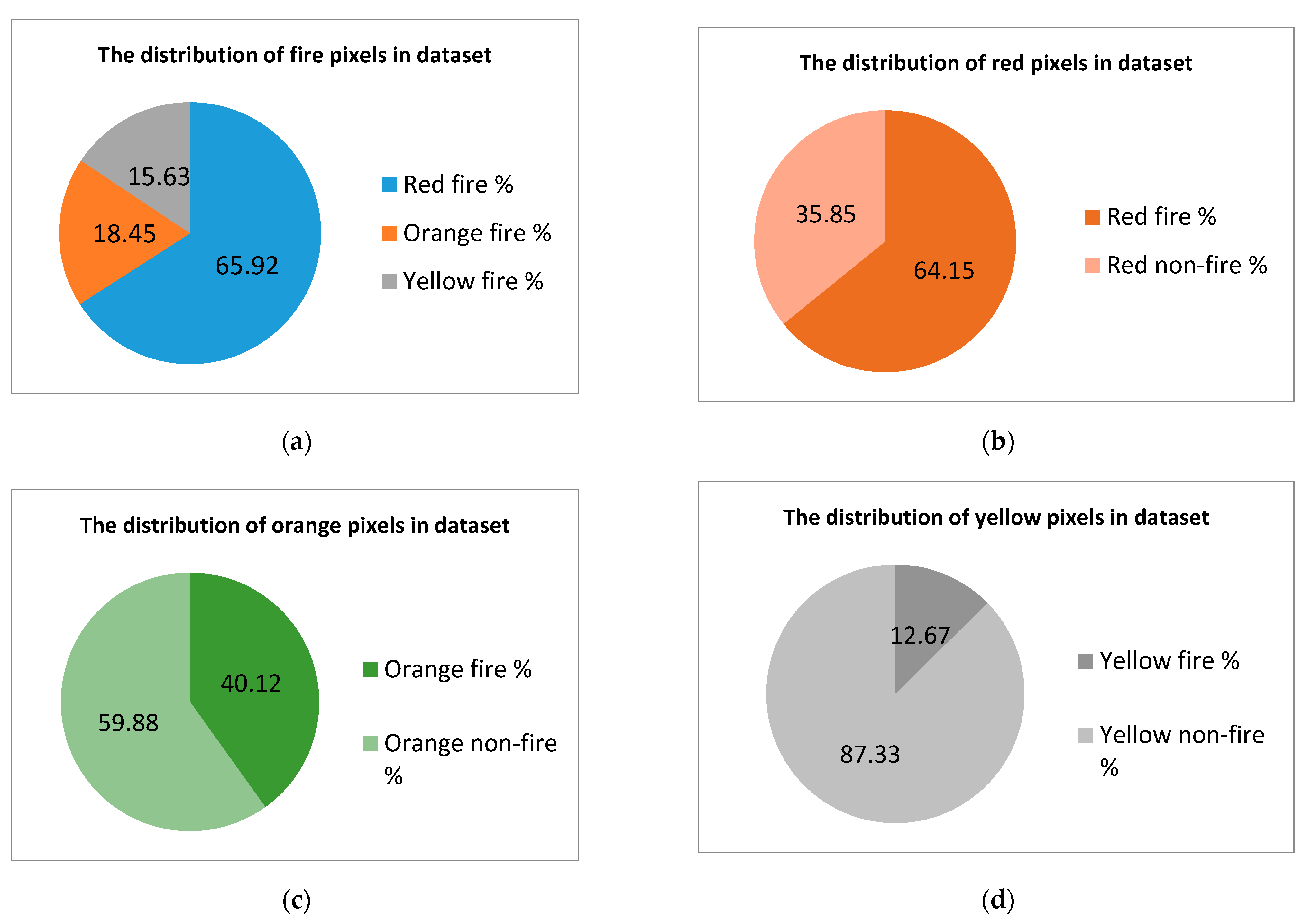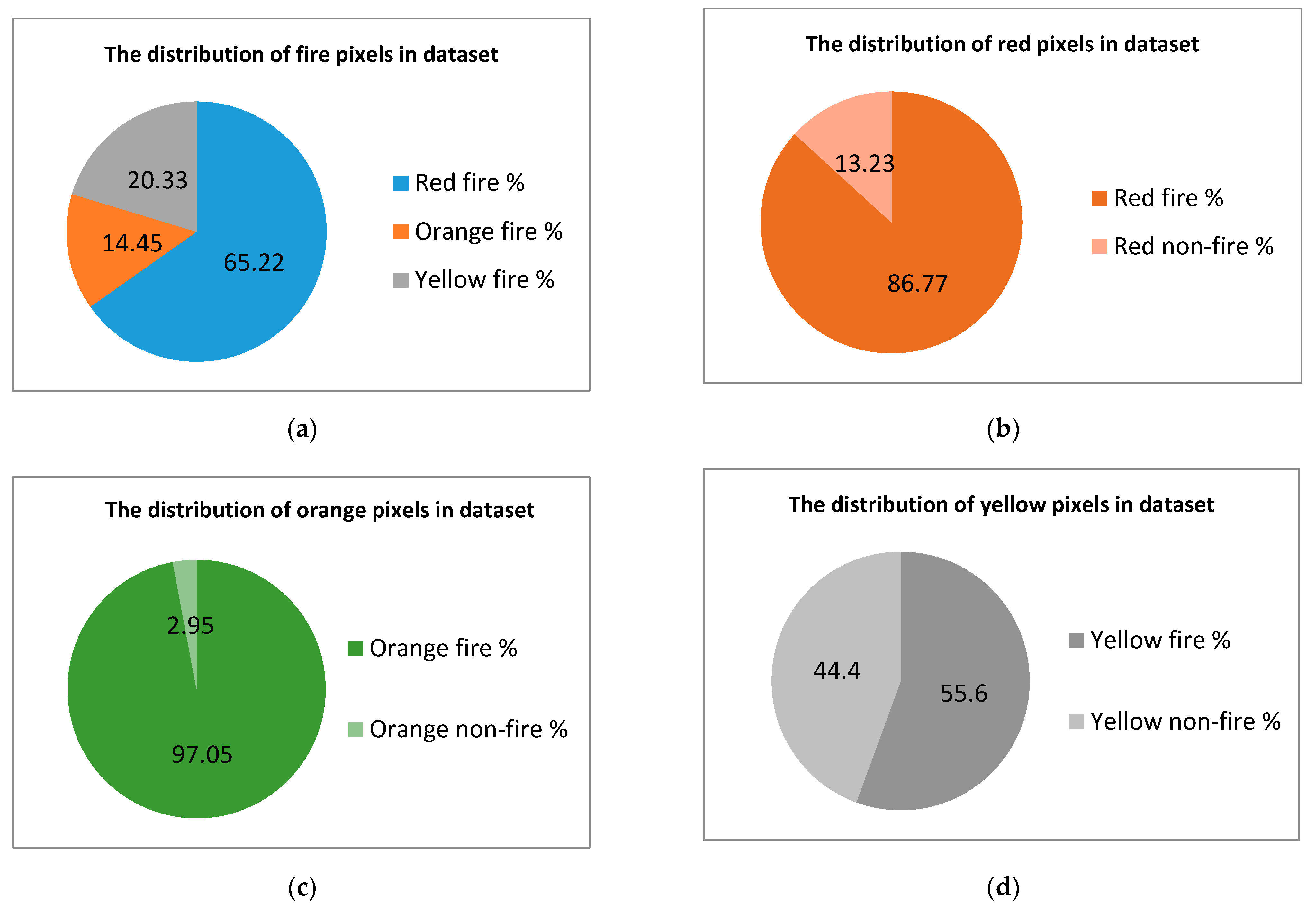wUUNet: Advanced Fully Convolutional Neural Network for Multiclass Fire Segmentation

Abstract

This article describes an AI-based solution to multiclass fire segmentation. The flame contours are divided into red, yellow, and orange areas. This separation is necessary to identify the hottest regions for flame suppression. Flame objects can have a wide variety of shapes (convex and non-convex). In that case, the segmentation task is more applicable than object detection because the center of the fire is much more accurate and reliable information than the center of the bounding box and, therefore, can be used by robotics systems for aiming. The UNet model is used as a baseline for the initial solution because it is the best open-source convolutional neural network. There is no available open dataset for multiclass fire segmentation. Hence, a custom dataset was developed and used in the current study, including 6250 samples from 36 videos. We compared the trained UNet models with several configurations of input data. The first comparison is shown between the calculation schemes of fitting the frame to one window and obtaining non-intersected areas of sliding window over the input image. Secondarily, we chose the best main metric of the loss function (soft Dice and Jaccard). We addressed the problem of detecting flame regions at the boundaries of non-intersected regions, and introduced new combinational methods of obtaining output signal based on weighted summarization and Gaussian mixtures of half-intersected areas as a solution. In the final section, we present UUNet-concatenative and wUUNet models that demonstrate significant improvements in accuracy and are considered to be state-of-the-art. All models use the original UNet-backbone at the encoder layers (i.e., VGG16) to demonstrate the superiority of the proposed architectures. The results can be applied to many robotic firefighting systems.

1. Introduction

Significant attention has been devoted to the problem of in-time forest fire detection. Considering the rapid development of convolutional neural networks, as well as their universality and effectivity in comparison with classic algorithms, such methods can be applied to flame detection tasks as well as their initial purpose (i.e., medical image segmentation).

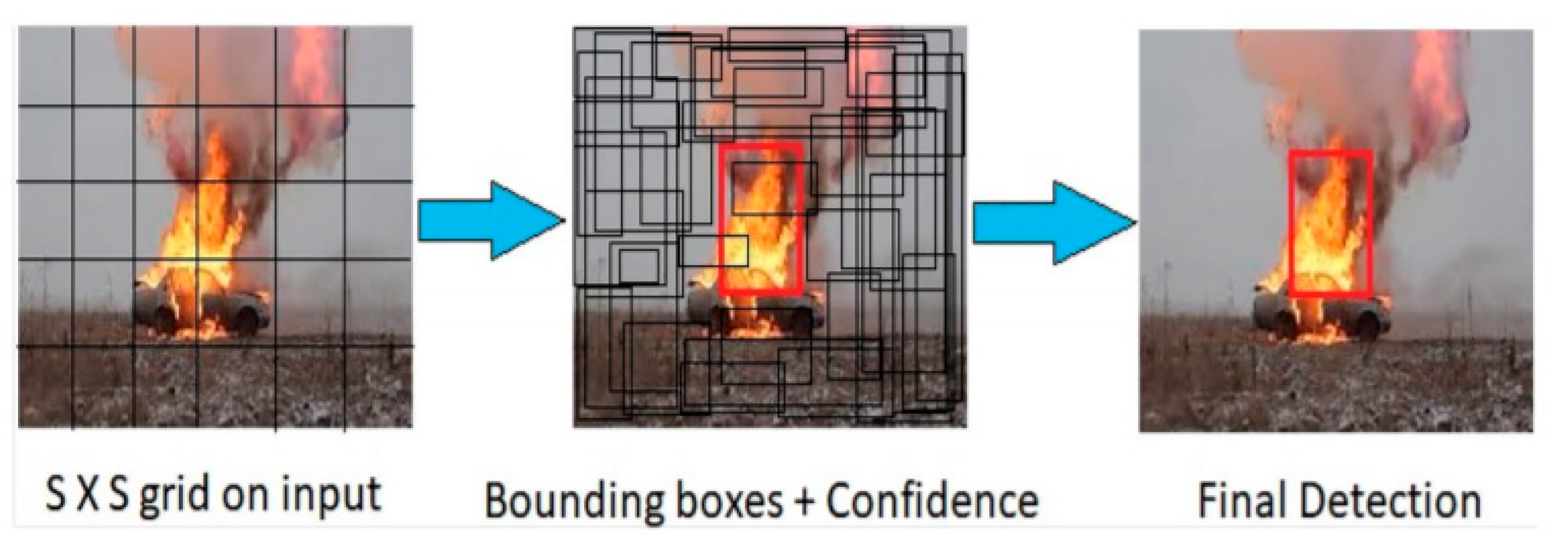
A previous study [1] described a fire object-detection solution using a YOLOv2 [2] model to obtain a bounding box for areas of flame without concretization of its class. The results are shown in Figure 1.

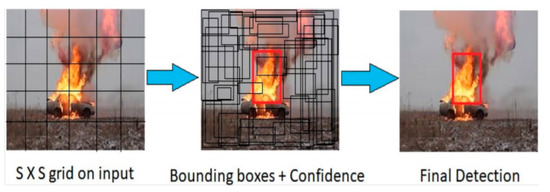
Figure 1. The application of the YOLOv2 method to obtain a fire bounding box represented in [1].

The application of object-detection methods for fires, however, has several drawbacks. The first is that fire has a wide variety of available contour configurations and, unlike regular convex objects, such as automobiles and pedestrians (signs used in advanced driver-assistance systems), fire objects cannot be optimally inscribed into a bounding box, which leads to the large variance of mAP metric accuracy. Additionally, the center mass of a fire represents much more accurate information of a non-regular contour than the center of the bounding box. As such, fire-segmentation is a more applicable class of computer-vision tasks than object detection.

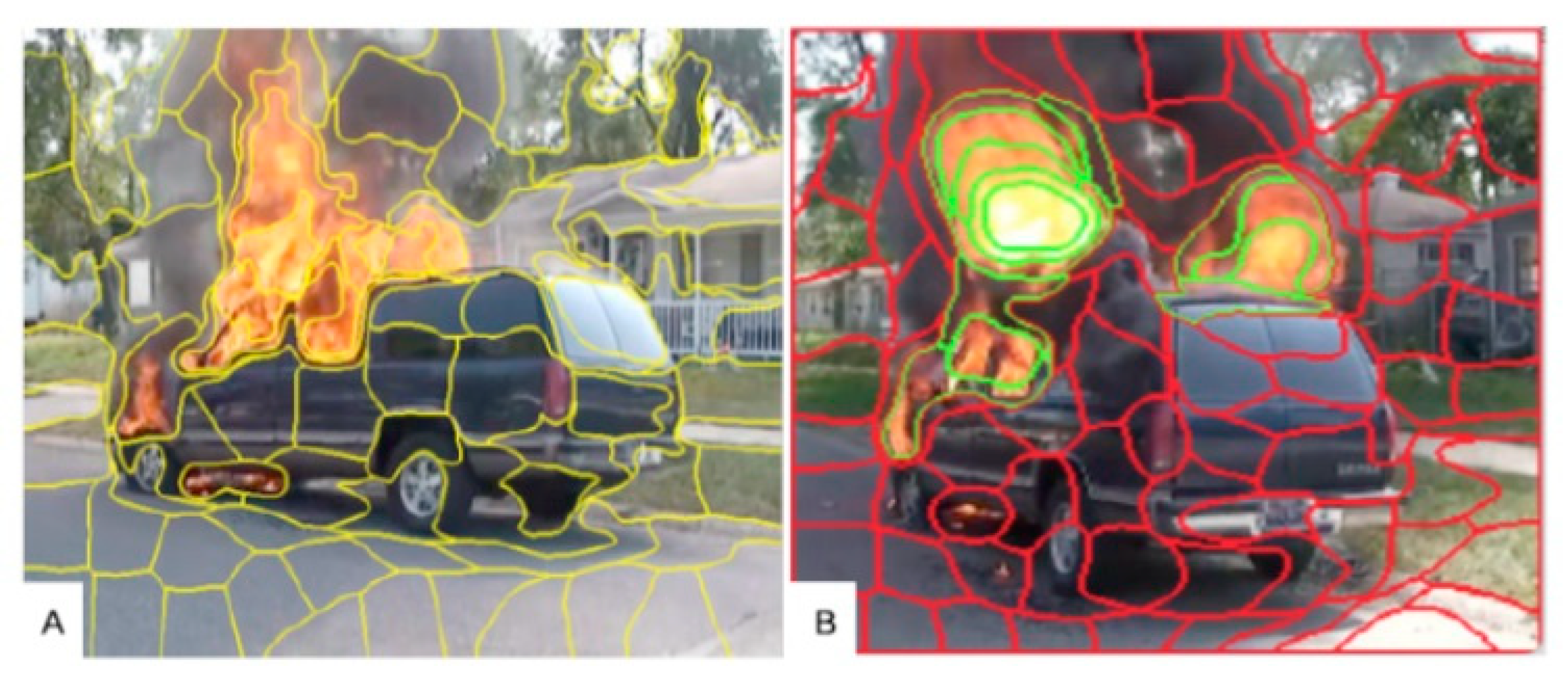
There are two methods of accurate fire-contour segmentation. The first is represented via a two-step pipeline: obtaining regions of interest (ROIs) represented by the same color and fire recognition for each region. Such methods have been described in previous studies [3,4]. The results of ROI recognition are shown in Figure 2.

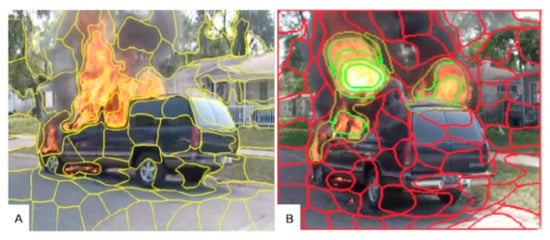
Figure 2. The results of extraction (A) and recognition (B) of super-pixel flame areas, reported in a previous study [4].

An aspect of super-pixel extractions is the main drawback of this method. Its calibration (the setup of color range) affects the form of concrete flame areas. It impacts the accuracy of the following recognition. Secondly, it is a sequential algorithm. As such, it cannot be applied to the conception of massive paralleling systems implemented in real-time GPU computations.

The second method of accurate fire-contour segmentation is one-shot semantic-segmentation models. Recent research achievements have been obtained in the area of using the Depplabv3+ [5] method for binary fire segmentation, as described in [6,7]. This architecture is used with heavy backbones such as XCeption to obtain fire contours without concretization of color (i.e., binary fire segmentation).

We solve the problem of multiclass fire segmentation because shooting at the hottest regions of the fire is a very important action for optimal firefighting [8]. The temperature of burning is correlated with the color of flame—that is, yellow-white regions are the hottest, whereas red areas are the coldest.

We used the UNet method [9] in our task of multiclass fire segmentation with the original lightweight backbone VGG16 for two reasons. While extinguishing a fire, it is important to obtain real-time information about the fire’s vulnerable points [10]. In addition, the lightweight model can be easily ported to Jetson architectures, which are widely used in robotics systems. Finally, it allows for a faster training process, with the ability to train the model on medium batches with an inexpensive GPU such as the Nvidia RTX2070.

We investigated the accuracy of image segmentation for an input data size of 224 × 224 and 448 × 448 pixels. We used two calculation schemes. The first fits the input image to the size of the CNN input (one-window). The second obtains non-intersected sub-areas of original images using a sliding window (non-intersected). Additionally, we suggest innovative methods to improve segmentation accuracy based on the composition of partially intersected areas via weighted addition and Gaussian mixtures of calculation results.

In the next step, we describe a new deep-learning architecture known as UUNet-concatenative, as a modernization of UNet. This model is the combination of binary and multiclass UNet methods. It enables the multiclass (differentiated by color) segmentation of signal obtained from the binary part of acquired single-nature objects (flame areas). Unlike the combination of two UNets, UUNet adds additional skip connections from the binary decoder to the encoder of the multiclass model. The concatenative suffix means that the result of binary segmentation joins with the input image via concatenation and goes to the multiclass UNet part as an input. wUUNet is the next step in the improvement of the UUNet model. It uses the entire combinatorial set of skip-connectors.

We prepared a custom dataset, including 6250 samples with a resolution of 224 × 224 pixels. We use soft Dice [11,12] and Jaccard [13] as target loss functions. We use the Adam [14] method to change CNN matrix weights with the initialization used by He et al. [15]. We use the SGDR [16] method for every 300 epochs with initial learning rate (lr) = 0.001 and 10× annealing of learning rates every 60 epochs.

2. Materials and Methods

2.1. Dataset

We collected a dataset, the characteristics of which are summarized in Table 1.

Table 1. The multiclass fire-segmentation dataset.

Type of Dataset	Number of Video Fragments	Number of Images 640 × 360	Number of Images 640 × 480	Number of Images with a Fire	Number of Images without a Fire
Training	21	234	8	186	56
Validation	15	172	0	162	10

The number of real samples depends on the configuration of the model. The splitting of input images is shown schematically in Figure 3.

Figure 3. The splitting of input image into sub-areas depends on the segmentation configuration.

In order to deal with problem of overfitting the CNN, we used many image augmentations: horizontal reflection, Gaussian, median noise, motion blur, random contrast and brightness variances, increasing of sharpness, and emboss filters.

The size of the dataset is equal to the values reported in Table 1 multiplied by two (including horizontally flipped images) for 448 × 448 single-window mode. We used a sliding window for 448 × 448 full-size network input to obtain three samples from one image. The sliding window was applied both vertically and horizontally to obtain 15 samples from the input image in the case of a full-size 224 × 224 calculation scheme. Therefore, the number of samples increased from 414 (one-window mode) to 6250 (full-size 224 mode).

The characteristics of the dataset shown in Table 1 enable us to conclude that the dataset is imbalanced. However, unlike image recognition, when we have only one result label for each image, we are dealing with image segmentation, wherein a label is set for each pixel in the image. The imbalance is also shown in Table 2 for pixel characteristics, but it shows that there are more non-fire pixels than fire pixels.

Table 2. The pixel characteristics of the binary segmentation dataset.

Type of Dataset	Total Pixel Number	Number of Pixels Marked as Fire (%)	Number of Pixels Not Marked as Fire (%)
Training	56,371,200	2.7	97.3
Test	39,628,800	8.33	91.67

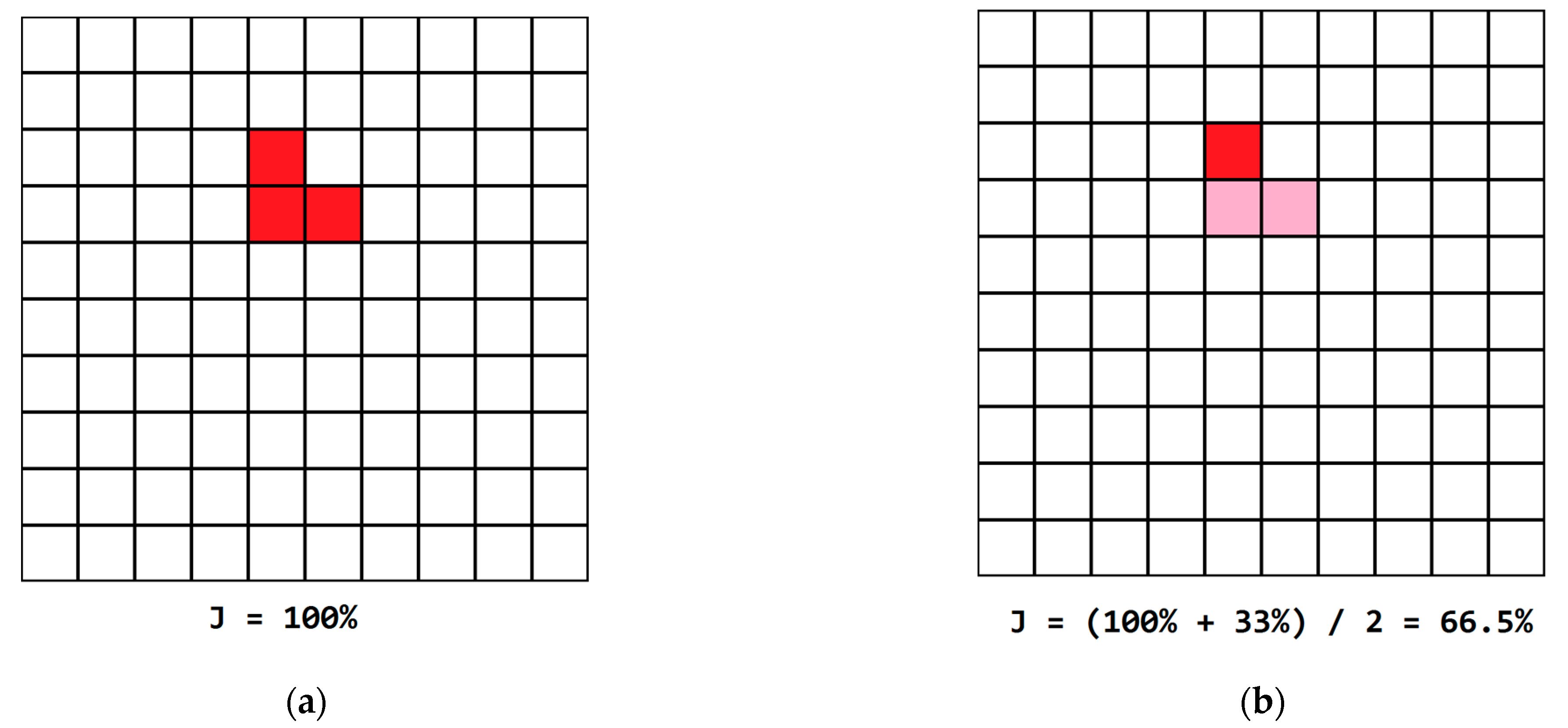
Fortunately, Dice and Jaccard scores address this situation and enable the training of the segmentation model to detect even small contours of objects. This is shown in Figure 4, where it can be seen that if a labeled object contour is small in frame, then the Jaccard or Dice score will score the detection of only this object.

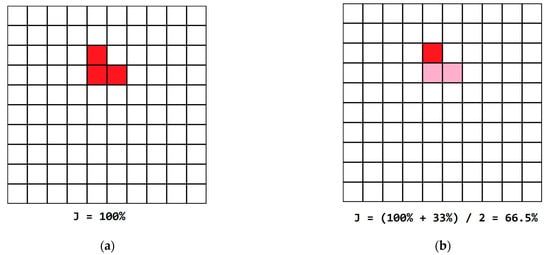
Figure 4. An example of Jaccard score evaluation of segmentation results. (a) The target object is fully detected and accurately segmented. (b) Only one of three pixels of the object is detected, which results in a low Jaccard score.

Therefore, we can conclude that the ratio between the number of pixels of interest and those that are not of interest is not critical. The most important characteristics of the dataset are represented between target classes and pixels that have the same colors but are not marked with fire. These characteristics are shown in Figure 5 and Figure 6.

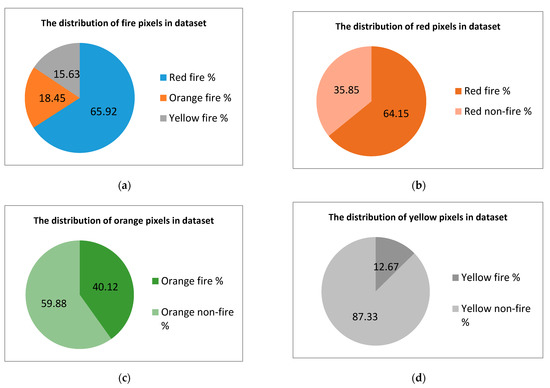
Figure 5. Important parameters of the training dataset. (a) Distribution of fire pixels in the dataset. (b) Distribution of red pixels in the dataset. (c) Distribution of orange pixels in the dataset. (d) Distribution of yellow pixels in the dataset.

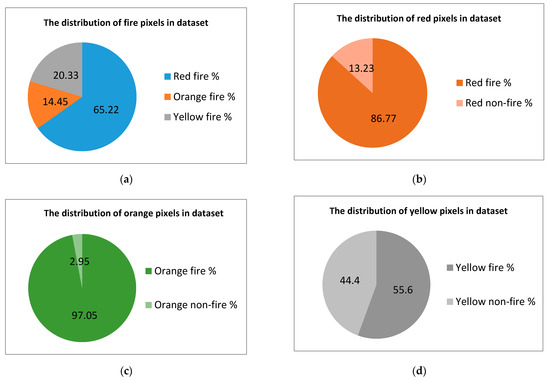
Figure 6. Important parameters of the test dataset. (a) Distribution of fire pixels in the dataset. (b) Distribution of red pixels in the dataset. (c) Distribution of orange pixels in the dataset. (d) Distribution of yellow pixels in the dataset

The plots shown in parts (b–d) of the figures show that simple methods of color threshold or color mapping are not sufficient to obtain the flame. The model must be able to distinguish between objects filled with the same color in order to select the correct label (e.g., to be able to recognize a fire truck as not fire, despite it being painted red, while also being able to recognize fire).

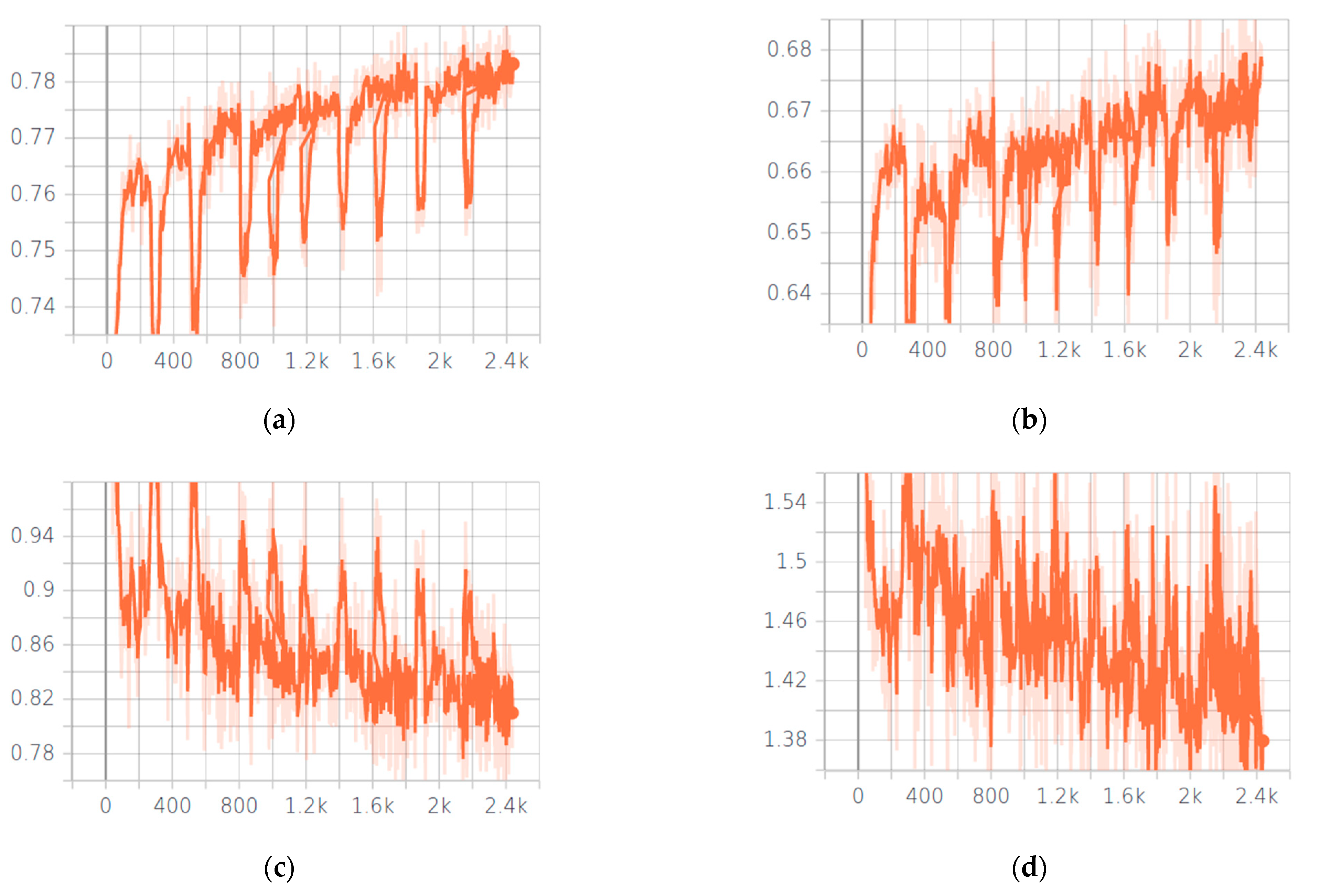
Considering the smaller number of training weights for the fully convolutional network UNet compared to recognition networks using fully connected layers, focusing on the localization of some feature (since the convolutional structure uses a neighbor from the target nodes) and the severity of the loss function, this dataset configuration is sufficient to avoid the overfitting problem. The UNet model training plots are shown in Figure 7, and demonstrate accuracy progress for both training and validation datasets. The periodic decrease in accuracy is caused by the use of a SGDR method to shake the network and reach a new saddle point(s).

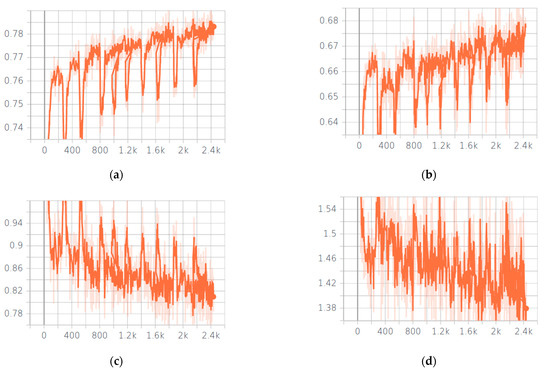
Figure 7. Plots of training UNet for multiclass fire segmentation. (a) Increasing the Jaccard accuracy of multiclass segmentation on the training dataset. (b) Increasing the Jaccard accuracy of multiclass segmentation on the validation dataset. (c) Reducing the soft Jaccard loss on a training dataset. (d) Reducing the soft Jaccard loss on a validation dataset.

Dataset collection and labeling was performed by several elaborators. Because the color sensitivity of visual data is a subjective human factor, we used alignment of the labels using look-up tables. The meaning of this method is as follows: first, we collect a frequency map of the color F:

$$\left\{\forall P_{i,j}\in IMG,P_{i,j}=C\in RGB,C=\{r,g,b\},{F(M_R,M_O,M_Y)|}_{P(i,j)}=\{\begin{array}{c}{M}_R=M_R+1|V(P_{i,j})=R\\ M_O=M_O+1|V(P_{i,j})=O\\ M_Y=M_Y+1|V(P_{i,j})=Y\end{array}\right\}$$

(1)

Then, in the next iteration, all pixels identified as a flame (red, yellow, or orange) are reinitialized based on maximal frequency with one of three types of flames detected during the first iteration (collection):

$$\overline{V}=\{\begin{array}{c}0|V(P_{i,j})=0\\ \arg \max (M_R,M_O,M_Y)|V(P_{i,j})>0\end{array}$$

(2)

2.2. Proposed Segmentation Schemes

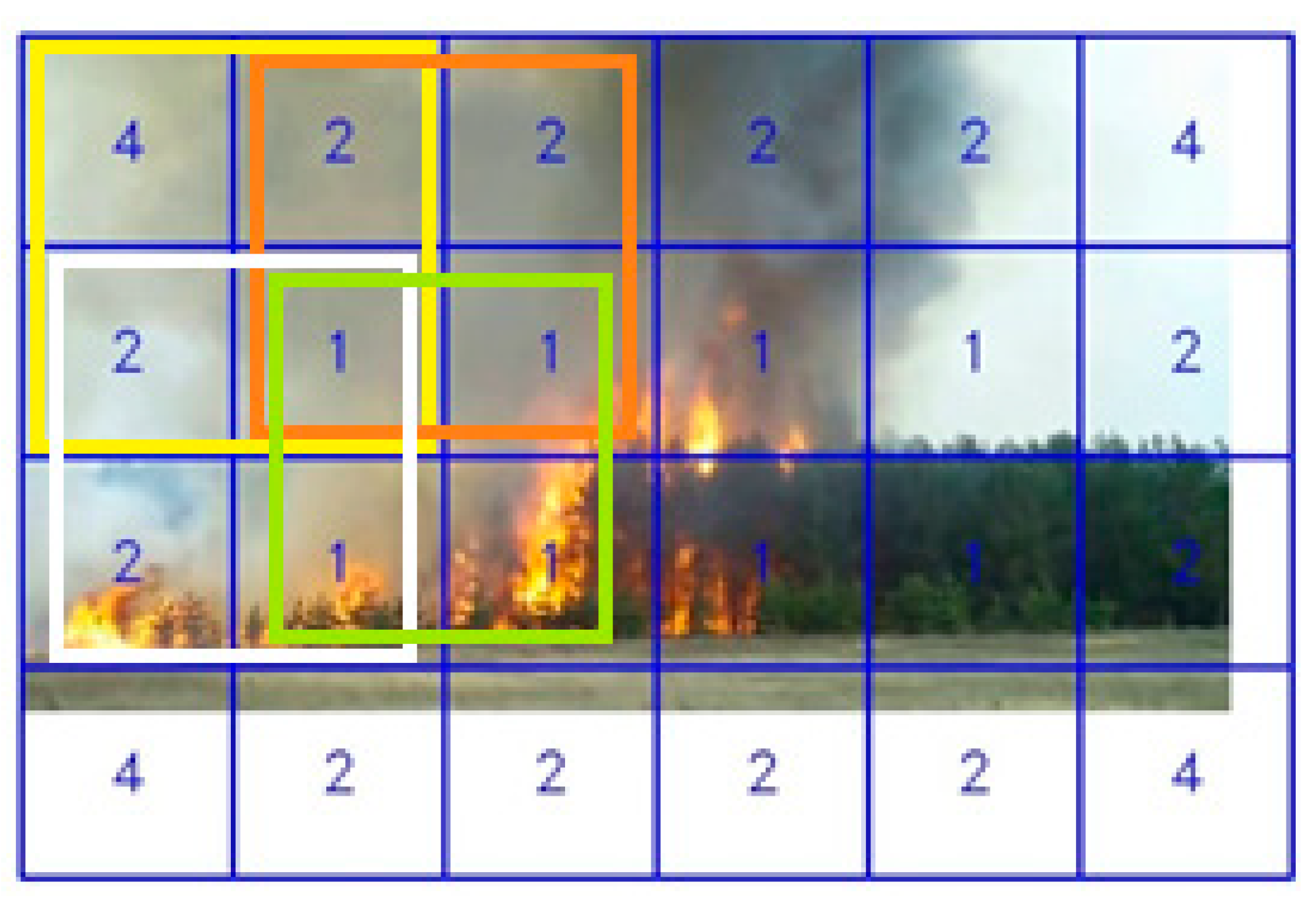
Considering that the full-size model UNet 224 × 224 mentioned in the previous section calculates non-intersected areas of the image, we are faced with the problem of detecting a flame at the border of one node, which is shown in Figure 8.

Figure 8. Fire edge pixel detection problem.

The undetected flame zone is shown schematically as the intersection of horizontal and vertical lines, which negatively affects the segmentation accuracy. This article describes two methods for solving this problem based on the composition of partially intersected areas of the frame.

The first method describes the addition of half-intersected areas. This combination is applied with multiplication of weights due to the presence of areas on the frame that are used by four nodes of the network simultaneously (internal half-zones), two nodes (bordering vertical and horizontal half-zones), and only one node (boundary diagonal subregions). We apply multiplicative factors in order to normalize the segmentation values for each region. This method is illustrated in Figure 9.

Figure 9. Schematic representation of the normalized addition of half-intersected sub-areas.

The second method is based on combining half-intersected areas using a Gaussian distribution of the fire signal centered at the center of the sub-area, with variance given by the following equation:

$$\sigma =\frac{224}{n}$$

(3)

where n is the divisor of window size. The Gaussian distribution represented by multiplying the fire signal elementwise (without the last row and column) by the Gaussian kernel of 223 × 223 elements:

$$\overline{S}=S\cdot G(223,\sigma )$$

(4)

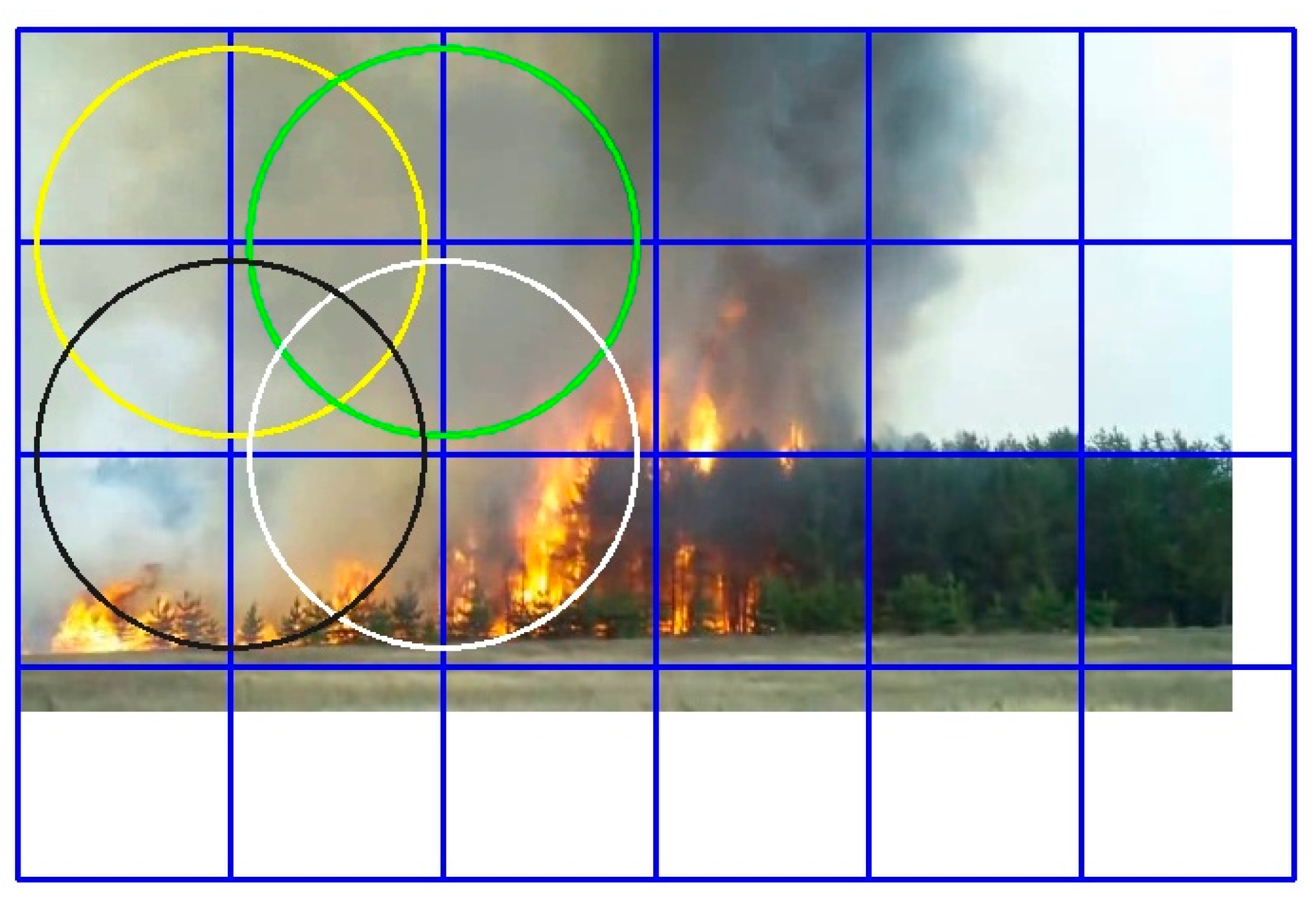
Considering the signal fading at the boundary of one node, this pixel region will be located near the center of the neighboring node. This enables normalization of the mixtures. Therefore, we do not need to introduce additional coefficients, as for the first method. The Gaussian mixture method is shown in Figure 10.

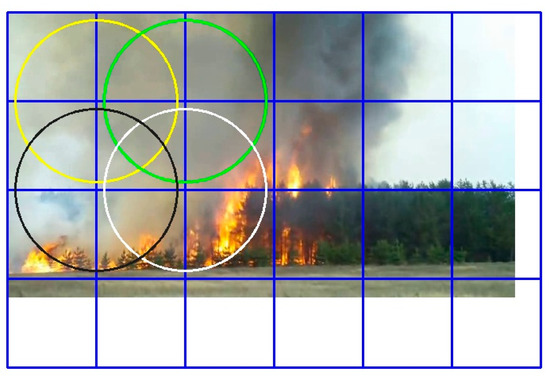
Figure 10. The combination of Gaussian-distributed signal sub-areas underlying the second approach.

2.3. UUNet-Concantine and wUUNet

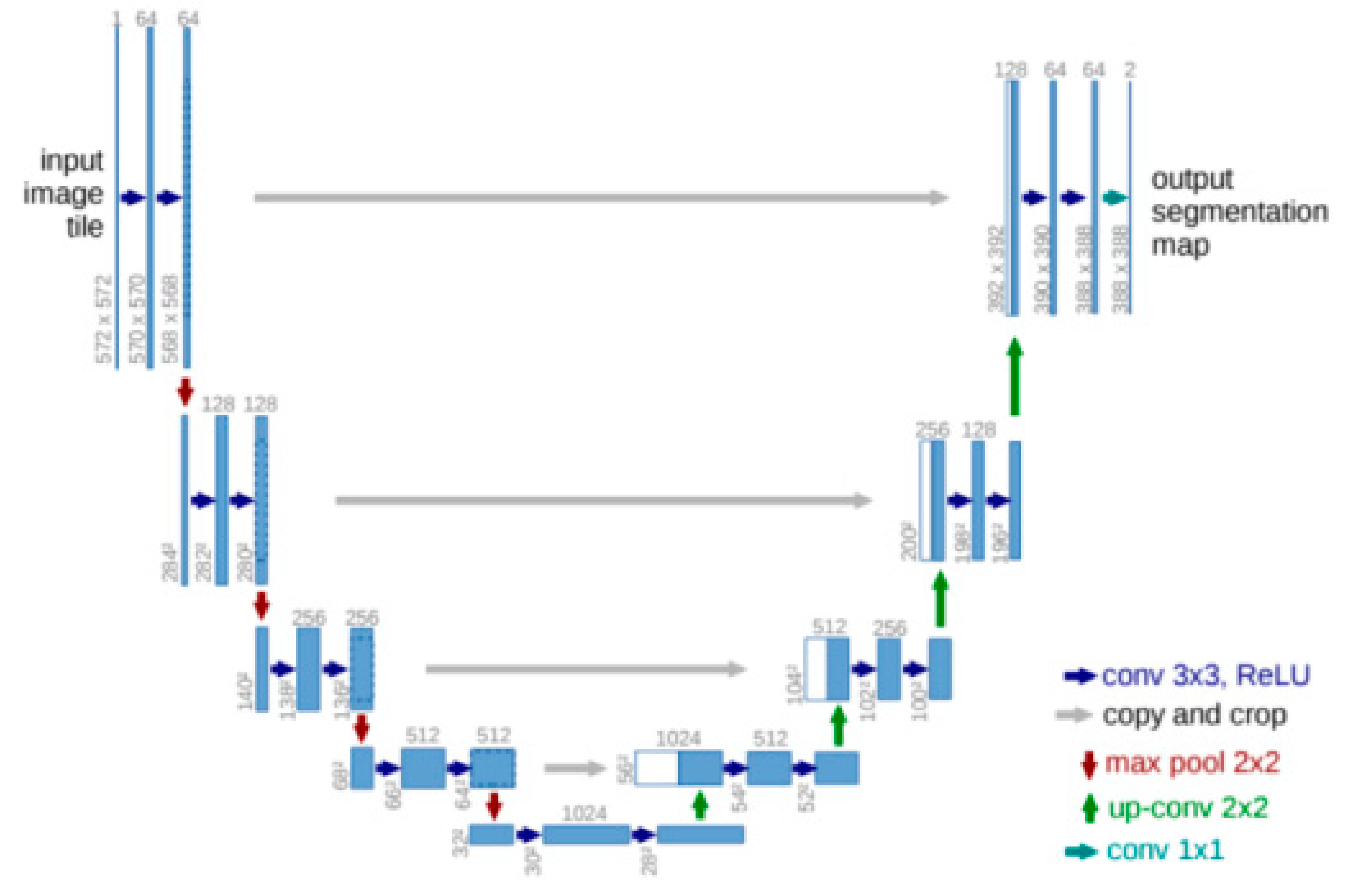
Earlier, we examined the UNet architecture, which directly assigns a flame class to the image. This architecture is shown schematically in Figure 11. It contains an encoding (compression) path on the left to indicate low-, medium-, and high-level fire features, a bottleneck in the center, and decoding (decompression) levels yielding one-level encoding results via skip connections to indicate the heat output of the flame image with a size equal to the input frame.

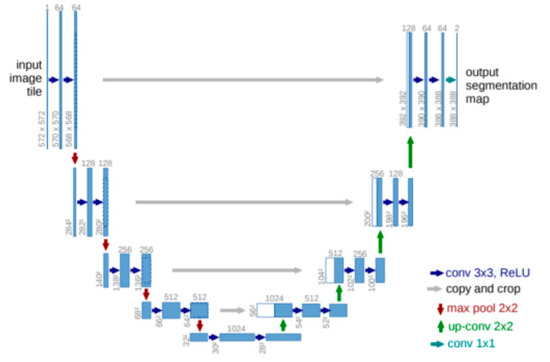
Figure 11. The UNet architecture.

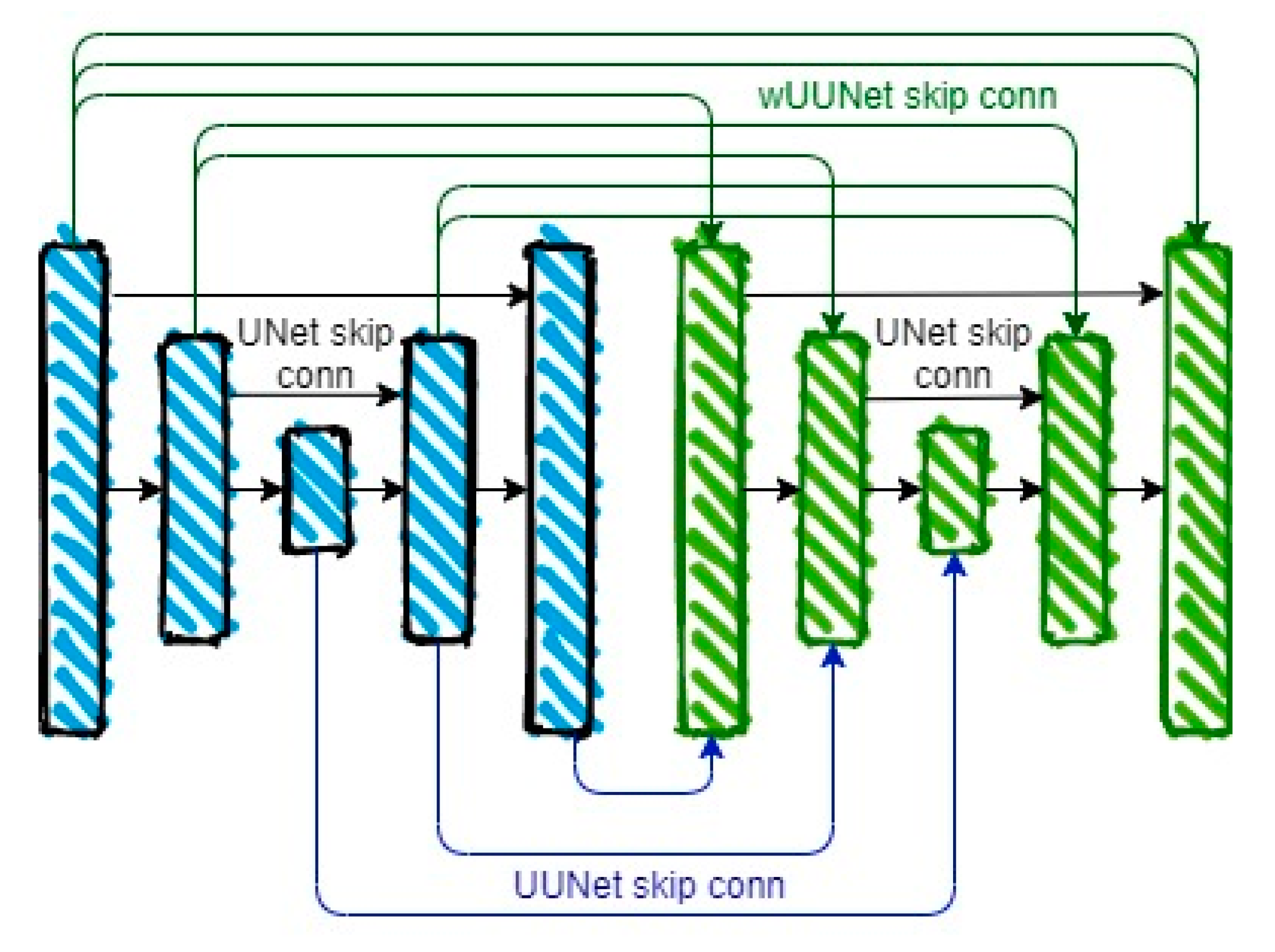
As part of the task of multiclass fire-segmentation task, we developed the UUNet-concatenative architecture shown in Figure 12. One of the main features of this architecture is the consistent use of two UNet models. The first provides a binary result of flame segmentation. The second uses the input image concatenated with the results of the first part to indicate the specific fire class (red, orange, yellow). An additional feature of this model is the use of skip connections between the binary model decoder and the multiclass model encoder (marked in blue). This is needed to account for the results of binary flame segmentation over the entire range of model levels.

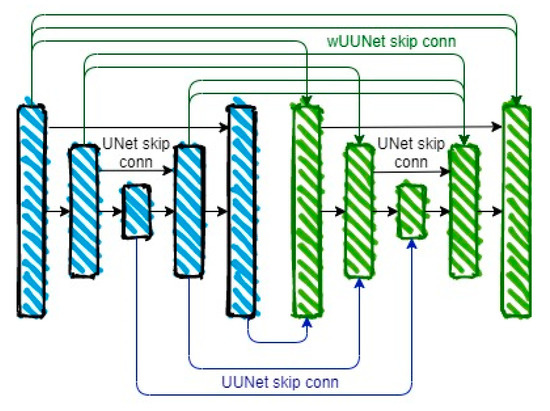
Figure 12. The wide-UUNet concatenative model (wUUNet) architecture.

As additional enhancement to the UUNet-concatenative model, we developed a wide-UUNet concatenative model (wUUNet). This model contains the maximum possible number of skip connections illustrated in Figure 12 (marked in green).

The loss function of the UUNet model (wUUNet) is represented by the composition of cross-entropy with soft-Jaccard for both binary and multiclass segmentation sub-models:

$$L(\sigma ,y)=BC{E}_B(\sigma ,y)+BC{E}_M(\sigma ,y)-\ln (J_B(\sigma ,y))-\ln (J_M(\sigma ,y))$$

(5)

3. Results

This section compares the models and calculation schemes presented in Section 2 to determine the best approach to fire segmentation. First, we obtain the best UNet model with a simple schema to assign a baseline. Then, we apply the proposed methods and models described in this article to demonstrate the improvement in segmentation accuracy.

3.1. UNet One-Window vs. Full-Size

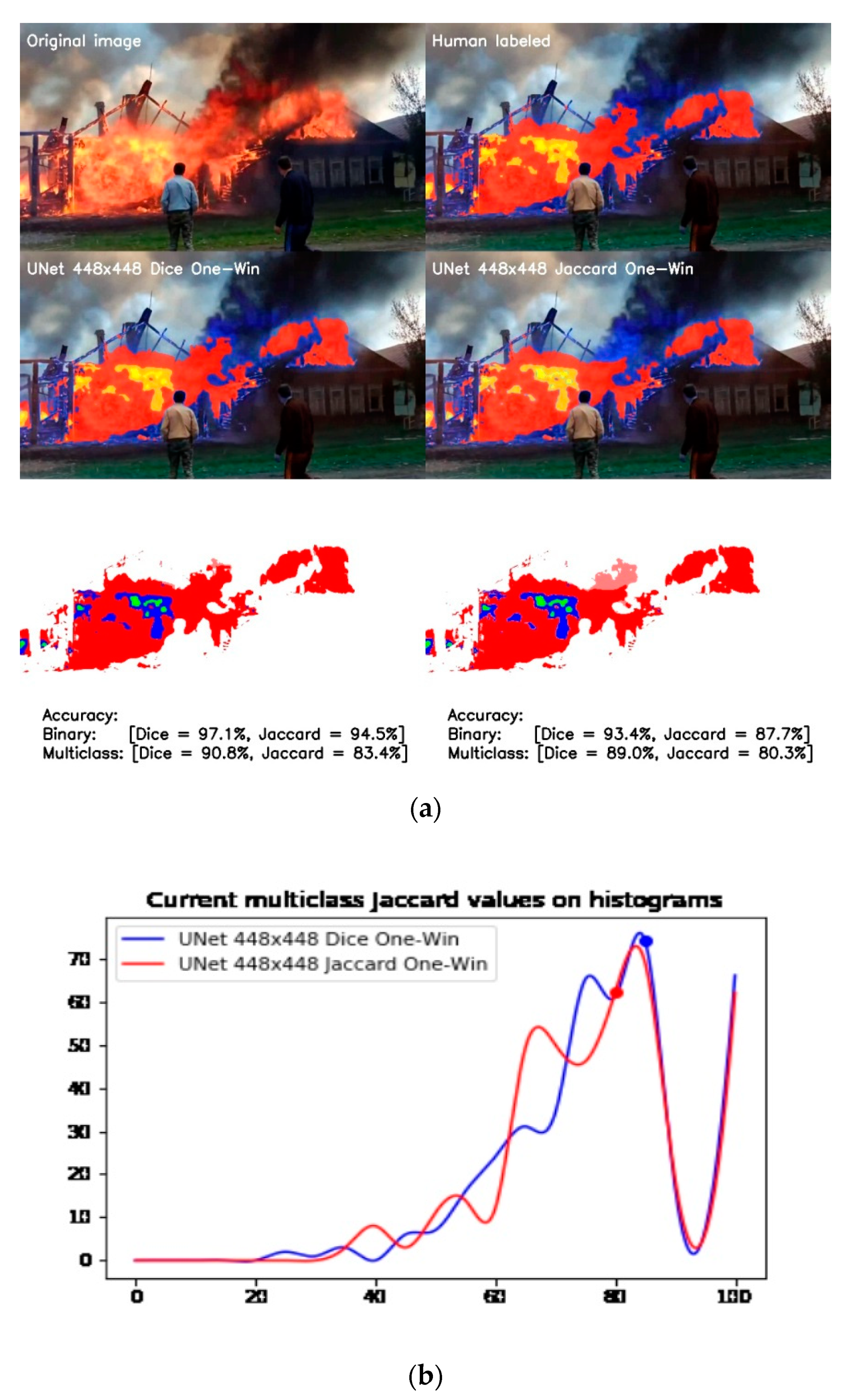
The first comparison in this study was between one-window models trained using soft Dice–Sørensen and Jaccard loss functions. The results are shown in Figure 13.

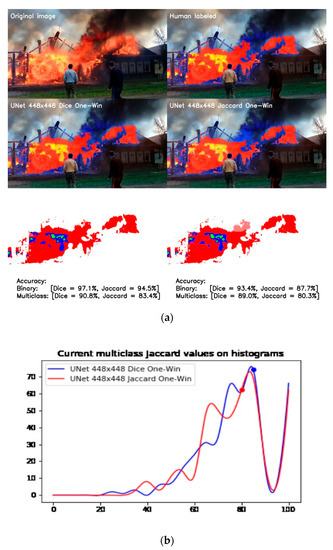
Figure 13. Comparison of one-window models trained on soft Dice and Jaccard loss functions: (a) Difference between actual data and ground truth; (b) Histogram of accuracy distribution.

There are hints for each part of the image describing its purpose. On the left side of Figure 13a, we see the result of the UNet model based on soft Dice loss and, on the right side, the Jaccard result. The last line of the image demonstrates the difference between ground truth and actual data, which also shows that the Jaccard model does not recognize significant red flare, resulting in lower scores for both binary and multiclass segmentation. In fact, the model trained on soft Dice–Sørensen loss performs better, as can be seen from the frequency histogram of accuracy distribution in the validation dataset shown in Figure 13b.

Although the peak of this histogram is in the same range of multiclass Jaccard accuracy (i.e., 82–84%), another significant peak of the model trained by the soft Jaccard function is at 66–68%, which negatively affects the average precision of the entire dataset.

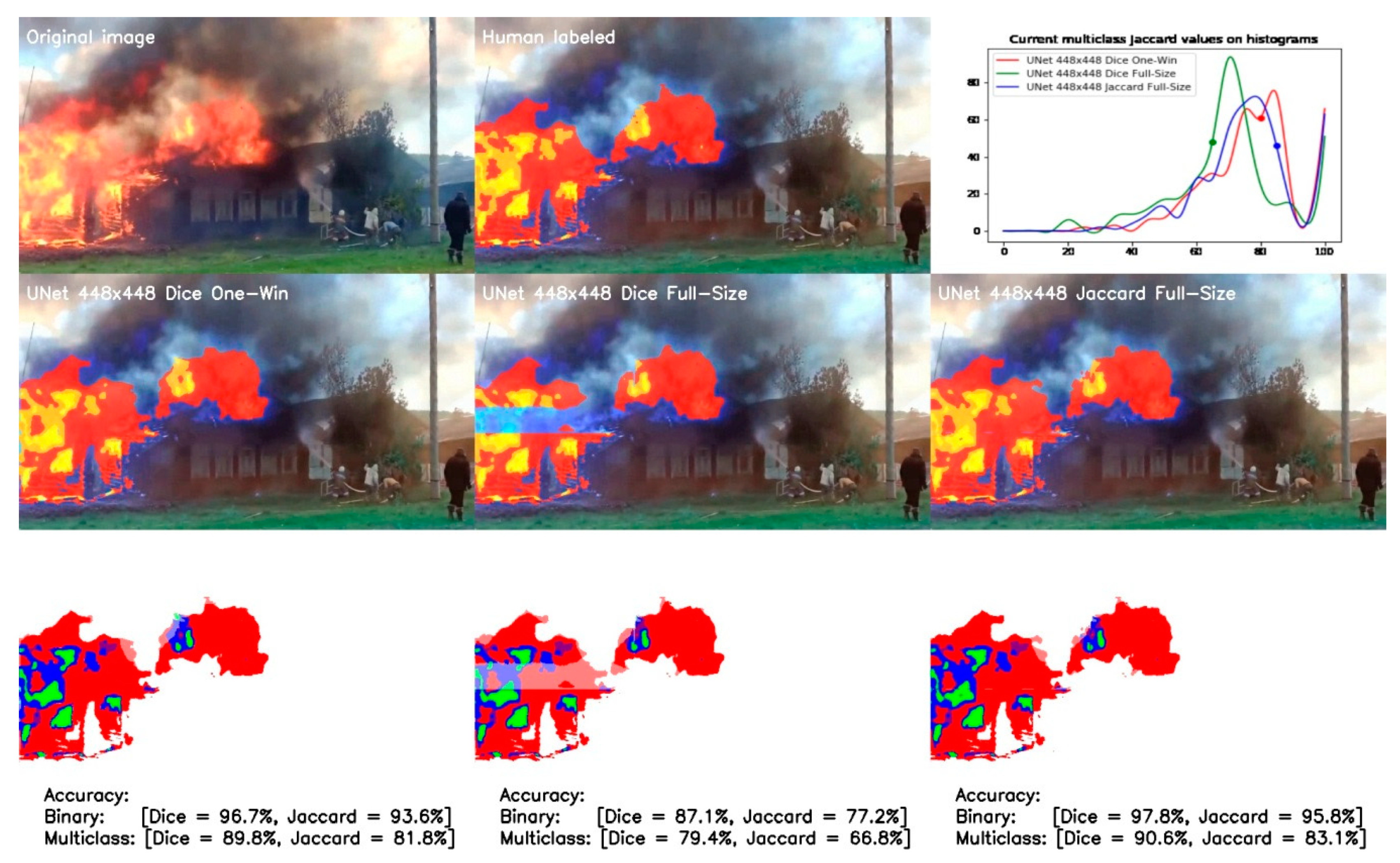
The following comparison concerns the results of one-window and full-size modes of the UNet 448 × 448 model shown in Figure 14. It can be clearly concluded that the full-size mode outperforms the one-window model; however, significantly better results are obtained when the soft Jaccard loss function is used.

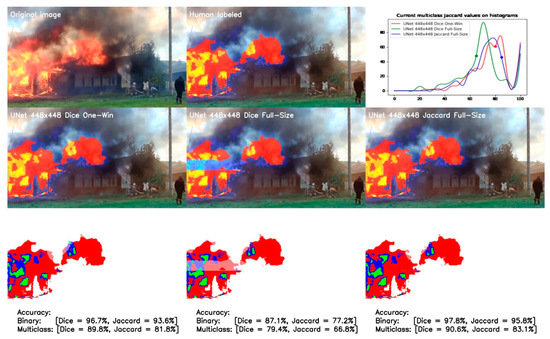
Figure 14. Comparison of one-window and full-size models UNet 448 × 448 trained on soft Dice and Jaccard loss functions.

The full-size model trained by Dice yields an unsatisfactory result, as evidenced by the absence of the detected flame in the center of the real one. However, considering the first and third differences, the full-size model recognizes flares better than the one-window model. This also has a positive effect on the accuracy of full-size model.

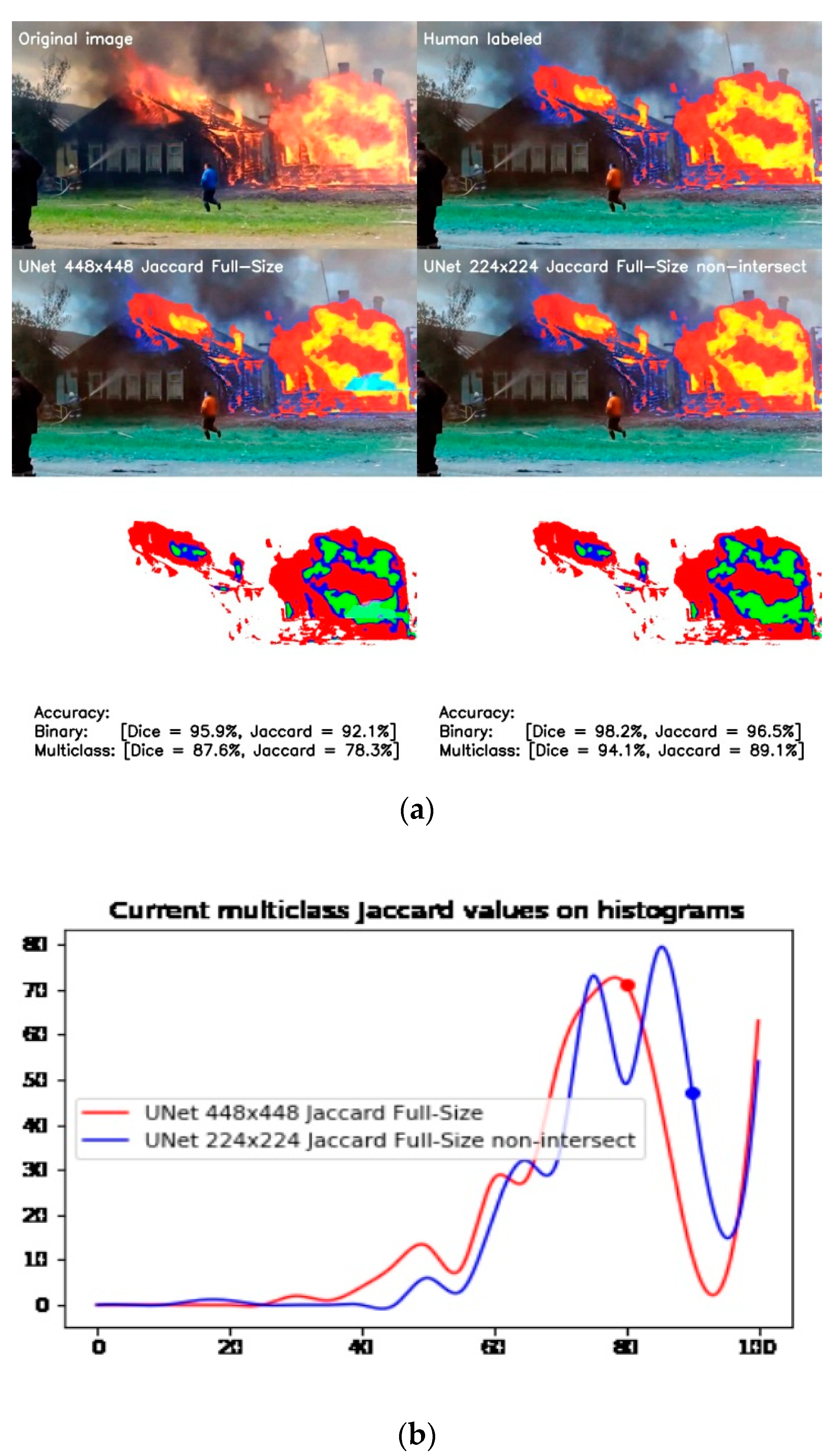
The last comparison in this section is shown in Figure 15, between UNet 448 × 448 and 224 × 224 full-size models.

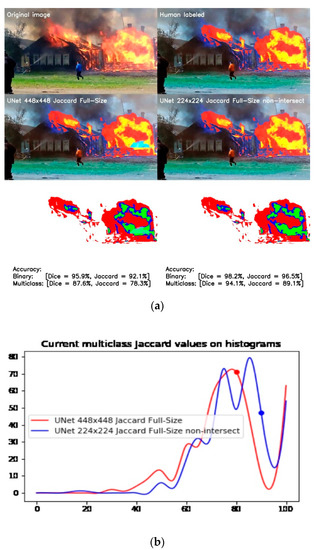
Figure 15. Comparison of full-size UNet 448 × 448 and 224 × 224 models trained by soft Jaccard loss functions: (a) The difference between actual data and ground truth; (b) Histogram of accuracy distribution.

The UNet 224 × 224 model performs significantly better, showing the corresponding difference in binary and multiclass precision metrics. This is also confirmed by the difference of accuracies histogram shown in Figure 15b, where we see the shifting of peaks towards higher accuracy.

To complete this section, Table 3 reports the mean and variance of the binary and multiclass segmentation precision for the previously analyzed models. You can see that the full-size model of UNet 224 × 224 shows the best results in the context of multiclass segmentation, but the 448 × 448 model works better for binary segmentation. Additionally, the 224 × 224 full-size model exhibits the largest accuracy variation. The improved accuracy of the 224 × 224 full-size is shown in the next section.

Table 3. The accuracy parameters (%) of the mean and variance for the model analyzed in this section. The maximum value of the corresponding metrics is in bold.

Model	Binary Dice		Binary Jaccard		Multiclass Dice		Multiclass Jaccard
OW Jacc	88.78	19.57	83.44	19.96	83.37	10.69	74.51	12.25
OW Dice	91.74	15.04	86.89	15.79	85.12	9.95	76.56	11.99
FS Dic 448	91.45	15.11	86.52	15.63	85.36	9.09	76.64	11.60
FS Jacc 448	92.71	12.41	88.01	13.42	85.89	8.98	77.33	11.48
FS Jacc 224	91.55	18.04	87.43	18.30	85.98	11.05	78.26	12.08

3.2. Non-Intersected vs. Averaged Half-Intersected Calculation Schemes

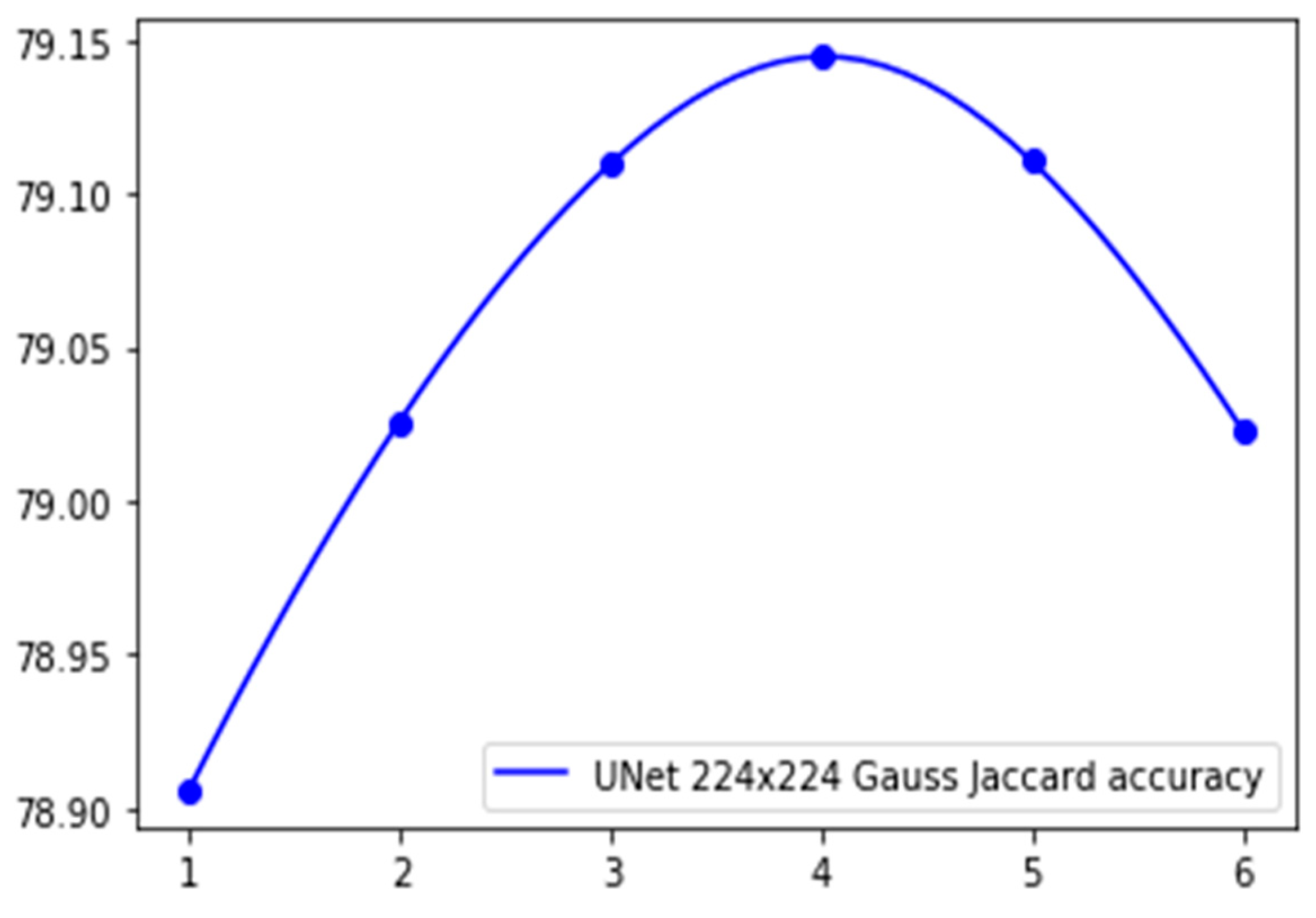
Returning to the discussion of the use of a full-size non-intersected calculation scheme (Section 2.2), with an illustration of the segmentation problem at the boundaries of non-intersected nodes, we propose new calculation schemes based on averaging the segmentation of half-intersected areas. In the process of looking for an optimal divisor n in Equation (3), we obtained the graph of the multiclass Jaccard accuracy shown in Figure 16.

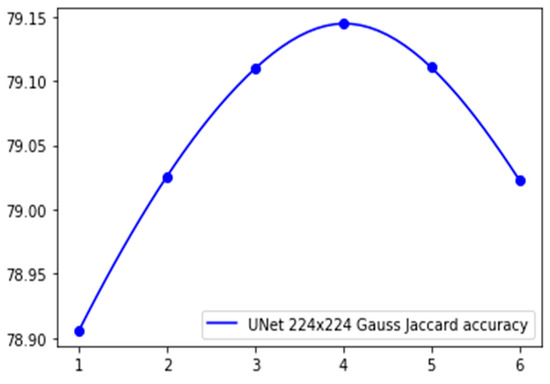
Figure 16. The values of multiclass accuracy depending on the value of n.

This figure demonstrates that the accuracy of the function, depending on the value of n, corresponds to a local maximum, which can be additionally approximated by a dichotomy. The result of applying this algorithm demonstrates maximal accuracy when n = 4.07512.

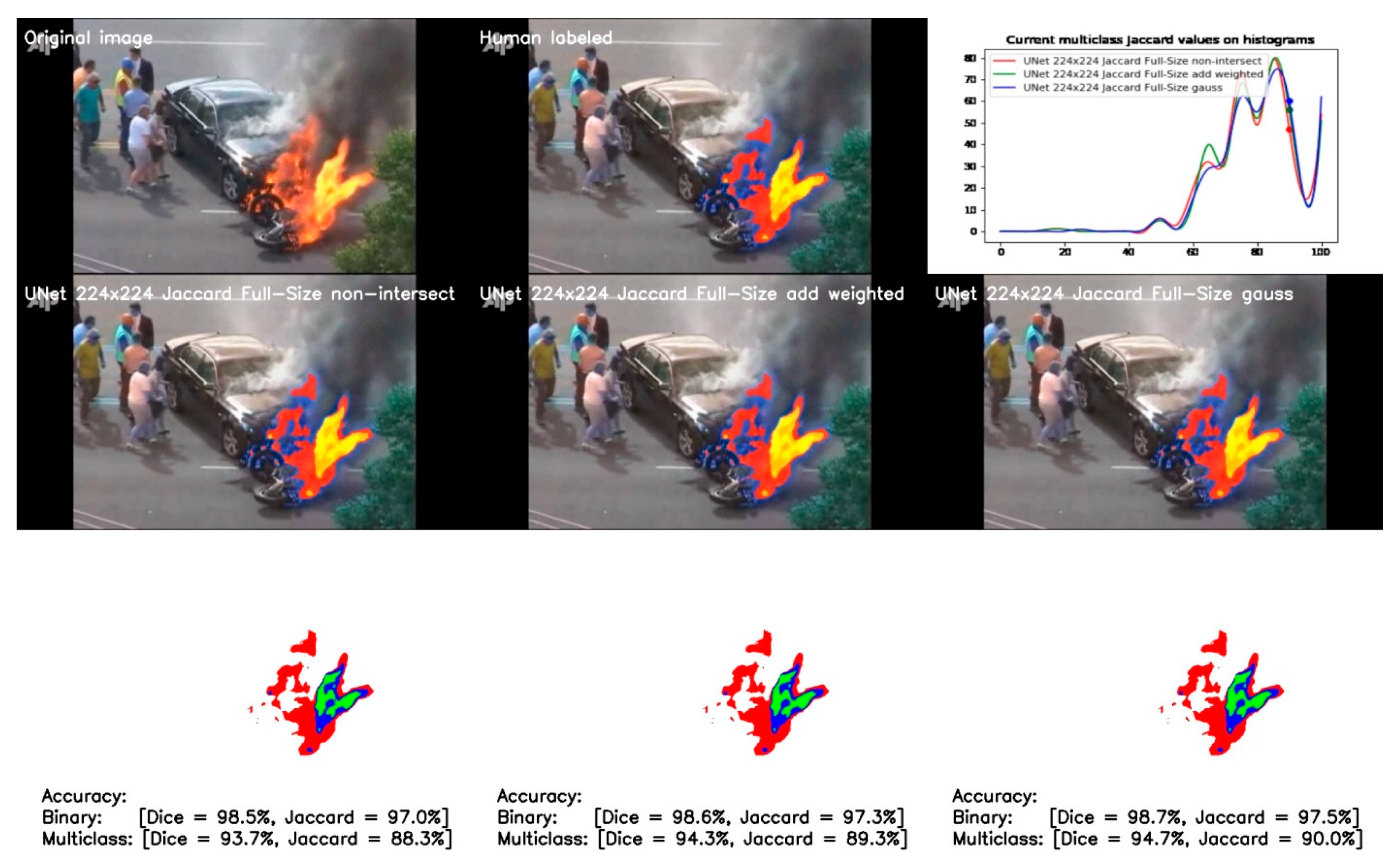
Comparison results for full-size non-intersected and half-intersected models using both methods are shown in Figure 17.

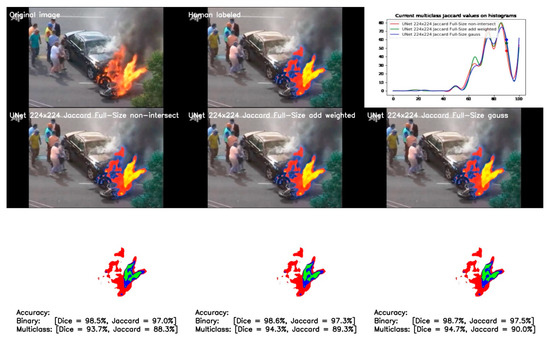
Figure 17. Comparison of full-size UNet model results based on non-intersected and half-intersected methods of calculation.

The results demonstrate the improved model accuracy with both methods. The shape of the accuracy histogram does not change significantly; however, the methods improve the accuracy for almost all samples in the validation dataset. This demonstrates the effectiveness of the methods and the corresponding mean accuracy and variance values provide further confirmation of this (see Table 4). The application of the Gaussian distribution demonstrates the best values of accuracy, as well as significantly better variances than other full-size UNet 224 × 224 models for both multiclass and binary segmentation.

Table 4. Mean and variance of accuracy (%) for the models analyzed in this section. The maximum value of the corresponding metrics is in bold.

Model	Binary Dice		Binary Jaccard		Multiclass Dice		Multiclass Jaccard
UNet 448	92.71	12.41	88.01	13.42	85.89	8.98	77.33	11.48
UNet non-int	91.74	18.04	87.43	18.30	85.98	11.05	78.26	12.08
UNet addw	91.57	18.07	87.49	18.41	86.31	11.04	78.75	12.10
UNet Gauss	92.10	16.53	87.96	17.04	86.69	10.05	79.15	11.45

3.3. UUNet and wUUNet

The proposed models are described in Section 2.3, and the comparison results are summarized in Table 5. The wUUNet with Gauss half-intersected schema model represents the best segmentation quality, and yields an accuracy above 80% according to the multiclass Jaccard metric.

Table 5. The mean and variance of accuracy (%) for the models analyzed in this section. The maximum value of the corresponding metrics is in bold.

Model	Binary Dice		Binary Jaccard		Multiclass Dice		Multiclass Jaccard
UNet 448	92.71	12.41	88.01	13.42	85.89	8.98	77.33	11.48
UNet non-int	91.74	18.04	87.43	18.30	85.98	11.05	78.26	12.08
UNet addw	91.57	18.07	87.49	18.41	86.31	11.04	78.75	12.10
UNet Gauss	92.10	16.53	87.96	17.04	86.69	10.05	79.15	11.45
UUNet addw	93.32	12.25	89.02	13.02	87.06	9.42	79.29	11.30
UUNet Gauss	93.77	12.33	89.92	13.00	87.47	9.37	79.91	11.12
wUUNet non-int	94.09	10.34	89.99	11.45	87.04	9.63	79.20	11.60
wUUNet addw	94.71	8.23	90.68	9.63	87.45	9.50	79.74	11.56
wUUNet Gauss	95.34	3.99	91.35	6.79	87.87	8.80	80.23	11.15

The performance characteristics are shown in Table 6. We use an Nvidia RTX2070-based workstation as the target device and pure PyTorch model to obtain FPS values, minimum memory consumption, and the number of video streams able to run in parallel. The table shows that all of UNet based models can run in real time. We do not take into account the time taken to move the input frame from CPU to GPU because robotics systems will fetch and save the frame directly to video RAM memory.

Table 6. The performance of the models used.

Model	FPS	Number of Parallel Video Streams (RTX2070 8G)	Minimal Memory Consumption (RTX2070 8G, 1 Stream) in G
UNet 448 OW	103	14	1.7
UNet 448 FS	102	7	2.1
UNet 224 FS	98	5	2.7
UNet Gauss	64	3	4.0
UNet addw	83	3	3.9
UUNet Gauss	63	2	4.1
wUUNet Gauss	63	2	5.5

To complete the investigation of the multiclass fire-segmentation task, it is worth noting that the methods can be used in different environmental conditions, as shown in Figure 18 and Figure 19. For each original image CNN calculates accurate fire-segmentation mask and we visualize it bellow by swapping red and blue channel of image and mark by red, orange and yellow the areas of detected flame.

Figure 18. The visualization of the algorithm on the training and validation datasets.

Figure 19. The visualization of the algorithm on the training and validation datasets.

The visualization demonstrates effective segmentation in cases of video capturing from the air and on the ground, as well as a large and a small fire. Additionally, it shows the reliable elimination of false alarms represented by firefighting vehicles and other objects of red, yellow, and orange colors.

4. Discussion

This article describes a detailed solution to multiclass fire image segmentation using an advanced neural-network architecture known as UNet. Because this problem has been solved for the first time, we collected and labeled datasets for training, and suggested some configurations for the UNet model. We analyzed the best configuration for fire segmentation and suggested innovative methods to improve accuracy. Based on the UNet architecture, we developed a wUUNet-concatenative model that demonstrates the best results in the task of multiclass fire segmentation. It outperforms the UNet model by 2% and 3% in case of binary and multiclass segmentation accuracy, respectively.

The software was developed using a PyTorch DL-framework. The open GitHub repository of the implementation can be accessed at (https://github.com/VSBochkov/wUUNet_fireSegm).

The next steps are to run the proposed model and calculation schemes in Jetson Nano board to perform real-time computations from the connected CSI camera module, and to create a prototype for fire detection system to provide automatic forest fire segmentation and effective suppression.