Dynamics of Cardiovascular Muscle Using a Non-Linear Symmetric Oscillator
Abstract
1. Introduction
1.1. Review on Cardiovascular Conduction Process towards the Prosthetic Heart
1.2. Importance of van der Pol Equation
1.3. Why Hamiltonian Approach
1.4. Background and Related Work
1.5. Contributions and Organization
1.6. General Objective of the Study
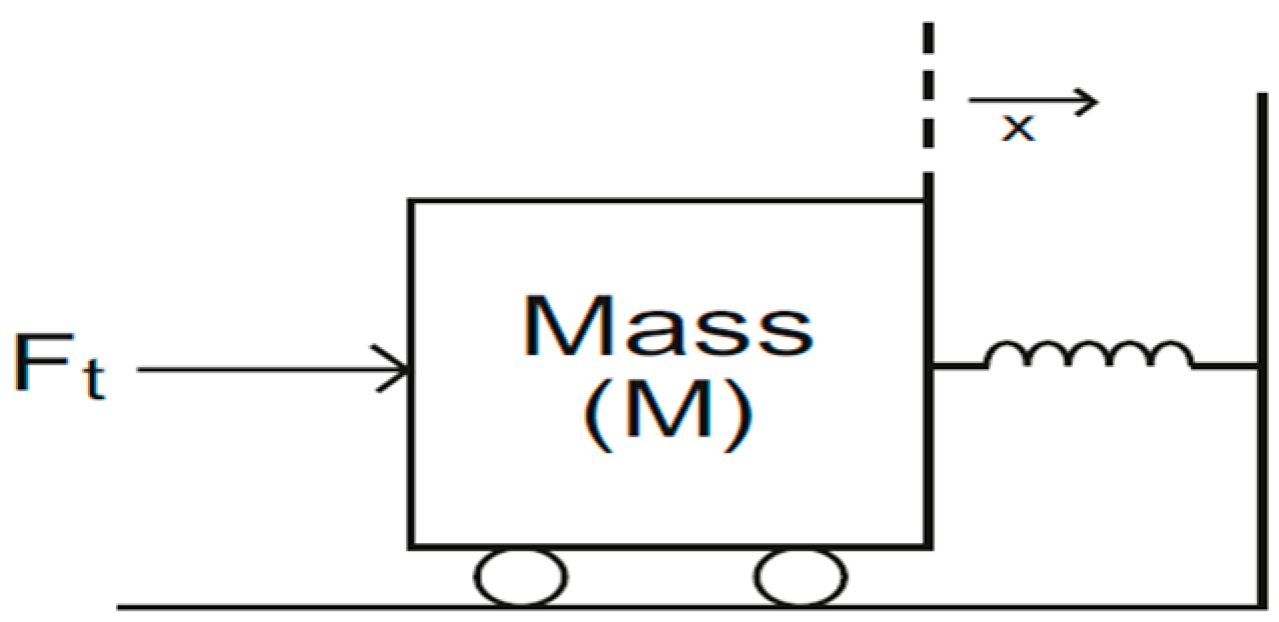
2. Modified Symmetric Oscillator Equation-Based Non-Linear Model of the Proposed Design
3. Hamiltonian Approach for Linear System
4. Hamiltonian Approach for Non-Linear System
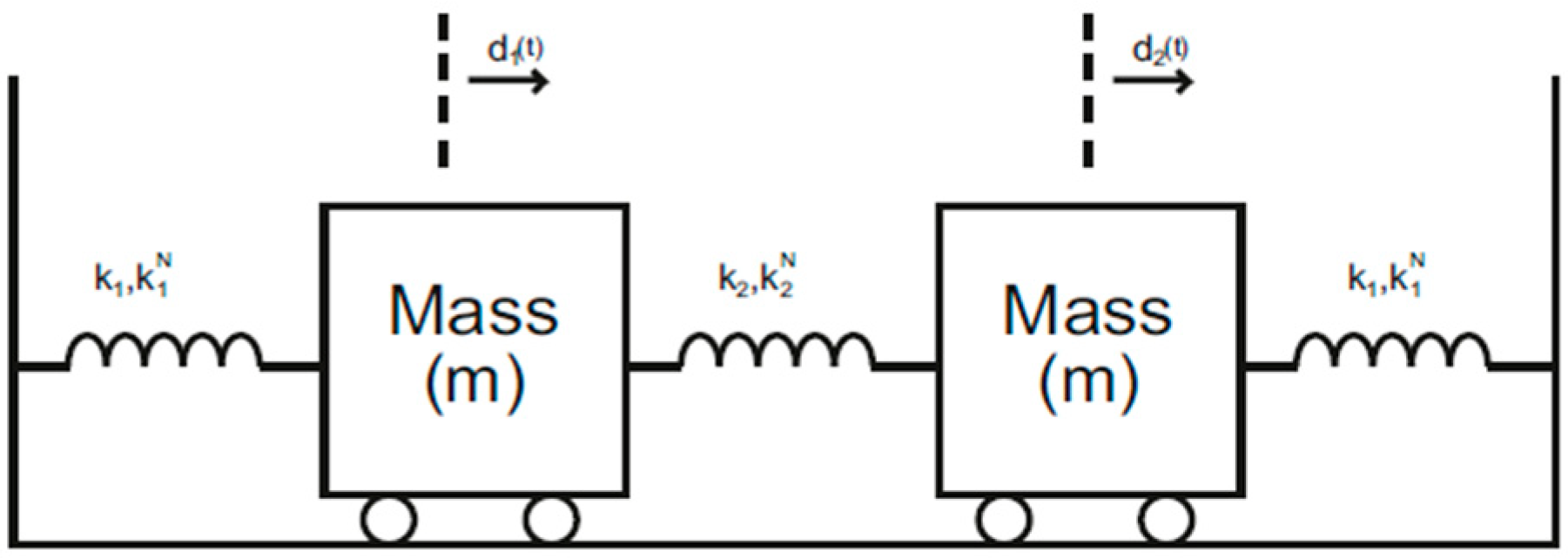
5. Modeling of the Proposed Design
6. Generation of Action Potential and Coupling of Nodes
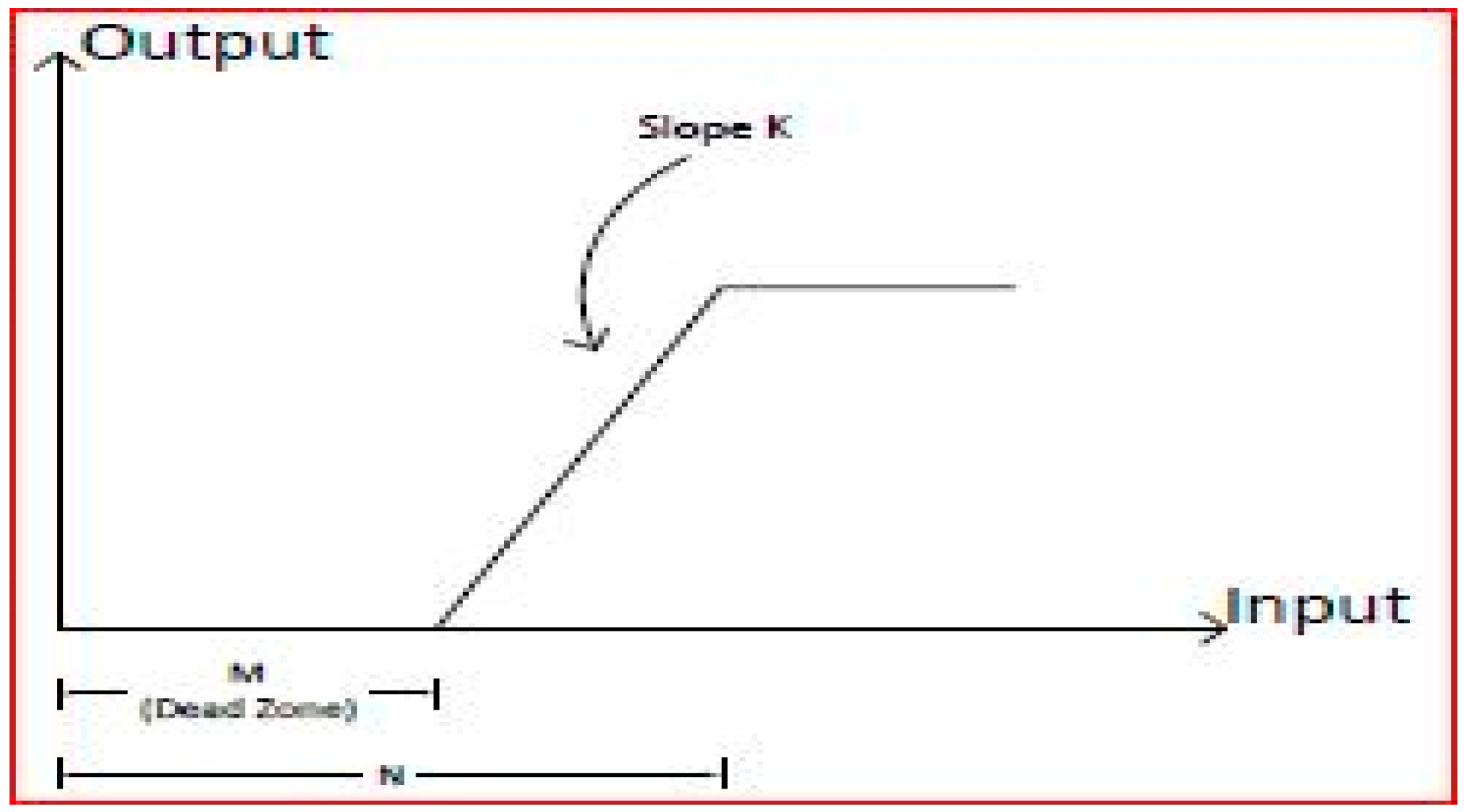
7. Muscle Dynamics Traditional Describing Function Method to Determine Nonlinearity
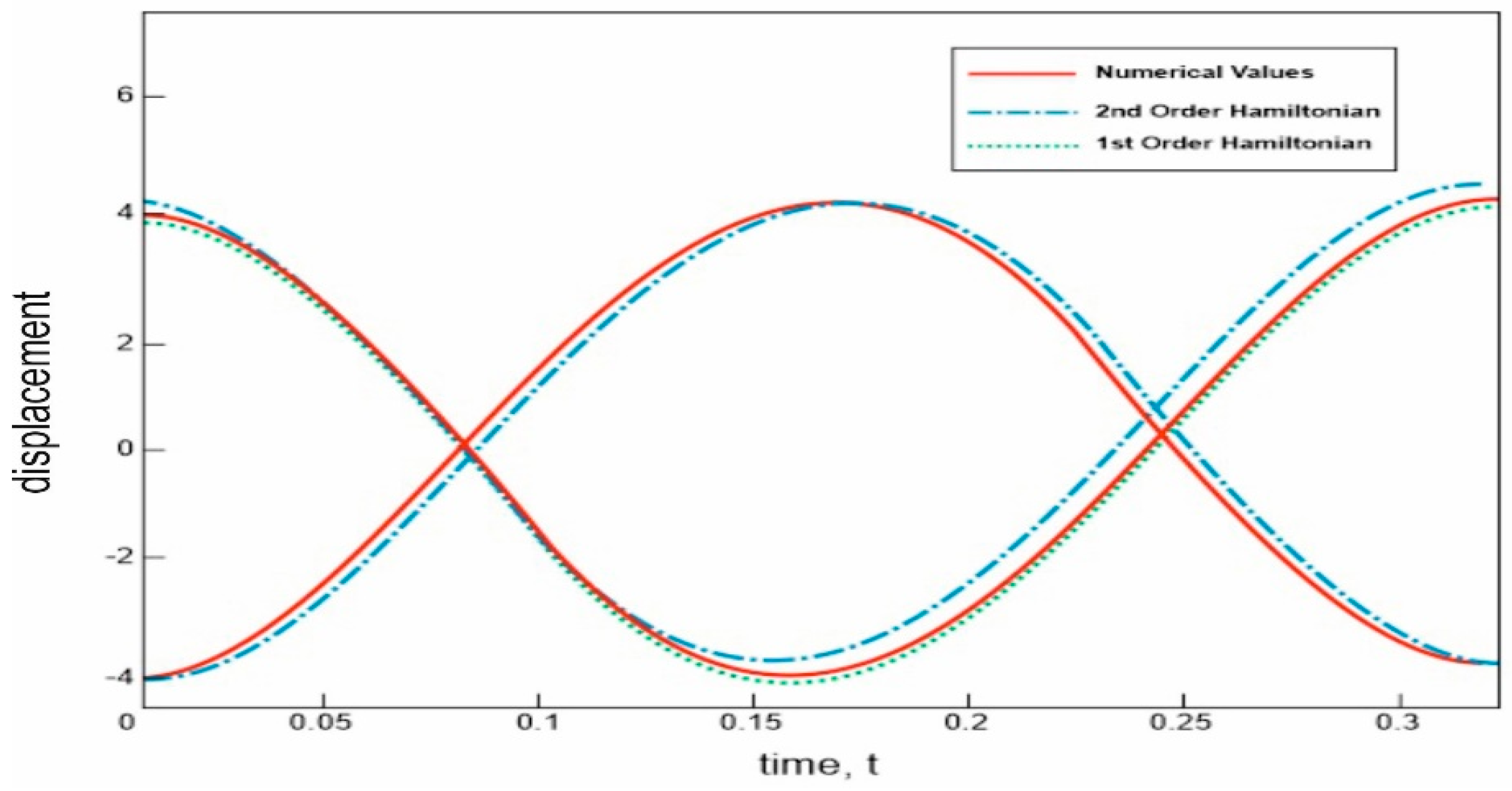
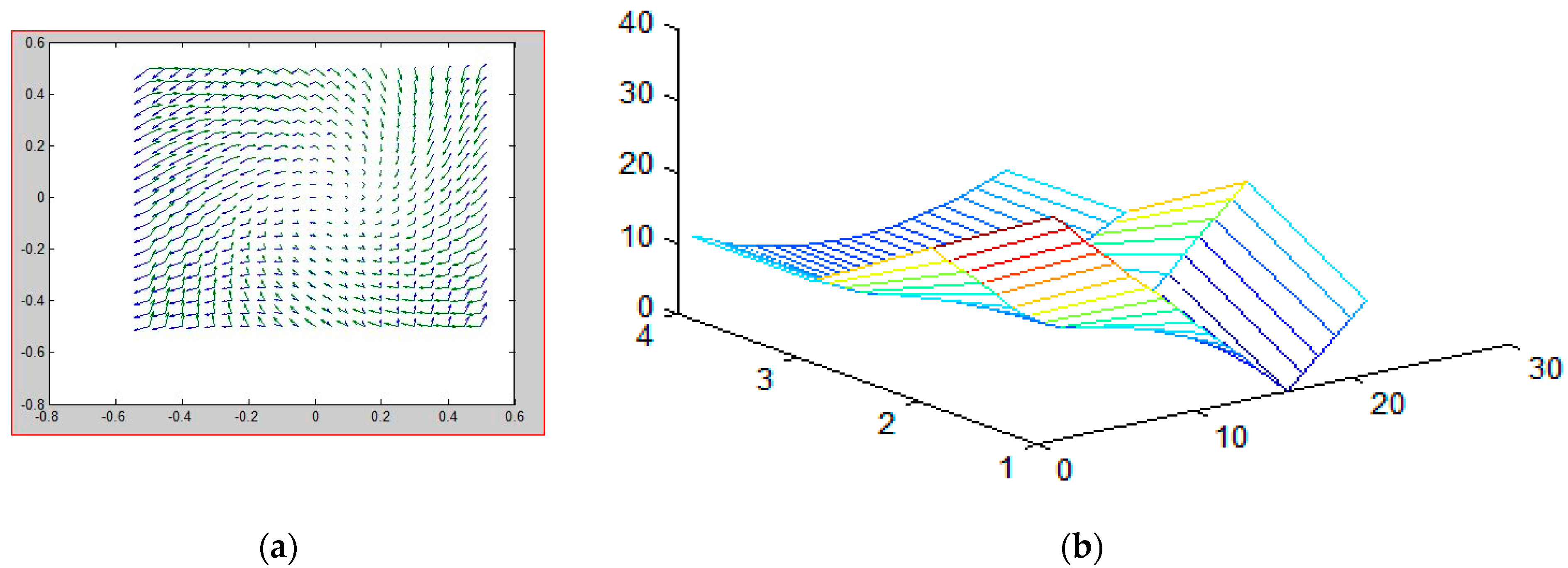
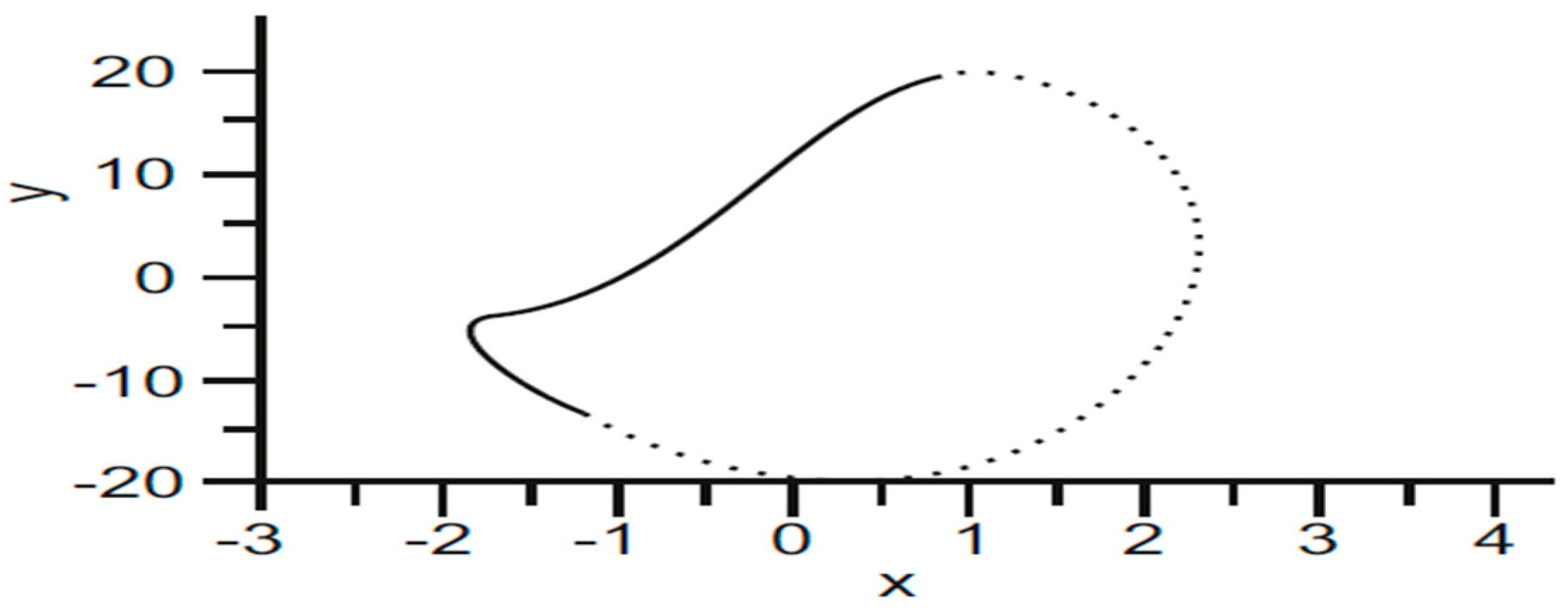
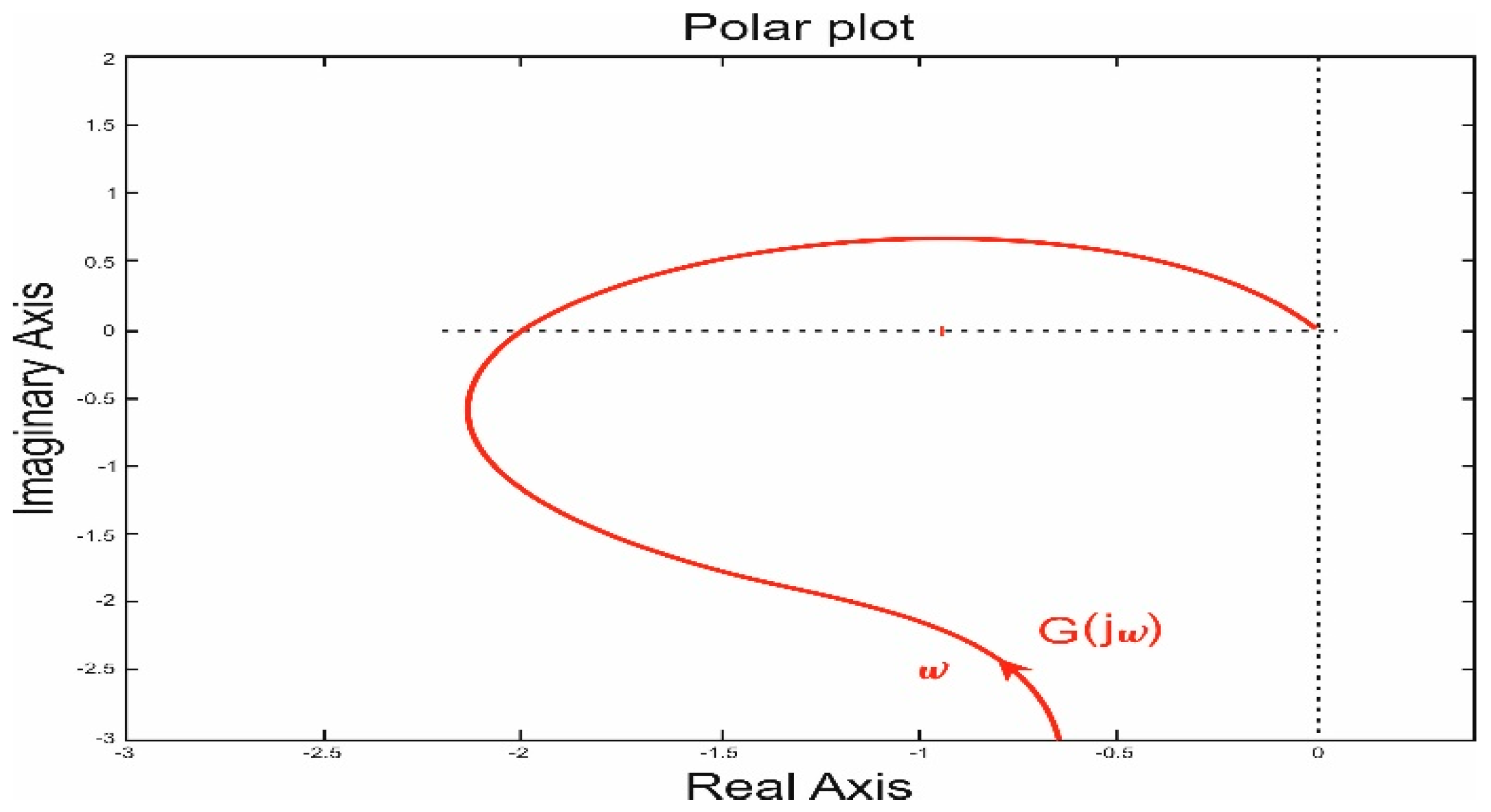
8. Simulation Result
9. Comparative Study of Our Proposed Design with Traditional Describing Function and Future Scope
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Islam, M.R.; Zulkarnain, M.I. Effect of pump characteristic (HQ) curves on the efficiency of Total Artificial Heart. In Proceedings of the 2015 International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 17–19 December 2015; pp. 55–58. [Google Scholar]
- Frazier, O. First use of an untethered, vented electric left ventricular assist device for long-term support. Circulation 1994, 89, 2908–2914. [Google Scholar] [CrossRef]
- Ghosal, S.; Darbar, R.; Neogi, B.; Das, A.; Tibarewala, D.N. Application of swarm intelligence computation techniques in PID controller tuning: A review. In Proceedings of the International Conference on Information Systems Design and Intelligent Applications 2012 (INDIA 2012), Visakhapatnam, India, 5–7 January 2012; pp. 195–208. [Google Scholar]
- Choi, S.W.; Min, B.G. Ventricular Assist Device Cannula and Ventricular Assist Device Including the Same. U.S. Patent 8,771,165, 8 July 2014. [Google Scholar]
- Sarkar, B. Mathematical and analytical approach for the management of defective items in a multi-stage production system. J. Clean. Prod. 2019, 218, 896–918. [Google Scholar] [CrossRef]
- Tayyab, M.; Jemai, J.; Han, L.; Sarkar, B. A sustainable development framework for a cleaner multi-item multi-stage textile production system with a process improvement initiative. J. Clean. Prod. 2020, 246, 119055. [Google Scholar] [CrossRef]
- Dey, B.K.; Pareek, S.; Tayyab, M.; Sarkar, B. Autonomation policy to control work-in-process inventory in a smart production system. Int. J. Prod. Res. 2020, in press. [Google Scholar] [CrossRef]
- Zhao, C.J.; Sun, Y.X.; Zhu, H.Q.; Liu, X.X. Axial suspension fuzzy pid control for axial artificial heart pump. Appl. Mech. Mater. 2015, 703, 323–326. [Google Scholar] [CrossRef]
- Castro, V.J.F.; Malathi, R. Design of advanced control strategies for cardiovascular system. Mater. Today Proc. 2018, 5, 1960–1966. [Google Scholar] [CrossRef]
- Sarkar, B.; Sana, S.S.; Chaudhuri, K.S. An imperfect production process for time-varying demand with inflation and time value of money—An EMQ model. Expert Syst. Appl. 2011, 38, 13543–13548. [Google Scholar] [CrossRef]
- Sarkar, B. An inventory model with reliability in an imperfect production process. Appl. Math. Comput. 2012, 218, 4881–4891. [Google Scholar] [CrossRef]
- Sarkar, B. An EOQ model with delay in payments and stock dependent demand in the presence of imperfect production. Appl. Math. Comput. 2012, 218, 8295–8308. [Google Scholar] [CrossRef]
- Pakar, I.; Bayat, M. Analytical study on the non-linear vibration of Euler-Bernoulli beams. J. Vibroeng. 2012, 14, 216–224. [Google Scholar]
- Pakar, I.; Bayat, M.; Bayat, M. On the Approximate Analytical solution for parametrically excited nonlinear oscillators. J. Vibroeng. 2012, 14, 423–429. [Google Scholar]
- Bazzani, A.; Giovannozzi, M.; Servizi, G.; Todesco, E.; Turchetti, G. Resonant normal forms, interpolating Hamiltonians and stability of area preserving maps. Physica D 1993, 64, 66–93. [Google Scholar] [CrossRef]
- Vesely, V.; Korosi, L. Robust PID Controller Design for Nonlinear Systems; De Gruyter: Berlin, Germany, 2018; pp. 65–71. [Google Scholar]
- Van der Pol, B.; van der Mark, J. The heartbeat considered as a relaxation oscillation and an electrical model of the heart. Philos. Mag. 1928, 6, 763–775. [Google Scholar] [CrossRef]
- Boro, B. Review of Stability Analysis of Non-Linear Control Systems. IJERG 2016, 4, 193–199. [Google Scholar]
- Yamada, H.; Yamaguchi, M.; Kobayashi, K.; Matsuura, Y.; Takano, H. Development and test of a linear motor-driven total artificial heart. IEEE Eng. Med. Biol. Mag. 1995, 14, 84–90. [Google Scholar] [CrossRef]
- Love, H.C.; Timms, D.L.; Nestler, F.; Frazier, O.H.; Cohn, W.E. A mock circulatory loop for designing and evaluating total artificial hearts. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 5667–5670. [Google Scholar]
- Kurita, N.; Ishikawa, T.; Saito, N.; Masuzawa, T.; Timms, D. A double-sided stator type axial self-bearing motor development for total artificial heart. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–6. [Google Scholar]
- Konieczny, G.; Opilski, Z.; Pustelny, T.; Gacek, A.; Gibinski, P.; Kustosz, R. Results of experiments with fiber pressure sensor applied in the polish artificial heart prosthesis. Acta Phys. Pol. Ser. A Gen. Phys. 2010, 118, 1183. [Google Scholar] [CrossRef]
- Baldoni, J.A.; Yellen, B.B. Magnetic tracking system: Monitoring heart valve prostheses. IEEE Trans. Magn. 2007, 43, 2430–2432. [Google Scholar] [CrossRef]
- Rosli, R.S.B.; Olanrewaju, R.F. Mobile Heart Rate Detection System (MoHeRDS) for Early Warning of Potentially-Fatal Heart Diseases. In Proceedings of the 2016 International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 26–27 July 2016; pp. 422–427. [Google Scholar]
- Marom, G.; Chiu, W.C.; Slepian, M.J.; Bluestein, D. Numerical model of total artificial heart hemodynamics and the effect of its size on stress accumulation. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014; pp. 5651–5654. [Google Scholar]
- Shi, W.; Chew, M.S. Mathematical and physical models of a total artificial heart. In Proceedings of the IEEE International Conference on Control and Automation, Christchurch, New Zealand, 9–11 December 2009; pp. 637–642. [Google Scholar]
- Pohlmann, A.; Leßmann, M.; Hameyer, K. Comparative study on optimization methods for a motor-drive of artificial hearts. In Proceedings of the 2010 International Conference on Electrical Machines and Systems (ICEMS), Incheon, Korea, 10–13 October 2010; pp. 1754–1758. [Google Scholar]
- Das, S.; Nandi, D.; Neogi, B.; Sarkar, B. Nonlinear system stability and behavioral analysis for effective implementation of artificial lower limb. Symmetry 2020, 12, 1727. [Google Scholar] [CrossRef]
- Pakar, I.; Bayat, M. Nonlinear free vibration analysis of tapered beams by Hamiltonian approach. J. Vibroeng. 2011, 13, 654–661. [Google Scholar]
- Bayat, M.; Pakar, I. Nonlinear dynamics of two degree of freedom systems with linear and nonlinear stiffnesses. Earthq. Eng. Eng. Vib. 2013, 12, 411–420. [Google Scholar] [CrossRef]
- Holden, A.V.; Biktashev, V.N. Computational biology of propagation in excitable media models of cardiac tissue. Chaos Solitons Fractals 2002, 13, 1643–1658. [Google Scholar] [CrossRef]
- Bazzani, A.; Mazzanti, P.; Servizi, G.; Turchetti, G. Normal forms for hamiltonian maps and non linear effects in a particle accelerator. IL Nuovo Cim. B 1988, 102, 51–80. [Google Scholar] [CrossRef]
- Katholi, C.R.; Urthaler, F.; Macy, J., Jr.; James, T.N. Mathematical model of automaticity in the sinus node and AV junction based on weakly coupled relaxation symmetric oscillators. Comput. Biomed. Res. 1977, 10, 529–543. [Google Scholar] [CrossRef]
- Di Bernardo, D.; Signorini, M.G.; Cerutti, S. A model of two nonlinear coupled symmetric oscillator s for the study of heartbeat dynamics. Int. J. Bifurc. Chaos Appl. Sci. Eng. 1998, 8, 1975–1985. [Google Scholar] [CrossRef]
- Nollo, G.; Del Greco, M.; Ravelli, F.; Disertori, M. Evidence of low and high-frequency oscillations in human AV interval variability: Evaluation with spectral analysis. Am. J. Physiol. 1994, 267, H1410–H1418. [Google Scholar] [CrossRef]
- Zhang, H.; Holden, A.V.; Kodama, I.; Honjo, H.; Lei, M.; Varghese, T.; Boyett, M.R. Mathematical models of action potentials in the periphery and center of the rabbit sinoatrial node. Am. J. Physiol. Heart Circ. Physiol. 2000, 279, H397–H421. [Google Scholar] [CrossRef]
- Saha, S.; Chatterjee, D.; Sarkar, B. The ramification of dynamic investment on the promotion and preservation technology for inventory management through a modified flower pollination algorithm. J. Retail. Con. Ser. 2021, 58, 102326. [Google Scholar] [CrossRef]
- Honerkamp, J. The heart as a system of coupled nonlinear symmetric oscillators. J. Math. Biol. 1983, 18, 69–88. [Google Scholar] [CrossRef]
- Żebrowski, J.J.; Baranowski, R. Type I intermittency in nonstationary systems—Models and human heart rate variability. Phys. A 2014, 336, 74–83. [Google Scholar] [CrossRef]
- Keener, J.; Sneyd, J. Mathematical Physiology, Interdisciplinary Applied Mathematics 8; Springer: New York, NY, USA, 1998. [Google Scholar]
- West, J.; Goldberger, A.L.; Rovner, G.; Bhargava, V. Nonlinear dynamics of the heartbeat. The AV junction: Passive conduit or active symmetric oscillator? Physica D 1985, 17, 198–206. [Google Scholar] [CrossRef]
- Jemai, J.; Sarkar, B. Optimum design of a transportation scheme for healthcare supply chain management: The effect of energy consumption. Energies 2019, 12, 2789. [Google Scholar] [CrossRef]
- Grudziński, K.; Żebrowski, J.J. Modeling cardiac pacemakers with relaxation symmetric oscillators. Phys. A 2004, 336, 153–162. [Google Scholar] [CrossRef]
- Hodgkin, L.; Huxley, A.F. A quantitative description of membrane current and its applications to conduction and excitation in nerve. J. Physiol. Lond. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Postnov, D.; Seung, K.H.; Hyungtae, K. Synchronization of diffusively coupled symmetric oscillator s near the homoclinic bifurcation. Phys. Rev. E 1999, 60, 2799–2807. [Google Scholar] [CrossRef]
- Meirovitch, L. Principles, and Techniques of Vibrations; Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Joyner, R.W.; van Capelle, F.J.L. Propagation through electrically coupled cells: How a small SA node drives a large atrium. Biophys. J. 1986, 50, 1157–1164. [Google Scholar] [CrossRef]
- Jadlovska, A.; Hrubina, K.; Majercak, J. Application of Stability Theory of NonLinear Systems and Lyapnov Transformation in Control of Artificial Pneumatic Muscle. Ann. Fac. Eng. 2011, 3, 97–102. [Google Scholar]
- Barbosa, J.R.S.; Machado, J.A.T. Describing Function Analysis of Systems with Impacts and Backlash. Nonlinear Dyn. 2002, 29, 235–250. [Google Scholar] [CrossRef]
- Davison, E.J.; Kurak, E.M. A computational method for determining quadratic Lyapunov functions for non Linear system. Automatica 1971, 7, 627–636. [Google Scholar] [CrossRef]



| An Author with Reference Number | Theme | Future Scope | Limitation |
|---|---|---|---|
| Yamada [19] | An implantable motor-driven artificial heart was tested. | The pump-based system tested on some animals may improve system efficiency. | The control analogy of this non-linear system is not illustrated. |
| Love [20] | A mechanical, hydraulic circulation system was tested for developing an artificial heart system. | This mechanical circulation system generates an initial idea of the artificial heart. | The system and control dynamics is not mentioned. |
| Kurita [21] | The whole operation is described as the development of an artificial heart. | Modification of the pump system provides development towards the artificial heart. | The heart model’s pumping operation is proposed, but the other operational parameters are not considered. For example, transportation delay, nonlinearity |
| Konieczny [22] | The non-invasive pressure monitoring system in an artificial heart was proposed and analyzed. | The future scope is aimed at the development of non-invasive heart prostheses or assistive devices. | The pressure sensing technique for various conditions was not illustrated. |
| Baldoni [23] | A magnetic heart valve sensing system was proposed for tracking heart valve prosthetic. | The monitoring system will be a step towards the development of the entire prosthetic heart monitoring system | The valve activity during monitoring is elaborated in this study, but the controlling analogy is not exact. |
| Rosli [24] | A smart wireless heart monitoring system was developed that uses heartbeat data for alarming. | This system may recognize the specific heart problem and alert the medical person. | The parametric analysis on several critical factors like system stability, sensitivity, and reliability was not pointed out. |
| Marom [25] | Three different Numerical models of artificial heart systems were developed in the aspect of flow control. | The various numerical model may develop the artificial model of the human heart. | The proposed design is incapable of generating a transfer function analogy. |
| Shi [26] | The proposed artificial heart model was based on physical and numerical analysis. | The actual artificial heart model may be developed by electrical and mathematical analysis, comparing with a simulative approach. | Analysis of disease-related issues with cardiovascular system is depicted in this article. |
| Pohlmann [27] | Some optimization techniques were realized in the artificial heart for optimal system performance. | The optimization technique drives towards functional improvement in the development of the artificial heart. | Optimization parameters of artificial heart modeling systems have not been considered. |
| Symbol | Meaning | Unit |
|---|---|---|
| β | Damping constant | lbfs/inch |
| Constant of van der Pol model | NA | |
| x | Displacement | cm |
| Velocity | cm/s | |
| X | The amplitude of input sinusoidal signal for non-linear analysis | V |
| M | The distance between nodes | mm |
| Y | The output of the non-linear system | V |
| M | Mass of cardiovascular muscle | g |
| K | Spring constant | N/m |
| B | Viscous drug | P |
| N | Order of spring constant | NA |
| K | The slope of non-linear section | NA |
| Kronecker delta | NA | |
| KE | Kinetic energy | J |
| PE | Potential energy | J |
| Px | Momentum | kg. m/s |
| H | Hamiltonian operator | NA |
| (v) | Hamiltonian considering multiple inputs | NA |
| L | Lagrangian operator | NA |
| Angular frequency | rad/s | |
| T | Period | s |
| Phase shift | rad | |
| V | Describing function | NA |
| Amplitude of oscillation | V |
| Parameter | Values |
|---|---|
| 1,3 | |
| 5,7 | |
| M | 1 |
| B | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharjee, S.; Banerjee, A.; Rakshit, A.; Bhattacharyya, S.; Chowdhuri, S.; Sarkar, B.; Neogi, B. Dynamics of Cardiovascular Muscle Using a Non-Linear Symmetric Oscillator. Symmetry 2021, 13, 151. https://doi.org/10.3390/sym13010151
Bhattacharjee S, Banerjee A, Rakshit A, Bhattacharyya S, Chowdhuri S, Sarkar B, Neogi B. Dynamics of Cardiovascular Muscle Using a Non-Linear Symmetric Oscillator. Symmetry. 2021; 13(1):151. https://doi.org/10.3390/sym13010151
Chicago/Turabian StyleBhattacharjee, Soumyendu, Aishwarya Banerjee, Amit Rakshit, Swapan Bhattacharyya, Swati Chowdhuri, Biswajit Sarkar, and Biswarup Neogi. 2021. "Dynamics of Cardiovascular Muscle Using a Non-Linear Symmetric Oscillator" Symmetry 13, no. 1: 151. https://doi.org/10.3390/sym13010151
APA StyleBhattacharjee, S., Banerjee, A., Rakshit, A., Bhattacharyya, S., Chowdhuri, S., Sarkar, B., & Neogi, B. (2021). Dynamics of Cardiovascular Muscle Using a Non-Linear Symmetric Oscillator. Symmetry, 13(1), 151. https://doi.org/10.3390/sym13010151









