Picture Fuzzy Geometric Aggregation Operators Based on a Trapezoidal Fuzzy Number and Its Application
Abstract
1. Introduction
1.1. Introduction for Picture Fuzzy Sets
1.2. The Development State for Picture Fuzzy Aggregation Operators
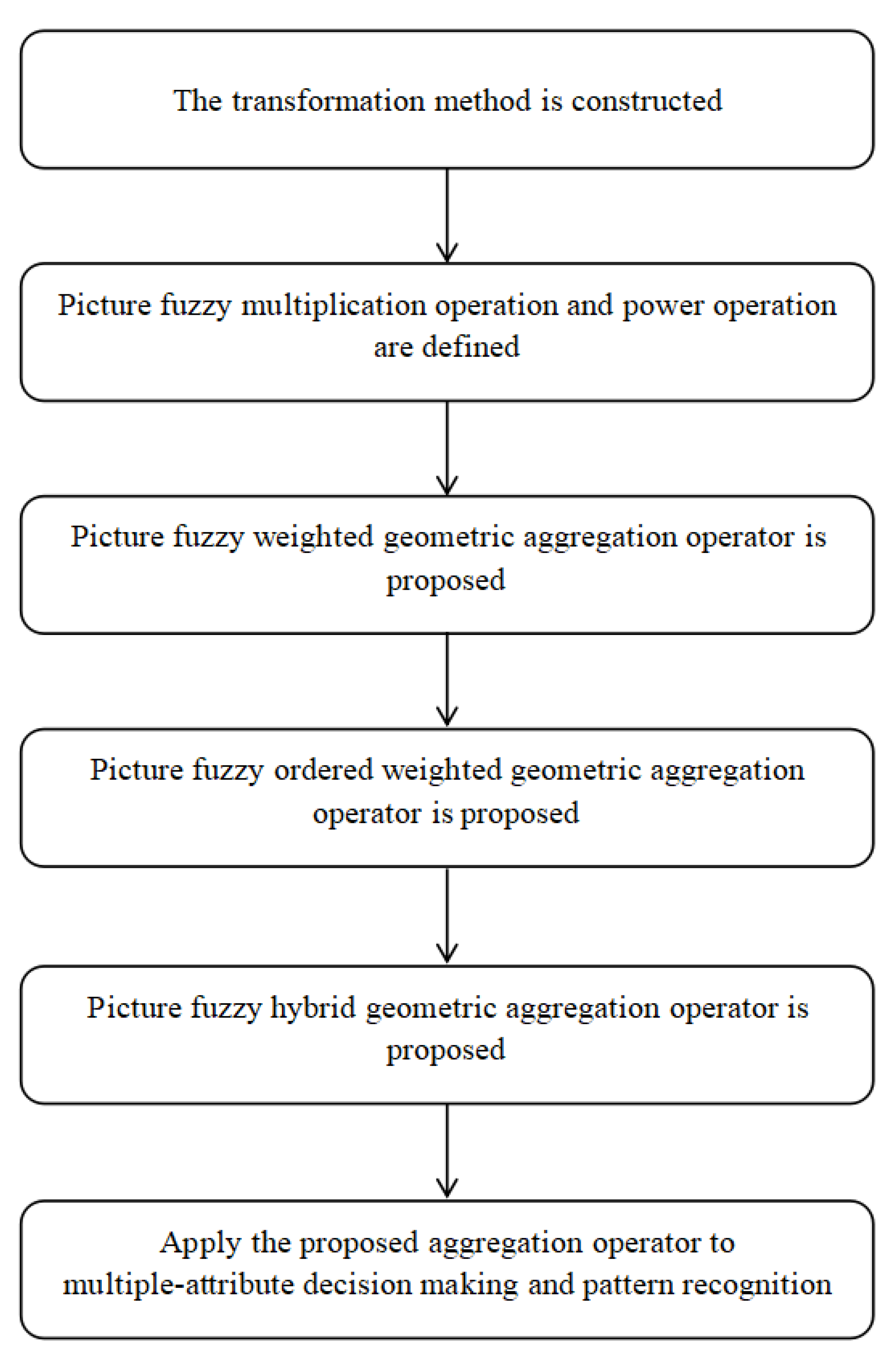
1.3. Main Contributions for This Paper
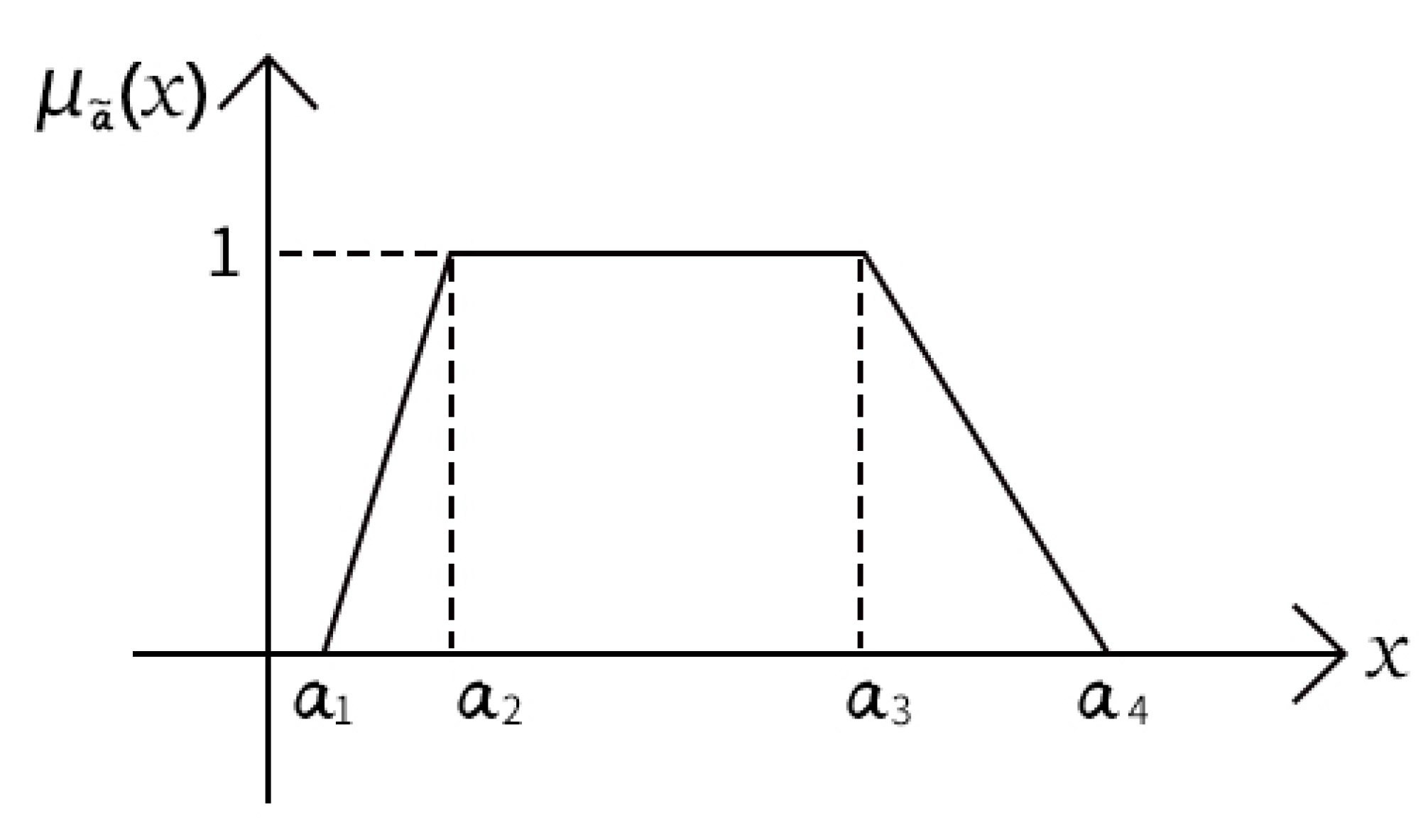
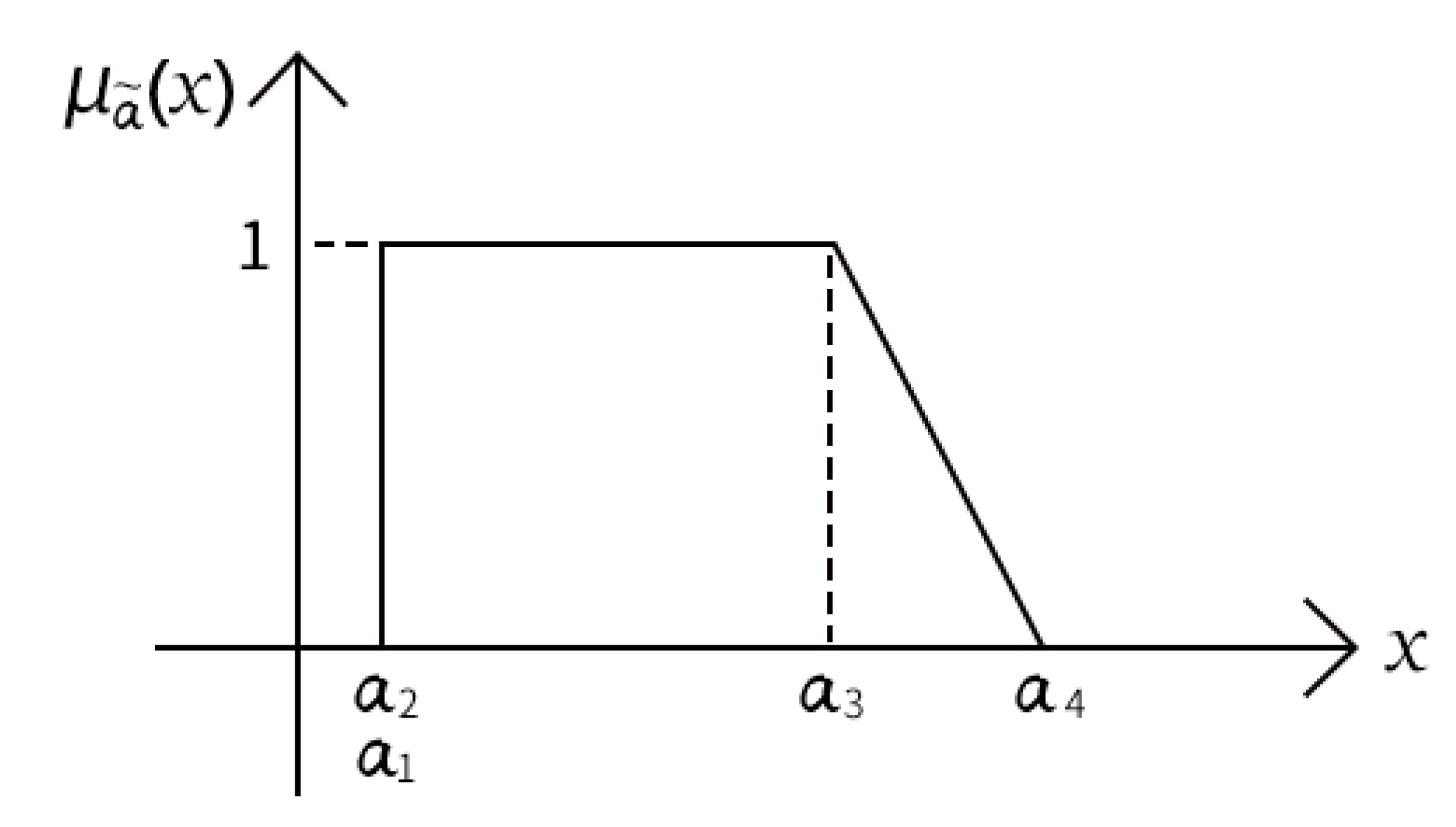
2. Basic Concepts and Properties for Picture Fuzzy Sets
3. New Transformation Approach for Picture Fuzzy Sets
4. New Geometric Aggregation Operators for Picture Fuzzy Sets
5. Application to Multi-Criteria Decision Making
5.1. Numerical Example
5.2. Application to Multi-Criteria Decision Making
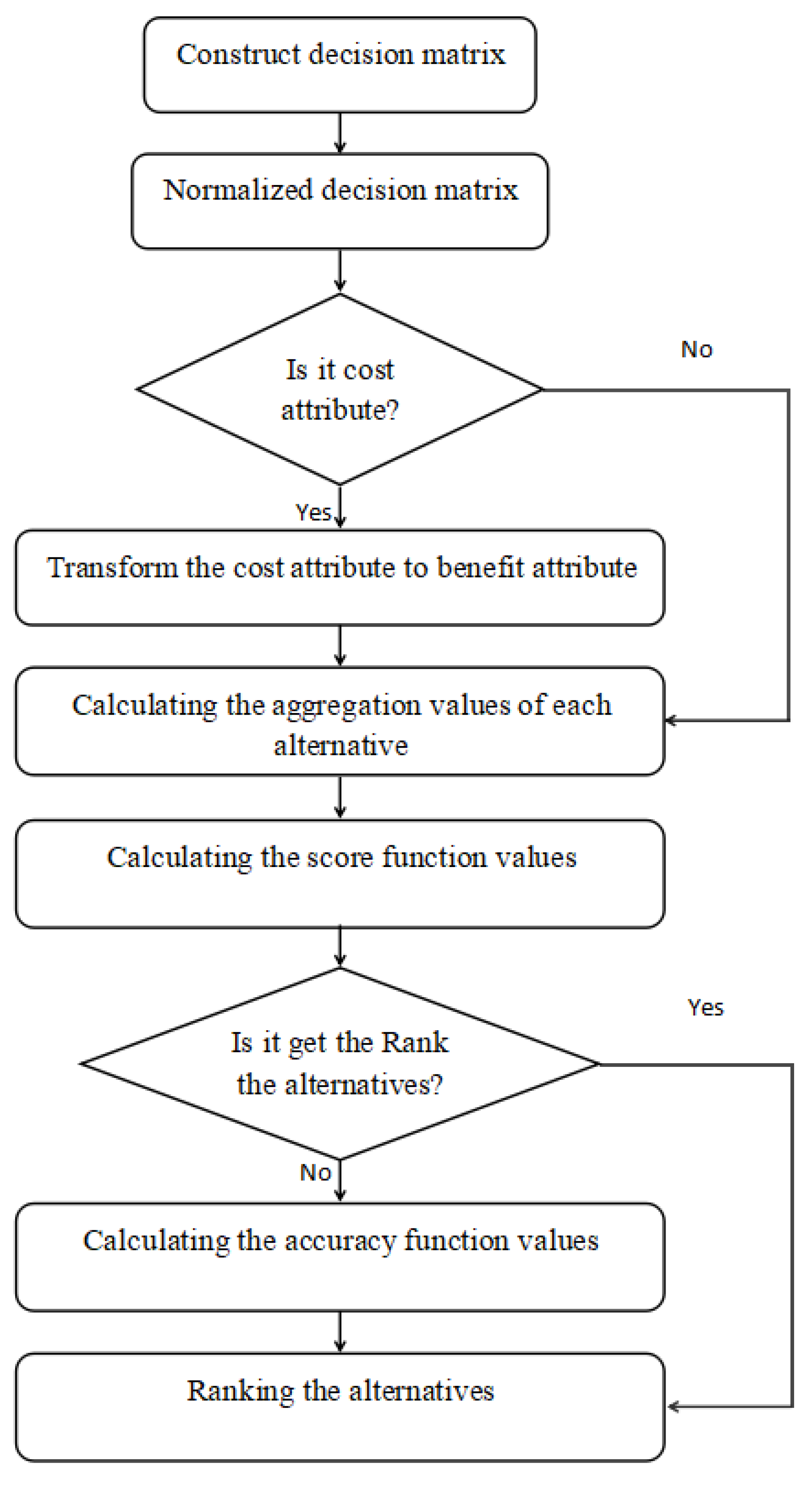
5.2.1. Algorithm for Multi-Criteria Decision Making
5.2.2. Application to Multi-Criteria Decision Making
5.3. Comparative Analysis the Conditions of Using Some Aggregation Operators
6. Application to Pattern Recognition
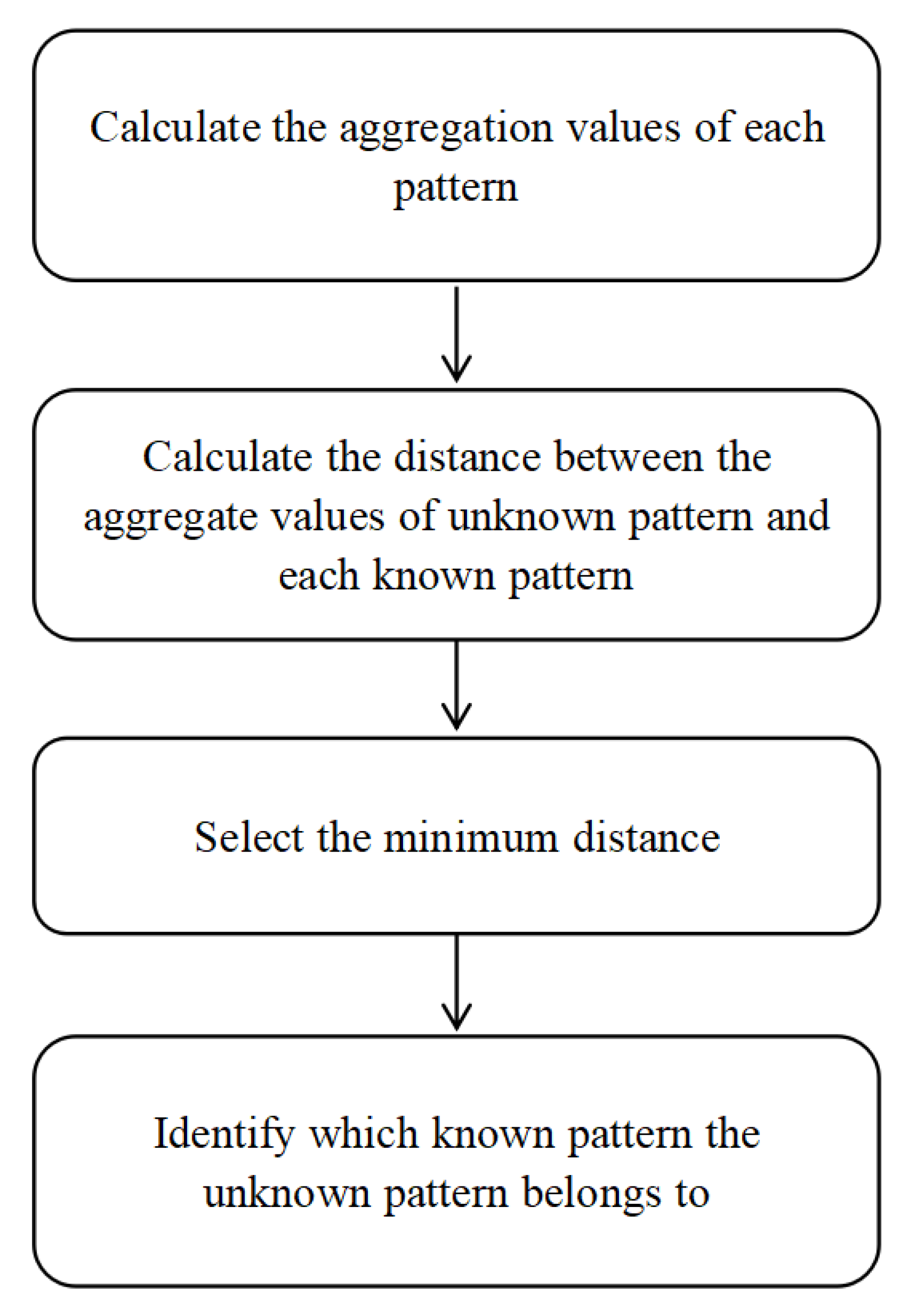
6.1. Algorithm for Pattern Recognition
6.2. Application to Pattern Recognition
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Luo, M.X.; Zhao, R.R. A distance between intuitionistic fuzzy sets and its application in medical diagnosis. Artif. Intell. Med. 2018, 89, 34–39. [Google Scholar] [CrossRef]
- Ngan, R.T.; Son, L.H.; Cuong, B.C.; Ali, M. H-max distance measure of intuitionistic fuzzy sets in decision making. Appl. Soft Comput. 2018, 69, 393–425. [Google Scholar] [CrossRef]
- Iancu, I. Intuitionistic fuzzy similarity measures based on Frank t-norms family. Pattern. Recognit. Lett. 2014, 42, 128–136. [Google Scholar] [CrossRef]
- Singh, P.; Mishra, N.K.; Kumar, M.; Saxena, S.; Singh, V. Risk analysis of flood disaster based on similarity measures in picture fuzzy environment. Afr. Mat. 2018, 29, 1019–1038. [Google Scholar] [CrossRef]
- Song, Y.F.; Wang, X.D.; Quan, W.; Huang, W.L. A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Comput. 2019, 23, 1985–1998. [Google Scholar] [CrossRef]
- Rahman, K.; Abdullah, S.; Jamil, M.; Khan, M.Y. Some generalized intuitionistic fuzzy einstein hybrid aggregation operators and their application to multiple attribute group decision making. Int. J. Fuzzy Syst. 2018, 20, 1–9. [Google Scholar] [CrossRef]
- Xu, Z.S. Additive intuitionistic fuzzy aggregation operators based on fuzzy measure. Int. J. Uncertain. Fuzz. 2016, 24, 1–12. [Google Scholar] [CrossRef]
- Ye, J. Intuitionistic fuzzy hybrid arithmetic and geometric aggregation operators for the decision-making of mechanical design schemes. Appl. Intell. 2017, 47, 743–751. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. General Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets-a new concept for computational intelligence problems. Inf. Commun. Technol. 2013, 1–6. [Google Scholar] [CrossRef]
- Son, L.H. Generalized picture distance measure and applications to picture fuzzy clustering. Appl. Soft Comput. 2016, 46, 284–295. [Google Scholar] [CrossRef]
- Dinh, N.V.; Thao, N.X. Some measures of picture fuzzy sets and their application in multi-attribute decision making. Int. J. Math. Sci. Comput. 2018, 4, 23–41. [Google Scholar] [CrossRef]
- Guleria, A.; Bajaj, R.K. A novel probabilistic distance measure for picture fuzzy sets with its application in classification problems. Hacet. J. Math. Stat. 2020, 49, 2134–2153. [Google Scholar] [CrossRef]
- Wei, G.W. Some similarity measures for picture fuzzy sets and their applications. Iran. J. Fuzzy Syst. 2018, 15, 77–89. [Google Scholar] [CrossRef]
- Wei, G.W. picture fizzy cross-entropy for multiple attribute desision making problems. J. Bus. Econ. Manag. 2016, 17, 491–502. [Google Scholar] [CrossRef]
- Wei, G.W.; Alsaadi, F.E.; Hayat, T.; Alsaed, A. Picture 2-tuple linguistic aggregation operators in multiple attribute decision making. Soft Comput. 2018, 22, 989–1002. [Google Scholar] [CrossRef]
- Joshi, R. A novel decision-making method using R-Norm concept and VIKOR approach under picture fuzzy environment. Expert Syst. Appl. 2020, 147, 113228. [Google Scholar] [CrossRef]
- Jana, C.; Senapati, T.; Pal, M.; Yager, R.R. Picture fuzzy Dombi aggregation operators: Application to MADM process. Appl. Soft Comput. 2019, 74, 99–109. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Fundam. Inform. 2018, 157, 271–320. [Google Scholar] [CrossRef]
- Jana, C.; Pal, M. Assessment of enterprise performance based on picture fuzzy hamacher aggregation operators. Symmetry 2019, 11, 75. [Google Scholar] [CrossRef]
- Harish, G. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Shahzaib, A.; Tahir, M.; Saleem, A.; Qaisar, K. Different approaches to multi-criteria group decision making problems for picture fuzzy environment. Bull. New Ser. Am. Math Soc. 2018, 1–25. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhou, X.Q.; Tu, H.N.; Tao, S.D. Some geometric aggregation operators based on picture fuzzy sets and their application in multiple attribute decision making. Ital. J. Pure Appl. Math. 2017, 37, 477–492. [Google Scholar]
- Yanbing, J.; Dawei, J.; Santibanez, G.E.D.R.; Giannakis, M.; Wang, A. Study of site selection of electric vehicle charging station based on extended GRP method under picture fuzzy environment. Comput. Ind. Eng. 2019, 135, 1271–1285. [Google Scholar] [CrossRef]
- Tian, C.; Peng, J.J.; Zhang, S.; Zhang, W.Y.; Wang, J.Q. Weighted picture fuzzy aggregation operators and their applications to multi-criteria decision-making problems. Comput. Ind. Eng. 2019, 137, 106037. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J.; Gao, H.; Wei, G.W. Methods for MADM with picture fuzzy Muirhead mean operators and their application for evaluating the financial investment risk. Symmetry 2019, 11, 6. [Google Scholar] [CrossRef]
- Xu, Y.; Shang, X.P.; Wang, J.; Zhang, R.T.; Li, W.Z.; Xing, Y.P. A method to multi-attribute decision making with picture fuzzy information based on Muirhead mean. J. Intell. Fuzzy Syst. 2018, 1–17. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Stupnanova, A. Picture fuzzy sets and 3-fuzzy sets. In Proceedings of the 2018 IEEE International Conference Fuzzy Syst, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Kaufmann, A.; Gupta, M.M. Introduction to fuzzy arithmetic: Theory and applications. Math. Comput. 1986, 47, 141–143. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Deschrijiver, G.; Kerre, E.E. Implicators based on binary aggregation operators in interval-valued fuzzy set theory. Fuzzy Sets Syst. 2005, 153, 229–248. [Google Scholar] [CrossRef]
- Kolesárová, A. Limit properties of quasi-arithmetic means. Fuzzy Sets Syst. 2001, 124, 65–71. [Google Scholar] [CrossRef]
- Chen, S.M.; Tan, J.M. Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Chen, S.M.; Chang, C.H. Fuzzy multiattribute decision making based on transformation techniques of intuitionistic fuzzy values and intuitionistic fuzzy geometric averaging operators. Inform. Sci. 2016, 133–149. [Google Scholar] [CrossRef]
- Xu, Z.S. An overview of methods for determining OWA weights. Int. J. Intell. Syst. 2005, 20, 843–865. [Google Scholar] [CrossRef]
- Khan, M.J.B.; Kumam, P.; Deebani, W.; Kumam, W.; Shah, Z. Bi-parametric distance and similarity measures of picture fuzzy sets and their applications in medical diagnosis. Egypt. Inform. J. 2020. [Google Scholar] [CrossRef]
| References | Aggregation Operators |
|---|---|
| Jana et al. [21] | |
| Wei [22] | |
| Ashraf et al. [25] | |
| Wang et al. [26] | |
| Wei [31] | |
| PFWG | PFOWG | PFHG | |
|---|---|---|---|
| Jana et al. [21] () | Cannot be calculated | Cannot be calculated | Cannot be calculated |
| Wei [22] () | |||
| Ashraf et al. [25] | |||
| Wang et al. [26] | |||
| Wei [31] | |||
| The proposed |
| References | PFWG | PFOWG | PFHG |
|---|---|---|---|
| Jana et al. [21] | Cannot be calculated | Cannot be calculated | Cannot be calculated |
| Wei [22] | |||
| Ashraf et al. [25] | |||
| Wang et al. [26] | |||
| Wei [31] | |||
| The proposed operator |
| 0.3584 | 0.4457 | 0.3456 | |
| 0.4452 | 0.2232 | 0.3205 | |
| 0.5222 | 0.3005 | 0.4018 | |
| 0.3451 | 0.3404 | 0.2652 | |
| 0.4066 | 0.4047 | 0.3032 |
| Ranking | |
|---|---|
| References | |||
|---|---|---|---|
| Jana et al. [21] | |||
| Wei [22] | |||
| Ashraf et al. [25] | |||
| Wang et al. [26] | |||
| Wei [31] | |||
| The proposed |
| References | Condition 1 | Condition 2 | Condition 3 | Condition 4 |
|---|---|---|---|---|
| Jana et al. [21] | Yes | No Yes | No No No | No |
| Wei [22] | Yes | No Yes | No No No | No |
| Ashraf et al. [25] | Yes | No No | No No No | No |
| Wang et al. [26] | Yes | Yes No | Yes No No | No |
| Wei [31] | Yes | No Yes | No No No | No |
| The proposed operators | Yes | Yes Yes | Yes Yes Yes | Yes |
| Patterns | |||
|---|---|---|---|
| S |
| Patterns | Aggregation Values |
|---|---|
| S |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, M.; Long, H. Picture Fuzzy Geometric Aggregation Operators Based on a Trapezoidal Fuzzy Number and Its Application. Symmetry 2021, 13, 119. https://doi.org/10.3390/sym13010119
Luo M, Long H. Picture Fuzzy Geometric Aggregation Operators Based on a Trapezoidal Fuzzy Number and Its Application. Symmetry. 2021; 13(1):119. https://doi.org/10.3390/sym13010119
Chicago/Turabian StyleLuo, Minxia, and Huifeng Long. 2021. "Picture Fuzzy Geometric Aggregation Operators Based on a Trapezoidal Fuzzy Number and Its Application" Symmetry 13, no. 1: 119. https://doi.org/10.3390/sym13010119
APA StyleLuo, M., & Long, H. (2021). Picture Fuzzy Geometric Aggregation Operators Based on a Trapezoidal Fuzzy Number and Its Application. Symmetry, 13(1), 119. https://doi.org/10.3390/sym13010119





