Multi Body Dynamic Equations of Belt Conveyor and the Reasonable Starting Mode
Abstract
1. Introduction
2. Rigid Finite Element Model of a Conveyor Belt
2.1. Discrete Model of the Conveyor Belt
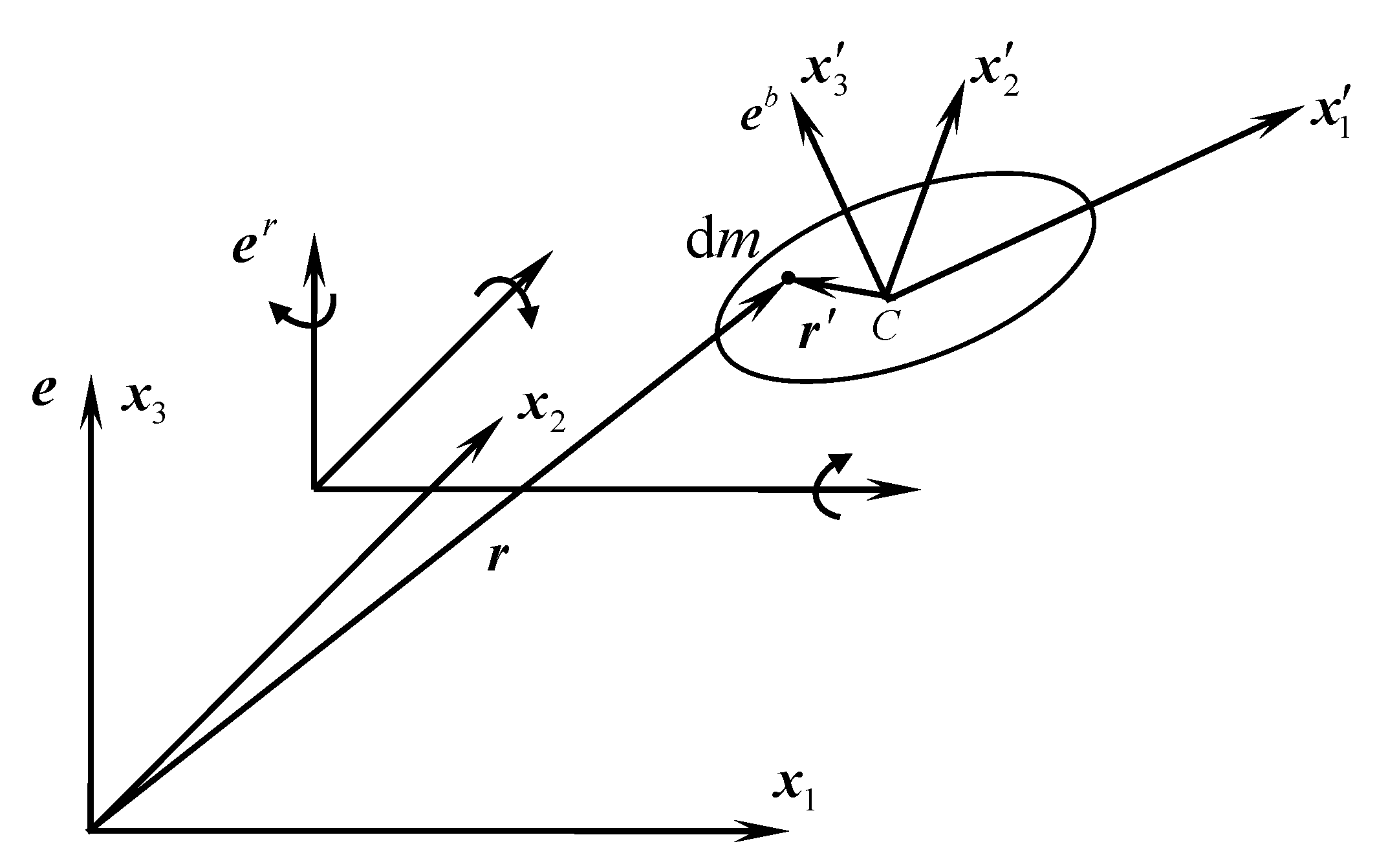
2.2. Coordinate Description
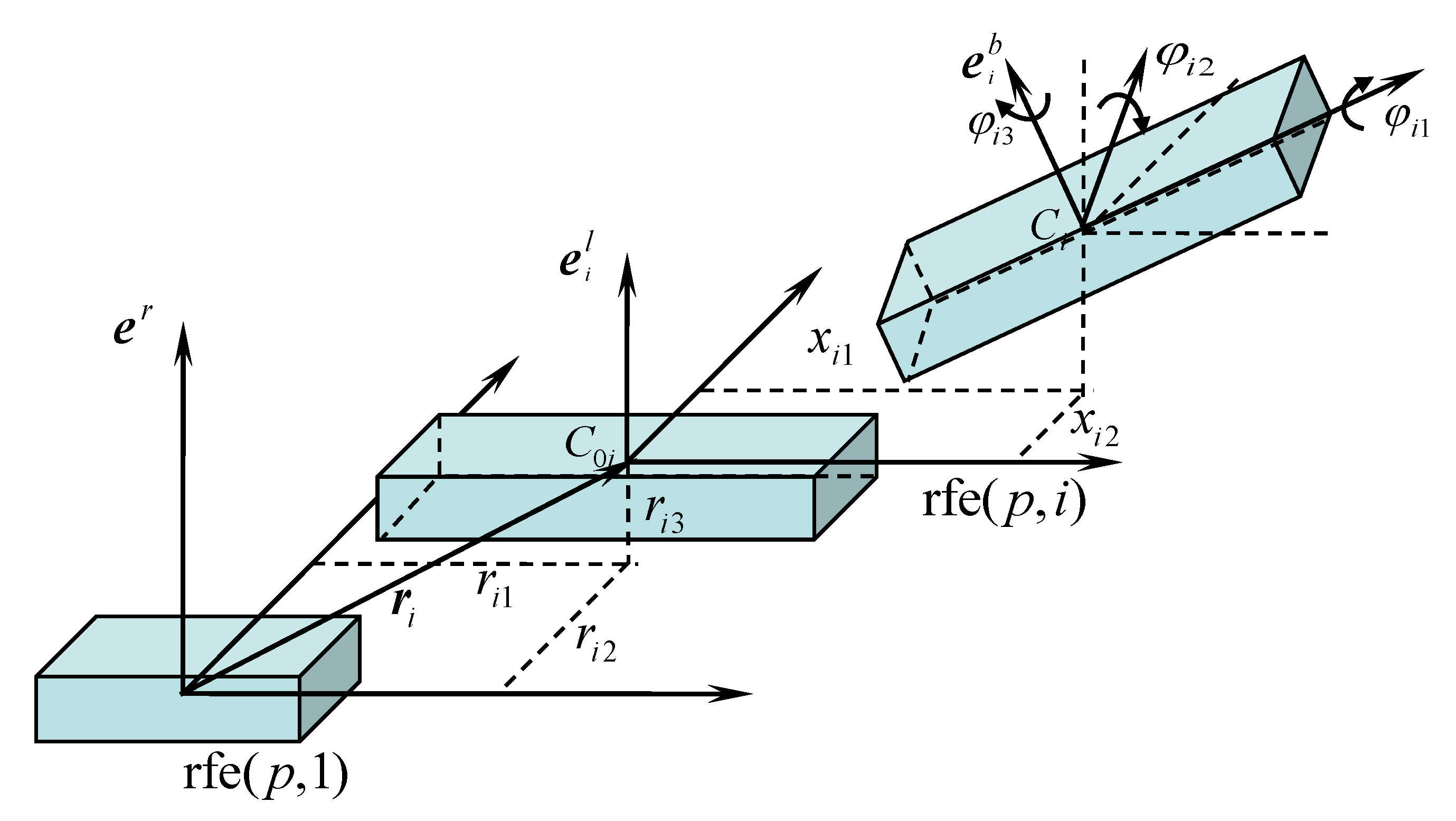
2.2.1. Rigid Finite Element
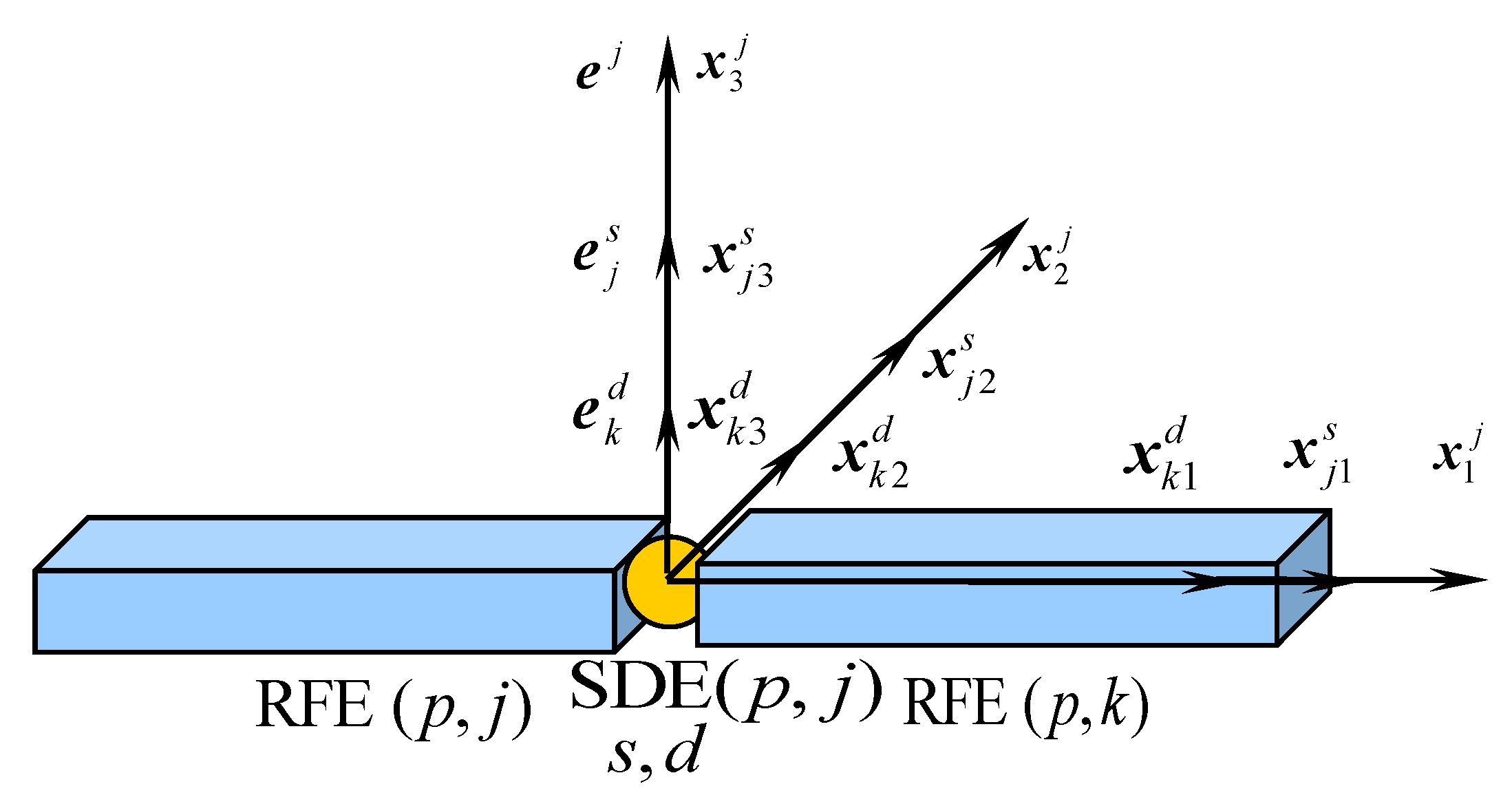
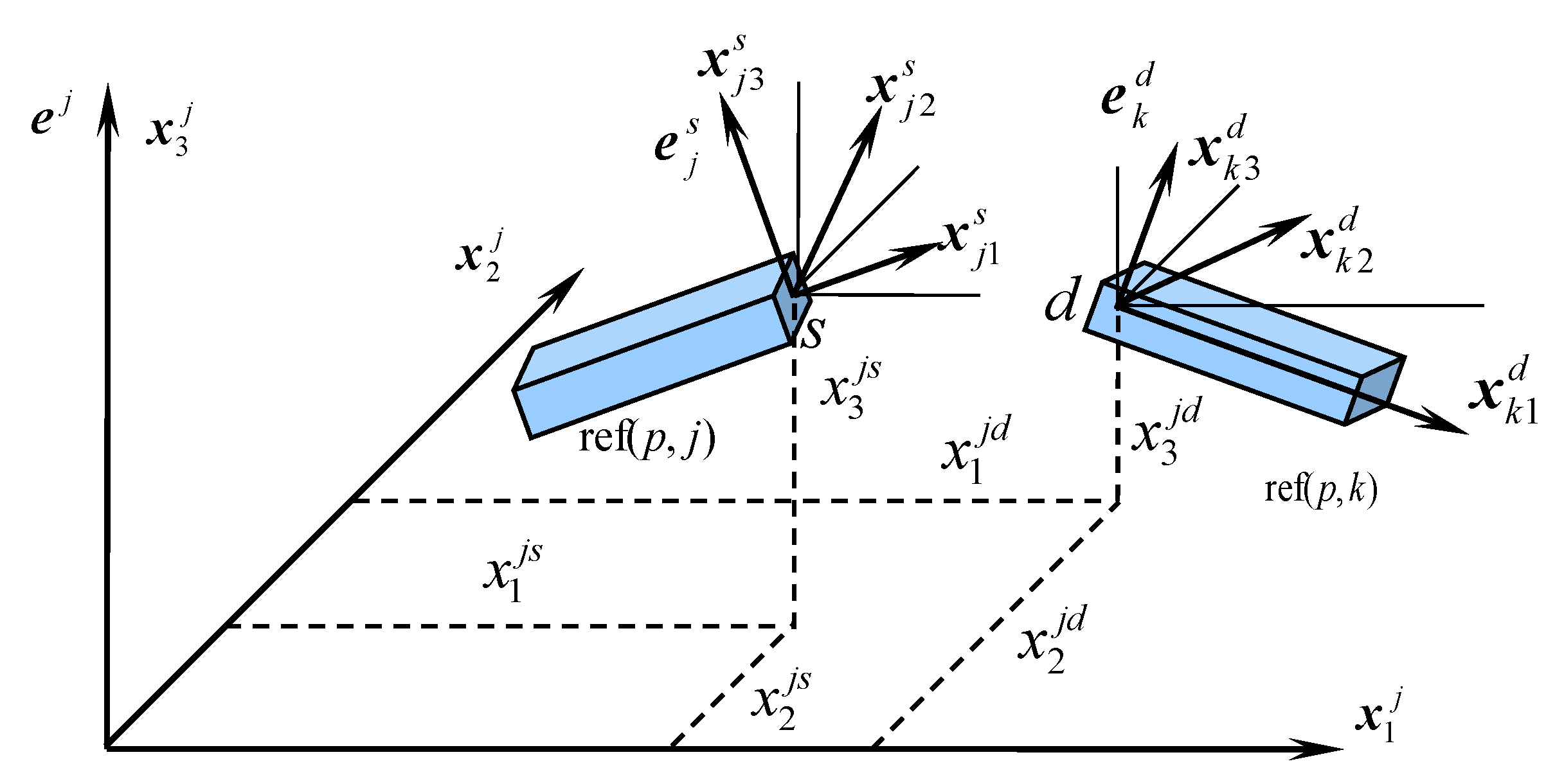
2.2.2. Spring Damping Element (SDE)
2.3. Spring Damping Element Parameters
2.3.1. Potential Energy and Generalized Stiffness Matrix
2.3.2. Coefficients of the Stiffness and Damping
- Each RFE can be simplified into an equal length beam element with a rectangular section shape;
- The deformation mode and velocity of the actual conveyor belt are the same as that of its equivalent SDE;
- The stress of each section in the conveyor belt section is equal, and its mechanical properties can be described by the Voigt model [20]:
2.4. Rigid Finite Element Parameters
2.4.1. Kinetic Energy and Lagrangian Operator
2.4.2. Gravitational Potential Energy and Generalized Force
2.4.3. Elastic Potential Energy
2.5. Multibody Dynamic Equation
2.5.1. Forward Recursive Formulation
2.5.2. Dynamic Equation of the Rigid Flexible Multibody System
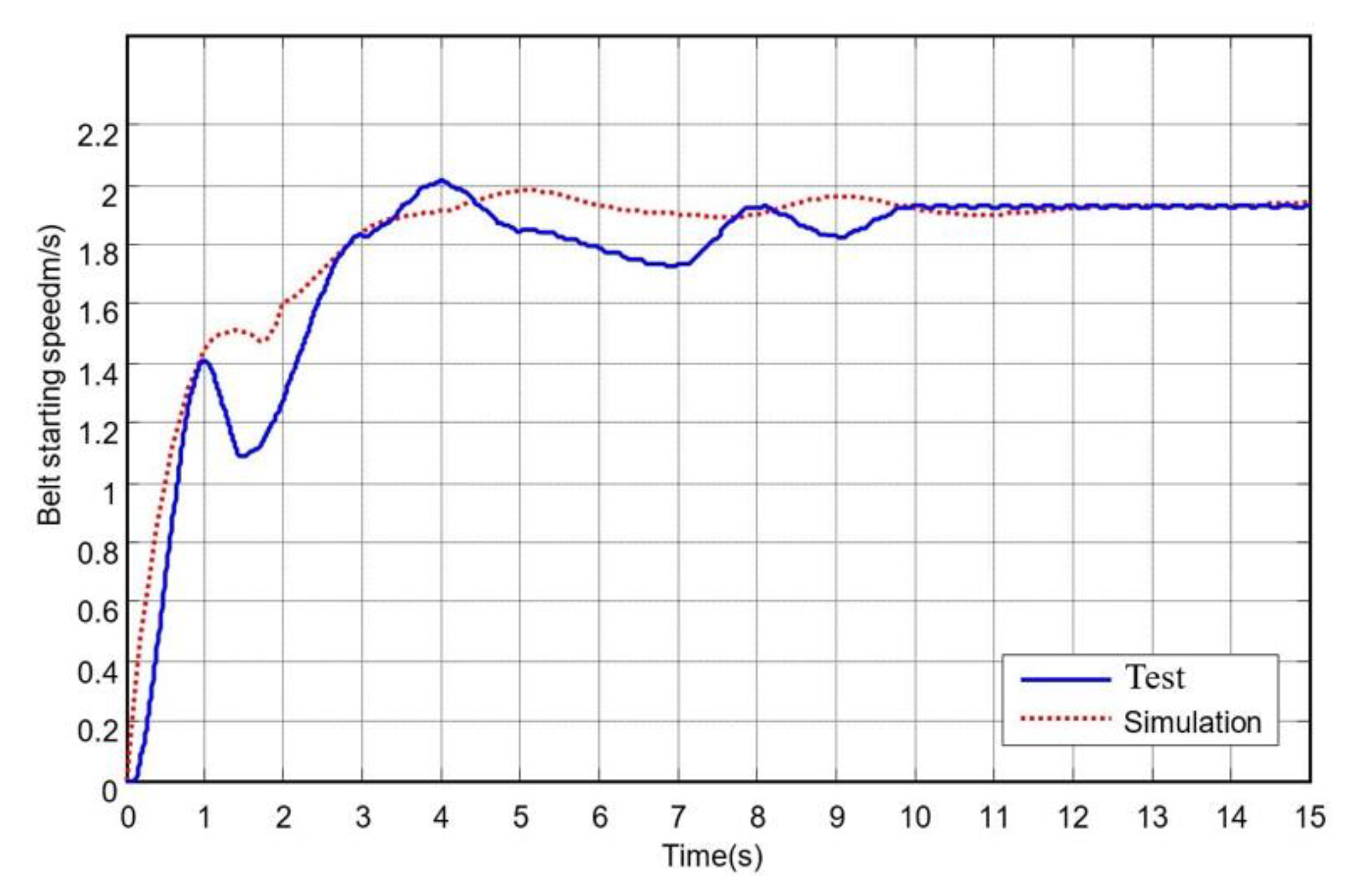
3. Verification of Belt Conveyor Simulation Model
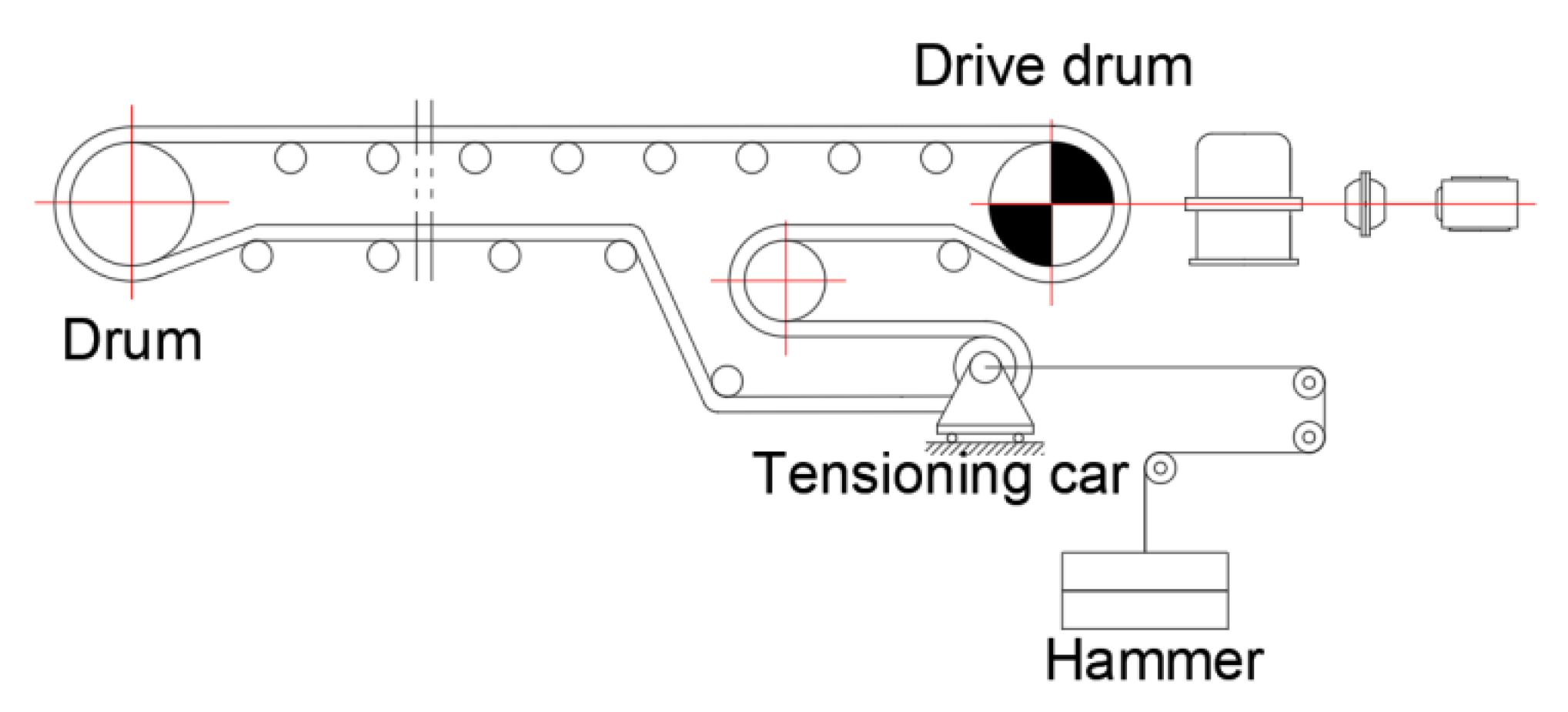
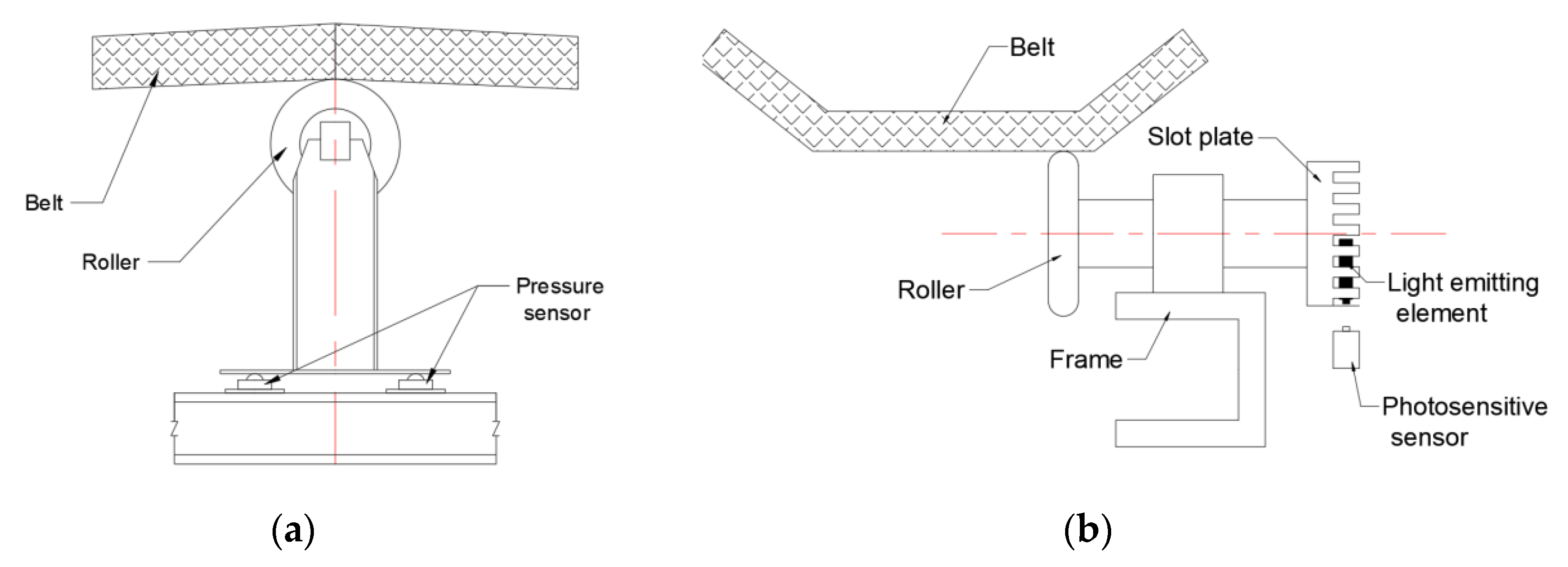
3.1. Field Test
Simulation Model
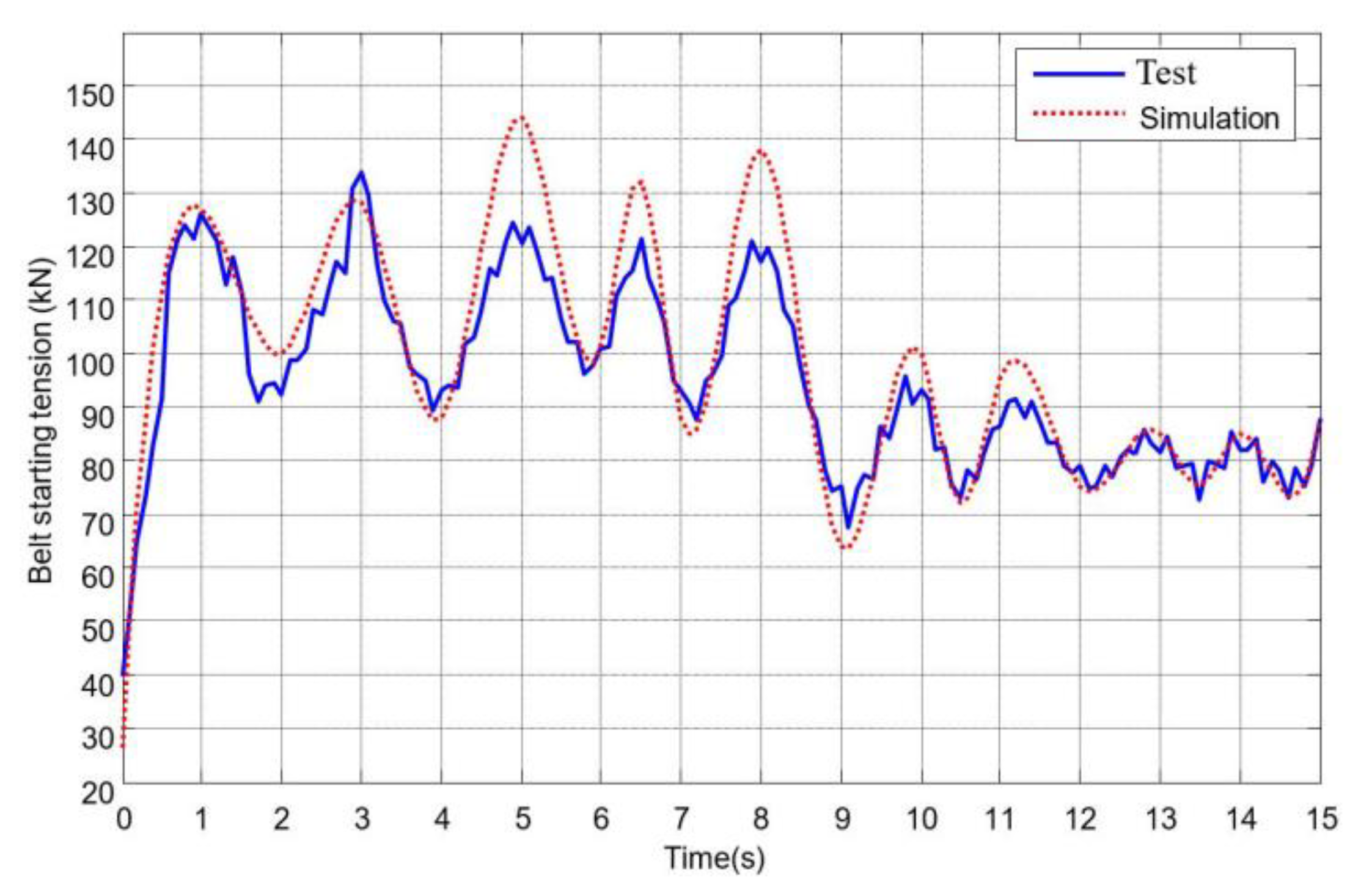
3.2. Verification
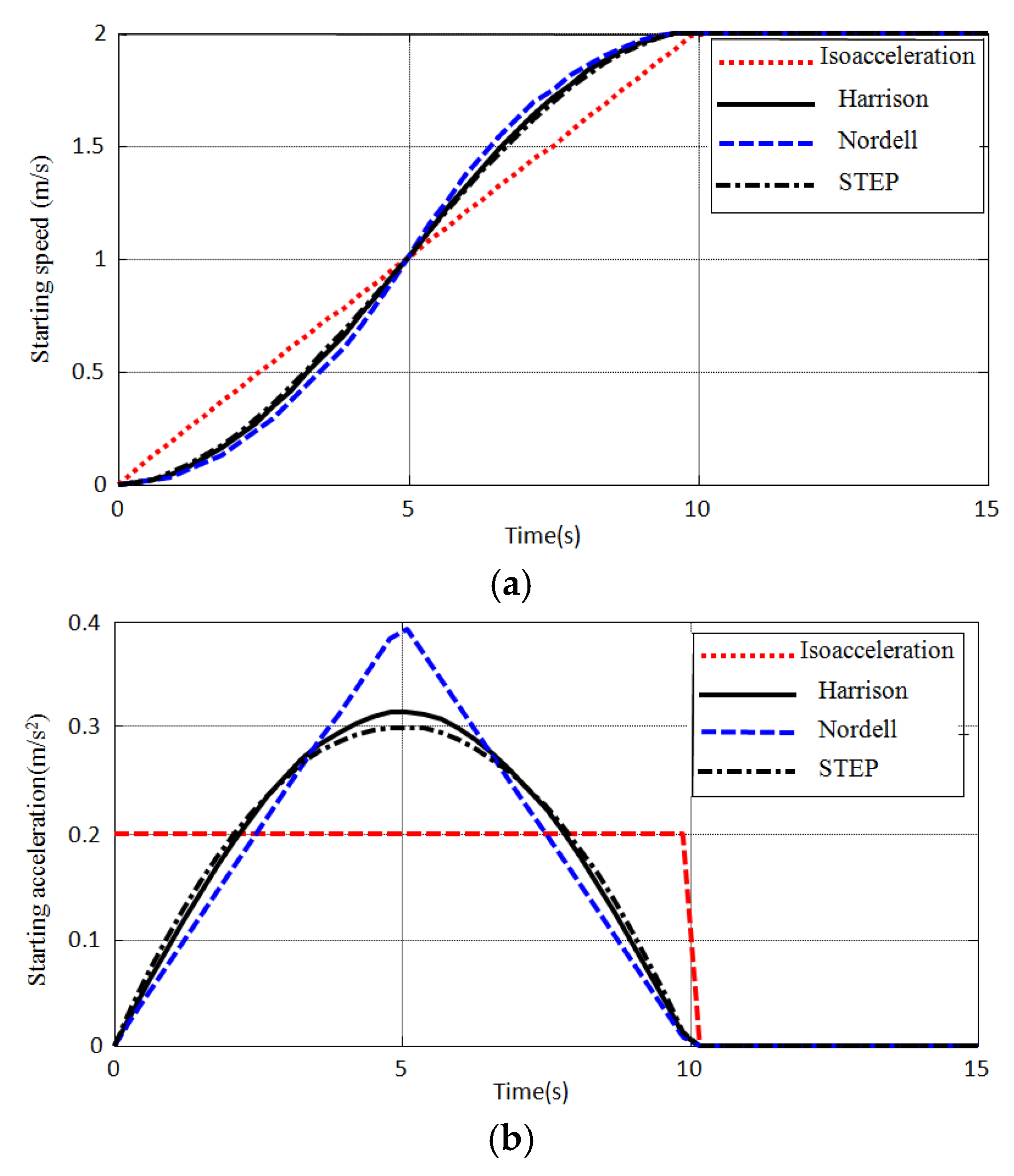
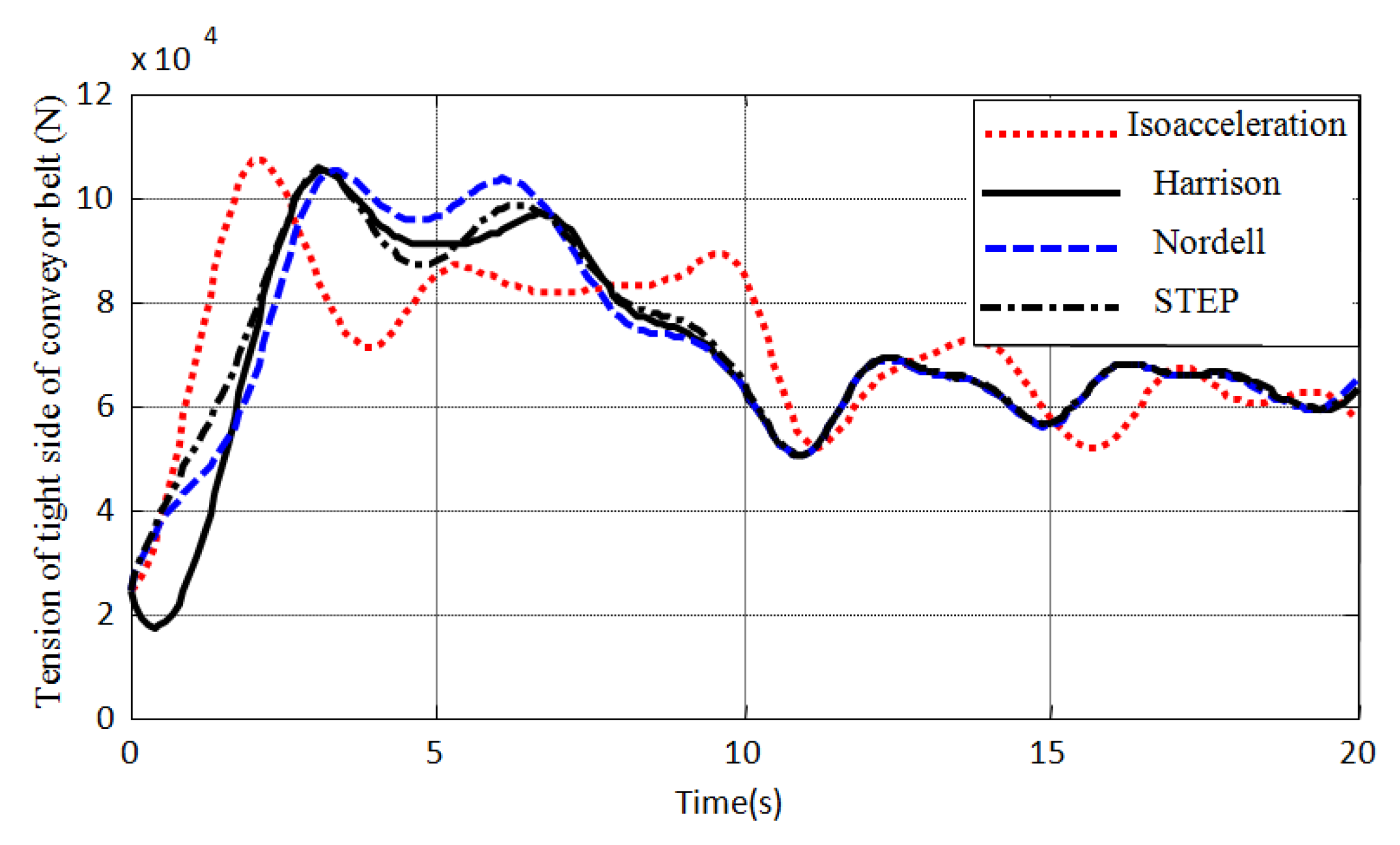
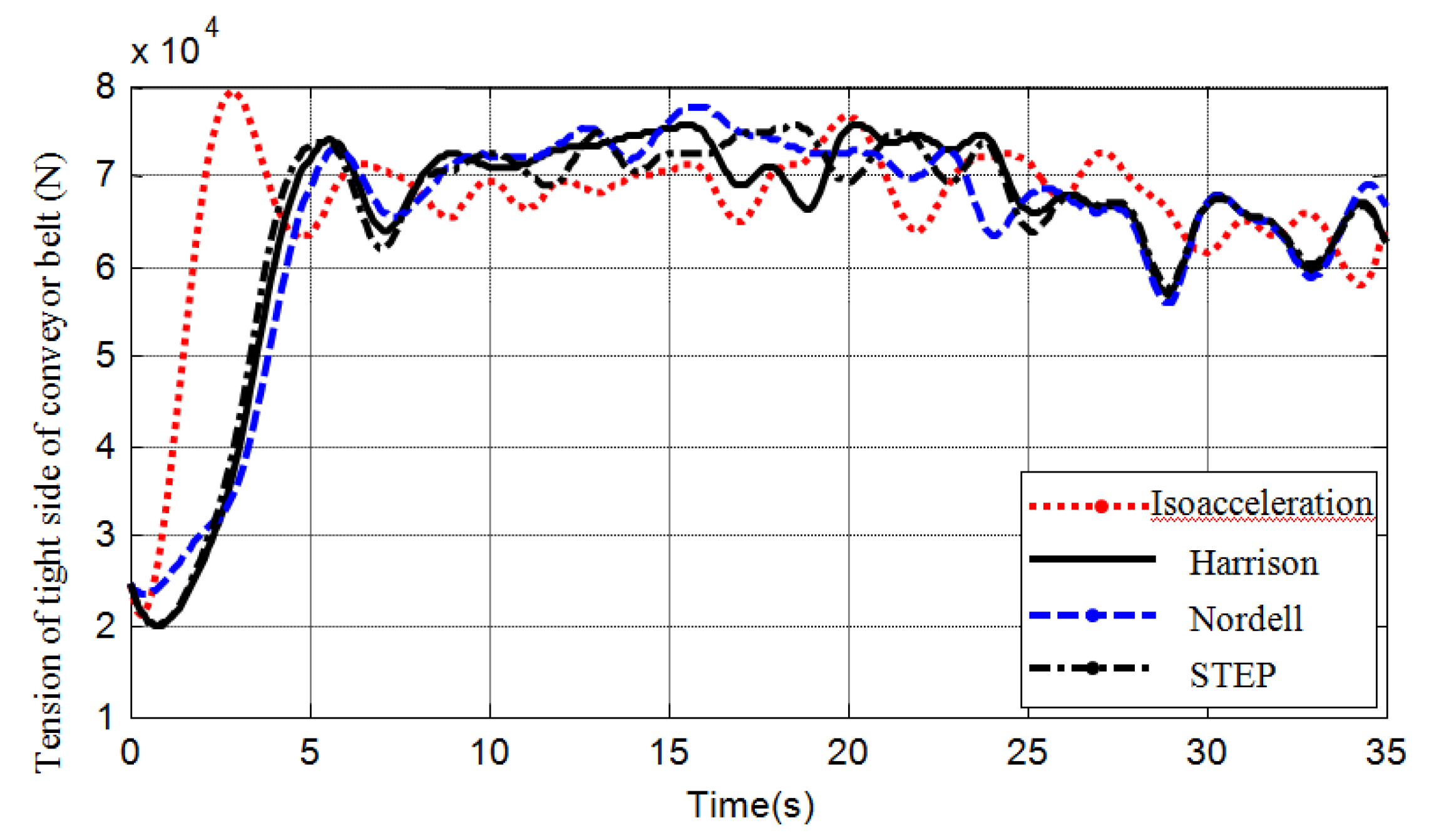
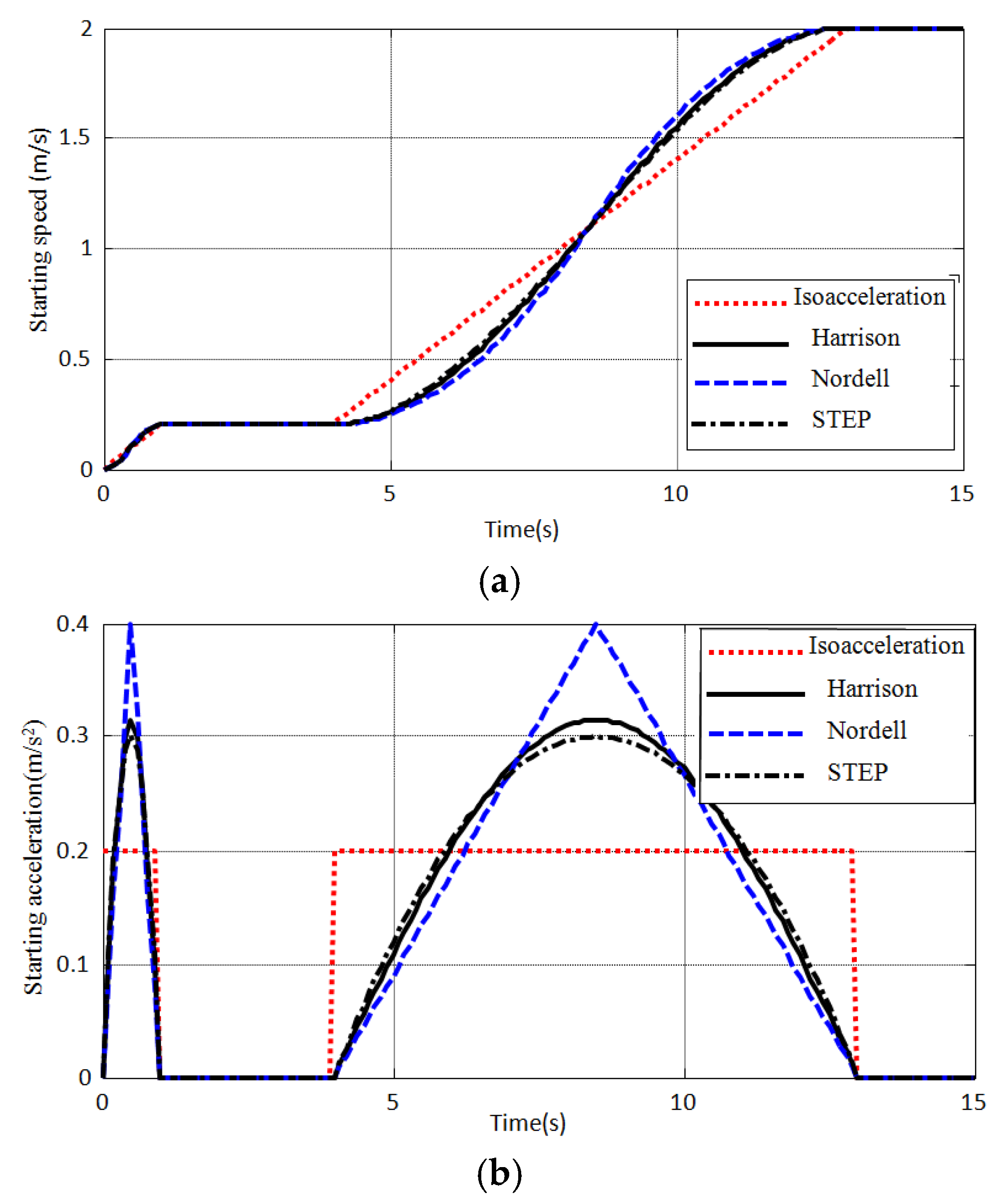
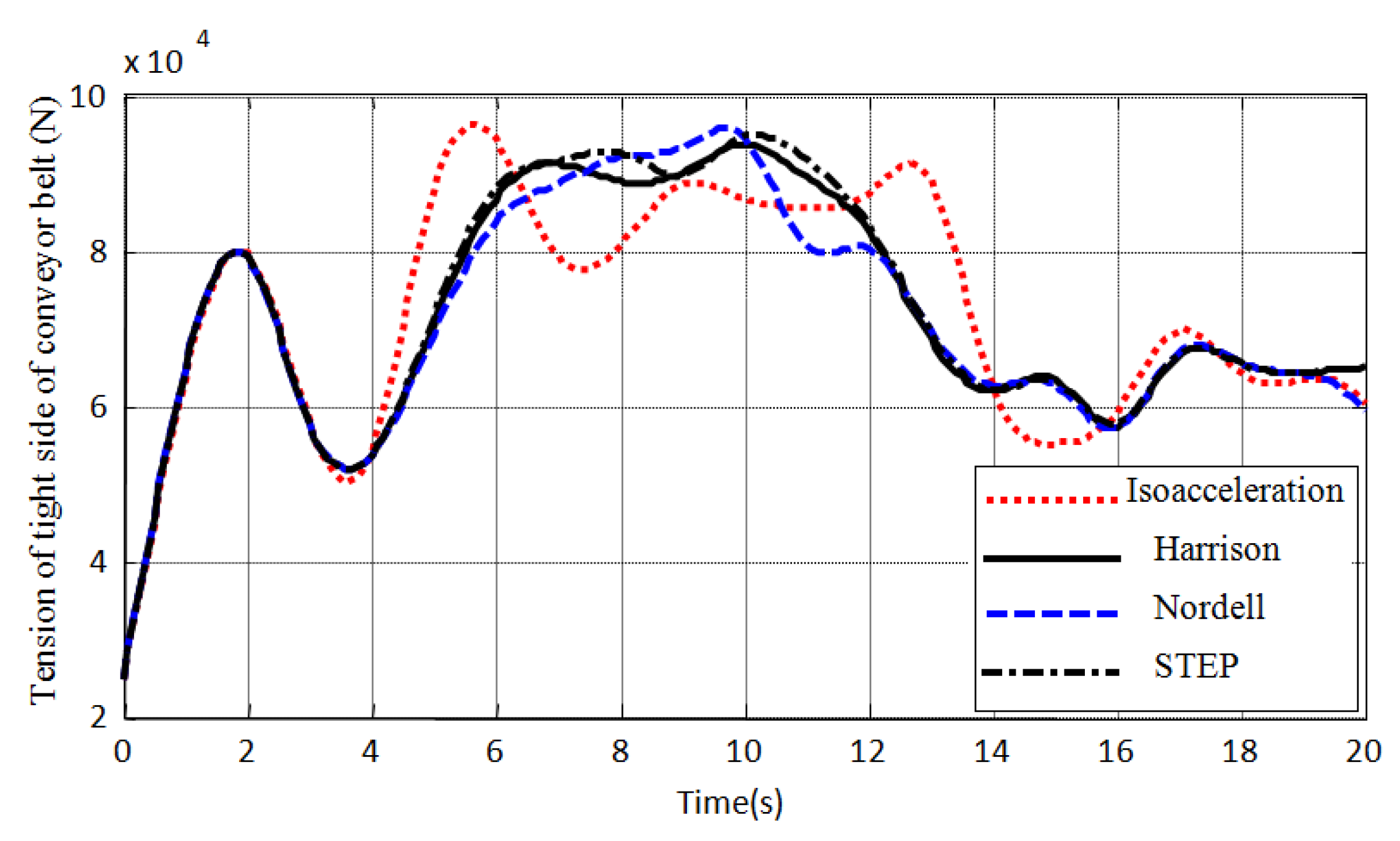
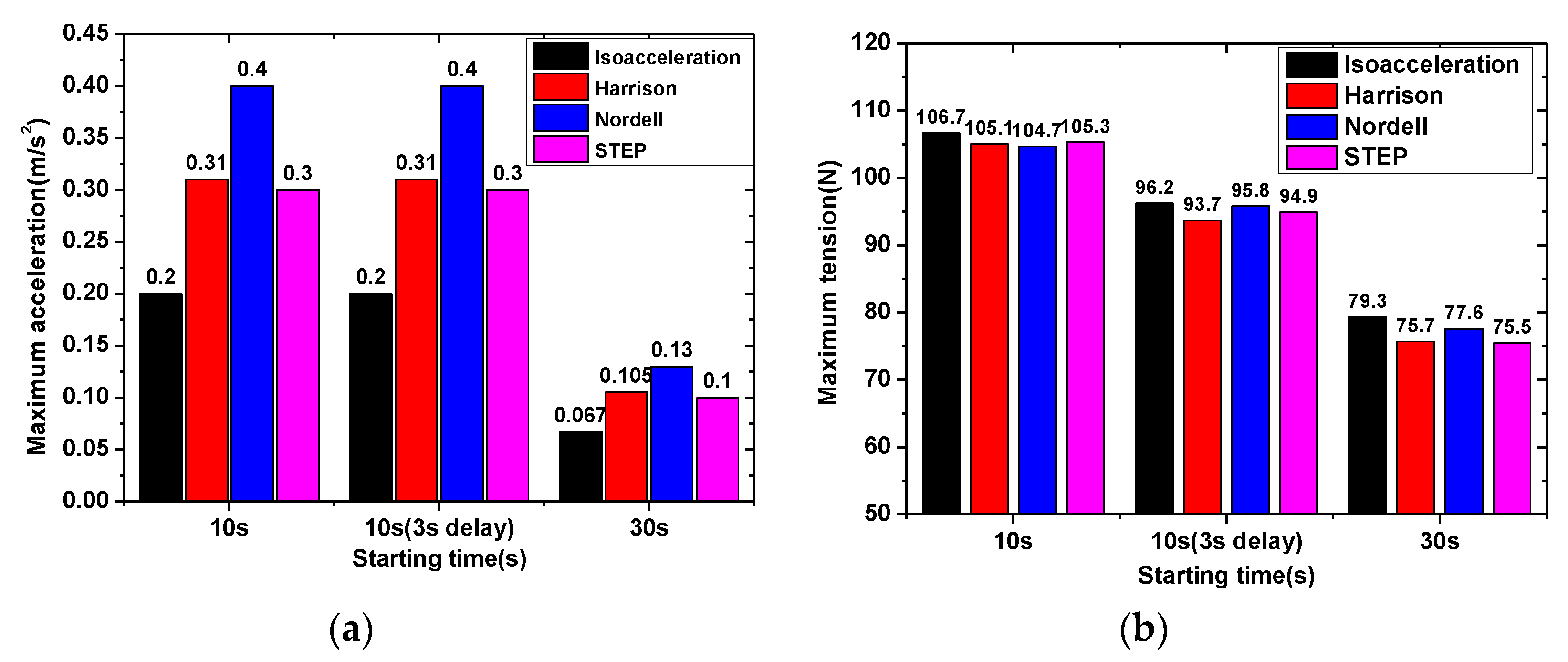
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Bajda, M.; Blazej, R.; Jurdziak, L. Analysis of changes in the length of belt sections and the number of splices in the belt loops on conveyors in an underground mine. Eng. Fail. Anal. 2019, 101, 436–446. [Google Scholar] [CrossRef]
- Fan, J.; Liu, T.; Chen, S. Analysis of dynamical behaviors of a 2-DOF friction-induced oscillator with one-sided impact on a conveyor belt. Nonlinear Dyn. 2019, 97, 797–830. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, M.; Li, G.; Meng, G. Dynamic characteristic analysis and startup optimization design of an intermediate drive belt conveyor with non-uniform load. Sci. Prog. 2019, 103, 39951860. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.H.; Mao, J.; Li, C.L. Study of indentation resistance of conveyor belt. J. China Coal Soc. 2010, 35, 149–153. [Google Scholar]
- Czaplicka, K. Analysis of stress relaxation processes in conveyor belts. Mech. Compos. Mater. 1994, 30, 411–415. [Google Scholar] [CrossRef]
- Li, W.; Xin, Z. Flexural fatigue life prediction of a tooth V-belt made of fiber reinforced rubber. Int. J. Fatigue 2018, 111, 269–277. [Google Scholar] [CrossRef]
- Li, G.; Li, R. Belt Conveyor modeling and performance simulation based on AMESim. In Proceedings of the 2009 Second International Conference on Information and Computing Science, Manchester, UK, 21–22 May 2009. [Google Scholar]
- Kulinowski, P. Analytical method of designing and selecting take-up systems for mining belt conveyors. Arch. Min. Sci. 2013, 58, 1301–1315. [Google Scholar]
- Kulinowski, P. Simulation method of designing and selecting tensioning systems for mining belt conveyors. Arch. Min. Sci. 2014, 59, 123–138. [Google Scholar] [CrossRef]
- Schulz, G. Comparison of drives for long belt conveyors. Bulk Solids Handl. 1995, 15, 247–251. [Google Scholar]
- Carretero, L.; Valero, J. Existence of periodic solutions for a scalar differential equation modelling optical conveyor belts. J. Math. Anal. Appl. 2019, 480, 123385. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Q. A regression model for prediction of idler rotational resistance on belt conveyor. Meas. Control 2019, 52, 441–448. [Google Scholar] [CrossRef]
- Munzenberger, P.J.; OShea, J.I.; Wheeler, C.A. A comparison of rubber stress relaxation models for conveyor belt indentation rolling resistance calculations. Int. J. Mech. Mater. Des. 2019, 15, 213–224. [Google Scholar] [CrossRef]
- Li, J.; Pang, X. Belt Conveyor Dynamic Characteristics and Influential Factors. Shock Vib. 2018, 8106879. Available online: https://doi.org/10.1155/2018/8106879 (accessed on 12 August 2020).
- Suweken, G.; Van Horssen, W.T. On the transversal vibrations of a conveyor belt with a low and time-varying velocity. Part II: The beam-like case. J. Sound Vib. 2003, 267, 1007–1027. [Google Scholar] [CrossRef]
- Shen, J.; Wheeler, C.; O’Shea, J.; Ilic, D. Investigation of the dynamic deflection of conveyor belts via experimental and modelling methods. Measurement 2018, 127, 210–220. [Google Scholar] [CrossRef]
- Ilic, D.; Wheeler, C. Measurement and simulation of the bulk solid load on a conveyor belt during transportation. Powder Technol. 2017, 307, 190–202. [Google Scholar] [CrossRef]
- Woźniak, D. Laboratory tests of indentation rolling resistance of conveyor belts. Measurement 2020, 150, 107065. [Google Scholar] [CrossRef]
- Wittbrodt, E.; Adamiec-Wójcik, I.; Wojciech, S. Dynamics of Flexible Multibody Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hou, Y.F.; Meng, Q.R. Dynamic characteristics of conveyor belts. J. China Univ. Min. Technol. 2008, 18, 629–633. [Google Scholar] [CrossRef]
- Gaull, A. A rigorous proof for the equivalence of the projective Newton–Euler equations and the Lagrange equations of second kind for spatial rigid multibody systems. Multibody Syst. Dyn. 2019, 45, 87–103. [Google Scholar] [CrossRef]
- Wang, F.S. Research on flexible multibody dynamics modeling of conveyor belt. Mech. Transm. 2018, 042, 43–46. [Google Scholar]
- Wang, F.S.; Jiang, H.Q. Analysis for boundary element of sag resistance of belt conveyer. Hoisting Conveying Mach. 2014, 45, 97–100. [Google Scholar]
- Wang, F.S.; Hou, Y.F. Analysis on contact problem of rigid cylinder with viscoelastic foundation. J. Mach. Des. 2010, 27, 15–17. [Google Scholar]
- Hunter, S.C. The rolling contact of a rigid cylinder with a viscoelastic half space. J. Appl. Mech. 1961, 28, 611. [Google Scholar] [CrossRef]
- Mao, J.; Shi, J.G.; Zhang, D.S. Starting characteristics and controllable starting technology of belt conveyor. Min. Process. Equip. 2004, 2, 19–22. [Google Scholar]
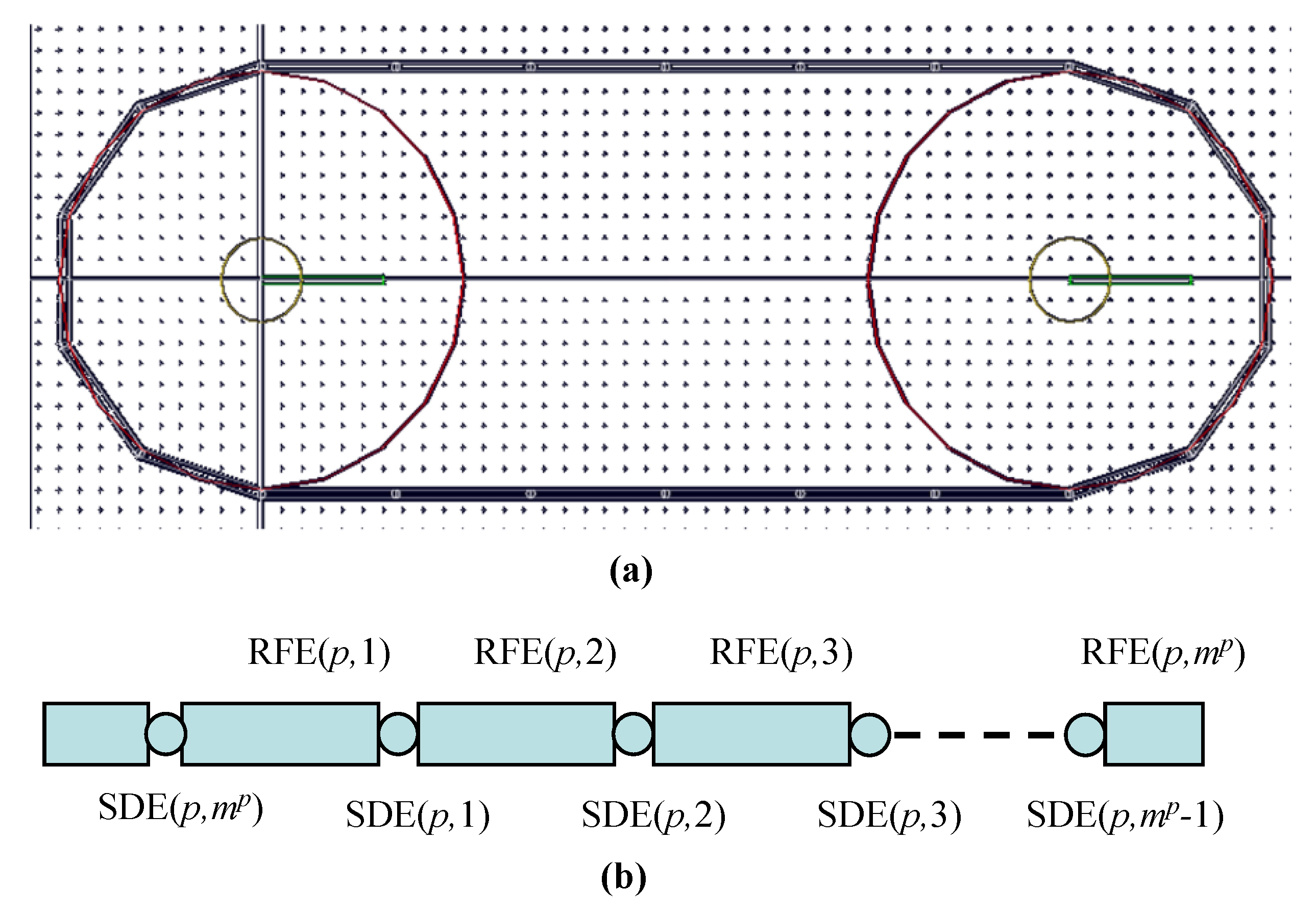

| Performance parameter | Transportation distance: 972 m Transportation capacity: 400 t/h Belt speed: 2 m/s |
| Driving device | Rated power of motor: 150 KW Rated speed: 1000 rpm Diameter of driving drum: 0.8 m Drum mass: 800 kg |
| Conveyor belt | Tensile strength: 1250 N/m Belt width: 1 m Mass per unit length of conveyor belt: 24.5 kg/m |
| Conveying materials | 56 kg/m |
| Model parameters and running resistance | Length of belt section: 314.23 mm Number of belt sections: 170 System degree of freedom: 309 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Wang, F. Multi Body Dynamic Equations of Belt Conveyor and the Reasonable Starting Mode. Symmetry 2020, 12, 1489. https://doi.org/10.3390/sym12091489
Guo Y, Wang F. Multi Body Dynamic Equations of Belt Conveyor and the Reasonable Starting Mode. Symmetry. 2020; 12(9):1489. https://doi.org/10.3390/sym12091489
Chicago/Turabian StyleGuo, Yongbo, and Fansheng Wang. 2020. "Multi Body Dynamic Equations of Belt Conveyor and the Reasonable Starting Mode" Symmetry 12, no. 9: 1489. https://doi.org/10.3390/sym12091489
APA StyleGuo, Y., & Wang, F. (2020). Multi Body Dynamic Equations of Belt Conveyor and the Reasonable Starting Mode. Symmetry, 12(9), 1489. https://doi.org/10.3390/sym12091489





