Multi-Stage Quantum Secure Direct Communication Using Secure Shared Authentication Key

Abstract

The security of Quantum Secure Direct Communication (QSDC) and its authentication procedure based on multiple stages is analyzed. The security analysis shows that the process of authentication is required to be done three times based on the usage of unitary transformation that is only known between Alice and Bob. In the proposed protocol, a secure quantum handshake is utilized to share the secret polarization angle and an authentication key at the initial stage of authentication over the quantum channel. The symmetry key is used in this work to protect user data communication within the QSDC protocol, where the same secret key is used to encrypt and decrypt the message. This work adopts the information travel time (ITT) by allowing the sender to detect any interference from third parties. In addition, the operation of the Pauli-X quantum gate increases Eve’s difficulty in stealing the information. The information transmitted is then continued by sending photons once in the quantum channel, which improves the efficiency without losing the message’s security. In addition, to securely transfer the stream of messages, the proposed protocol is operated in single-stage, and the authentication is applied bit-by-bit, thus reducing the transmission time. Security checks are carried out along the data transmission process. Compared to previous protocols, this new initial authentication protocol has remarkable advantages since it does not require public communication to pre-share the authentication key and secret angles before the onset of the transmission, therefore, reducing the communication cost. Moreover, the secret authentication key and polarization angles are updated after a number of bits are sent to increase the security level. The verification process is also conducted to ensure the symmetry of the sender and receiver. The analyses presented herein demonstrate that the proposed authentication protocol is simple and secure in order to ensure the legitimacy of the users.

1. Introduction

Quantum Secure Direct Communication (QSDC) protocol is one of the quantum cryptography concepts that securely transmits the message directly in the quantum channel, where all the information deals with the quantum state. QSDC promotes a high level of protocol security by instantly transmitting the message directly to the quantum channel. Long and Liu introduced the first QSDC protocol in 2002, which securely and directly transmitted the secret message without using a key in advanced [1]. The modified version of the basic QSDC protocol has been introduced, which are (Einstein–Podolsky–Rosen) EPR QSDC [2] and single-photon QSDC. EPR QSDC utilized the block of EPR pairs as carriers to directly transmit information, while single photon QSDC combined a one-time pad protocol with the secret message [3].

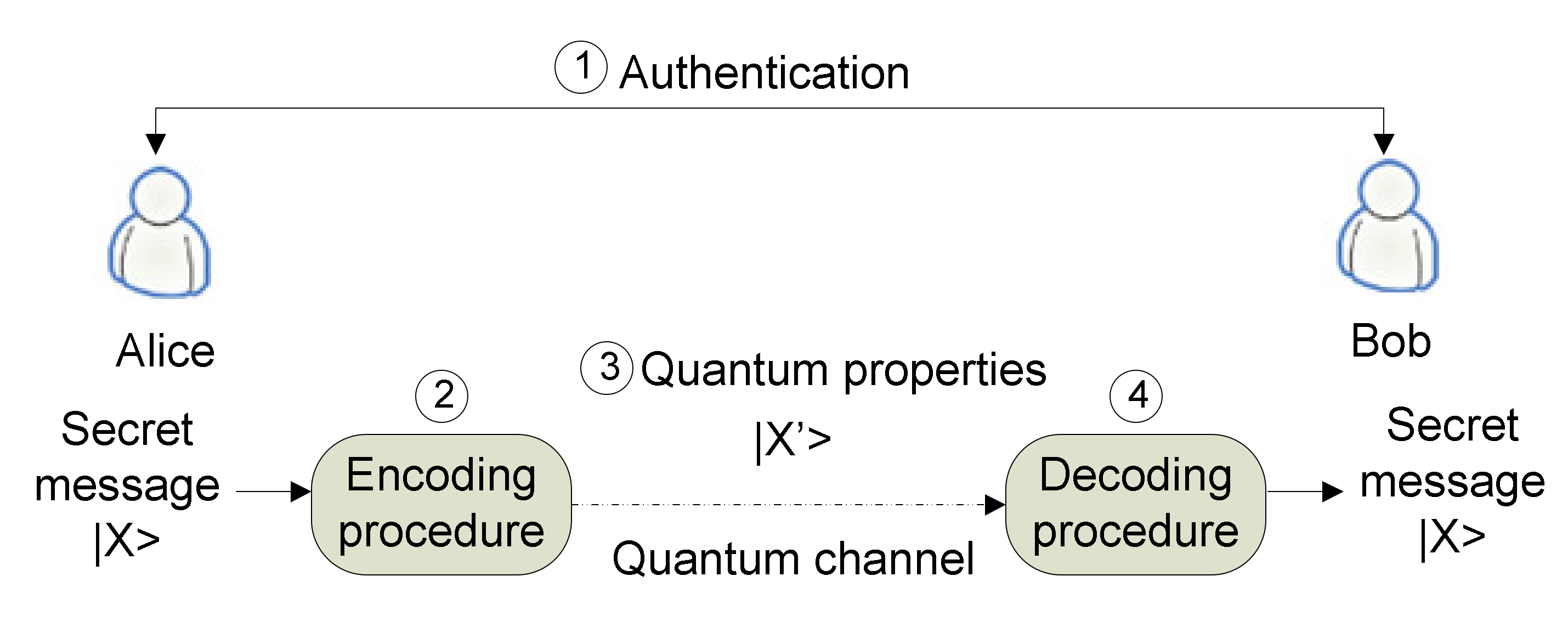
The security requirement in QSDC is stricter compared to Quantum Key Distribution (QKD) since an eavesdropper must not uncover the transmitted messages. Like QKD, QSDC is divided into three approaches: Quantum entanglement [4], single-photon [5,6], and multiple photons [7]. All of the QSDC protocols consist of four parts: Authentication, encoding, the transformation of quantum properties, and decoding, as illustrated in Figure 1. QSDC starts with the authentication process to verify the identity of Alice and Bob. After the successful authentication process, Alice embeds the sensitive information using the proposed QSDC encoding procedure and sends the secret message over the quantum channel. To encode the information, various properties of photons can be employed such as phase, polarization, EPR quantum correlation pairs, wavelength, or quadrature components of squeezed state of light [8]. Bob will then retrieve the contents of the secret message through the proposed decoding process.

One of the biggest limitations of QSDC is the low transfer rate in the long-distance quantum channel [7,9]. To overcome this limitation, a concept of multi-photon was proposed by Subhash Kak [10], namely the three-stage protocol that can directly share the message over the multi-stages of the quantum channel using a rotational change in polarization. The multi-photon provides security features without the involvement of the key distribution step, and no entanglement is required. In the multi-photon protocol, photons act as the carrier to carry the quantum information by polarizing their quantum properties, i.e., |$0⟩$ and |$1⟩$.

Given the advantages of multi-photon QSDC, it remains a challenge to enforce QSDC authentication on behalf of each entity. Throughout quantum communication, a good authentication component is essential to ensure the legitimacy of users. Moreover, the participants in the communication must be authenticated to secure the transmitted message from the man-in-the-middle (MITM) attack [11,12]. The problem of today’s authentication is the complex environment of networks. A network administrator, therefore, finds it very difficult to apply a consistent set of authentication, quality of service, and security schemes that are safe from security breaches and comply with regulations [13].

Unlike our previous work [14] that focused on increasing the transmission rates by reducing the transmission time in multi-photon over multi-stage protocol, here, the issue of authentication is focused. The aim of this paper is, therefore, to recommend a secure way to share the initial secret angle and authentication key between users over a multi-stage quantum channel. In this work, the symmetry key is applied to secure the user’s data communications in QSDC protocol, where the same secret key is used to encrypt and decrypt the message. Therefore, the secret key must be exchanged securely over the communication channel, thus that the sender and receiver are symmetry on both sides. To solve the problem of initial communication in the authentication phase, a quantum handshake protocol is proposed to share Alice’s secret angle and the authentication key [15]. In addition, an update function of the secret angle and the authentication key is proposed based on a mutually agreed algorithm. The proposed protocol in this paper sends multi-photon over the single-stage and implements bit-by-bit authentication to defend against a MITM attack. It should be noted that Alice is a trusted party that does not mislead the information. This protocol will significantly improve the existing multi-photon works of references [7,9] that need to share the secret angle at the onset of the transmission over the secret channel. This protocol significantly improves communication efficiency without losing security. The main contributions of this work are as follows:

(1)

The secret angle and authentication key are generated by Alice, and no third party is involved in the process to enhance the confidentiality of the communication. Thus, no pre-shared authentication key and initial secret angle are exchanged between Alice and Bob at the onset of the communication, which occurs in public channels.

(2)

The secret angles and the authentication key are updated using a mutually agreed algorithm after a number of bits sent to increase the security level.

(3)

The QSDC protocol is operated in single-stage, and the authentication is applied bit-by-bit, thus reducing the transmission time, and the security check is done along with the data transmission process.

The remainder of this paper is organized as follows. In Section 2, the importance of the authentication procedure in QSDC is discussed. Related works are presented in Section 3, while Section 4 presents the secure shared authentication key protocol. Section 5 shows the example of the proposed protocol. Section 6 discusses the performance analysis, while Section 7 provides the implementation issues of the proposed protocol. Finally, the conclusion of this paper is summarized in Section 8.

2. The Importance of Authentication for QSDC

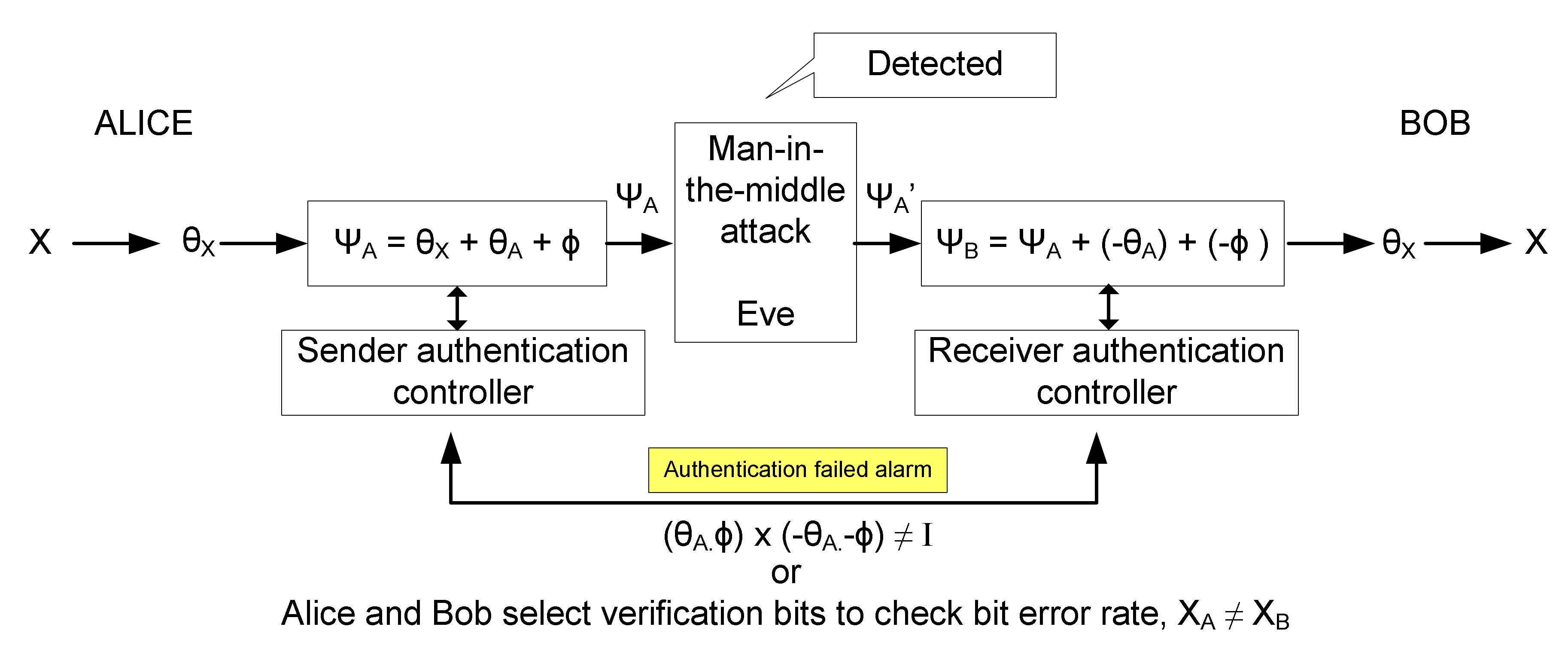
The authentication procedure is significant to avoid the legitimate parties’ identities being impersonated by an eavesdropper that contributes to the leak of secret messages. In order to avoid eavesdroppers’ attacks, existing quantum cryptography protocols typically require a third-party authentication for Alice and Bob to initiate the communication. However, some drawbacks may occur when a third party is involved in the communication. Third-party authentication is typically based on the classical cryptography assumptions that utilize computational complexity. Another problem noted is Eve can still attack the quantum communication channels after Alice and Bob are authenticated to circumvent the third party authentication, leaving such attack undetected as revealed in reference [16]. This type of attack is called the Intercept-Resend attack, which will be discussed later in this paper.

Thus, to overcome the aforementioned problem, the authentication process should be performed during the quantum data communication process. It is important to ensure that the parties involved in the protocol are whom they are supposed to be; this is what we call identity authentication. In addition, the data origin authentication can be done on a bit-by-bit basis to eliminate the possibility that Eve attacks the quantum channel after Alice and Bob are authenticated. This step is important to ensure that the data originate from the right sender and is received by the right receiver. The important part of the authentication is to share the authentication key between Alice and Bob to allow the recognition process [16]. The authentication key is important to avoid a MITM attack launched by Eve, who is pretending to be Alice and Bob at the same time. The authentication key must not be revealed to Eve and needs to be shared secretly between Alice and Bob before the process of authentication has started. This process is done in the initial part of the authentication by sharing the sender’s secret angle and the authentication key since pre-shared is not suitable to be adapted because it deals with the public channel.

In quantum communication, it is essential to reduce the level of complexity and, at the same time, maintain the security of the system against eavesdropping attacks. However, a direct link between Alice and Bob will significantly be affected where an eavesdropper can overhear, jam, or spoof the communication between them [17]. Recent work by [18] showed that an eavesdropper might span into multiple smart attackers that can overhear the secure message depending on their location between the transmitter and the receiver. In addition, the investigation by reference [19] proved that an attacker might use several transmitter antennas to increase the attack rate. It can be concluded that the eavesdroppers can utilize various types of attacks to intercept secret messages. Thus, the improvement of data and transmission secrecy is an urgent issue to be solved in the communication area.

3. Related Works

In the last few years, several authentication protocols for multiphoton QSDC have been proposed. The main objective of those approaches was to ensure that the messages are delivered securely to the legitimate parties. This section reviews several multiphoton QSDC’s authentication approaches over multi-stage to validate the parties involved in quantum communication, discussing their basic concepts, and describing their advantages and drawbacks.

In reference [20], a single-stage protocol was proposed to transmit the photon in a stage using secret unitary transformation. The security strength of this protocol relies on the secret value of the polarization angle, θ, and it must be secret along with the communication between Alice and Bob. Otherwise, the security of this protocol cannot be compromised anymore when the eavesdropper is able to get the value of θ. This protocol assumes that there is another protocol operated, such as a trusted certificate exchanged before the secure transmission begins. The authors in [9] presented a secure quantum communication over a single-stage, hereafter called it a Braided Single Stage protocol. The idea of Braided Single Stage protocol is to overcome the drawback of the three-stage protocol by reducing the overhead to encode the photons. Later, the IV Three-stage protocol [7] was proposed based on the adoption of an Initialization Vector (IV) to be a one-time pad key as the extra dimension of security for the three-stage protocol.

All of the mentioned approaches utilized the three-stage protocol to handle the authentication process in the first phase by sharing the initial value of secret polarization angle $\theta$ (e.g., 0°, 25°, 50°, …, 180°) that is predetermined among users. The set is usually exchanged via a secret channel [21,22] over the public channel or using face to face communication. However, the technique of exchanging the secret angle is omitted. Besides, the reviewed multi-photon approaches only assumed that the sender and receiver to be mutually trusted parties, and they are already authenticated to each other [7,23]. The usage of the authentication key that is only known by legal parties is able to provide secrecy in the authentication of QSDC [16,24,25]. Hence, combining the unitary transformation with the authentication key has become an appropriate strategy to construct high-level security of the cryptographic protocol. Therefore, an important question in this research is how to share the secret angle and authentication key securely in the quantum channel? Most of the authentication schemes are based on pre-shared secret information, which is not so practical for the initial communication of trusted parties [15]. To mitigate these issues, a secure shared authentication key (SSAK) is proposed in this paper. The SSAK protocol shares the secret angle and authentication key using the quantum handshake mechanism. The main objective of the proposed SSAK protocol is to improve the efficiency of authentication and reduce the communication cost by avoiding public channel usage.

4. Secure Shared Authentication Key (SSAK) Protocol

This section presents the proposed SSAK protocol. The SSAK protocol focuses on the idea of sharing a secret angle and an authentication key between Alice and Bob over a multi-stage quantum channel. In the proposed protocol, an Information Travel Time (ITT) or Time Stamp technique associated with the data [26] is adopted to detect the presence of eavesdroppers in the initial authentication procedure. In the condition, Eve is located midway between Alice and Bob, the ITT is obviously different due to the fact that the distances between Alice and Bob are greater than the distance between Alice and Eve as well as Eve and Bob. However, in the case of Eve located far away from Alice and Bob, the ITT would be doubled and shows a sign of eavesdroppers’ attack. Thus, when quantum particles pass through optical polarization devices on the sender’s site, and an eavesdropper is present in the communication to read the photon, the response by the receiver might induce abnormal timing information. Moreover, this work utilizes the Pauli-X quantum gate to increase the difficulty for Eve to steal the information. Theoretically, a wire of transmission carries a qubit of information, and the quantum gate will take that qubit as an input. Here, the function of the quantum gate is to perform the unitary transformation on this qubit and produce a new state of qubit as an output. Pauli-X gate is also known as a bit flip operator that is responsible for altering the qubit state by flipping bit 0 to 1 and vice versa. Based on previous research, the quantum gate provides many benefits such as being easy-to-use as the information related to the operators is not necessarily shared between the parties, has less precision requirement compared to in arbitrary rotation such as half-wave plate (HWP), and provides accurate measurement [27].

The details of the proposed protocol can be described in three phases: Initial authentication, secure message sharing, and security checking. Figure 2 shows the whole process of the proposed SSAK protocol.

4.1. Initial Authentication Procedure

Alice is the party that supposedly sends a message to Bob. For Alice, it is extremely important to ensure the messages are only received by the authenticated user who is Bob. However, Bob faces difficulties when he receives the message; he does not know whether it comes from Alice or an eavesdropper. The initial part of authentication is important to verify the party that initiates the communication. Therefore, in this paper, a novel quantum handshake for sharing initial secret angle and authentication key, which is utilized before the quantum communication session is proposed. The objective of the proposed protocol is to allow Alice to identify herself to Bob and Bob can prove that Alice is a legitimate party. Note that operator $E_K\left[·\right]$ and $D_K\left[·\right]$ operators in Figure 2 are defined as encrypt and decrypt operations with key $K$.

The steps of the proposed protocol are discussed below:

• First item, Alice prepares a private orthogonal state ${\psi }_0$ and generates a random quantum state ${\theta }_A$ using a random number generator. Based on the decimal value of ${\theta }_A$, she prepares five binary digits and do Pauli-X quantum gate operation to produce ${\theta }_A{}^{\prime }$. She then encrypts ${\theta }_A$ with ${\psi }_0$ to produce the quantum state ${\psi }_1$. The $TimeStamp$ is set to $t_A\left(1\right)=0.$
• Second item, Bob generates a random quantum state ${\theta }_B$ using a random number generator and encrypts it with the received quantum state ${\psi }_1$ and produces ${\psi }_2$. The $TimeStamp$ is set to $t_B\left(1\right)=2.$
• Third item, Alice decrypts the received ${\psi }_2$ with $(-{\theta }_A)$ to generate ${\psi }_3$ and sends it back to Bob. At this stage, Alice is able to extract ${\theta }_B.$ Alice will verify the $TimeStamp$ after she gets the photon replied by Bob. Alice starts to analyze the difference between the sending and receiving time. If Alice gets $TimeStamp\ne 4$, an eavesdropper is detected and she will terminate the communication. Otherwise, the communication will be continued. Then, the $TimeStamp$ is set to 4.
• Bob applies $(-{\theta }_B)$ to obtain the ${\psi }_0$ and successfully extracted ${\psi }_0$. Bob gets the value of ${\theta }_A$ and converts it into five binary digits. He then does the Pauli-X quantum gate operation to generate new value of ${\theta }_B$. Next, he encrypts it with the received quantum state ${\psi }_0$ to produce quantum state ${\psi }_4$ and sends it to Alice.
• Alice authenticates Bob by comparing and analysing ${\theta }_B$ using measurement. If the value is correct, she will then send the authentication key ${\Phi }_{initial}$ that is generated using a random number generator. The${\Phi }_{initial}$ is then encrypted with the ${\theta }_B$ that she had extracted in step 3 to produce ${\psi }_5$ and passed it back to Bob. If the value is different, the communication will be terminated and needs to be restarted.
• Bob couples the receiving ${\psi }_5$ with $(-{\theta }_B)$, to get the authentication key $\Phi$.

After the authentication is successfully completed, Alice will start to convert the string of bit message into the photons and directly sends it to Bob using the initial secret polarization angle (${\theta }_{initial})$ and authentication key (${\Phi }_{initial})$.

4.2. Secure Message Sharing Procedure

It is assumed that Alice and Bob have the same secret angle and authentication key that they shared in the initial stage of authentication in Section 4.1. Suppose that Alice’s secret message $X$ is a series of classical bit of 0 and 1 in order, $X\left(x_{i, }{x}_{i+1 }\dots x_n\right)$.

• Alice encrypts her secret message $x_i$ by generating a state with a linear polarization using a 0° polarizer as bit 0 or using 90° polarizer as bit 1 to get ${\theta }_X$.
• Quantum state ${\theta }_X$ is then coupled with initial ${\theta }_A$ and sent along with the initial authentication key $\Phi$ by Alice. The combination of ${\theta }_X$, ${\theta }_A$ and $\Phi$ generates ${\psi }_A$ are sent to Bob.
• Bob receives the quantum state ${\psi }_A$ and couples it with $(-{\theta }_A)$ and $(-\Phi )$ obtains information $X_i$.
• Alice and Bob frame the received bits and convert the last $n \mathrm{bits}$ to integer value $N$, given by

  $$N={\displaystyle \sum }_{i=k-n+1}^k{b}_i\times 2^i$$

  (1)

  where k is the number of transmitted keys, b is the sequence of the transmitted bits (i.e., the bits $b_{k-n+1},\dots ,b_k$) using the last n bits to generate the new angle θ.
• Alice and Bob compute new value of θ and $\mathsf{\Phi }$, given by

  $${\theta }_{Next}=\frac{N\pi }{2^k}+ {\theta }_{initial}$$

  (2)

  $${\Phi }_{Next}=\frac{N\pi }{2^k}+ {\Phi }_{initial}$$

  (3)

4.3. Security Checking Procedure

Alice and Bob will check the authenticity between them by performing a measurement. By doing so, if there is no eavesdropper, Alice will be ensured that she received the same value as Bob, given by

$$({\theta }_{Next}.{\Phi }_{Next}) \times \left(-{\theta }_{Next}.-{\Phi }_{Next}\right)=I$$

(4)

where “$·$” is the multiplication operator and $I$ is the identity matrix. If there is an eavesdropper, in the case of Alice’s result is not the same with Bob, then Alice will announce to Bob to abort the communication, where

$$({\theta }_{Next}.{\Phi }_{Next}) \times \left(-{\theta }_{Next}.-{\Phi }_{Next}\right)\ne I$$

(5)

5. Example of the Proposed Protocol

Let us illustrate an example of the proposed protocol and describe the three parts of secure QSDC, which is the initial authentication procedure, message sharing procedure, and security phase procedure. The implementation of proposed SSAK has been tested using a simulation developed via Python programming language. Python is chosen due to its capabilities to simulate the quantum state in superposition via mathematical form. The pseudo-code of SSAK protocol is detailed in Algorithm 1.

5.1. Initial Authentication Procedure

The initial authentication procedure is explained as follows:

• Suppose that Alice prepares a photon ${\psi }_0=|0⟩$ and generates a random secret angle, ${\theta }_A=1°$. Based on the decimal value of ${\theta }_A$, she converts it into binary digits $|00001⟩$ and employs Pauli-X quantum gate operation to produce $|11110⟩$. She converts it back to decimal value,${\theta }_A{}^{\prime }=30°$. The new value will be used as the security check for the next procedure. She starts to encrypt$X=|0⟩$ using ${\theta }_A$ and produce quantum state ${\psi }_1$. The $TimeStamp$ is set to $t_A\left(1\right)=0$.
• Bob generates a random secret angle ${\theta }_B=15°$ and encrypts it with the received quantum state ${\psi }_1$ and produces ${\psi }_2$. The$TimeStamp$ is set to $t_B\left(1\right)=2$.
• Alice decrypts the received ${\psi }_2$ with $-{\theta }_A$ to generate ${\psi }_3$ and sends it back to Bob. At this stage, Alice gets ${\theta }_B=15°.$ Alice will verify the $TimeStamp=4$ after she gets the photon replied by Bob. If Alice gets the $TimeStamp\ne 4$, an eavesdropper is detected, and she will terminate the communication. Otherwise, the communication will be continued. The$TimeStamp$ is set to $t_A\left(2\right)=4$.
• Bob applies $-{\theta }_B$ to obtain ${\psi }_0=|0⟩$. He gets the value of ${\theta }_A=1°$ and converts it into the binary digits $|00001⟩$. Using the Pauli-X quantum gate, he gets $|11110⟩$, and he converts it back into decimal value and generates ${\theta }_B=30°$. He then encrypts it with the received quantum state ${\psi }_0=|0⟩$ to produce quantum state ${\psi }_4$ and sends it to Alice. The$TimeStamp$ is set to $t_B\left(2\right)=6$.
• Alice authenticates Bob by comparing and analyzing ${\theta }_B$ using measurement. If ${\theta }_B ={\theta }_A{}^{\prime }$, she sends the initial authentication key ${\Phi }_{initial}=20°$ that is generated using a random number generator and encrypts it with ${\theta }_B=30°$. If ${\theta }_B\ne {\theta }_A{}^{\prime }$, the communication will be terminated and need to be restarted.
• Finally, Bob couples the receiving ${\psi }_5$ with ${\theta }_B=30°$ to get the authentication key ${\Phi }_{initial}$.
• It can be concluded that the security of the proposed scheme depends entirely on the initial authentication procedure, where the eavesdropping check and identity authentication are implemented at the same time.

5.2. Message Sharing Procedure

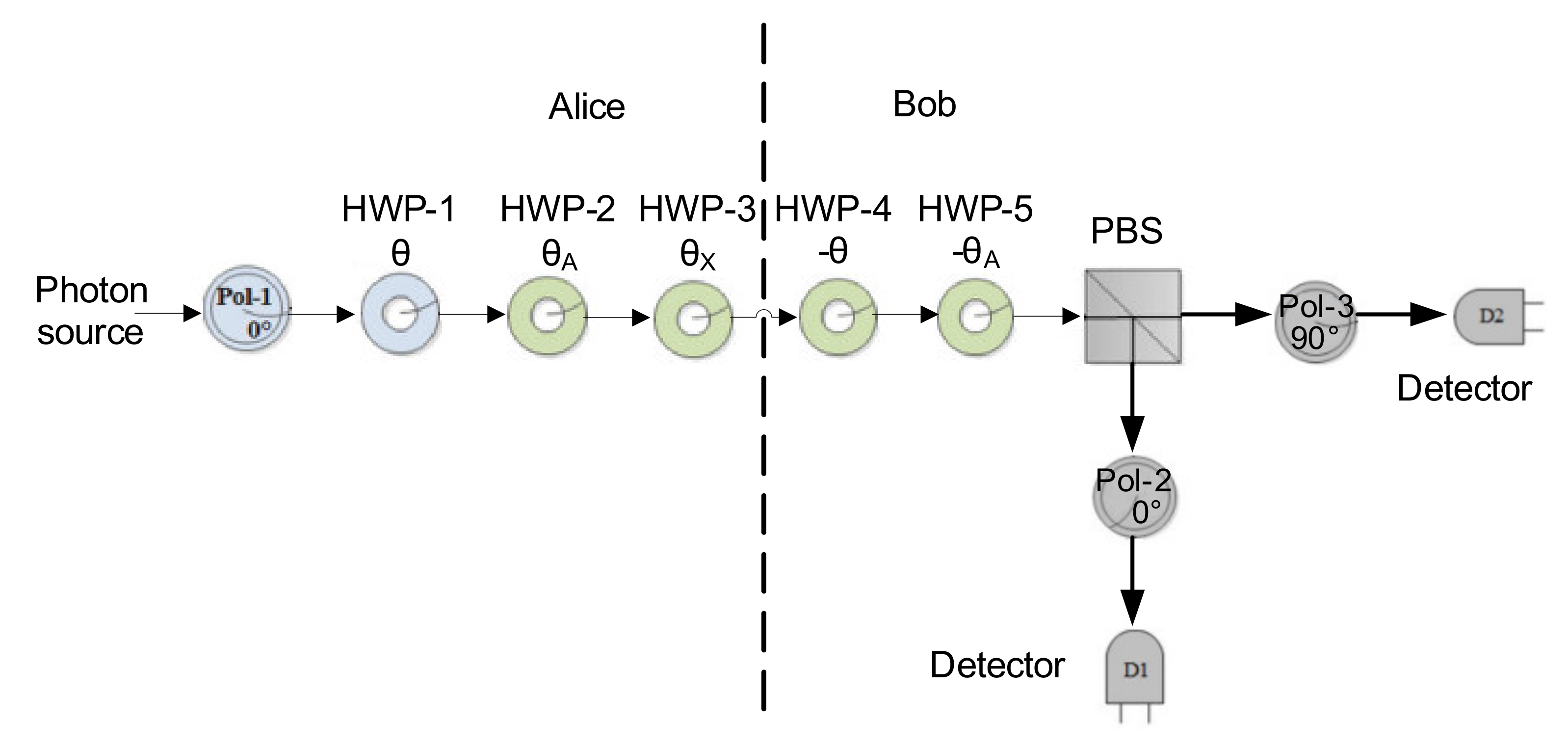
In this section, the implementation of SSAK protocol over free space optics using passive optical components is discussed. Figure 3 shows the setup of the implementation.

Alice will have three half-wave plates (HWPs) in her possession while Bob will have two HWPs. A linearly polarized laser is used as the photon source in our implementation [28]. At the beginning of the protocol, Alice generates a state with a 0° linear polarization using a 0° polarizer. The polarization procedure is to encrypt the classical bits using the photons to produce the quantum bit (qubit). After the classical bits are encrypted to the photons, she will apply a transformation using HWP-1 at the angle θ and apply her second HWP-2 at angle ${\theta }_A$, which results in the superposition state, |$\psi ⟩$. The superposition states carry the secret message that will be shared between Alice and Bob in quantum manners [27]. The rotation of HWP operation is represented as

$$M_{HWP}\left(\theta \right)= \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\left(4\theta \right)& sin\left(4\theta \right)& 0\\ 0& sin\left(4\theta \right)& -cos\left(4\theta \right)& 0\\ 0& 0& 0& -1\end{array}\right]$$

(6)

where

$$0°<\theta <45°$$

(7)

It is noted that HWP-1 at the angle θ is the authentication key set from 0° to 45°, coupled with information $X$ to make the protocol more secure. Alice then applies the transformation associated with the encoded bit using HWP-3 that will be set at an angle ${\theta }_X=$0° in the case of bit 0 being sent or ${\theta }_X=$45° if bit 1 is being sent.

$$\begin{array}{c}Message X\Rightarrow bits\in {\left\{0,1\right\}}^n\\ {\left\{0,1\right\}}^n\Rightarrow \left\{\begin{array}{c}|0⟩,|S_{out}=M_{HWP}\left(0°\right)\times S_{in}\\ |1⟩,|S_{out}=M_{HWP}\left(45°\right)\times S_{in}\end{array}\right.\end{array}$$

(8)

where $S_{in}$ is the Stokes parameter’s sequence of the input light that is illustrated as

$$S_{in}=\left[\begin{array}{c}{S}_0\\ S_1\\ S_2\\ S_3\end{array}\right]=\left[\begin{array}{c}1\\ 1\\ 0\\ 0\end{array}\right]$$

(9)

while $S_{out}$ is the Stokes parameter’s sequence of the output light

$$S_{out}=\left[\begin{array}{c}S{\prime }_0\\ S{\prime }_1\\ S{\prime }_2\\ S{\prime }_3\end{array}\right]$$

(10)

$$S_{out}=M_{HWP}\times S_{in}$$

(11)

The light polarization angle after passing through the HWP can be measured [28,29] by

$$\theta ={\cos }^{-1}\frac{S_{in}\left[1:3\right].S_{out}\left[1:3\right]}{\parallel S_{in}\left[1:3\right]\parallel \times \parallel S_{out}\left[1:3\right]\parallel }$$

(12)

where “$··$ ” is the multiplication operator and $\left|\left|·\right|\right|$ is the norm operator.

Alice will send the optical beam containing the message to Bob, who will first pass it through his first HWP (HWP-4). Then he will remove his transformation using a HWP-5 sets at the angle ${\theta }_A$. Bob will receive a beam polarizer at either 0° or 90° and pass it through a polarization beam splitter. The detectors will detect whether it is bit 0 or bit 1.

A basic description of the proposed protocol is discussed here. First, the message that is translated into the binary code is encrypted into a single particle called a quantum bit or qubit. The quantum bit is then transmitted from Alice to Bob using the proposed protocol as follows.

• Suppose that Alice prepares a photon. Alice wants to send the first qubit, |$0⟩,$ the qubit is then encrypted to the photons using the first agreed angle from the first procedure, ${\theta }_A=30°$. Alice prepares photons based on Equation (9) and encrypts it using the rotation of HWP based on Equation (6).

  $$\begin{array}{ccc}{\phi }_1& =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(4\left(30\right))& sin\left(4\left(30\right)\right)& 0\\ 0& sin\left(4\left(30\right)\right)& -cos\left(4\left(30\right)\right)& 0\\ 0& 0& 0& -1\end{array}\right]\times \left[\begin{array}{c}1\\ 1\\ 0\\ 0\end{array}\right]\\ & =& \left[\begin{array}{c}1\\ -0.5\\ 0.8660254\\ 0\end{array}\right].\end{array}$$

  (13)
• Alice encrypts the ${\phi }_1$ with the authentication key, which is previously shared in the initial authentication procedure, $\Phi =20°$.

  $$\begin{array}{ccc}{\phi }_2& =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(4\left(20\right))& sin\left(4\left(20\right)\right)& 0\\ 0& sin\left(4\left(20\right)\right)& -cos\left(4\left(20\right)\right)& 0\\ 0& 0& 0& -1\end{array}\right]\times \left[\begin{array}{c}1\\ -0.5\\ 0.8660254\\ 0\end{array}\right]\\ & =& \left[\begin{array}{c}1\\ 0.76604444\\ -0.64278761\\ 0\end{array}\right].\end{array}$$

  (14)
• Alice then applies the transformation associated with the encoded bit. In the case of bit 0 is being sent, the angle is set at ${\theta }_X=$0° or ${\theta }_X=$45° if bit 1 is being sent.

  $$\begin{array}{ccc}{\phi }_3& =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(4\left(0\right))& sin\left(4\left(0\right)\right)& 0\\ 0& sin\left(4\left(0\right)\right)& -cos\left(4\left(0\right)\right)& 0\\ 0& 0& 0& -1\end{array}\right]\times \left[\begin{array}{c}1\\ 0.76604444\\ -0.64278761\\ 0\end{array}\right]\\ & =& \left[\begin{array}{c}1\\ 0.76604444\\ 0.64278761\\ 0\end{array}\right].\end{array}$$

  (15)
• Bob receives ${\phi }_3$ and decrypts it by rotating it back with the angle $–{\theta }_A$.

  $$\begin{gathered} \begin{array}{ccc}{\phi }_4& =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(4\left(-30\right))& sin\left(4\left(-30\right)\right)& 0\\ 0& sin\left(4\left(-30\right)\right)& -cos\left(4\left(-30\right)\right)& 0\\ 0& 0& 0& -1\end{array}\right]\times \left[\begin{array}{c}1\\ 0.76604444\\ 0.64278761\\ 0\end{array}\right] \\ \\ & =& \left[\begin{array}{c}1\\ -0.5\\ -0.8660254\\ 0\end{array}\right].\end{array} \end{gathered}$$

  (16)
• Bob receives ${\phi }_4$ and decrypts it by rotating it back using the angle of authentication key ${\Phi }_A.$ Bob receives the original message.

  $$\begin{gathered} \begin{array}{ccc}{\phi }_5& =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos(4\left(-20\right))& sin\left(4\left(-20\right)\right)& 0\\ 0& sin\left(4\left(-20\right)\right)& -cos\left(4\left(-20\right)\right)& 0\\ 0& 0& 0& -1\end{array}\right]\times \left[\begin{array}{c}1\\ -0.5\\ -0.8660254\\ 0\end{array}\right] \\ \\ & =& \left[\begin{array}{c}1\\ 1\\ 0\\ 0\end{array}\right].\end{array} \end{gathered}$$

  (17)

5.3. Security Check Procedure

After ${\phi }_5$ is delivered successfully, the process continues with the remaining qubits using the same procedure. Alice and Bob will check the authenticity between them by comparing Alice’s and Bob’s secret rotations using Equation (4).

$$\begin{array}{ccc}{\mathit{Auth}}_{\mathit{AB}}& =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0.76604444& -0.64278761& 0\\ 0& 0.64278761& 0.76604444& 0\\ 0& 0& 0& 1\end{array}\right]\times \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0.76604444& 0.64278761& 0\\ 0& -0.64278761& 0.76604444& 0\\ 0& 0& 0& 1\end{array}\right]\\ & =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right].\end{array}$$

(18)

Algorithm 1 SSAK protocol

1: Notation: 2: TimeStamp ← calibration using time synchronization/time stamp 3: $\theta$ ← is the secret polarization angle 4: f(Pauli $-X$)← is a function bit flip operator using Pauli-X gate 5: 1. Initialization authentication procedure 6: ${\phi }_{i\dots n}$ ← is the random string message of (0,1) 7: $R\left(\theta \right)$ ← is the rotation of HWP using Equation (6) 8: $\left|{\phi }_{i\dots n}\right.⟩$ ← is the photon associate with ${\phi }_{i\dots n}$ 9: Alice prepares a photon using Equation (8) 10: Alice converts the decimal of $\theta$ into binary and does Pauli-X operation 11: $\theta {}^{\prime }$ ← f(Pauli$-X$) 12: Alice initializes the authentication by sharing secret polarization 13: $R\left({\theta }_A\right)\left|{\phi }_0⟩\right.=\left|{\phi }_1⟩\right.$ 14: TimeStamp=0 15: $R\left({\theta }_B\right)\left|{\phi }_1⟩\right.=\left|{\phi }_2⟩\right.$ 16: TimeStamp = 2 17: $R\left(-{\theta }_A\right)\left|{\phi }_2⟩\right.=\left|{\phi }_3⟩\right.$ 18: TimeStamp = 4 19: if TimeStamp ≠4 then 20:   detect Eve and terminate communication 21: elif 22:   $R\left(-{\theta }_B\right)\left|{\phi }_3⟩\right.=\left|{\phi }_0⟩\right.$ 23:   TimeStamp = 6 24: end if 25: Bob analyzed the result 26: Determine the value of ${\theta }_A$ using Equation (12) and the corresponding bit 27: ${\theta }_A{}^{\prime }$← f(Pauli $-X$) 28: Generate new ${\theta }_B$ 29: $R\left({\theta }_B\right)\left|{\phi }_0⟩\right.=\left|{\phi }_4⟩\right.$ 30: Alice compares and analyses new${\theta }_B$according to her previous calculation, verifies Bob and sends authentication key 31: Determine the new value of ${\theta }_B$ using Equation (12) and the corresponding bit 32: if$R\left({\theta }_A{}^{\prime }\right)$ ≠$R\left({\theta }_B\right)$ then 33:   detect Eve and terminate communicatione 34: elif 35:   Alice sends authentication key using ${\theta }_B$ to Bob 36:   $R\left({\theta }_B\right)\left|\Phi \right.=\left|{\phi }_5⟩\right.$ 37: end if 38: Bob gets authentication key 39: $R\left(-{\theta }_B\right)\left|{\phi }_5⟩\right.=\left|\Phi \right.⟩$ 40: 2. Message sharing procedure of bit sequence, B 41: B ← A bit sequence 42: len(B) ← is the length of bit sequence B is set to 8 photons per block 43: Alice prepares photons based on Equation (8), encrypts it using${\mathit{\theta }}_{\mathit{A}}$and$\mathit{\Phi }$. 44: Notation: 45: f(B, $\theta$, $\Phi$) ← is the function that returns the updated secret polarization angle and authentication key for every block of photon (8 photons per block) 46: for i ($\theta$,$\Phi$) in enumerate (f(B, $\theta$, $\Phi$)) do 47:    for j = 1 in range B do 48:    Transmission of photon using single-stage 49:     if i * B + j ≥ len(B) then 50:    break transmission; 51:     end if 52:    end for 53: end for 54: Alice and Bob checks for authenticity 55: if$({\theta }_A.\Phi ) \times \left(-{\theta }_A.-\Phi \right)=I$then 56:   Alice and Bob are authenticated 57: else 58:   detect Eve and terminate communication 59: end if

6. Performance Analysis

6.1. Mutual Authentication

It has been found that the authentication procedure in the IV Three-stage and Braided Single Stage protocol is unidirectional, which means that only Alice can authenticate Bob. In this work, a mutual authentication procedure is presented by applying the unitary transformation in the process of authentication. Mutual authentication between legal parties is necessary to avoid an eavesdropper stealing the secret message. Mutual authentication requires the parties to prove their identity with each other in the communication. Therefore, the mutually agreed algorithm of the authentication keys is changed every eight bits of transactions. The keys are updated based on every last $n$ bit photons to prevent the message from leaking. The frequent change of the authentication key has helped to enhance the level of security, but a longer time is needed to change the polarization angle due to the limitations of the mechanical components [28].

As discussed in the previous section, the transformation needs to be commutative in which the rotation is only known to the parties that apply them [30]. Therefore, in the case where Alice and Bob are not mutually authenticated, Equation (5) is fulfilled, where ${\theta }_A.\Phi$ is the polarization at Alice that acts as encryption angle, $-{\theta }_A.-\Phi$ is the polarization at Bob that acts as decryption angle and $I$ is the identity matrix, as shown in Equation (18). As shown in Figure 4, the sender and receiver authentication controllers provide an authentication function by the evaluation of information sent by both parties [16]. Besides, the controller also monitors the bit error rate of the received photons. For instance, Alice and Bob can check the legitimacy of each other by comparing their polarizations. If the result is not equal to $I$, the failed authentication alarm will be triggered, and the procedure would be stopped. The procedure needs to start over again.

6.2. Low Cost and Low Complexity

Table 1. Performance comparison between three-stage variants and proposed authentication protocol.

Protocol	IV Three-Stage	Braided Single Stage	Proposed Protocol
1. Public Communication (pre-shared angle)	Yes	Yes	No
2. Authentication key	Yes	No	Yes
3. No. of HWP for information exchange	7	5	5
4. Information exchange stage	3 times	1 times	1 times
5.Quantum communication complexity of authentication	$Q^{*}\left(f_I\right)=\Omega \left(3n+3IV\right)$	$Q^{*}\left(f_I\right)=\Omega \left(3n\right)$	$Q\left(f_I\right)=5n$

shows that the previous protocols, IV Three-stage and Braided Single Stage, use the public channel to share the initial secret angle between Alice and Bob, therefore, making the secret angle vulnerable to attacks. The proposed protocol, on the other hand, uses the quantum channel to share the initial angle and the authentication key. Thus it is hard for the attacker to obtain the value since the quantum state is implemented from the beginning of the procedure. It makes the authentication of the users simpler without sharing the secret polarization angle and authentication key onset of the protocol. Similar to previous protocols, there is no need for a third party to verify the authentication in the proposed protocol. Despite the IV Three-stage protocol that used four variables [7] during the message sharing, the proposed authentication only consists of three variables, which are ${\theta }_X$, ${\theta }_A$, and $\Phi$. It shows that the consumption of photonic devices is less compared to the previous protocols.

Instead of the classical authentication, which is based on the computational complexity of certain mathematical problems, quantum authentication utilizes quantum mechanics, which provides absolute security [15,16,31]. Thus, to evaluate the quantum authentication protocol, quantum communication complexity measurement was conducted. Quantum communication complexity can be defined as the amount of communications carried out between the parties to accomplish information distribution tasks [32]. The protocol that uses quantum and classical resources to authenticate users is denoted by $Q^{*}\left(f_I\right)$, while the protocol that fully uses quantum channel to authenticate users is denoted by $Q\left(f_I\right)$, where $Q$ is the quantum communication complexity and $f_I$ is the identity authentication [32,33]. It can be seen from Table 1 that the IV Three-stage and Braided Single Stage protocol require a classical channel ($\Omega$) to share a set of polarization states predetermined amongst them for authentication functionalities [30]. For the IV Three-stage protocol, a three-stage transformation over the quantum channel ($n$) is required to perform the authentication process between the parties and to exchange the initialization vector that acts as an authentication key. Due to no authentication key in the Braided Single Stage [9], the three-stage transformation is only used for authentication tasks. Indeed, the proposed protocol does not need a predetermined polarization state before the effective authentication process starts. The secret polarization angle and authentication key can be shared in a fully quantum channel within five stages. It can be considered a good quantum authentication protocol if a minimum number of communications are held between parties. In order to make the authentication process more secure and efficient, classical communication is not necessary.

6.3. Security Analysis

Security analysis is the critical assessment standard for any quantum protocol to ensure that the proposed protocol is secure against any eavesdropper attacks. The security of the proposed QSDC authentication protocol relies not only on the quantum non-cloning theorem and the quantum uncertainty principle of the secret message to prevent an unconditional attack, but the quantum state is also applied to the authentication key that secures the messages. The security analysis is explained in detail herein.

6.3.1. Man-in-the-Middle Attack

Due to the two secret polarization angles, the attacker must know the value of ${\theta }_A$ and $\Phi$ at the same time. However, it is very difficult for the attacker to guess the exact value due to the secure handshake mechanism that has been conducted to share that value between Alice and Bob. If the $\Phi$ and the quantum states ${\theta }_X$ are exposed to Eve during transmission, she has no means to understand the value of $\Phi$ or X. Even if Alice sends multiple photons with the same polarization, Eve cannot obtain the useful information since different values of authentication keys are generated for each block of the bit transfer. Bob is able to decode the information X if he possesses the correct ${\theta }_A$ and $\Phi$. Hence, Eve cannot pretend to be Alice or Bob if she does not know the authentication key. As shown in Figure 4, Alice and Bob will compare the bits to determine if a MITM attack has been launched. For example, Eve may disturb the message by interrupting the quantum channel several times, and this situation will lead to the re-initialization of the communication between the legitimate parties. If an interception occurs, Alice and Bob will immediately detect it, and Eve will never get the original message. If the bit error rate is high, this means that Eve’s attack has been started as the quantum states are disturbed. Thus, if the error rate is higher than the threshold, the transmission will be canceled. During the MITM attack, Eve will impersonate Alice and Bob to extract information. Eve does not know the value of ${\theta }_A$ and $\Phi$ to send a fake sequence of messages prepared by herself to Bob because Alice and Bob share the ${\theta }_{initial}$ and ${\Phi }_{initial}$ by utilizing a quantum handshake scheme. The possible cases on how the proposed protocol defends MITM attacks are discussed here.

Case 1:

Eve has no knowledge of the ${\theta }_{initial}$ or the ${\Phi }_{initial}$, thus she is incapable of getting anything about the secret message. Thus, the proposed protocol is secure against MITM attack. As stated in Section 5, Eve needs to guess 45 possibilities of angle for each qubit transmitted. Eve can predict the true angle for ${\theta }_{initial}$ and ${\Phi }_{initial}$ with the probability $p=\frac{1}{45}\times \frac{1}{45}=\frac{1}{2025}$.

Case 2:

Eve succeeds in guessing the ${\theta }_{initial}$. However, Eve does not get any useful information about the message since she does not know ${\Phi }_{initial}$.

In order to investigate the impact of Eve’s information on the secret angles of the SSAK and the benchmark protocol, a random character from 5 to 25 with random message generation is selected. The messages are shared over the QSDC protocol. The simulations have been tested using Python programming language. Figure 5 shows an average of 30 simulation runs for each data point. The leakage angle in average, $Lea{k}_{AB}$ can be calculated as:

$$Lea{k}_{AB}=\frac{LeakAngle}{SecretAngle}$$

(19)

where $LeakAngle$ is the number of angles that are successfully recovered by Eve and $SecretAngle$ is the number of secret angles agreed by Alice and Bob.

As shown in Figure 5, the average covered angle by Eve is 0% in the proposed protocol. This means that Eve does not have any clue to guess the true angles, $\Phi$ and $\theta$ simultaneously. Therefore, Eve has completely no knowledge about the polarized photon that represents the message. However, in benchmark protocols (IV Three-stage and Braided Single Stage), as the number of bits increases, Eve still has chances to guess the secret angle by 2% on average. The line plotted in the graph shows the maximum average covered angles by Eve after 30 simulation runs for the benchmark protocol. It can be seen that Eve is able to guess up to 7% of the secret angles in the lowest number of characters shared.

6.3.2. Intercept/Resend Attack

After Alice encodes the photons, Eve attempts to steal the photons and substitutes them with fake photons prepared in advance. In the proposed SSAK protocol, Alice shares the secret θ and Φ securely with Bob that is only known to them. Eve cannot measure the intercepted photons correctly because she cannot know the right value of θ and Φ. Eve’s ability to obtain useful information is limited because the quantum states are transmitted in the quantum mechanical property, which means that the states are the non-orthogonal. The authentication keys and polarization states of photons are used to generate the non-orthogonal quantum states. It shows that the security relies on the no-cloning theorem, which means no one can make a copy of any unknown no-orthogonal states. Besides, when Eve tries to measure the superposition states during the transformation phase, the result could be any non-orthogonal state. Thus, no information regarding the polarization angle is detected. Assuming that Eve managed to intercept the transmitted photons from Alice, Eve will resend the photons to Bob after doing a measurement. However, Eve cannot break the protocol because she does not know the polarization angles and authentication keys set by Alice and Bob. Let us assume that Alice transmits a quantum state of $|\phi ⟩$, i.e., |$1⟩$ in 45° polarization angle and encrypts it using the authentication key. Then, Eve tries to intercept them. Eve will fail to get the $|\phi ⟩$ since she does not possess the secret polarization angle and the authentication key. In the proposed protocol, Eve needs to guess two secret angles in high precision. Eve can be detected if her polarization angle is not the same as Alice and Bob keys’ possession. Since this protocol applies bit-by-bit authentication, Eve cannot spend a long time analyzing the statistics of a large number of photons that she gets during her attack, or she will be exposed. Consequently, Eve’s attack can be exposed as Alice’s and Bob’s measurements on the fake bit are not identical to the original one. Moreover, Eve cannot gain any profit from this attack.

6.3.3. Beam Splitting Attack

In this attack, Eve will locate the beam splitter between Alice and Bob to collect the photons illegally. Without being detected at Bob, Eve will get the probability of 50% of the correct photons. However, this attack is not possible against the proposed protocol. Even if Eve is able to collect the fraction of the transmitted photons without being detected by Bob, it is very difficult to find the secret polarization angles since the angle will never be disclosed publicly. In addition, the angles of polarization will be updated after a number of photons using the mutually agreed secret algorithm to maintain the level of secrecy and to obtain unconditional security [7,28]. Apart from that, the newly updated keys will prevent information related to the keys and messages from being sniffed by an eavesdropper.

7. Implementation Issues of the Proposed Protocol

The security of the protocol proposed is based on how hard it is for an eavesdropper to construct the authentication key and secret angle that Alice and Bob exchange. Eve has to find Alice’s secret information using a probability of up to $\frac{1}{2025}$ by intercepting their communications. The ease of implementation is one of the key factors in the design of QSDC. It can be observed that there are no entangled states, which are difficult to implement in the proposed protocol. The performance analysis showed that the proposed protocol is low-cost, and it can be implemented with today’s technology using optical devices, as discussed in Section 4. As discussed in the literature, the proposed work intends to secure the information against an eavesdropper’s attack. In the real implementation of the QSDC protocol, several practical issues need to be considered other than security issues. The practical issues that will impact the implementation of quantum communication are the noise and error in the quantum channel. Besides, photon loss may occur in the large communication distance due to the features of quantum mechanics [34]. The channel loss will lead to photon loss, which results in the secret information loss due to the information been encoded into individual photons. In addition, an eavesdropper could hide her presence in the channel noise and take the advantages to gain a certain amount of information [6]. Thus, a quantum error correction is necessary during transmission via a noisy channel.

8. Conclusions

This work implements a secure mutual authentication to ensure the legitimacy of users without any involvement of the third party. Unlike the most well-known QSDC protocols that rely on a slight classical communication to share the pre-shared authentication key at the onset of communication, the proposed protocol fully utilizes the quantum channel to share the secret angle and authentication key at the initial stage of authentication. Firstly, the proposed scheme is enhanced with ITT implementation by allowing the sender to detect any disturbance by the third party. When quantum particles pass through optical polarization devices at the sender’s site, and an eavesdropper is present in the communication to read the photon, the response by the receiver might induce additional time. Secondly, Pauli-X quantum gate operation is employed where the received qubit is flipped according to the numerical secret rotation angle to increase the difficulty for Eve to steal the information. The proposed protocol can be concluded that public communication or public states are not used to transmit a secret message or verify the parties. The security of the proposed scheme is discussed in the context of eavesdropping attacks during initial authentication and transmission of messages. Security analysis of initial authentication and transmission of messages has shown that the eavesdropper is unable to reveal any information about the authentication key or the transmitted message. That is because Alice only knows the secret angle of polarization and authentication key, and this is successfully shared with Bob through the quantum channel without being exposed to Eve.

The authentication is also prepared before the message is exchanged, and bit-by-bit checks are performed during quantum communication. The security analysis demonstrates that the suggested quantum authentication scheme is secure against most of the well-known attacks. There is no chance Eve could impersonate either Alice or Bob. In the proposed protocol, we only considered two parties involved in the communication. Recently, the authors of [35] proposed an effective way to share the authentication key among three parties using a single photon in polarization and spatial-mode degree of freedom. Following their work, we will study the authentication parts of three-party on multi-stage using unitary transformation of QSDC in the future. The problem of photon loss in the real implementation of the QSDC protocol has been studied in our work [14]. Therefore, the implementation of practical QSDC in a realistic environment of high information loss and noise using the proposed protocol should be focused on in our future research.