Symmetrical and Asymmetrical Rectifications Employed for Deeper Ocean Extrapolations of In Situ CTD Data and Subsequent Sound Speed Profiles
Abstract
1. Introduction
2. Materials and Methods
2.1. The Proposed Extrapolation Methodology
- The Chen and Millero Equation (1977) [16];
2.2. Sound Speed Profile (SSP) Computations
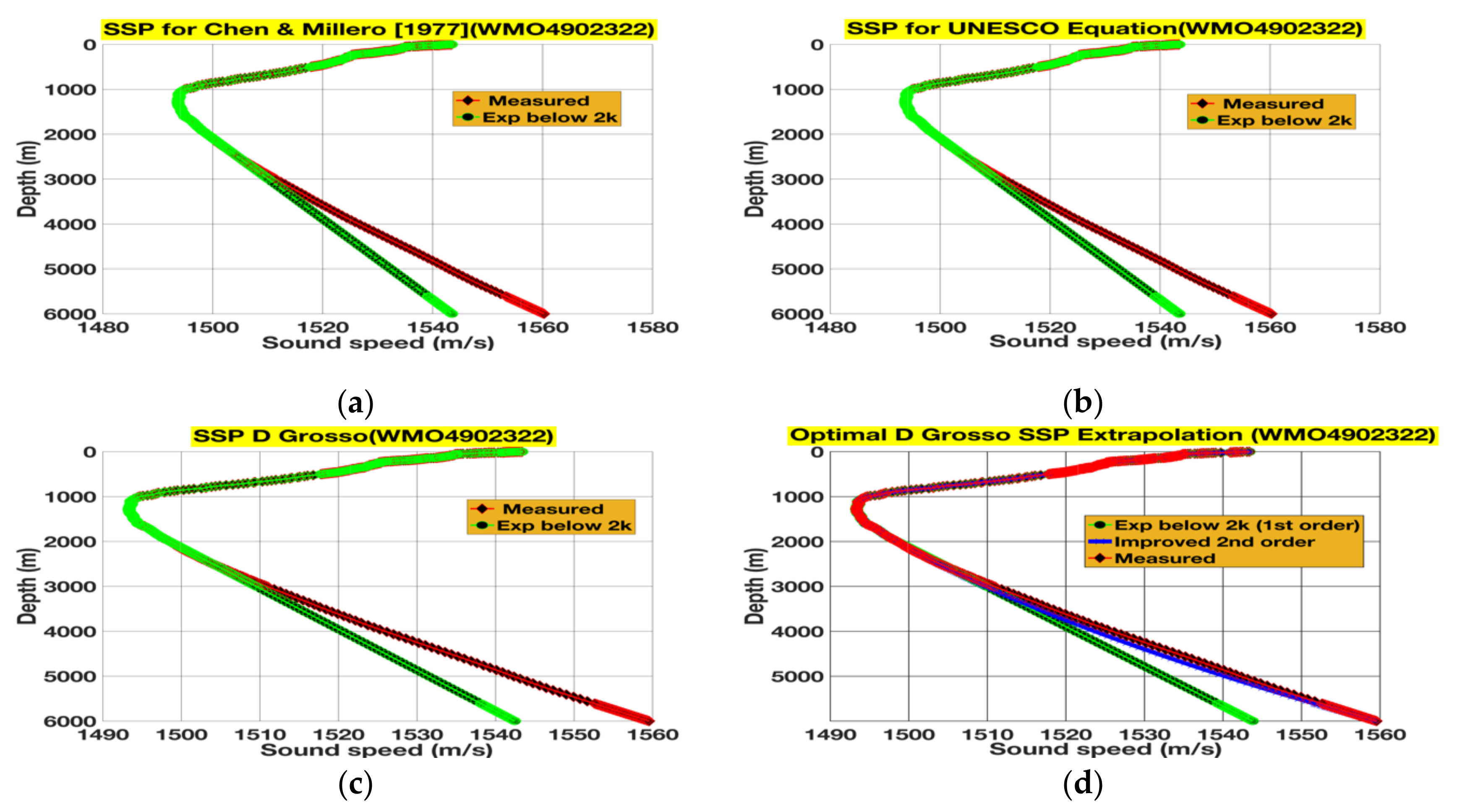
2.2.1. SSP Computations Using the Chen and Millero Equation (1977)
2.2.2. SSP Computations Using the UNESCO Algorithm
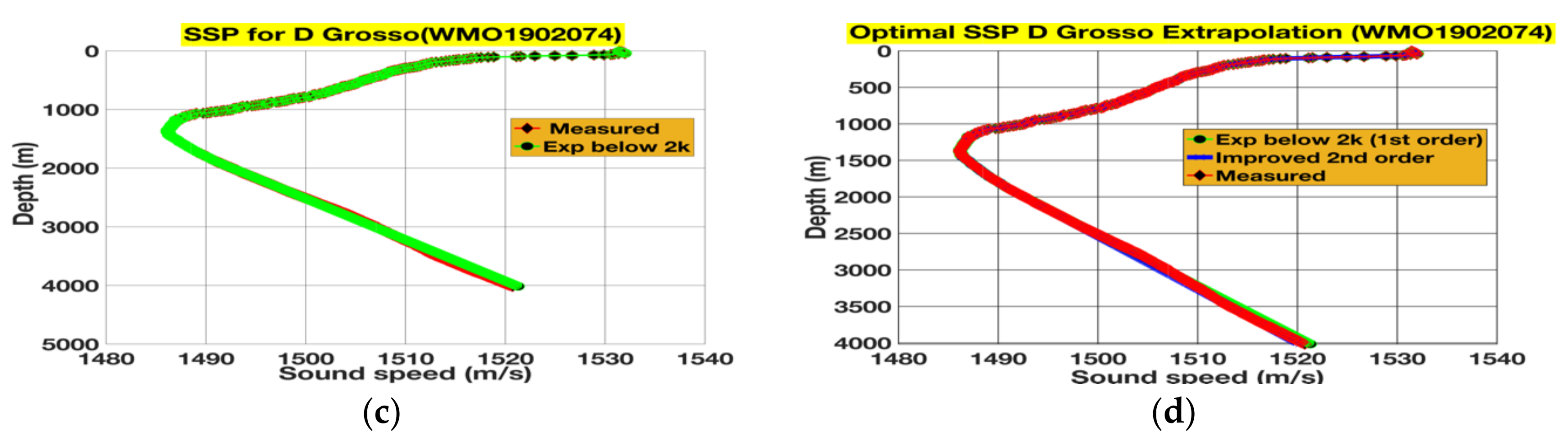
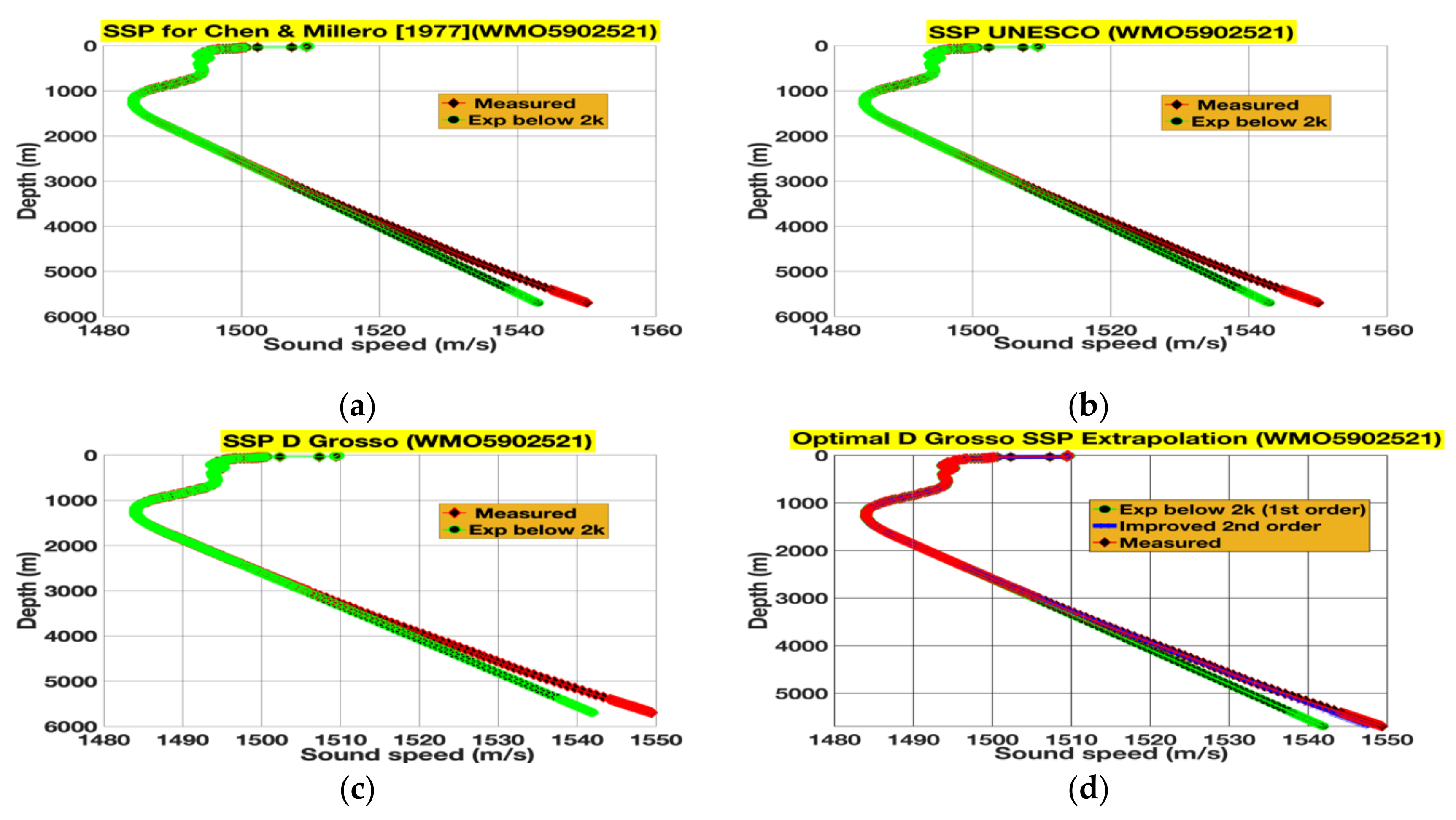
2.2.3. SSP Computations Using the Del Grosso Equation (1974)
3. Results
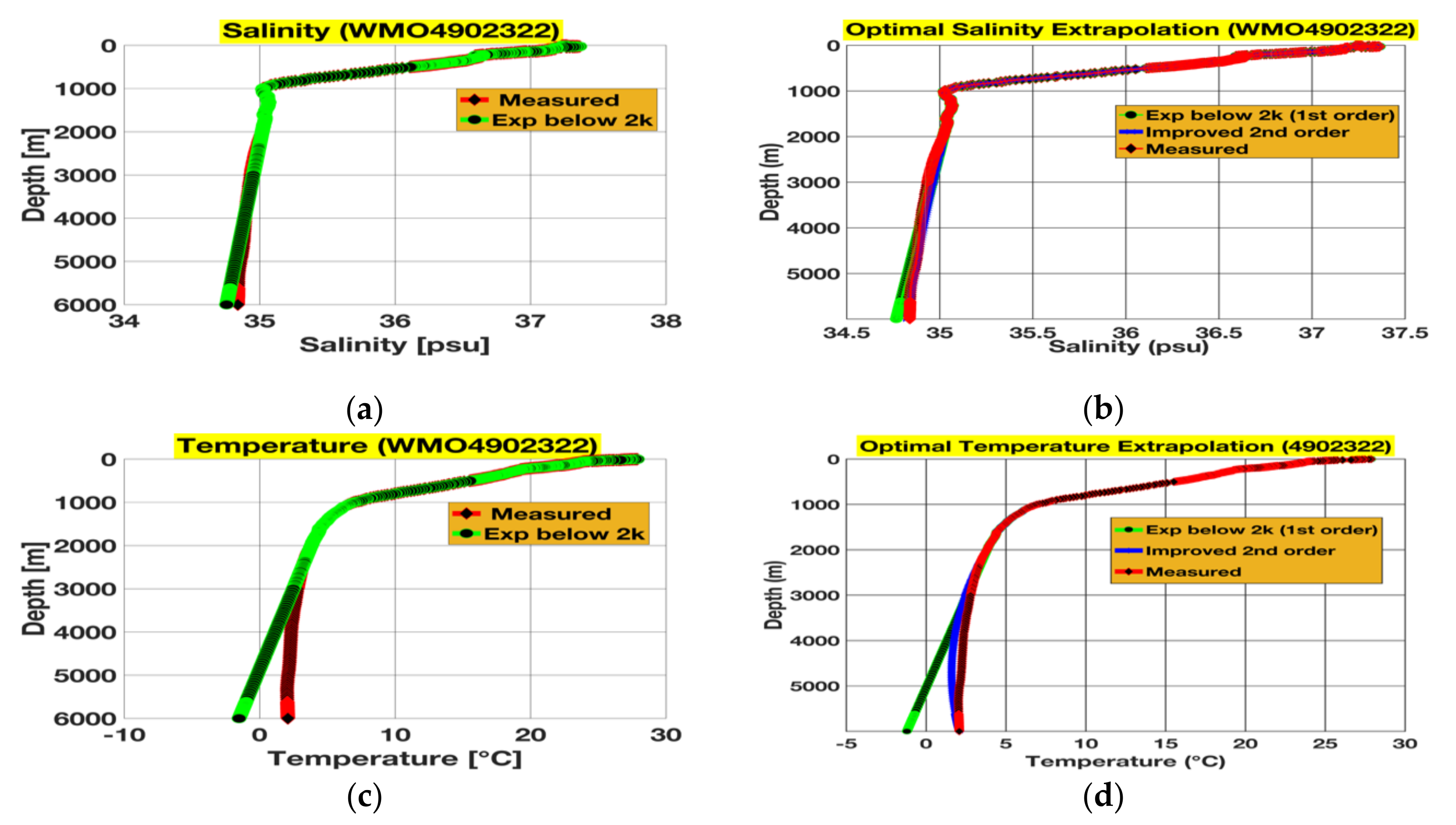
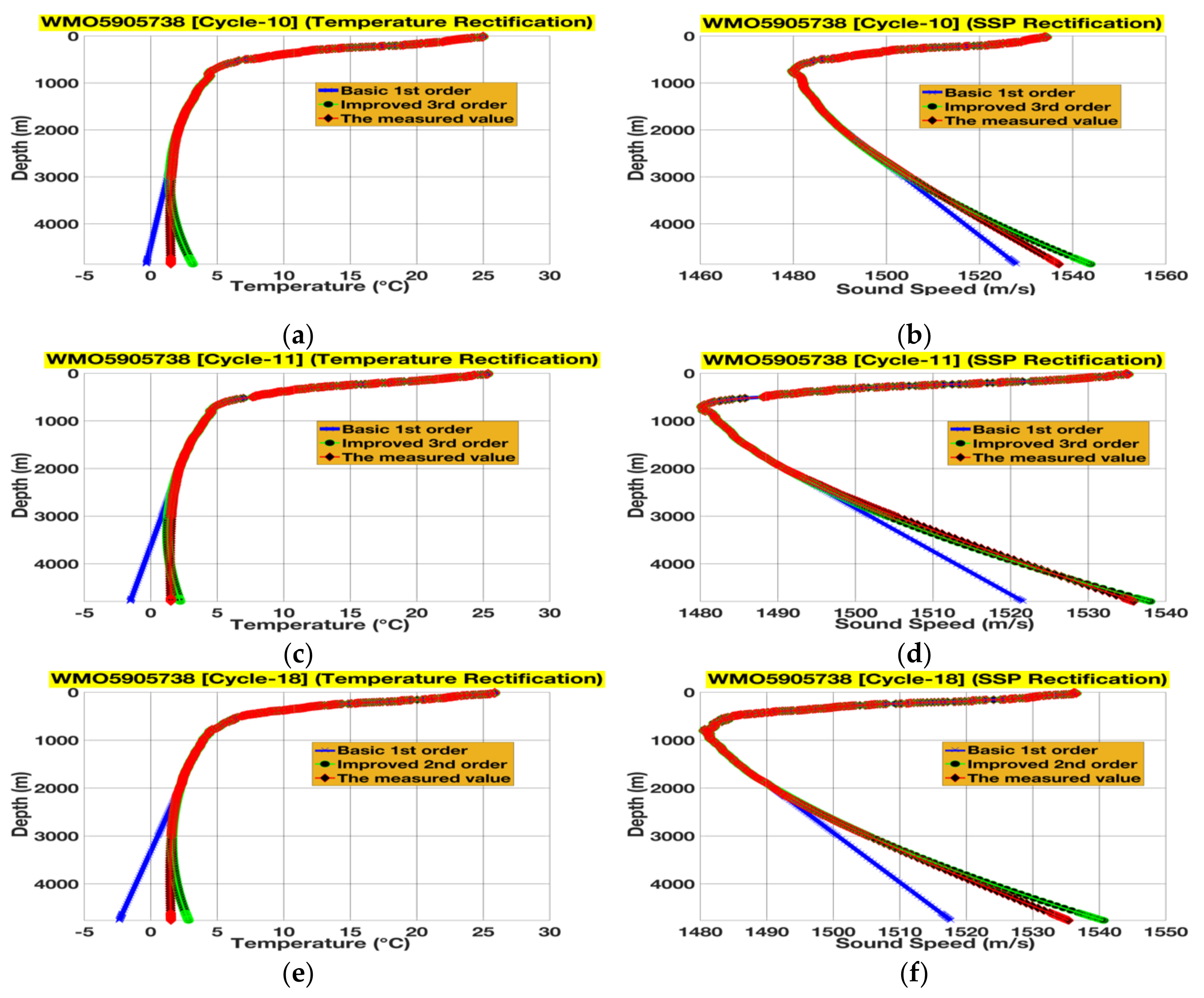
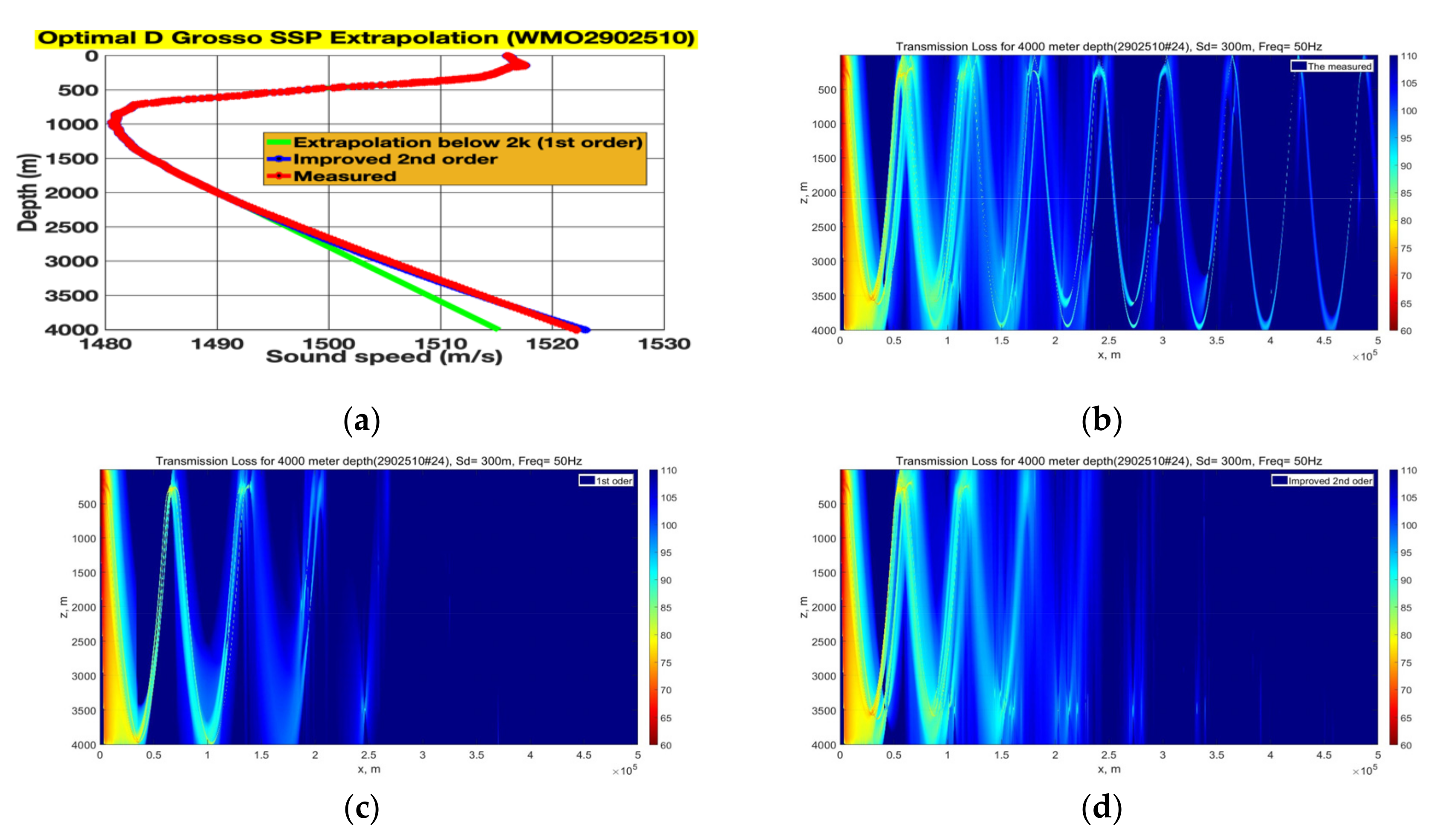
3.1. Extrapolations and Their Subsequent Rectifications for 4000 m Floats
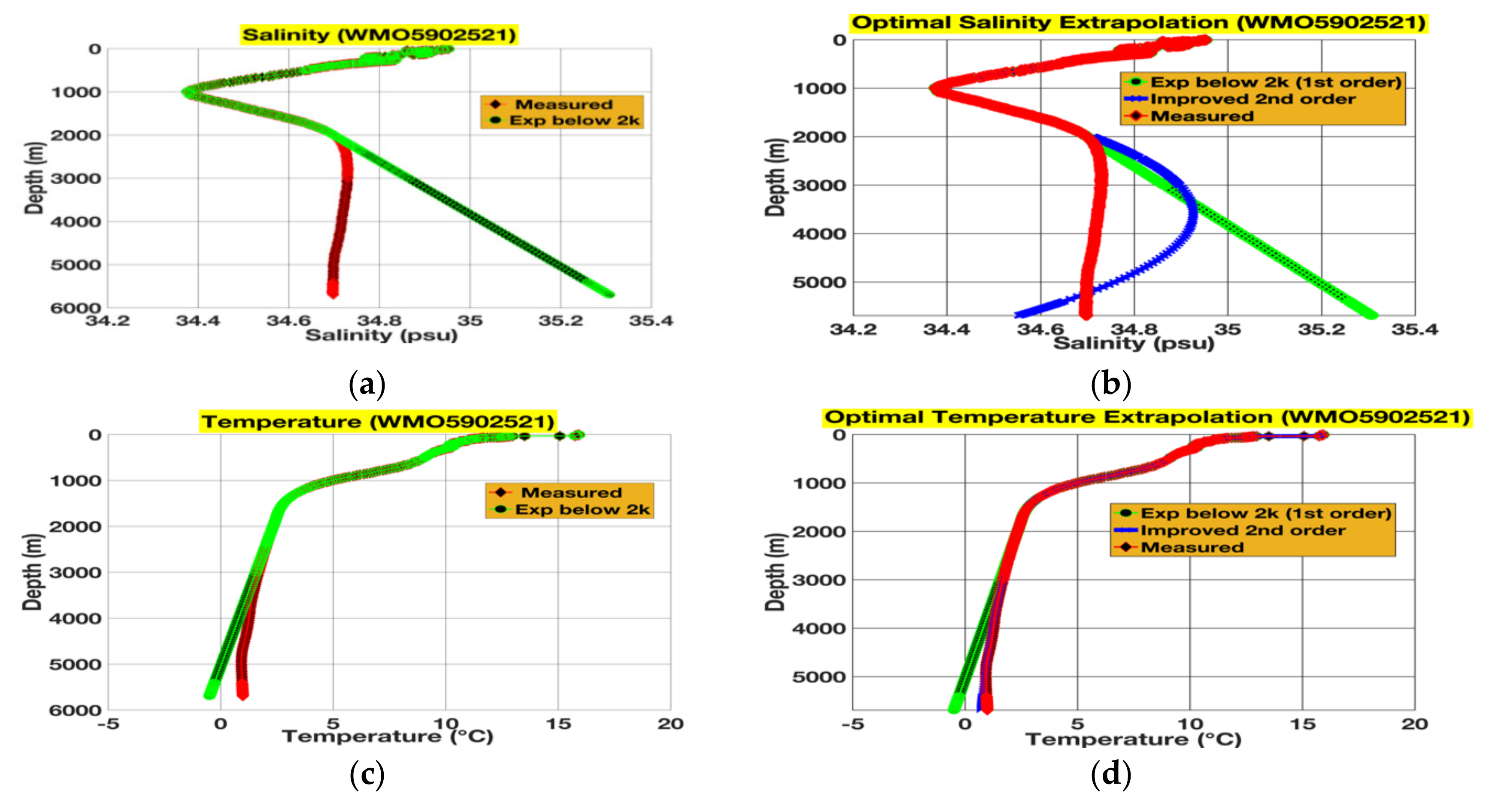
3.2. Extrapolations and Their Subsequent Rectifications for 6000 m Floats
3.3. Experimentation in the Pacific Ocean for Spatiotemporal Coverage and Asymmetric Rectification
3.3.1. Spatiotemporal Coverage through Extrapolations
3.3.2. Symmetric and Asymmetric SSP Rectifications
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Iqbal, K.; Zhang, M.; Piao, S.; He, G. Gradual but Persistent Quest for the Ocean Observation by Employing Multifarious Sensing Gadgets: A Preview. In Proceedings of the OCEANS 2019—Marseille, Marseille, France, 17–20 June 2019. [Google Scholar] [CrossRef]
- Iqbal, K.; Zhang, M.; Piao, S.; He, G. Advent of Deep Argo Data & an Attempt at Analyzing the Deeper Sound Speed Profiles for Extrapolation Corrections. Underwater Acoustics Conference & Exhibition, UACE2019, Conference Proceedings. ISSN: 2408-0195, HERSONISSOS, CRETE—GREECE|30.06—05.07.2019. Available online: http://www.uaconferences.org/docs/2019_papers/UACE2019_1007_Iqbal.pdf (accessed on 1 September 2020).
- Roemmich, D.; Johnson, G.; Riser, S.; Davis, R.E.; Gilson, J.; Owens, W.B.; Garzoli, S.L.; Schmid, C.; Ignaszewski, M. The Argo Program: Observing the Global Oceans with Profiling Floats. Oceanography 2009, 22, 34–43. [Google Scholar] [CrossRef]
- Gasparin, F.; Hamon, M.; Rémy, E.; Le Traon, P.-Y. How Deep Argo Will Improve the Deep Ocean in an Ocean Reanalysis. J. Clim. 2019, 33, 77–94. [Google Scholar] [CrossRef]
- Katsaros, K. BOOK REVIEW|Atmosphere-Ocean Interactions (Volume 1). Oceanography 2003, 16, 106–108. [Google Scholar] [CrossRef][Green Version]
- Bigg, G.R.; Jickells, T.D.; Liss, P.S.; Osborn, T.J. The role of the oceans in climate. Int. J. Clim. 2003, 23, 1127–1159. [Google Scholar] [CrossRef]
- Meyssignac, B.; Boyer, T.; Zhao, Z.; Hakuba, M.Z.; Landerer, F.W.; Stammer, D.; Köhl, A.; Kato, S.; L’Ecuyer, T.; Ablain, M.; et al. Measuring Global Ocean Heat Content to Estimate the Earth Energy Imbalance. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Le Reste, S.; Dutreuil, A.V.; André, A.X.; Thierry, V.; Renaut, B.C.; Le Traon, P.-Y.; Maze, G.; A, L. “Deep-Arvor”: A New Profiling Float to Extend the Argo Observations Down to 4000-m Depth. J. Atmos. Ocean. Technol. 2016, 33, 1039–1055. [Google Scholar] [CrossRef]
- Bittig, H.; Maurer, T.L.; Plant, J.N.; Schmechtig, C.; Wong, A.P.S.; Claustre, H.; Trull, T.W.; Bhaskar, T.V.S.U.; Boss, E.; Dall’Olmo, G.; et al. A BGC-Argo Guide: Planning, Deployment, Data Handling and Usage. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Durack, P.; Laboratory, L.L.N.; Gleckler, P.; Purkey, S.; Johnson, G.; Lyman, J.; Boywe, T. Ocean Warming: From the Surface to the Deep in Observations and Models. Oceanography 2018, 31, 41–51. [Google Scholar] [CrossRef]
- Zilberman, N.; King, B.; Purkey, S.; Thierry, V.; Roemmich, D. Report on the 2nd Deep Argo Implementation Workshop, Hobart, Australia, 13–15 May 2019. Available online: https://archimer.ifremer.fr/doc/00507/61873/ (accessed on 1 June 2020).
- Roemmich, D.; Sherman, J.T.; Davis, R.E.; Grindley, K.; McClune, M.; Parker, C.J.; Black, D.N.; Zilberman, N.; Purkey, S.G.; Sutton, P.J.H.; et al. Deep SOLO: A Full-Depth Profiling Float for the Argo Program. J. Atmos. Ocean. Technol. 2019, 36, 1967–1981. [Google Scholar] [CrossRef]
- Roemmich, D.; Alford, M.H.; Claustre, H.; Johnson, K.; King, B.A.; Moum, J.; Oke, P.; Owens, W.B.; Pouliquen, S.; Purkey, S.; et al. On the Future of Argo: A Global, Full-Depth, Multi-Disciplinary Array. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Steven, J.M. The Methods of Least Squares. Mathematics Department Brown University, Providence, RI, 02912. Available online: https://web.williams.edu/Mathematics/sjmiller/public_html/BrownClasses/54/handouts/MethodLeastSquares.pdf (accessed on 1 September 2020).
- Schmid, C.; Molinari, R.L.; Sabina, R.; Daneshzadeh, Y.-H.; Xia, X.; Forteza, E.; Yang, H. The Real-Time Data Management System for Argo Profiling Float Observations. J. Atmos. Ocean. Technol. 2007, 24, 1608–1628. [Google Scholar] [CrossRef]
- Fofonoff, N.P.; Millard, R.C., Jr. Algorithms for Computation of Fundamental Properties of Seawater. Unesco Technical Papers in Marine Science, Endorsed by: Unesco/SCOR/IAPSO Joint Panel on Oceanographic Tables and Standards and SCOR Working Group 51, Unesco 1983. Available online: https://pdfs.semanticscholar.org/42f5/eabc0051566f9d5b4ef469d89a505e6b0f64.pdf (accessed on 1 September 2020).
- Underwater Acoustics: Technical Guides—Speed of Sound in Sea-Water. National Physical Laboratory, Teddington, Middlesex, UK, TW11 0LW. Available online: http://resource.npl.co.uk/acoustics/techguides/soundpurewater/speedpw.pdf (accessed on 1 September 2020).
- Wong, G.S.K.; Zhu, S.-M. Speed of sound in seawater as a function of salinity, temperature, and pressure. J. Acoust. Soc. Am. 1995, 97, 1732. [Google Scholar] [CrossRef]
- Bretscher, O. Linear Algebra with Applications, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- These Data Were Collected and Made Freely Available by the Coriolis Project and Programmes that Contribute to It. Available online: http://www.coriolis.eu.org (accessed on 1 September 2020).
- Millero, F.J.; Li, X. Comments on “On equations for the speed of sound in seawater” J. Acoust. Soc. Am. 93, 255–275 (1993). J. Acoust. Soc. Am. 1994, 95, 2757. [Google Scholar] [CrossRef]
- Ali, M.M.; Jain, S.; Rachandran, R. Effect of Temperature and Salinity on Sound Speed in the Central Arabian Sea. Open Ocean Eng. J. 2011, 4, 71–76. [Google Scholar]
- Ridgway, N.M. Temperature and salinity of sea water at the ocean floor in the New Zealand region. N. Z. J. Mar. Freshw. Res. 1969, 3, 57–72. [Google Scholar] [CrossRef]
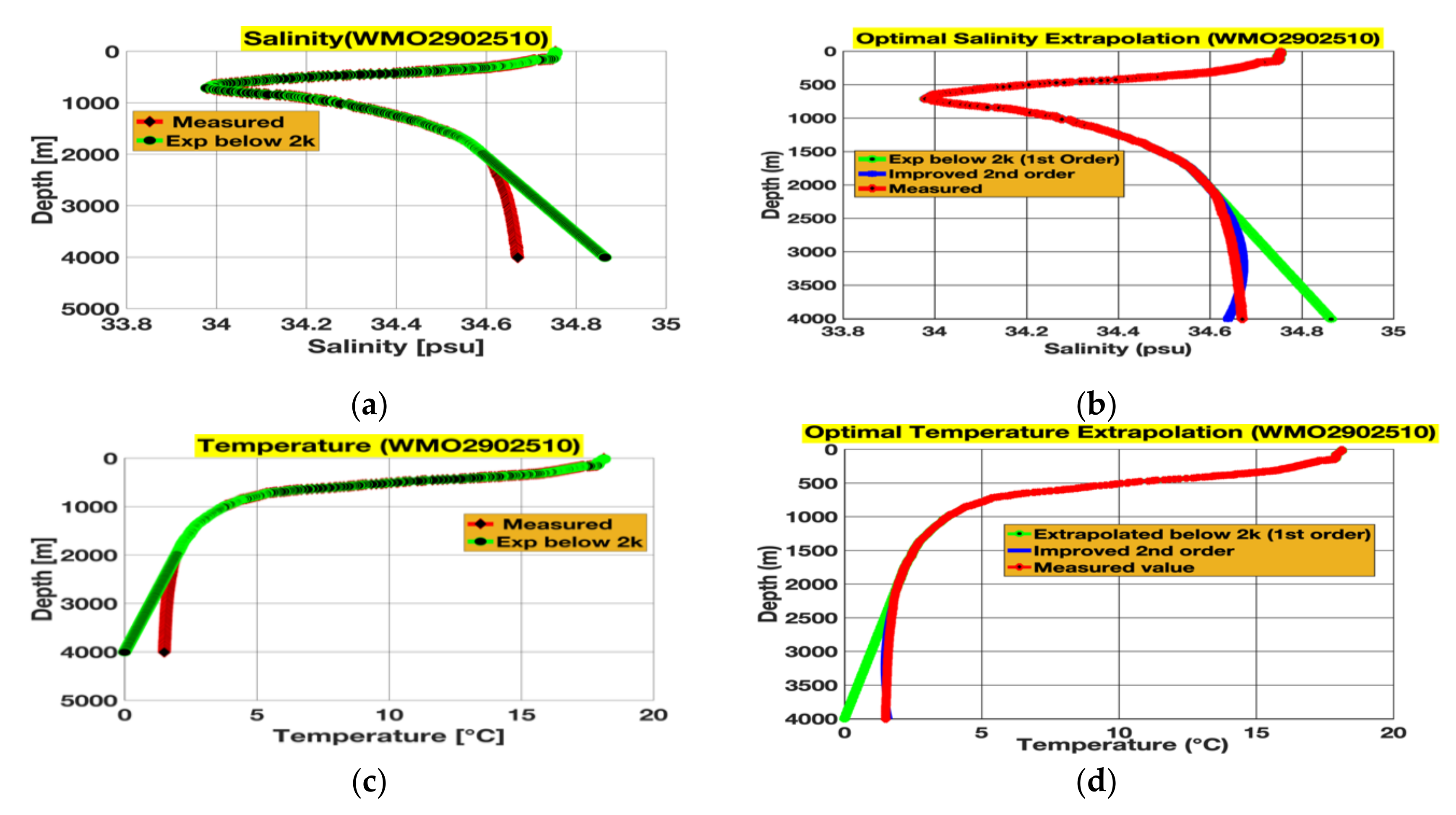
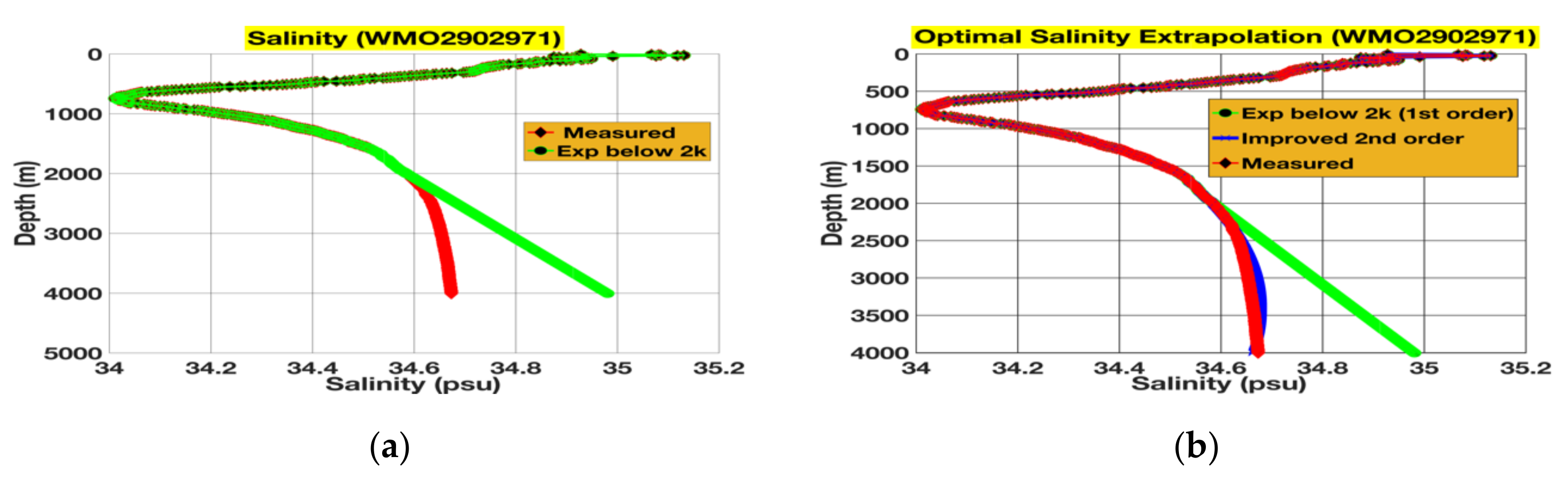
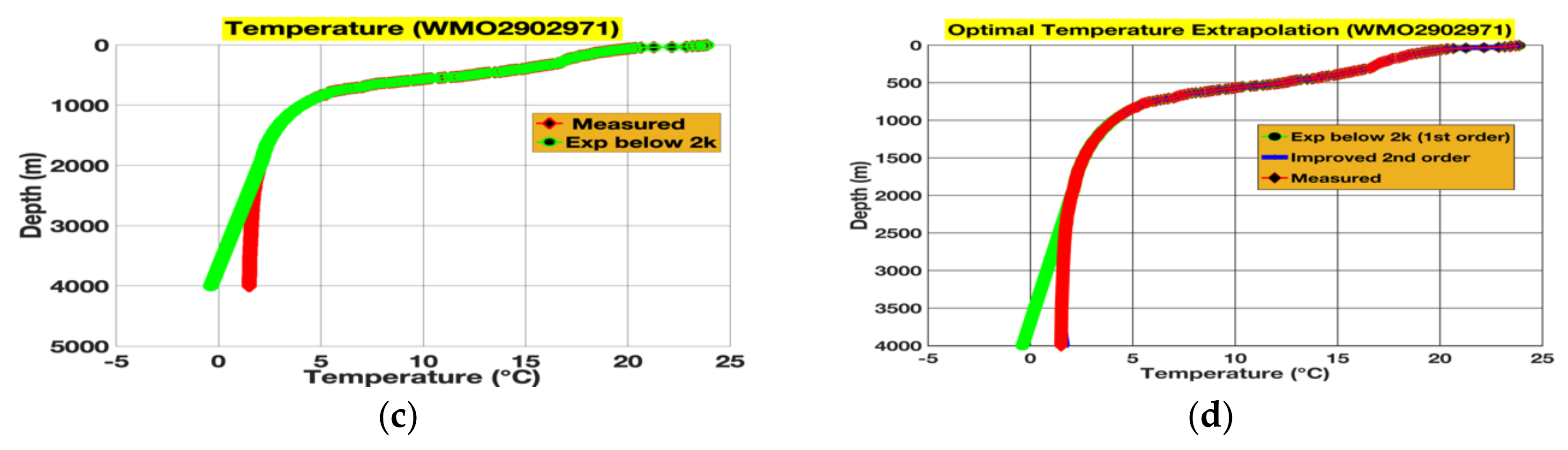
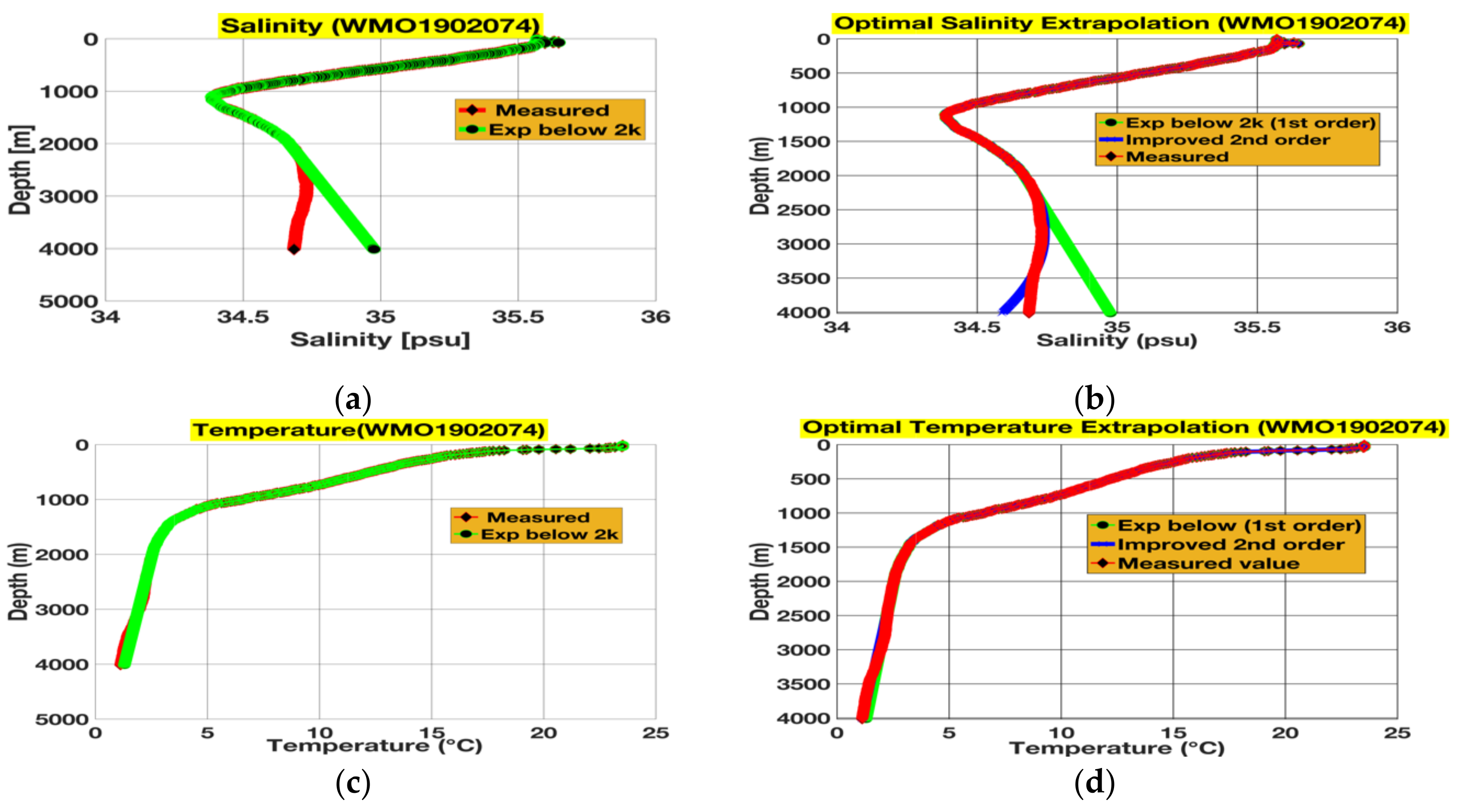
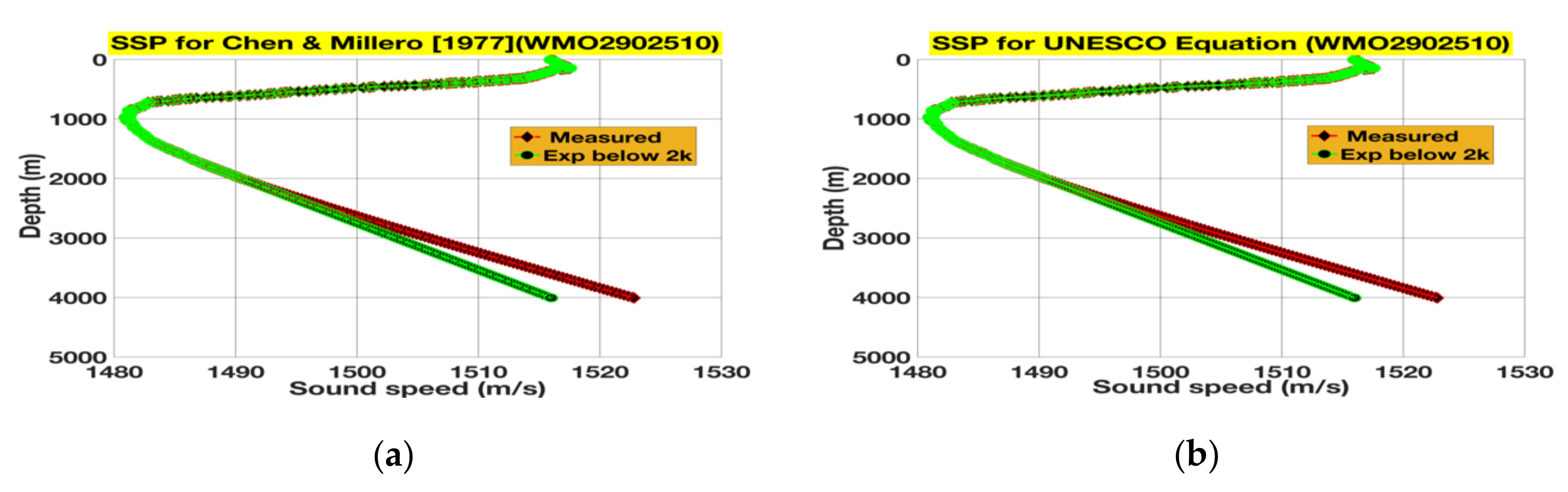
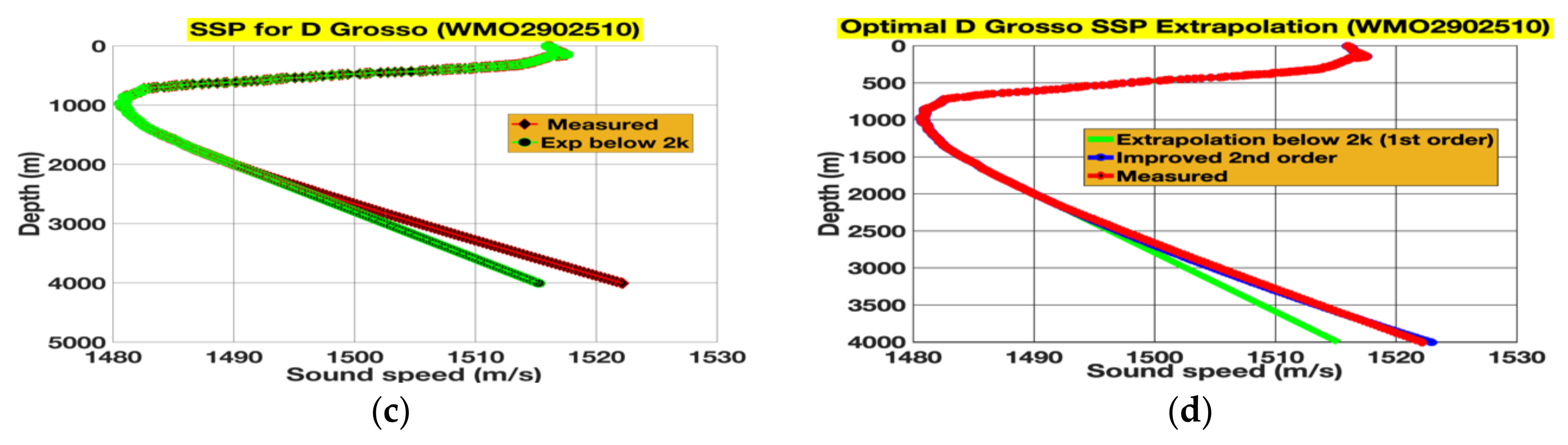
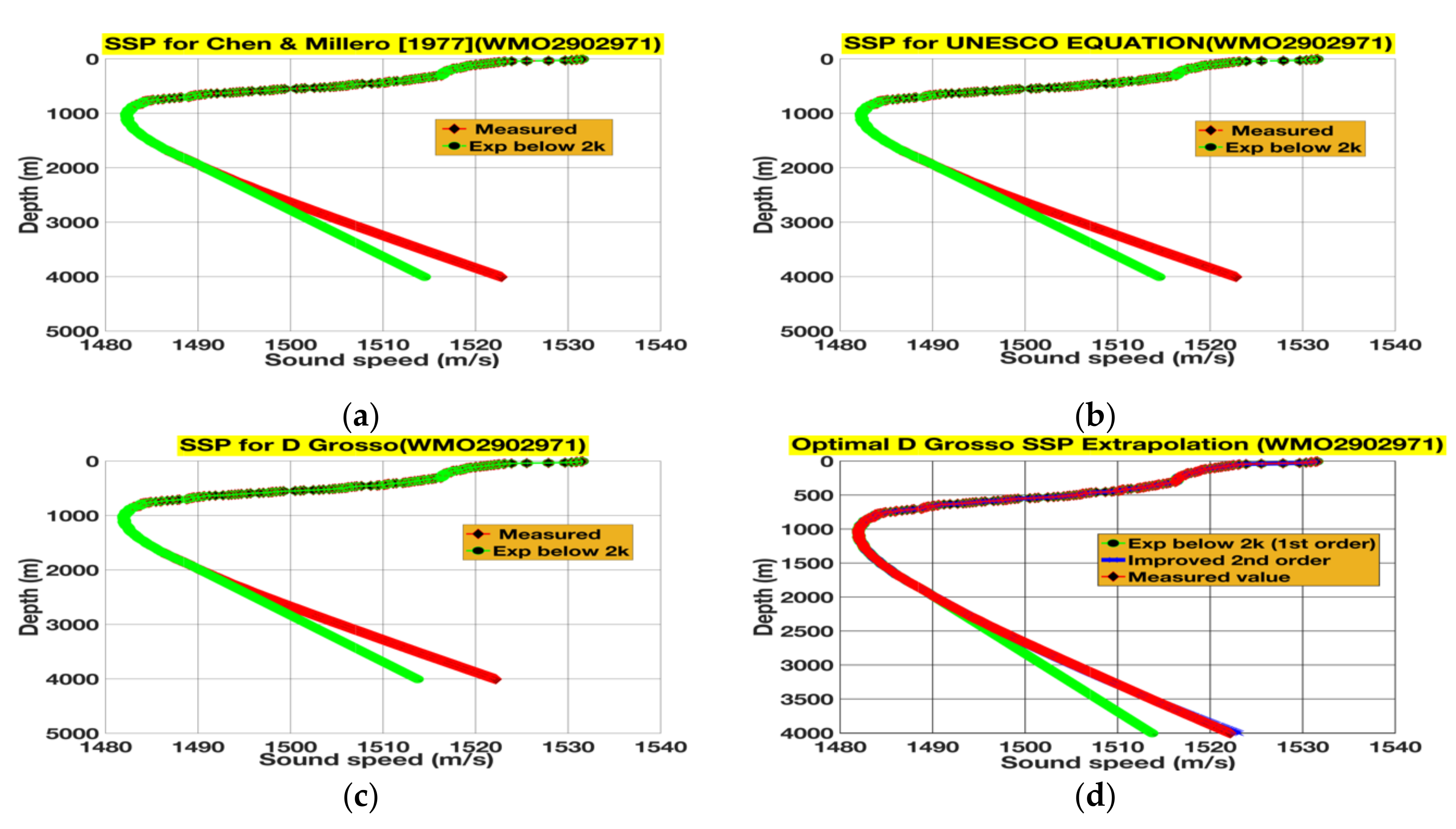
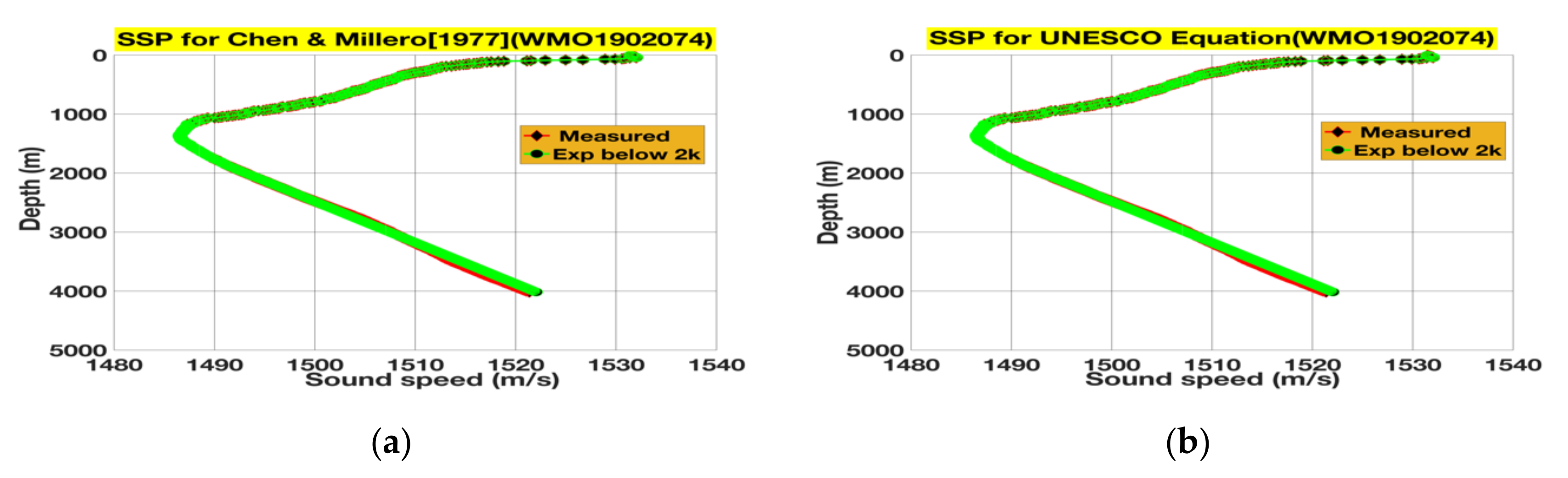

| Float Identity | Cycle Number | Date | Lat, Long. | Location |
|---|---|---|---|---|
| WMO2902510 | 24 | 2 March 2014 | 30.447 N, 146.004 E | Pacific Ocean |
| WMO2902971 | 08 | 12 May 2016 | 29.566 N, 146.364 E | Pacific Ocean |
| WMO1902074 | 08 | 11 April 2016 | 28.998 S, 52.16 E | Indian Ocean |
| Float Identity | Cycle Number | Date | Lat, Long. | Location |
|---|---|---|---|---|
| WMO4902322 | 15 | 17 June 2017 | 24.8972 N, 58.4255 E | Atlantic Ocean |
| WMO5902521 | 71 | 5 Jane 2019 | 38.7563 S, 128.6227 E | Indian Ocean |
| Float Identity | Cycle | Lat, Long. | Date | Time |
|---|---|---|---|---|
| WMO5905738 | 10 | 22.9324 N, 158.5839 W | 31 May 2018 | 05:43:00 |
| WMO5905738 | 11 | 22.9638 N, 158.705 W | 5 June 2018 | 02:14:00 |
| WMO5905738 | 18 | 22.9121 N, 158.715 W | 9 July 2018 | 14:39:00 |
| Float Identity | Cycle | Lat, Long. | Date | Time |
|---|---|---|---|---|
| WMO5905738 | 20 | 22.6443 N, 158.6656 W | 19 July 2018 | 11:52:11 |
| WMO5905739 | 20 | 22.8836 N, 158.7888 W | 3 July 2018 | 04:03:52 |
| WMO5902521 | 20 | 12.0588 N, 154.0620 W | 19 September 2018 | 07:54:23 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, K.; Zhang, M.; Piao, S. Symmetrical and Asymmetrical Rectifications Employed for Deeper Ocean Extrapolations of In Situ CTD Data and Subsequent Sound Speed Profiles. Symmetry 2020, 12, 1455. https://doi.org/10.3390/sym12091455
Iqbal K, Zhang M, Piao S. Symmetrical and Asymmetrical Rectifications Employed for Deeper Ocean Extrapolations of In Situ CTD Data and Subsequent Sound Speed Profiles. Symmetry. 2020; 12(9):1455. https://doi.org/10.3390/sym12091455
Chicago/Turabian StyleIqbal, Kashif, Minghui Zhang, and Shengchun Piao. 2020. "Symmetrical and Asymmetrical Rectifications Employed for Deeper Ocean Extrapolations of In Situ CTD Data and Subsequent Sound Speed Profiles" Symmetry 12, no. 9: 1455. https://doi.org/10.3390/sym12091455
APA StyleIqbal, K., Zhang, M., & Piao, S. (2020). Symmetrical and Asymmetrical Rectifications Employed for Deeper Ocean Extrapolations of In Situ CTD Data and Subsequent Sound Speed Profiles. Symmetry, 12(9), 1455. https://doi.org/10.3390/sym12091455





