Deep-Learning Steganalysis for Removing Document Images on the Basis of Geometric Median Pruning
Abstract
1. Introduction
2. Related Technologies
2.1. Active Steganalysis
2.2. Pruning Methods
3. Deep-Learning Steganography Removal Model
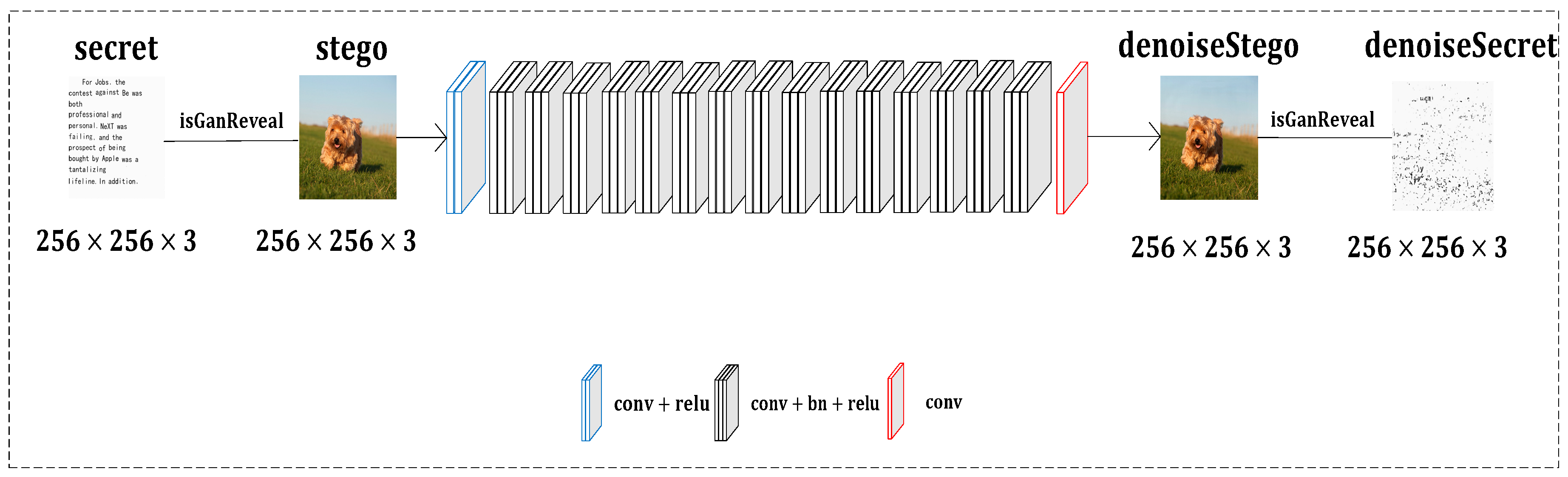
3.1. DnCNN Model
3.2. HGD Model
4. Methods
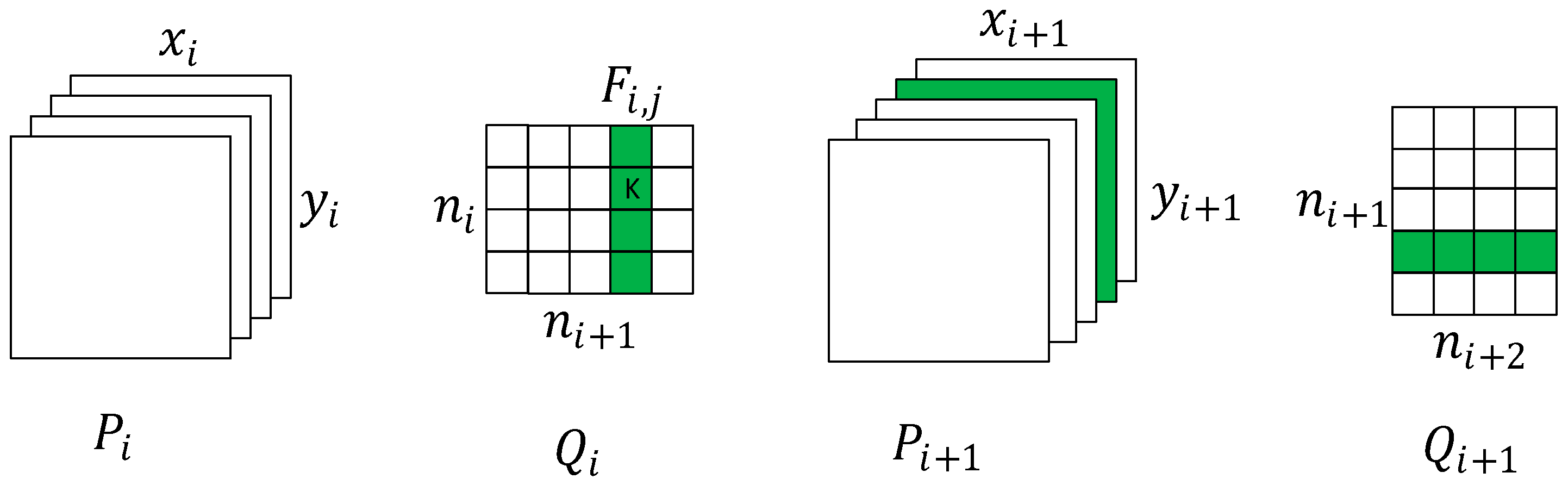
4.1. Pruning Strategy for the Deep-Learning Steganography Removal Model
4.2. Geometric Median Pruning
4.3. Overall Iterative Pruning of Deep-Learning Steganography Removal Model Based on Geometric Median
| Algorithm 1 Pruning the deep-learning steganography removal model via geometric median |
| 1: Prepare the pre-trained DnCNN and HGD models; |
| 2: Calculate geometric median on all filters of a convolutional layer in the deep-learning steganography removal model, as in Formula (2), find the data center point f of filters in the convolutional layer; |
| 3: Filters that have redundant information are closed to the geometric median according to Formula (3). We prune these redundant filters to achieve the purpose of pruning, while maintaining the performance of the models; |
| 4: Prune a filter in a convolution layer, which will affect the kernel matrix and corresponding feature map channels in the next convolutional layer, As analyzed in 4.1. Therefore, it is necessary to remove the number of feature maps channels and corresponding weights involved in pruning. and to match the number of input and output channels of the relevant convolution layer; |
| 5: Retain the remaining kernel matrix after removing filters of one convolution layer of the deep-learning steganography removal model, complete a filter pruning operation based on geometric median. |
| Algorithm 2 Iterative pruning process of the deep-learning steganography removal model |
| 1: Input: Prepare the pre-trained DnCNN and HGD models; |
| 2: Initialization: Set m pruning layers; set the maximum channels pruning rate r; set the channels iteration pruning rate p of the deep-learning steganography removal model. According to the maximum channels pruning rate and channels iterative pruning rate, set the number of iterative pruning channels of each convolutional layer, ; |
| 3: Conditions: Set the DIQA threshold while ensuring the image quality, that is, SSIM > 0.9 for the original image and purified image, SSIM > 0.9 for the stego image and purified image, PSNR > 26 for the original image and purified image, PSNR > 26 for the stego image and purified image; |
| 4: for i = 1:m do for j in C do Call Algorithm 1 to perform a geometric median pruning; Verify the network after each pruning. If the network after pruning meets the DIQA threshold and image-quality assessment, we should prune more channels for this convolutional layer. If the network after pruning does not meet the DIQA threshold and image-quality assessment, jump out of this layer loop, determine the final pruning result of the convolutional layer, save the pruning model and start pruning of the next convolutional layer; end end |
| 5: Output: The pruned models. |
4.4. ABC Automatic Pruning of Deep-Learning Steganography Removal Model Based on Geometric Median
- Nectar sources: Its value is composed of many factors, such as the amount of nectar, the distance from the hive and the difficulty of obtaining nectar. The fitness of nectar source is used to express the above factors;
- Employed bees: The number of employed bees and nectar sources is usually equal. Employed bees have memory function to store relevant information of a certain nectar source, including the distance, direction and abundance of nectar source and share this information with a certain probability to other bees;
- Unemployed bees: The responsibility of unemployed bees including onlooker bees and scout bees is to find the nectar source to be mined. Onlooker bees observe the swinging dance of the employed bees to obtain important nectar source information and choose the bees that they are satisfied with to follow. The number of onlooker bees and employed bees is equal. Scout bees that account for 5–20% of total bee colonies do not follow any other bees and randomly search for nectar sources around the hive.
4.4.1. Initialization of Nectar Sources
4.4.2. Search Process of Employed Bees
4.4.3. Search Process of Onlooker Bees
4.4.4. Search Process of Scout Bees
| Algorithm 3 ABC automatic pruning of deep-learning steganography removal model based on geometric median |
| 1: Input: Prepare the pre-trained DnCNN and HGD models. |
| 2: Initialization: Set t pruning rounds; initialization of nectar sources according to Formula (4); set n pruning layers; maximum channel pruning of each convolutional layer of the model; maximum of poor quality of nectar source is ; the number of iteration search for poor quality of nectar source is . |
| 3: Conditions: Set the DIQA threshold while ensuring the image quality, that is, SSIM > 0.9 for the original image and purified image, SSIM > 0.9 for the stego image and purified image, PSNR > 26 for the original image and purified image, PSNR > 26 for the stego image and purified image, params and flops as small as possible. Use the above conditions as the nectar source fitness value . |
| 4: for i = 1:t do for j = 1:D do The employed bee searches for a new nectar source around the nectar source through formula (5), and calls algorithm 1 to obtain the combinations of each convolutional layer channels of the model, and calculates the fitness value ; if then else end for j = 1:D do Calculate the probability of nectar being selected through formula (6); Generate a random number ; if then The employed bee searches for a new nectar source around the nectar source through formula (5), and calls algorithm 1 to obtain the combinations of each convolutional layer channels of the model, and calculates the fitness value ; if then else end for j = 1:n do if thenperform formula (7); end end |
| 5: endend Output: The pruned models. |
4.5. Analysis of Algorithm
5. Experiments
5.1. Experimental Preparation and Environment
5.2. Results of Pruning Experiments
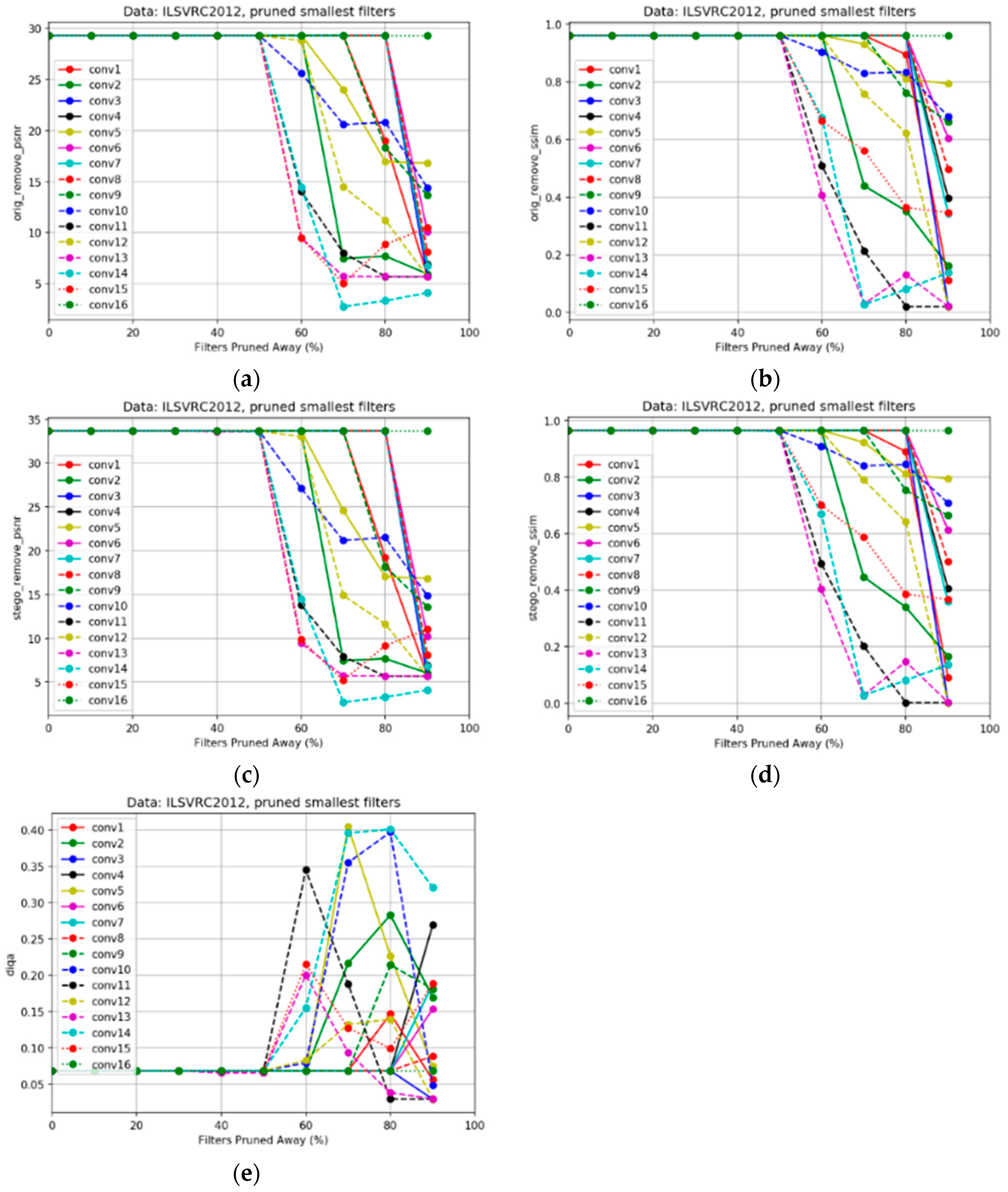
5.2.1. Sensitivity Analysis of the Individual Pruning
5.2.2. Analysis of the Overall, Iterative Pruning
5.2.3. Analysis of the Overall Iterative Pruning Threshold
5.2.4. Analysis of the ABC Automatic Pruning
5.2.5. Analysis of Pruning Rate Based on the Geometric Median Pruning
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Neural Information Processing Systems 25 (NIPS); Curran Associates Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; IEEE: New York, NY, USA, 2015; pp. 1–9. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26–30 June 2016; IEEE: New York, NY, USA, 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Baluja, S. Hiding Images in Plain Sight: Deep Steganography. In Neural Information Processing Systems (NIPS); Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 2069–2079. [Google Scholar]
- Wu, P.; Yang, Y.; Li, X. StegNet: Mega Image Steganography Capacity with Deep Convolutional Network. Future Internet 2018, 10, 54. [Google Scholar] [CrossRef]
- Zhang, R.; Dong, S.; Liu, J. Invisible Steganography via Generative Adversarial Networks. Multimed. Tools Appl. 2018. [Google Scholar] [CrossRef]
- Xu, G.; Liu, B.; Jiao, L.; Li, X.; Feng, M.; Liang, K.; Ma, L.; Zheng, X. Trust2Privacy: A Novel Fuzzy Trust-to-Privacy Mechanism for Mobile Social Networks. IEEE Wirel. Commun. 2020, 27, 72–78. [Google Scholar] [CrossRef]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; IEEE: New York, NY, USA, 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Kang, L.; Ye, P.; Li, Y.; Doermann, D. A deep learning approach to document image quality assessment. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; IEEE: New York, NY, USA; pp. 2570–2574. [Google Scholar] [CrossRef]
- Johnson, N.F.; Jajodia, S. Steganalysis of Images Created Using Current Steganography Software. In International Workshop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 1998; pp. 273–289. [Google Scholar] [CrossRef]
- Jung, D.; Bae, H.; Choi, H.S.; Yoon, S. PixelSteganalysis: Pixel-wise Hidden Information Removal with Low Visual Degradation. arXiv 2019, arXiv:1902.10905. [Google Scholar]
- Oord, A.V.D.; Kalchbrenner, N.; Vinyals, O.; Espeholt, L.; Graves, A.; Kavukcuoglu, K. Conditional Image Generation with PixelCNN Decoders. In Proceedings of the 30th International Conference on Neural Information Processing, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. ntriguing properties of neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Jia, X.; Wei, X.; Cao, X.; Foroosh, H. ComDefend: An Efficient Image Compression Model to Defend Adversarial Examples. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; IEEE: New York, NY, USA, 2019; pp. 6084–6092. [Google Scholar]
- Lei, B.J.; Caurana, R. Do Deep Nets Really Need to be Deep? In Proceedings of the Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–11 December 2014; Curran Associates Inc.: Red Hook, NY, USA, 2014; pp. 2654–2662. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Cun, Y.L.; Denker, J.S.; Solla, S.A. Optimal brain damage. In Neural Information Processing Systems (NIPS); Curran Associates Inc.: Red Hook, NY, USA, 1990; pp. 598–605. [Google Scholar]
- Liu, Z.; Sun, M.; Zhou, T.; Huang, G.; Darrell, T. Rethinking the Value of Network Pruning. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning both Weights and Connections for Efficient Neural Networks. In Neural Information Processing Systems (NIPS); Curran Associates Inc.: Red Hook, NY, USA, 2015; pp. 1135–1143. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Fridrich, J.; Goljan, M.; Hogea, D. Steganalysis of JPEG Images: Breaking the F5 Algorithm. In 5th International Workshop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 2002; pp. 310–323. [Google Scholar] [CrossRef]
- Gou, H.; Swaminathan, A.; Wu, M. Noise Features for Image Tampering Detection and Steganalysis. IEEE Int. Conf. Image Process. 2007, 6, VI-97–VI-100. [Google Scholar] [CrossRef]
- Amritha, P.P.; Sethumadhavan, M.; Krishnan, R. On the Removal of Steganographic Content from Images. Def. Ence J. 2016, 66, 574–581. [Google Scholar] [CrossRef]
- Corley, I.; Lwowski, J.; Hoffman, J. Destruction of Image Steganography using Generative Adversarial Networks. arXiv 2019, arXiv:1912.10070. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Kim, T.; Nowozin, S.; Ermon, S.; Kushman, N. PixelDefend: Leveraging Generative Models to Understand and Defend against Adversarial Examples. arXiv 2017, arXiv:1710.10766. [Google Scholar]
- Liao, F.; Liang, M.; Dong, Y.; Pang, T.; Hu, X.; Zhu, J. Defense against Adversarial Attacks Using High-Level Representation Guided Denoiser. arXiv 2017, arXiv:1712.02976. [Google Scholar]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning Filters for Efficient ConvNets. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- He, Y.; Kang, G.; Dong, X.; Fu, Y.; Yang, Y. Soft Filter Pruning for Accelerating Deep Convolutional Neural Networks. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI), Stockholm, Sweden, 13–19 July 2018. [Google Scholar] [CrossRef]
- He, Y.; Liu, P.; Wang, Z.; Hu, Z.; Yang, Y. Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Li, C. Self-Adaptive Network Pruning. arXiv 2019, arXiv:1910.08906v1. [Google Scholar]
- Madaan, D.; Shin, J.; Hwang, S.J. Adversarial Neural Pruning with Latent Vulnerability Suppression. arXiv 2020, arXiv:1908.04355. [Google Scholar]
- Luo, J.-H.; Wu, J.; Lin, W. ThiNet: A Filter Level Pruning Method for Deep Neural Network Compression. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Sun, J. Channel Pruning for Accelerating Very Deep Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef]
- Yu, R.; Li, A.; Chen, C.-F.; Lai, J.-H.; Morariu, V.I.; Han, X.; Gao, M.; Lin, C.-Y.; Davis, L.S. NISP: Pruning Networks using Neuron Importance Score Propagation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9194–9203. [Google Scholar]
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning Efficient Convolutional Networks through Network Slimming. In IEEE International Conference on Computer Vision (ICCV); IEEE: New York, NY, USA, 2017; pp. 2755–2763. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, N. Data-Driven Sparse Structure Selection for Deep Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Lin, S.; Ji, R.; Yan, C.; Zhang, B.; Cao, L.; Ye, Q.; Huang, F.; Doermann, D. Towards Optimal Structured CNN Pruning via Generative Adversarial Learning. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, X.-Y.; Han, Q.; Cheng, M.-M. Dependency Aware Filter Pruning. arXiv 2020, arXiv:2005.02634. [Google Scholar]
- Guerra, L.; Zhuang, B.; Reid, I.; Drummond, T. Automatic Pruning for Quantized Neural Network. arXiv 2020, arXiv:2002.00523. [Google Scholar]
- Dong, X.; Yang, Y. Network Pruning via Transformable Architecture Search. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2019; pp. 760–771. [Google Scholar]
- Liu, N.; Ma, X.; Xu, Z.; Wang, Y.; Ye, J. AutoCompress: An Automatic DNN Structured Pruning Framework for Ultra-High Compression Rates. AAAI 2020. [Google Scholar] [CrossRef]
- Lin, M.; Ji, R.; Zhang, Y.; Zhang, B.; Wu, Y.; Tian, Y. Channel Pruning via Automatic Structure Search. IJCAI 2020. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the International Conference on Machine Learning, Helsinki, Finland, 5–9 June 2008. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015. [Google Scholar] [CrossRef]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge Distillation: A Survey. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, DC, USA, 16–18 June 2020. [Google Scholar]
- Zhou, G.; Xu, G.; Hao, J.; Chen, S.; Xu, J.; Zheng, X. Generalized Centered 2-D Principal Component Analysis. IEEE Trans. Cybern. 2019, 1–12. [Google Scholar] [CrossRef] [PubMed]

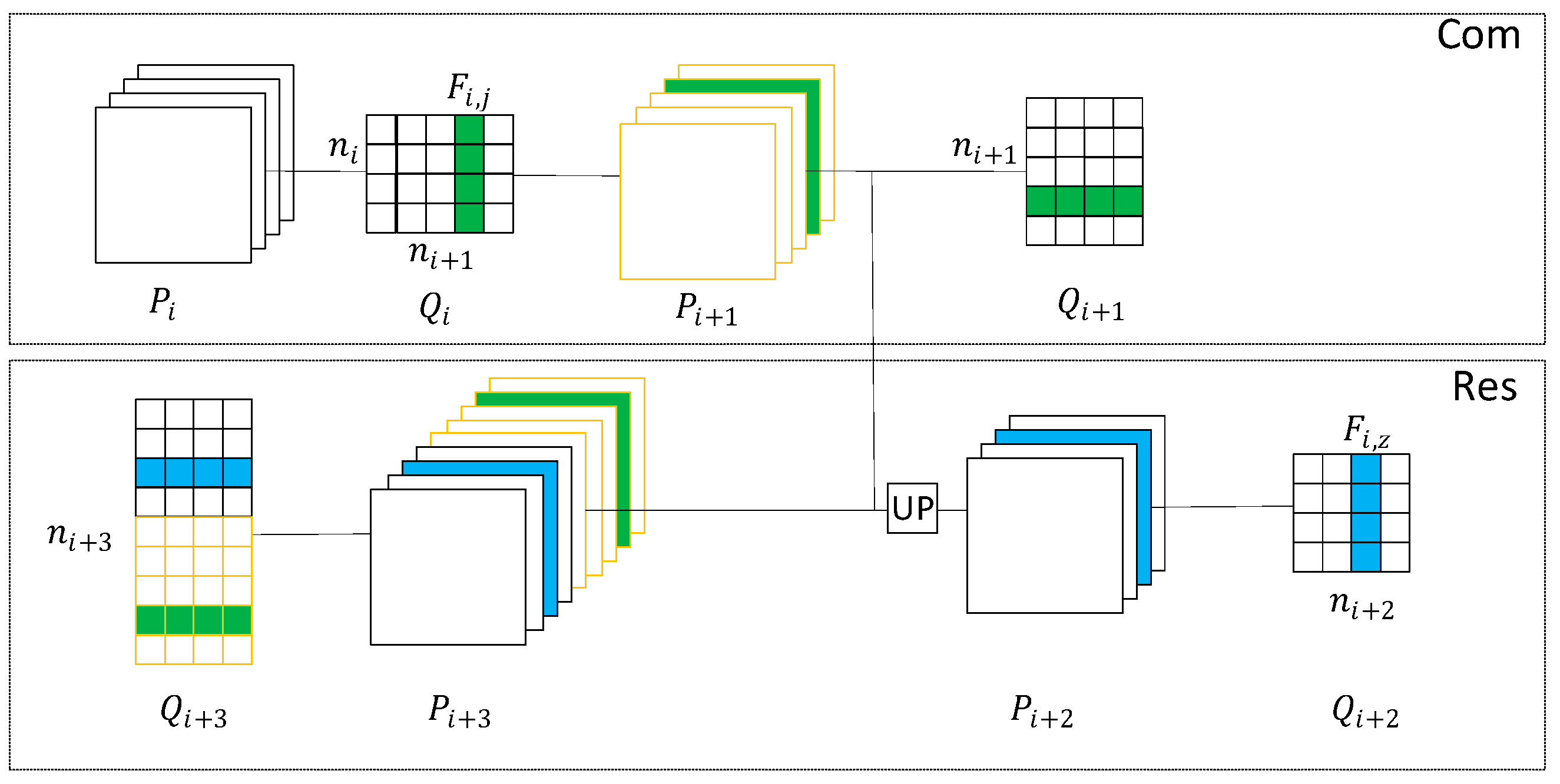
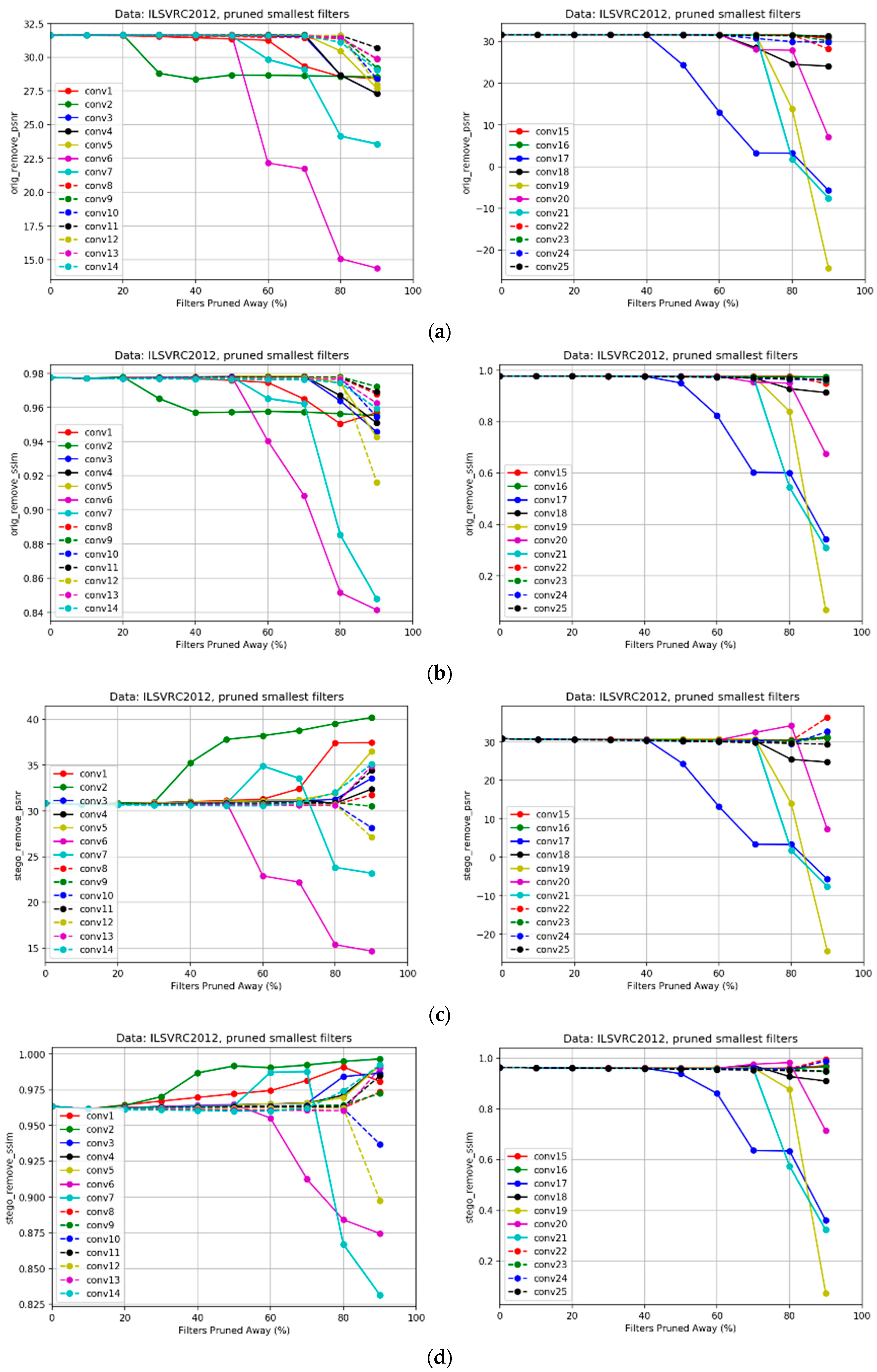
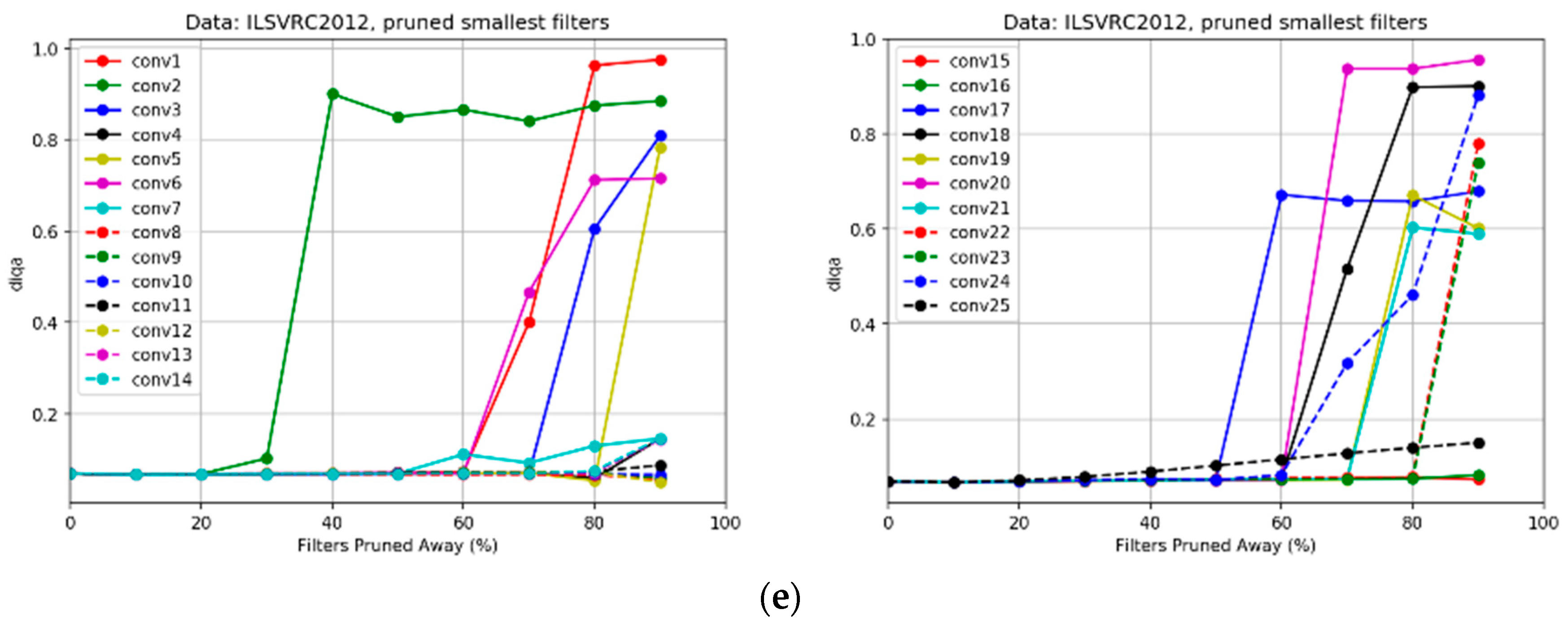




| Model | Orig_Remove_SSIM | Orig_Remove_PSNR | Stego_Remove_SSIM | Stego_Remove_PSNR | DIQA | Params (M) | Flops (G) |
|---|---|---|---|---|---|---|---|
| DnCNN | 0.961 | 29,323 | 0.966 | 33,696 | 0.068 | 0.558 | 36,591 |
| HGD | 0.978 | 31,618 | 0.963 | 30,868 | 0.069 | 11,034 | 50,937 |
| Foraging Behavior of ABC | Channel Pruning Problem of the Deep-Learning Steganography Removal Model |
|---|---|
| Nectar sources | The combinations of each convolutional layer channels of model. |
| Quality of nectar sources | The quality of combinations is achieved by calculating the combination fitness value, that is, sets the DIQA threshold, SSIM > 0.9, PSNR > 26 and params and flops of the model as small as possible. |
| Optimal quality of nectar sources | The params and flops of the model are the smallest and the image quality and document image quality are guaranteed. |
| Pick nectar | Search the pruning structure of the model. |
| Prune | Orig_Remove_SSIM | Orig_Remove_PSNR | Stego_Remove_SSIM | Stego_Remove_PSNR | DIQA | Params (M) | Flops (G) |
|---|---|---|---|---|---|---|---|
| oralModel | 0.961 | 29,323 | 0.966 | 33,696 | 0.068 | 0.558 | 36,591 |
| conv1_rm_44channels (70%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.532 | 34,852 |
| conv2_rm_38channels (60%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.503 | 32,965 |
| conv3_rm_50channels (80%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.462 | 30,304 |
| conv4_rm_50channels (80%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.427 | 27,997 |
| conv5_rm_38channels (60%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.400 | 26,244 |
| conv6_rm_50channels (80%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.360 | 23,583 |
| conv7_rm_50channels (80%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.325 | 21,276 |
| conv8_rm_50channels (80%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.289 | 18,969 |
| conv9_rm_44channels (70%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.258 | 16,939 |
| conv10_rm_31channels (50%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.235 | 15,399 |
| conv11_rm_31channels (50%) | 0.961 | 29,323 | 0.966 | 33,695 | 0.068 | 0.208 | 13,622 |
| conv12_rm_38channels (60%) | 0.956 | 28,811 | 0.962 | 33,018 | 0.083 | 0.175 | 11,443 |
| conv13_rm_38channels (60%) | 0.954 | 28,560 | 0.959 | 32,554 | 0.091 | 0.144 | 9420 |
| conv14_rm_31channels (50%) | 0.954 | 28,548 | 0.957 | 32,497 | 0.092 | 0.119 | 7771 |
| conv15_rm_31channels (50%) | 0.954 | 28,548 | 0.957 | 32,497 | 0.092 | 0.091 | 5993 |
| conv16_rm_57channels (90%) | 0.954 | 28,548 | 0.957 | 32,497 | 0.092 | 0.073 | 4775 |
| Prune | Orig_Remove_SSIM | Orig_Remove_PSNR | Stego_Remove_SSIM | Stego_Remove_PSNR | DIQA | Params (M) | Flops (G) |
|---|---|---|---|---|---|---|---|
| oralModel | 0.978 | 31,618 | 0.963 | 30,868 | 0.069 | 11,034 | 50,937 |
| conv1_rm_38channels (60%) | 0.978 | 31,618 | 0.963 | 30,868 | 0.069 | 11,011 | 49,430 |
| conv2_rm_19channels (30%) | 0.963 | 29,368 | 0.966 | 31,257 | 0.090 | 10,974 | 48,060 |
| conv3_rm_89channels (70%) | 0.963 | 29,368 | 0.966 | 31,257 | 0.090 | 10,835 | 45,787 |
| conv4_rm_89channels (70%) | 0.963 | 29,368 | 0.966 | 31,257 | 0.090 | 10,701 | 43,593 |
| conv5_rm_102channels (80%) | 0.958 | 28,823 | 0.978 | 35,270 | 0.159 | 10,312 | 40,115 |
| conv6_rm_127channels (50%) | 0.958 | 28,823 | 0.978 | 35,270 | 0.159 | 9990 | 38,794 |
| conv7_rm_178channels (70%) | 0.952 | 28,457 | 0.988 | 34,200 | 0.145 | 9373 | 36,266 |
| conv8_rm_204channels (80%) | 0.952 | 28,457 | 0.988 | 34,200 | 0.145 | 8289 | 33,271 |
| conv9_rm_230channels (90%) | 0.952 | 28,654 | 0.987 | 34,693 | 0.175 | 7651 | 32,618 |
| conv10_rm_230channels (90%) | 0.952 | 28,495 | 0.988 | 35,965 | 0.132 | 7067 | 32,020 |
| conv11_rm_230channels (90%) | 0.949 | 27,910 | 0.988 | 35,346 | 0.172 | 5953 | 31,286 |
| conv12_rm_230channels (90%) | 0.943 | 26,070 | 0.988 | 30,255 | 0.128 | 5369 | 31,136 |
| conv13_rm_230channels (90%) | 0.950 | 28,292 | 0.991 | 37,972 | 0.144 | 4784 | 30,987 |
| conv14_rm_230channels (90%) | 0.950 | 28,076 | 0.987 | 36,073 | 0.184 | 4200 | 30,427 |
| conv15_rm_230channels (90%) | 0.951 | 28,334 | 0.987 | 36,249 | 0.137 | 3562 | 29,774 |
| conv16_rm_230channels (90%) | 0.949 | 28,031 | 0.990 | 36,867 | 0.155 | 2978 | 29,176 |
| conv17_rm_102channels (40%) | 0.949 | 28,041 | 0.990 | 36,803 | 0.154 | 2719 | 28,184 |
| conv18_rm_153channels (60%) | 0.949 | 28,041 | 0.990 | 36,803 | 0.154 | 2082 | 25,577 |
| conv19_rm_178channels (70%) | 0.949 | 28,041 | 0.990 | 36,803 | 0.154 | 1507 | 23,220 |
| conv20_rm_153channels (60%) | 0.949 | 28,041 | 0.990 | 36,803 | 0.154 | 1223 | 19,863 |
| conv21_rm_89channels (70%) | 0.949 | 28,041 | 0.990 | 36,803 | 0.154 | 1017 | 16,488 |
| conv22_rm_102channels (80%) | 0.949 | 28,041 | 0.990 | 36,803 | 0.154 | 0.863 | 13,973 |
| conv23_rm_102channels (80%) | 0.949 | 28,041 | 0.990 | 36,803 | 0.154 | 0.781 | 9654 |
| conv24_rm_38channels (60%) | 0.948 | 27,994 | 0.990 | 36,519 | 0.160 | 0.734 | 6623 |
| conv25_rm_57channels (90%) | 0.948 | 27,994 | 0.990 | 36,519 | 0.160 | 0.721 | 5731 |
| Model | Orig_Remove_SSIM | Orig_Remove_PSNR | Stego_Remove_SSIM | Stego_Remove_PSNR | DIQA | Params (M) | Flops (G) |
|---|---|---|---|---|---|---|---|
| oralModel | 0.961 | 29,323 | 0.966 | 33,696 | 0.068 | 0.558 | 36,591 |
| DIQA < 0.2 | 0.954 | 28,548 | 0.957 | 32,497 | 0.092 | 0.073 | 4775 |
| DIQA < 0.4 | 0.954 | 28,548 | 0.957 | 32,497 | 0.092 | 0.073 | 4775 |
| DIQA < 0.6 | 0.954 | 28,548 | 0.957 | 32,497 | 0.092 | 0.073 | 4775 |
| Model | Orig_Remove_SSIM | Orig_Remove_PSNR | Stego_Remove_SSIM | Stego_Remove_PSNR | DIQA | Params (M) | Flops (G) |
|---|---|---|---|---|---|---|---|
| oralModel | 0.978 | 31,618 | 0.963 | 30,868 | 0.069 | 11,034 | 50,937 |
| DIQA < 0.2 | 0.948 | 27,994 | 0.990 | 36,519 | 0.160 | 0.721 | 5731 |
| DIQA < 0.4 | 0.953 | 27,925 | 0.981 | 33,609 | 0.321 | 0.603 | 4349 |
| DIQA < 0.6 | 0.946 | 27,296 | 0.990 | 33,878 | 0.275 | 0.758 | 5642 |
| Threshold | Nectar Source | |
|---|---|---|
| DIQA < 0.2 | 9 | [7, 6, 7, 8, 5, 8, 7, 8, 7, 5, 4, 4, 4, 4, 4, 3] |
| 6 | [4, 6, 6, 5, 5, 5, 5, 4, 6, 5, 5, 5, 5, 4, 5, 4] | |
| DIQA < 0.4 | 9 | [7, 6, 8, 8, 6, 8, 7, 7, 7, 3, 5, 6, 3, 5, 5, 2] |
| 6 | [6, 6, 6, 6, 6, 4, 6, 5, 4, 5, 5, 6, 4, 4, 5, 2] | |
| DIQA < 0.6 | 9 | [7, 6, 7, 7, 5, 6, 3, 8, 5, 4, 3, 6, 6, 4, 4, 3] |
| 6 | [3, 5, 5, 6, 6, 6, 6, 6, 6, 4, 4, 6, 6, 4, 5, 4] |
| Threshold | Nectar Source | |
|---|---|---|
| DIQA < 0.2 | 9 | [5, 2, 3, 4, 7, 4, 9, 5, 9, 8, 7, 2, 5, 4, 4, 5, 3, 5, 7, 5, 7, 8, 6, 6, 1] |
| 6 | [2, 2, 6, 5, 6, 6, 6, 5, 6, 6, 6, 6, 6, 3, 3, 6, 3, 2, 6, 3, 6, 6, 3, 5, 2] | |
| DIQA < 0.4 | 9 | [6, 2, 9, 3, 9, 4, 7, 4, 9, 5, 9, 7, 2, 2, 9, 7, 3, 8, 3, 3, 5, 8, 4, 5, 4] |
| 6 | [4, 2, 6, 6, 5, 3, 5, 6, 6, 6, 6, 6, 5, 6, 6, 6, 3, 6, 6, 6, 6, 1, 5, 4, 4] | |
| DIQA < 0.6 | 9 | [3, 3, 7, 7, 6, 5, 9, 9, 9, 4, 3, 9, 4, 7, 9, 8, 3, 4, 4, 6, 3, 7, 5, 7, 2] |
| 6 | [3, 4, 6, 4, 6, 6, 6, 4, 2, 4, 5, 4, 6, 2, 4, 6, 3, 6, 4, 4, 6, 4, 3, 6, 2] |
| Threshold | Orig_Remove_SSIM | Orig_Remove_PSNR | Stego_Remove_SSIM | Stego_Remove_PSNR | DIQA | Params (M) | Flops (G) | |
|---|---|---|---|---|---|---|---|---|
| oralModel | 0.961 | 29,323 | 0.966 | 33,696 | 0.068 | 0.558 | 36,591 | |
| DIQA < 0.2 | 9 | 0.944 | 27,499 | 0.956 | 31,491 | 0.061 | 0.116 | 7626 |
| 6 | 0.960 | 29,291 | 0.965 | 33,586 | 0.066 | 0.136 | 8900 | |
| DIQA < 0.4 | 9 | 0.955 | 28,797 | 0.960 | 32,940 | 0.084 | 0.104 | 6807 |
| 6 | 0.956 | 28,788 | 0.962 | 32,930 | 0.077 | 0.141 | 9264 | |
| DIQA < 0.6 | 9 | 0.938 | 26,901 | 0.950 | 30,541 | 0.131 | 0.131 | 8565 |
| 6 | 0.954 | 28,560 | 0.959 | 32,556 | 0.091 | 0.133 | 8709 |
| Threshold | Orig_Remove_SSIM | Orig_Remove_PSNR | Stego_Remove_SSIM | Stego_Remove_PSNR | DIQA | Params (M) | Flops (G) | |
|---|---|---|---|---|---|---|---|---|
| oralModel | 0.978 | 31,618 | 0.963 | 30,868 | 0.069 | 11,034 | 50,937 | |
| DIQA < 0.2 | 9 | 0.944 | 28,458 | 0.942 | 30,541 | 0.061 | 2261 | 10,723 |
| 6 | 0.957 | 28,420 | 0.995 | 35,815 | 0.105 | 2993 | 15,843 | |
| DIQA < 0.4 | 9 | 0.955 | 27,726 | 0.985 | 34,092 | 0.385 | 1832 | 10,529 |
| 6 | 0.978 | 31,617 | 0.964 | 30,886 | 0.071 | 2312 | 13,967 | |
| DIQA < 0.6 | 9 | 0.949 | 28,044 | 0.985 | 34,651 | 0.398 | 1556 | 10,451 |
| 6 | 0.953 | 28,291 | 0.993 | 38,681 | 0.582 | 3329 | 14,303 |
| Model | Threshold | Channels | Pruned | Params (M) | Pruned | Flops (G) | Pruned | |
|---|---|---|---|---|---|---|---|---|
| oralModel | 9 | 1030 | 0% | 0.558 | 0% | 36,591 | 0% | |
| overall iterative pruning | DIQA < 0.2 | 9 | 359 | 65.14% | 0.073 | 86.92% | 4775 | 86.95% |
| DIQA < 0.4 | 9 | 359 | 65.14% | 0.073 | 86.92% | 4775 | 86.95% | |
| DIQA < 0.6 | 9 | 359 | 65.14% | 0.073 | 86.92% | 4775 | 86.95% | |
| ABC pruning | DIQA < 0.2 | 9 | 455 | 55.83% | 0.116 | 79.21% | 7626 | 79.16% |
| 6 | 515 | 50.00% | 0.136 | 75.63% | 8900 | 75.68% | ||
| DIQA < 0.4 | 9 | 441 | 57.18% | 0.104 | 81.36% | 6807 | 81.40% | |
| 6 | 524 | 49.13% | 0.141 | 74.73% | 9264 | 74.68% | ||
| DIQA < 0.6 | 9 | 499 | 51.55% | 0.131 | 76.52% | 8565 | 76.59% | |
| 6 | 511 | 50.39% | 0.133 | 76.16% | 8709 | 76.20% |
| Model | Threshold | Channels | Pruned | Params (M) | Pruned | Flops (G) | Pruned | |
|---|---|---|---|---|---|---|---|---|
| oralModel | 9 | 4870 | 0% | 11,034 | 0% | 50,937 | 0% | |
| overall iterative pruning | DIQA < 0.2 | 9 | 1210 | 75.15% | 0.721 | 93.47% | 5731 | 88.75% |
| DIQA < 0.4 | 9 | 1134 | 76.71% | 0.603 | 94.54% | 4349 | 91.46% | |
| DIQA < 0.6 | 9 | 1263 | 74.07% | 0.758 | 93.13% | 5642 | 88.92% | |
| ABC pruning | DIQA < 0.2 | 9 | 2242 | 53.96% | 2261 | 79.51% | 10,723 | 78.95% |
| 6 | 2536 | 47.93% | 2993 | 72.87% | 15,843 | 68.90% | ||
| DIQA < 0.4 | 9 | 2185 | 55.13% | 1832 | 83.40% | 10,529 | 79.33% | |
| 6 | 2324 | 52.28% | 2312 | 79.05% | 13,967 | 72.58% | ||
| DIQA < 0.6 | 9 | 1906 | 60.86% | 1556 | 85.90% | 10,451 | 79.48% | |
| 6 | 2725 | 44.05% | 3329 | 69.83% | 14,303 | 71.92% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, S.; Weng, W.; Chen, K.; Lai, J. Deep-Learning Steganalysis for Removing Document Images on the Basis of Geometric Median Pruning. Symmetry 2020, 12, 1426. https://doi.org/10.3390/sym12091426
Zhong S, Weng W, Chen K, Lai J. Deep-Learning Steganalysis for Removing Document Images on the Basis of Geometric Median Pruning. Symmetry. 2020; 12(9):1426. https://doi.org/10.3390/sym12091426
Chicago/Turabian StyleZhong, Shangping, Wude Weng, Kaizhi Chen, and Jianhua Lai. 2020. "Deep-Learning Steganalysis for Removing Document Images on the Basis of Geometric Median Pruning" Symmetry 12, no. 9: 1426. https://doi.org/10.3390/sym12091426
APA StyleZhong, S., Weng, W., Chen, K., & Lai, J. (2020). Deep-Learning Steganalysis for Removing Document Images on the Basis of Geometric Median Pruning. Symmetry, 12(9), 1426. https://doi.org/10.3390/sym12091426





