In this section, we will discuss how to obtain a positive region reduct by using PR-SADT in theory. Next, two efficient subalgorithms are proposed. Finally, the complete reduction algorithm based on PR-SADT is presented.
4.1. Positive Region Reduction Method Based on PR-SADT
PR-SADT is different from the original decision table because it changes and deletes some objects. To obtain a positive region reduct of the original decision table, it is necessary to provide the related description.
In general, a positive region reduction keeps the positive region of the target decision table unchanged. Although all of the granules or objects in the positive region are exact, the rough granules or objects cannot be ignored. In [
10], we noted that a positive region reduction method should satisfy the following discernibility matrix
M = (
m(
i,
j)).
Matrix
M illustrates the discernibility relationships corresponding to positive region reduction. To explain these relationships, we classified and listed them in
Table 3.
For the original inconsistent decision table, it is necessary to analyze the “type of granule pairs” and the “decision value set” for judging whether a granule pair should be discerned.
If the original decision table is reformed to a PR-SADT by using Algorithm 1, all of the rough granules in the original decision table are changed to exact granules with the new decision value dnew. This means that the third type is changed to the first type. In a similar way, the fourth type of the granule pair is changed to the second type.
In conclusion, the discernibility relationships corresponding to positive region reduction in PR-SADT are described in
Table 4.
It is worth noting that there are no rough granules or repeating objects in a PR-SADT calculated by Algorithm 1. Each granule in a PR-SADT only has one object. Therefore, the object pair is used to judge the discernibility relationship for convenience. In
Table 4, there are only two items, which are less than those in
Table 3, and only the “decision value set” is necessary.
Based on
Table 4, we gave a new definition on the positive region reduct, which is described as follows.
Definition 3. Let Sp be a PR-SADT without repeated objects. An attribute set R⊆C is called a positive region reduct if and only if R satisfies the following two conditions:
The first condition ensures the discernibility relationship corresponding to an unchanged positive region reduct. This means that each object pair with different decision values in PR-SADT should be discerned. The second condition means that each attribute in a reduct is necessary. They are jointly sufficient and individually necessary to represent a positive region reduct if a PR-SADT is constructed.
4.2. Fast Core Attribute Calculation Based on PR-SADT
In this section, a special core attribute calculation algorithm is presented for the novel heuristic reduction method.
Theorem 1. Let a PR-SADT without repeated objects Sp and the last conditional attribute, Ifis a core attribute, then, which satisfies the conditions: (xk,xk+1) ,, and, where B = {a1,a2,…,an−1}.
Proof. In a consistent decision table, if , then and |Id([xi]B)|>1. This means that , it has . Considering that Sp is a PR-SADT, it also has . □
Theorem 1 shows three necessary conditions on the last condition attribute an. At the same time, the conditions (xk,xk+1), mean that the attribute an is the unique attribute that discerns the object pair (xk, xk+1), and means that the object pair should be discerned according to Definition 3. Hence, the three conditions in Theorem 1 are also sufficient to check whether an is a core attribute or not. Based on the above conclusion, an algorithm is given as follows.
If flag = 1, then the last condition attribute is a core attribute. In the worst case, Algorithm 2 iterates through the data set and has a time complexity of O(|U||C|).
The output of Algorithm 2 has two possibilities. If the last condition attribute is not a core attribute (
flag = 0), one can efficiently check a core attribute by applying Theorem 2, which is described as follows.
| Algorithm 2. Check the last condition attribute an. |
| Input: a PR-SADT |
| Output: flag |
| 1: Begin |
| 2: flag = 0; |
| 3: for k = 1: |U|-1 |
| 4: if (xk,xk+1), , and |
| 5: flag = 1 and return |
| 6: End |
| 7: End |
| 8: end |
Theorem 2. Suppose S1 is the new decision table when the last column data of a PR-SADT Sp is deleted. If, then RED(S1)RED(Sp) and RED(S1)≠.
Proof. Let RED(Sp)= R1∪R2, where R2 is the set of reducts that includes the last condition attribute an. Owing to , R1≠. According to the relationship between Sp and S1, it has R1= RED(S1). Thus, RED(S1) RED(Sp) and RED(S1)≠. □
Theorem 2 shows that the column data corresponding to the last condition attribute is redundant for a heuristic reduction algorithm if an is not a core attribute. Namely, it is effective for obtaining a reduct of the original decision table based on S1 because RED(S1) RED(Sp) and RED(S1)≠. To reduce the running time of all of the remaining heuristic steps, it is necessary to delete the data of column an.
It is worth noting that it is impossible to obtain a reduct including an if the last column data is deleted. This shortcoming is acceptable because only one reduct is required in a heuristic reduction algorithm.
Algorithm 3 has several special features. First, it only calculates a single core attribute. Second, it deletes some redundant column data. Third, the output of Algorithm 3 is a relative core attribute. In other words, owing to some redundant column data have been deleted in Algorithm 3, the output is just a core attribute of S1. Considering RED(S1) RED(Sp), it has . Thus, the output may not be a core attribute of the original decision table Sp.
The time complexity is dependent on the number of redundant condition attributes. In the worst case that the output is
a1, the time complexity is
O(|
U||
C|
2/2). The more exact analysis on time complexity is shown in
Section 4.4.
| Algorithm 3. The special core attribute calculation algorithm. |
| Input: a PR-SADT |
| Output: a core attribute |
| 1: Step 1: check the last condition attribute by Algorithm 2. |
| 2: Step 2: if flag = 0, then delete the data corresponding to the last condition attribute and jump to step1; else step3. |
| 3: Step 3: output the last condition attribute |
4.3. Fast Positive Region Calculation Based on PR-SADT
In this section, a fast method based on PR-SADT is presented to calculate the positive region with respect to attribute set R.
Theorem 3. Let attribute set R = {a1,a2,…,am}, U/R = {X1,X2,…,XK}. For, if, then, and it satisfies: Id(xk)≠Id (xk+1).
Proof. In a PR-SADT, the objects in a granule with respect to attribute set R are adjacent. Suppose, where q = |Xi|. Owing to , it has |Id (Xi)| >1. Hence, and it satisfies Id (xk)≠Id (xk+1). □
Theorem 3 illustrates a simple way to discern the positive region with respect to R. The related algorithm is described as follows.
Algorithm 4 calculates the positive region with respect to
R by scanning a PR-SADT once. The time complexity is
O(|
U||
R|), where |
R|≤|
C|. As a contrast, the time complexity of a classical positive region calculation is
O(|
U|
2|
C|). The positive region calculation algorithm in [
29] has the complexity of
O(|
U||
C|
2). In [
32], the complexity of calculating the positive region is
O(|
U||
C|log|
U|).
| Algorithm 4. Calculate the positive region with respect to R in a PR-SADT. |
| Input: a PR-SADT, attribute set R = {c1,c2,…,cm}. |
| Output: the positive region with respect to R. |
| 1: Step 1: set the default value. |
| PR =, gra = {x1}, flag = 0. |
| 2: Step 2: compare the adjacent object pair |
| For i = 1: |U|−1 |
| gra = gra {xi+1} if ;//discern the object in a granule; |
| flag = 1 if and Id (xi)≠Id (xi+1);//the granule is rough if flag is 1; |
| PR = PR gra if and flag == 0;//record the exact granule; |
| gra = {xi+1}, flag = 0 if ;//prepare for the next granule |
| end |
| 3: Step 3: record the last exact granule. |
| If flag==0 |
| PR=PR gra;//record the last exact granule |
| end |
| 4: Step 4: output PR. |
Example 2. According to Algorithm 4, the positive region of the PR-SADT in Table 2 is calculated by the following process. Suppose
R = {
a1,
a2}. In step 1,
PR=,
gra = {
x1},
flag =0. In step 2, these parameters were calculated in
Figure 1.
In step 3, the last object x5 is added into PR. Finally, output the positive region .
4.4. The Attribute Reduction Algorithm Based on PR-SADT
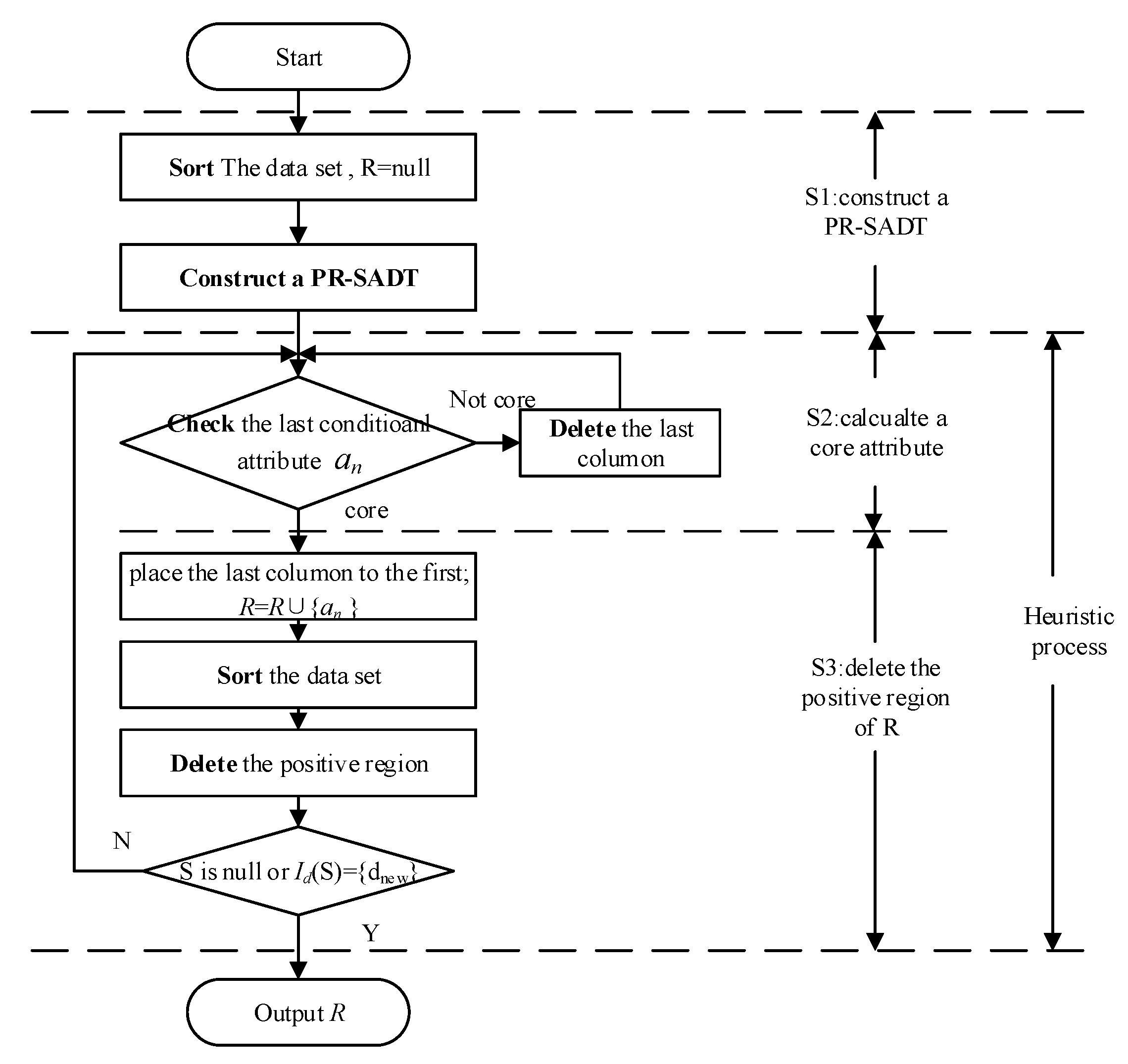
The fast positive region reduction algorithm based on PR-SADT (FPRA) was proposed as Algorithm 5, and the related flow chart is described as
Figure 2.
| Algorithm 5. The fast positive region reduction algorithm based on PR-SADT (FPRA) |
| Input: a decision table S. |
| Output: a complete reduct. |
| 1: Step 1. R =. Sort the original decision table. |
| 2: Step 2. Delete the repeated objects, and calculate a PR-SADT by Algorithm 1. |
| 3: Step 3. Check the last condition attribute an by Algorithm 2. If it is a core attribute, then jump to step 5; else, step 4. |
| 4: Step 4. Delete the last column data, and jump to step 3. |
| 5: Step 5. R = R∪{ak }. Place the last column to the first column, and sort the decision table. |
| 6: Step 6. Calculate the positive region with respect to R by Algorithm 4. Delete the positive region. |
| 7: If Sp is null or Id(Sp) is dnew, then output the reduct R; else, jump to step 3. |
Analysis on the completeness of FPRA:
FPRA satisfies two key features. First, it adopts the reduct construction by deletion. Second, each attribute in R is a core attribute with respect to the related heuristic steps. Thus, R is a complete reduct.
The detail proof is described as follows.
Considering any attribute , there is a object pair (xk,xk+1), which satisfies the conditions according to step 3 in FPRA: (xk,xk+1), , and , where B=Ri∪{a1,a2,…,ai−1}, . This means that the object pair (xk,xk+1) cannot be discerned by B. At the same time, owing to , it is concluded that the object pair (xk,xk+1) cannot be discerned by R-{ai}. However, the object pair can be discerned by R according to Algorithm 5. Thus, attribute ai is essential for attribute set R.
In conclusion, the attributes of R are jointly sufficient and individually necessary for the original data set. Thus, R is a complete reduct.
Analysis on time complexity:
FPRA includes three subprocesses: the S1 process of constructing a PR-SADT (step 1 and step 2), the S2 process of calculating a core attributes (step 3->step 4->step 3) and the S3 process (step 5->step 6).
Considering an original decision table, one adopts the algorithm in [
27,
30] to construct a PR-SADT with the time complexity of
O(|
U||
C|). However, the real running times of algorithms in [
27,
30] are dependent on the good programming style or habit. In the related experimental section, we apply the sortrows function to sort a decision table. Step 2 is accomplished by Algorithm 1, and the time complexity is
O(|
U||
C|). Thus, the time complexity of the S1 subprocess is
O(|
U||
C|).
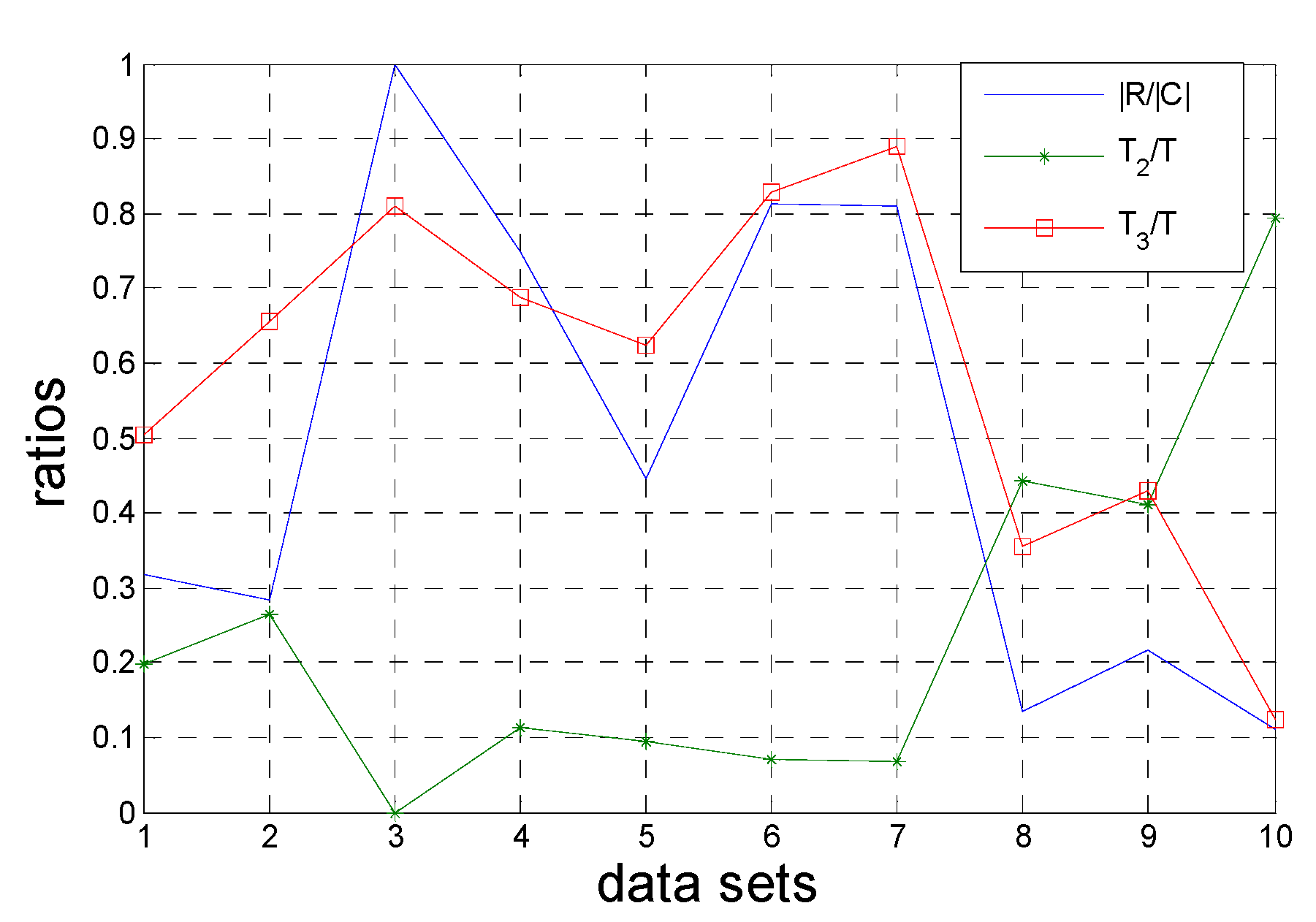
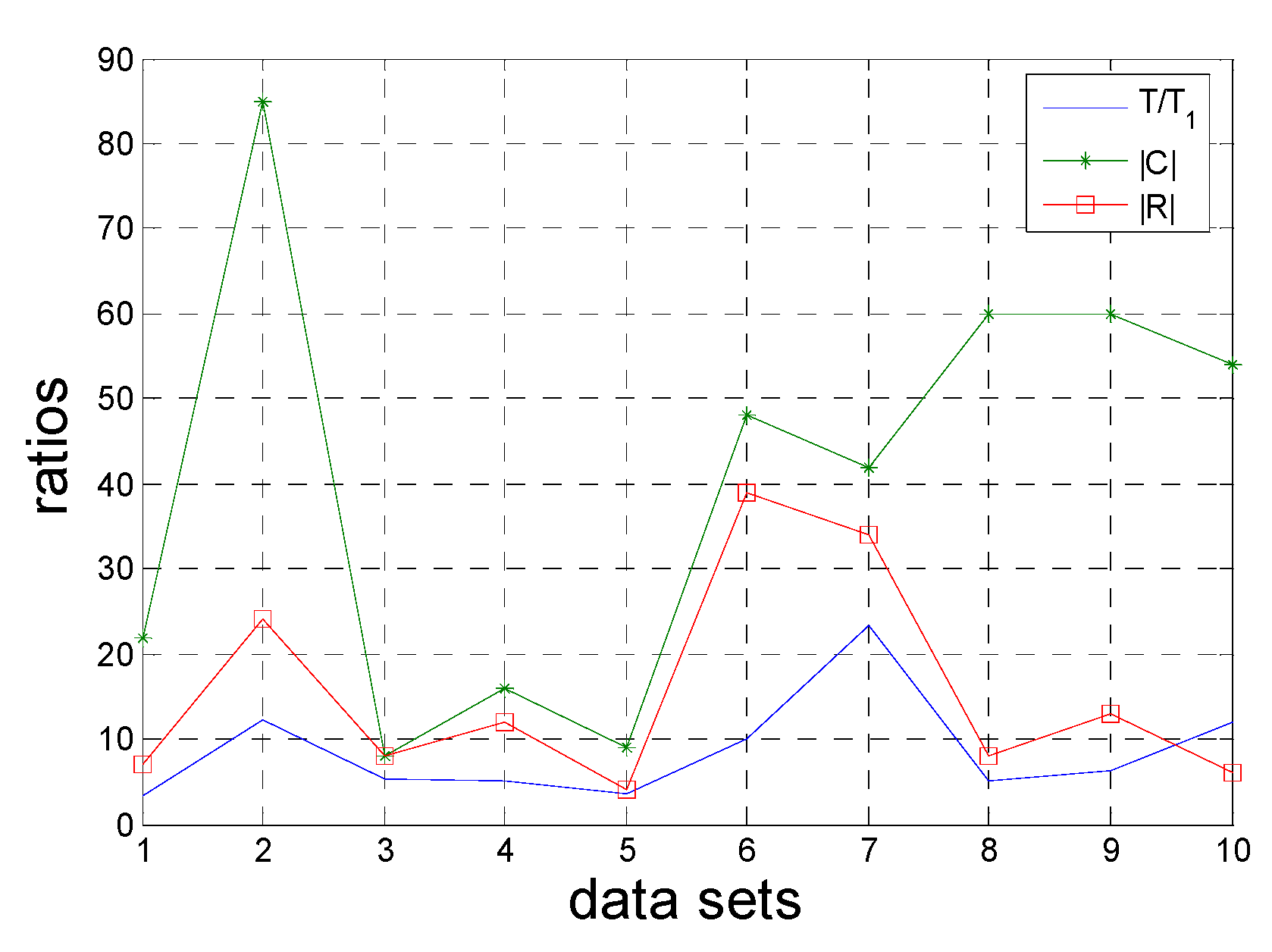
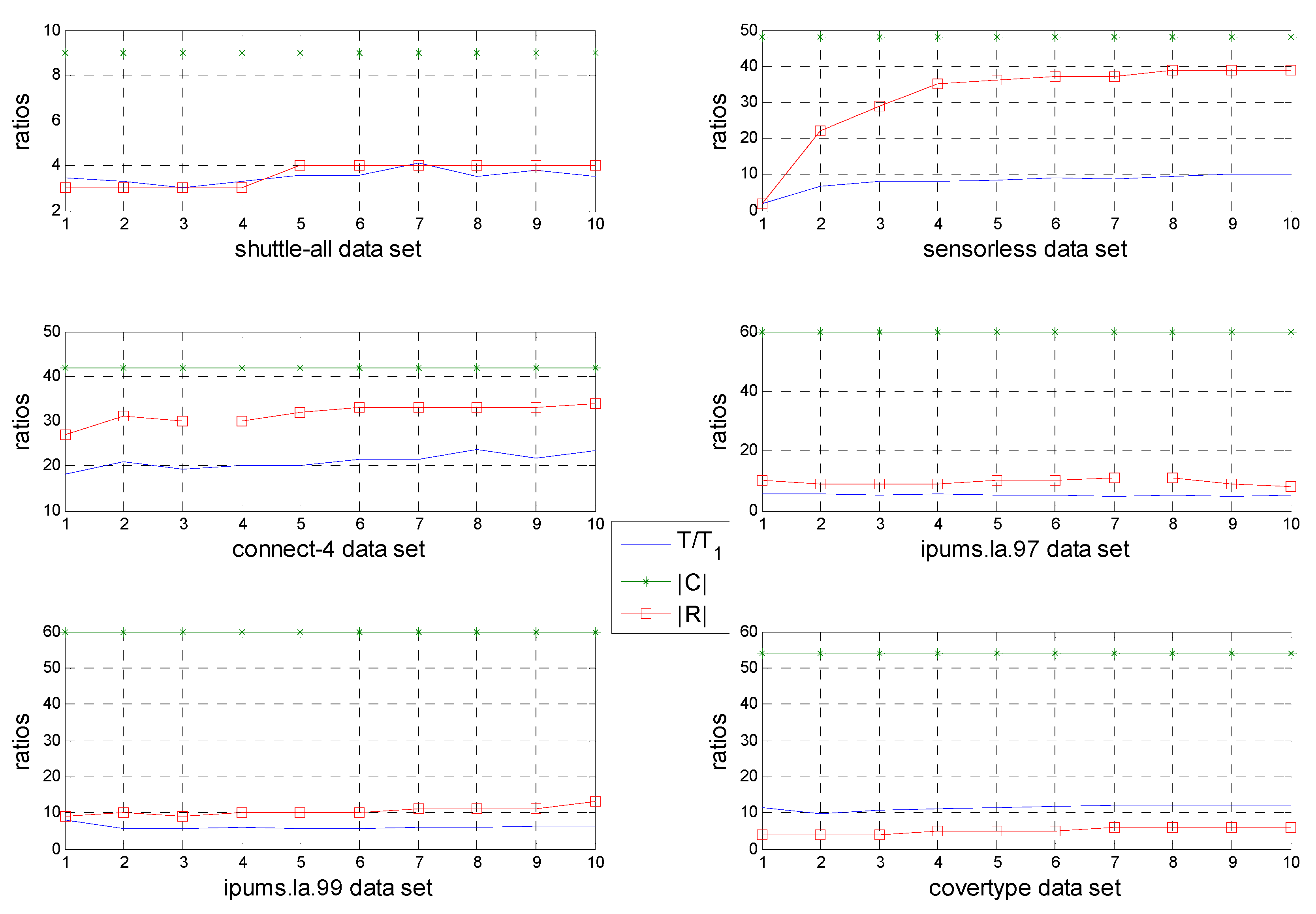
In the next steps, the number of object sets and condition attribute sets are different in each heuristic process. The S2 process (step 3->step 4) deletes some related columns of data set, and the S3 process (step 5->step 6) rearranges the PR-SADT and deletes the related positive regions (some rows of data set). These two subprocesses reduce |U| and |C| and are highly efficient in optimizing the time complexity of FPRA.
Let Ui and Ci represent the object set and condition attribute set of the ith heuristic process, respectively. It has ,, where k = |R| is the number of attributes in reduct R, C1 = C, and |U1| = |U/C|.
Step 3 is calculated with Algorithm 2, and the time complexity is O(|Ui||Ci|). Step 5 sorts the decision table, and the complexity of the ith heuristic process is O(|Ui||Ci|). The time complexity of step 6 includes two parts. One comes from Algorithm 4 and is represented as O(i |Ui|), where i is the number of attributes of R for the ith heuristic process. The other part originated by deleting the positive region, and it also has a time complexity of O(i |Ui|).
In Algorithm 5, S2 subprocess will be performed |R| times and thus has a time complexity of where Qi = |Ci|-|Ci+1|. S3 will also be performed |R| times with time complexity of .
Finally, the total time complexity is
. In the best case where
R = {
c|C|}, even the speed of O(|
C||
U|) is possible. In the worst case where
R = C, the time complexity is
. Considering
R is the output of FPRA, the time complexity is treated as
. The time complexity of FPRA is considerably less than those of traditional algorithms, which has a time complexity of
O(|
U|
2|
C|
2) [
2,
27]. To stress the advantage of Algorithm 4, some excellent reduction algorithms are compared and listed in
Table 5.
Obviously, the time complexity of FPRA is less than those of the algorithms in [
2,
38,
39]. It is worth noting that the
Ui of the algorithm in [
1] is different from
Ui of FPRA. This means that it is hard to compare the efficiencies of the two algorithms (algorithm in [
1] and FPRA) by the time complexity in
Table 5. The related experiments in
Section 5 will propose the more effective evidence to represent the advantage of FPRA.
Analysis on the characteristic of FPRA:
To summarize, FPRA is complete and efficient. It has the following important features and advantages.
- 1.
FPRA is dependent on an efficient sort function.
FPRA just repeats a simple procedure: sort->compare->delete. Only the most efficient sort function is considered in FPRA. Thus, all the comparisons sort algorithms, such as Bubble sort (O(n2)), Shell sort (O(nlogn)), Merge sort (O(nlogn)), Quick sort (O(nlogn)), etc., are not suitable for FPRA because of the limit of O(nlogn). Instead, bucket sort algorithms are considered because their time complexities below O(nlogn). In fact, we did not pay attention to how to design a sort function because many tools or software provide the efficient sort functions. Additionally, the sortrows function or the Shuffle in MapReduce is highly recommended.
- 2.
FPRA does not calculate any attribute significances.
Most of traditional heuristic attribute reduction algorithms would provide a simple or complex definition to calculate attribute significances of all the condition attributes. No matter how simple the definition is, it is necessary to calculate and compare the significances of all the attributes and select the most significant attribute. This calculation process on significance would be run (2|C|-|R|+1) ×|R|/2 times if the addition construction was adopted, or (|C|+|R|+1|)×(|C|-|R|)/2 times if the deletion construction was adopted. As a comparison, the special core attribute calculation in FPRA only would be run |C| times.
- 3.
The heuristic method of FPRA is more efficient and concise.
The traditional heuristic algorithms include two kinds of calculation: the entire core set calculation before the heuristic process and attribute significance calculation in heuristic processes, respectively. As a comparison, FPRA only has a kind of calculation: core attribute calculation in heuristic processes. In detail, FPRA calculates a single core attribute in each heuristic process, while the traditional algorithms have to calculate the attribute significances of all the existed condition attributes.
Besides, each conditional attribute of FPRA is checked at most once. In the traditional heuristic algorithms, a conditional attribute would be checked (2|C|-|R|+1)×|R|/(2|C|) or (|C|+|R|+1|)×(|C|-|R|)/(2|C|) times in average. Therefore, FPRA is more efficient and concise than the traditional heuristic algorithms.