A Confront between Amati and Combo Correlations at Intermediate and Early Redshifts
Abstract
1. Introduction
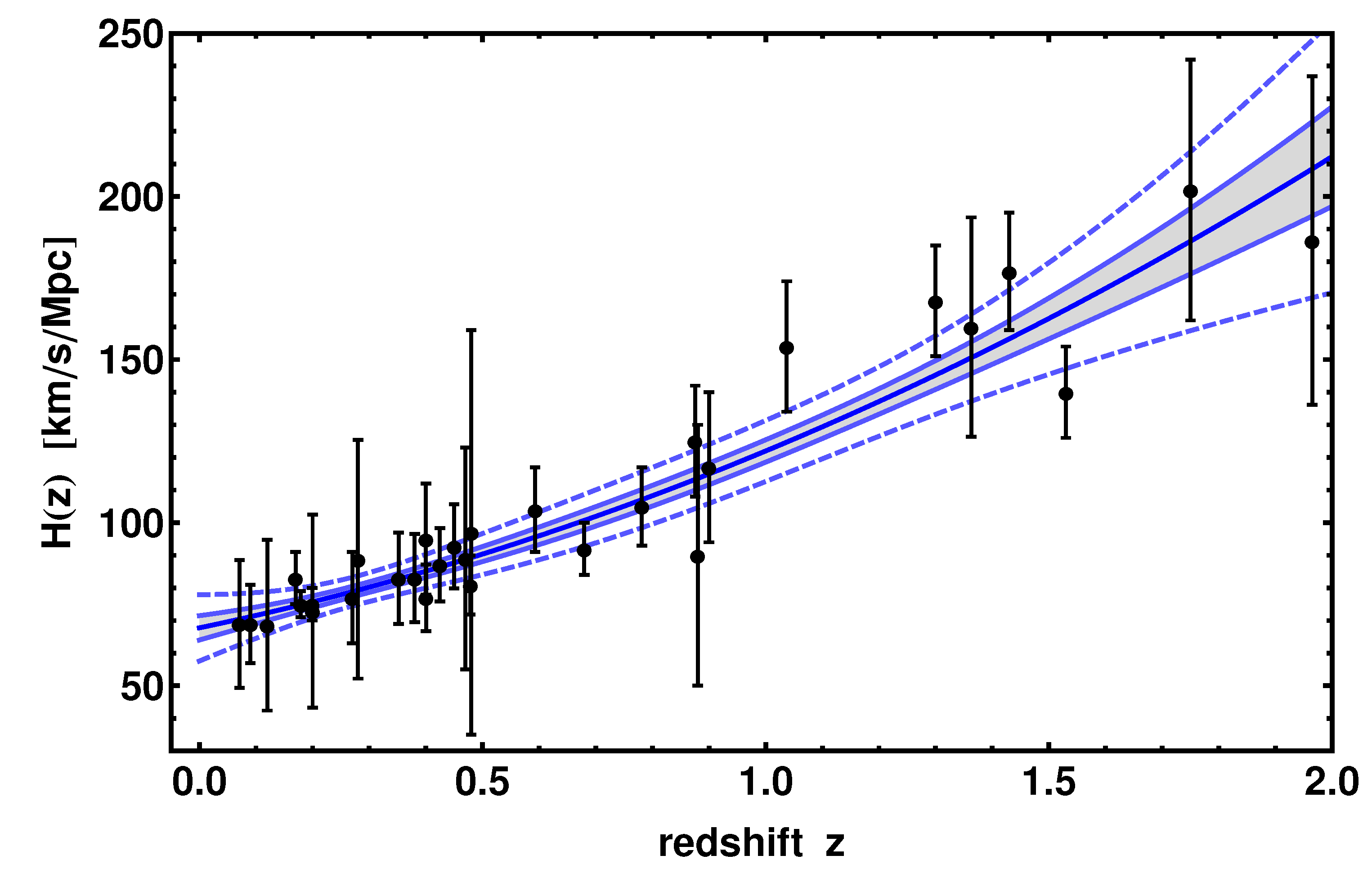
2. The OHD Model-Independent Calibration Method
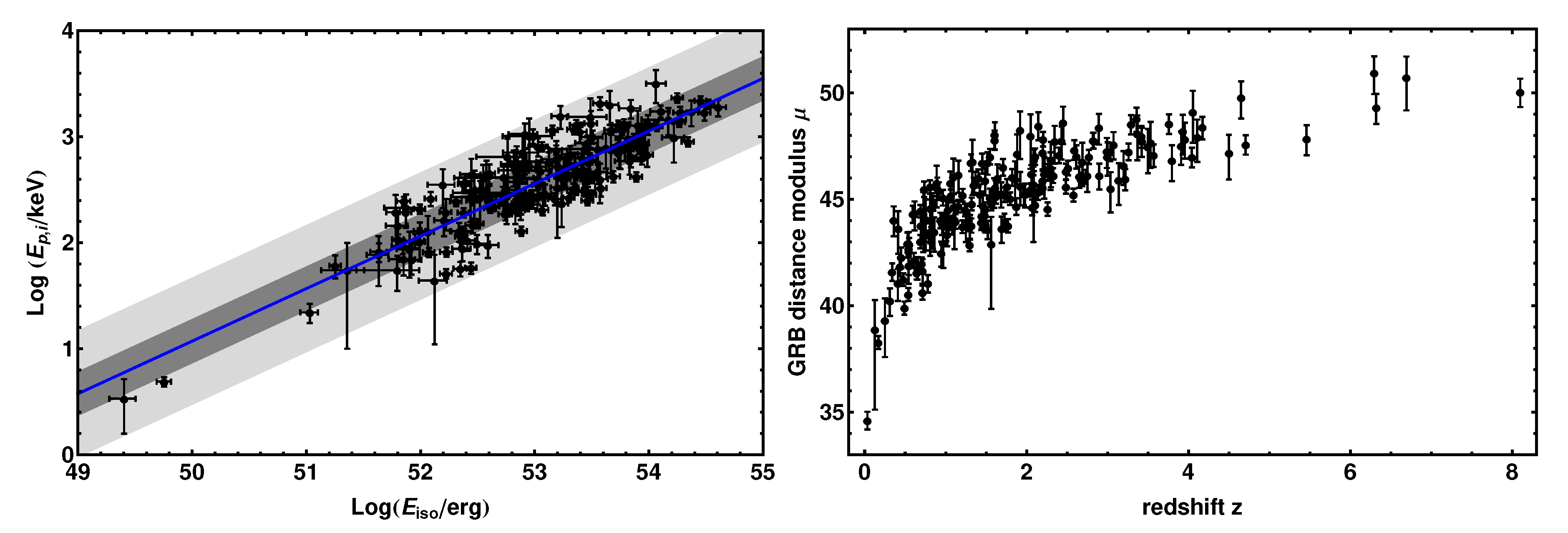
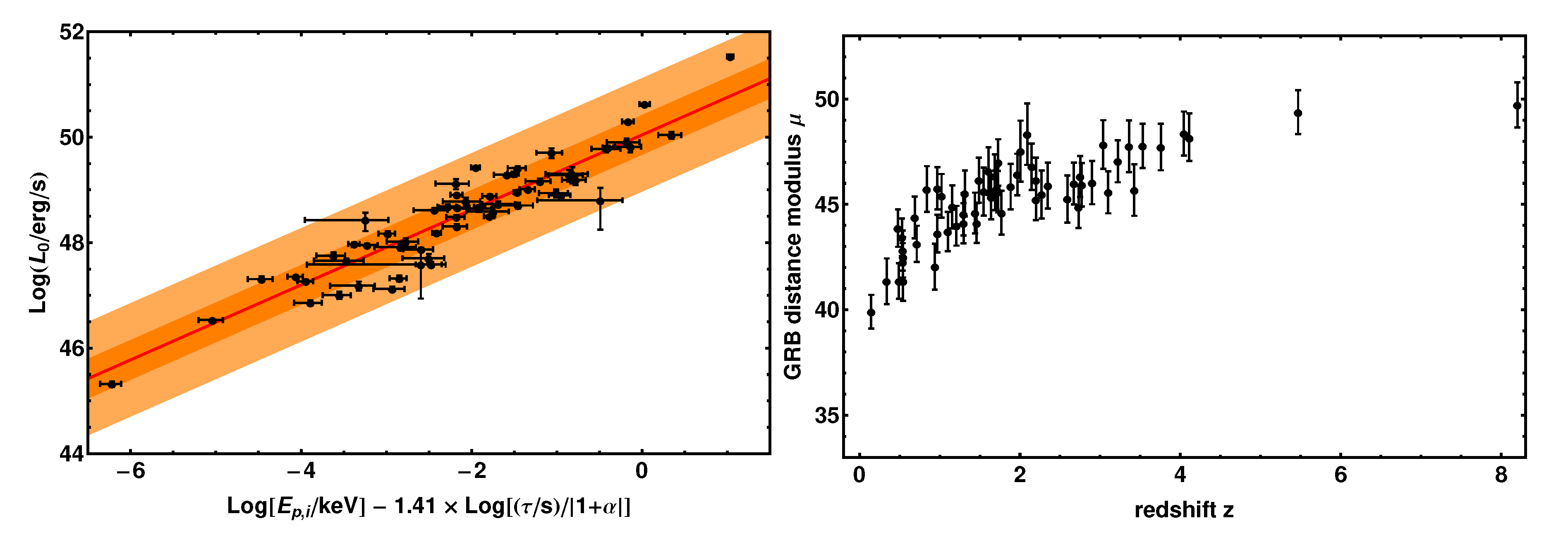
3. The Calibrated Amati and Combo Correlations
4. Results from Cosmological Fits
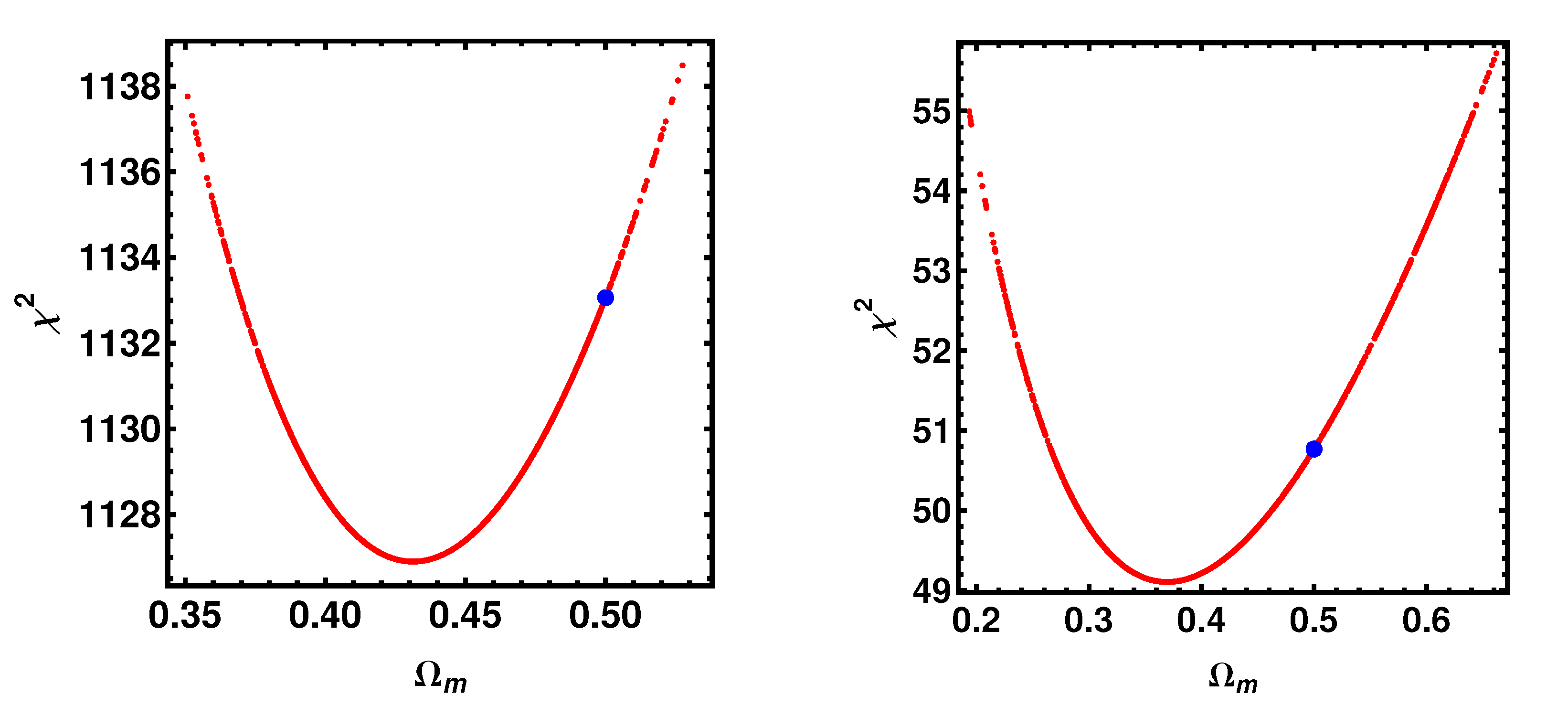
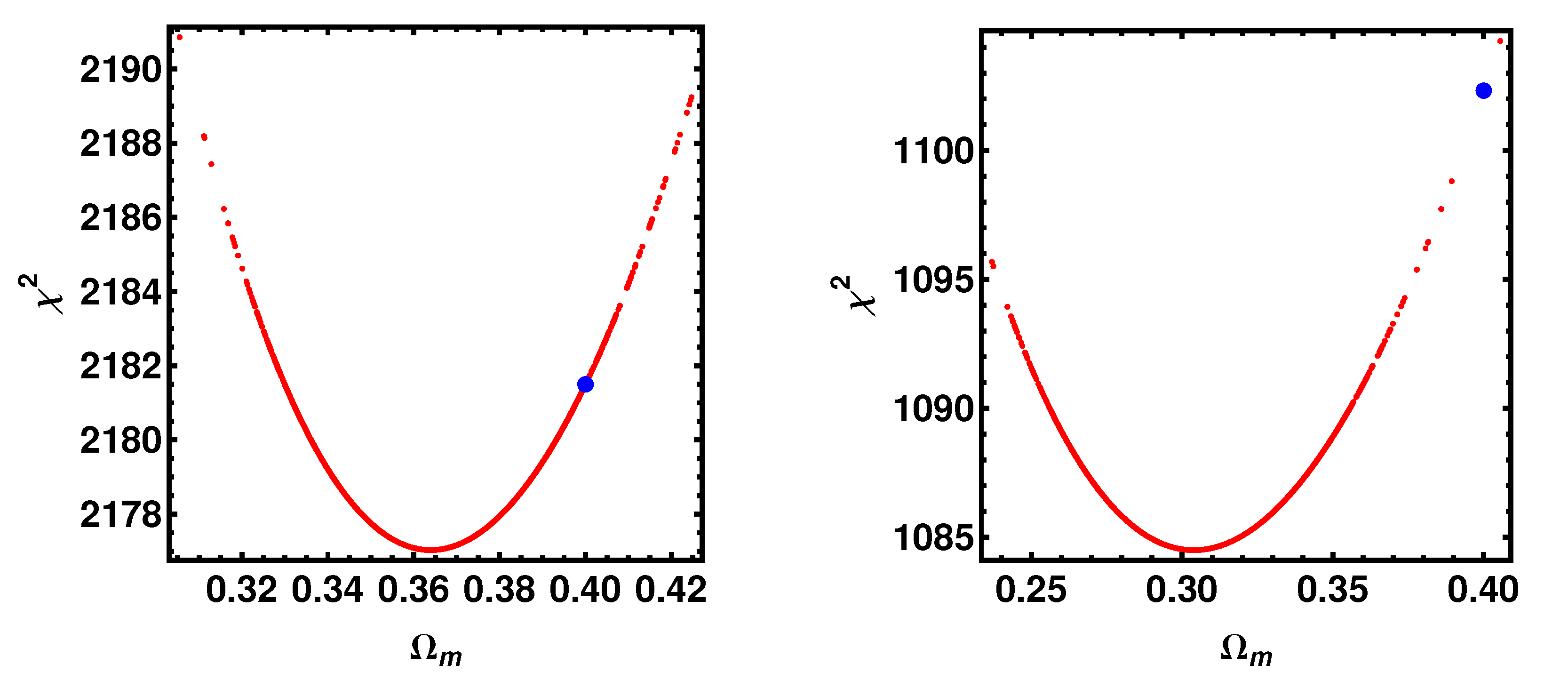
4.1. The CDM Model
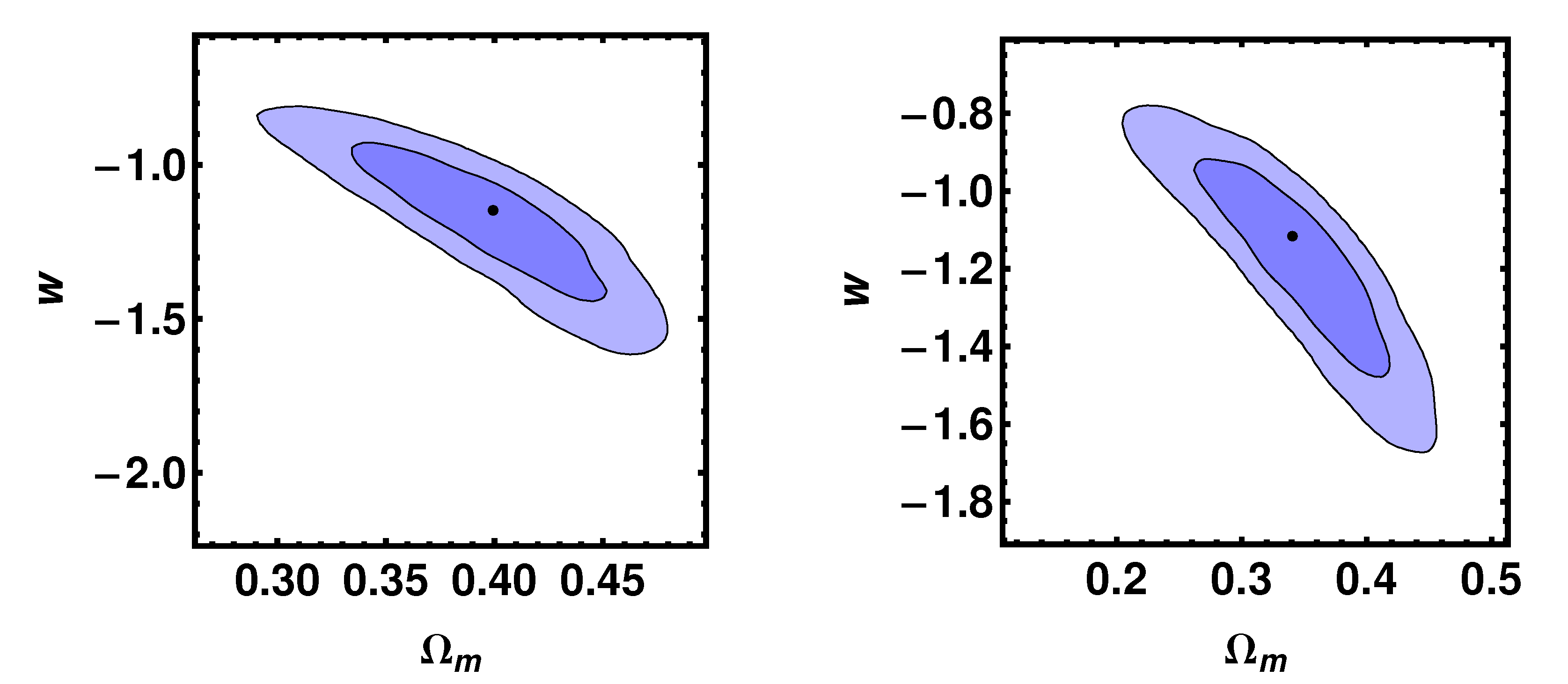
4.2. The wCDM Model
4.3. Results
5. Conclusions and Discussions
Funding
Acknowledgments
Conflicts of Interest
References
- Phillips, M.M. The absolute magnitudes of Type IA supernovae. Astrophys. J. 1993, 413, L105–L108. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; della Valle, M.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; et al. Discovery of a supernova explosion at half the age of the universe. Nature 1998, 391, 51. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Schmidt, B.P.; Suntzeff, N.B.; Phillips, M.M.; Schommer, R.A.; Clocchiatti, A.; Kirshner, R.P.; Garnavich, P.; Challis, P.; Leibundgut, B.; Spyromilio, J.; et al. The High-Z Supernova Search: Measuring Cosmic Deceleration and Global Curvature of the Universe Using Type IA Supernovae. Astrophys. J. 1998, 507, 46–63. [Google Scholar] [CrossRef]
- Kang, Y.; Lee, Y.W. Investigation of Stellar Populations in the Early type Host Galaxies of Type Ia Supernovae. Am. Astron. Soc. Meet. Abstr. 2019, 233, 312.03. [Google Scholar]
- Rodney, S.A.; Riess, A.G.; Scolnic, D.M.; Jones, D.O.; Hemmati, S.; Molino, A.; McCully, C.; Mobasher, B.; Strolger, L.G.; Graur, O.; et al. Two SNe Ia at Redshift ∼2: Improved Classification and Redshift Determination with Medium-band Infrared Imaging. Astron. J. 2015, 150, 156. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Luongo, O.; Ruggeri, A. Cosmographic Constraints and Cosmic Fluids. Galaxies 2013, 1, 216–260. [Google Scholar] [CrossRef]
- Luongo, O.; Battista Pisani, G.; Troisi, A. Cosmological degeneracy versus cosmography: A cosmographic dark energy model. arXiv 2015, arXiv:1512.07076. [Google Scholar] [CrossRef]
- Salvaterra, R.; Della Valle, M.; Campana, S.; Chincarini, G.; Covino, S.; D’Avanzo, P.; Fernández-Soto, A.; Guidorzi, C.; Mannucci, F.; Margutti, R.; et al. GRB090423 at a redshift of z˜8.1. Nature 2009, 461, 1258. [Google Scholar] [CrossRef] [PubMed]
- Tanvir, N.R.; Fox, D.B.; Levan, A.J.; Berger, E.; Wiersema, K.; Fynbo, J.P.U.; Cucchiara, A.; Krühler, T.; Gehrels, N.; Bloom, J.S.; et al. A γ-ray burst at a redshift of z˜8.2. Nature 2009, 461, 1254. [Google Scholar] [CrossRef] [PubMed]
- Cucchiara, A.; Levan, A.J.; Fox, D.B.; Tanvir, N.R.; Ukwatta, T.N.; Berger, E.; Krühler, T.; Küpcü Yoldaş, A.; Wu, X.F.; Toma, K.; et al. A Photometric Redshift of z˜9.4 for GRB 090429B. Astrophys. J. 2011, 736, 7. [Google Scholar] [CrossRef]
- Salvaterra, R.; Campana, S.; Vergani, S.D.; Covino, S.; D’Avanzo, P.; Fugazza, D.; Ghirlanda, G.; Ghisellini, G.; Melandri, A.; Nava, L.; et al. A Complete Sample of Bright Swift Long Gamma-Ray Bursts. I. Sample Presentation, Luminosity Function and Evolution. Astrophys. J. 2012, 749, 68. [Google Scholar] [CrossRef]
- Coward, D.M.; Howell, E.J.; Branchesi, M.; Stratta, G.; Guetta, D.; Gendre, B.; Macpherson, D. The Swift gamma-ray burst redshift distribution: Selection biases and optical brightness evolution at high z? Mon. Not. R. Astron. Soc. 2013, 432, 2141–2149. [Google Scholar] [CrossRef]
- Amati, L. The Ep,i-Eiso correlation in gamma-ray bursts: Updated observational status, re-analysis and main implications. Mon. Not. R. Astron. Soc. 2006, 372, 233–245. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Firmani, C. Gamma-ray bursts as standard candles to constrain the cosmological parameters. New J. Phys. 2006, 8, 123. [Google Scholar] [CrossRef]
- Nava, L.; Salvaterra, R.; Ghirlanda, G.; Ghisellini, G.; Campana, S.; Covino, S.; Cusumano, G.; D’Avanzo, P.; D’Elia, V.; Fugazza, D.; et al. A complete sample of bright Swift long gamma-ray bursts: Testing the spectral-energy correlations. Mon. Not. R. Astron. Soc. 2012, 421, 1256–1264. [Google Scholar] [CrossRef]
- Amati, L.; Della Valle, M. Measuring Cosmological Parameters with Gamma Ray Bursts. Int. J. Mod. Phys. D 2013, 22, 1330028. [Google Scholar] [CrossRef]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. Cosmology with gamma-ray bursts. I. the Hubble diagram through the calibrated Ep,i-Eiso correlation. Astron. Astrophys. 2017, 598, A112. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; in’t Zand, J.J.M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; et al. Intrinsic spectra and energetics of BeppoSAX Gamma-Ray Bursts with known redshifts. Astron. Astrophys. 2002, 390, 81. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Ghisellini, G.; Lazzati, D.; Firmani, C. Gamma-Ray Bursts: New Rulers to Measure the Universe. Astrophys. J. 2004, 613, L13–L16. [Google Scholar] [CrossRef]
- Amati, L.; Guidorzi, C.; Frontera, F.; Della Valle, M.; Finelli, F.; Landi, R.; Montanari, E. Measuring the cosmological parameters with the Ep,i–Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2008, 391, 577. [Google Scholar] [CrossRef]
- Schaefer, B.E. The Hubble Diagram to Redshift > 6 from 69 Gamma-Ray Bursts. Astrophys. J. 2007, 660, 16. [Google Scholar] [CrossRef]
- Capozziello, S.; Izzo, L. Cosmography by gamma ray bursts. Astron. Astrophys. 2008, 490, 31–36. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Cardone, V.F.; Capozziello, S. A time-luminosity correlation for γ-ray bursts in the X-rays. Mon. Not. R. Astron. Soc. 2008, 391, L79–L83. [Google Scholar] [CrossRef]
- Bernardini, M.G.; Margutti, R.; Zaninoni, E.; Chincarini, G. A universal scaling for short and long gamma-ray bursts: EX,iso-Eγ,iso-Epk. Mon. Not. R. Astron. Soc. 2012, 425, 1199–1204. [Google Scholar] [CrossRef]
- Wei, J.J.; Wu, X.F.; Melia, F.; Wei, D.M.; Feng, L.L. Cosmological tests using gamma-ray bursts, the star formation rate and possible abundance evolution. Mon. Not. R. Astron. Soc. 2014, 439, 3329–3341. [Google Scholar] [CrossRef]
- Izzo, L.; Muccino, M.; Zaninoni, E.; Amati, L.; Della Valle, M. New measurements of Ωm from gamma-ray bursts. Astron. Astrophys. 2015, 582, A115. [Google Scholar] [CrossRef]
- Demianski, M.; Piedipalumbo, E.; Sawant, D.; Amati, L. Cosmology with gamma-ray bursts. II. Cosmography challenges and cosmological scenarios for the accelerated Universe. Astron. Astrophys. 2017, 598, A113. [Google Scholar] [CrossRef]
- Kodama, Y.; Yonetoku, D.; Murakami, T.; Tanabe, S.; Tsutsui, R.; Nakamura, T. Gamma-ray bursts in 1.8 < z < 5.6 suggest that the time variation of the dark energy is small. Mon. Not. R. Astron. Soc. 2008, 391, L1–L4. [Google Scholar] [CrossRef]
- Amati, L.; D’Agostino, R.; Luongo, O.; Muccino, M.; Tantalo, M. Addressing the circularity problem in the Ep-Eiso correlation of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2019, 486, L46–L51. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Amati, L. Gamma-ray Burst Prompt Correlations: Selection and Instrumental Effects. Publ. Astron. Soc. Pac. 2018, 130, 051001. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining Cosmological Parameters Based on Relative Galaxy Ages. Astrophys. J. 2002, 573, 37–42. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Cosmographic analysis with Chebyshev polynomials. Mon. Not. R. Astron. Soc. 2018, 476, 3924–3938. [Google Scholar] [CrossRef]
- Montiel, A.; Cabrera, J.I.; Hidalgo, J.C. Improving sampling and calibration of GRBs as distance indicators. arXiv 2020, arXiv:2003.03387. [Google Scholar]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Liang, N.; Xiao, W.K.; Liu, Y.; Zhang, S.N. A Cosmology-Independent Calibration of Gamma-Ray Burst Luminosity Relations and the Hubble Diagram. Astrophys. J. 2008, 685, 354–360. [Google Scholar] [CrossRef]
- Luongo, O. Cosmography with the Hubble Parameter. Mod. Phys. Lett. A 2011, 26, 1459–1466. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Updated constraints on f(R) gravity from cosmography. Phys. Rev. D 2013, 87, 044012. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Cosmographic reconstruction of f(T) cosmology. Phys. Rev. D 2013, 87, 064025. [Google Scholar] [CrossRef]
- Luongo, O. Dark Energy from a Positive Jerk Parameter. Mod. Phys. Lett. A 2013, 28, 1350080. [Google Scholar] [CrossRef]
- Gruber, C.; Luongo, O. Cosmographic analysis of the equation of state of the universe through Padé approximations. Phys. Rev. D 2014, 89, 103506. [Google Scholar] [CrossRef]
- Capozziello, S.; Farooq, O.; Luongo, O.; Ratra, B. Cosmographic bounds on the cosmological deceleration-acceleration transition redshift in f(R) gravity. Phys. Rev. D 2014, 90, 044016. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Precision cosmology with Padé rational approximations: Theoretical predictions versus observational limits. Phys. Rev. D 2014, 90, 043531. [Google Scholar] [CrossRef]
- Capozziello, S.; Luongo, O.; Saridakis, E.N. Transition redshift in f (T ) cosmology and observational constraints. Phys. Rev. D 2015, 91, 124037. [Google Scholar] [CrossRef]
- de la Cruz-Dombriz, Á.; Dunsby, P.K.S.; Luongo, O.; Reverberi, L. Model-independent limits and constraints on extended theories of gravity from cosmic reconstruction techniques. J. Cosmol. Astropart. Phys. 2016, 2016, 042. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Model-independent reconstruction of f( T) teleparallel cosmology. Gen. Relativ. Gravit. 2017, 49, 141. [Google Scholar] [CrossRef]
- Calzá, M.; Casalino, A.; Luongo, O.; Sebastiani, L. Kinematic reconstructions of extended theories of gravity at small and intermediate redshifts. Eur. Phys. J. Plus 2020, 135, 1. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. High-redshift cosmography: Auxiliary variables versus Padé polynomials. Mon. Not. R. Astron. Soc. 2020, 494, 2576–2590. [Google Scholar] [CrossRef]
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2019, arXiv:1807.06209. [Google Scholar]
- Luongo, O.; Muccino, M. Speeding up the Universe using dust with pressure. Phys. Rev. D 2018, 98, 103520. [Google Scholar] [CrossRef]
- Conley, A.; Guy, J.; Sullivan, M.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D.; et al. Supernova Constraints and Systematic Uncertainties from the First Three Years of the Supernova Legacy Survey. ApJS 2011, 192, 1. [Google Scholar] [CrossRef]
- Goliath, M.; Amanullah, R.; Astier, P.; Goobar, A.; Pain, R. Supernovae and the nature of the dark energy. Astron. Astrophys. 2001, 380, 6–18. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Luković, V.V.; D’Agostino, R.; Vittorio, N. Strong evidence for an accelerating universe. Astron. Astrophys. 2017, 600, L1. [Google Scholar] [CrossRef]
- Yang, T.; Banerjee, A.; Colgáin, E.Ó. On cosmography and flat ΛCDM tensions at high redshift. arXiv 2019, arXiv:1911.01681. [Google Scholar]
- Risaliti, G.; Lusso, E. Cosmological Constraints from the Hubble Diagram of Quasars at High Redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef]
- Ooba, J.; Ratra, B.; Sugiyama, N. Planck 2015 Constraints on the Non-flat ΛCDM Inflation Model. Astrophys. J. 2018, 864, 80. [Google Scholar] [CrossRef]
- Wei, J.J.; Melia, F. Model-independent Distance Calibration and Curvature Measurement Using Quasars and Cosmic Chronometers. Astrophys. J. 2020, 888, 99. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Kinematic model-independent reconstruction of Palatini f(R) cosmology. Gen. Relativ. Gravit. 2019, 51, 2. [Google Scholar] [CrossRef]
| Sample | Amati | Combo | ||||
|---|---|---|---|---|---|---|
| w | DoF | w | DoF | |||
| ΛCDM | ||||||
| GRB | ||||||
| GRB+SN | ||||||
| wCDM | ||||||
| GRB+SN | ||||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muccino, M. A Confront between Amati and Combo Correlations at Intermediate and Early Redshifts. Symmetry 2020, 12, 1118. https://doi.org/10.3390/sym12071118
Muccino M. A Confront between Amati and Combo Correlations at Intermediate and Early Redshifts. Symmetry. 2020; 12(7):1118. https://doi.org/10.3390/sym12071118
Chicago/Turabian StyleMuccino, Marco. 2020. "A Confront between Amati and Combo Correlations at Intermediate and Early Redshifts" Symmetry 12, no. 7: 1118. https://doi.org/10.3390/sym12071118
APA StyleMuccino, M. (2020). A Confront between Amati and Combo Correlations at Intermediate and Early Redshifts. Symmetry, 12(7), 1118. https://doi.org/10.3390/sym12071118




