Time for Change: Implementation of Aksentijevic-Gibson Complexity in Psychology
Abstract
1. String Complexity
1.1. Complexity as Magnitude
1.2. Complexity as Structure
Suppose we divide the space into little volume elements. If we have black and white molecules, how many ways could we distribute them among the volume elements so that white is on one side and black is on the other? On the other hand, how many ways could we distribute them with no restriction on which goes where? Clearly, there are many more ways to arrange them in the latter case. We measure "disorder" by the number of ways that the insides can be arranged, so that from the outside it looks the same… The number of ways in the separated case is less, so the entropy is less, or the “disorder” is less.[23]; p. 1
1.3. Complexity as Change
1.4. Computing and Testing AG Complexity
1.5. Examined Studies
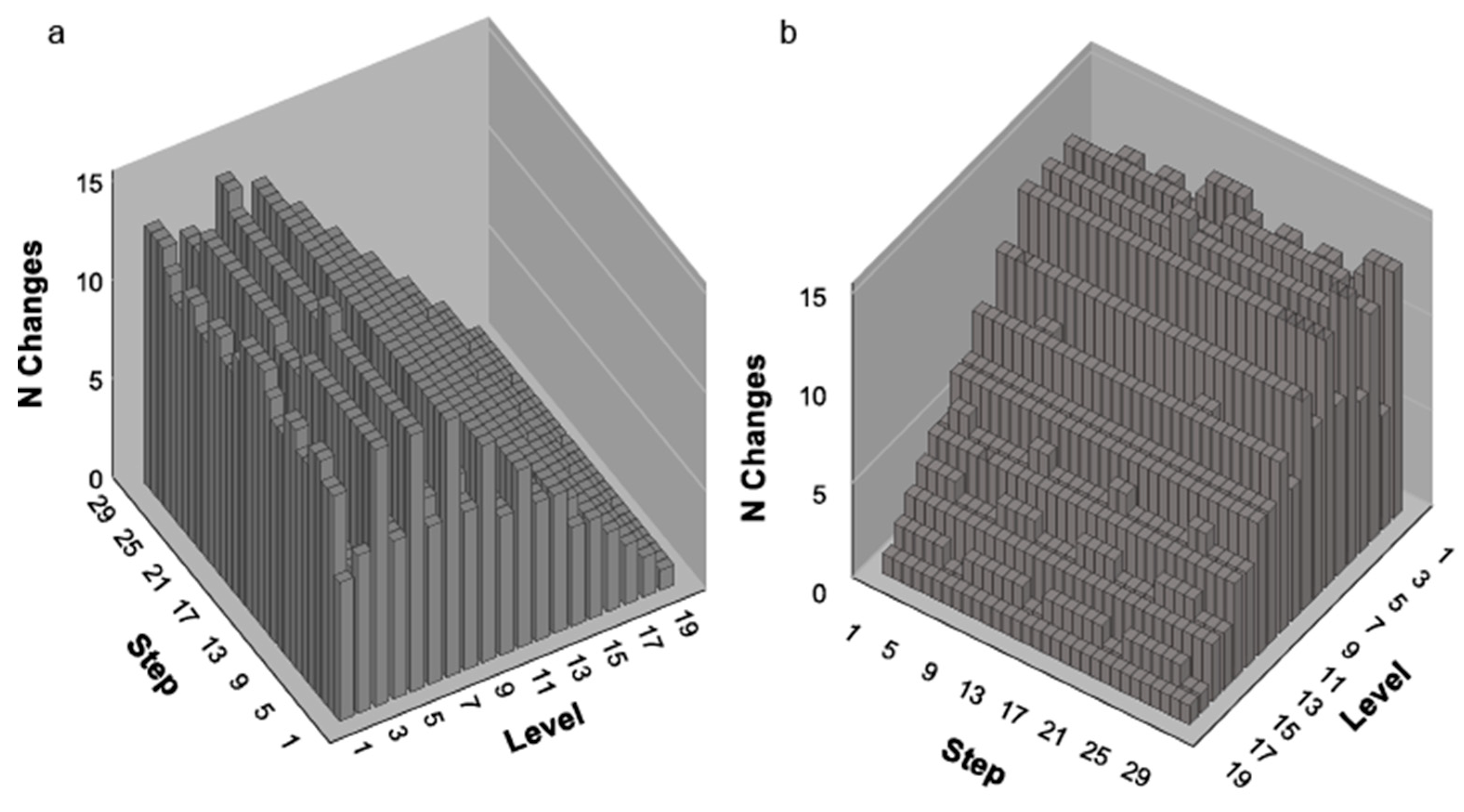
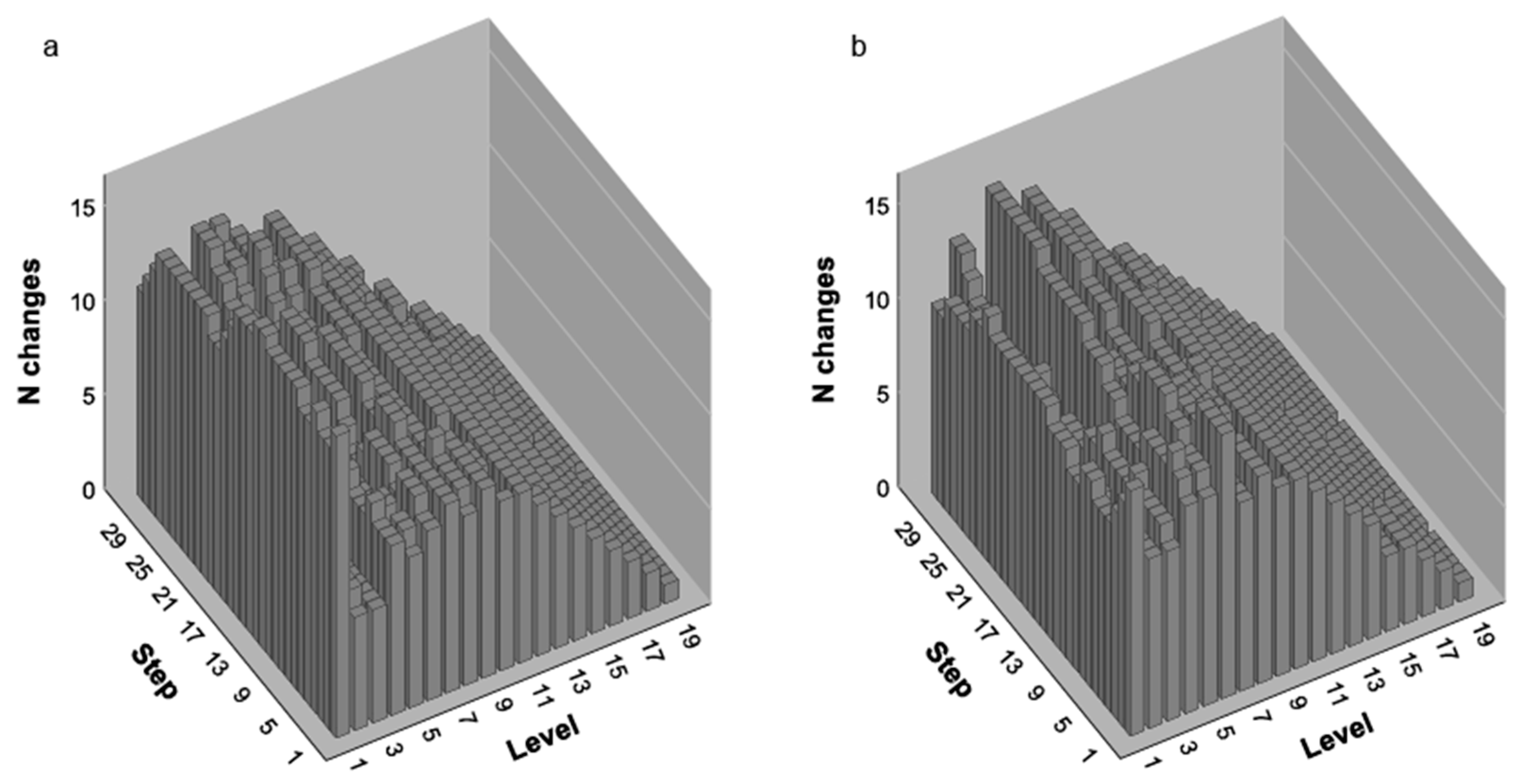
1.6. Results
1.6.1. General Findings
1.6.2. Usefulness of Complexity Profiles
2. Complexity of Visual Form
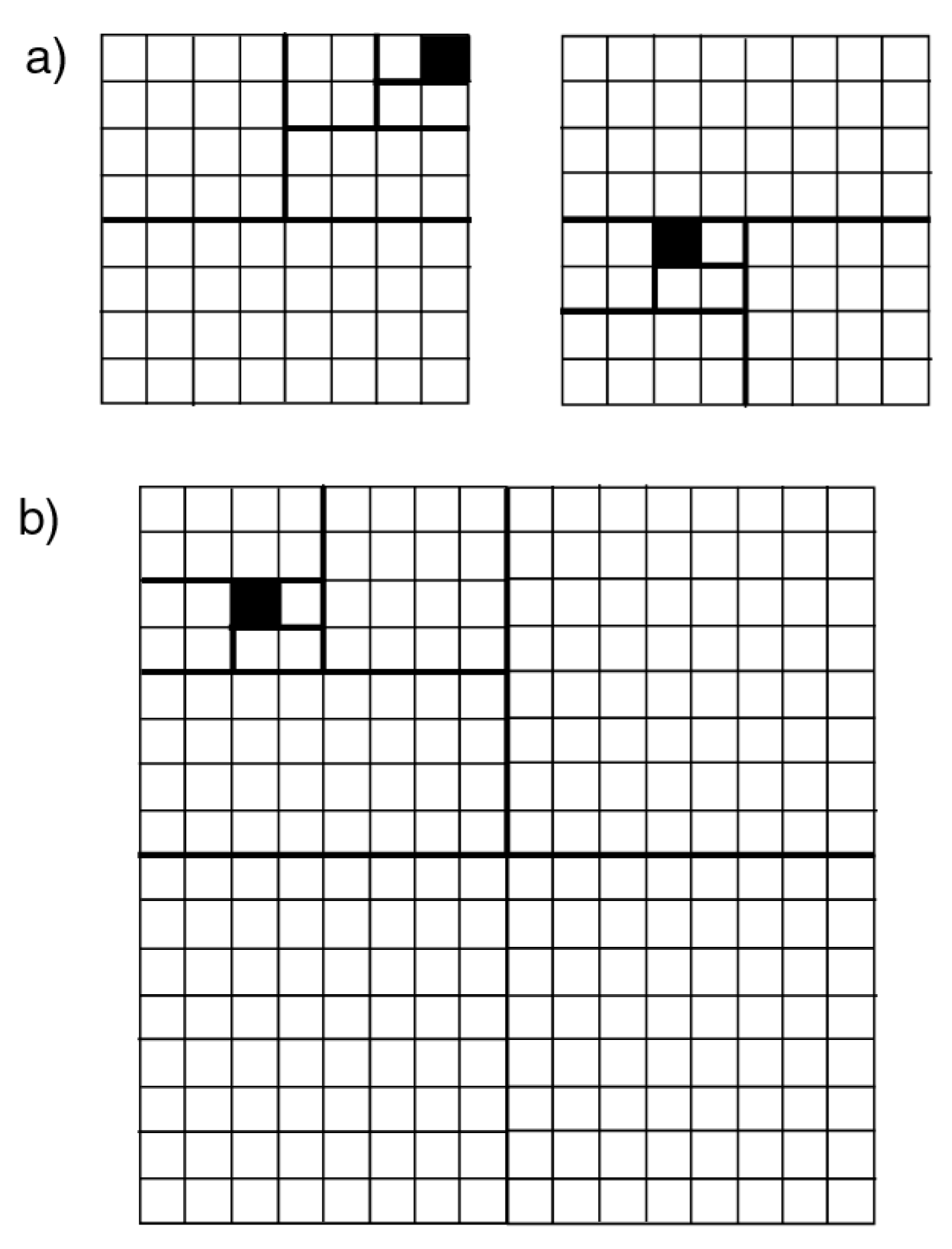
2.1. Computing 2D AG Complexity
- -
- create a zero matrix
- -
- for : If , then set
- -
- for to If then set and continue to the next value of ,
- -
- calculate , to and obtain which is a change profile of ,
- -
- the complexity of is , where
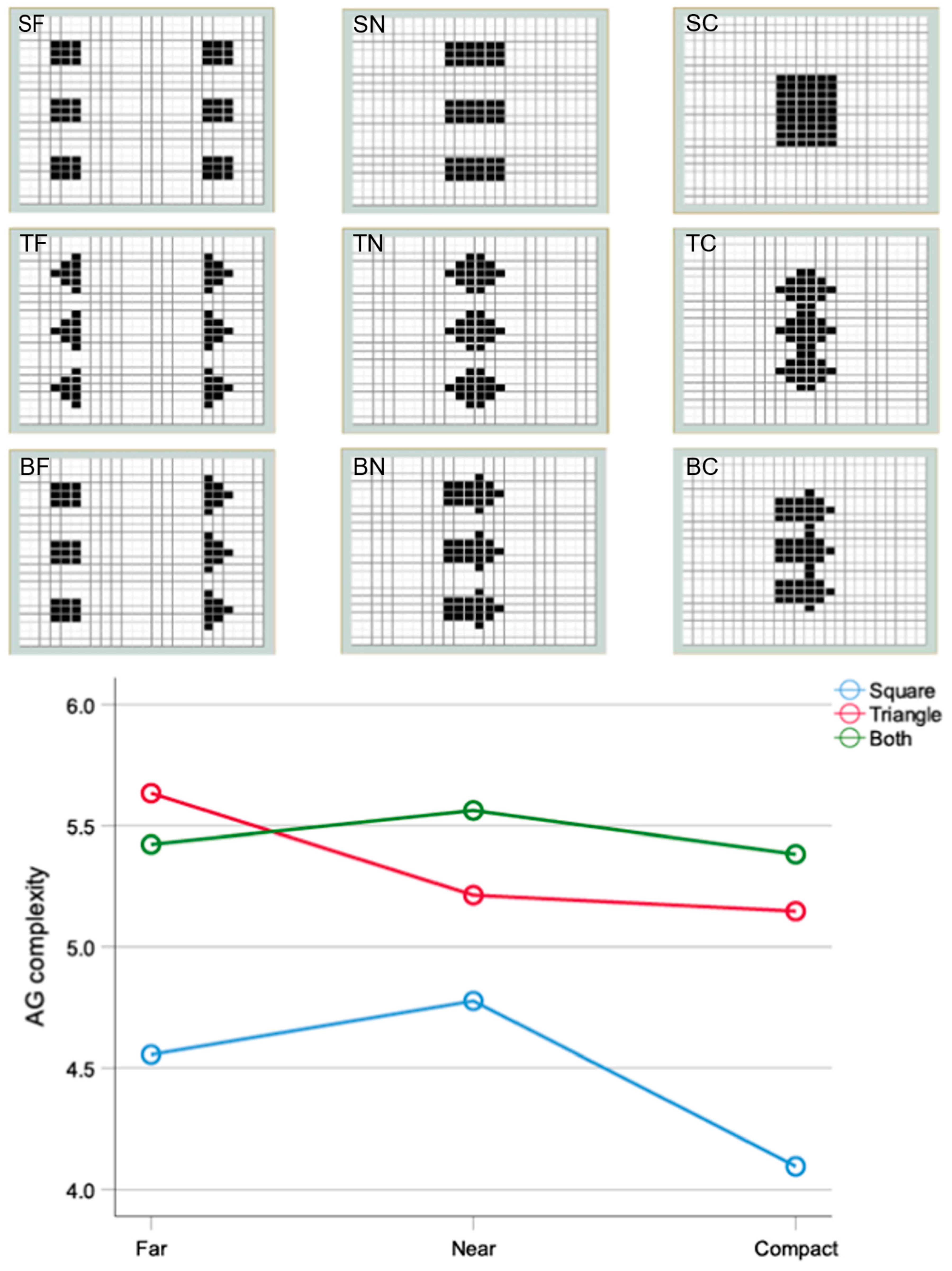
2.2. Applying 2D AG
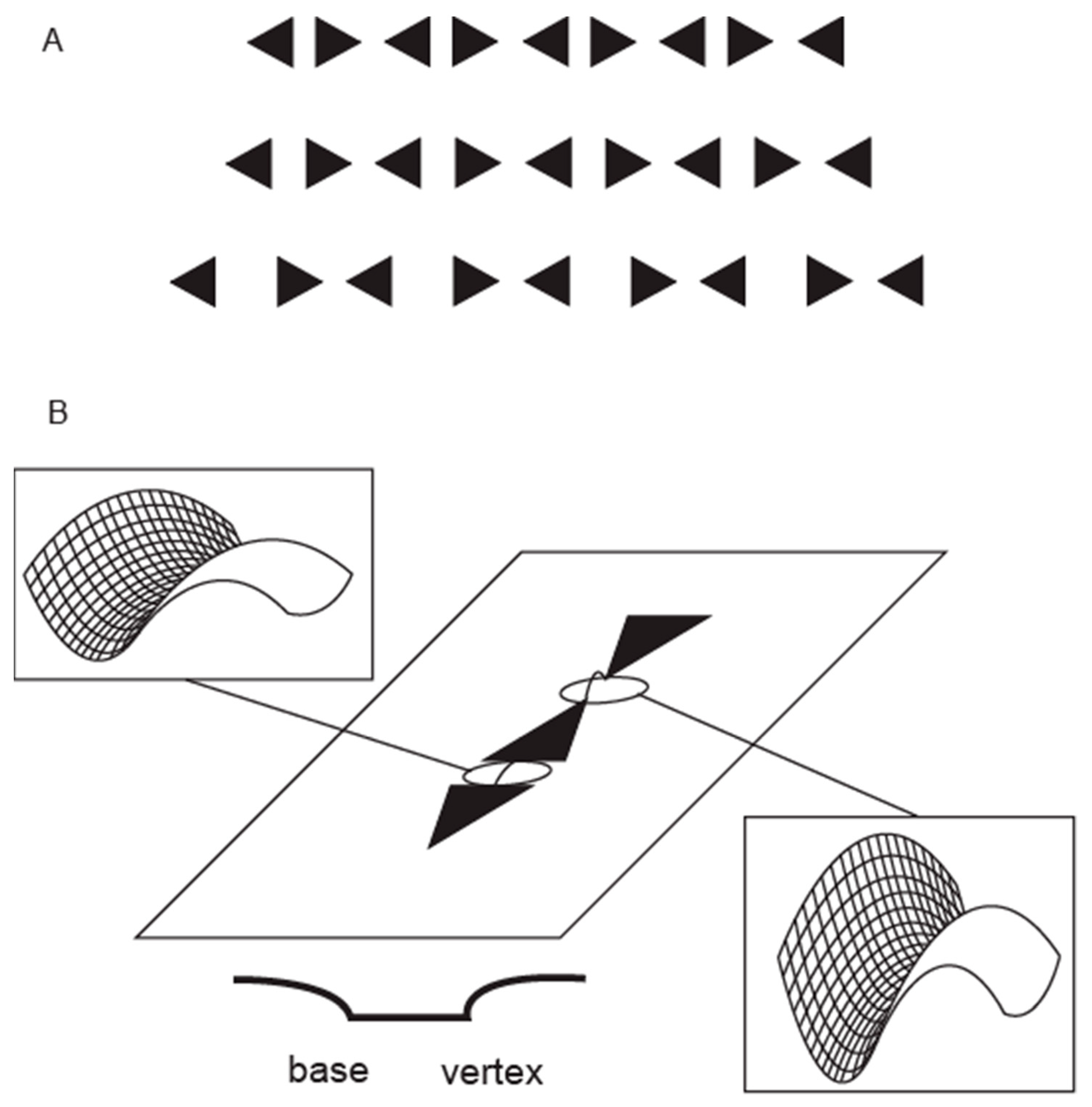
2.2.1. Subjective Complexity/Goodness
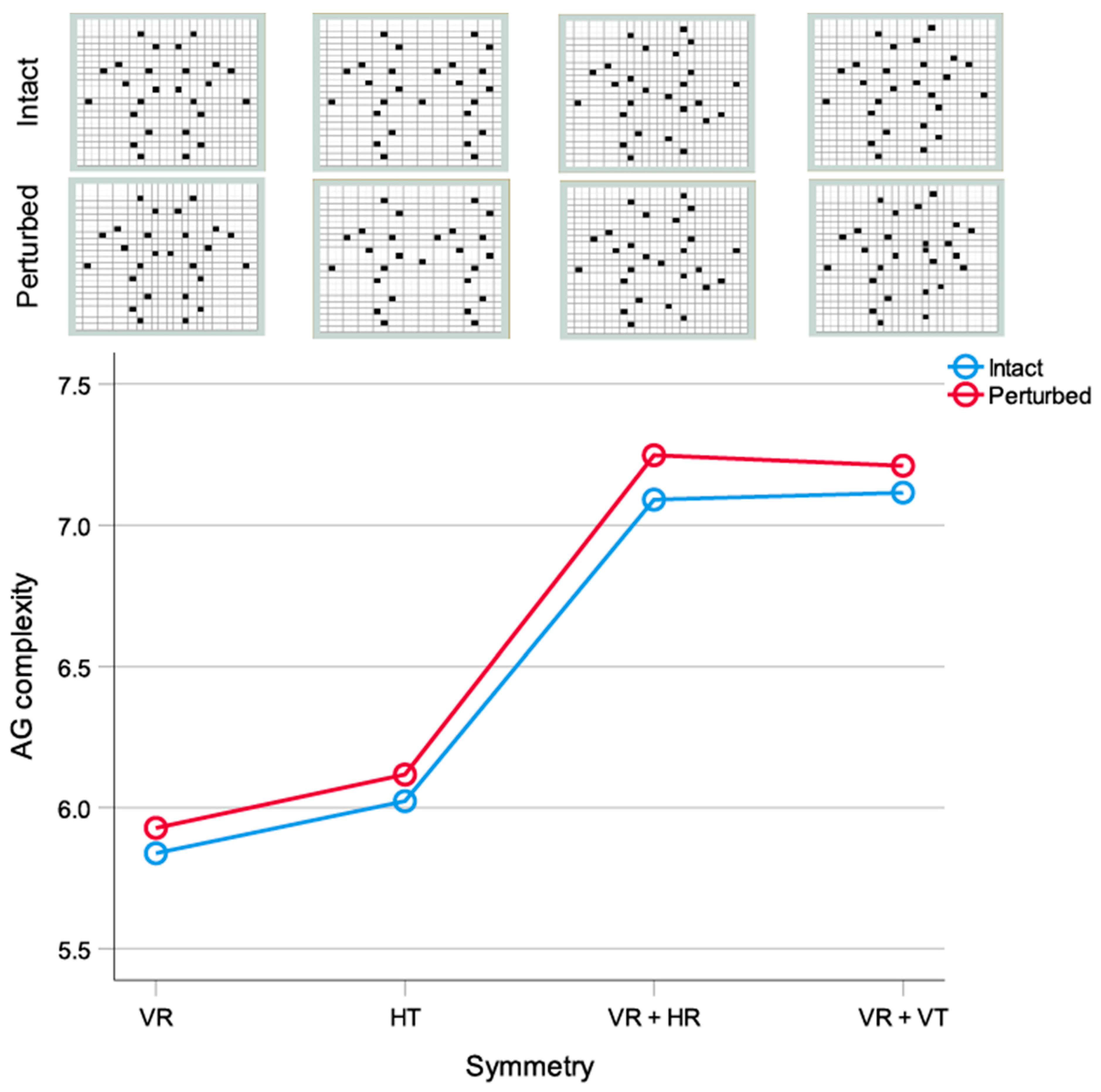
2.2.2. Geometric Transformations
2.2.3. Form and Complexity
2.2.4. Proximity and Similarity
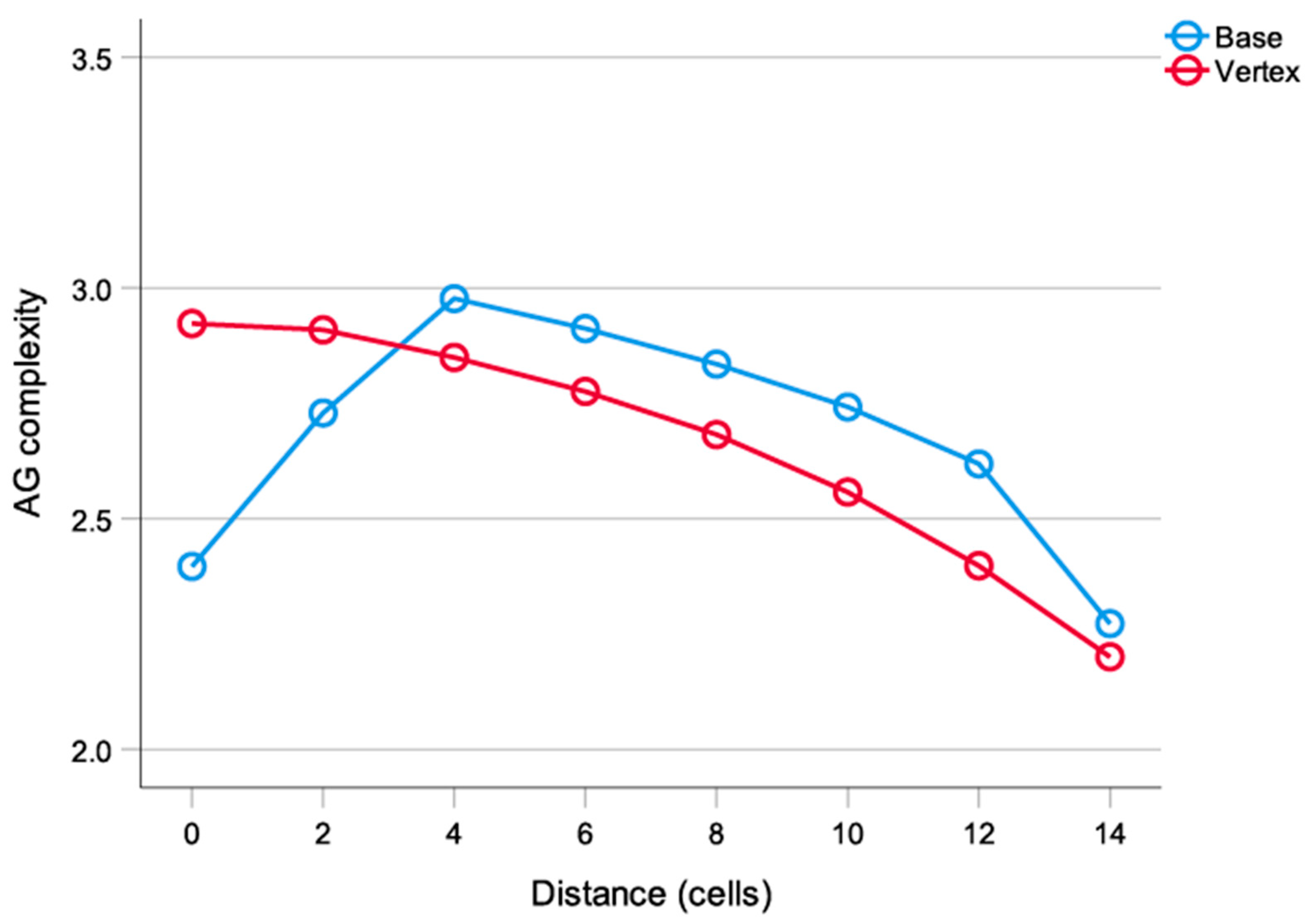
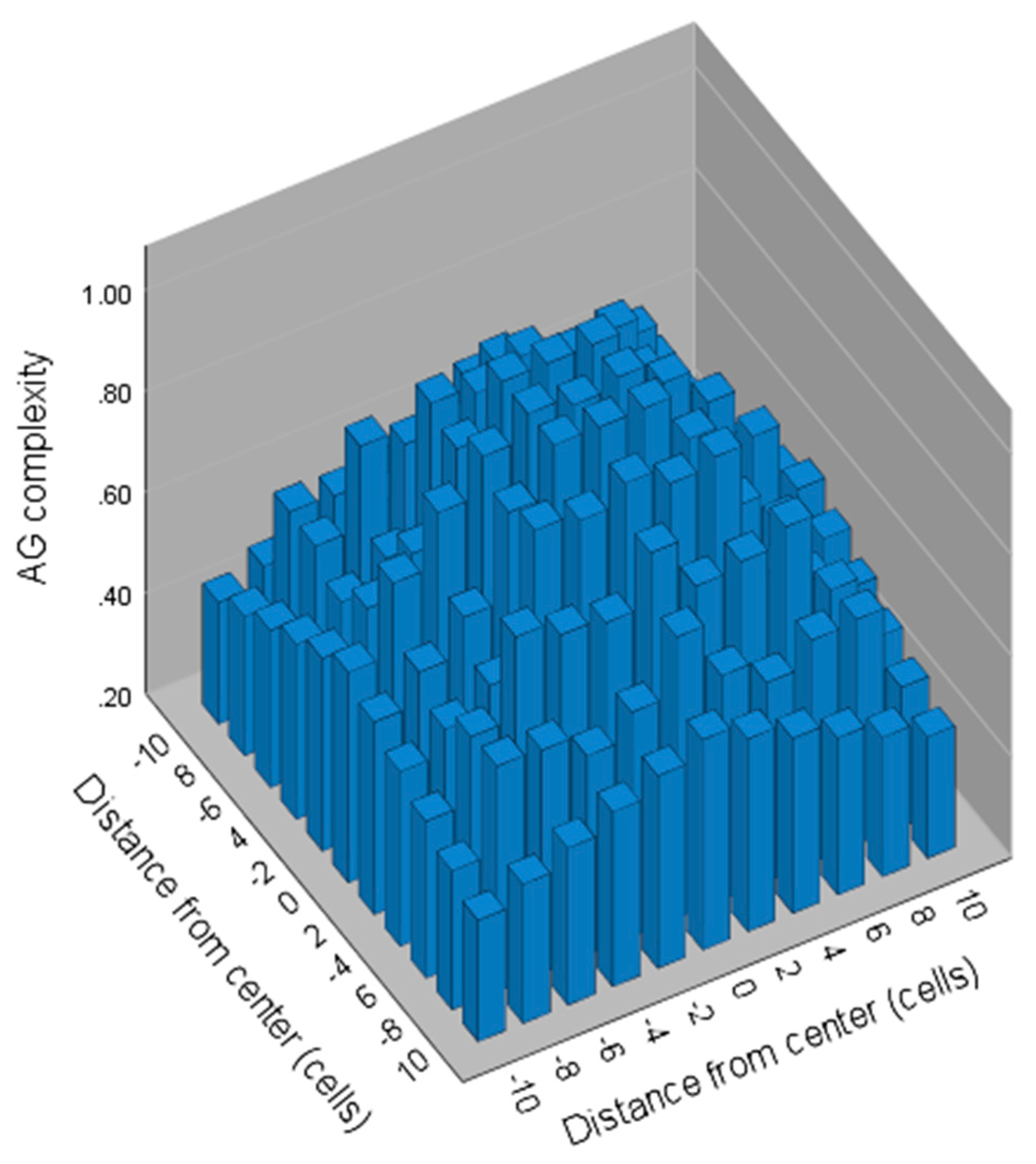
2.2.5. Local Field Interactions
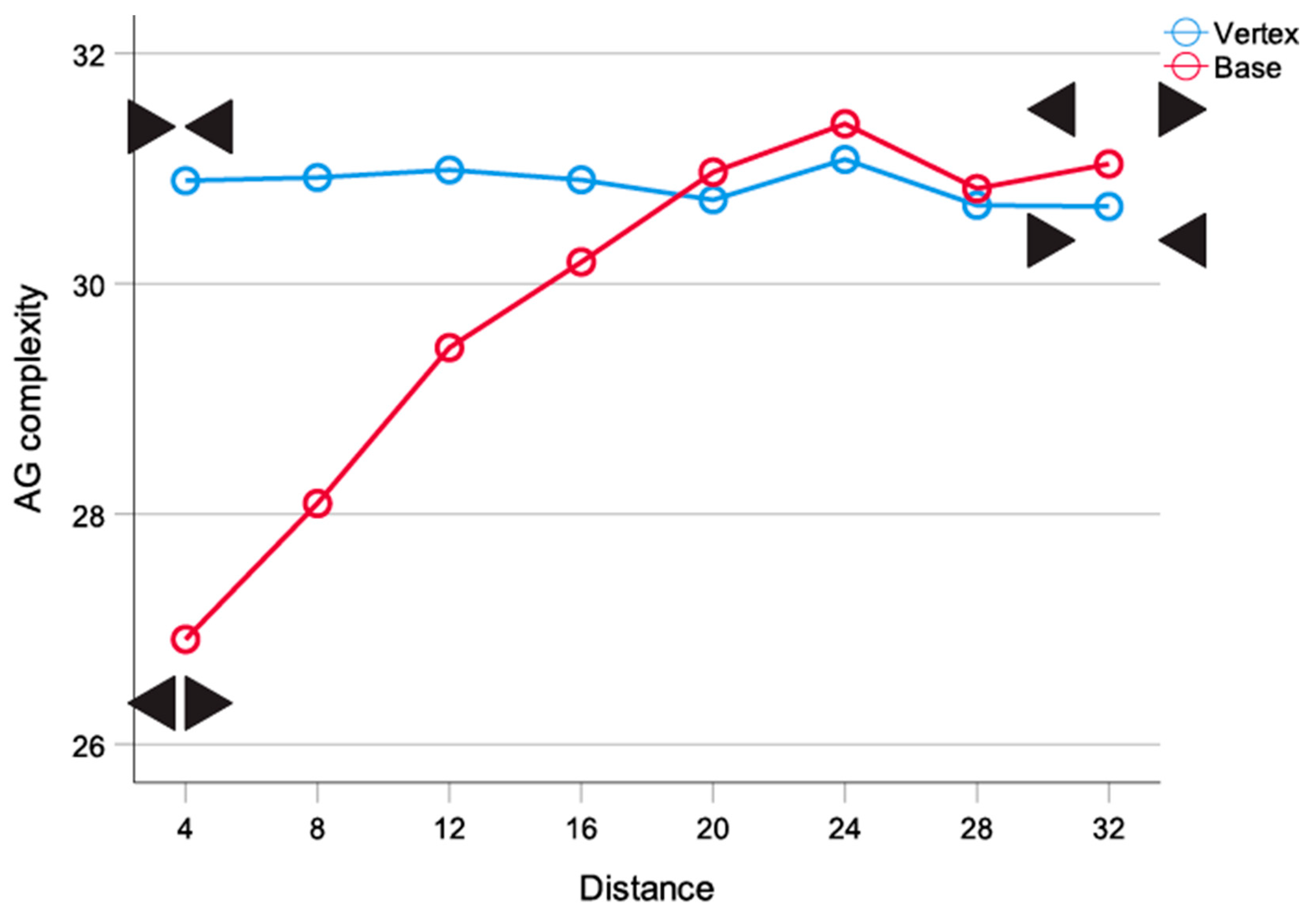
2.2.6. Global Field Interactions
2.2.7. AG and Transition to Disorder
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aksentijevic, A.; Mihailovic, D.T.; Kapor, D.; Crvenkovic, S.; Nikolic-Djoric, E.; Mihailovic, A. Complementarity of information obtained by Kolmogorov and Aksentijevic-Gibson complexities in the analysis of binary time series. Chaos Solitons Fractals 2020, 130, 109394. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Attneave, F. Applications of Information Theory to Psychology: A Summary of Basic Concepts, Methods, and Results; Henry Holt: New York, NY, USA, 1959. [Google Scholar]
- Berlyne, D.E. The influence of complexity and change in visual figures on attention. J. Exp. Psychol. 1958, 55, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Fitts, P.M.; Weinstein, M.; Rappaport, M.; Anderson, N.; Leonard, J.A. Stimulus correlates of visual pattern correlation: A probability approach. J. Exp. Psychol. 1956, 51, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Aksentijevic, A. Randomness: Off with its heads (and tails). Mind Soc. 2015, 16, 1–16. [Google Scholar] [CrossRef]
- Vernon, M.D. A Further Study of Visual Perception; Cambridge University Press: New York, NY, USA, 1952. [Google Scholar]
- Attneave, F. Some informational aspects of visual perception. Psychol. Rev. 1954, 61, 183–193. [Google Scholar] [CrossRef]
- Sternberg, S. The discovery of processing stages: Extensions of Donders’ method. In Attention and Performance II. Acta Psychologica; Koster, W.G., Ed.; North Holland Publishing Company: Amsterdam, The Netherlands, 1969; Volume 30, pp. 276–315. [Google Scholar]
- Miller, G. The magical number seven plus minus two: Some limits on our capacity for processing information. Psychol. Rev. 1956, 63, 81–97. [Google Scholar] [CrossRef]
- Garner, W.R. Uncertainty and Structure as Psychological Concepts; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Kemps, E. Effects of complexity on visuo-spatial working memory. Eur. J. Cogn. Psychol. 1999, 11, 335–356. [Google Scholar] [CrossRef]
- Payne, B. The relationship between a measure of organization for visual patterns and their judged complexity. J. Verbal Learn. Verbal Behav. 1966, 5, 338–343. [Google Scholar] [CrossRef]
- Uttal, W.R. A Behaviorist Looks at Form Recognition; Lawrence Erlbaum: Mahwah, NJ, USA, 2002. [Google Scholar]
- Luce, R.D. Whatever happened to information theory in psychology? Rev. Gen. Psychol. 2003, 7, 183–188. [Google Scholar] [CrossRef]
- Aksentijevic, A.; Gibson, K. Complexity and the cost of information processing. Theory Psychol. 2012, 22, 572–590. [Google Scholar] [CrossRef]
- Koffka, K. Principles of Gestalt Psychology; Lund Humphries: London, UK, 1935. [Google Scholar]
- Hyman, R. Stimulus information as a determinant of reaction time. J. Exp. Psychol. 1953, 45, 188–196. [Google Scholar] [CrossRef] [PubMed]
- Pollack, I. The information of elementary auditory displays, II. J. Acoust. Soc. Am. 1952, 24, 745–749. [Google Scholar] [CrossRef]
- Quastler, H. Information theory in psychology: Problems and methods. In Proceedings of the Conference on the Estimation of Information Flow, Monticello, Illinois, 5–9 July 1954 and related papers; Quastler, H., Ed.; Ill Free Press: Glencoe, UK, 1955. [Google Scholar]
- Garner, W.R.; Clement, D.E. Goodness of pattern and pattern uncertainty. J. Verbal Learn. Verbal Behav. 1963, 2, 446–452. [Google Scholar] [CrossRef]
- Garner, W.R. The Processing of Information and Structure; Lawrence Erlbaum: Potomac, MD, USA, 1974. [Google Scholar]
- Feynman, R.P.; Leighton, R.B.; Sands, M. Ratchet and Pawl. Reading. In The Feynman Lectures on Physics; Addison-Wesley: Boston, MA, USA, 1963. [Google Scholar]
- von Helmholtz, H. Physiological Optics. Volume 3. The Theory of the Perceptions of Vision; Translated from the 3rd German edition, 1910; reprinted in Dover: New York, NY, USA, 1925. [Google Scholar]
- Glanzer, M.; Clark, W.H. Accuracy of perceptual recall: An analysis of organization. J. Verbal Learn. Verbal Behav. 1962, 1, 289–299. [Google Scholar] [CrossRef]
- Leeuwenberg, E.L.J. Quantitative specification of information in sequential patterns. Psychol. Rev. 1969, 76, 216–220. [Google Scholar] [CrossRef]
- Restle, F. Theory of serial pattern learning: Structural trees. Psychol. Rev. 1970, 77, 481–495. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Li, M.; Vitanyi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: New York, NY, USA, 1997. [Google Scholar]
- Grassberger, P. How to measure self-generated complexity. Phys. A 1986, 140, 319–325. [Google Scholar] [CrossRef]
- Chater, N. Reconciling simplicity and likelihood principles in perceptual organisation. Psychol. Rev. 1996, 103, 566–581. [Google Scholar] [CrossRef]
- Aksentijevic, A.; Gibson, K. Complexity equals change. Cogn. Syst. Res. 2012, 15–16, 1–16. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Gauvrit, N.; Singmann, H.; Soler-Toscano, F.; Zenil, H. Algorithmic complexity for psychology: A user-friendly implementation of the coding theorem method. Beh. Res. Met. 2015, 48, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Faires, D.J.; Burden, R.L. Numerical Methods; Brooks/Cole: Boston, MA, USA, 1998. [Google Scholar]
- Galanter, E.H.; Smith, W.A.S. Some experiments on a simple thought-problem. Am. J. Psychol. 1958, 71, 359–366. [Google Scholar] [CrossRef] [PubMed]
- Alexander, C.; Carey, S. Subsymmetries. Percept. Psychophys. 1968, 4, 73–77. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Tenenbaum, J.B. Probability, algorithmic complexity and subjective randomness. In Proceedings of the 25th Annual Conference of the Cognitive Science Society; Cognitive Science Society: Boston, MA, USA, 2003; pp. 480–485. [Google Scholar]
- Vitz, P.C. Information, run structure & binary pattern complexity. Percept. Psychophys. 1968, 3, 275–280. [Google Scholar]
- Psotka, J. Simplicity, symmetry, and syntely. Mem. Cogn. 1975, 3, 434–444. [Google Scholar] [CrossRef]
- Garner, W.R.; Gottwald, R.L. Some perceptual factors in the learning of sequential patterns of binary events. J. Verbal Learn. Verbal Behav. 1967, 6, 582–589. [Google Scholar] [CrossRef]
- Royer, F.L.; Garner, W.R. Response uncertainty and perceptual difficulty of auditory temporal patterns. Percept. Psychophys. 1966, 1, 41–47. [Google Scholar]
- Falk, R.; Konold, C. Making sense of randomness: Implicit encoding as a bias for judgment. Psychol. Rev. 1997, 104, 301–318. [Google Scholar] [CrossRef]
- De Fleurian, R.; Blackwell, T.; Ben-Tal, O.; Müllensiefen, D. Information-theoretic measures predict the human judgment of rhythm complexity. Cogn. Sci. 2016, 41, 800–813. [Google Scholar] [CrossRef] [PubMed]
- Shmulevich, I.; Povel, D.-J. Measures of temporal pattern complexity. J. New Music Res. 2000, 29, 61–69. [Google Scholar] [CrossRef]
- Royer, F.L.; Garner, W.R. Perceptual organization of nine-element auditory temporal patterns. Percept. Psychophys. 1970, 7, 115–120. [Google Scholar] [CrossRef]
- Aksentijevic, A.; Monje Garcia, L. Cross-modal facilitation of mental rotation: Effects of pattern modality and complexity. Br. J. Psychol. 2013, 104, 181–192. [Google Scholar] [CrossRef] [PubMed]
- MacGregor, J. A measure of temporal patterns. Percept. Psychophys. 1985, 38, 97–100. [Google Scholar] [CrossRef] [PubMed]
- Delahaye, J.-P.; Zenil, H. Numerical evaluation of algorithmic complexity for short strings: A glance into the innermost structure of randomness. Appl. Math. Comput. 2012, 219, 63–77. [Google Scholar] [CrossRef]
- Soler-Toscano, F.; Zenil, H.; Delahaye, J.-P.; Gauvrit, N. Calculating Kolmogorov complexity from the output frequency distributions of small Turing Machines. PLoS ONE 2014, 9, e96223. [Google Scholar] [CrossRef]
- Zenil, H.; Hernández-Orozco, S.; Kiani, N.A.; Soler-Toscano, F.; Rueda-Toicen, A.; Tégner, J. A Decomposition method for global evaluation of Shannon entropy and local estimations of algorithmic complexity. Entropy 2018, 20, 605. [Google Scholar] [CrossRef]
- Köhler, W. Gestalt Psychology: An Introduction to New Concepts in Modern Psychology; Liveright: New York, NY, USA, 1947. [Google Scholar]
- Wertheimer, M. Experimentelle Studien über das Sehen von Bewegung (Experimental studies on motion vision). Z. Psychol. 1912, 61, 161–265. [Google Scholar]
- Arnheim, R. Art and Visual Perception: A Psychology of the Creative Eye; University of California Press: Berkeley, CA, USA, 1974. [Google Scholar]
- Evans, S.H.; Mueller, M.R. VARGUS 9: Computed stimuli for schema research. Psychon. Sci. 1966, 6, 511–512. [Google Scholar] [CrossRef][Green Version]
- Lane, S.H. Preference for complexity as a function of schematic orderliness and redundancy. Psychon. Sci. 1968, 13, 209–210. [Google Scholar] [CrossRef][Green Version]
- Schnore, M.M.; Partington, J.T. Immediate memory for visual patterns: Symmetry and amount of information. Psychon. Sci. 1967, 8, 421–422. [Google Scholar] [CrossRef]
- Attneave, F. Symmetry, information and memory for patterns. Am. J. Psychol. 1955, 68, 209–222. [Google Scholar] [CrossRef] [PubMed]
- Attneave, F.; Arnoult, M.D. The quantitative study of shape and pattern perception. Psychol. Bull. 1956, 53, 452–471. [Google Scholar] [CrossRef] [PubMed]
- Attneave, F. Physical determinants of the judged complexity of shapes. J. Exp. Psychol. 1957, 53, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Stenson, H.H. The physical factor structure of random forms and their judged complexity. Percept. Psychophys. 1966, 1, 303–310. [Google Scholar] [CrossRef][Green Version]
- Terwilliger, R.F. Pattern complexity and affective arousal. Percept. Mot. Skills 1963, 17, 387–395. [Google Scholar] [CrossRef]
- Lordahl, D.S. An hypothesis approach to sequential predictions of binary events. J. Math. Psychol. 1970, 7, 339–361. [Google Scholar] [CrossRef]
- Leeuwenberg, E.L.J. A perceptual coding language for visual and auditory patterns. Am. J. Psychol. 1971, 84, 307–349. [Google Scholar] [CrossRef]
- van der Helm, P.A. Simplicity versus likelihood in visual perception: From surprisals to precisals. Psychol. Bull. 2000, 126, 770–800. [Google Scholar] [CrossRef]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Palmer, S.E. Goodness, Gestalt, groups, and Garner: Local symmetry subgroups as a theory of figural goodness. In The Perception of Structure; Lockhead, G.R., Pomerantz, J.R., Eds.; American Psychological Association: Washington, DC, USA, 1991; pp. 23–39. [Google Scholar]
- Wagemans, J. Characteristics and models of human symmetry perception. Trends Cogn. Sci. 1997, 1, 346–352. [Google Scholar] [CrossRef]
- Treder, M.S. Behind the looking glass: A review of human symmetry perception. Symmetry 2010, 2, 1510–1543. [Google Scholar] [CrossRef]
- Corcoran, D.J.W. Pattern Recognition; Penguin Books: London, UK, 1971. [Google Scholar]
- Baylis, G.C.; Driver, J. Parallel computation of symmetry but not repetition within single visual shapes. Visual Cogn. 1994, 1, 377–400. [Google Scholar] [CrossRef]
- Chipman, S. Complexity and structure in visual patterns. J. Exp. Psychol. Gen. 1977, 106, 269–301. [Google Scholar] [CrossRef]
- Yodogawa, E. Symmetropy, an entropy-lie measure of visual symmetry. Percept. Psychophys. 1982, 32, 230–240. [Google Scholar] [CrossRef]
- Howe, E. Effects of partial symmetry, exposure time, and backward masking on judged goodness and reproduction of visual patterns. Q. J. Exp. Psychol. 1980, 32, 27–55. [Google Scholar] [CrossRef]
- Wenderoth, P.; Welsh, S. Effects of pattern orientation and number of symmetry axes on the detection of mirror symmetry in dot and solid patterns. Perception 1998, 27, 965–976. [Google Scholar] [CrossRef]
- Dakin, S.C.; Watt, R.J. Detection of bilateral symmetry using spatial filters. Spat. Vis. 1994, 8, 393–413. [Google Scholar] [CrossRef]
- Wagemans, J.; van Gool, L.; Swinnen, V.; van Horebeek, J. Higher-order structure in regularity detection. Vision Res. 1993, 33, 1067–1088. [Google Scholar] [CrossRef]
- Nucci, M.; Wagemans, J. Goodness of regularity in dot patterns: Global symmetry, local symmetry, and their interactions. Perception 2007, 36, 1305–1319. [Google Scholar] [CrossRef]
- Corballis, M.C.; Roldan, C.E. On the perception of symmetrical and repeated patterns. Percept. Psychophys. 1974, 16, 136–142. [Google Scholar] [CrossRef]
- Aksentijevic, A.; Elliott, M.A.; Barber, P.J. Dynamics of perceptual grouping: Similarities in the organization of visual and auditory groups. Visual Cogn. 2001, 8, 349–358. [Google Scholar] [CrossRef]
- Aksentijevic, A.; Elliott, M.A. Local spatial distortion caused by simple geometrical figures. Q. J. Exp. Psychol. 2016, 70, 1535–1548. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, F.C. The Mind at Work and Play; Allen and Unwin: London, UK, 1951. [Google Scholar]
- Stadler, M.; Richter, P.H.; Pfaf, S.; Kruse, P. Attractors and perceptual fields of homogeneous stimulus areas. Psychol. Res. 1991, 53, 102–112. [Google Scholar] [CrossRef]
- Goude, G.; Hjortzberg, I. An Experimental Prövning; University of Stockholm: Stockholm, Sweden, 1967. [Google Scholar]
- Palmer, S.E.; Guidi, S. Mapping the perceptual structure of rectangles through goodness-of-fit ratings. Perception 2011, 40, 1428–1446. [Google Scholar] [CrossRef]
- Zurek, W. Algorithmic randomness and physical entropy. Phys. Rev. A 1989, 40, 4731–4751. [Google Scholar] [CrossRef]
- van der Helm, P.A. Symmetry perception. In The Oxford Handbook of Perceptual Organization; Wagemans, J., Ed.; Oxford University Press: Oxford, UK, 2014. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular automata. Los Alamos Sci. 1983, 9, 2–21. [Google Scholar]






| Study | N (Patterns) | Mode | Presentation | Length | Measure | Correlation with AG | Correlation with KC a |
|---|---|---|---|---|---|---|---|
| Galanter & Smith (1958) | 6 | S | Seq | 2–5 | Prediction accuracy | 0.94 ** | 0.77 |
| Glanzer & Clark (1962) | 256 | V | Sim | 8 | Reproduction accuracy | −0.39 *** (−0.71 ***) | −0.18 * |
| Alexander & Carey (1967) | 35 | V | Sim | 7 | Overall goodness | −0.73 *** | 0.05 |
| Exp. 1 Search | −0.41 * | −0.15 | |||||
| Exp. 2 Sorting | −0.61 *** | 0.01 | |||||
| Exp. 3a Time | −0.58 *** | 0.19 | |||||
| Exp. 3b Confusion | −0.68 *** | −0.06 | |||||
| Exp. 4 Description | −0.68 *** | −0.06 | |||||
| Griffiths & Tenenbaum (2003) | 127 | V | Seq | 8 | Perceived randomness | 0.66 *** | 0.31 *** |
| Vitz (1968) | 26 | V | Seq | 1–8 | Judged complexity | 0.87 *** | 0.77 *** |
| Psotka (1975) | 35 | V | Seq | 8 | Judged complexity | 0.68 *** | −0.02 |
| Judged symmetry | −0.80 *** | −0.30 | |||||
| Judged syntely | −0.26 | 0.06 | |||||
| Garner & Gottwald (1967) | 10 | V | Seq | 5 | Trials to criterion | 0.75 * | −0.58 |
| Number of errors | 063† | −0.69 * | |||||
| Royer & Garner (1966) | 19 | A | Seq | 8 | Response uncertainty | 0.71 ** | 0.36 |
| Response delay | 0.69 ** | 0.40 † | |||||
| Error rate | 0.65 ** | 0.44 † | |||||
| 138 | Freq. SP | 0.09 | 0.02 | ||||
| Response delay | 0.49 *** | 0.20 * | |||||
| Error rate | 0.52 *** | 0.26 ** | |||||
| Falk & Kondold (1997) | 40 | V | Sim | 21 | Apparent randomness | 0.72 *** | 0.77 |
| Memorization difficulty | 0.79 *** | −0.18 * | |||||
| Copying difficulty | 0.80 *** | 0.05 | |||||
| Memorization time | 0.86 *** | −0.15 | |||||
| De Fleurian et al. (2016) | 48 | A | Seq | 49 | Correct ending | −0.32 * | 0.01 |
| Ease | −0.75 *** | 0.19 |
| String | Algorithm | KC |
|---|---|---|
| 10111011101110101011101110111010101110111011101010 | P16 | 0.00178 |
| 10110110101101010101101101010101101111010110101111 | GM | 0.0415 |
| 01010110100111011011111010110100101101111001100110 | B-0.5 | 0.0574 |
| Study | N (Patterns) | Dimensions | Measure | Correlation with 2D AG |
|---|---|---|---|---|
| Chipman (1977) | 45 | 6 × 6 | Subjective complexity | 0.74 *** |
| Howe (1980) | 60 | 5 × 5 | Subjective goodness | 0.72 *** |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aksentijevic, A.; Mihailovic, A.; T. Mihailovic, D. Time for Change: Implementation of Aksentijevic-Gibson Complexity in Psychology. Symmetry 2020, 12, 948. https://doi.org/10.3390/sym12060948
Aksentijevic A, Mihailovic A, T. Mihailovic D. Time for Change: Implementation of Aksentijevic-Gibson Complexity in Psychology. Symmetry. 2020; 12(6):948. https://doi.org/10.3390/sym12060948
Chicago/Turabian StyleAksentijevic, Aleksandar, Anja Mihailovic, and Dragutin T. Mihailovic. 2020. "Time for Change: Implementation of Aksentijevic-Gibson Complexity in Psychology" Symmetry 12, no. 6: 948. https://doi.org/10.3390/sym12060948
APA StyleAksentijevic, A., Mihailovic, A., & T. Mihailovic, D. (2020). Time for Change: Implementation of Aksentijevic-Gibson Complexity in Psychology. Symmetry, 12(6), 948. https://doi.org/10.3390/sym12060948





