Superstabilization of Descriptor Continuous-Time Linear Systems via State-Feedback Using Drazin Inverse Matrix Method

Abstract

In this paper the descriptor continuous-time linear systems with the regular matrix pencil $(E,A)$ are investigated using Drazin inverse matrix method. Necessary and sufficient conditions for the stability and superstability of this class of dynamical systems are established. The procedure for computation of the state-feedback gain matrix such that the closed-loop system is superstable is given. The effectiveness of the presented approach is demonstrated on numerical examples.

1. Introduction

Many of the dynamical systems require mathematical model represented by a combined set of differential and algebraic equations. The latter usually refer to constraints imposed on the system in a natural way, resulting from physical laws (e.g., the law of conservation of energy) or defined by the designer (e.g., constrainted motion of the object related to its area of work).

The considered class of systems has different nomenclature in the literature. They are usually called descriptor systems [1], singular systems [2], generalized state-space systems [3] or differential-algebraic equations (DAEs) [4]. In this paper we will use the term “descriptor systems”.

The history of descriptor systems dates back to the 19th century. In 1868 Weierstrass laid the foundations for this theory considering elementary divisors of regular matrix pencils [5], which was then generalized by Kronecker in 1890 for singular pencils [6]. These problems were also investigated by Gantmacher in his monograph in 1959 [7].

A matrix pencil is a set of matrices of the form $A+\lambda B$, where $\lambda$ is a parameter and A, B are matrices of the same size. Regularity of the matrix pencil guarantees the existence and uniqueness of the solution to the state equation of the considered class of dynamical systems [1,8]. The pencil is said to be regular if A, B are square matrices and $\det [A+\lambda B]\ne 0$.

The descriptor systems theory flourished in the second half of the 20th century. In 1958 Drazin introduced a generalized inverse of a square matrix [9], which was used in 1976 by Campbell et al. to derive the solution to the state equation of the descriptor continuous-time linear system [10]. Other forms of the solution were obtained by: Rose in 1978 using the Laurent series expansion [11], Yip and Sincovec in 1981 using the Weierstrass–Kronecker canonical form [12]. In subsequent years, lots of papers on analysis and design of descriptor systems were written.

There are many applications of the descriptor systems theory such as analysis of electrical, mechanical and multibody systems as well as modelling of problems in robotics, fluid mechanics, chemical engineering, economy and demography, see, e.g., [1,13,14,15,16,17,18]. Some of complex systems require hybrid models, which are not only based on ordinary differential equations (ODEs) [19].

An overview of state of the art in descriptor systems theory is given in [1,2,8]. Stability of this class of dynamical systems was investigated in [1,8,20,21]. Descriptor closed-loop systems were also studied: with state-feedback [1,8,22], with output-feedback [1,8,23] and with dynamical feedback [1,8,24,25,26]. However, all these works focused mainly on the problems of the pole assignment and regularization of descriptor systems.

Local and global stability criteria for a population model with two age classes were considered in [27]. A special class of stable systems are superstable systems with more restricted dynamics requirements, i.e., with the norm of the state vector decreasing monotonically to zero [28,29,30].

In this paper superstabilization of descriptor continuous-time linear systems via state-feedback using Drazin inverse matrix method will be investigated. The paper is organized as follows. In Section 2, basic definitions and theorems concerning descriptor systems and the Drazin inverse are recalled. The stability and superstability of this class of dynamical systems are discussed in Section 3. In Section 4, descriptor continuous-time linear systems with state-feedback are examined and the procedure for computation of the gain matrix such that the closed-loop system is superstable is presented. Numerical examples and concluding remarks are given in Section 5 and Section 6, respectively.

The following notation will be used: $\mathbb{R}$—the set of real numbers, ${\mathbb{R}}^{n\times m}$—the set of $n\times m$ real matrices and ${\mathbb{R}}^n={\mathbb{R}}^{n\times 1}$, $\mathbb{C}$—the set of complex numbers, ${\mathbb{I}}_n$—the $n\times n$ identity matrix.

2. Preliminaries

In this paper we will consider the continuous-time linear state-space model in the form

$$E\dot{x}(t)=Ax(t)+Bu(t),$$

(1)

where $x(t)\in {\mathbb{R}}^n$ is the state vector, $u(t)\in {\mathbb{R}}^m$ is the input vector and $E,A\in {\mathbb{R}}^{n\times n}$, $B\in {\mathbb{R}}^{n\times m}$. The characteristic feature of descriptor systems is that $\det E=0$, i.e., the matrix E is not invertible. We distinguish two subclasses of the considered class of systems:

• descriptor systems with the regular matrix pencil $(E,A)$, i.e.,

  $$\det [Es-A]\ne 0\mathrm{for}\mathrm{some}s\in \mathbb{C};$$

  (2)
• descriptor systems with the singular matrix pencil $(E,A)$, i.e.,

  $$\det [Es-A]=0\mathrm{for}\mathrm{some}s\in \mathbb{C}.$$

  (3)

There are several techniques for analyzing the system (1) with (2), e.g., the Laurent series expansion method [11], the Weierstrass–Kronecker decomposition method [12] and the Drazin inverse matrix method [10]. In this paper, we will focus on the last one.

Assuming that for some chosen $c\in \mathbb{C}$ we have $\det [Ec-A]\ne 0$ and premultiplying (1) by ${[Ec-A]}^{-1}$ we obtain

$$\overline{E}\dot{x}(t)=\overline{A}x(t)+\overline{B}u(t),$$

(4)

where

$$\overline{E}={[Ec-A]}^{-1}E,\overline{A}={[Ec-A]}^{-1}A,,\overline{B}={[Ec-A]}^{-1}B.$$

(5)

Note that this transformation can be done only for descriptor systems with the regular matrix pencil $(E,A)$. Observe that Equations (1) and (4) have the same solution $x(t)$.

Definition 1

([8,10]). The smallest non-negative integer q is called the index of the matrix $\overline{E}\in {\mathbb{R}}^{n\times n}$ if

$$\mathrm{rank}{\overline{E}}^q=\mathrm{rank}{\overline{E}}^{q+1}.$$

(6)

Definition 2

([8,10]). A matrix ${\overline{E}}^D\in {\mathbb{R}}^{n\times n}$ is called the Drazin inverse of $\overline{E}\in {\mathbb{R}}^{n\times n}$ if it satisfies the conditions

$$\overline{E}{\overline{E}}^D={\overline{E}}^D\overline{E},$$

(7)

$${\overline{E}}^D\overline{E}{\overline{E}}^D={\overline{E}}^D,$$

(8)

$${\overline{E}}^D{\overline{E}}^{q+1}={\overline{E}}^q,$$

(9)

where q is the index of $\overline{E}$ defined by (6).

The Drazin inverse, like the standard matrix inverse, always exists and it is unique [8,10]. From (7)–(9) it follows that if $\det \overline{E}\ne 0$, then ${\overline{E}}^D={\overline{E}}^{-1}$. Some methods for computation of the Drazin inverse are given in [8,31,32].

Lemma 1

([8,10]). The matrices $\overline{E}$ and $\overline{A}$ defined by (5) have the following properties

$$\overline{A}\overline{E}=\overline{E}\overline{A},{\overline{A}}^D\overline{E}=\overline{E}{\overline{A}}^D,{\overline{E}}^D\overline{A}=\overline{A}{\overline{E}}^D,{\overline{A}}^D{\overline{E}}^D={\overline{E}}^D{\overline{A}}^D,$$

(10)

$$\ker \overline{A}\cap \ker \overline{E}=\left\{0\right\},$$

(11)

$$({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)\overline{A}{\overline{A}}^D={\mathbb{I}}_n-\overline{E}{\overline{E}}^D,({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){(\overline{E}{\overline{A}}^D)}^q=0.$$

(12)

Also, the matrices $\overline{E}$, ${\overline{E}}^D$ and $\overline{A}$ can be written in the form

$$\overline{E}=T\left[\begin{array}{cc}J& 0\\ 0& N\end{array}\right]T^{-1},{\overline{E}}^D=T\left[\begin{array}{cc}{J}^{-1}& 0\\ 0& 0\end{array}\right]T^{-1},\overline{A}=T\left[\begin{array}{cc}{A}_1& 0\\ 0& A_2\end{array}\right]T^{-1},$$

(13)

where $\det T\ne 0$, $J\in {\mathbb{R}}^{n_1\times n_1}$ is nonsingular, $N\in {\mathbb{R}}^{n_2\times n_2}$ is nilpotent, i.e., for some μ, $N^{\mu -1}\ne 0$, $N^{\mu }=0$ and $A_1\in {\mathbb{R}}^{n_1\times n_1}$, $A_2\in {\mathbb{R}}^{n_2\times n_2}$, $n_1+n_2=n$.

Let $U\subset {\mathbb{R}}^m$ be the set of admissible inputs $u(t)\in U$ and $X_0\subset {\mathbb{R}}^n$ be the set of consistent initial conditions $x_0\in X_0$ for which Equation (1) has a solution $x(t)$ for $u(t)\in U$.

Theorem 1

([8,10]). The solution to Equation (4) (or equivalently (1)) for $x_0\in X_0$ and $u(t)\in U$ is given by

$$x(t)=e^{{\overline{E}}^D\overline{A}t}\overline{E}{\overline{E}}^D{x}_0+{\int }_0^t{e}^{{\overline{E}}^D\overline{A}(t-\tau )}\overline{B}u(\tau )d\tau +(\overline{E}{\overline{E}}^D-{\mathbb{I}}_n)\sum _{k=0}^{q-1}{({\overline{A}}^D\overline{E})}^k{\overline{A}}^D\overline{B}{u}^{(k)}(t),$$

(14)

where $u^{(k)}(t)$ is the k-th time derivative of the input vector and q is the index of $\overline{E}$.

From (14) for $t=0$ we obtain consistent initial conditions for the system

$$x_0=\overline{E}{\overline{E}}^D\gamma +(\overline{E}{\overline{E}}^D-{\mathbb{I}}_n)\sum _{k=0}^{q-1}{({\overline{A}}^D\overline{E})}^k{\overline{A}}^D\overline{B}{u}^{(k)}(0),$$

(15)

where $\gamma \in {\mathbb{R}}^n$ is an arbitrary vector.

Note that the matrices (5) depend of the choice of the parameter c. However, in the solution (14) they appear as products $\overline{E}{\overline{E}}^D$, ${\overline{E}}^D\overline{A}$, ${\overline{A}}^D\overline{E}$, ${\overline{E}}^D\overline{B}$, ${\overline{A}}^D\overline{B}$, which are independent of the choice of c [8].

3. Stability and Superstability of Descriptor Continuous-Time Linear Systems

In this section the stability and superstability of descriptor continuous-time linear systems will be discussed. Necessary and sufficient conditions for these properties will be given using Drazin inverse matrix method.

3.1. Stability

In the following considerations it is assumed that $\det A\ne 0$, i.e., the descriptor continuous-time linear system (1) has exactly one equilibrium point [8].

Definition 3.

The descriptor continuous-time linear system (1) is called asymptotically stable if

$$\underset{t\to \infty }{lim}x(t)=0$$

(16)

for all consistent initial conditions $x_0\in X_0$ and $u(t)=0$.

In contrast to standard dynamical systems (i.e., with $E={\mathbb{I}}_n$), where we can study their stability based on the eigenvalues of the matrix A, in descriptor systems we analyze the eigenvalues of the matrix pair $(E,A)$.

Definition 4.

The characteristic equation of the matrix pair $(E,A)$ has the form

$$p_{(E,A)}(s)=\det [Es-A]=a_r{s}^r+a_{r-1}{s}^{r-1}+\dots +a_{1}s+a_0=0,$$

(17)

where $r<n$ and $p_{(E,A)}(s)$ is the characteristic polynomial of the matrix pair $(E,A)$.

Theorem 2

([8]). The matrix pair $(E,A)$ (or equivalently the system (1)) is asymptotically stable if and only if its eigenvalues $s_k$, $k=1,\dots ,r$ (roots of the characteristic equation) satisfy the condition

$$\mathrm{Re}{s}_k<0,k=1,\dots ,r.$$

(18)

Taking into account that Equations (1) and (4) have the same solution $x(t)$, we expect that both models also have the same set of eigenvalues.

Definition 5.

The characteristic equation of the matrix pair $(\overline{E},\overline{A})$ is given by

$$p_{(\overline{E},\overline{A})}(s)=\det [\overline{E}s-\overline{A}]={\overline{a}}_r{s}^r+{\overline{a}}_{r-1}{s}^{r-1}+\dots +{\overline{a}}_{1}s+{\overline{a}}_0=0,$$

(19)

where $r<n$ and $p_{(\overline{E},\overline{A})}(s)$ is the characteristic polynomial of the matrix pair $(\overline{E},\overline{A})$.

Lemma 2.

The characteristic polynomials of the matrix pairs $(E,A)$ and $(\overline{E},\overline{A})$ are related by

$$p_{(\overline{E},\overline{A})}(s)=\frac{p_{(E,A)}(s)}{\det [Ec-A]}.$$

(20)

Proof. 

The characteristic polynomial of the pair $(\overline{E},\overline{A})$ has the form

$$\begin{array}{cc}\hfill p_{(\overline{E},\overline{A})}(s)& =\det [\overline{E}s-\overline{A}]=\det \{{[Ec-A]}^{-1}Es-{[Ec-A]}^{-1}A\}\hfill \\ \hfill & =\det \left\{{[Ec-A]}^{-1}[Es-A]\right\}=\det {[Ec-A]}^{-1}\det [Es-A]\hfill \\ \hfill & ={\left\{\det [Ec-A]\right\}}^{-1}{p}_{(E,A)}(s),\hfill \end{array}$$

(21)

which is equivalent to (20). □

Note that the characteristic equations of the matrix pairs $(E,A)$ and $(\overline{E},\overline{A})$ have the same form. Therefore, both pairs have the same set of eigenvalues and Theorem 2 can be used for the roots of Equation (19).

The following approach can also be used to test the stability of the descriptor continuous-time linear system (1).

Lemma 3.

The matrix ${\overline{E}}^D\overline{A}$ has $r=\mathrm{rank}{\overline{E}}^D\overline{A}$ eigenvalues of the pair $(\overline{E},\overline{A})$ (or $(E,A)$) and additionally $n-r$ zero eigenvalues, i.e., its characteristic equation has the form

$$p_{{\overline{E}}^D\overline{A}}(s)=\det [{\mathbb{I}}_{n}s-{\overline{E}}^D\overline{A}]=s^{n-r}{p}_{(\overline{E},\overline{A})}(s)=0,$$

(22)

where $p_{{\overline{E}}^D\overline{A}}(s)$ is the characteristic polynomial of the matrix ${\overline{E}}^D\overline{A}$.

Proof. 

Using (13) we have

$$\begin{array}{cc}\hfill p_{{\overline{E}}^D\overline{A}}(s)& =\det [{\mathbb{I}}_{n}s-{\overline{E}}^D\overline{A}]=\det \left\{T\left[\begin{array}{cc}{\mathbb{I}}_{n_1}s-J^{-1}{A}_1& 0\\ 0& {\mathbb{I}}_{n_2}s\end{array}\right]T^{-1}\right\}\hfill \\ \hfill & =\det T\det [{\mathbb{I}}_{n_1}s-J^{-1}{A}_1]\det \left[{\mathbb{I}}_{n_2}s\right]\det T^{-1}=s^{n_2}\det [{\mathbb{I}}_{n_1}s-J^{-1}{A}_1],\hfill \end{array}$$

(23)

since $\det T\det T^{-1}={\mathbb{I}}_n$. It is easy to see that $n_1=r$ and $n_2=n-r$.

Using again (13) we can write

$$\begin{array}{cc}\hfill p_{(\overline{E},\overline{A})}(s)& =\det [\overline{E}s-\overline{A}]=\det \left\{T\left[\begin{array}{cc}Js-A_1& 0\\ 0& Ns-A_2\end{array}\right]T^{-1}\right\}\hfill \\ \hfill & =\det T\det [Js-A_1]\det [Ns-A_2]\det T^{-1}=\det [Js-A_1]\det [Ns-A_2],\hfill \end{array}$$

(24)

since $\det T\det T^{-1}={\mathbb{I}}_n$.

Note that $\overline{E}\overline{A}=\overline{A}\overline{E}$. Then from (13) we have $N{A}_2=A_{2}N$ if and only if $A_2=\alpha {\mathbb{I}}_{n_2}$, where $\alpha \in \mathbb{R}$, i.e., $A_2$ is a scalar matrix (a nilpotent matrix N can not be scalar). Hence, Equation (24) can be written in the form

$$p_{(\overline{E},\overline{A})}(s)=\det [Js-A_1]\det [Ns-\alpha {\mathbb{I}}_{n_2}]={(-\alpha )}^{n_2}\det [Js-A_1]={(-\alpha )}^{n_2}\det [{\mathbb{I}}_{n_1}s-J^{-1}{A}_1],$$

(25)

since $\det [Ns-\alpha {\mathbb{I}}_{n_2}]={(-\alpha )}^{n_2}$.

Equating (23) and (25) to zero we have

$$p_{{\overline{E}}^D\overline{A}}(s)=s^{n_2}\det [{\mathbb{I}}_{n_1}s-J^{-1}{A}_1]=0,$$

(26)

$$p_{(\overline{E},\overline{A})}(s)=\det [{\mathbb{I}}_{n_1}s-J^{-1}{A}_1]=0,$$

(27)

which is equivalent to (22). □

Theorem 3.

The descriptor continuous-time linear system (1) is asymptotically stable if and only if the matrix ${\overline{E}}^D\overline{A}$ has r stable eigenvalues (satisfying the condition (18)) and $n-r$ zero eigenvalues.

Proof. 

The proof follows directly from Lemma 3. □

Based on the above considerations we have the following Theorem.

Theorem 4.

The descriptor continuous-time linear system (1) is asymptotically stable if and only if one of the following equivalent conditions are met:

• roots of the characteristic Equation (19) satisfy the condition (18);
• the matrix ${\overline{E}}^D\overline{A}$ has $r=\mathrm{rank}{\overline{E}}^D\overline{A}$ stable eigenvalues and $n-r$ zero eigenvalues.

3.2. Superstability

The asymptotic stability of a dynamical system ensures that its free response decreases to zero for $t\to \infty$, however its value may increase significantly in the initial part of the state vector trajectory. In superstable systems the norm of the state vector decreases monotonically to zero for $t\to \infty$, which prevents such undesirable effects [28,29,30].

The following norms will be used:

• ∞-norm of a vector $x(t)=\left[x_i(t)\right]\in {\mathbb{R}}^n$

  $$\parallel x(t)\parallel =\underset{1\le i\le n}{max}\left|x_i(t)\right|,$$

  (28)
• ∞-norm of a matrix $A=\left[a_{ij}\right]\in {\mathbb{R}}^{n\times n}$

  $$\parallel A\parallel =\underset{1\le i\le n}{max}\left(\sum _{j=1}^n\left|a_{ij}\right|\right).$$

  (29)

Definition 6

([29]). A matrix $A\in {\mathbb{R}}^{n\times n}$ of the continuous-time linear system

$$\dot{x}(t)=Ax(t)$$

(30)

is called superstable if

$$\sigma (A)=\sigma =\underset{1\le i\le n}{min}\left(-a_{ii}-\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^n\left|a_{ij}\right|\right)>0.$$

(31)

Quantity $\sigma (A)$ is called the superstability degree of the matrix A. If the matrix is superstable, then it is also stable, however the reverse implication does not hold.

Lemma 4

([29]). For a superstable matrix A we have

$$\parallel e^{At}\parallel \le e^{-\sigma t}.$$

(32)

Theorem 5

([29]). If the system (30) is superstable, then

$$\parallel x(t)\parallel \le \parallel x_0\parallel e^{-\sigma t},t\in [0,+\infty ).$$

(33)

Now let us consider the descriptor continuous-time linear system (1). The solution to Equation (4) (or equivalently (1)) for $u(t)=0$ has the form

$$x(t)=e^{{\overline{E}}^D\overline{A}t}\overline{E}{\overline{E}}^D{x}_0.$$

(34)

Lemma 5.

The matrices ${\overline{E}}^D\overline{A}$ and ${\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$, where $G\in {\mathbb{R}}^{n\times n}$ is arbitrary, satisfy the equality

$$e^{{\overline{E}}^D\overline{A}t}\overline{E}{\overline{E}}^D=e^{[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\overline{E}{\overline{E}}^D.$$

(35)

Proof. 

The matrix $e^{[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\overline{E}{\overline{E}}^D$ can be written in the form

$$\begin{array}{cc}\hfill e^{[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\overline{E}{\overline{E}}^D& =\left({\mathbb{I}}_n+[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t+\frac{{[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]}^2{t}^2}{2!}+\dots \right)\overline{E}{\overline{E}}^D\hfill \\ \hfill & =\left({\mathbb{I}}_n+{\overline{E}}^D\overline{A}t+\frac{{({\overline{E}}^D\overline{A})}^2{t}^2}{2!}\right)\overline{E}{\overline{E}}^D=e^{{\overline{E}}^D\overline{A}t}\overline{E}{\overline{E}}^D,\hfill \end{array}$$

(36)

since $({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)\overline{E}{\overline{E}}^D=0$. □

Using Lemma 5 Equation (34) can be rewritten in the form

$$x(t)=e^{{\overline{E}}^D\overline{A}t}\overline{E}{\overline{E}}^D{x}_0=e^{[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\overline{E}{\overline{E}}^D{x}_0,$$

(37)

where $G\in {\mathbb{R}}^{n\times n}$ is an arbitrary matrix.

Taking into account (14) and (15) for $u(t)=0$ it is easy to see that if $x_0\in \mathrm{Im}\overline{E}{\overline{E}}^D$, then $x_0=\overline{E}{\overline{E}}^D{x}_0$. Therefore, from (37) we have

$$\parallel x(t)\parallel \le \parallel e^{[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\parallel \parallel x_0\parallel .$$

(38)

If the matrix ${\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$ is superstable (i.e., it satisfies the condition (31)), then by Lemma 4 we have $\parallel e^{[{\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\parallel \le e^{-\sigma t}$. From the inequality (38) we obtain

$$\parallel x(t)\parallel \le \parallel x_0\parallel e^{-\sigma t},$$

(39)

and the norm of the state vector decreases monotonically to zero. Therefore, the following theorem has been proved.

Theorem 6.

The descriptor continuous-time linear system (1) is superstable if and only if there exists a matrix $G\in {\mathbb{R}}^{n\times n}$ such that the matrix ${\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$ satisfies the condition (31).

The matrix G shall be chosen so that the superstability degree of the matrix ${\overline{E}}^D\overline{A}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$ takes value higher than zero, i.e., the term $G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$ eliminates from the matrix ${\overline{E}}^D\overline{A}$ unimportant entries that are further canceled through multiplication by $x_0\in \mathrm{Im}\overline{E}{\overline{E}}^D$.

4. Descriptor Continuous-Time Linear Systems with State-Feedback

In this section descriptor continuous-time linear systems with state-feedback will be examined. The procedure for computation of the gain matrix such that the closed-loop system is superstable will be presented.

First we shall show that Equation (4) can be decomposed into two equations as follows.

Lemma 6.

Let

$$x_1(t)=\overline{E}{\overline{E}}^{D}x(t),x_2(t)=({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)x(t),$$

(40)

$$x_1(t)+x_2(t)=x(t).$$

(41)

The Equation (4) is equivalent to the following equations:

$${\dot{x}}_1(t)={\overline{E}}^D\overline{A}{x}_1(t)+{\overline{E}}^D\overline{B}u(t),$$

(42)

$$({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{E}{\dot{x}}_2(t)=x_2(t)+({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{B}u(t).$$

(43)

Proof. 

Premultilpying (4) by $\overline{E}{\overline{E}}^D$ we obtain

$${\overline{E}}^2{\overline{E}}^D\dot{x}(t)=\overline{A}\overline{E}{\overline{E}}^{D}x(t)+\overline{E}{\overline{E}}^D\overline{B}u(t),$$

(44)

which is equivalent to

$$\overline{E}{\dot{x}}_1(t)=\overline{A}{x}_1(t)+\overline{E}{\overline{E}}^D\overline{B}u(t).$$

(45)

Next, multiplying (45) by ${\overline{E}}^D$ we get

$$\overline{E}{\overline{E}}^D{\dot{x}}_1(t)={\overline{E}}^D\overline{A}{x}_1(t)+{\overline{E}}^D\overline{E}{\overline{E}}^D\overline{B}u(t)$$

(46)

and

$${\dot{x}}_1(t)={\overline{E}}^D\overline{A}{x}_1(t)+{\overline{E}}^D\overline{B}u(t),$$

(47)

since $\overline{E}{\overline{E}}^D{x}_1(t)=\overline{E}{\overline{E}}^D\overline{E}{\overline{E}}^{D}x(t)=\overline{E}{\overline{E}}^{D}x(t)=x_1(t)$. Then, subtracting (44) from (4) we have

$$\overline{E}({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)\dot{x}(t)=\overline{A}({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)x(t)+({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)\overline{B}u(t)$$

(48)

and

$$\overline{E}{\dot{x}}_2(t)=\overline{A}{x}_2(t)+({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)\overline{B}u(t).$$

(49)

Premultiplying (49) by ${\overline{A}}^D({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$ we obtain

$$({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{E}{\dot{x}}_2(t)=({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)\overline{A}{\overline{A}}^D{x}_2(t)+{({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)}^2{\overline{A}}^D\overline{B}u(t).$$

(50)

Using (12) and the fact that ${({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)}^k={\mathbb{I}}_n-\overline{E}{\overline{E}}^D$ for $k=1,2,\dots$ we have

$$({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{E}{\dot{x}}_2(t)=x_2(t)+({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{B}u(t),$$

(51)

since $({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)x_2(t)={({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)}^{2}x(t)=({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)x(t)=x_2(t)$. □

It is easy to check that the first two components of (14) are the solution to Equation (42) and the third component of (14) is the solution to Equation (43).

4.1. Problem Formulation

Let us consider the system (1) with the state-feedback

$$u(t)=v(t)-Kx(t)=v-K(x_1+x_2),$$

(52)

where $v\in {\mathbb{R}}^m$ is the new input vector, $x_1\in {\mathbb{R}}^n$, $x_2\in {\mathbb{R}}^n$ are defined by (40) and $K\in {\mathbb{R}}^{m\times n}$.

To simplify the notation we introduce

$${\overline{A}}_1={\overline{E}}^D\overline{A},{\overline{B}}_1={\overline{E}}^D\overline{B},{\overline{B}}_2=({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{B},\overline{N}=({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{E}.$$

(53)

Using (53) Equations (42), (43) can be rewritten in the form

$${\dot{x}}_1(t)={\overline{A}}_1{x}_1(t)+{\overline{B}}_{1}u(t),$$

(54)

$$\overline{N}{\dot{x}}_2(t)=x_2(t)+{\overline{B}}_{2}u(t).$$

(55)

Substituting (52) into (54), (55) we obtain

$${\dot{x}}_1(t)=({\overline{A}}_1-{\overline{B}}_{1}K)x_1(t)-{\overline{B}}_{1}K{x}_2(t)+{\overline{B}}_{1}v(t),$$

(56)

$$\overline{N}{\dot{x}}_2(t)=({\mathbb{I}}_n-{\overline{B}}_{2}K)x_2(t)-{\overline{B}}_{2}K{x}_1(t)+{\overline{B}}_{2}v(t).$$

(57)

The problem can be stated as follows. Given ${\overline{A}}_1$, ${\overline{B}}_1$, ${\overline{B}}_2$, $\overline{N}$ find K such that the closed-loop system is superstable.

4.2. Problem Solution

Lemma 7.

It is possible to choose the matrix K such that $K{x}_1(t)\ne 0$, $K{x}_2(t)=0$ or $K{x}_1(t)=0$, $K{x}_2(t)\ne 0$.

Proof. 

Let $K=\left[K_1{K}_2\right]$ and $\overline{K}=KT=\left[{\overline{K}}_1{\overline{K}}_2\right]$. Taking into account (13) and (40) we have

$$K{x}_1(t)=K\overline{E}{\overline{E}}^{D}x(t)=\left[K_1{K}_2\right]T\left[\begin{array}{cc}{\mathbb{I}}_{n_1}& 0\\ 0& 0\end{array}\right]T^{-1}x=\left[{\overline{K}}_{1}0\right]T^{-1}x(t),$$

(58)

$$K{x}_2(t)=K({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)x(t)=\left[K_1{K}_2\right]T\left[\begin{array}{cc}0& 0\\ 0& {\mathbb{I}}_{n_2}\end{array}\right]T^{-1}x=\left[0{\overline{K}}_2\right]T^{-1}x(t).$$

(59)

Hence, for $K\overline{E}{\overline{E}}^D=0$ we have $K{x}_1(t)=0$ and for $K({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)=0$ we have $K{x}_2(t)=0$. □

Choosing the matrix K such that $K{x}_2(t)=0$, i.e., $K({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)=0$, from (56), (57) we obtain

$${\dot{x}}_1(t)={\overline{A}}_{C1}{x}_1(t)+{\overline{B}}_{1}v(t),$$

(60)

$$\overline{N}{\dot{x}}_2(t)=x_2(t)-{\overline{A}}_{C2}{x}_1(t)+{\overline{B}}_{2}v(t),$$

(61)

where

$${\overline{A}}_{C1}={\overline{A}}_1-{\overline{B}}_{1}K,{\overline{A}}_{C2}={\overline{B}}_{2}K.$$

(62)

The solution to Equation (60) is well-known [8] and it is given by

$$x_1(t)=e^{{\overline{A}}_{C1}t}{x}_{10}+{\int }_0^t{e}^{{\overline{A}}_1(t-\tau )}{\overline{B}}_{1}v(\tau )d\tau =e^{{\overline{A}}_{C1}t}\overline{E}{\overline{E}}^D{x}_0+{\int }_0^t{e}^{{\overline{A}}_1(t-\tau )}{\overline{B}}_{1}v(\tau )d\tau$$

(63)

since $x_{10}=\overline{E}{\overline{E}}^D{x}_0$.

The solution to Equation (61) can be obtained using the approach given in [8] and it has the form

$$x_2(t)=-\sum _{k=0}^{q-1}{\overline{N}}^k\left({\overline{B}}_2{v}^{(k)}(t)-{\overline{A}}_{C2}{x}_1^{(k)}(t)\right),$$

(64)

where $v^{(k)}(t)$ and $x_1^{(k)}(t)$ are the k-th time derivatives of $v(t)$ and $x_1(t)$. Taking into account that

$$\begin{array}{cc}\hfill {\dot{x}}_1(t)& ={\overline{A}}_{C1}{x}_1(t)+{\overline{B}}_{1}v(t),\hfill \\ \hfill {\ddot{x}}_1(t)& ={\overline{A}}_{C1}{\dot{x}}_1(t)+{\overline{B}}_1\dot{v}(t)={\overline{A}}_{C1}^2{x}_1(t)+{\overline{A}}_{C1}{\overline{B}}_{1}v(t)+{\overline{B}}_1\dot{v}(t),\hfill \\ \hfill & ⋮\hfill \\ \hfill x_1^{(k)}(t)& ={\overline{A}}_{C1}{x}_1^{(k-1)}(t)+{\overline{B}}_1{v}^{(k-1)}(t)={\overline{A}}_{C1}^k{x}_1(t)+\sum _{j=0}^{k-1}{\overline{A}}_{C1}^{k-j-1}{\overline{B}}_1{v}^{(j)}(t)\hfill \end{array}$$

(65)

from (64) we have

$$x_2(t)=-\sum _{k=0}^{q-1}{\overline{N}}^k\left[{\overline{B}}_2{v}^{(k)}(t)-{\overline{A}}_{C2}\left({\overline{A}}_{C1}^k{x}_1(t)+\sum _{j=0}^{k-1}{\overline{A}}_{C1}^{k-j-1}{\overline{B}}_1{v}^{(j)}(t)\right)\right].$$

(66)

4.2.1. Stability of the Closed-Loop System

Lemma 8.

If $v(t)=0$ then for descriptor continuous-time linear system (1) with the state-feedback (52) such that $K{x}_2(t)=0$ we have $\underset{t\to \infty }{lim}{x}_2(t)=0$ if and only if $\underset{t\to \infty }{lim}{x}_1(t)=0$.

Proof. 

The proof follows immediately from (66) for $v(t)=0$, i.e.,

$$x_2(t)=\sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{\overline{A}}_{C1}^k{x}_1(t).$$

(67)

Therefore, if $\underset{t\to \infty }{lim}{x}_1(t)=0$ then also $\underset{t\to \infty }{lim}{x}_2(t)=0$. □

Hence, the stability of the closed-loop system (60), (61) depends only on Equation (60), i.e., on the matrix ${\overline{A}}_{C1}$. Thus, we can use the considerations presented in Section 3.1.

Theorem 7.

The descriptor continuous-time linear sysstem (1) with the state-feedback (52) such that $K{x}_2(t)=0$ is asymptotically stable if and only if one of the following equivalent conditions are met:

• roots of the characteristic equation $\det [\overline{E}s-(\overline{A}-\overline{B}K)]=0$ satisfy the condition (18);
• the matrix ${\overline{A}}_{C1}$ has $r=\mathrm{rank}{\overline{A}}_{C1}$ stable eigenvalues and $n-r$ zero eigenvalues.

4.2.2. Superstability of the Closed-Loop System

Theorem 8.

The descriptor continuous-time linear sysstem (1) with the state-feedback (52) such that $K{x}_2(t)=0$ is superstable if and only if there exists a matrix $G\in {\mathbb{R}}^{n\times n}$ such that:

• the matrix ${\overline{A}}_{C1}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$ satisfies the condition (31);
• the inequality

  $$∥\sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{[{\overline{A}}_{C1}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]}^k∥\le 1$$

  (68)
  is satisfied.

Proof. 

The first condition can be proven in a similar way as Theorem 6, so we will focus on the proof of the second condition. Assume $v(t)=0$. Using (41), (63) and (67) we have

$$x(t)=x_1(t)+x_2(t)=\left({\mathbb{I}}_n+\sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{\overline{A}}_{C1}^k\right)x_1(t)=\left({\mathbb{I}}_n+\sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{\overline{A}}_{C1}^k\right)e^{{\overline{A}}_{C1}t}\overline{E}{\overline{E}}^D{x}_0.$$

(69)

Let

$$\overline{B}=T\left[\begin{array}{c}{B}_1\\ B_2\end{array}\right],K=\left[\begin{array}{cc}{\overline{K}}_1& {\overline{K}}_2\end{array}\right]T^{-1}$$

(70)

and

$$\overline{B}K=T\left[\begin{array}{cc}{B}_1{\overline{K}}_1& B_1{\overline{K}}_2\\ B_2{\overline{K}}_1& B_2{\overline{K}}_2\end{array}\right]T^{-1}.$$

(71)

Taking into account (13) and using (71) for $K({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)=0$ (i.e., ${\overline{K}}_2=0$) we obtain

$$\begin{array}{cc}\hfill {\overline{A}}_{C1}& ={\overline{E}}^D\overline{A}-{\overline{E}}^D\overline{B}K\hfill \\ \hfill & =T\left(\left[\begin{array}{cc}{J}^{-1}{A}_1& 0\\ 0& 0\end{array}\right]-\left[\begin{array}{cc}{J}^{-1}{B}_1{\overline{K}}_1& 0\\ 0& 0\end{array}\right]\right)T^{-1}=T\left[\begin{array}{cc}{A}_{C1}& 0\\ 0& 0\end{array}\right]T^{-1},\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill {\overline{A}}_{C2}& =({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{B}K\hfill \\ \hfill & =T\left[\begin{array}{cc}0& 0\\ 0& {\mathbb{I}}_{n_2}\end{array}\right]\left[\begin{array}{cc}{A}_1^D& 0\\ 0& A_2^D\end{array}\right]\left[\begin{array}{cc}{B}_1{\overline{K}}_1& 0\\ B_2{\overline{K}}_1& 0\end{array}\right]T^{-1}=T\left[\begin{array}{cc}0& 0\\ A_2^D{B}_2{\overline{K}}_1& 0\end{array}\right]T^{-1}\hfill \\ \hfill & =T\left[\begin{array}{cc}0& 0\\ A_{C2}& 0\end{array}\right]T^{-1}\hfill \end{array}$$

(73)

$$\begin{array}{cc}\hfill \overline{N}& =({\mathbb{I}}_n-\overline{E}{\overline{E}}^D){\overline{A}}^D\overline{E}\hfill \\ \hfill & =T\left[\begin{array}{cc}0& 0\\ 0& {\mathbb{I}}_{n_2}\end{array}\right]\left[\begin{array}{cc}{A}_1^D& 0\\ 0& A_2^D\end{array}\right]\left[\begin{array}{cc}J& 0\\ 0& N\end{array}\right]T^{-1}=T\left[\begin{array}{cc}0& 0\\ 0& A_2^{D}N\end{array}\right]T^{-1}\hfill \\ \hfill & =T\left[\begin{array}{cc}0& 0\\ 0& \tilde{N}\end{array}\right]T^{-1}\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill e^{{\overline{A}}_{C1}t}& =\exp \left(T\left[\begin{array}{cc}{A}_{C1}& 0\\ 0& 0\end{array}\right]T^{-1}\right)=T\left[\begin{array}{cc}{e}^{A_{C1}t}& 0\\ 0& {\mathbb{I}}_{n_2}\end{array}\right]T^{-1},\hfill \end{array}$$

(75)

where $A_{C1}=J^{-1}(A_1-B_1{\overline{K}}_1)$, $A_{C2}=A_2^D{B}_2{\overline{K}}_1$, $\tilde{N}=A_2^{D}N$. It is easy to check that

$$\begin{array}{cc}\hfill x(t)& =\left({\mathbb{I}}_n+\sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{[{\overline{A}}_{C1}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]}^k\right)e^{[{\overline{A}}_{C1}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\overline{E}{\overline{E}}^D{x}_0\hfill \\ \hfill & =\left({\mathbb{I}}_n+\sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{\overline{A}}_{C1}^k\right)e^{{\overline{A}}_{C1}t}\overline{E}{\overline{E}}^D{x}_0\hfill \end{array}$$

(76)

since by Lemma 5 it follows that $e^{[{\overline{A}}_{C1}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]t}\overline{E}{\overline{E}}^D=e^{{\overline{A}}_{C1}t}\overline{E}{\overline{E}}^D$ and from (72), (75) we have $e^{{\overline{A}}_{C1}t}\overline{E}{\overline{E}}^D=\overline{E}{\overline{E}}^D{e}^{{\overline{A}}_{C1}t}$, ${[{\overline{A}}_{C1}+G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)]}^k\overline{E}{\overline{E}}^D={\overline{A}}_{C1}^k\overline{E}{\overline{E}}^D$. Using (13) and (72)–(76) we obtain

$$\begin{array}{cc}\hfill \sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{\overline{A}}_{C1}^k& =\sum _{k=0}^{q-1}\left(T\left[\begin{array}{cc}0& 0\\ 0& {\tilde{N}}^k\end{array}\right]\left[\begin{array}{cc}0& 0\\ A_{C2}& 0\end{array}\right]\left[\begin{array}{cc}{A}_{C1}^k& 0\\ 0& 0\end{array}\right]T^{-1}\right)\hfill \\ \hfill & =T\left[\begin{array}{cc}0& 0\\ {\displaystyle \sum _{k=0}^{q-1}}{\tilde{N}}^k{A}_{C2}{A}_{C1}^k& 0\end{array}\right]T^{-1}\hfill \end{array}$$

(77)

and

$$\begin{array}{c}\hfill x(t)=\left({\mathbb{I}}_n+\sum _{k=0}^{q-1}{\overline{N}}^k{\overline{A}}_{C2}{\overline{A}}_{C1}^k\right)e^{{\overline{A}}_{C1}t}\overline{E}{\overline{E}}^D{x}_0=T\left[\begin{array}{cc}{e}^{A_{C1}t}& 0\\ {\displaystyle \sum _{k=0}^{q-1}}{\tilde{N}}^k{A}_{C2}{A}_{C1}^k{e}^{A_{C1}t}& 0\end{array}\right]T^{-1}{x}_0\end{array}$$

(78)

Let $T={\mathbb{I}}_n$. The norm of (78) can be expressed by

$$\parallel x(t)\parallel \le \parallel e^{A_{C1}t}\parallel \parallel x_0\parallel or\parallel x(t)\parallel \le ∥\sum _{k=0}^{q-1}{\tilde{N}}^k{A}_{C2}{A}_{C1}^k∥\parallel e^{A_{C1}t}\parallel \parallel x_0\parallel .$$

(79)

Thus, for $∥{\displaystyle \sum _{k=0}^{q-1}}{\tilde{N}}^k{A}_{C2}{A}_{C1}^k∥\le 1$ we have $\parallel x(t)\parallel \le \parallel e^{A_{C1}t}\parallel \parallel x_0\parallel$. In general case for any matrix T we obtain the condition (68). Note that the matrix G does not change the solution $x(t)$ and its choice is arbitrary. The term $G({\mathbb{I}}_n-\overline{E}{\overline{E}}^D)$ is used to eliminate unnecessary elements that may occur in the matrix ${\overline{A}}_{C1}$. □

5. Numerical Examples

In this section the effectiveness of the presented approach will be demonstrated on two numerical examples. The first one shows how to test the superstability of the descriptor continuous-time linear system (1) using Theorem 6. The second one shows the procedure for the state-feedback synthesis such that the superstability of the closed-loop system (60), (61) is guaranteed (Theorem 8).

Example 1.

Check the superstability of the descriptor continuous-time linear system (1) with $u(t)=0$ and

$$E=\left[\begin{array}{ccc}-2.4& -2.6& -1.95\\ 0.6& 0.9& 0.675\\ 1.6& 0.4& 0.3\end{array}\right],A=\left[\begin{array}{ccc}2& 3& -1\\ 0& -2& -1\\ -4& 1& 0\end{array}\right].$$

(80)

It is easy to verify that the matrix pencil $(E,A)$ is regular, i.e.,

$$\det [Es-A]=-2.75s^2-19.25s-22\ne 0.$$

(81)

From (5) for $c=0$ we have

$$\overline{E}={[-A]}^{-1}E=\left[\begin{array}{ccc}0.5& 0.25& 0.1875\\ 0.4& 0.6& 0.45\\ -0.2& -0.3& -0.225\end{array}\right],\overline{A}={[-A]}^{-1}A=-{\mathbb{I}}_3=\left[\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right]$$

(82)

Using one of the known methods for computation of the Drazin inverse [8,31,32] we obtain

$${\overline{E}}^D=\left[\begin{array}{ccc}3& -2& -1.5\\ -3.2& 6.4& 4.8\\ 1.6& -3.2& -2.4\end{array}\right].$$

(83)

and

$${\overline{E}}^D\overline{A}=\left[\begin{array}{ccc}-3& 2& 1.5\\ 3.2& -6.4& -4.8\\ -1.6& 3.2& 2.4\end{array}\right],\overline{E}{\overline{E}}^D=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1.6& 1.2\\ 0& -0.8& -0.6\end{array}\right].$$

(84)

The matrix ${\overline{E}}^D\overline{A}$ defined by (84) does not satisfy the condition (31). However, using (84) and

$$G=\left[\begin{array}{ccc}0& 1.25& 0\\ 0& -4& 0\\ 0& 0& -4\end{array}\right]$$

(85)

we obtain

$${\overline{E}}^D\overline{A}+G({\mathbb{I}}_3-\overline{E}{\overline{E}}^D)=\left[\begin{array}{ccc}-3& 1.25& 0\\ 3.2& -4& 0\\ -1.6& 0& -4\end{array}\right],$$

(86)

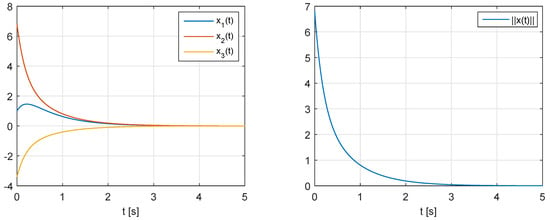
which satisfies (31). Therefore, by Theorem 6 the considered system is superstable. In Figure 1 we present time plots of the state variables and the norm of the state vector for $x_0=\left[\begin{array}{ccc}1& 6.8& -3.4\end{array}\right]$. We can see that the norm of the state vector decreases monotonically for $t\to \infty$ and the system is superstable. Similar result can be obtained for any $x_0\in \mathrm{Im}\overline{E}{\overline{E}}^D$.

Example 2.

Consider the descriptor continuous-time linear system (1) with

$$E=\left[\begin{array}{ccc}-3& -5& -0.5\\ 3.5& 7& 0.7\\ 3.5& 5.5& 0.55\end{array}\right],A=\left[\begin{array}{ccc}1& 0.95& 0\\ 0& -1.9& 2.85\\ -1.5& 0& 0.95\end{array}\right],B=\left[\begin{array}{cc}-1.715& -0.24\\ 7.98& -5.795\\ 5.85& 0.075\end{array}\right].$$

(87)

The matrix pencil $(E,A)$ is regular since

$$5.8633s^2+23.465s+5.8633\ne 0.$$

(88)

From (5) for $c=0$ we have

$$\overline{E}=\left[\begin{array}{ccc}2& 3& 0.3\\ 1.0526& 2.1053& 0.2105\\ -0.5263& -1.0526& -0.1053\end{array}\right],\overline{A}=\left[\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right],\overline{B}=\left[\begin{array}{cc}2& 1\\ -0.3& -0.8\\ -3& 1.5\end{array}\right].$$

(89)

Computation of the Drazin inverse of the matrix $\overline{E}$ yields

$${\overline{E}}^D=\left[\begin{array}{ccc}2& -3& -0.3\\ -1.0526& 2.1053& 0.2105\\ 0.5263& -1.0526& -0.1053\end{array}\right].$$

(90)

Note that $\mathrm{rank}\overline{E}=\mathrm{rank}{\overline{E}}^2$ and $q=1$. It is also worth noting that $\det \overline{A}\ne 0$, so ${\overline{A}}^D={\overline{A}}^{-1}=\overline{A}$. Using (89) and (90) we obtain

$$\begin{array}{c}{\overline{A}}_1={\overline{E}}^D\overline{A}=\left[\begin{array}{ccc}-2& 3& 0.3\\ 1.0526& -2.1053& -0.2105\\ -0.5263& 1.0526& 0.1053\end{array}\right],{\overline{B}}_1={\overline{E}}^D\overline{B}=\left[\begin{array}{cc}5.8& 3.95\\ -3.3684& -2.4211\\ 1.6842& 1.2105\end{array}\right]\\ \overline{E}{\overline{E}}^D=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1.0526& 0.1053\\ 0& -0.5263& -0.0526\end{array}\right],{\overline{B}}_2=(\overline{E}{\overline{E}}^D-{\mathbb{I}}_3){\overline{A}}^D\overline{B}=\left[\begin{array}{cc}0& 0\\ -0.3316& 0.1158\\ 3.3158& -1.1579\end{array}\right].\end{array}$$

(91)

It is easy to check that there does not exist a matrix $G\in {\mathbb{R}}^{3\times 3}$ such that ${\overline{A}}_1+G({\mathbb{I}}_3-\overline{E}{\overline{E}}^D)$ satisfies (31). Therefore, by Theorem 6 the considered system is not superstable. Now let us consider the state-feedback

$$u(t)=-Kx(t),$$

(92)

where

$$K=\left[\begin{array}{ccc}{k}_{11}& k_{12}& k_{13}\\ k_{21}& k_{22}& k_{23}\end{array}\right]$$

(93)

and

$$\begin{array}{ccc}K\overline{E}{\overline{E}}^D& =& \left[\begin{array}{ccc}{k}_{11}& 1.0526k_{12}-0.5263k_{13}& 0.1053k_{12}-0.0526k_{13}\\ k_{21}& 1.0526k_{22}-0.5263k_{23}& 0.1053k_{22}-0.0526k_{13}\end{array}\right],\\ K({\mathbb{I}}_3-\overline{E}{\overline{E}}^D)& =& \left[\begin{array}{ccc}0& -0.05263k_{12}+0.5263k_{13}& -0.1053k_{12}+1.0526k_{13}\\ 0& -0.05263k_{22}+0.5263k_{23}& -0.1053k_{22}+1.0526k_{23}\end{array}\right].\end{array}$$

(94)

Choosing $k_{13}=0.1k_{12}$, $k_{23}=0.1k_{22}$ yields $K({\mathbb{I}}_3-\overline{E}{\overline{E}}^D)=0$. From (91) and (93) for

$$K=\left[\begin{array}{ccc}0& 0.01& 0.001\\ 0.3& 0.0139& 0.0014\end{array}\right]$$

(95)

we have

$$\begin{array}{c}{\overline{A}}_{C1}={\overline{A}}_1-{\overline{B}}_{1}K=\left[\begin{array}{ccc}-3.185& 2.8871& 0.2887\\ 1.7789& -2.0379& -0.2038\\ -0.8895& 1.019& 0.1019\end{array}\right],\\ {\overline{A}}_{C2}={\overline{B}}_{2}K=\left[\begin{array}{ccc}0& 0& 0\\ 0.0347& -0.0017& -0.0002\\ -0.3474& 0.0171& 0.0017\end{array}\right].\end{array}$$

(96)

Using (91), (96) and

$$G=\left[\begin{array}{ccc}0& 2.8501& 0\\ 0& 0& 0.2\\ 0& 20& 0\end{array}\right]$$

(97)

we obtain

$${\overline{A}}_{C1}+G({\mathbb{I}}_3-\overline{E}{\overline{E}}^D)=\left[\begin{array}{ccc}-3.185& 2.7371& -0.0113\\ 1.7789& -1.9327& 0.0068\\ -0.8895& -0.0337& -2.0034\end{array}\right].$$

(98)

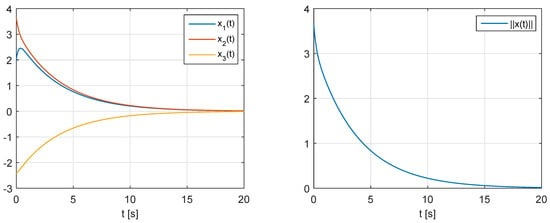
The matrix (98) satisfies (31) and $\parallel {\overline{A}}_{C2}\parallel =0.3661\le 1$. Therefore, by Theorem 8 the descriptor continuous-time linear system (1), (87) with the state-feedback (92), (95) is superstable. In Figure 2 we present time plots of the state variables and the norm of the state vector for the open-loop system with $x_0=\left[\begin{array}{ccc}2& 3.6& -1.8\end{array}\right]$. We can see that the norm of the state vector does not decrease monotonically for $t\to \infty$.

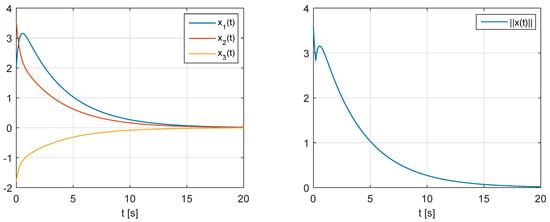
In Figure 3 we present time plots of the state variables and the norm of the state vector for the closed-loop system with $x_0=\left[\begin{array}{ccc}2& 3.6& -2.4\end{array}\right]$. Note that the set of consistent initial conditions for the system with the state-feedback is different, i.e., from (69) for $t=0$ and $q=1$ we have $x_0=({\mathbb{I}}_3+{\overline{A}}_{C2})\gamma$ for some $\gamma \in {\mathbb{R}}^3$. After applying the feedback, we can see that the norm of the state vector decrease monotonically for $t\to \infty$. Similar result can be obtained for any consistent initial conditions $x_0$.

6. Concluding Remarks

In this paper the descriptor continuous-time linear systems with regular matrix pencil $(E,A)$ have been investigated using Drazin inverse matrix method and the procedure of state-feedback synthesis such that the closed-loop system is superstable has been proposed.

The presented approach differs from those discussed in the literature, which are mainly focused on the problems of the pole assignment and regularization of descriptor systems, i.e., properties that can be determined basing on the state Equation (1). The method given in the paper allows to design the state-feedback that affects pole-independent system properties such as positivity or superstability for which the standard approach is not applicable. Although a superstable system is also an asymptotically stable one and its poles must have negative real parts, the superstability itself does not depend on the exact location of poles, i.e., from two systems with the same set of stable poles one may be superstable and the other one may not.

The main contributions of this paper can be summarized as follows:

• An alternative method for testing the stability of descriptor continuous-time linear systems has been proposed (Theorems 3 and 4);
• Necessary and sufficient conditions for the superstability of this class of dynamical systems have been established (Theorem 6);
• The procedure for computation of the state-feedback gain matrix such that the closed-loop system is stable (Theorem 7) and superstable (Theorem 8) has been given.

The effectiveness of the presented approach has been demonstrated on numerical examples. The considerations can be extended to fractional-order descriptor continuous-time linear systems.