Forms of the Symmetry Energy Relevant to Neutron Stars
Abstract
1. Introduction
2. Symmetry Energy: The Taylor Series
- the binding energy at saturation density :
- the symmetry energy with the symmetry energy coefficient
- the slope of the symmetry energy :
- the incompressibility of symmetric nuclear matter :
- the curvature of the symmetry energy: .
3. Symmetry Energy: The Padé Approximation
4. Isospin-Sensitive Properties of Neutron Stars
5. The Formalism
5.1. Nuclear Matter
5.2. Matter of a Neutron Star
6. Results
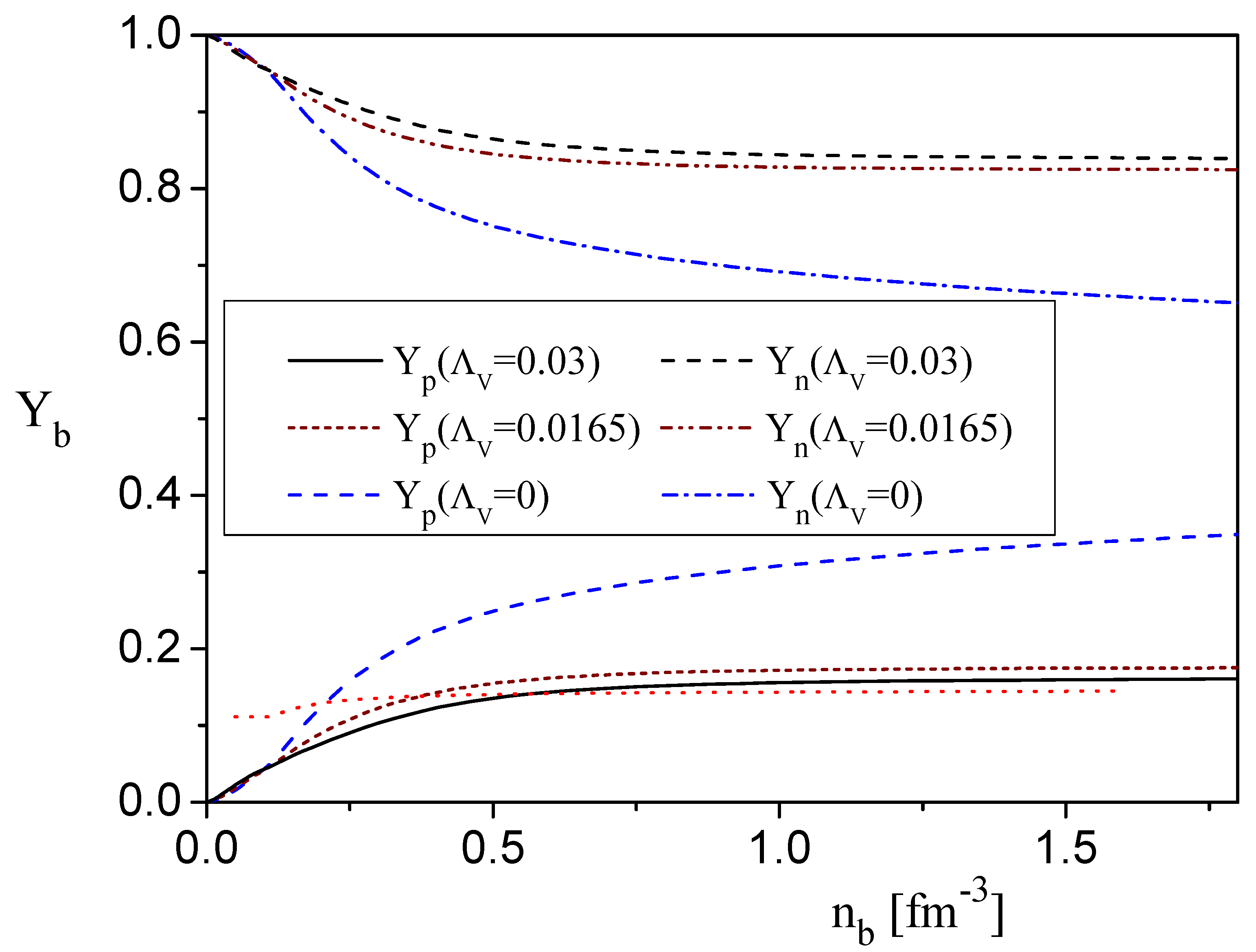
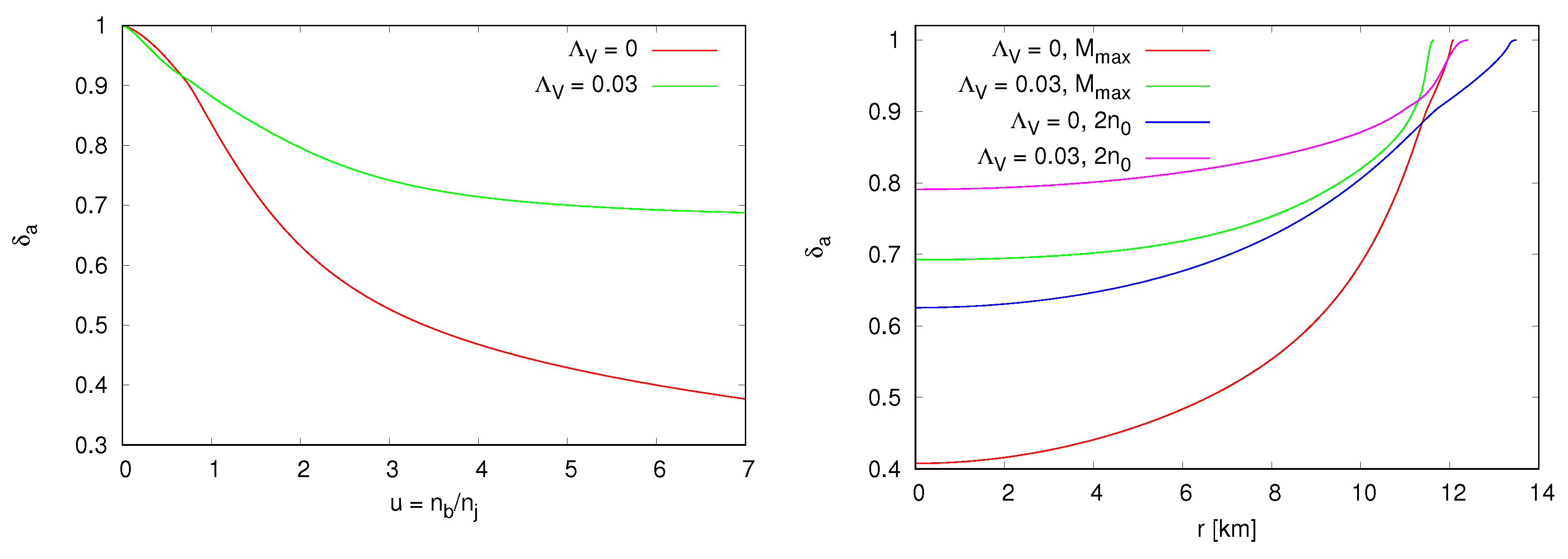
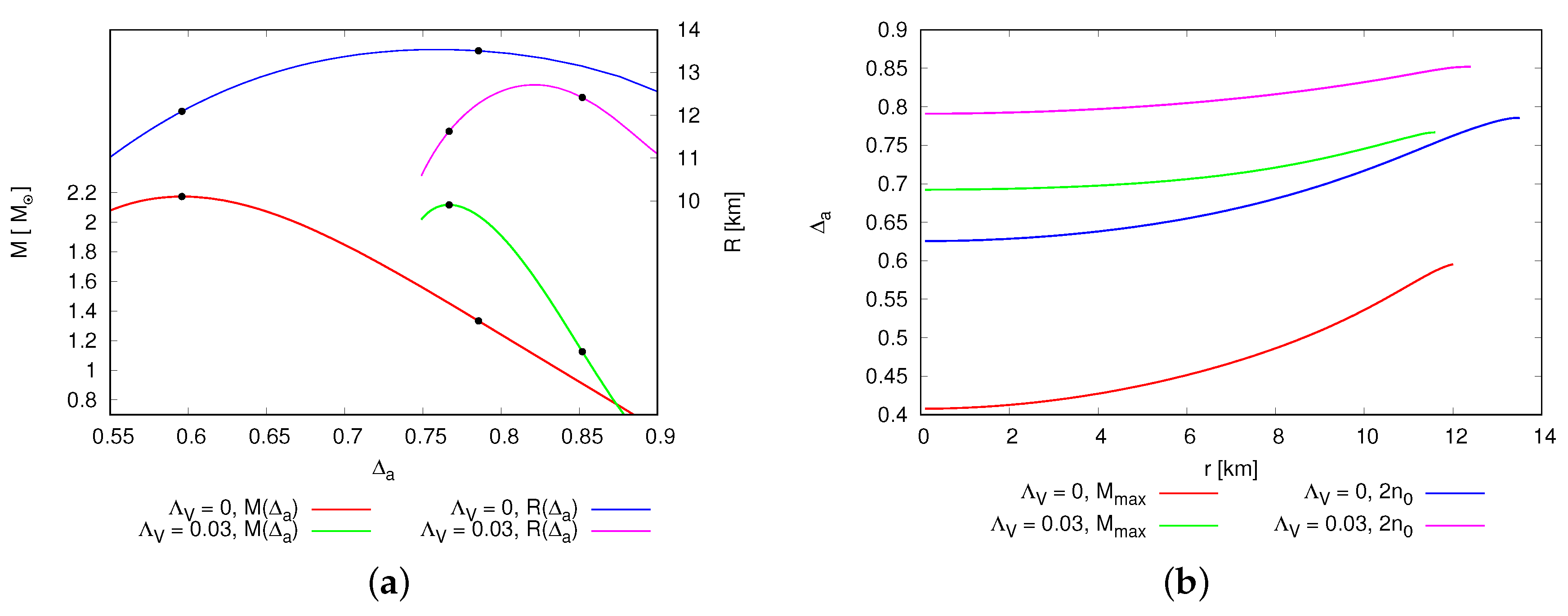
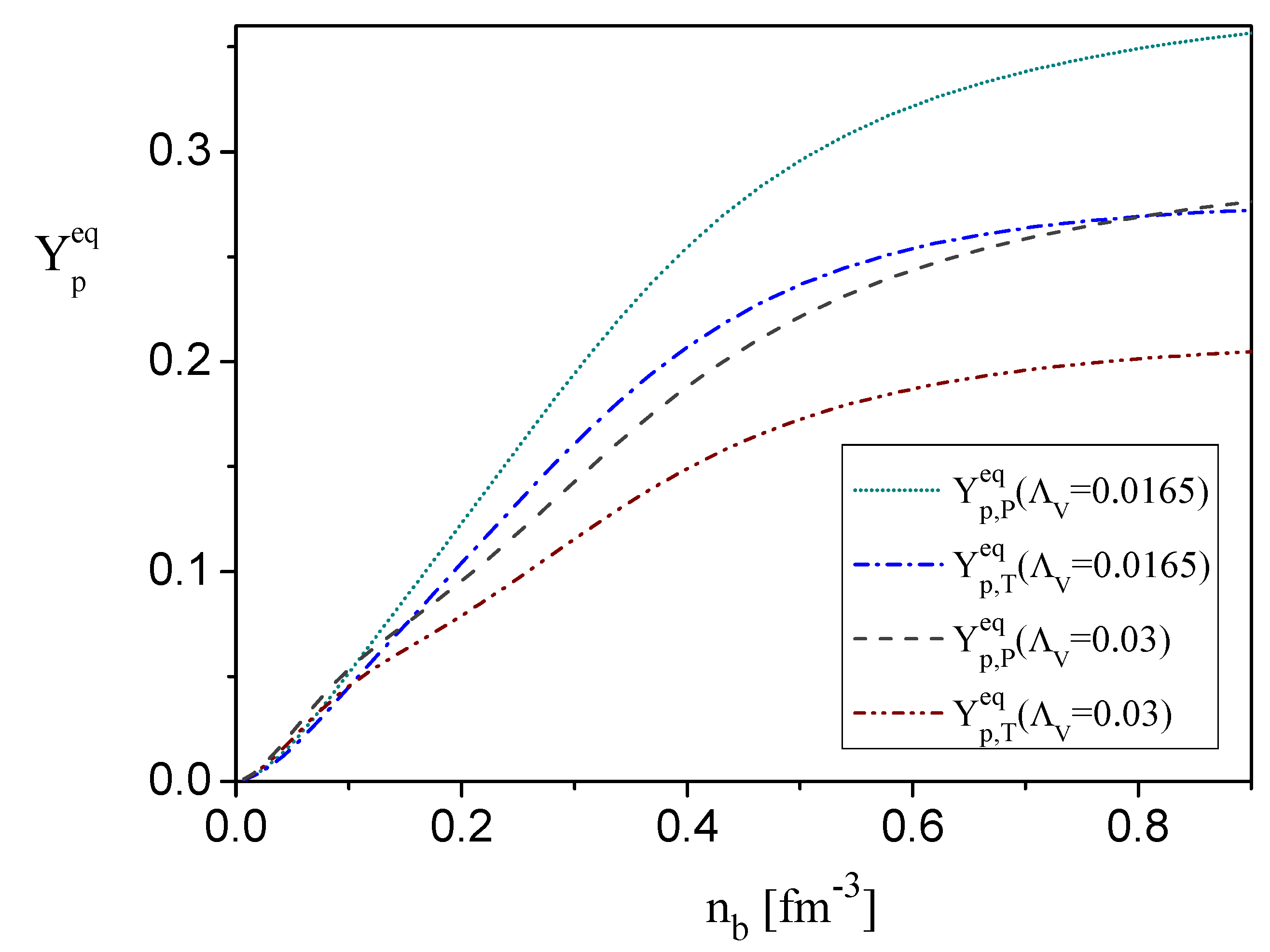
6.1. The Effect of the Symmetry Energy for Neutron Star Matter
6.2. The Effect of the Approximation Method for Neutron Star Matter
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1619. [Google Scholar] [CrossRef] [PubMed]
- Tonchev, A.P.; Tsoneva, N.; Bhatia, C.; Arnold, C.W.; Goriely, S.; Hammond, S.L.; Kelley, J.H.; Kwan, E.; Lenske, H.; Piekarewicz, J.; et al. Pygmy and core polarization dipole modes in 206Pb: Connecting nuclear structure to stellar nucleosynthesis. Phys. Lett. B 2017, 773, 20–25. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Brown, E.F.; Kim, Y.; Lynch, W.G.; Michaels, R.; Ono, A.; Piekarewicz, J.; Tsang, M.B.; Wolter, H.H. A way forward in the study of the symmetry energy: Experiment, theory, and observation. J. Phys. G Nucl. Part. Phys. 2014, 41, 093001–093019. [Google Scholar] [CrossRef]
- Baran, V.; Colonna, M.; Greco, V. Reaction dynamics with exotic beams. Phys. Rep. 2005, 410, 335–466. [Google Scholar] [CrossRef]
- Zhang, Y.; Danielewicz, P.; Famiano, M.; Li, Z.; Lynch, W.G.; Tsang, M.B. The influence of cluster emission and the symmetry energy on neutron-proton spectral double ratios. Phys. Lett. B 2008, 664, 145–148. [Google Scholar] [CrossRef]
- Zielinska-Pfabe, M. The density dependence of the nuclear symmetry energy in heavy ion collisions. Acta Phys. Pol. B 2017, 10, 153–164. [Google Scholar] [CrossRef]
- Russotto, P.; Gannon, S.; Lasko, P.; Acosta, L.; Adamczyk, M.; Al-Ajlan, A.; Al-Garawi, M.; Al-Homaidhi, S.; Amorini, F.; Auditore, L.; et al. Results of the ASY-EOS experiment at GSI: The symmetry energy at suprasaturation density. Phys. Rev. C 2016, 94, 034608–034632. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Soff, S.; Bleicher, M.; Stoecker, H. Probing the equation of state with pions. J. Phys. G Nucl. Part. Phys. 2006, 32, 151–164. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Soff, S.; Bleicher, M.; Stoecker, H. Medium modifications of the nucleon–nucleon elastic cross section in neutron-rich intermediate energy HICs. J. Phys. G Nucl. Part. Phys. 2006, 32, 407–416. [Google Scholar] [CrossRef]
- Leifels, Y.; Blaich, T.; Elze, T.W.; Emling, H.; Freiesleben, H.; Grimm, K.; Henning, W.; Holzmann, R.; Keller, J.G.; Klingler, H.; et al. (FOPI Collaboration). Exclusive studies of neutron and charged particle emission in collisions of 197Au+197Au at 400 MeV/nucleon. Phys. Rev. Lett. 1993, 71, 963–966. [Google Scholar] [CrossRef]
- Lambrecht, D.; Blaich, T.; Elze, T.W.; Emling, H.; Freiesleben, H.; Grimm, K.; Henning, W.; Holzmann, R.; Keller, J.G.; Klingler, H.; et al. Energy dependence of collective flow of neutrons and protons in 197Au+197Au collisions. Z. Phys. A 1994, 350, 115–120. [Google Scholar] [CrossRef]
- Gandolfi, S.; Lippuner, J.; Steiner, A.W.; Tews, I.; Du, X.; Al-Mamun, M. From the microscopic to the macroscopic world: From nucleons to neutro stars. J. Phys. G Nucl. Part. Phys. 2019, 46, 21. [Google Scholar] [CrossRef]
- Li, B.A.; Krastev, P.G.; Wen, D.H.; Zhang, N.B. Towards understanding astrophysical effects of nuclear symmetry energy. Euro. Phys. J. A 2019, 55, 117–193. [Google Scholar] [CrossRef]
- Heinke, C.O.; Jonker, P.G.; Wijnands, R.R.; Taam, R.E. Constraints on Thermal X-Ray Radiation from SAX J1808.4–3658 and Implications for Neutron Star Neutrino Emission. Astrophys. J. 2007, 660, 1424–1427. [Google Scholar]
- Providência, C.; Fortin, M.; Pais, H.; Rabhi, A. Hyperonic stars and the nuclear symmetry energy. Front. Astron. Space Sci. 2019, 6, 13. [Google Scholar] [CrossRef]
- Bednarek, I.; Sładkowski, J.; Syska, J. Modification of the Symmetry Energy by Strangeness. Acta Phys. Pol. B 2019, 50, 1849–1858. [Google Scholar] [CrossRef]
- Bednarek, I.; Manka, R.; Pienkos, M. The influence of the enhanced vector meson sector on the properties of the matter of neutron stars. PLoS ONE 2014, 9, e106368–e106383. [Google Scholar] [CrossRef][Green Version]
- Grigorian, H.; Voskresensky, D.N.; Maslov, K.A. Cooling of neutron stars in “nuclear medium cooling scenario” with stiff equation of state including hyperons. Nucl. Phys. A 2018, 980, 105–130. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro delay measurement of a two solar mass neutron star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Fonesca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The Nanograv Nine-Year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Kerkwijk, M.H.v.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131–6184. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Kolomeitsev, E.E.; Maslov, K.A.; Voskresensky, D.N. Delta isobars in relativistic mean-field models with σ-scaled hadron masses and couplings. Nucl. Phys. A 2017, 961, 106–141. [Google Scholar] [CrossRef]
- Sotani, H.; Iida, K.; Oyamatsu, K. Constraining the density dependence of the nuclear symmetry energy from an X-ray bursting neutron star. Phys. Rev. C 2015, 91, 015805–015809. [Google Scholar] [CrossRef]
- Maslov, K.A.; Kolomeitsev, E.E.; Voskresensky, D.N. Relativistic mean-field models with scaled hadron masses and couplings: Hyperons and maximum neutron star mass. Nucl. Phys. A 2016, 950, 64–109. [Google Scholar] [CrossRef]
- Gendreau, K.; Arzoumanian, Z.; Okaajima, T. The Neutron star Interior Composition ExploreR (NICER): An Explorer mission of opportunity for soft x-ray timing spectroscopy. Proc. SPIE 2012, 8443, 8. [Google Scholar]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabartyl, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Vidana, I. Nuclear symmetry energy and the r-mode instability of neutron stars. Phys. Rev. C 2012, 85, 045808–045816. [Google Scholar] [CrossRef]
- Tews, I.; Carlson, J.; Gandolfi, S.; Reddy, S. Constraining the speed of sound inside neutron stars with chiral effective field theory interactions and observations. Astrophys. J. 2018, 860, 24. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. A critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef]
- Bednarek, I.; Sładkowski, J.; Syska, J. A cross-validation check in the covariance analysis of isospin sensitive observables from heavy ion collisions. Nucl. Phys. A 2020, 997, 121727. [Google Scholar] [CrossRef]
- Cai, B.; Chen, L. Nuclear matter fourth-order symmetry energy in the relativistic mean field model. Phys. Rev. C 2012, 85, 024302–024311. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Fantina, A.F.; Goriely, S. Symmetry energy: Nuclear masses and neutron stars. Eur. Phys. J. A 2014, 50, 43. [Google Scholar] [CrossRef]
- Gonzalez-Boquera, C.; Centelles, M.; Viñas, X.; Rios, A. Higher-order symmetry energy and neutron star core-crust transition with Gogny forces. Phys. Rev. C 2017, 96, 065806. [Google Scholar] [CrossRef]
- Roth, R.; Langhammer, J. Padé-resummed high-order perturbation theory for nuclear structure calculations. Phys. Lett. B 2010, 6, 272–277. [Google Scholar] [CrossRef]
- Itô, K. Encyclopedic Dictionary of Mathematics; MIT Press: London, UK, 1987. [Google Scholar]
- Brezinski, C. Padé-type Approximation and General Orthogonal Polynomials; Birkhäuser: Basel, Switzerland, 1980. [Google Scholar]
- Suetin, S.P. Padé approximants and efficient analytic continuation of a power series. Russ. Math. Surv. 2002, 57, 43–141. [Google Scholar] [CrossRef]
- Baker, G.A., Jr.; Gammel, J.L.; Wills, J.G. An investigation of the applicability of the Padé approximant method. J. Math. Anal. Appl. 1961, 2, 405–418. [Google Scholar] [CrossRef]
- Stahl, H. The convergence of Padé approximants to functions with branch points. J. Approx. Theory. 1997, 91, 139. [Google Scholar] [CrossRef]
- Sasakawa, T. Scattering Theory; Shokabo: Tokyo, Japan, 1991. (In Japanese) [Google Scholar]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Clarendon Press: Oxford, UK, 1971. [Google Scholar]
- Gröber, R.; Maier, A.; Rauh, T. Reconstruction of top-quark mass effects in Higgs pair production and other gluon-fusion processes. J. High Energ. Phys. 2018, 20, 1–32. [Google Scholar] [CrossRef]
- Yang, C.N.; Lee, T.D. Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation. Phys. Rev. 1952, 87, 404–409. [Google Scholar] [CrossRef]
- Nickel, B. On the singularity structure of the 2D Ising model susceptibility. J. Phys. A Math. Gen. 1999, 32, 3889–3906. [Google Scholar] [CrossRef]
- Kubo, R.; Toda, M.; Hashizume, N.; Saito, N. Statistical Physics I: Equilibrium Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Kubo, R.; Toda, M.; Hashizume, N.; Saito, N. Statistical Physics II: Nonequilibrium Statistical Mechanics; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Berretti, A.; Chierchia, L. On the complex analytic structure of the golden invariant curve for the standard map. Nonlinearity 1990, 3, 39–44. [Google Scholar] [CrossRef]
- Bessis, D. Padé approximations in noise filtering. J. Comput. Appl. Math. 1996, 66, 85–88. [Google Scholar] [CrossRef][Green Version]
- Stahl, H. The convergence of diagonal Padé approximants and the Pade conjecture. J. Comput. Appl. Math. 1997, 86, 287–296. [Google Scholar] [CrossRef]
- Gilewicz, J.; Pindor, M. Padé approximants and noise: A case of geometric series. J. Comput. Appl. Math. 1997, 87, 199–214. [Google Scholar] [CrossRef]
- Bessis, D.; Perotti, L. Universal analytic properties of noise: Introducing the J-matrix formalism. J. Phys. A Math. Theor. 2009, 42, 365202. [Google Scholar] [CrossRef][Green Version]
- Falcolini, C.; Llave, R. Numerical calculation of domains of analyticity for perturbation theories in the presence of small divisors. J. Stat. Phys. 1992, 67, 645–666. [Google Scholar] [CrossRef]
- Llave, R.; Tompaidis, S. Computation of domains of analyticity for some perturbative expansions of mechanics. Phys. D Nonlinear Phenom. 1994, 71, 55–81. [Google Scholar] [CrossRef]
- Berretti, A.; Marmi, S. Scaling, perturbative renormalization and analyticity for the standard map and some generalizations. Chaos Solitons Fractals 1995, 5, 257–269. [Google Scholar] [CrossRef]
- Berretti, A.; Falcolini, C.; Gentile, G. Shape of analyticity domains of Lindstedt series: The standard map. Phys. Rev. E 2001, 64, 015202(R). [Google Scholar] [CrossRef]
- Paszkowski, S. Hermite-Padé approximation (basic notions and theorems). J. Comp. Appl. Math. 1990, 32, 229–236. [Google Scholar] [CrossRef][Green Version]
- Wallin, H. Convergence and Divergence of Multipoint Padé Approximants of Meromorphic Functions; Lecture Notes in Math. 1105; Springer: New York, NY, USA, 1984; pp. 272–284. [Google Scholar]
- Ibryaeva, O.L.; Adukov, V.M. An algorithm for computing a Padé approximant with minimal degree denominator. J. Comput. Appl. Math. 2013, 237, 529–541. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Nakazato, K.; Suzuki, H.; Hu, J.; Shen, H. Influence of density dependence of symmetry energy in hot and dense matter for supernova simulations. Astrophys. J. 2019, 887, 110–130. [Google Scholar] [CrossRef]
- Atta, D.; Basu, D.N. Stability of β -equilibrated dense matter and core-crust transition in neutron stars. Phys. Rev. C 2014, 90, 035802. [Google Scholar] [CrossRef]
- Lai, D. Resonant oscillations and tidal heating in coalescing binary neutron stars. Mon. Not. R. Astron. Soc. 1994, 270, 611–629. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J. Neutron star structure and the neutron radius of 208Pb. Phys. Rev. Lett. 2001, 86, 5647–5650. [Google Scholar] [CrossRef]
- Sharma, B.K.; Pal, S. Nuclear symmetry energy effects in finite nuclei and neutron star. Phys. Lett.B 2009, 682, 23–26. [Google Scholar] [CrossRef]
- Bednarek, I.; Pienkos, M. The influence of the symmetry energy on the structure of hyperon stars. Acta Phys. Pol. B 2015, 46, 2343–2350. [Google Scholar]
- Sugahara, Y.; Toki, H. Relativistic mean-field theory for unstable nuclei with non-linear σ and ω terms. Nucl. Phys. A 1994, 579, 557–572. [Google Scholar] [CrossRef]
- Manka, R.; Bednarek, I. The nucleon and mesons effective masses in the relativistic mean field theory. J. Phys. G 2001, 27, 1975–1986. [Google Scholar] [CrossRef]
- Bednarek, I.; Sładkowski, J.; Syska, J. Aspects of Approximation in Modeling of the Asymmetric Nuclear Matter. J. Phys. Soc. Jpn. 2019, 88, 124201. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1. Equation of State and Structure, 1st ed.; Sringer: New York, NY, USA, 2007; pp. 264–266. [Google Scholar]
- Steiner, A.W.; Prakash, M.; Lattimer, J.M.; Ellis, P.J. Isospin asymmetry in nuclei and neutron stars. Phys. Rep. 2005, 411, 325–375. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Xia, C.-J.; Li, Z.; Biswal, S.K. Constraints on the symmetry energy and its associated parameters from nuclei to neutron stars. Phys. Rev. C 2020, 101, 034303. [Google Scholar] [CrossRef]
- Wang, R.; Chen, L. Empirical information on nuclear matter fourth-order symmetry energy from an extended nuclear mass formula. Phys. Lett. B 2017, 773, 62–67. [Google Scholar] [CrossRef]




| MeV | 7.2327 fm | - | |||
| MeV | - | - | |||
| MeV | 0.0 | 0.0165 | 0.03 | ||
| 9.2644 | 10.037 | 11.10 |
| M[M] | R (km) | |||||
|---|---|---|---|---|---|---|
| M | 0.03 | 0.77 | 6.05 | 2.11 | 11.6 | 0.69 |
| 0.03 | 0.85 | 2.08 | 1.13 | 12.42 | 0.79 | |
| M | 0.0 | 0.6 | 5.71 | 2.17 | 12.09 | 0.41 |
| 0.0 | 0.79 | 2.05 | 1.33 | 13.05 | 0.63 |
| PA | Padé | ||||||
|---|---|---|---|---|---|---|---|
| n (fm | 0.0876 | 0.0932 | 0.0947 | n (fm | 0.0877 | 0.0931 | 0.0946 |
| Y | 0.037 | 0.041 | 0.0430 | Y | 0.041 | 0.047 | 0.05 |
| P | 1.256 | 0.378 | 0.410 | P | 1.285 | 0.400 | 0.423 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bednarek, I.; Sładkowski, J.; Syska, J. Forms of the Symmetry Energy Relevant to Neutron Stars. Symmetry 2020, 12, 898. https://doi.org/10.3390/sym12060898
Bednarek I, Sładkowski J, Syska J. Forms of the Symmetry Energy Relevant to Neutron Stars. Symmetry. 2020; 12(6):898. https://doi.org/10.3390/sym12060898
Chicago/Turabian StyleBednarek, Ilona, Jan Sładkowski, and Jacek Syska. 2020. "Forms of the Symmetry Energy Relevant to Neutron Stars" Symmetry 12, no. 6: 898. https://doi.org/10.3390/sym12060898
APA StyleBednarek, I., Sładkowski, J., & Syska, J. (2020). Forms of the Symmetry Energy Relevant to Neutron Stars. Symmetry, 12(6), 898. https://doi.org/10.3390/sym12060898






