Prediction of the Neutrino Mass Scale Using Coma Galaxy Cluster Data
Abstract
1. Introduction—What is at Stake Here
2. Using Coma Galaxy Cluster Data to Derive the Neutrino Mass Scale
2.1. The Fundamental Equation
- The location of the galaxy is at or near the center of the CNO.
- The measured speed of that galaxy will satisfy the equation
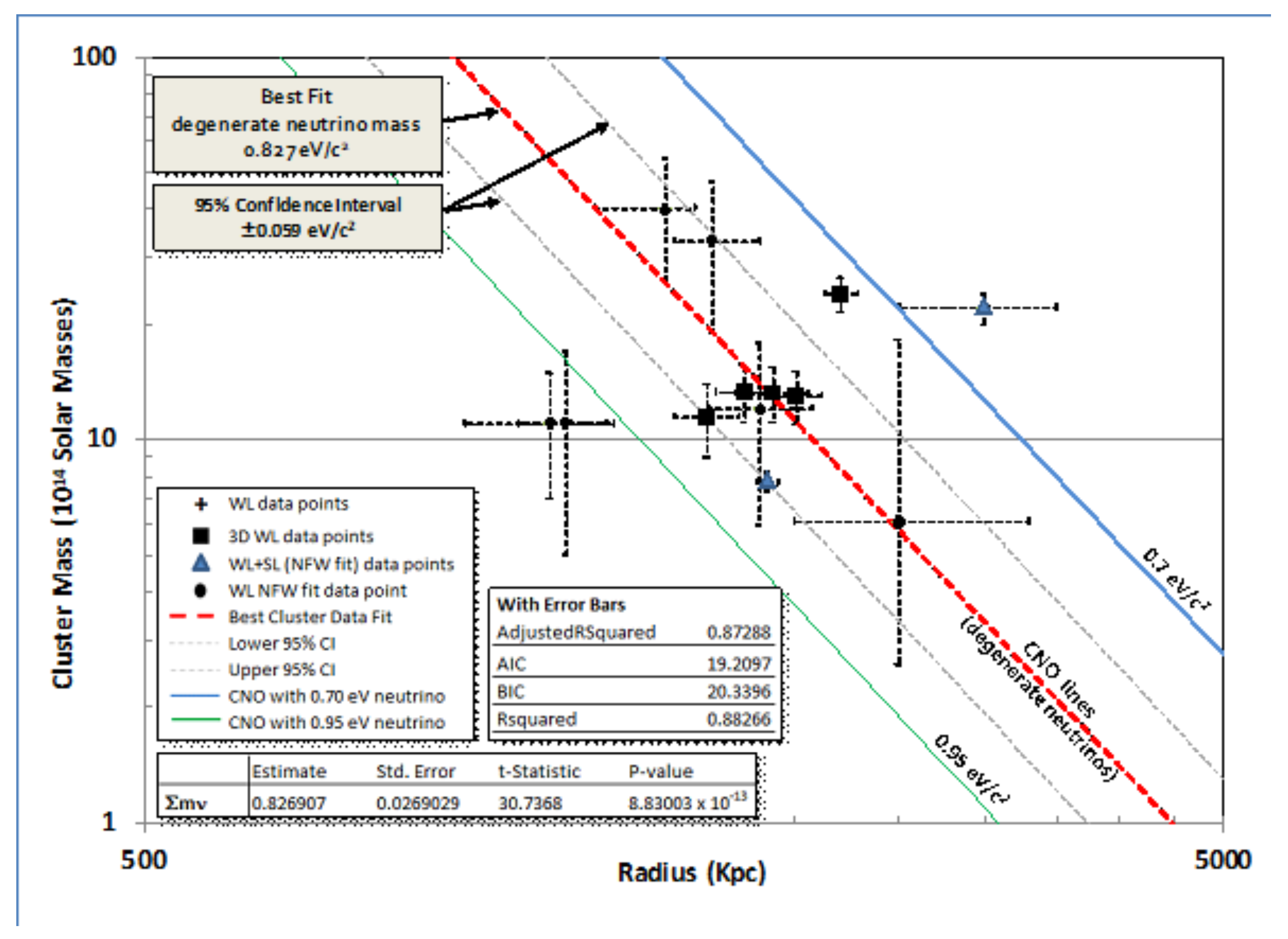
2.2. Experimental Data
3. Implications of a KATRIN Neutrino Mass Signal
- The KATRIN terrestrial experiment will have identified Dark Matter as Condensed Neutrino Objects.
- The raw Planck satellite microwave data will have to be re-processed with the neutrino degrees of freedom removed, and in their place, magnetic field degrees of freedom inserted.
- It is expected that the PSC value of the Hubble Constant will be changed.
- With the advent of CNO in the Universe, the dynamics of galaxies embedded in CNO can be studied. That is, the orbits of galaxies embedded in CNO can be computed.
- The section 26 ‘Dark Matter’ in the Review of Particle Physics [14] which describes Dark Matter as a collection of WIMPS, Axions, etc becomes fiction and the hundreds of references it cites become irrelevant.
- It is expected that CNO will greatly influence the evolution of structure in the Early Universe.
- CNO have a maximum mass that their internal pressure can support. Exceeding that mass results in CNO gravitational collapse to colossal Black Holes that greatly perturb the Cosmic Microwave Radiation field around them. This provides an experimental signature for their discovery.
Funding
Conflicts of Interest
References
- Morley, P.D.; Buettner, D.J. Instantaneous power radiated from magnetic dipole moments. Astropart. Phys. 2015, 62, 7–11. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. arXiv 2019, arXiv:1807.06209. [Google Scholar]
- KATRIN. Available online: https://www.katrin.kit.edu (accessed on 5 June 2020).
- KATRIN. An improved upper limit on the neutrino mass from a direct kinematic method by KATRIN. arXiv 2019, arXiv:1909.06048. [Google Scholar]
- Morley, P.D.; Buettner, D.J. A dark matter signature for condensed neutrinos. Int. J. Mod. Phys. D 2016, 25, 1650089. [Google Scholar] [CrossRef]
- Morley, P.D.; Buettner, D.J. Weak lensing data and condensed neutrino objects. Universe 2017, 3, 81. [Google Scholar] [CrossRef]
- Morley, P.D.; Buettner, D.J. Dark matter in the local group of galaxies. Int. J. Mod. Phys. D 2017, 26, 1750069. [Google Scholar] [CrossRef]
- Morley, P.D.; Buettner, D.J. SHM of galaxies embedded within condensed neutrino matter. Int. J. Mod. Phys. D 2015, 24, 15500042. [Google Scholar] [CrossRef]
- Colless, M.; Dunn, A.M. Structure and dynamics of the Coma cluster. Astrophys. J. 1996, 458, 435. [Google Scholar] [CrossRef]
- Godwin, J.G.; Metcalf, N.; Peach, J.V. Coma cluster 1. A catalogue of magnitudes, colours, ellipticities and position angles for 6724 galaxies in the field of the Coma cluster. Mon. Not. R. Astron. Soc. 1983, 202, 113–124. [Google Scholar] [CrossRef]
- Lokas, E.L.; Mamon, G.A. Dark matter distribution in the Coma cluster from galaxy kinematics: Breaking the mass-anisotropy degeneracy. Mon. Not. R. Astron. Soc. 2003, 343, 401. [Google Scholar] [CrossRef]
- Freedman, W.L. Cosmology at crossroads: Tension with the Hubble constant. arXiv 2017, arXiv:1706.02739. [Google Scholar]
- Chen, G.C.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; Chan, J.H.; Wong, K.C.; Auger, M.W.; Hilbert, S.; Bonvin, V.; Birrer, S.; et al. A SHARP view of HoLiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging. Mon. Not. R. Astron. Soc. 2019, 490, 1743. [Google Scholar] [CrossRef]
- Particle Data Group. Review of particle physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
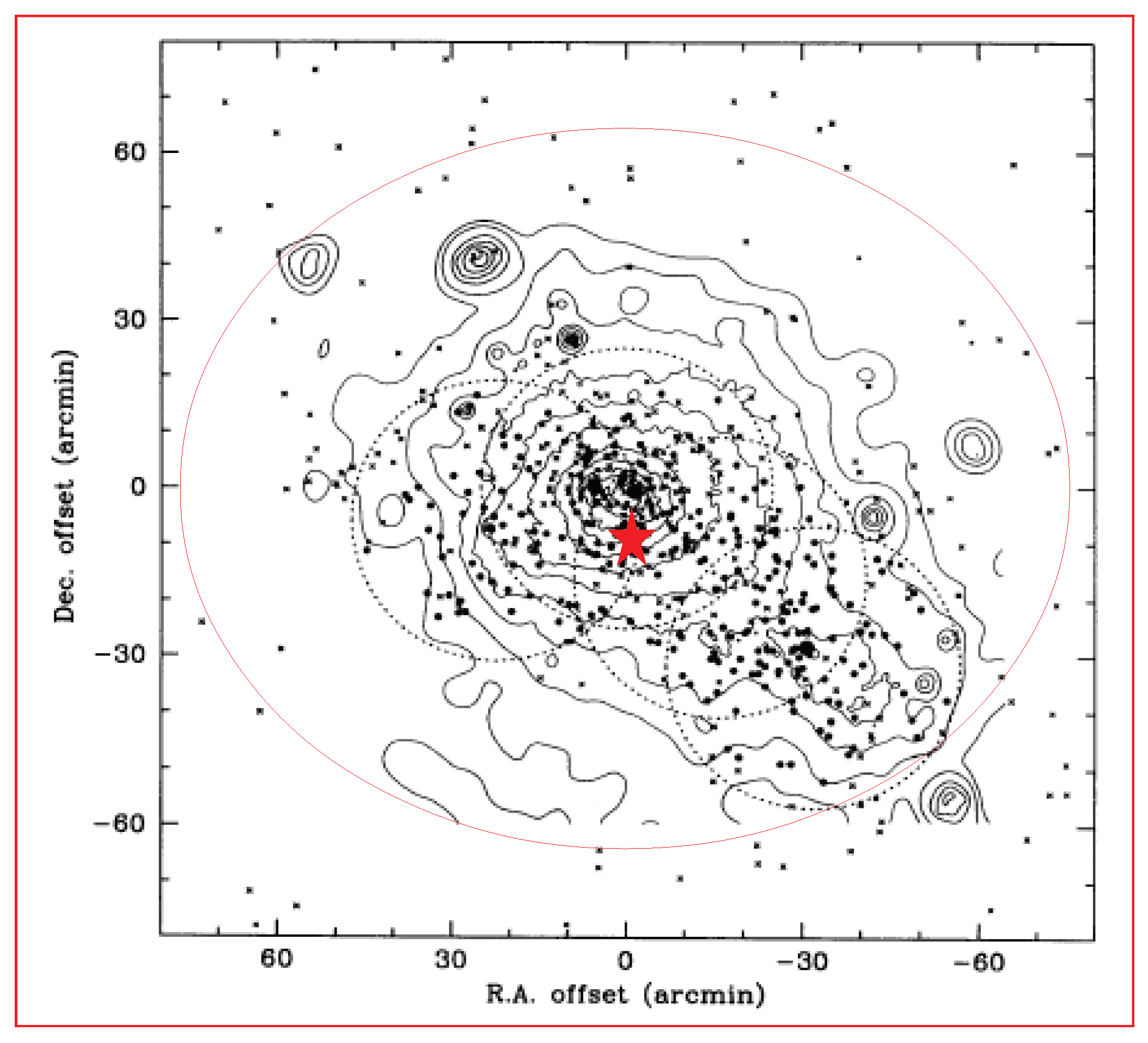
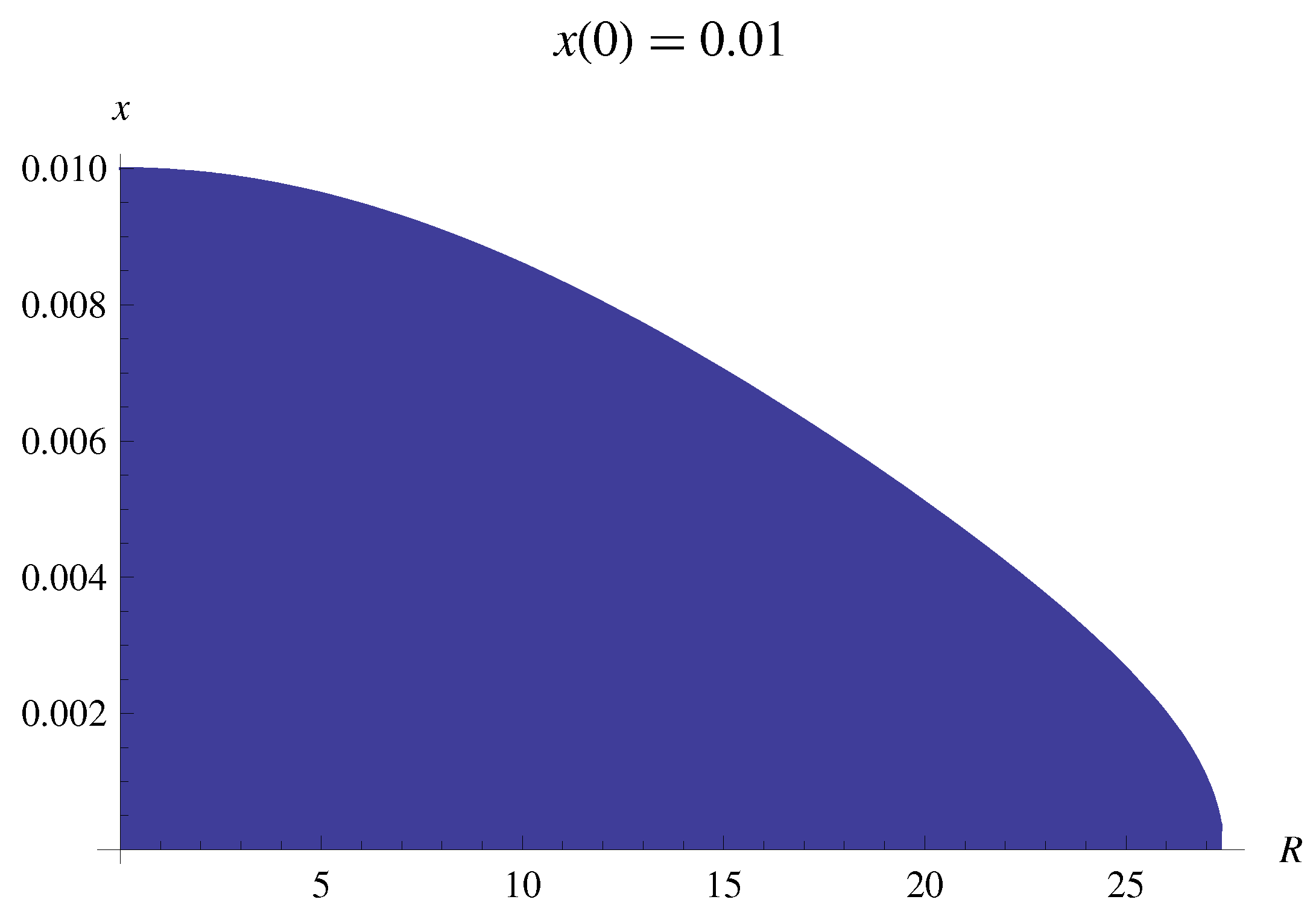
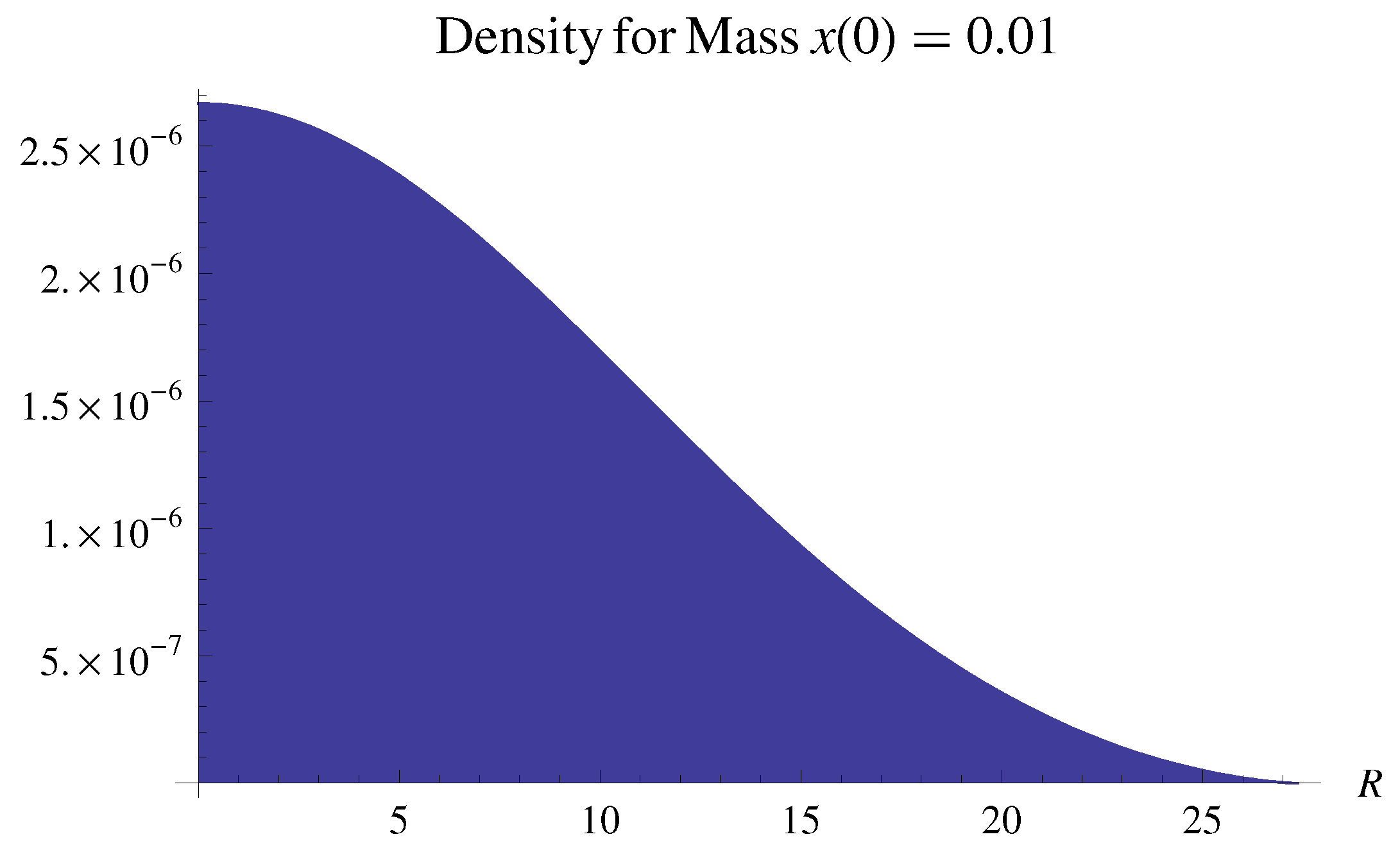
| Physical Parameter | Value | Value = 0.759 eV/c2 |
|---|---|---|
| CNO (Dark Mass) mass | M | M |
| CNO radius | Mpc | 2.191 Mpc |
| CNO center | (J2000) 12 59 46.28 +27 44 46.1 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morley, P.D. Prediction of the Neutrino Mass Scale Using Coma Galaxy Cluster Data. Symmetry 2020, 12, 1049. https://doi.org/10.3390/sym12061049
Morley PD. Prediction of the Neutrino Mass Scale Using Coma Galaxy Cluster Data. Symmetry. 2020; 12(6):1049. https://doi.org/10.3390/sym12061049
Chicago/Turabian StyleMorley, Peter D. 2020. "Prediction of the Neutrino Mass Scale Using Coma Galaxy Cluster Data" Symmetry 12, no. 6: 1049. https://doi.org/10.3390/sym12061049
APA StyleMorley, P. D. (2020). Prediction of the Neutrino Mass Scale Using Coma Galaxy Cluster Data. Symmetry, 12(6), 1049. https://doi.org/10.3390/sym12061049