A Vertex-Aligned Model for Packing 4-Hexagonal Clusters in a Regular Hexagonal Container
Abstract
1. Introduction
2. Problem Formulation
2.1. Formal Definition of Cluster Packing
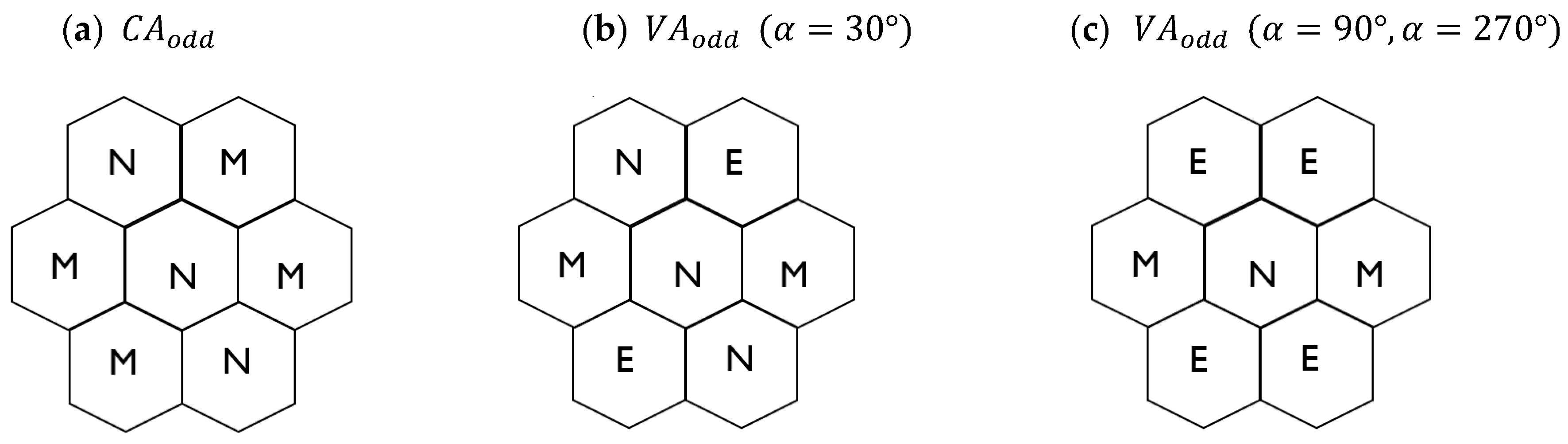
2.2. Cluster Plane Uniformity and Cluster Orientations
2.3. Research Problems
- Problem 1. How to cluster the tessellated plane of hexagonal cells, such that the cluster plane remains uniform?
- ○
- Is it possible to enclose all clusters inside a regular hexagonal container by using the existing models from the literature?
- ○
- How to calculate the total number of inner clusters inside the container and the total number of shared clusters at the container border?
- Problem 2. How to derive a model from obtaining a new structure for hexagonal clustering, with clusters entirely embedded inside the container while keeping the cluster plane uniform?
- Problem 3. What is the efficiency of the proposed geometrical structure compared to the existing models in terms of the total number of packed clusters inside the container?
2.4. Research Context
3. Clustering with the Existing Models
3.1. Centroid-Aligned Architecture
3.1.1. Packing 4-Hexagonal Clusters in the Even-Sized CA Container
3.1.2. Packing 4-Hexagonal Clusters in the Odd-Sized CA Container
3.2. Vertex-Aligned Architecture
3.2.1. Packing 4-Hexagonal Clusters in the Even-Sized VA Container
3.2.2. Packing 4-Hexagonal Clusters in the Odd-Sized VA Container
4. The Proposed Vertex-Aligned Architecture
4.1. General Description
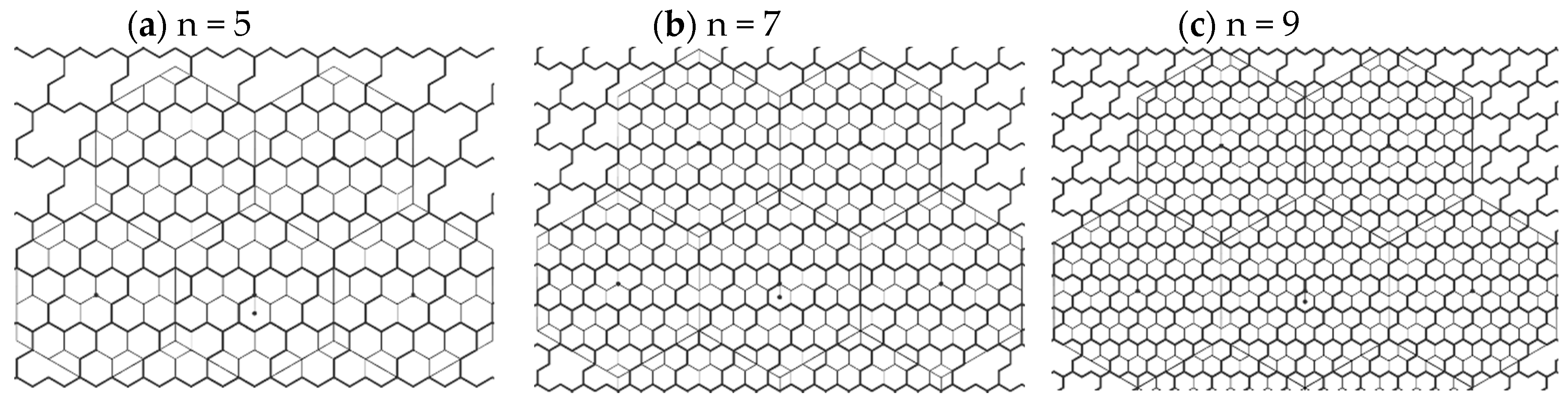
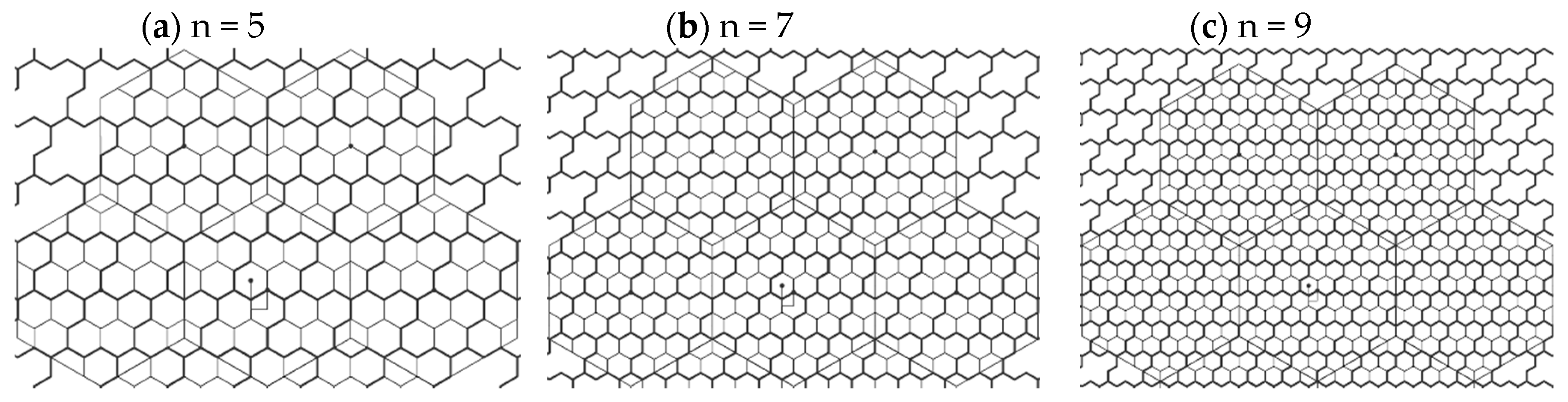
4.2. Uniform Clustering with the Proposed Model
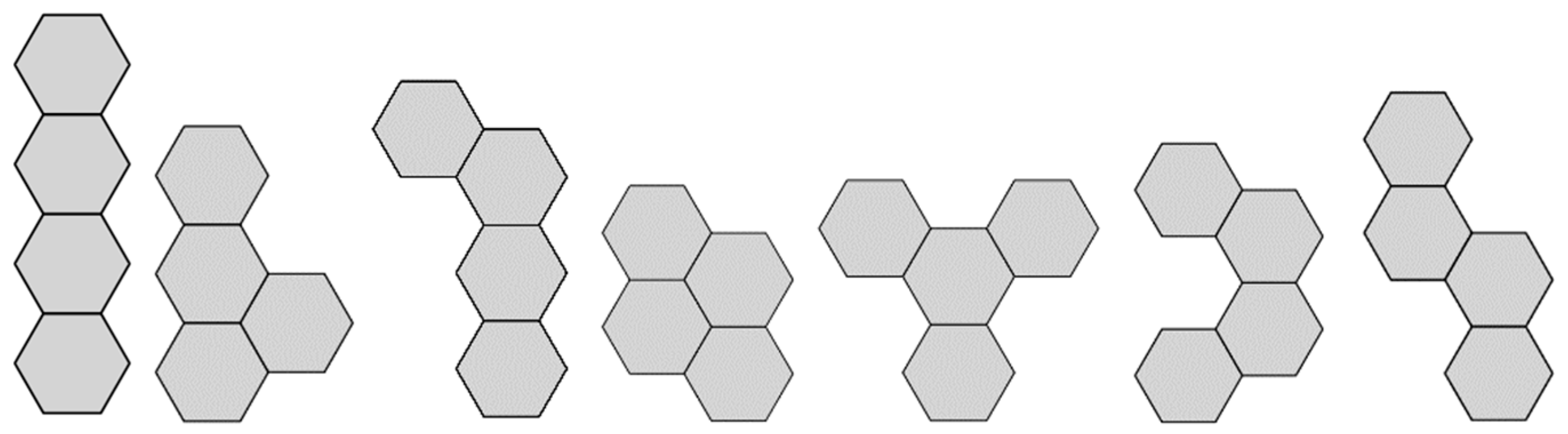
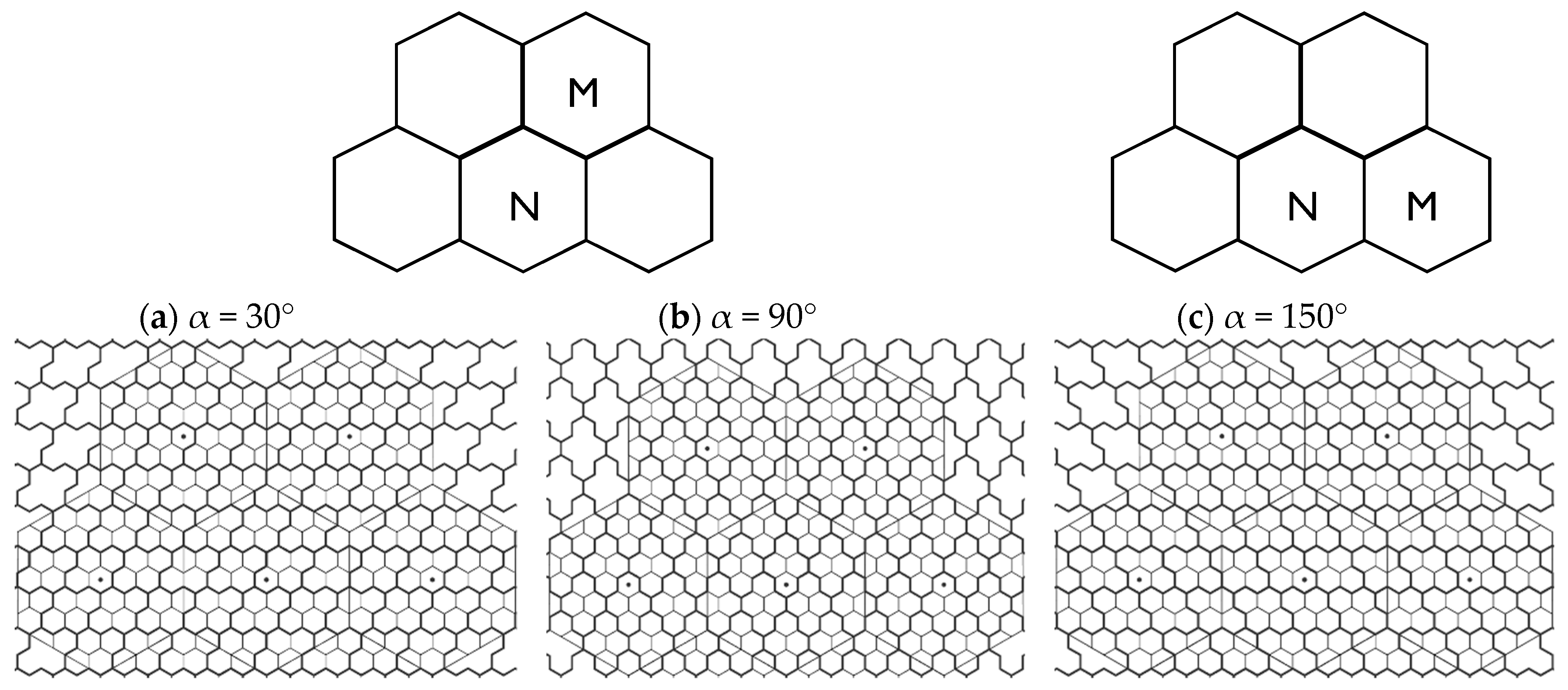
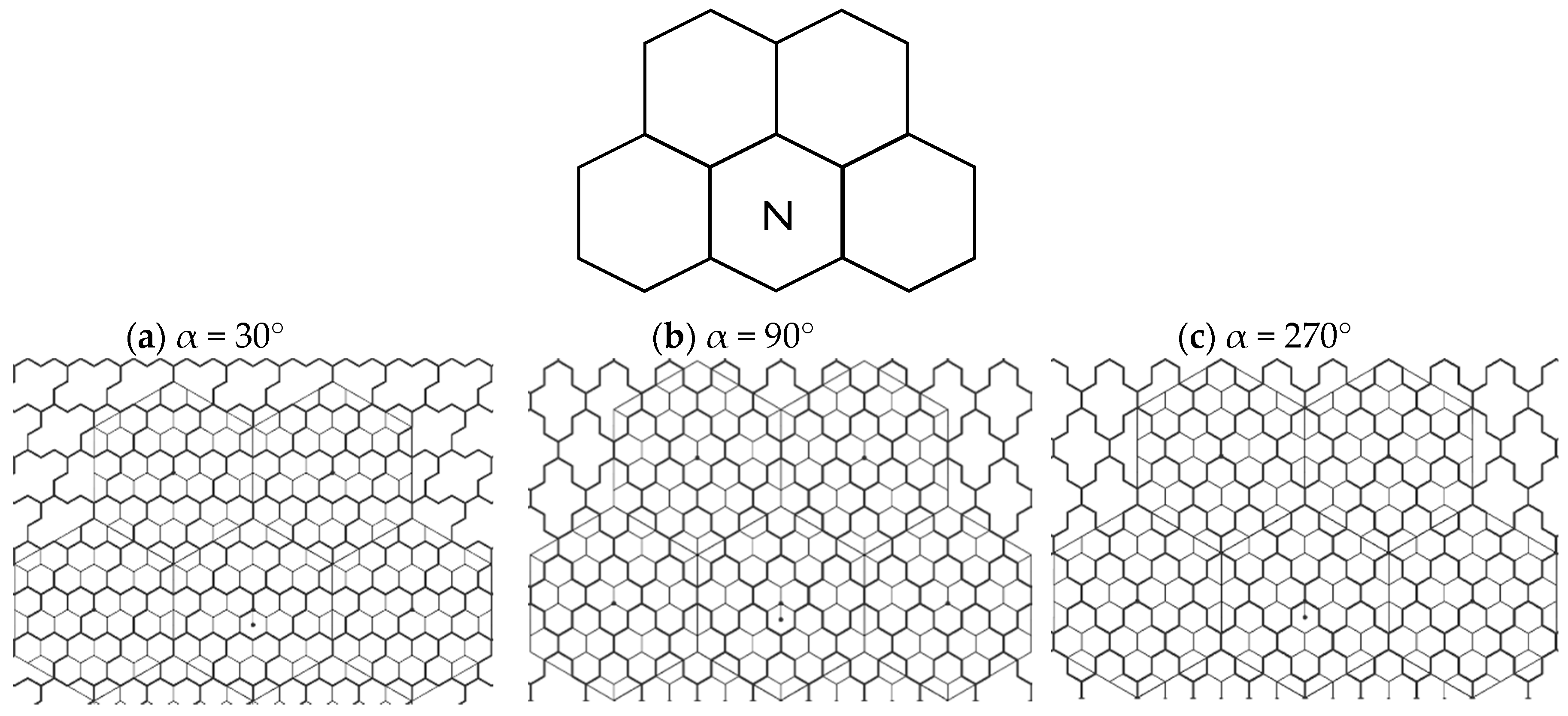
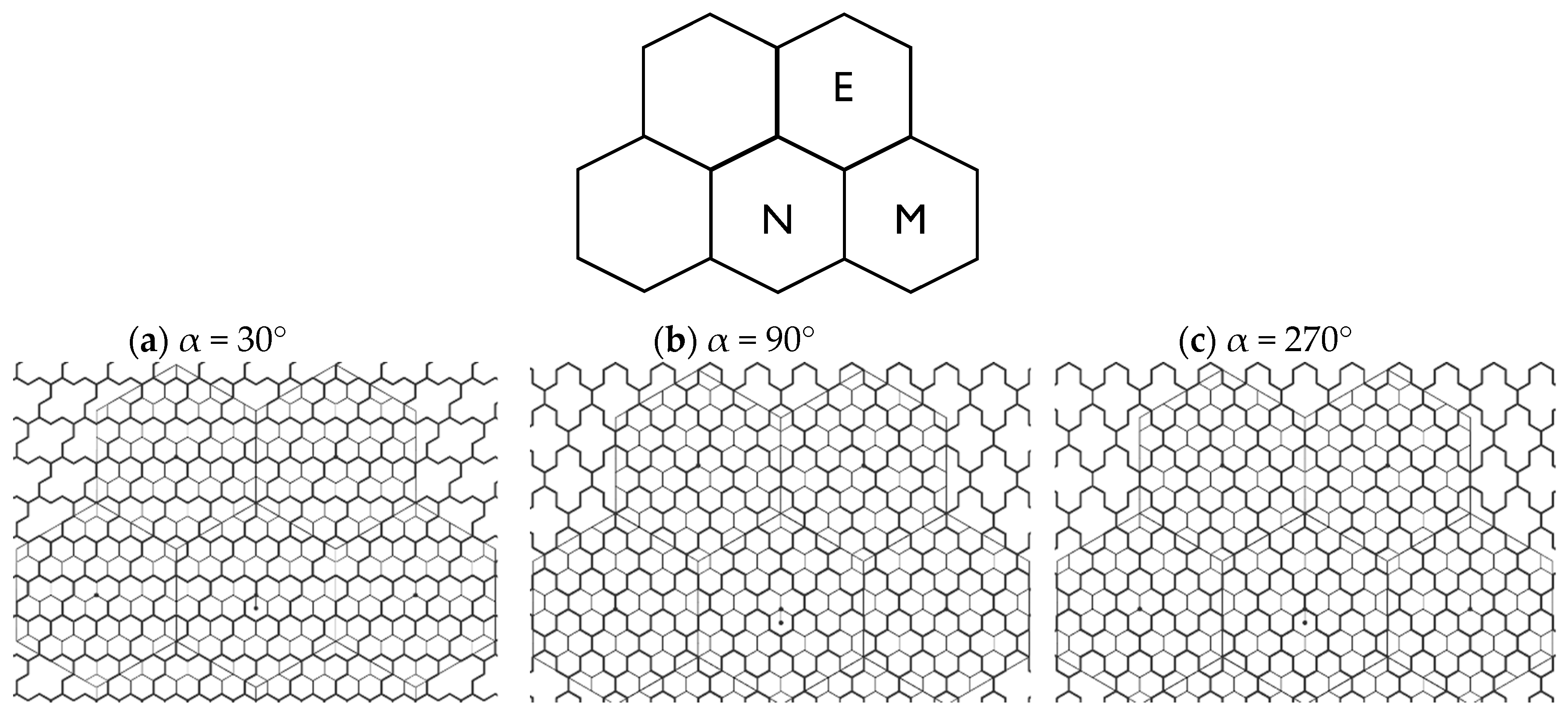
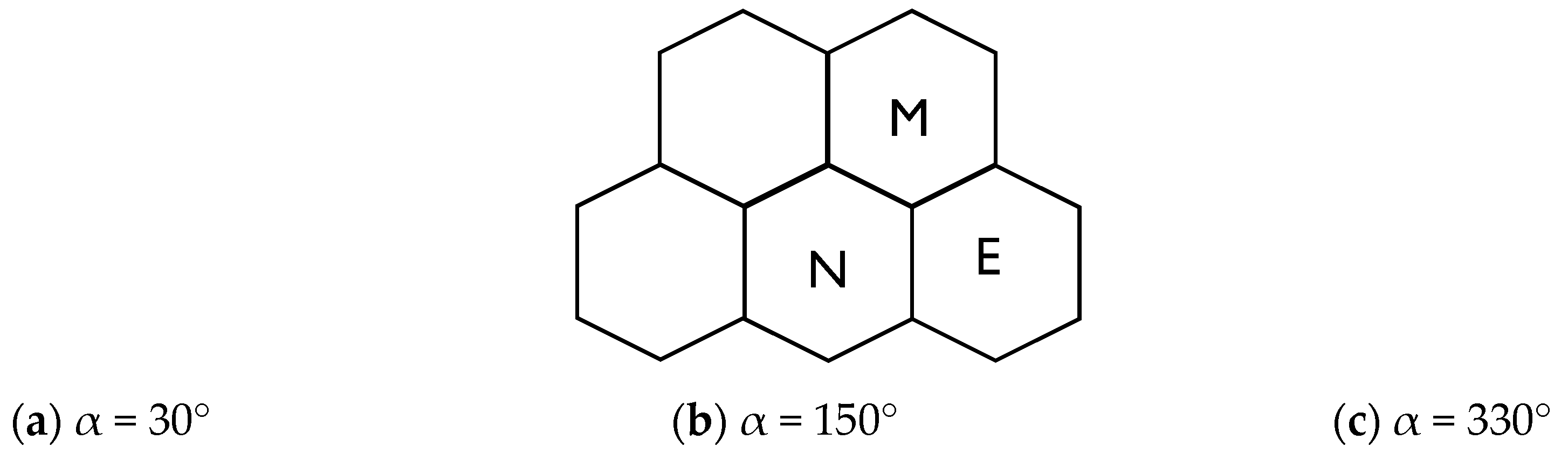
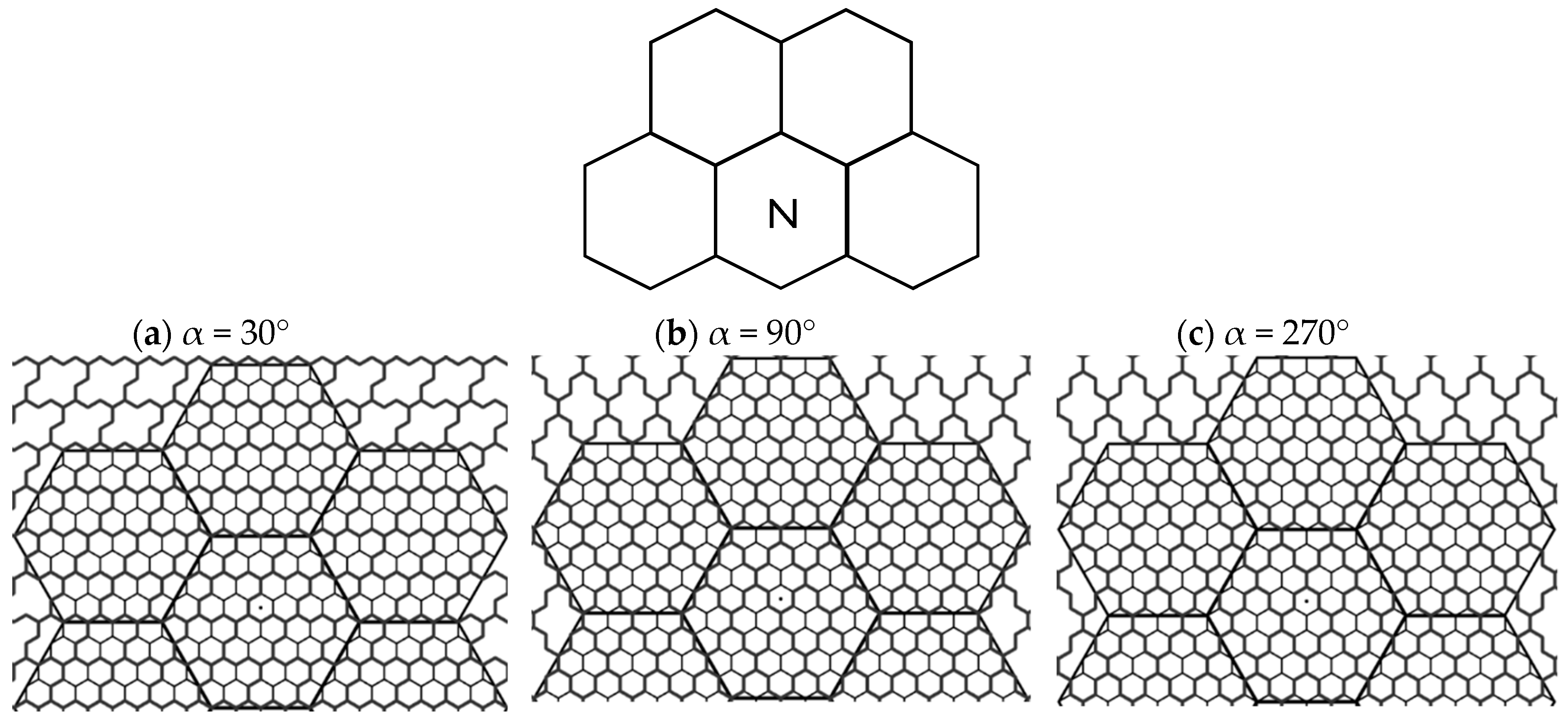
4.2.1. The 4-Hexagonal Cluster Rotations
4.2.2. The Geometrical Properties and Derived Formulas
4.3. The Proposed Non-Uniform Clustering Approach
5. Evaluation and Results
5.1. Summary of the Presented Models
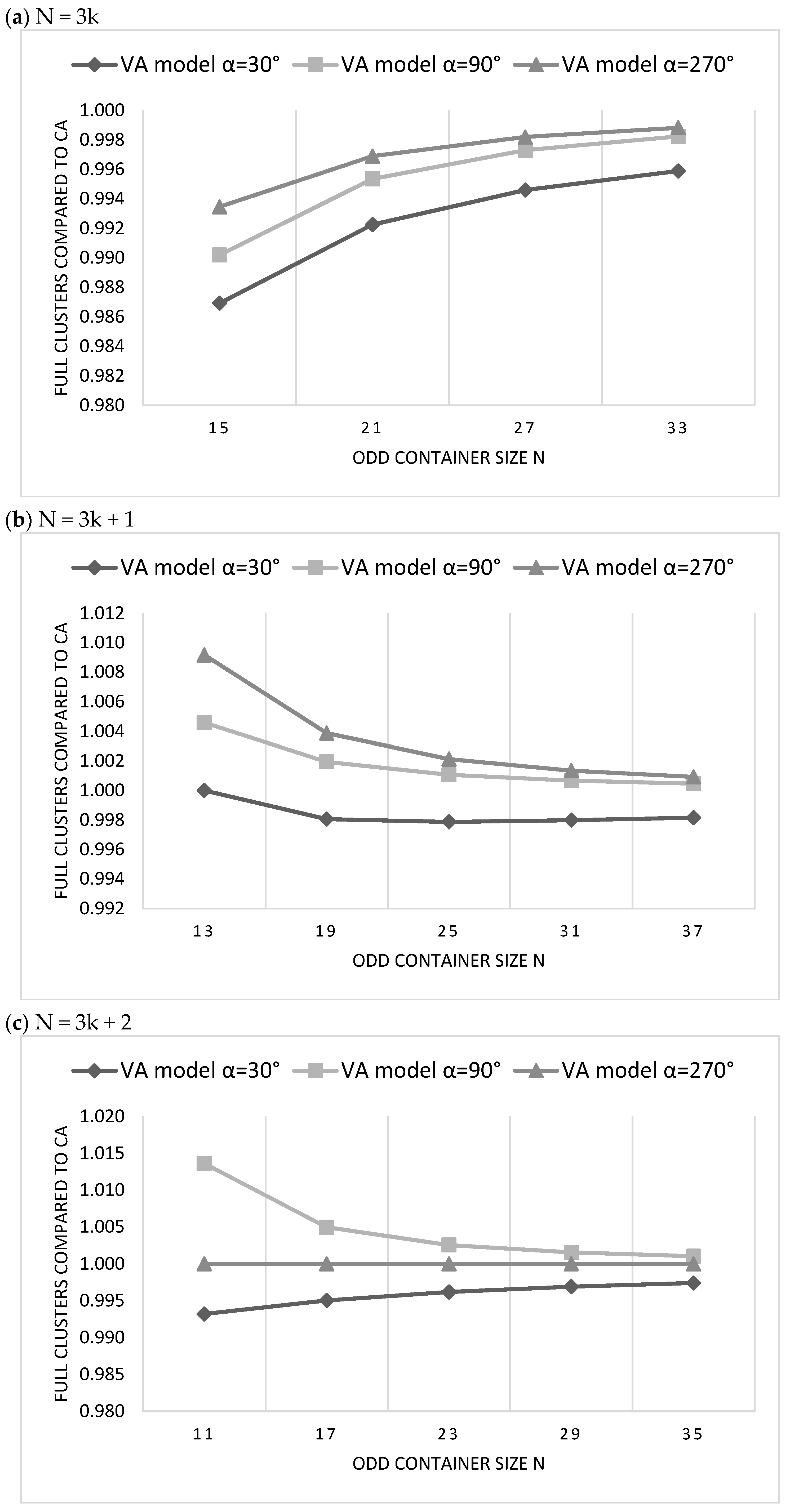
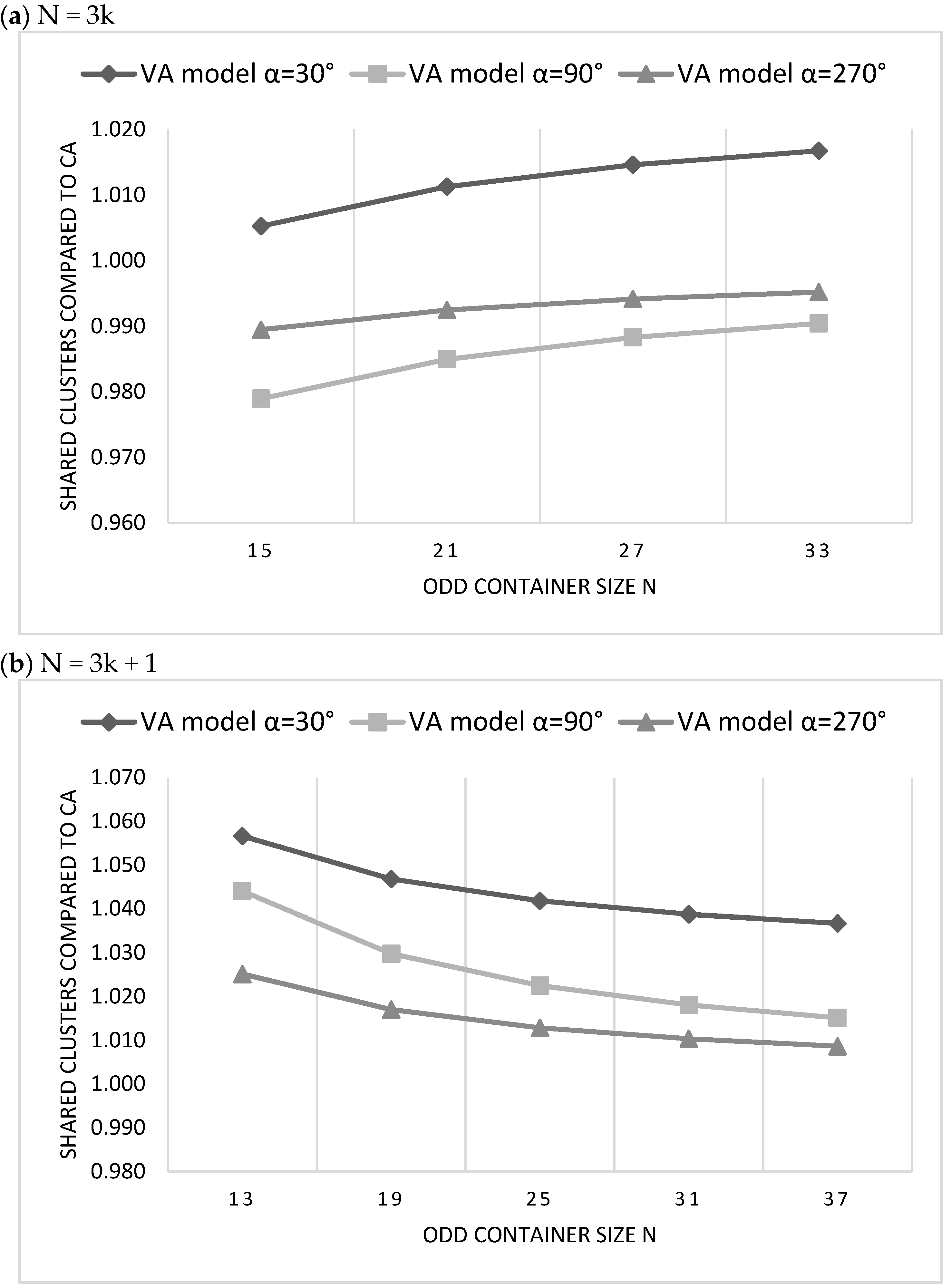
5.2. The Comparison of CA and VA Clustering Architectures
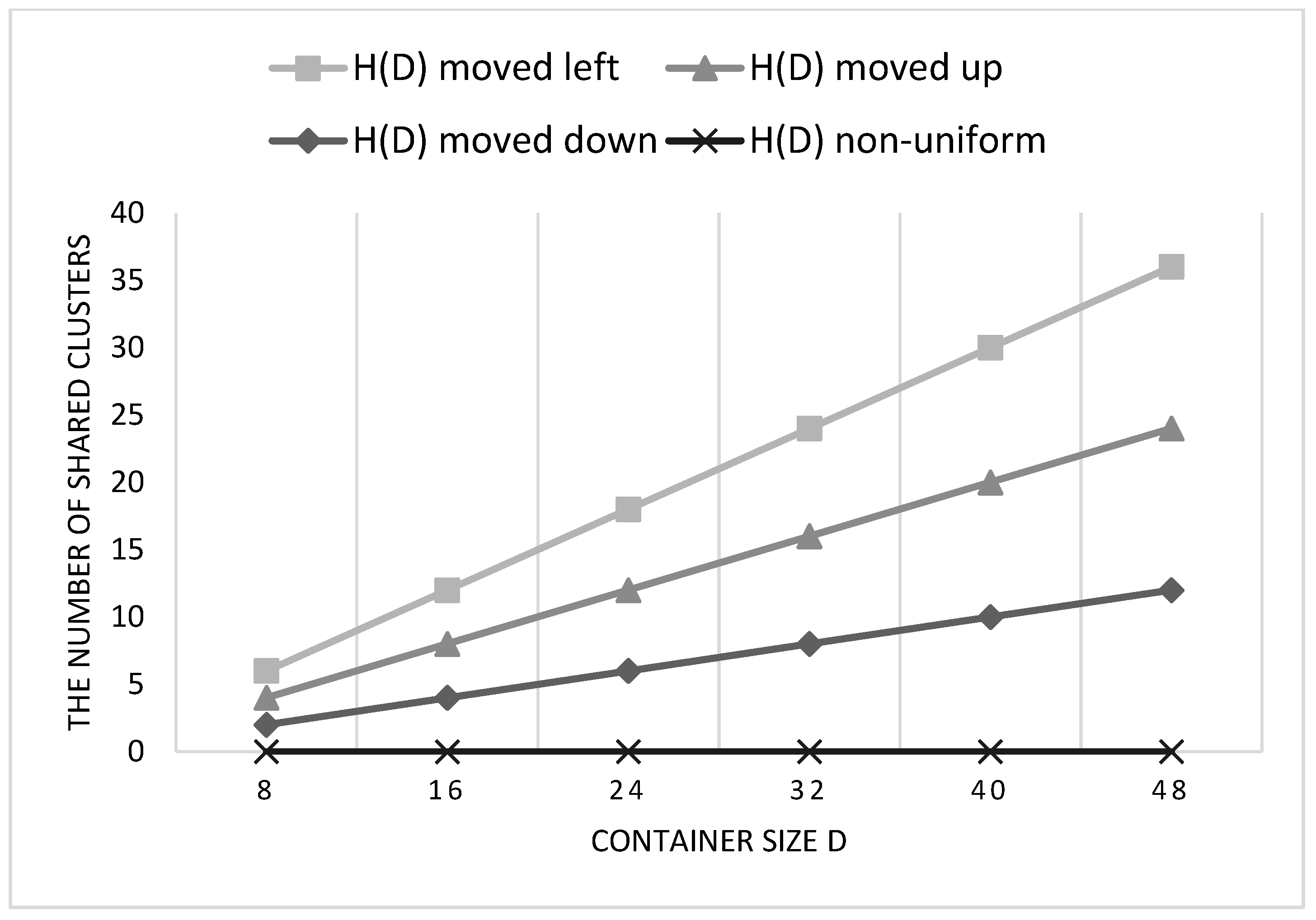
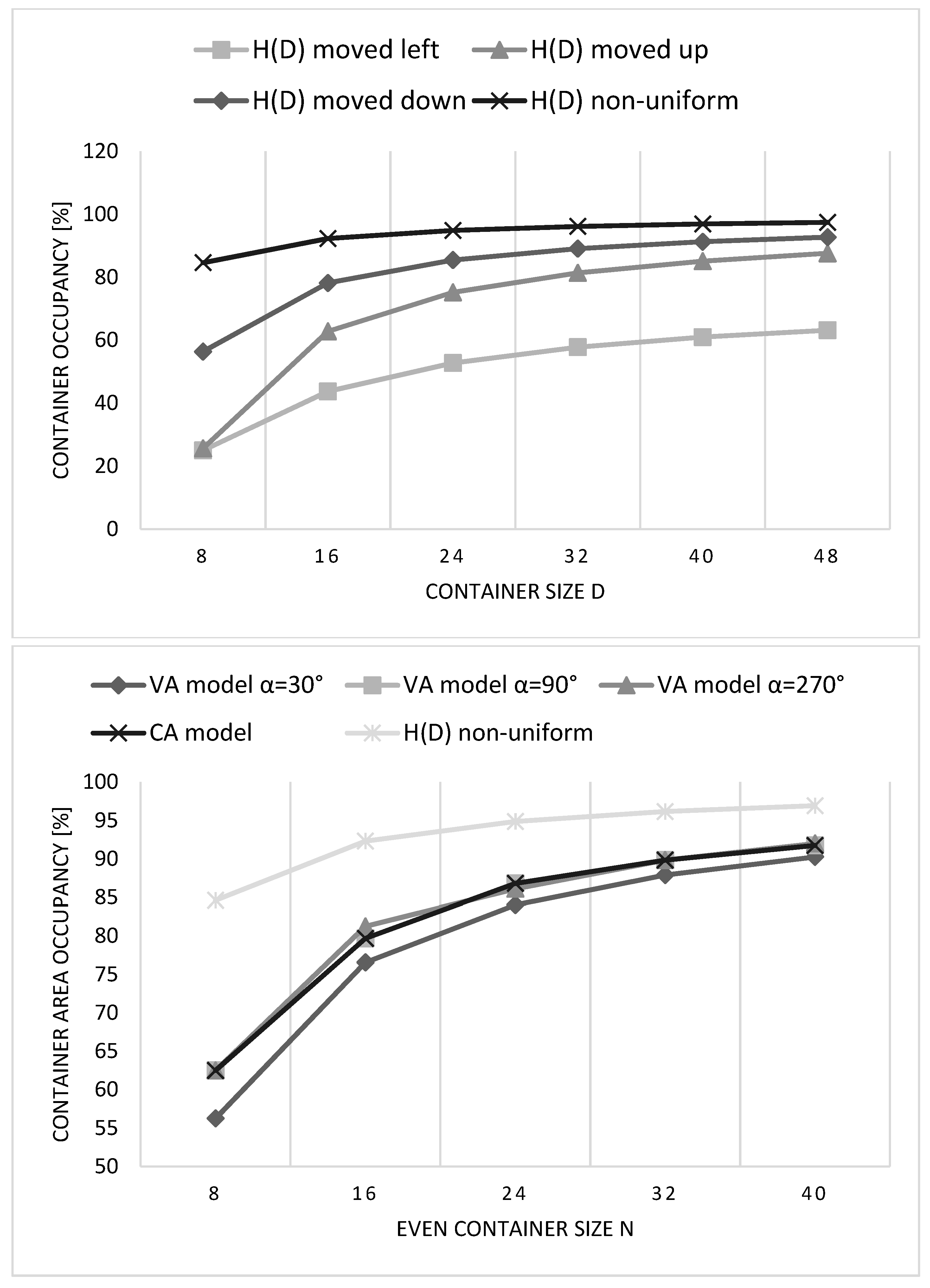
5.3. The Evaluation of the Proposed H(D) Clustering Model
6. Limitations of the Study
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CA | Center Aligned |
| CERN | European Laboratory for Particle Physics |
| CMS | Compact Muon Solenoid |
| HGCAL | High Granularity Calorimeter |
| LHC | Large Hadron Collider |
| NN | Nearest Neighbor |
| ROI | Region of Interest |
| VA | Vertex Aligned |
References
- Romanova, T.; Pankratov, A.; Litvinchev, I.; Pankratova, Y.; Urniaieva, I. Optimized Packing Clusters of Objects in a Rectangular Container. Math. Probl. Eng. 2019, 2019, 4136430. Available online: https://www.hindawi.com/journals/mpe/2019/4136430/ (accessed on 13 December 2019). [CrossRef]
- Litvinchev, I.; Infante, L.; Ozuna, L. Packing circular-like objects in a rectangular container. Comput. Syst. Sci. Int. 2015, 54, 259–267. [Google Scholar] [CrossRef]
- Torres-Escobar, R.; Marmolejo-Saucedo, J.A.; Litvinchev, I.; Vasant, P. Monkey Algorithm for Packing Circles with Binary Variables. Intell. Comput. Optim. Cham. 2019, 547–559. [Google Scholar] [CrossRef]
- Kampas, F.J.; Castillo, I.; Pintér, J.D. Optimized ellipse packings in regular polygons. Optim. Lett. 2019, 13, 1583–1613. [Google Scholar] [CrossRef]
- Kampas, F.J.; Pinter, J.D.; Castillo, I. Packing Ovals in Optimized Regular Polygons. arXiv 2019, arXiv:1901.07056. [Google Scholar] [CrossRef]
- Pankratov, A.; Romanova, T.; Litvinchev, I. Packing ellipses in an optimized convex polygon. J. Glob. Optim. 2019, 75, 495–522. [Google Scholar] [CrossRef]
- López, C.O.; Beasley, J.E. Packing a fixed number of identical circles in a circular container with circular prohibited areas. Optim. Lett. 2019, 13, 1449–1468. [Google Scholar] [CrossRef]
- Bennell, J.; Scheithauer, G.; Stoyan, Y.; Romanova, T.; Pankratov, A. Optimal clustering of a pair of irregular objects. J. Glob. Optim. 2015, 61, 497–524. [Google Scholar] [CrossRef]
- Peralta, J.; Andretta, M.; Oliveira, J.F. Packing Circles and Irregular Polygons using Separation Lines. In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems, Funchal, Portugal, 24–26 January 2018; pp. 71–77. [Google Scholar] [CrossRef]
- Galiev, S.; Lisafina, M. Numerical optimization method for packing regular convex polygons. Comput. Math. Math. Phys. 2016, 56, 1402–1413. [Google Scholar] [CrossRef]
- Prvan, M.; Ožegović, J.; Mišura, A.B. On Calculating the Packing Efficiency for Embedding Hexagonal and Dodecagonal Sensors in a Circular Container. Math. Probl. Eng. 2019, 2019, 9624751. Available online: https://www.hindawi.com/journals/mpe/2019/9624751/cta/ (accessed on 10 December 2019). [CrossRef]
- Wang, D.; Lin, L.; Xu, L. A study of subdividing hexagon-clustered WSN for power saving: Analysis and simulation. Ad Hoc Netw. 2011, 9, 1302–1311. [Google Scholar] [CrossRef]
- Stoyan, Y.; Yaskov, G. Packing equal circles into a circle with circular prohibited areas. Int. J. Comput. Math. 2012, 89, 1355–1369. [Google Scholar] [CrossRef]
- Galiev, S.I.; Lisafina, M.S. Linear models for the approximate solution of the problem of packing equal circles into a given domain. Eur. J. Oper. Res. 2013, 230, 505–514. [Google Scholar] [CrossRef]
- Toledo, F.M.B.; Carravilla, M.A.; Ribeiro, C.; Oliveira, J.F.; Gomes, A.M. The Dotted-Board Model: A new MIP model for nesting irregular shapes. Int. J. Prod. Econ. 2013, 145, 478–487. [Google Scholar] [CrossRef]
- Kazakov, A.L.; Lempert, A.A.; Nguyen, H.L. The Problem of the Optimal Packing of the Equal Circles for Special Non-Euclidean Metric. In International Conference on Analysis of Images, Social Networks and Texts; Springer: Berlin/Heidelberg, Germany, 2017; pp. 58–68. [Google Scholar]
- López, C.O.; Beasley, J.E. Packing unequal rectangles and squares in a fixed size circular container using formulation space search. arXiv 2018, arXiv:1802.07519. [Google Scholar]
- Ekanayake, D.B.; Ranpatidewage, M.M.; LaFountain, D.J. Optimal Packings for Filled Rings of Circles. Appl. Math. 2020, 65, 1–22. [Google Scholar] [CrossRef]
- Lintzmayer, C.N.; Miyazawa, F.K.; Xavier, E.C. Online Circle and Sphere Packing. arXiv 2017, arXiv:1708.08906. [Google Scholar]
- Coffin, S.T. The Puzzling World of Polyhedral Dissections; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Parween, R.; Shi, Y.; Parasuraman, K.; Vengadesh, A.; Sivanantham, V.; Ghanta, S.; Mohan, R.E. Modeling and Analysis of hHoneycomb—A Polyhex Inspired Reconfigurable Tiling Robot. Energies 2019, 12, 2517. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, W.; Su, J.; Xiang, F. Hexagonal Convolutional Neural Networks for Hexagonal Grids. IEEE Access 2019, 7, 142738–142749. [Google Scholar] [CrossRef]
- Uher, V.; Gajdoš, P.; Snášel, V.; Lai, Y.-C.; Radecký, M. Hierarchical Hexagonal Clustering and Indexing. Symmetry 2019, 11, 731. [Google Scholar] [CrossRef]
- Sauvan, J.-B. Concepts and design of the CMS high granularity calorimeter Level-1 trigger. J. Phys. Conf. Ser. 2017, 928, 012026. [Google Scholar] [CrossRef]
- Collaboration, C.M.S. The Phase-2 Upgrade of the CMS Endcap Calorimeter. CERN Document Server, 21 November 2017. Available online: https://cds.cern.ch/record/2293646 (accessed on 10 December 2019).
- Maier, A.A. Sensors for the CMS High Granularity Calorimeter. J. Instrum. 2017, 12, C06030. [Google Scholar] [CrossRef][Green Version]
- Yang, W. Maximal and Minimal Polyhexes; University of Wisconsin-Madison: Madison, WI, USA, 2002. [Google Scholar]
- Mahdavi-Amiri, A.; Harrison, E.; Samavati, F. Hexagonal connectivity maps for Digital Earth. Int. J. Digit. Earth 2015, 8, 750–769. [Google Scholar] [CrossRef]
- Holub, P.; Miller, M.; Pérez-Rosés, H.; Ryan, J. Degree diameter problem on honeycomb networks. Discrete Appl. Math. 2014, 179, 139–151. [Google Scholar] [CrossRef]
- Tong, X.; Ben, J.; Wang, Y. A new effective Hexagonal Discrete Global Grid System: Hexagonal quad balanced structure. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Van de Ville, D.; Blu, T.; Unser, M.; Philips, W.; Lemahieu, I.; Van de Walle, R. Hex-Splines: A Novel Spline Family for Hexagonal Lattices. IEEE Trans. Image Process. 2004, 13, 758–772. [Google Scholar] [CrossRef]




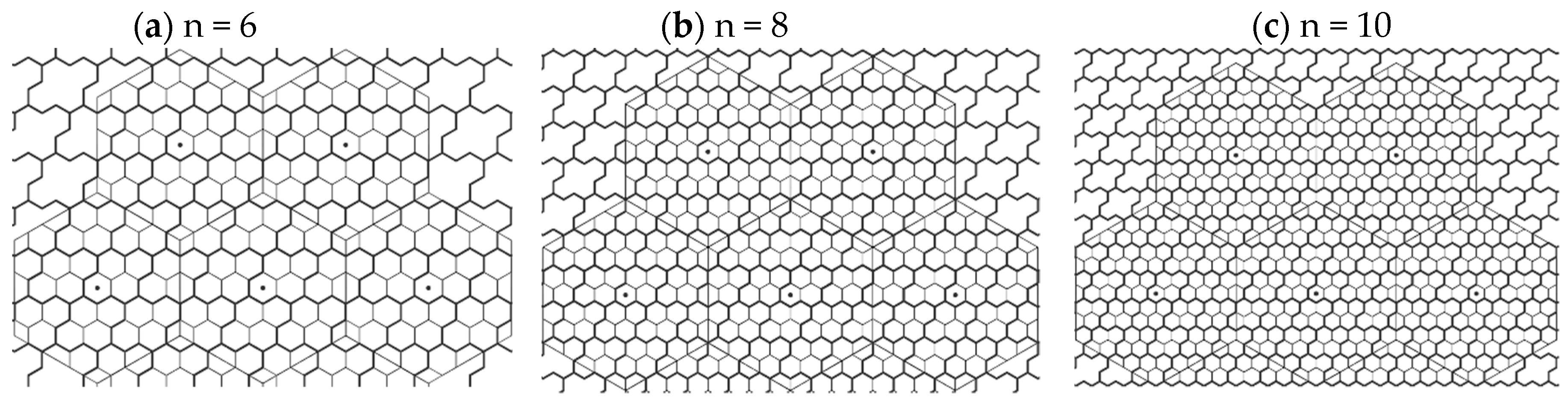



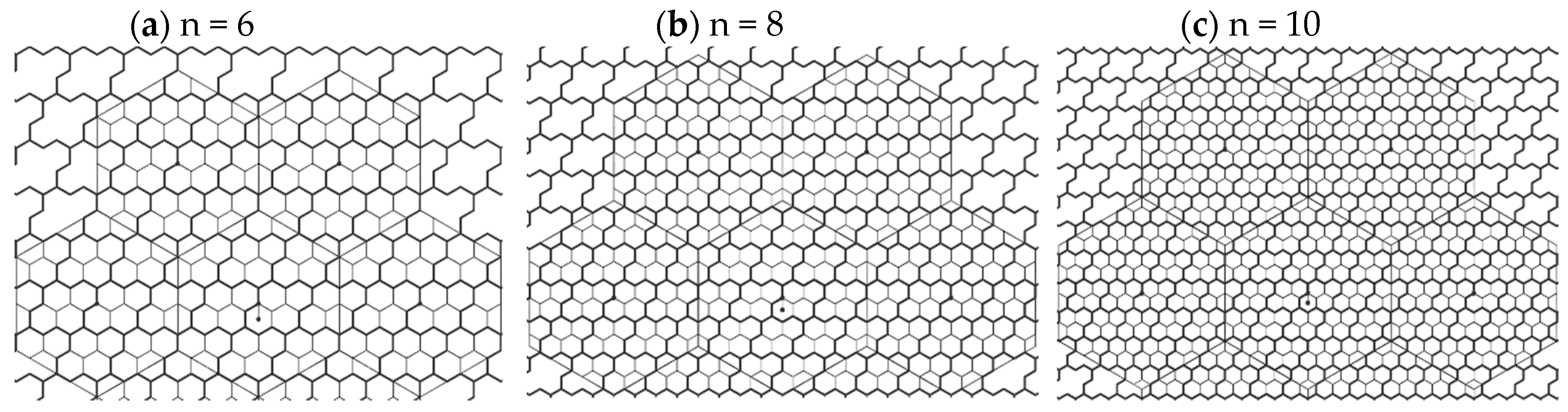






| Container Size (n) | #Full (Inner) Clusters | #Border (Shared) Clusters |
|---|---|---|
| 6 | 5 | 10 |
| 8 | 10 | 13 |
| 10 | 17 | 17 |
| 12 | 27 | 20 |
| 14 | 38 | 23 |
| 16 | 51 | 27 |
| Container Size (n) | #Full (Inner) Clusters | #Border (Shared) Clusters | ||
|---|---|---|---|---|
| 5 | 3 | 2 | 9 | 9 |
| 7 | 6 | 7 | 13 | 11 |
| 9 | 12 | 14 | 18 | 15 |
| 11 | 21 | 21 | 21 | 19 |
| 13 | 30 | 32 | 25 | 21 |
| 15 | 42 | 45 | 30 | 25 |
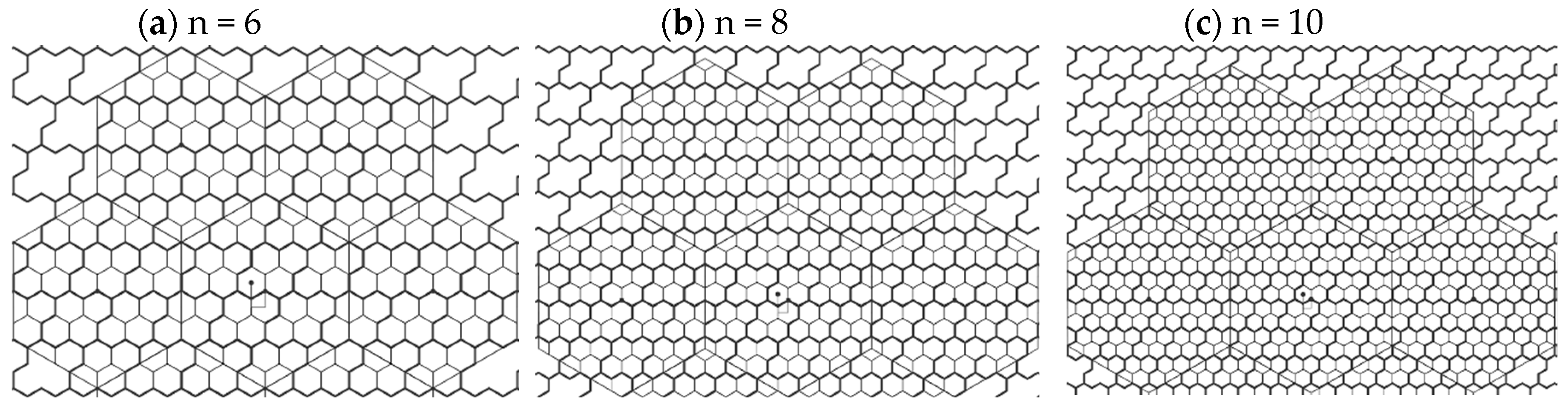
| Container Size (n) | #Full (Inner) Clusters | #Border (Shared) Clusters |
|---|---|---|
| 6 | 4 | 11 |
| 8 | 9 | 15 |
| 10 | 16 | 20 |
| 12 | 25 | 23 |
| 14 | 36 | 27 |
| 16 | 49 | 32 |
| , | , | |
| α = 30° | Formula (10), (11) | Formula (10), (11) |
| α = 90° | Formula (1), (4) | Formula (10), (11) |
| α = 270° | Formula (12), (9) | Formula (10), (11) |
| α = 150° | Formula (10), (11) | Formula (12), (9) |
| α = 330° | Formula (10), (11) | Formula (1), (4) |
| Container Size (n) | #Full (Inner) Clusters | #Border (Shared) Clusters | ||||
|---|---|---|---|---|---|---|
| 5 | 3 | 1 | 3 | 8 | 10 | 9 |
| 7 | 7 | 7 | 6 | 12 | 12 | 15 |
| 9 | 13 | 13 | 12 | 15 | 18 | 16 |
| 11 | 22 | 19 | 21 | 18 | 22 | 21 |
| 13 | 32 | 31 | 30 | 22 | 24 | 27 |
| 15 | 44 | 43 | 42 | 25 | 30 | 28 |
| , , , , , | , , , , , | |
| α = 30° | Formula (14), (15), (6), (16), (17), (18) | Formula (6), (15), (14), (18), (17), (16) |
| α = 90° | Formula (15), (6), (14), (17), (18), (16) | Formula (6), (15), (14), (18), (17), (16) |
| α = 270° | Formula (6), (15), (14), (18), (17), (16) | Formula (6), (15), (14), (18), (17), (16) |
| α = 150° | Formula (14), (15), (6), (16), (17), (18) | Formula (6), (15), (14), (18), (17), (16) |
| α = 330° | Formula (14), (15), (6), (16), (17), (18) | Formula (15), (6), (14), (17), (18), (16) |
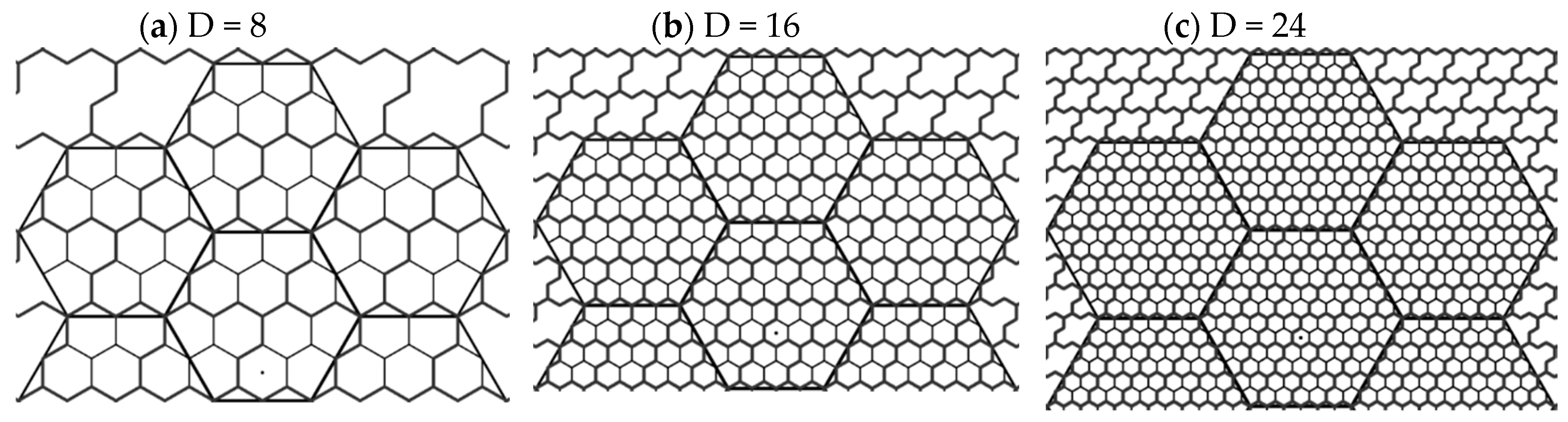
| Container Size (D) | #Full (Inner) Clusters | #Border (Shared) Clusters |
|---|---|---|
| 8 | 2 | 2 |
| 16 | 10 | 4 |
| 24 | 24 | 6 |
| 32 | 44 | 8 |
| 40 | 70 | 10 |
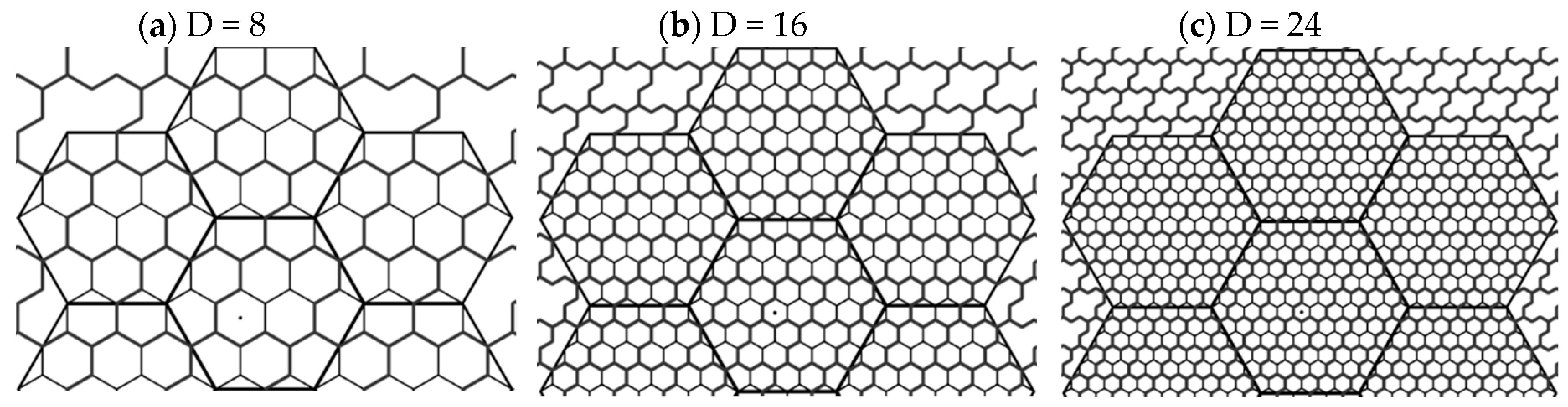
| Container Size (D) | #Full (Inner) Clusters | #Border (Shared) Clusters |
|---|---|---|
| 8 | 1 | 6 |
| 16 | 7 | 12 |
| 24 | 19 | 18 |
| 32 | 37 | 24 |
| 40 | 61 | 30 |
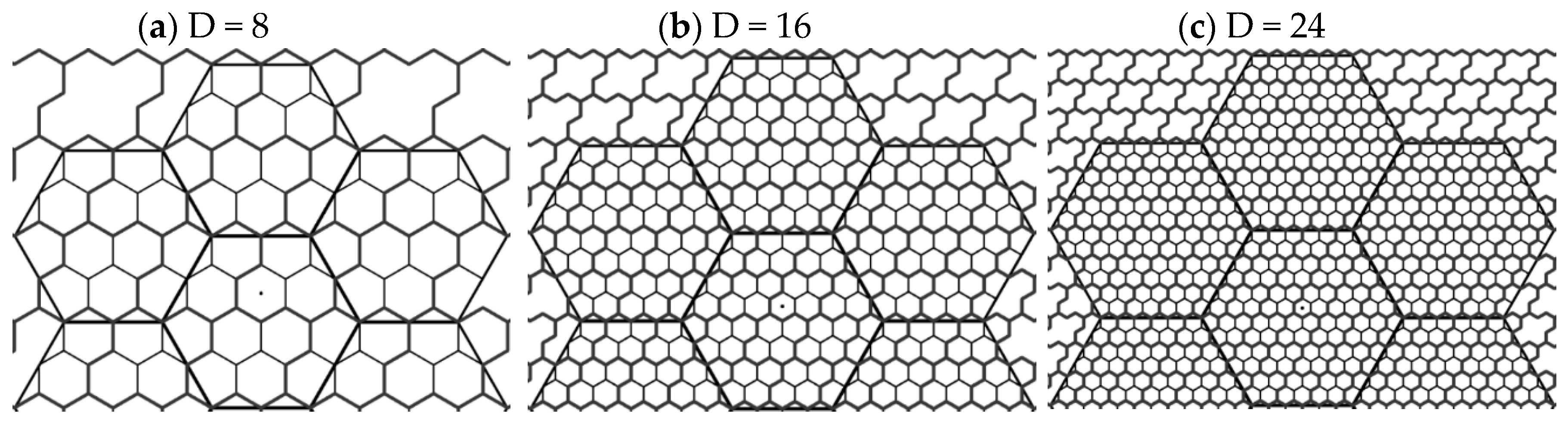
| Container Size (D) | #Full (Inner) Clusters | #Border (Shared) Clusters |
|---|---|---|
| 8 | 1 | 4 |
| 16 | 8 | 8 |
| 24 | 21 | 12 |
| 32 | 40 | 16 |
| 40 | 65 | 20 |
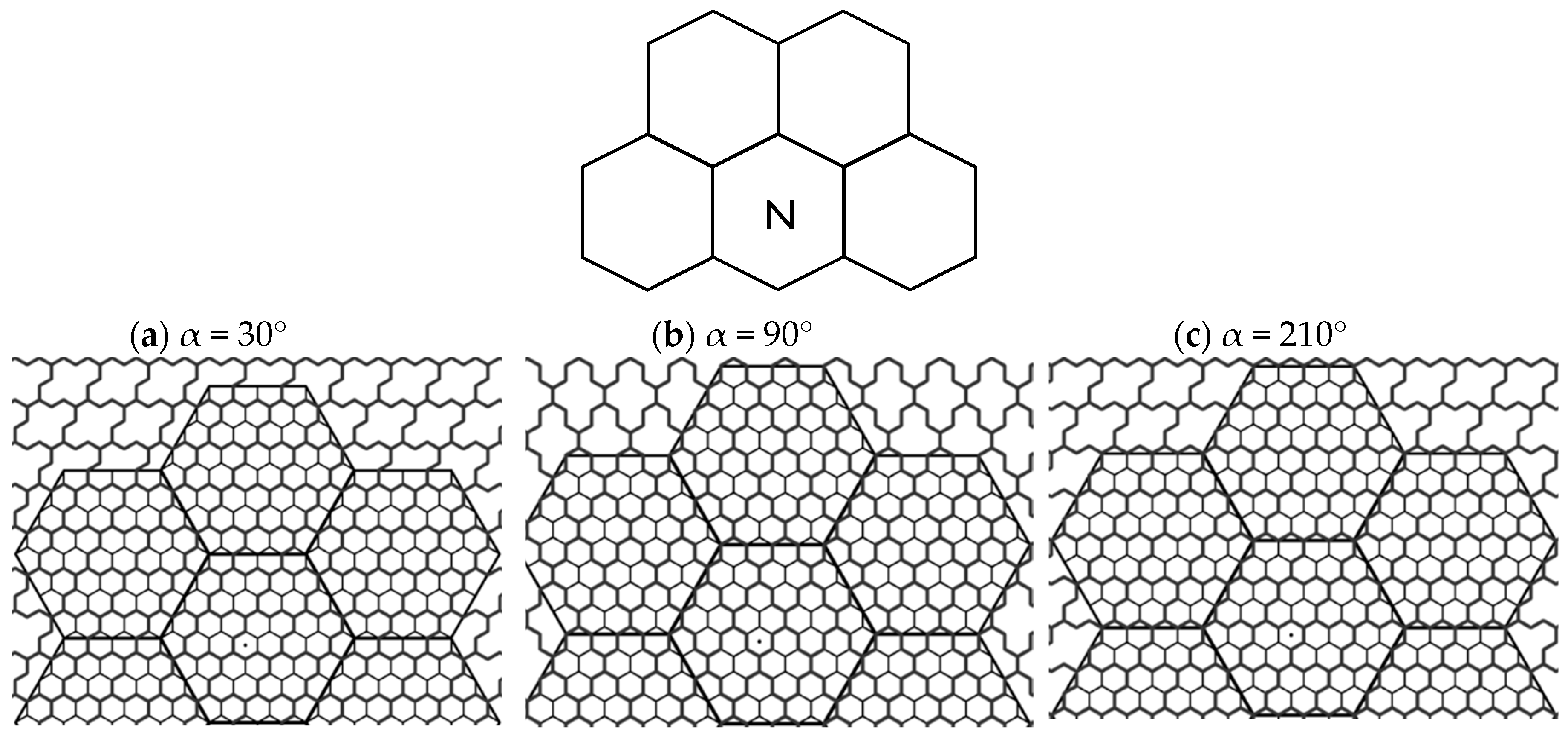
| , | , | , | |
| α = 30° | Formula (19), (20) | Formula (21), (22) | Formula (23), (24) |
| α = 90° | Formula (21), (22) | Formula (23), (24) | Formula (19), (20) |
| α = 210° | Formula (21), (22) | Formula (19), (20) | Formula (19), (20) |
| α = 270° | Formula (19), (20) | Formula (23), (24) | Formula (21), (22) |
| Container Size (D) | #Full (Inner) Clusters | #Border (Shared) Clusters |
|---|---|---|
| 8 | 3 | 0 |
| 16 | 12 | 0 |
| 24 | 27 | 0 |
| 32 | 48 | 0 |
| 40 | 75 | 0 |
| 48 | 108 | 0 |
| Model | Sub-Type | Sub-Classes | Center Position | Orientations | Chosen Model |
|---|---|---|---|---|---|
| CA () | () | - no movements needed | , | ||
() | - no movements needed | , | |||
| VA () | () | - moved down - moved left | , , | - moved down , | |
( | - moved down - moved left | , , | - moved down , | ||
| uniform | - moved down - moved left - moved up | , , | - all positions | ||
| non-uniform | - with voids - no voids |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prvan, M.; Burazin Mišura, A.; Gecse, Z.; Ožegović, J. A Vertex-Aligned Model for Packing 4-Hexagonal Clusters in a Regular Hexagonal Container. Symmetry 2020, 12, 700. https://doi.org/10.3390/sym12050700
Prvan M, Burazin Mišura A, Gecse Z, Ožegović J. A Vertex-Aligned Model for Packing 4-Hexagonal Clusters in a Regular Hexagonal Container. Symmetry. 2020; 12(5):700. https://doi.org/10.3390/sym12050700
Chicago/Turabian StylePrvan, Marina, Arijana Burazin Mišura, Zoltan Gecse, and Julije Ožegović. 2020. "A Vertex-Aligned Model for Packing 4-Hexagonal Clusters in a Regular Hexagonal Container" Symmetry 12, no. 5: 700. https://doi.org/10.3390/sym12050700
APA StylePrvan, M., Burazin Mišura, A., Gecse, Z., & Ožegović, J. (2020). A Vertex-Aligned Model for Packing 4-Hexagonal Clusters in a Regular Hexagonal Container. Symmetry, 12(5), 700. https://doi.org/10.3390/sym12050700





