Planetary Systems and the Hidden Symmetries of the Kepler Problem
Abstract
1. Introduction
2. Methods
2.1. Transformations of Planetary Orbits
- :Me, 0:V, 1:E, 2:Ma, 3:A, 4:J, 5:S, 6:U, 7:P.
- 1:Me, 2:V, 3:E, 4:Ma, 5:A, 6:J, 7:S, 8:U, 9:N, 10:P.
2.2. Symmetries of the Kepler Problem
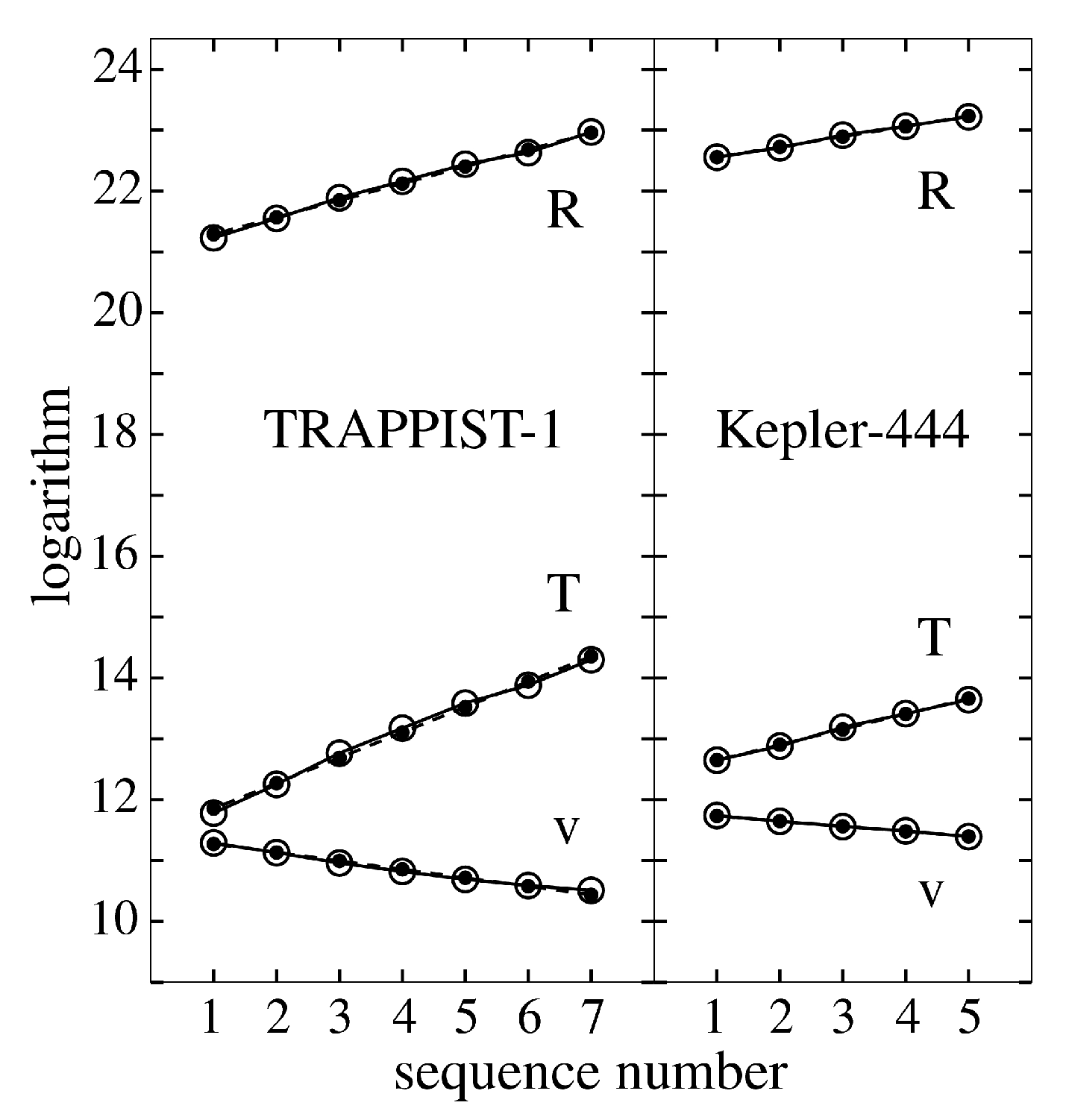
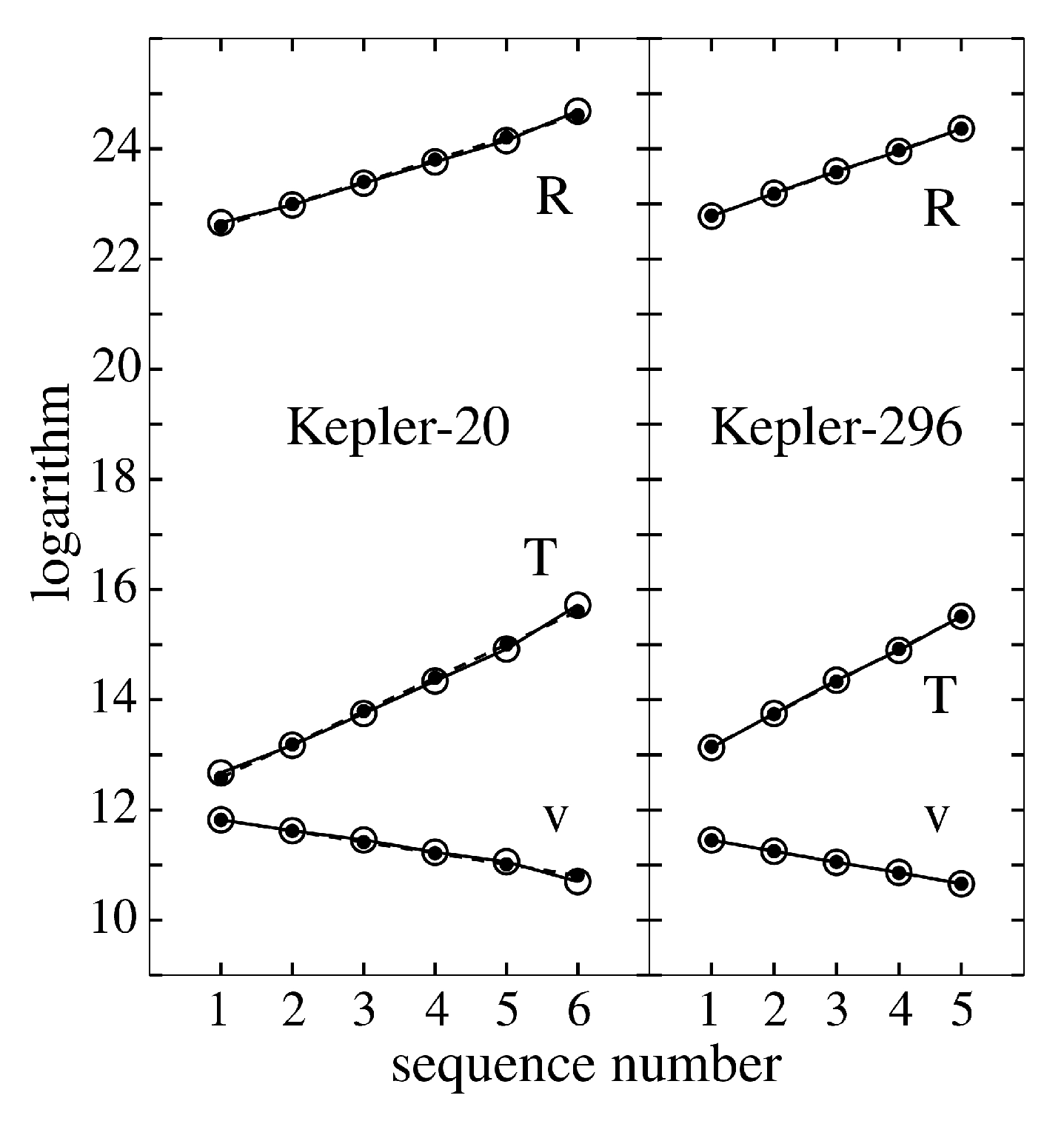
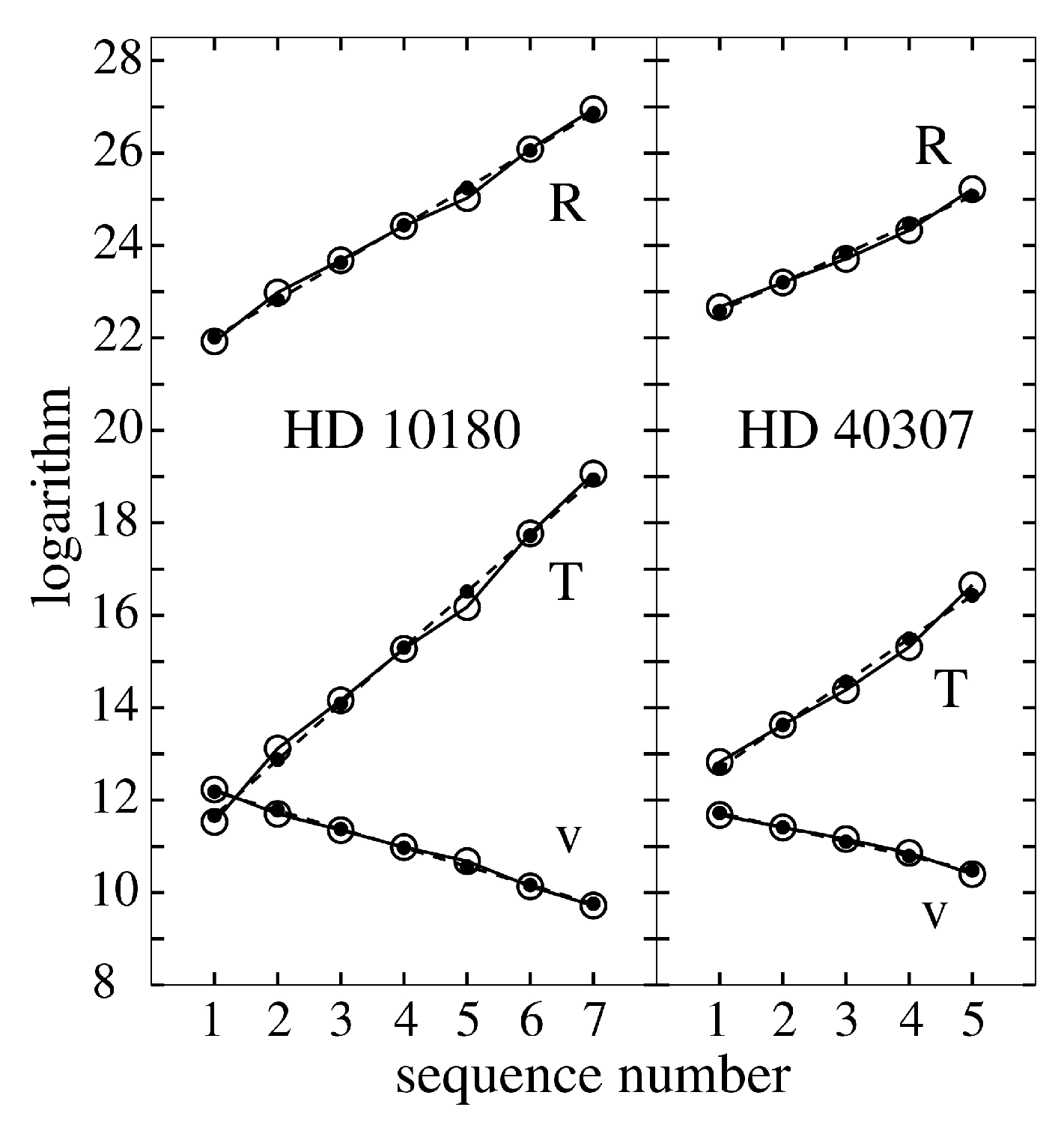
3. Results
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kepler, J. Astronomia Nova; Casper, M., Translator; Green Lion Press: Oldenburg, München, Germany, 1609. [Google Scholar]
- Kepler, J. Harmonices Mundi; Casper, M., Translator; Linz: Oldenburg, München, Germany, 1619. [Google Scholar]
- Kepler, J. Mysterium Cosmographicum; ETH-Bibliothek Zürich: Tübingen, Germany, 1596. [Google Scholar]
- Nieto, M. The Tititus-Bode Low of Planetary Distances: Its History and Theory; Pergamon Press: Oxford, UK, 1972. [Google Scholar]
- Nieto, M. The letters between Titius and Bonnet and the Tititus-Bode low of planetary distances. Am. J. Phys. 1985, 53, 22–24. [Google Scholar] [CrossRef]
- Barut, A.O. Symmetry and dynamics: Two distinct methodologies from Kepler to supersymmetry. In Symmetries in Science II; Gruber, B., Lenczewski, R., Eds.; Plenum Press: New York, NY, USA, 1989; pp. 37–50. [Google Scholar]
- Ksanfomality, L.V. Planets, dwarf planets, and small bodies in the Solar System. Sol. Syst. Res. 2007, 41, 174–176. [Google Scholar] [CrossRef]
- Buta, A. Toward an atomic model of the planetary system. Rev. Romaine Phys. 1982, 27, 321. [Google Scholar]
- Graner, F.; Dubrulle, B. Titius-Bode laws in solar system: I. Scale invariance explains everything. Astron. Astrophys. 1994, 301, 262–268. [Google Scholar]
- Graner, F.; Dubrulle, B. Titius-Bode laws in solar system: II. Build your own law from disk models. Astron. Astrophys. 1994, 301, 269–276. [Google Scholar]
- Ragnarsson, S.I. Planetary distances: A new simplified model. Astron. Astrophys. 1994, 282, 609–612. [Google Scholar]
- Poveda, A.; Lara, P. The exo-planetary system of 55 Cancri and the Titius-Bode law. Rev. Mexicana Astron. Astrofis. 2008, 44, 243–246. [Google Scholar]
- Lynch, P. On the significance of the Titius–Bode law for the distribution of the planets. Mon. Not. R. Astron. Soc. 2003, 341, 1174–1178. [Google Scholar] [CrossRef]
- Wybourne, B.G. Classical Groups for Physicists; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Fock, V. Zur Theorie des Wasserstoffatoms. Z. Physik 1935, 98, 145. [Google Scholar] [CrossRef]
- Bargmann, V. Zur Theorie des Wasserstoffatoms. Z. Physik 1936, 99, 576. [Google Scholar] [CrossRef]
- Györgyi, G. Kepler’s Equation, Fock Variables, Bacry’s Generators and Dirac Brackets. Nuovo Cimento 1968, 53A, 717. [Google Scholar] [CrossRef]
- Györgyi, G. Kepler’s Equation, Fock Variables, Bacry’s Generators II. Classical and quantum group dynamics of the Kepler problem. Nuovo Cimento 1969, 62A, 449. [Google Scholar] [CrossRef]
- Wulfman, C.E. Dynamical Symmetry; World Scientific: Singapore, 2011. [Google Scholar]
- Quesne, C. Symmetry and dynamical Lie algebras in classical and quantum mechanics. In Symmetries in Physics; Frank, A., Wolf, K.B., Eds.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 325–348. [Google Scholar]
- Barut, A.O.; Bornzin, G.L. Unification of the external conformal symmetry group and the internal conformal dynamical group. J. Math. Phys. 1974, 15, 1000–1006. [Google Scholar] [CrossRef]
- Maclay, G.J. Dynamical Symmetries of the H Atom. Symmetry 2020, 12, 1323. [Google Scholar] [CrossRef]
- Available online: https://exoplanetarchive.ipac.caltech.edu (accessed on 12 January 2020).
- Stöcker, H.; Harris, J.W. Handbook of Mathematics and Computational Science; Springer: Berlin/Heidelberg, Germany, 1998; p. 386. [Google Scholar]
- Gillon, M.; Triaud, A.H.M.J.; Demory, B.; Jehin, E.; Agol, E.; Deck, K.M.; Lederer, S.M.; de Wit, J.; Burdanov, A.; Ingalls, J.G.; et al. Seven temperate terrestrial planets around the nearby ultracool dwarf star. Nature 2017, 542, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Campante, T.L.; Barclay, T.; Swift, J.J.; Huber, D.; Adibekyan, V.Z.; Cochran, W.; Burke, C.J.; Isaacson, H.; Quintana, E.V.; Davies, G.R.; et al. An Ancient Extrasolar System with Five Sub-Earth-size Planets. Astrophys. J. 2015, 799, 170–186. [Google Scholar] [CrossRef]
- Buchhave, L.A.; Dressing, C.D.; Dumusque, X.; Rice, K.; Vanderburg, A.; Mortier, A.; Lopez-Morales, M.; Lopez, E.; Lundkvist, M.S.; Kjeldsen, H.; et al. A 1.9 Earth Radius Rocky Planet and the Discovery of a Non-transiting Planet in the Kepler-20 System. Astron. J. 2016, 152, 160–171. [Google Scholar] [CrossRef]
- Barclay, T.; Quintana1, E.V.; Adams, F.C.; Ciardi, D.R.; Huber, D.; Foreman-Mackey, D.; Montet, B.T.; Caldwell, D. The Five Planets in the Kepler-296 Binary System All Orbit the Primary: A Statistical and Analytical Analysis. Astrophys. J. 2015, 809, 7–16. [Google Scholar] [CrossRef]
- Kane, S.R.; Gelino, D.M. On the Inclination and Habitability of the HD 10180 System. Astrophys. J. 2014, 792, 111–117. [Google Scholar] [CrossRef][Green Version]
- Tuomi, M.; Anglada-Escudé, G.; Gerlach, E.; Jones, H.R.A.; Reiners, A.; Rivera, E.J.; Vogt5, S.S.; Butler, R.P. Habitable-zone super-Earth candidate in a six-planet system around the K2.5V star HD 40307. Astron. Astrophys. 2013, 549, A48. [Google Scholar] [CrossRef]
| Planets | T (Day) | Smax (AU) | ecc. |
|---|---|---|---|
| TRAPPIST-1b | 1.51087 | 0.0111 | 0.081 |
| TRAPPIST-1c | 2.42182 | 0.0152 | 0.083 |
| TRAPPIST-1d | 4.04961 | 0.0214 | 0.070 |
| TRAPPIST-1e | 6.09962 | 0.0282 | 0.085 |
| TRAPPIST-1f | 9.20669 | 0.0371 | 0.063 |
| TRAPPIST-1g | 12.35294 | 0.0451 | 0.061 |
| TRAPPIST-1h | 18.76700 | 0.0630 | 0.000 |
| HD 10,180 b | 1.17766 | 0.0222 | 0.001 |
| HD 10,180 c | 5.75969 | 0.0641 | 0.073 |
| HD 10,180 d | 16.35700 | 0.1286 | 0.131 |
| HD 10,180 e | 49.74800 | 0.2699 | 0.051 |
| HD 10,180 f | 122.74400 | 0.4929 | 0.119 |
| HD 10,180 g | 604.67000 | 1.4270 | 0.263 |
| HD 10,180 h | 2205.00000 | 3.3810 | 0.095 |
| HD 40,307 b | 4.31230 | 0.0468 | 0.200 |
| HD 40,307 c | 9.61840 | 0.0799 | 0.060 |
| HD 40,307 d | 20.43200 | 0.1321 | 0.070 |
| HD 40,307 f | 51.76000 | 0.2470 | 0.020 |
| HD 40,307 g | 197.80000 | 0.6000 | 0.290 |
| Kepler-20 b | 3.69612 | 0.0463 | 0.030 |
| Kepler-20 e | 6.09852 | 0.0639 | 0.280 |
| Kepler-20 c | 10.85409 | 0.0949 | 0.160 |
| Kepler-20 f | 19.57758 | 0.1396 | 0.320 |
| Kepler-20 g | 34.94000 | 0.2055 | 0.150 |
| Kepler-20 d | 77.61130 | 0.3506 | 0.600 |
| Kepler-296 c | 5.84164 | 0.0521 | 0.330 |
| Kepler-296 b | 10.86438 | 0.0790 | 0.330 |
| Kepler-296 d | 19.85029 | 0.1180 | 0.330 |
| Kepler-296 e | 34.14211 | 0.1690 | 0.330 |
| Kepler-296 f | 63.33627 | 0.2550 | 0.330 |
| Kepler-444 b | 3.60011 | 0.0418 | 0.160 |
| Kepler-444 c | 4.54588 | 0.0488 | 0.310 |
| Kepler-444 d | 6.18939 | 0.0600 | 0.180 |
| Kepler-444 e | 7.74349 | 0.0696 | 0.100 |
| Kepler-444 f | 9.74049 | 0.0811 | 0.290 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cseh, J. Planetary Systems and the Hidden Symmetries of the Kepler Problem. Symmetry 2020, 12, 2109. https://doi.org/10.3390/sym12122109
Cseh J. Planetary Systems and the Hidden Symmetries of the Kepler Problem. Symmetry. 2020; 12(12):2109. https://doi.org/10.3390/sym12122109
Chicago/Turabian StyleCseh, József. 2020. "Planetary Systems and the Hidden Symmetries of the Kepler Problem" Symmetry 12, no. 12: 2109. https://doi.org/10.3390/sym12122109
APA StyleCseh, J. (2020). Planetary Systems and the Hidden Symmetries of the Kepler Problem. Symmetry, 12(12), 2109. https://doi.org/10.3390/sym12122109




