Symmetries of Magnetic Fields Driven by Spherical Dynamos of Exoplanets and Their Host Stars

Abstract

Observations of exoplanets open a new area of scientific activity and the structure of exoplanet magnetospheres is an important part of this area. Here we use symmetry arguments and experiences in spherical dynamo modeling to obtain the set of possible magnetic configurations for exoplanets and their corresponding host stars. The main part of our results is that the possible choice is much richer than the basic dipole magnetic field of both exoplanets and stars. Other options, for example, are quadrupole configurations or mixed parity solutions. Expected configurations of current sheets for the above mentioned exoplanet host star systems are presented as well.

1. Introduction

Exoplanets is a new area for scientific investigations that accumulates ideas from various more traditional scientific branches [1,2,3,4]. The process of accumulation is far from being straightforward because of the novelty of the topic. In particular, it seems very attractive to suppose that the exoplanets have magnetic fields that are to some extent similar to the geomagnetic field as well as the stars in the planetary system with particular exoplanets having a magnetic field that is to some extent similar to the solar magnetic field [5,6]. In regards to first attempts to observe the magnetic fields of exoplanets see, e.g., [7]. It becomes possible to use for the exoplanet studies, the available bulk knowledge concerning solar magnetosphere, solar wind, and related topics of space physics. The point however is that we know quite a lot about the solar and Earth’s magnetic field from long term studies using various tracers. Of course, we extrapolate the ideas together with available knowledge concerning planetary magnetism in the solar system to the much wider sample of exoplanets. It is far from clear to see in advance how wide a variety of options lost in straightforward extrapolation could be.

The available understanding of the magnetic field origin in celestial bodies in the framework of dynamo theory helps in this extrapolation (basic ideas of dynamo theory for astrophysical applications can be found in various books, e.g., [8]). Theoretical abilities, here, are however limited because our knowledge concerning stellar and planetary hydrodynamics required from theoretical prediction is much more limited than one for the Sun and Earth. The point is that the intensive motions of electroconducting media in the form of convection or turbulence and differential rotation seems to be required for dynamo action in exoplanets and their host stars however one needs to know various delicate properties of convection to predict the shape of dynamo-driven configuration. One such fine property is the degree of mirror asymmetry of convective flows. Quantification of such values is far from an easy undertaking even for laboratory experiments with liquid metals. The available experiences in laboratory dynamo experiments confirm the point that moderate changes in delicate properties of the flow can result in a substantial modification in dynamo-driven magnetic configuration, see, e.g., [9]. Of course, extensive numerical simulations remain a useful tool for the understanding of exoplanetary dynamos however it looks unrealistic to predict the magnetic configuration based on several integral parameters of an exoplanet. Of course, the magnetic field of an exoplanet similar to Jupiter is expected to be similar to the magnetic field of Jupiter. A non-rotating exoplanet or an exoplanet without any liquid envelope is expected to have no pronounced internal magnetic field. It is natural to expect that a larger rotational moment of a celestial body results in its higher magnetic moments. Stellar activity observations support this expectation (e.g., [10]; remarkably, this early finding in the topic is simultaneously an early paper in exoplanetary studies). However deeper thoughts are required on an approach directed on exoplanet studies specifically.

Looking for a way to resolve to some extent the problem, we suggest to base a list of possible magnetic configurations relevant to the problem on the symmetry properties of spherical dynamos as well as experiences in the field of playing parameters in quite a rich history of spherical dynamo modeling. An immediate message from this business (say, [11]) is that the variety of options here is much wider rather than one suggested by a straightforward extrapolation from solar system experiences. The aim of our paper is to present a variety of options known from the experiences in dynamo modeling and briefly explain how dramatic the corresponding changes required could be in the basic concept of magnetospheric studies for exoplanet-star systems. We note that the results from dynamo theory collected below are already discussed in the scientific literature and (we give their corresponding references) however the attention of the authors was concentrated mainly on magnetic configurations typical for the Sun or Earth so it is from easy for a reader to extract the variety of dynamo-driven magnetic configuration from the original papers. As a result researchers interested in current sheets systematically ignore many options. Our paper aims to fill this gap.

We appreciate various specific mechanisms like compression of magnetic field, frozen in stellar wind, relic magnetic field, or battery effects which may be responsible for magnetic field formation in some celestial bodies. We concentrate however on the message from dynamo theory as a main stream of explanation in stellar and planetary magnetic studies. It would be risky to insist that dynamo successfully explains any particular observation in the field however the general progress here looks remarkable.

2. Spherical Dynamos

As we know the choice of possible mechanisms for magnetic field self-excitation in stars and planets is very limited. If we are not ready to admit new physics to explain magnetic field generation in an isolated celestial body, we have to consider its self-excitation (and then it being self-sustained) by electromagnetic induction. In other words, we have to consider magnetic field self-excitation by a flow of electrically-conducting media. This idea was suggested by Larmor as early as 1919 and the corresponding physical mechanism is known now as a dynamo [12]. Numerous attempts to somehow modify this starting point in dynamo studies remain unsuccessful and we accept that dynamo is responsible for magnetic fields in celestial bodies, ignoring some rare exceptions (say, relic magnetism in some stars [13]) irrelevant for our problem.

The point is that according to the so-called Lenz rule, electromagnetic induction acting in an electrical circuit suppresses a seed magnetic field. In order to obtain the magnetic field self-excitation, we have to consider two systems of magnetic lines and a flow which produces an induction effect for one system, which enhances magnetic field in the second one and vice versa (e.g., [14]). Around 2000, the possibility of such self-excitation was demonstrated experimentally in Latvia and later in Germany using a device with moving liquid sodium. From that time, the dynamo process can be considered an experimental fact rather than theoretical speculation (see, e.g., [9], for review about laboratory dynamo experiments).

Several particular ways to obtain a dynamo self-excitation are known, however one that is relevant in stellar and planetary context was suggested by Parker in 1955 [15]. Consider poloidal magnetic field $B_P$ which looks more or less similar to the field of one or several magnetic dipoles situated at the rotation axis and toroidal magnetic field $B_T$ situated deep under the surface of the body and directed in the azimuthal direction. Then differential rotation produces toroidal magnetic field from the poloidal one. This is one part of dynamo self-excitation. In order to get a dynamo, we have to restore the poloidal magnetic field from the toroidal one. Parker [15] suggested that it occurs due to a mirror asymmetry of the convective or turbulent flows. This mirror asymmetry can be created by various effects however Parker [15] considered Coriolis force acting on convective vortexes in rotating stratified convection. In 1965 Steenbeck, Krause, and Rädler independently developed a consistent theory of this effect known after their work as the $\alpha$-effect (e.g., [16]). The $\alpha$-effect was also obtained in laboratory experiments [17] and can be considered now as an experimental fact. Dynamo models based on the joint action of the differential rotation with angular velocity $\omega$ and the $\alpha$-effect known as the spherical $\alpha \omega$-dynamos are extensively investigated numerically nowadays.

The governing equation for magnetic field $\mathbf{B}$ averaged over convective pulsations reads:

$$\frac{\partial \mathbf{B}}{\partial t}=\mathrm{curl}\left([\mathbf{V}\times \mathbf{B}]+\alpha \mathbf{B}-\beta \mathrm{curl}\left(\mathbf{B}\right)\right),$$

where $\mathbf{V}$ is large-scale velocity (mainly differential rotation), $\alpha$ is the so-called $\alpha$-effect which quantifies mirror asymmetry of convective flows, and $\beta$ is the coefficient of convective magnetic diffusivity. The first term in the r.h.s. of this equation is usually at least 10 times larger than the second one however it is insufficient for dynamo action. The quantity $\alpha$ is measured in the same units as a large-scale velocity $\mathbf{V}$ and convective r.m.s. velocity v which determines $\beta$. Usually the convective velocity $\mathbf{v}$ is much smaller than $\mathbf{V}$ and $\alpha$ is an order of magnitude weaker than $\mathbf{v}$ however $\alpha$ remains a key driver and can not be ignored. Of course, it is difficult to estimate $\alpha$ observationally or even theoretically for an exoplanet. Contemporary computational physics can perform direct numerical dynamo simulations without averaging over convective vortexes and avoid to involve quantities like $\alpha$ and $\beta$ directly in the model however it does not help in the estimation of tiny properties of convection in a particular exoplanet responsible for the dynamo-driven configuration. In regards to various approaches to simulate solar and stellar dynamos as well as general situation in dynamo modeling see e.g., [18].

Note that dynamo (considered independent of other physical processes) as an instability predicts, strictly speaking, an unbounded magnetic field growth. For particular celestial bodies, this growth is saturated by a magnetic field action on dynamo drivers. In order to include these effects in a dynamo model one needs use in dynamo equations additional physical effects and quantities which is far from easy for determination for exoplanets. It seems to be easier to start here from symmetries of dynamo-driven magnetic configurations and move to the estimates of saturated magnetic field strength on further stage of research only. About the spatial scales under discussion, we expect something similar to what happens in the Sun-Earth system, i.e., averaging over the convective vortices inside the spherical shell, the scale of the dynamo driven magnetic field is few time smaller rather than the radius of exoplanet or hosting star respectively (approximately on the order of one tenth of the planetary or stellar radii, see, e.g., [19,20,21,22]) and the scale of the dynamo-driven magnetic field is the order of the radius of the exoplanet or hosting star.

The key point in the $\alpha \omega$ dynamos is that the drivers, namely differential rotation and $\alpha$-effect, have different symmetries with respect to the rotation axes and equator of the body. Differential rotation is symmetric with respect to the equator, while $\alpha$-effect is antisymmetric.

3. Earth’s and Solar Magnetism in the Spherical Dynamo Framework

The geomagnetic field of the Earth’s surface is a poloidal magnetic field close to the magnetic field of a magnetic dipole, which is almost parallel to the rotation axis. A deviation of the magnetic dipole from the rotation axis is considered a large-scale fluctuation. The toroidal component of the geomagnetic field is presumed to be located somewhere deep inside the Earth, being inaccessible for contemporary observations, because the Earth’s mantle prevents its propagation to the surface. In regards to initial ideas on the Earth’s toroidal magnetic field observations, see [23].

Solar magnetic field contains a poloidal component that is also closed to the field of magnetic dipole parallel to the rotation axis. The toroidal component of the solar magnetic field is also mainly located deep in the solar interior, however, it is traced at the solar surface due to sunspots. Concerning the current understanding of dynamo aspects of solar magnetic studies, see e.g., [24].

Symmetries of both magnetic fields is known as dipole one, i.e., toroidal magnetic field is antisymmetric with respect to the equator while the poloidal magnetic field is symmetric with respect to the solar equator. In particular, toroidal magnetic field vanishes at the solar equator. Correspondingly, sunspots are rare just in the vicinity of the equator. The symmetry of poloidal magnetic field determines the structure of the heliospheric current sheet. The poloidal magnetic field is parallel to the rotation axis at the solar equator, meaning that the current sheet (area of magnetic field changing) is situated nearby this equator.

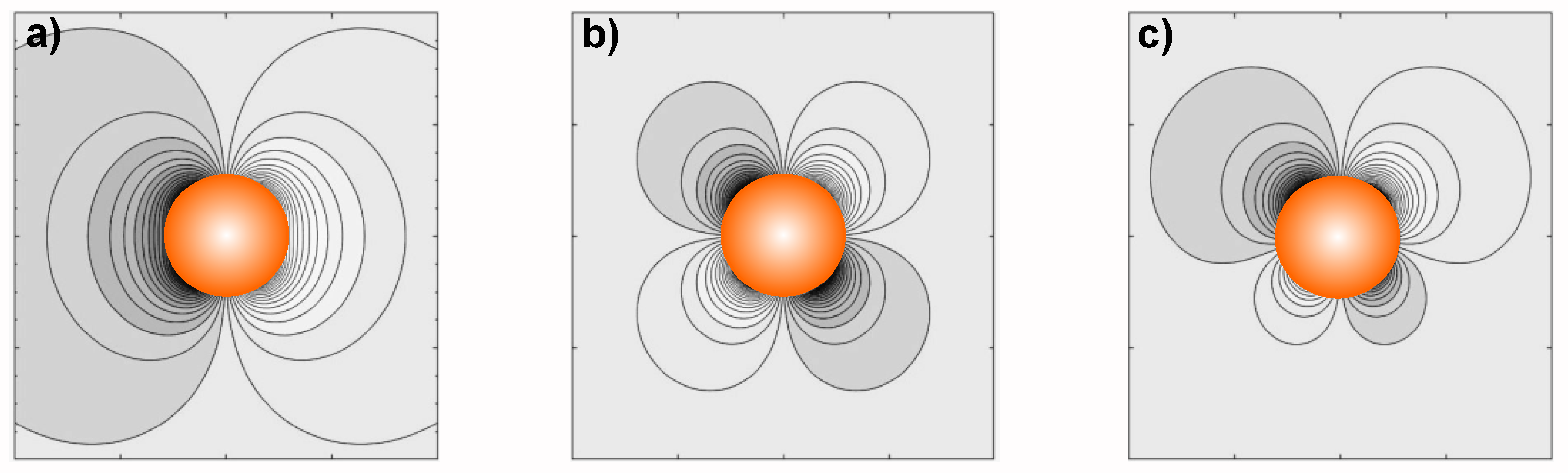
The magnetic field symmetry of dipole type agrees with the symmetry of dynamo driver, and one can verify this fact by a direct calculation (e.g., [14]). The point however is that it is not the only symmetry compatible with the symmetry of classical dynamo equations. Typical magnetic field configurations in the exterior of the spherical body include dipole, quadrupole structures, and their mixed parity configurations, see examples in Figure 1.

4. Magnetic Configurations Known for Spherical Dynamos

Of course, conventional dipole configuration do excites by $\alpha \omega$-spherical dynamo for an appropriate choice of dynamo drivers.

Another magnetic field symmetry compatible with the symmetry of dynamo drivers is so-called the quadrupole symmetry (e.g., [14]). Toroidal magnetic field is symmetric with respect to the equator, in particular, it means that $B_T$ may be maximal just at it. In contrast, $B_P$ is antisymmetric with respect to the equator, where it vanishes. Magnetic field around the dynamo active sphere is closed to the magnetic field of quadrupole. In particular, regions where the magnetic field is parallel to the rotation axis and equatorial projection of magnetic force changes the sign to the opposite are located in the middle latitudes symmetrically relative to the equatorial plane. As a result, instead of the one disk-like current sheet typical for the heliosphere, we have to expect the formation of two conic-like current sheets at approximate latitudes near $\pm {30}^{\circ }$, see [25,26].

Dynamo models with magnetic fields of quadrupole symmetry systematically arise in spherical dynamo models almost as easy as magnetic fields with dipole symmetry (e.g., [27]). From the viewpoint of dynamo modeling, it would be natural to expect that a substantial part of stars and planets have a magnetic field of quadrupole symmetry however it remains difficult to verify this option by available observations. A short epoch with sunspots concentrated at the solar equator is known for XVIII century [28]. Maybe, it gives some hint concerning the possible quardupole symmetry for the solar magnetic field at these times [29]. Note, that higher symmetries, say, octupole one, are different from the symmetry of dynamo drivers. Correspondingly, there is no reason to expect stellar or planetary magnetic fields with symmetries higher than quadrupole one. Observation of an exoplanet and/or host star with a magnetic structure with a pronounced octupole symmetry and negligible dipole and quadrupole magnetic moments would be a challenge for contemporary dynamos. In principle, it might happen that a dynamo system excites a magnetic configuration with a poloidal magnetic field antisymmetric with respect to the equator however its magnetic dipole moment vanishes due to certain reasons and the only octupole magnetic moments survives however we have never faced such an example in dynamo modeling. Solar magnetic configuration do contains octupole component and even higher zonal harmonics (e.g., [30]) which are interesting for the current sheet studies (e.g., [26]) and can be included in corresponding modeling (e.g., [31]) however dipole component in solar magnetic field is presented as well.

A straightforward way to obtain a dynamo generated magnetic configuration with octupolar symmetry would be to consider a spherical shell with two dynamo waves with equal in strength oppositely directed toroidal magnetic field propagating equatorwards in each hemisphere. The poloidal field produced by dynamo action from such a toroidal field has the desired configuration. If the number of dynamo waves of opposite parities is even higher, the magnetic fields with even higher symmetries can be excited. Dynamo equations allow in principle such kind of configurations and they are mentioned in exploratory papers in dynamo theory (e.g., [32] and references therein). An excitation of such configurations requires dynamo drivers much more intensive rather than what happens in the Sun and Earth. There are no hints concerning such intensive dynamo action in contemporary observations. In contrast, excitation of another magnetic configurations under discussion is possible with more or less conventional dynamo drivers. An observation of exoplanets and/or host stars with pronounced octupolar magnetic field would be a message that we basically miSunderstand to what extent solar or Earth’s magnetism are instructive for the problem.

The symmetry of a dynamo-driven magnetic field is expected to be determined by the symmetry of dynamo drivers in a linear instability problem only. Dynamo-driven magnetic field is governed however by linear equations for quite a short time. As the growing magnetic field becomes strong enough to affect the motion of conducting medium the problem becomes nonlinear and dynamo driven configurations with symmetries lower then that one of dynamo drivers becomes possible. Such mixed-parity solutions are known from the dynamo modeling ([11,33]). One can consider a mixed parity solution at a superposition of dipole and quadrupole solutions [34].

Mixed parity solution occurring in numerical simulations are substantially more rare than dipole or quadrupole configurations. The number of papers discussed mixed parity solutions may be estimated as few percent of the whole bulk of papers addressing spherical dynamo modeling. The dynamo models exciting mixed parity solution do not however require anything very specific and it is natural to expect that they have to be presented in a sample of exoplanets and/or host stars, provided it will contain hundreds of cases. A mixed-parity configuration of activity tracers was however isolated in historical solar activity data as recorded in sunspot observations at the end of Maunder minimum [35]. It was suggested that solar dynamo that time produced a mixed-parity magnetic field [34]. More specifically, according to this interpretation, magnetic activity at the end of the Maunder minimum happened in one solar hemisphere only. During such times, only one current sheet was available in the solar vicinity, however, the sheet was located in the middle latitudes rather than in the equatorial plane. Of course, one must be careful in the interpretation of archive data [36,37,38] however it looks plausible that mixed parity configuration could be expected in some celestial bodies.

Experiences in spherical dynamo modeling contain one more message that may be important for exoplanet studies. The point is that both the dynamo drivers, namely the differential rotation and $\alpha$-effect, can be positive as well as negative. In particular, $\alpha$ being antisymmetric with respect to the stellar equator, have to be positive in one hemisphere and negative in another one. Differential rotation being symmetric with respect to the stellar can be larger near the stellar surface at the stellar equator or may be smaller there in middle latitudes. Correspondingly, the dimensionless number D known as the dynamo number, which measures the intensity of dynamo action, may be positive as well as negative. What combination of drivers is called positive is a conventional agreement. For the sake of definiteness, we accept here that $D<0$ in solar case.

Note that the abilities of contemporary science to estimate the size of the dynamo number D in particular celestial bodies are very limited. The point is that direct observations of mirror asymmetry of convection in stellar or planetary interior remain unrealistic. Scattering in theoretical estimates may be as large as order of magnitudes. The viewpoint of [39] that solar dynamo is just above the excitation threshold is close to our understanding of the situation however it is too far to be unanimously accepted by the community. Of course, some very qualitative scalings for D are possible. Say, rapid rotation is helpful for dynamo action however the gap between such general ideas and a quantitative estimate of a dynamo number in a particular celestial body is quite wide (see, e.g., [40] which is often cited in this context).

Solar activity can be described as a sequence of activity wave propagating equatorwards. If the stellar dynamo number D is positive, the activity wave propagates polarwards (e.g., [41]) and activity manifestations are expected to be much more pronounced rather for the Sun. In particular, the conic polar current sheets [42] are expected to be much more pronounced than in solar magnetoshere.

One more option for the stars with positive D are standing magnetic configurations with a magnetic field substantially stronger for the Sun [43,44,45]. In particular, stellar flares are substantially more intensive than solar ones expected for such stars. Contemporary observations of solar flares say that such superflares are possible on stars which seems to be at first sight similar to the Sun [46].

5. Symmetries for ${\mathbf{\alpha }}^{\mathbf{2}}$ Spherical Dynamos

One more option in a variety of possible magnetic configurations relevant for the exoplanet studies and host stars can be presented as follows. Classical $\alpha \omega$ dynamo presumes that it is the differential rotation responsible from the transformation of the poloidal magnetic field in the toroidal one. The point however is that the $\alpha$-effect is able to produce this transformation as well. A violation of mirror symmetry measured by $\alpha$ is usually quite small, a conventional estimate is that excess of, say, right hand rotating vortexes over the left-hand ones in a given hemisphere is about 5–10% only. The point however is that the low rotation of a spherical body may not be very different from the solid body one as well. A naive expectation is that a differential rotation is still more important in toroidal field production than the $\alpha$-effect. Correspondingly, the $\alpha \omega$-dynamo is considered a more attractive scheme than a dynamo based on $\alpha$-effect only. The later is known as ${\alpha }^2$-dynamo. Indeed, ${\alpha }^2$-dynamo equations can be formulated in a form that explicitly depends on the driver in the form ${\alpha }^2$ [47]. Quantity $\alpha$ being antisymmetric with respect to the stellar equator have to vanish just at the equator. However, the symmetry of the dynamo drivers for ${\alpha }^2$ occurs to be much less pronounced than that of the $\alpha \omega$-dynamo. It is why the ${\alpha }^2$-dynamo excites a magnetic configuration that is highly inclined to the rotation axis much easier more so than the $\alpha \omega$-dynamo. In particular, magnetic configurations in the form of equatorial dipole are welcome for the ${\alpha }^2$-dynamo (e.g., [48]). An observation of a substantial equatorial component of magnetic dipole at Uranus supports the idea that ${\alpha }^2$-dynamo may be an important option in a mechanism to excite the magnetic field of exoplanets. Strictly speaking, magnetic dipole for the $\alpha \omega$-driven configuration can be directed in the equatorial plane at instants of magnetic field reversals (e.g., [49,50]) however this looks to be an unlikely option.

6. The Structure of Astrosphere as the Possible Indication to the Dynamo Symmetries

Now let us consider some aspects of observations of exoplanet/host star magnetic fields and their extension in the surrounding space. While the existence of magnetized stars has been known for quite a long time, there are little data about exoplanetary magnetic fields. They were discovered and estimated recently by indirect measurements based particularly on the observations of anomalous enhanced emissions ( in radio, UV, or X-ray) that likely indicate the existence of the magnetic field of exoplanets [3,51,52]. The irradiation of planet outer layers by star wind can lead to a substantial atmospheric outflow and therefore give the observable signatures for a distant observer (e.g., [53,54]). This phenomenon can not be directly related to planet-host star magnetic interactions, but magnetic fields can influence and accelerate the outflows of ionized gas [55]. The exact method was recently proposed [56] for direct detecting of the presence of magnetic fields in the atmospheres of transiting exoplanets. This method is similar to one that has been initially introduced in solar physics by [57] based on detecting radiation polarization in the helium line triplet at 1083 nm during transits of close-in exoplanets with extended or escaping atmospheres. This method is defined by authors as exact and extremely sensitive to the presence of magnetic fields in exoplanet atmospheres. Therefore one can expect the further rapid development of investigations in this area.

The magnetic fields of extrasolar planets are of great interest because they can play a substantial role in the shielding of planetary atmospheres from cosmic rays and in the regulation of atmospheric losses, which, in turn, are important for the estimates of their interior and atmospheric contents and, finally, their habitability. In addition, the magnetic fields of exoplanets can be influenced strongly by mutual exoplanets – host star interactions. As a result, the investigations of impact of host star magnetic fields and the corresponding environment are also the object of intensive research. In this context, hot Jupiters (exoplanets with masses M greater than 13 mass of Jupiter ($M>13M_J$) orbiting close to their host stars at distances less than 10 stars radii $d>10R_{*}$, as well as brown dwarfs (a separate group of celestial bodies with $12<M<80M_J$ moving alone or with their satellites) are the important objects for observations of magnetic activities. First observations of their magnetic fields were done in [58]. Recently, the auroral emission for four dwarfs was detected and corresponded to magnetic fields from about 3.2 to 6.2 kG [59]. It was concluded that rapid dwarf rotation may be important for producing strong dipole fields in convective dynamos and it possibly contributes for driving the current systems powering auroral radio emission.

Observations of the Ly$\alpha$ line (that is a signature of neutral H atoms moving with high velocities toward and away from the star) during exoplanet HD 209458b transit in front of its host star revealed the motion of stellar wind with a velocity $v_{sw}\approx 400$ km/s, plasma density $n_{sw}\approx 5\times {10}^2$m${}^{-3}$ and finally allowed estimating the planetary magnetic moment as $D_p\approx 1.6\times {10}^{26}$A/m${}^2$, that is approximately 10 percent from the Jupiterian one [60]. The star-planet interactions in the form of the planet-modulated chromospheric emission of the star were investigated for four hot Jupiters [7]. Magnetic star-planet interactions involving the release of energy of both stellar and planetary magnetic fields allow one to estimate exoplanetary magnetic fields. It was found that the value of the surface magnetic field for hot Jupiters is in a range from 20 G to 120 G. That is approximately one–two order larger than it is predicted by dynamo scaling laws, but is in agreement with scaling laws relating the internal heat flux and planetary magnetic field.

We should mention here that these first results of experimental researches of exoplanetary magnetic fields are very important, on the one side, but, on the other side, are sometimes quite difficult for interpretation because of observational complexities of such remote planetary systems and the limited set of methods generally providing indirect data. For a comparison with the above-mentioned results, the dipole magnetic moment of the Earth is about $8\times {10}^{22}$A· m${}^2$ while the Jupiterian one is approximately $2\times {10}^4$ times larger [61]. The values of magnetic induction at the surfaces are equal, correspondingly, (0.3–0.6) G at the Earth and about 5G at Jupiter. We see that magnetic fields of the planets of the solar system and extrasolar planets can be substantially different and the later ones sometimes could not agree with the theory. It depends on many factors that may be missing in our knowledge about extrasolar planets and their interactions with parent stars. The fact that exoplanets have a much stronger magnetic field than Jupiter makes them suitable objects for further research. As a result the known methods of the Sun’s observations principally can be applied for investigations of their magnetic fields and interactions with their host stars.

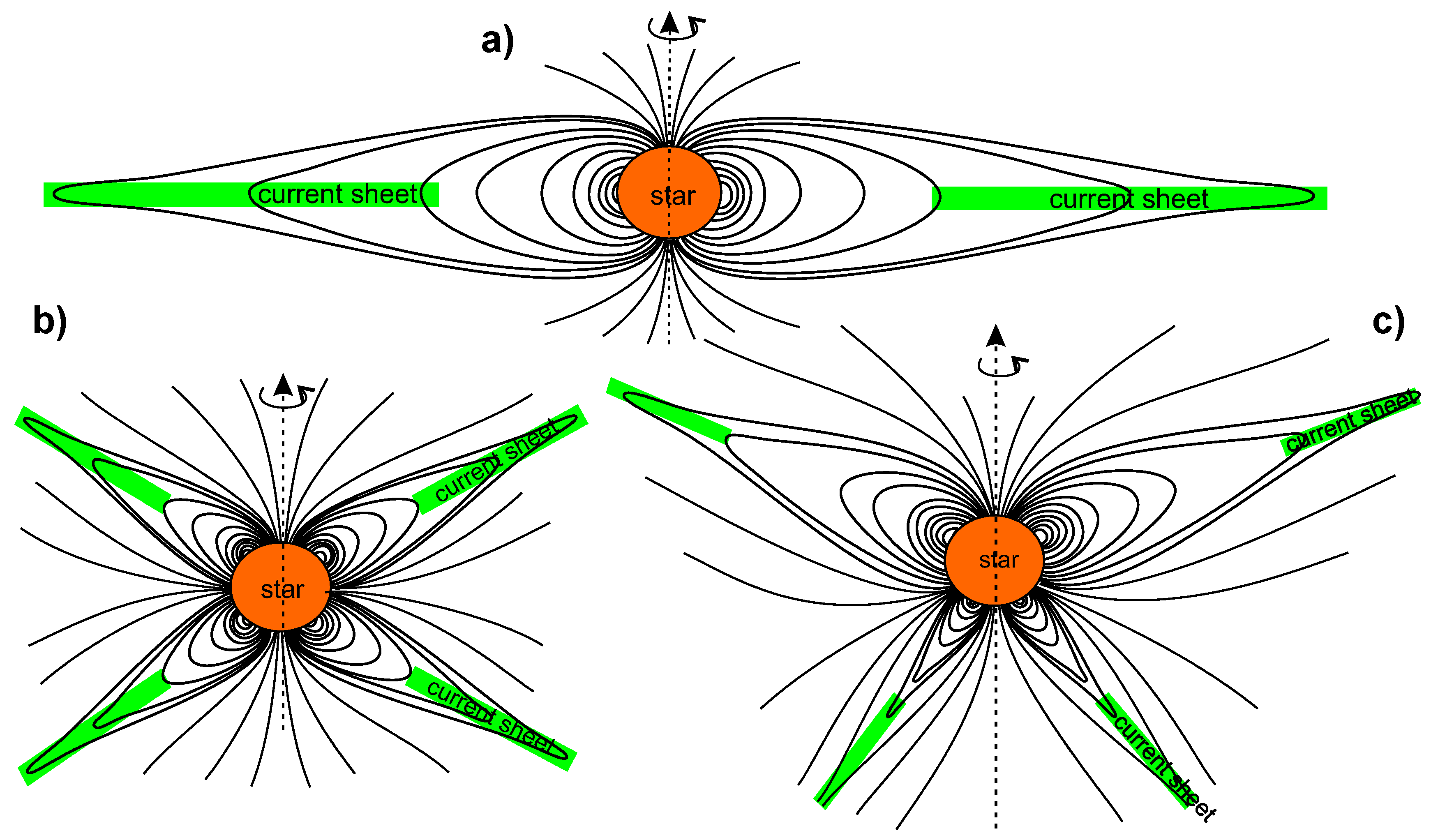
Concerning the consequences of dynamo symmetry for the formation of the astrosphere structure (by analogy with the heliosphere we name such region around the star where both magnetic field and plasma environment of the star dominate), one can highlight two problems of internal and external factors, i.e., (1) dynamo processes in the interiors of stars and planets and their influence on the shape of the magnetic field of celestial bodies in the surrounding space and (2) the mutual influence of magneto-plasma shells of stars and planets, leading to the formation of sufficiently stable structures as astrospheres, magnetospheres, and large-scale current systems. The large magneto-plasma structures in the surrounding of the star depend generally on its magnetic field shape, plasma density, temperature, rotation speed, tilt of the magnetic axis to the rotation, and other factors. The stars dynamo processes can indirectly lead to the formation of a system of currents sheets with characteristic scales comparable with the whole astrosphere, analogous to the heliospheric current sheet in the heliosphere. This system of currents is important for the transport of ionized matter of the star and for the interaction of the stellar environment with exoplanets. Due to the interior dynamo processes in the interiors of stars are practically inaccessible for observations we might suppose that these large-scale current systems in astrospheres, if they can be observed and estimated, can be the good indicators of the stars magnetic configurations.

Large-scale currents in the astrosphere, as in the heliosphere, are supposed to be the extension of neutral lines in the stars corona separating regions with oppositely directed magnetic fluxes [62,63,64]. In the solar system, during the period of minimum solar activity (i.e., the predominance of the dipole heliomagnetic field), a disk-like heliospheric current sheet is formed in the near-equatorial region of the heliosphere. During the periods of maximum of solar activity when the quadrupole field dominates two quasi-stationary conical current sheets can be formed at high latitudes as the continuation of neutral lines of quadrupole [26,31]. Figure 2 illustrates the structure of possible large-scale currents in the astrosphere for different stars, including the Sun, with the dipole magnetic configuration (Figure 2a) and axisymmetric quadrupole field (Figure 2b). Figure 2c shows the corresponding configuration of currents in a mixed dipole-quadrupole configuration, which is characterized by the asymmetry of the magnetic field and current sheets localizations in the Northern and Southern hemispheres (see also Figure 1c with the basic magnetic configuration).

Here one can mention the remote measurements in the heliosphere of the Lyman-$\alpha$ radiation scattered on interstellar hydrogen atoms that can be the useful tool to investigate both hydrogen atom concentration and the mass flux of the solar wind. In [65], the observed by SOHO spacecraft celestial maps of the intensity of scattered Lyman-alpha radiation allowed a reconstruction of the dependence of the solar wind mass flux on heliolatitude. It is shown that during the periods of solar minima, the dependence of solar wind concentration on heliolatitude has a maximum in the Sun’s equatorial region and minima at the poles. However, concentration maxima are clearly seen at mid-latitudes of ± (30–50) during periods of weaker solar activity. These observational data are in good qualitative agreement with the results of MHD modeling [25,26] indicating the formation of two quasi-stationary large-scale conic current and plasma sheets during solar maximum. Figure 2a–c illustrate our view that two current density maxima at high heliolatitudes indicate the dominant quadrupole structure of the Sun’s magnetic field while one current sheet at equatorial region is characteristic for the dipole field.

Let us continue our analogy between characteristic properties of the solar system that can be useful in investigations of exoplanetary systems. It is known that large-scale current sheets as well as a heliospheric current sheet can be formed at the distances beyond the Sun’s Alfven surface (the surface around the Sun where the velocity of accelerating solar wind becomes equal to the Alfven velocity), i.e., they are observed at the distances approximately larger than approximately 10 of the Sun’s radii. If we use the analogy of the Sun and host star with closely moving hot Jupiters (their usual separation from the host star is less than about 10 stars radii [7]), one can expect that hot Jupiters should move in the regions of subsonic plasma flows and do not cross surfaces of large-scale current sheet. In other words, the shape of the average stars magnetic field seen from the hot Jupiters should be dipole or quadrupole-like as it is presented in Figure 1a–c. Due to close orbiting hot Jupiters as well as Mercury in the solar system, might strongly depend on magneto-plasma structures in the stars corona and non-stationary processes in them. In addition, their magnetic field, if they have for example a dipole shape, should be like that of Ganymede (the largest Galilean satellite of Jupiter), having its own magnetosphere and rotating in the subsonic magneto-plasma environment [66]. Thus the Ganymede’s magnetosphere can be reconnected with the high-latitude of Jupiter’s magnetic field, which can result in noticeable auroral emissions in polar regions. The similar effects, but more pronounced, should be expected in the systems hot Jupiters–host stars [67].

During their motion, the exoplanets located at larger distances (e.g., the most common type of multiple planets system in the Galaxy having masses between 1 and 20 Earth masses are orbiting within 0.5–1 AU [2]) from their host stars like solar system should probably cross the current sheets of the astrosphere. Therefore during their rotation in the gravitational field of the star, their magnetospheres can be perturbed due to the influence of both the plasma and magnetic environment of the star. In [68,69], the characteristic shape of exoplanetary magnetosphere streamlined by star wind flow are considered with magnetopause, magnetosheath, and magnetotail. In such conditions, we expect similar processes of magnetospheric perturbation as magnetic storms and substorms (e.g., [6]). Like the Earth, the processes of atmospheric escape from exoplanets should be considered, taking into account the form of planetary magnetic fields. The differences of atmospheric escape in the quadrupole and dipole magnetic fields are considered, particularly, in [70].

7. Conclusions and Discussion

Let us summarize magnetic field configurations that appear relevant for exoplanet studies. The main message here is that the same dynamo mechanism based on differential rotation and mirror asymmetric convective flows, which generates oscillating dipole solar magnetic field and quasi-stationary Earth’s dipole with chaotic inversions in geological time scales can, for relative moderate modifications of dynamo drivers, excite magnetic configurations with substantially different symmetry. Thus, both the exoplanet and host star may have a dipole/quadrupole magnetic configuration as well as mixed parity magnetic fields.

We stress again that dynamo models which generate magnetic field with quadrupole symmetry in a spherical shell exactly symmetric in respect to the equator is just the same as that one producing magnetic field with dipole symmetry. The evolution of eigenmodes with quadrupole symmetry is independent from the evolution of dipole modes. The difference in the corresponding growth rate is very moderate. A moderate variation of dynamo governing parameters is sufficient to make the growth rate for the quadrupole mode larger then that one for the dipole mode. For a spherical shell, which is approximately symmetric only, a growing almost quadrupole mode obtains an admixture of the mode of dipole symmetry and vice versa, however the basic shape of solution remains similar to that one for an exactly symmetric shell. Symmetry in respect to the equator may be violated by a magnetic field than a mixed parity solution arises. This option is expected however to be quite rare.

Dynamo can be driven by mirror asymmetry only (${\alpha }^2$-dynamo). It can happen in bodies with a rotation law extremely close to the solid body one. It is difficult to expect that this kind of dynamo happens very often. ${\alpha }^2$-dynamo demonstrates much less pronounced symmetries in respect to the equator rather than the $\alpha \omega$-dynamo.

A variety of dynamo configurations excited by $\alpha \omega$-dynamo means that observing exoplanetary magnetic configurations we learn more about corresponding magnetospheres rather than about hydrodynamics of planetary interiors. In contrast, if future observations will demonstrate that dipole magnetic configuration dominate in most cases and no quadrupole ones exist it will be a message that something basically is wrong in our understanding of dynamo and/or hydrodynamics of stellar and planetary interiors.

Future observations of exoplanets and/or host stars with mixed parity solutions would be interesting as confirmation of our current understanding of dynamo nonlinear saturation and instructive concerning the possibility to get one more solar mixed parity configuration in the visible future.

Magnetic fields substantially more intensive than ones obtained based on a comparison with solar and Earth’s experiences are possible. Configurations with a significantly more pronounced polar field rather at the Sun are admissible.

Additionally, magnetic dipole highly inclined to the rotation axis may occur for exoplanets as well as for host stars.

Of course, a further understanding of physical properties of exoplanets and/or host stars may remove some of the above options from the list of possible magnetic configurations or require further development.