Computational Costs of Multi-Frontal Direct Solvers with Analysis-Suitable T-Splines
Abstract
1. Introduction
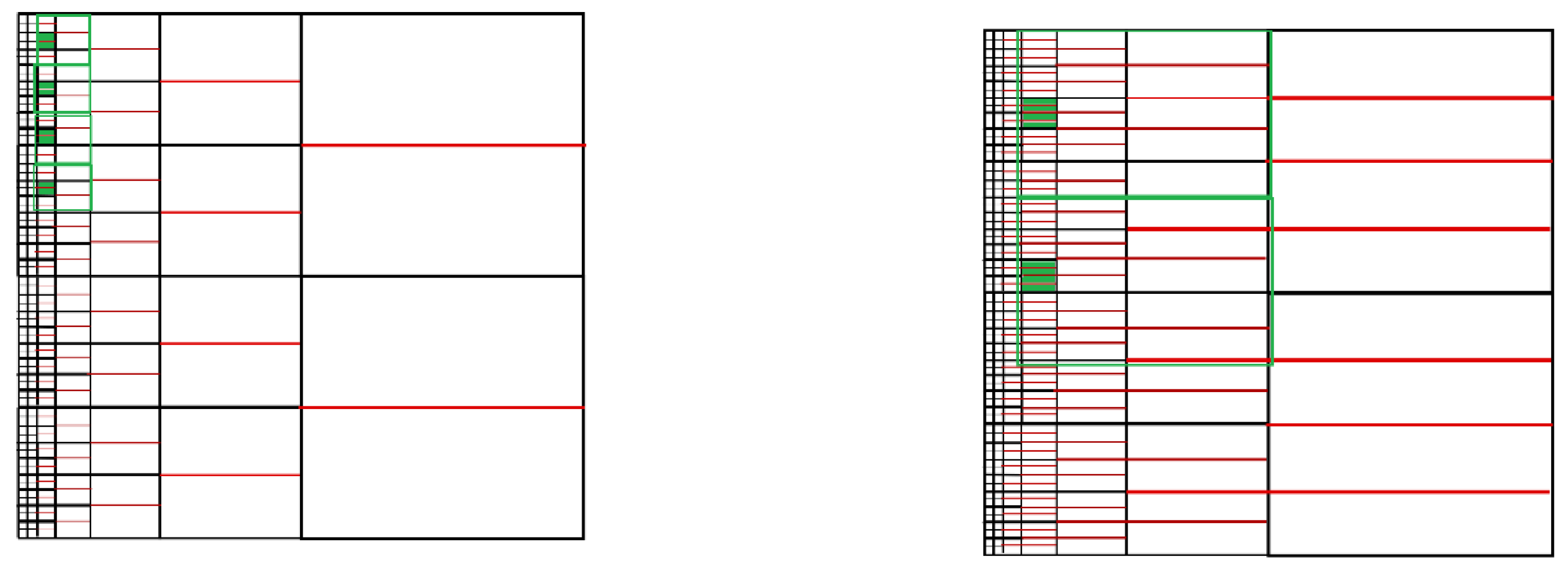
- 1,2,6,7, which can be performed on a local sub-matrix of the global sparse matrix, called the frontal matrix. These rows represent B-splines that overlap with B-splines 3,8,11,12, and 13. Thus, this frontal matrix has a size of nine (with rows 1,2,6,7,3,8,11,12, and 13), and this step eliminates four rows (1,2,6, and 7).
- 4,5,9,10, which can be performed on another frontal matrix, and these B-splines overlap with 3,8,13,14, and 15. This frontal matrix has a size of nine (with rows 4,5,9,10,3,8,13,14, and 15), and this step eliminates four rows (4,5,9, and 10).
- 16,17,21,22 (the third frontal matrix); they overlap with 18, 23, and 11,12, and 13. This frontal matrix has, again, a size of nine (with rows 16,17,21,22,18,23,11,12, and 13), and this step eliminates four rows (16,17,21, and 22).
- 19,20,24,25 (the fourth frontal matrix); they overlap with 18,23,13,14, and 15. This frontal matrix, as with the previous ones, has a size of nine (with rows 19,20,24,25,18,23,13,14, and 15), and this step eliminates four rows (19,20,24, and 25).
- Merge the first and the second frontal matrices into a fifth frontal matrix, and eliminate rows 3 and 8. This time, the frontal matrix has a size of seven (it contains rows 3,8,11,12,13,14, and 15) and this step eliminates two rows (3 and 8).
- Merge the third and fourth frontal matrices into a sixth frontal matrix and eliminate rows 18 and 23. This time, the frontal matrix has a size of seven (it contains rows 18,23,11,12,13,14, and 15) and this step eliminates two rows (18 and 23).
- Merge the fifth and the sixth frontal matrices and eliminate all the rows. This frontal matrix has a size of five (it contains rows 11,12,13,14, and 15) and this step eliminates all the rows.
2. Motivation
3. Uniform Mesh
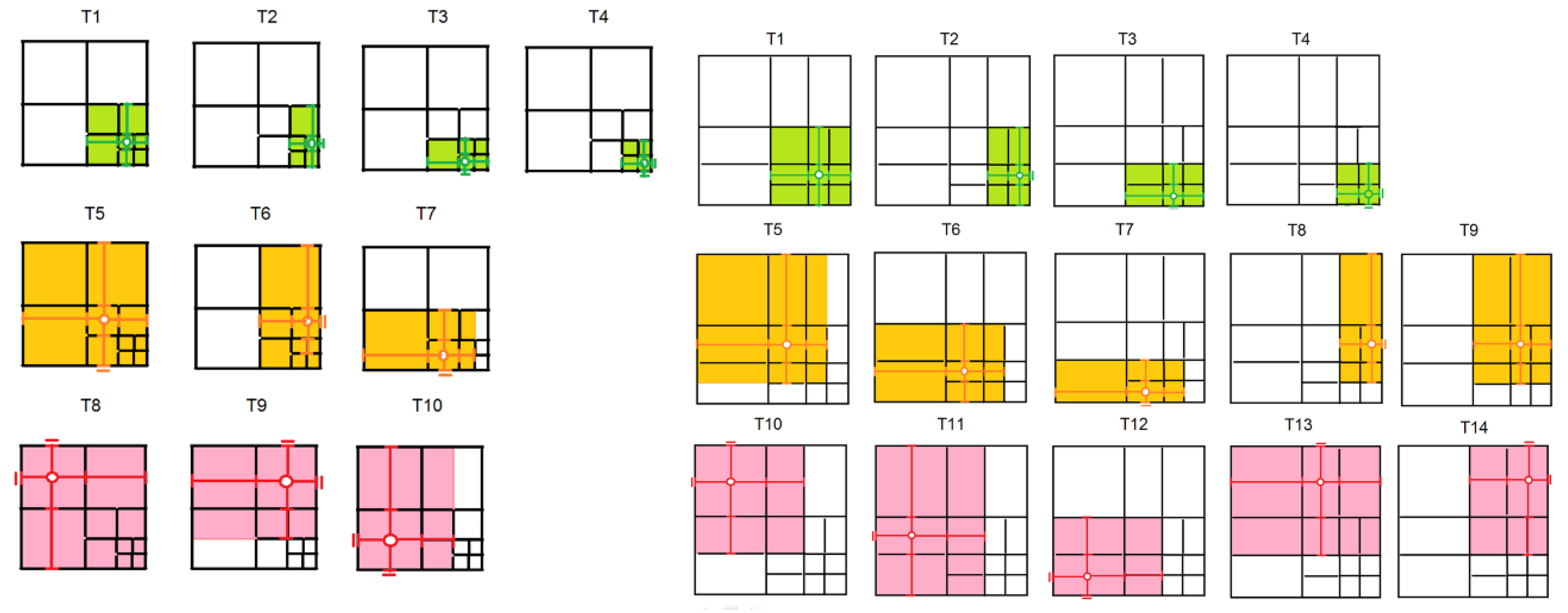
4. Refined Meshes with T-Spline Basis Functions
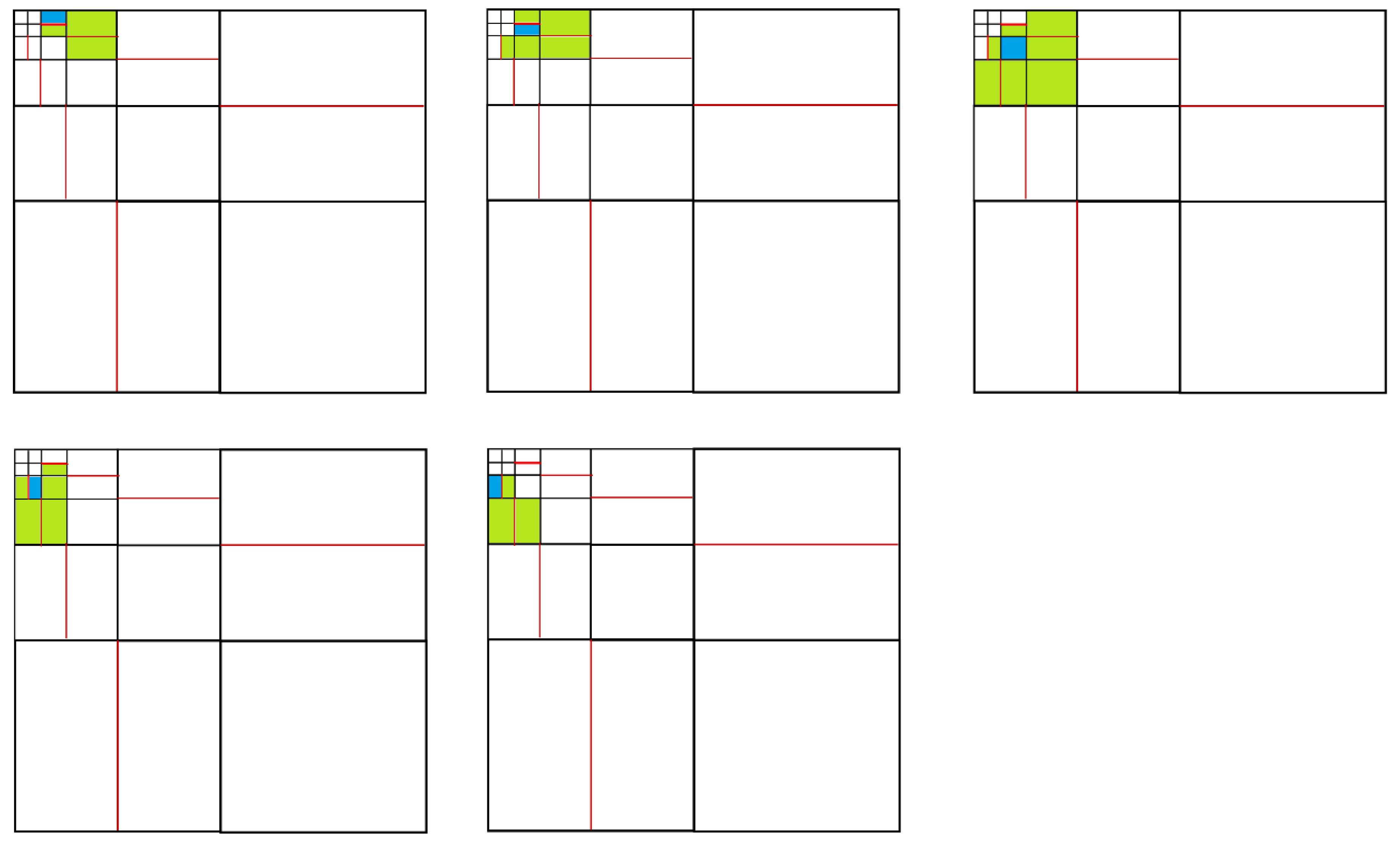
4.1. Mesh with Point Singularity
4.2. Mesh with Edge Singularity
5. Refined Meshes with Analysis Suitable T-Splines
5.1. Mesh with Point Singularity
5.2. Mesh with Edge Singularity
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cottrell, A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric Analysis: Toward Unification of CAD and FEA; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Bazilevs, Y.; Calo, V.M.; Cottrell, J.A.; Evans, J.A.; Lipton, S.; Scott, M.A.; Sederberg, T.W. Isogeometric analysis using T-splines. Comput. Methods Appl. Mech. Eng. 2010, 199, 229–263. [Google Scholar] [CrossRef]
- Bornemann, P.B.; Cirak, F. A subdivision-based implementation of the hierarchical B-spline finite element method. Comput. Methods Appl. Mech. Eng. 2013, 253, 584–598. [Google Scholar] [CrossRef]
- Giannelli, C.; Juttler, B.; Speleers, H. THB-splines: The truncated basis for hierarchical splines. Comput. Aided Geom. Des. 2012, 29, 485–498. [Google Scholar] [CrossRef]
- Dokken, T.; Lyche, T.; Pettersen, K. Polynomial splines over locally refined box-partitions. Comput. Aided Geom. Des. 2013, 30, 331–356. [Google Scholar] [CrossRef]
- Johannessen, K.; Kvamsdal, T.; Dokken, T. Isogeometric analysis using LR B-splines. Comput. Methods Appl. Mech. Eng. 2014, 269, 471–514. [Google Scholar] [CrossRef]
- Burkhart, D.; Hamann, B.; Umlauf, G. Iso-geometric Finite Element Analysis Based on Catmull-Clark: Subdivision Solids. Comput. Graph. Forum 2010, 29, 1575–1584. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Y.; Hughes, T.J.R.; Scott, M. Truncated hierarchical Catmull-Clark subdivision with local refinement. Comput. Methods Appl. Mech. Eng. 2015, 291, 1–20. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Y.; Hughes, T.J.R.; Scott, M. Extended Truncated hierarchical Catmull-Clark subdivision with local refinement. Comput. Methods Appl. Mech. Eng. 2016, 299, 316–336. [Google Scholar] [CrossRef]
- Li, X.; Wei, X.; Zhang, Z. Hybrid non-uniform recursive subdivision with improved convergence rates. Comput. Methods Appl. Mech. Eng. 2019, 352, 606–624. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Duff, I.S. Multifrontal parallel distributed symmetric and unsymmetric solvers. Comput. Methods Appl. Mech. Eng. 2000, 184, 501–520. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Duff, I.S.; Koster, J.; L’Excellent, J.-L. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Appl. 2001, 1, 15–41. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Guermouche, A.; L’Excellent, J.-Y.; Pralet, S. Hybrid scheduling for the parallel solution of linear systems. Comput. Methods Appl. Mech. Eng. 2001, 2, 136–156. [Google Scholar] [CrossRef]
- Collier, N.; Pardo, D.; Dalcin, L.; Paszyński, M.; Calo, V.M. The cost of continuity: A study on performance of isogeometric finite elements using direct solvers. Comput. Methods Appl. Mech. Eng. 2012, 213–216, 353–361. [Google Scholar] [CrossRef]
- Paszyński, M.; Pardo, D.; Calo, V.M. Direct solvers performance on h-adapted grids. Comput. Math. Appl. 2015, 70, 282–295. [Google Scholar] [CrossRef]
- Garcia, D.; Pardo, D.; Dalcin, L.; Paszyński, M.; Collier, N.; Calo, V.M. The value of continuity: Refined isogeometric analysis and fast direct solvers. Comput. Methods Appl. Mech. Eng. 2017, 316, 586–605. [Google Scholar] [CrossRef]
- Heggernes, P.; Eisenstat, S.C.; Kumfert, G.; Pothen, A. The Computational Complexity of the Minimum Degree Algorithm; ICASE Report No. 2001–42; Institute for Computer Applications in Science and Engineering: Hampton, VA, USA, 2001. [Google Scholar]
- Schulze, J. Toward a tighter coupling of bottom-up and top-down sparse matrix ordering methods. BIT 2001, 41, 800. [Google Scholar] [CrossRef]
- Karypis, G.; Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1998, 20, 359–392. [Google Scholar] [CrossRef]
- Liu, J.W.H. The multifrontal method for sparse matrix solution: Theory and practice. SIAM Rev. 1992, 34, 82–109. [Google Scholar] [CrossRef]
- Paszyńska, A.; Paszyński, M.; Jopek, K.; Woźniak, M.; Goik, D.; Gurgul, P.; AbouEisha, H.; Moshkov, M.; Calo, V.M.; Lenharth, A.; et al. Quasi-optimal elimination trees for 2D grids with singularities. Sci. Program. 2015, 2015, 303024. [Google Scholar] [CrossRef]
- Paszyńska, A. Volume and neighbors algorithm for finding elimination trees for three dimensional h-adaptive grds. Comput. Math. Appl. 2014, 68, 1467–1478. [Google Scholar] [CrossRef]
- AbouEisha, H.; Moshkov, M.; Calo, V.; Paszynski, M.; Goik, D.; Jopek, K. Dynamic programming algorithm for generation of optimal elimination trees for multi-frontal direct solver over h-refined grids. Procedia Comput. Sci. 2014, 29, 947–959. [Google Scholar] [CrossRef]
- AbouEisha, H.; Calo, V.M.; Jopek, K.; Moshkov, M.; Paszyńska, A.; Skotniczny, M. Element partition trees for h-refined meshes to optimize direct solver performance. Part 1, Dynamic programming. Int. J. Appl. Math. Comput. Sci. 2017, 27, 351–365. [Google Scholar] [CrossRef]
- Balay, S.; Abhyankar, S.; Adams, M.F.; Brown, J.; Brune, P.; Buschelman, K.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; et al. PETSc Web Page. 2014. Available online: http://www.mcs.anl.gov/petsc (accessed on 12 October 2020).
- Blackford, L.S.; Choi, J.; Cleary, A.; D’Azevedo, E.; Demmel, J.; Dhillon, I.; Dongarra, J.; Hammarling, S.; Henry, S.; Petitet, A.; et al. ScaLAPACK Users’ Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Hnon, P.; Ramet, P.; Roman, J. PaStiX: A High-Performance Parallel Direct Solver for Sparse Symmetric Definite Systems. Parallel Comput. 2002, 28, 301–321. [Google Scholar] [CrossRef]
- Li Xiaoye, S. An Overview of SuperLU: Algorithms, Implementation, and User Interface. Trans. Math. Softw. 2005, 31, 302–325. [Google Scholar]
- Gurgul, P. A Linear Complexity Direct Solver for H-adaptive Grids with Point Singularities. Procedia Comput. Sci. 2014, 29, 1090–1099. [Google Scholar] [CrossRef][Green Version]
- Da Veiga, L.B.; Buffa, A.; Sangalli, G.; Vazquez, R. Analysis-suitable T-splines of arbitrary degree: Definition and properties. Math. Models Methods Appl. Sci. 2013, 23, 1979–2003. [Google Scholar] [CrossRef]
- Calo, V.M.; Collier, N.; Pardo, D.; Paszyński, M. Computational complexity and memory usage for multi-frontal direct solvers used in p finite element analysis. Procedia Comput. Sci. 2011, 4, 1854–1861. [Google Scholar] [CrossRef]
- Skotniczny, M. Computational Complexity of Hierarchically Adapted Meshes. In Computational Science—ICCS 2020, Proceedings of the 20th International Conference, Amsterdam, The Netherlands, 3–5 June 2020; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12139, pp. 226–239. [Google Scholar]
- Gomez, H.; Calo, V.M.; Bazilevs, Y.; Hughes, T.J.R. Isogeometric analysis of the Cahn-Hilliard phase-field model. Comput. Methods Appl. Mech. Eng. 2008, 197, 4333–4352. [Google Scholar] [CrossRef]
- Gomez, H.; Hughes, T.J.R.; Nogueira, X.; Calo, V.M. Isogeometric analysis of the isothermal Navier-Stokes-Korteweg equations. Comput. Methods Appl. Mech. Eng. 2010, 199, 1828–1840. [Google Scholar] [CrossRef]
- Hsu, M.-C.; Akkerman, I.; Bazilevs, Y. High-performance computing of wind turbine aerodynamics using isogeometric analysis. Comput. Fluids 2011, 49, 93–100. [Google Scholar] [CrossRef]
- Duddu, R.; Lavier, L.; Hughes, T.J.R.; Calo, V.M. A finite strain Eulerian formulation for compressible and nearly incompressible hyper-elasticity using high-order NURBS elements. Int. J. Numer. Methods Eng. 2012, 89, 762–785. [Google Scholar] [CrossRef]
- Calo, V.M.; Brasher, N.; Bazilevs, Y.; Hughes, T.J.R. Multiphysics Model for Blood Flow and Drug Transport with Application to Patient-Specific Coronary Artery Flow. Comput. Mech. 2008, 43, 161–177. [Google Scholar] [CrossRef]
































Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paszyńska, A.; Paszyński, M. Computational Costs of Multi-Frontal Direct Solvers with Analysis-Suitable T-Splines. Symmetry 2020, 12, 2070. https://doi.org/10.3390/sym12122070
Paszyńska A, Paszyński M. Computational Costs of Multi-Frontal Direct Solvers with Analysis-Suitable T-Splines. Symmetry. 2020; 12(12):2070. https://doi.org/10.3390/sym12122070
Chicago/Turabian StylePaszyńska, Anna, and Maciej Paszyński. 2020. "Computational Costs of Multi-Frontal Direct Solvers with Analysis-Suitable T-Splines" Symmetry 12, no. 12: 2070. https://doi.org/10.3390/sym12122070
APA StylePaszyńska, A., & Paszyński, M. (2020). Computational Costs of Multi-Frontal Direct Solvers with Analysis-Suitable T-Splines. Symmetry, 12(12), 2070. https://doi.org/10.3390/sym12122070



