Topological Structures via Interval-Valued Neutrosophic Crisp Sets

Abstract

In this paper, we introduce the new notion of interval-valued neutrosophic crisp sets providing a tool for approximating undefinable or complex concepts in real world. First, we deal with some of its algebraic structures. We also define an interval-valued neutrosophic crisp (vanishing) point and obtain some of its properties. Next, we define an interval-valued neutrosophic crisp topology, base (subbase), neighborhood, and interior (closure), respectively and investigate some of each property, and give some examples. Finally, we define an interval-valued neutrosophic crisp continuity and quotient topology and study some of each property.

1. Introduction

Numerous mathematicians have been trying to find a mathematical expression of the complexation and uncertainty in real world for a long time. For example, Zadeh [1] defined a fuzzy set as a generalization of a classical set in 1965. Zadeh [2] (1975), Pawlak [3] (1982), Atanassov [4] (1983), Atanassov and Gargov [5] (1989), Gau and Buchrer [6] (1993), Smarandache [7] (1998), Molodtsov [8] (1999), Lee [9], Torra [10], Jun et al. [11] (2012), and Lee et al. [12] (2020) introduced the concept of interval-valued fuzzy sets, rough sets, intuitionistic fuzzy sets, interval-valued intuitionistic fuzzy sets, vague sets, neutrosophic sets, soft sets, bipolar fuzzy sets, hessitant fuzzy sets, cubic sets combined by interval-valued fuzzy sets and fuzzy sets, and octahedron sets combined by interval-valued fuzzy sets, intuitionistic fuzzy sets, and fuzzy sets, in turn, in order to solve various complex and uncertain problems.

In 1996, cCoker [13] proposed the concept of an intuitionistic set as the generalization of a classical set and the special case of an intuionistic fuzzy set and he studied topological structures based on intuitionistic sets in [14]. Kim et al. [15] dealt with categorical structures based on intuitionistic sets. They also obtained further properties of intuionistic topology in [16]. In 2014, Salama et al. [17] defined neutrosophic crisp sets as the generalization of classical sets and the special case of neutrosophic sets proposed by Smarandache [7,18,19], and studied some of its properties. Moreover, they dealt with topological structures based on the neutrosophic crisp sets in [17]. Hur et al. [20] investigated categorical structures via neutrosophic crisp sets. Many researchers [21,22,23,24,25,26,27,28,29] have discussed topological structures via neutrosophic crisp sets. Recently, Kim et al. [30] introduced the concept of an interval-valued set as the generalization of a classical set and the specialization of an interval-valued fuzzy set, and applied it to topological structures.

This paper considers two perspectives. First, we define the interval-valued neutrosophic crisp set, a new concept that combines the interval-valued set and neutrosophic crisp set. As an example, suppose a country conducts a poll during an election that determines the highest head of administration. At this time, the preference for Candidate A is divided into three groups: Favor, neutral, and rejection among its citizens from the viewpoint of neutrosophic crisp set, but the minimum and maximum for each of a favor, neutral, and rejection from the viewpoint of interval-valued neutrosophic crisp set. The group is considered. Then, it is believed that the results of the poll by the new concept are more accurate than those by the neutrosophic crisp set. Thus, this new concept is needed. Second, since the topology can be applied to high dimensional data sets, big data, and computational evaluations (see [31,32,33], respectively), we study topological structures based on interval-valued neutrosophic crisp sets. In order to accomplish such research, first, we recall some definitions related to intuitionistic sets, interval-valued sets, and neutrosophic crisp sets. Secondly, we introduce the new concept of interval-valued neutrosophic crisp set and obtain some of its algebraic structures, and give some examples. We also define interval-valued neutrosophic crisp points of two types and discuss the characterizations of the inclusion, equality, intersection, and union of interval-valued neutrosophic crisp sets. Thirdly, we define an interval-valued neutrosophic crisp topology, an interval-valued neutrosophic crisp base and subbase, and study some of their properties. Fourthly, we introduce the concepts of interval-valued neutrosophic crisp neighborhoods of two types and find some of their properties. In particular, we prove that there is an IVNCT under the hypothesis satisfying some properties of interval-valued neutrosophic crisp neighborhoods. Moreover, we define an interval-valued neutrosophic crisp interior and closure and deal with some of their properties. In particular, we show that there is a unique IVNCT for interval-valued neutrosophic crisp interior [resp. closure] operators. Finally, we introduce the concepts of interval-valued neutrosophic crisp continuous [resp. open and closed] mappings and quotient topologies and obtain some of their properties.

Throughout this paper, we assume that $X,Y$ are non-empty sets, unless otherwise stated.

2. Preliminaries

In this section, we recall the concept of an intuitionistic set proposed in [13]. We also recall some concepts and results introduced and studied in [30,34,35], respectively.

Definition 1

([13]). The form $A=(A^{\in },A^{\notin })$ such that $A^{\in },A^{\notin }\subset X$, and $A^{\in }\cap A^{\notin }=\mathsf{\varnothing }$ is called an intuitionistic set (briefly, IS) of X, where $A^{\in }$ [resp. $A^{\notin }$] represents the set of memberships [resp. non-memberships] of elements of X to A. In fact, $A^{\in }$ [resp. $A^{\notin }$] is a subset of X agreeing or approving [resp. refusing or opposing] for a certain opinion, suggestion, or policy.

The intuitionistic empty set [resp. the intuitionistic whole set] of X, denoted by $\overline{\mathsf{\varnothing }}$ [resp. $\overline{\mathrm{X}}$], is defined by $\overline{\mathsf{\varnothing }}=(\mathsf{\varnothing },X)$ [resp. $\overline{X}=(X,\mathsf{\varnothing })$]. The set of all ISs of X will be denoted by $IS\left(X\right)$. It is also clear that for each $A\in IS\left(X\right)$, ${\chi }_A=({\chi }_{A^{\in }},{\chi }_{A^{\notin }})$ is an intuitionistic fuzzy set in X proposed by Atanassov [4]. Thus we can consider the intuitionistic set A in X as an intuitionistic fuzzy set in X.

Furthermore, we can easily check that for each $A\in IS\left(X\right)$, $A^{\in }\cup A^{\notin }\ne X$ (in fact, ${A^{\in }}^c\cap {A^{\notin }}^c\ne \mathsf{\varnothing }$) in general (see Example 1) but if $A^{\in }\cup A^{\notin }=X$, then ${A^{\in }}^c\cap {A^{\notin }}^c=\mathsf{\varnothing }$. We denote the family $\{A\in IS\left(X\right):A^{\in }\cup A^{\notin }=X\}$ as $I{S}^{*}\left(X\right)$.

Example 1.

Let $X=\{a,b,c,d,e\}$ be a set and consider the IS A in X given by:

$$A=\left(\right\{a,b,c\},\{d\left\}\right).$$

Then clearly, $A^{\in }\cup A^{\notin }\ne X$. In fact, ${A^{\in }}^c\cap {A^{\notin }}^c\ne \mathsf{\varnothing }$.

For the inclusion, equality, union, and intersection of intuitionistic sets, and the complement of an intuitionistic set, the operations $\left[\right]$ and $<>$ on $IS\left(X\right)$, refer to [13].

Definition 2

([34,36]). The form $A=〈A^T,A^I,A^F〉$ such that $A^T,A^I,A^F\subset X$ is called a neutrosophic crisp set (briefly, NCS) in X, where $A^T$, $A^I$, and $A^F$ represent the set of memberships, indeterminacies, and non-memberships respectively of elements of X to A.

We consider neutrosophic crisp empty [resp. whole] sets of two types in X, denoted by ${\mathsf{\varnothing }}_{1,N},{\mathsf{\varnothing }}_{2,N}$ [resp. $X_{1,N},X_{2,N}$] and defined by (see Remark 1.1.1 in [34]):

$${\mathsf{\varnothing }}_{1,N}=〈\mathsf{\varnothing },\mathsf{\varnothing },X〉,{\mathsf{\varnothing }}_{2,N}=〈\mathsf{\varnothing },X,X〉[resp.X_{1,N}=〈X,X,\mathsf{\varnothing }〉,X_{2,N}=〈X,\mathsf{\varnothing },\mathsf{\varnothing }〉].$$

We will denote the set of all NCSs in X denoted by $NC\left(X\right).$

It is obvious that $A=〈A,\mathsf{\varnothing },A^c〉\in NC\left(X\right)$ for each ordinary subset A of X. Then we can consider an NCS in X as the generalization of an ordinary subset of X. It is also clear that $A=〈A^{\in },\mathsf{\varnothing },A^{\notin }〉$ is an NCS in X for each $A\in IS\left(X\right)$. Thus an NCS in X can be considered as the generalization of an intuitionistic set in X. Furthermore, we can easily see that for each $A\in N\left(X\right)$,

$${\chi }_A=〈{\chi }_{A^T},{\chi }_{A^I},{\chi }_{A^F}〉$$

is a neutrosophic set in X introduced by Salama and Smarandache [7,18,19]. So an NCS is a special case of a neutrosophic set.

Definition 3

([34]). Let $A\in NC\left(X\right)$. Then the complement of A, denoted by $A^{i,c}$ ($i=1,2$) and defined by:

$$A^{1,c}=〈A^F,{A^I}^c,A^T〉,A^{2,c}=〈A^F,A^I,A^T〉.$$

Definition 4

([34]). Let $A,B\in NC\left(X\right)$. Then A is said to be:

(i) 

A 1-type subset of B, denoted by $A{\subset }_{1}B$, if it satisfies the following conditions:

$$A^T\subset B^T,A^I\subset B^I,A^F\supset B^F,$$

(ii) 

A 2-type subset of B, denoted by $A{\subset }_{2}B$, if it satisfies the following conditions:

$$A^T\subset B^T,A^I\supset B^I,A^F\supset B^F.$$

Definition 5

([34]). Let $A,B\in NC\left(X\right)$.

(i) 

The i-intersection of A and B, denoted by $A{\cap }^{i}B$ ($i=1,2$) and defined by:

$$A{\cap }^{1}B=〈A^T\cap B^T,A^I\cap B^I,A^F\cup B^F〉,A{\cap }^{2}B=〈A^T\cap B^T,A^I\cup B^I,A^F\cup B^F〉.$$

(ii) 

The i-union of A and B, denoted by $A{\cup }^{i}B$ ($i=1,2$) and defined by:

$$A{\cup }^{1}B=〈A^T\cup B^T,A^I\cup B^I,A^F\cap B^F〉,A{\cup }^{2}B=〈A^T\cup B^T,A^I\cap B^I,A^F\cap B^F〉.$$

(iii) 

$\left[\right]A=〈A^T,A^I,{A^T}^c〉,〈〉A=〈{A^F}^c,A^I,A^F〉.$

The followings are immediate results of Definitions 3, 4, and 5.

Proposition 1

(See Proposition 3.3 in [20] and also compare it with Proposition 3.5 in [15]). Let $A,B,C\in NC\left(X\right)$ and let $i=1,2$. Then we have:

(1) 

(See Proposition 1.1.1 in [34]) ${\mathsf{\varnothing }}_{i,N}{\subset }_{i}A{\subset }_i{X}_{i,N}$,

(2) 

If $A{\subset }_{i}B$ and $B{\subset }_{i}C$, then $A{\subset }_{i}C$,

(3) 

$A{\cap }^{i}B{\subset }_{i}A$ and $A{\cap }^{i}B{\subset }_{i}B$,

(4) 

$A{\subset }_{i}A{\cup }^{i}B$ and $B{\subset }_{i}A{\cup }^{i}B$,

(5) 

$A{\subset }_{i}B$ if and only if $A{\cap }^{i}B=A$,

(6) 

$A{\subset }_{i}B$ if and only if $A{\cup }^{i}B=B$.

Proposition 2

(See Proposition 3.4 in [20] and also compare it with Proposition 3.6 in [15]). Let $A,B,C\in NC\left(X\right)$ and let $i=1,2$. Then we have:

(1) 

(Idempotent laws): $A{\cup }^{i}A=A$, $A{\cap }^{i}A=A$,

(2) 

(Commutative laws): $A{\cup }^{i}B=B{\cup }^{i}A$, $A{\cap }^{i}B=B{\cap }^{i}A$,

(3) 

(Associative laws): $A{\cup }^i\left(B{\cup }^{i}C\right)=\left(A{\cup }^{i}B\right){\cup }^{i}C$, $A{\cap }^i\left(B{\cap }^{i}C\right)=\left(A{\cap }^{i}B\right){\cap }^{i}C$,

(4) 

(Distributive laws): $A{\cup }^i\left(B{\cap }^{i}C\right)=\left(A{\cup }^{i}B\right){\cap }^i\left(A{\cup }^{i}C\right)$,

$A{\cap }^i\left(B{\cup }^{i}C\right)=\left(A{\cap }^{i}B\right){\cup }^i\left(A{\cap }^{i}C\right)$,

(5) 

(Absorption laws): $A{\cup }^i\left(A{\cap }^{i}B\right)=A$, $A{\cap }^i\left(A{\cup }^{i}B\right)=A$,

(6) 

(DeMorgan’s laws):${\left(A{\cup }^{1}B\right)}^{1,c}=A^{1,c}{\cap }^1{B}^{1,c}$, ${\left(A{\cup }^{1}B\right)}^{2,c}=A^{2,c}{\cap }^2{B}^{2,c}$,

${\left(A{\cup }^{2}B\right)}^{1,c}=A^{1,c}{\cap }^2{B}^{1,c}$, ${\left(A{\cup }^{2}B\right)}^{2,c}=A^{2,c}{\cap }^1{B}^{2,c}$,

${\left(A{\cap }^{1}B\right)}^{1,c}=A^{1,c}{\cup }^1{B}^{1,c}$, ${\left(A{\cap }^{1}B\right)}^{2,c}=A^{2,c}{\cup }^2{B}^{2,c}$,

${\left(A{\cap }^{2}B\right)}^{1,c}=A^{1,c}{\cup }^2{B}^{1,c}$, ${\left(A{\cap }^{2}B\right)}^{2,c}=A^{2,c}{\cup }^1{B}^{2,c}$,

(7) 

${\left(A^{i,c}\right)}^{i,c}=A$,

(8) (8a)

$A{\cup }^i{\mathsf{\varnothing }}_{i,N}=A$, $A{\cap }^i{\mathsf{\varnothing }}_{i,N}={\mathsf{\varnothing }}_{i,N}$,

  (8b)

$A{\cup }^i{X}_{i,N}=X_{i,N}$, $A{\cap }^i{X}_{i,N}=A$,

  (8c)

${X_{i,N}}^{i,c}={\mathsf{\varnothing }}_{i,N}$, ${{\mathsf{\varnothing }}_{i,N}}^{i,c}=X_{i,N}$,

  (8d)

$A{\cup }^i{A}^{i,c}\ne {X_{i,N}}^{i,c}$, $A{\cap }^i{A}^{i,c}\ne {\mathsf{\varnothing }}_{i,N},$ in general.

Definition 6

(See [34,37]). Let $a\in X$. Then the form $a_{{}_N}=〈\left\{a\right\},\mathsf{\varnothing },{\left\{a\right\}}^c〉$ [resp. $a_{{}_{NV}}=〈\mathsf{\varnothing },\left\{a\right\},{\left\{a\right\}}^c〉$] is called a neutrisophic crisp [resp. vanishing] point in X.

We denote the set of all neutrisophic crisp points and all neutrisophic crisp vanishing points in X by $N_P\left(X\right)$.

Definition 7

(See [34,37]). Let $a\in X$ and let $A\in NC\left(X\right)$. Then,

(i) 

$a_{{}_N}$ said to belong to A, denoted by $a_{{}_N}\in A$, if $a\in A^T$,

(ii) 

$a_{{}_{NV}}$ said to belong to A, denoted by $a_{{}_{NV}}\in A$, if $a\notin A^F$.

Result 1

([34], Proposition 1.2.6). Let $A\in NC\left(X\right)$. Then,

$$A=A_N{\cup }^1{A}_{NV},$$

where $A_N={\bigcup }_{a_{{}_N}\in A}^1{a}_{{}_N},A_{NV}={\bigcup }_{a_{{}_{NV}}\in A}^1{a}_{NV}.$ In fact, $A_N=〈A^T,\mathsf{\varnothing },{A^T}^c〉$ and $A_{NV}=〈\mathsf{\varnothing },A^I,A^F〉$.

Definition 8

([30,35]). The form $[A^{-},A^{+}]=\{B\subset X:A^{-}\subset B\subset A^{+}\}$ such that $A^{-},A^{+}\subset X$ is called an interval-valued sets (briefly, IVS) in X, where $A^{-}$ [resp. $A^{+}$] represents the set of minimum [resp. maximum] memberships of elements of X to A. In fact, $A^{-}$ [resp. $A^{+}$] is a minimum [resp. maximum] subset of X agreeing or approving for a certain opinion, suggestion, or policy.

$[\mathsf{\varnothing },\mathsf{\varnothing }]$ [resp. $[X,X]$] is called the interval-valued empty [resp. whole] set in X and denoted by $\tilde{\mathsf{\varnothing }}$ [resp. $\tilde{X}$]. The set of all IVSs in X will be denoted by $IVS\left(X\right)$.

For any classical subset A of X, $[A,A]\in IVS\left(X\right)$ is obvious. Then we can consider an IVS in X as the generalization of a classical subset of X. Also, if $A=[A^{-},A^{+}]\in IVS\left(X\right)$, then ${\chi }_{{}_A}=[{\chi }_{{}_{A^{-}}},{\chi }_{{}_{A^{+}}}]$ is an interval-valued fuzzy set in X introduced by Zadeh [2]. Thus an interval-valued fuzzy set can be considered as the generalization of an IVS.

Furthermore, we can easily check that for each $A\in IVS\left(X\right)$, $A^{-}\ne A^{+}$ (in fact, $A^{+}\cap {A^{-}}^c\ne \mathsf{\varnothing }$) in general (see Example 2) but if $A^{-}=A^{+}$, then $A^{+}\cap {A^{-}}^c=\mathsf{\varnothing }$. We denote the family $\{A\in IVS\left(X\right):A^{-}=A^{+}\}$ as $IV{S}^{*}\left(X\right)$.

Example 2.

Let $X=\{a,b,c,d,e\}$ and consider the IVS A in X given by:

$$A=\left[\right\{a,b\},\{a,,b,c\left\}\right].$$

Then we can easily calculate that $A^{-}\ne A^{+}$ and $A^{+}\cap {A^{-}}^c\ne \mathsf{\varnothing }.$

For the inclusion, equality, union, and intersection of intuionistic sets, and the complement of an intuitionistic set refer to [30,35].

3. Interval-Valued Neutrosophic Crisp Sets

In this section, we introduce the concept of an interval-valued neutrosophic crisp set combined by a neutrosophic crisp set and an interval-valued set, and obtain some of its properties.

Definition 9.

The form $〈[A^{T,-},A^{T,+}],[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉$ is called an interval-valued neutrosophic crisp set (briefly, IVNCS) in X, where $[A^{T,-},A^{T,+}],[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]\in IVS\left(X\right)$.

In this case, $[A^{T,-},A^{T,+}]$, $[A^{I,-},A^{I,+}]$, and $[A^{F,-},A^{F,+}]$ represent the IVS of memberships, indeterminacies, and non-memberships respectively of elements of X to A.

In particular, an IVNCS is defined as three types below.

An IVNCS $A=〈[A^{T,-},A^{T,+}],[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉$ in X is said to be of:

(i) 

Type 1, if it satisfies the following conditions:

$$[A^{T,-},A^{T,+}]\cap [A^{I,-},A^{I,+}]=\tilde{\mathsf{\varnothing }},[A^{T,-},A^{T,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }},$$

$$[A^{I,-},A^{I,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }},$$

equivalently, $A^{T,+}\cap A^{I,+}=\mathsf{\varnothing },A^{T,+}\cap A^{F,+}=\mathsf{\varnothing },A^{I,+}\cap A^{F,+}=\mathsf{\varnothing },$

(ii) 

Type 2, if it satisfies the following conditions:

$$[A^{T,-},A^{T,+}]\cap [A^{I,-},A^{I,+}]=\tilde{\mathsf{\varnothing }},[A^{T,-},A^{T,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }},$$

$$[A^{I,-},A^{I,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }},[A^{T,-},A^{T,+}]\cup [A^{I,-},A^{I,+}]\cup [A^{F,-},A^{F,+}]=\tilde{X},$$

equivalently, $A^{T,+}\cap A^{I,+}=\mathsf{\varnothing },A^{T,+}\cap A^{F,+}=\mathsf{\varnothing },A^{I,+}\cap A^{F,+}=\mathsf{\varnothing },$

$A^{T,-}\cup A^{I,-}\cup A^{F,-}=X,$

(iii) 

Type 3, if it satisfies the following conditions:

$$[A^{T,-},A^{T,+}]\cap [A^{I,-},A^{I,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }},$$

$$[A^{T,-},A^{T,+}]\cup [A^{I,-},A^{I,+}]\cup [A^{F,-},A^{F,+}]=\tilde{X},$$

equivalently, $A^{T,+}\cap A^{I,+}\cap A^{F,+}=\mathsf{\varnothing },A^{T,-}\cup A^{I,-}{A}^{F,-}=X.$

The set of all IVNCSs of Type 1 [resp. Type 2 and Type 3] in X is denoted by $IV{N}_1\left(X\right)$ [resp. $IV{N}_2\left(X\right)$ and $IV{N}_3\left(X\right)$], and $IVNCS\left(X\right)=IV{N}_1\left(X\right)\cup IV{N}_2\left(X\right)\cup IV{N}_3\left(X\right)$, where $IVNCS\left(X\right)$ is the set of all IVNCSs in X.

For any classical subset A of X, $〈[A,A],\tilde{\mathsf{\varnothing }},[A^c,A^c]〉\in IVNCS\left(X\right)$ is clear. Then we can consider an INCS in X can be considered as the generalization of a classical subset of X. Moreover, if $A=〈[A^{T,-},A^{T,+}],[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉\in IVNCS\left(X\right)$, then:

$${\chi }_{{}_A}=([{\chi }_{{}_{A^{T,-}}},{\chi }_{{}_{A^{T,+}}}],[{\chi }_{{}_{A^{I,-}}},{\chi }_{{}_{A^{I,+}}}],[{\chi }_{{}_{A^{F,-}}},{\chi }_{{}_{A^{F,+}}}])$$

is an interval neutrosophic set in X proposed by Ye [38]. Thus we can consider an IVS as the generalization of an IVNCS.

Remark 1

(1) 

$IV{N}_2\left(X\right)\subset IV{N}_1\left(X\right),IV{N}_2\left(X\right)\subset IV{N}_3\left(X\right),$

(2) 

$IV{N}_1\left(X\right)\not\subset IV{N}_2\left(X\right),IV{N}_1\left(X\right)\not\subset IV{N}_3\left(X\right)$ in general,

(3) 

$IV{N}_3\left(X\right)\not\subset IV{N}_1\left(X\right),IV{N}_3\left(X\right)\not\subset IV{N}_2\left(X\right)$ in general.

Example 3.

Let $X=\{a,b,c,d,e,f,g,h,i\}$. Consider two IVNCSs in X given by:

$$A=〈\left[\right\{a,b,c\},\{a,b,c,d\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉,$$

$$B=〈\left[\right\{a,b,c\},\{a,b,c\left\}\right],\left[\right\{a,e,f\},\{a,e,f\left\}\right],\left[\right\{g,h,i\},\{g,h,i\left\}\right]〉.$$

(i) 

$[A^{T,-},A^{T,+}]\cap [A^{I,-},A^{I,+}]=\tilde{\mathsf{\varnothing }},[A^{T,-},A^{T,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }},$

$[A^{I,-},A^{I,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }}.$ But

$[A^{T,-},A^{T,+}]\cup [A^{I,-},A^{I,+}]\cup [A^{F,-},A^{F,+}]=[\{a,b,c,d,e,f,g,h\},X\}]\ne \tilde{X}.$ Then $A\in IV{N}_1\left(X\right)$ but $A\notin IV{N}_2\left(X\right)$. Moreover, we have:

$$[A^{T,-},A^{T,+}]\cap [A^{I,-},A^{I,+}]\cap [A^{F,-},A^{F,+}]=\tilde{\mathsf{\varnothing }}.$$

Thus $A\notin IV{N}_3\left(X\right)$. So we can confirm that Remark 1 (2) holds.

(ii) 

$[B^{T,-},B^{T,+}]\cap [B^{I,-},B^{I,+}]\cap [B^{F,-},B^{F,+}]=\tilde{\mathsf{\varnothing }},$

$[B^{T,-},B^{T,+}]\cup B{C}^{I,-},B^{I,+}]\cup [B^{F,-},B^{F,+}]=\tilde{X}.$ But

$[B^{T,-},B^{T,+}]\cap [B^{I,-},B^{I,+}]=[\left\{a\right\},\left\{a\right\}]\ne \tilde{\mathsf{\varnothing }}.$

Then $B\in IV{N}_3\left(X\right)$ but $B\notin IV{N}_1\left(X\right),B\notin IV{N}_2\left(X\right)$. Thus we can confirm that Remark 1 (3) holds.

Definition 10.

We may define the interval-valued neutrosophic crisp empty sets and the interval-valued neutrosophic crisp whole sets, denoted by ${\mathsf{\varnothing }}_{i,IVN}$ and $X_{i,IVN}$ ($i=1,2,3,4$), respectively as follows:

(i) 

${\mathsf{\varnothing }}_{1,IVN}=〈\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }},\tilde{X}〉,{\mathsf{\varnothing }}_{2,IVN}=〈\tilde{\mathsf{\varnothing }},\tilde{X},\tilde{X}〉,$

${\mathsf{\varnothing }}_{3,IVN}=〈\tilde{\mathsf{\varnothing }},\tilde{X},\tilde{\mathsf{\varnothing }}〉,{\mathsf{\varnothing }}_{4,IVN}=〈\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$

(ii) 

$X_{1,IVN}=〈\tilde{X},\tilde{X},\tilde{\mathsf{\varnothing }}〉,X_{2,IVN}=〈\tilde{X},\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$

$X_{3,IVN}=〈\tilde{X},\tilde{\mathsf{\varnothing }},\tilde{X}〉,X_{4,IVN}=〈\tilde{X},\tilde{X},\tilde{X}〉.$

Definition 11.

Let $A\in IVNCS\left(X\right)$. Then the complements of A, denoted by $A^{i,c}$ ($i=1,2,3$), is an IVNCS in X, respectively as follows:

$$A^{1,c}=〈{[A^{T,-},A^{T,+}]}^c,{[A^{I,-},A^{I,+}]}^c,{[A^{F,-},A^{F,+}]}^c〉,$$

$$A^{2,c}=〈[A^{F,-},A^{F,+}],[A^{I,-},A^{I,+}],[A^{T,-},A^{T,+}]〉,$$

$$A^{3,c}=〈[A^{F,-},A^{F,+}],{[A^{I,-},A^{I,+}]}^c,[A^{T,-},A^{T,+}]〉.$$

Example 4.

Let $A=〈\left[\right\{a,b,c\},\{a,b,c,d\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉$ be the IVNCS in X given in Example 3. Then we can easily check that:

$A^{1,c}=<[\{e,f,g,h,i\},\{d,e,f,g,h,i\}],[\{a,b,c,d,g,h,i\},\{a,b,c,d,f,g,h,i\}],$

$\left[\right\{a,b,c,d,e,f\},\{a,b,c,d,e,f,i\left\}\right]>,$

$A^{2,c}=〈\left[\right\{g,h\},\{g,h,i\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{a,b,c\},\{a,b,c,d\left\}\right]〉,$

$A^{3,c}=<[\{g,h\},\{g,h,i\}],[\{a,b,c,d,g,h,i\},\{a,b,c,d,f,g,h,i\}],$

$\left[\right\{a,b,c\},\{a,b,c,d\left\}\right]>.$

Definition 12.

Let $A,B\in IVNCS\left(X\right)$. Then we may define the inclusions between A and B, denoted by $A{\subset }_{i}B$ ($i=1,2$), as follows:

$A{\subset }_{1}B$ iff $[A^{T,-},A^{T,+}]\subset [B^{T,-},B^{T,+}],[A^{I,-},A^{I,+}]\subset [B^{I,-},B^{I,+}],$

$[A^{F,-},A^{F,+}]\supset [B^{F,-},B^{F,+}],$

$A{\subset }_{2}B$ iff $[A^{T,-},A^{T,+}]\subset [B^{T,-},B^{T,+}],[A^{I,-},A^{I,+}]\supset [B^{I,-},B^{I,+}],$

$[A^{F,-},A^{F,+}]\supset [B^{F,-},B^{F,+}].$

Proposition 3.

For any $A\in IVNCS\left(X\right)$, the followings hold:

(1) 

${\mathsf{\varnothing }}_{1,IVN}{\subset }_{1}A{\subset }_1{X}_{1,IVN},{\mathsf{\varnothing }}_{2,IVN}{\subset }_{2}A{\subset }_2{X}_{2,IVN}$,

(2) 

${\mathsf{\varnothing }}_{i,IVN}{\subset }_j{\mathsf{\varnothing }}_{i,IVN}$, $X_{i,IVN}{\subset }_j{X}_{i,IVN}$,($i=1,2,3,4$, $j=1,2$).

Proof. 

Straightforward. ‎‎□‎‎

Definition 13.

Let $A,B\in IVNCS\left(X\right)$, ${\left(A_j\right)}_{j\in J}\subset IVNCS\left(X\right)$.

(i) 

The intersection of A and B, denoted by $A{\cap }^{i}B$ ($i=1,2$), is an IVNCS in X defined by:

$A{\cap }^{1}B=<[A^{T,-},A^{T,+}]\cap [B^{T,-},B^{T,+}],[A^{I,-},A^{I,+}]\cap [B^{I,-},B^{I,+}],$

$[A^{F,-},A^{F,+}]\cup [B^{F,-},B^{F,+}]>,$

$A{\cap }^{2}B=<[A^{T,-},A^{T,+}]\cap [B^{T,-},B^{T,+}],[A^{I,-},A^{I,+}]\cup [B^{I,-},B^{I,+}],$

$[A^{F,-},A^{F,+}]\cup [B^{F,-},B^{F,+}]>.$

(i’) 

The intersection of ${\left(A_j\right)}_{j\in J}$, denoted by ${\bigcap }_{j\in J}^i{A}_j$ ($i=1,2$), is an IVNCS in X defined by:

$$\bigcap _{j\in J}^1{A}_j=〈\bigcap _{j\in J}[A_j^{T,-},A_j^{T,+}],\bigcap _{j\in J}[A_j^{I,-},A_j^{I,+}],\bigcup _{j\in J}[A_j^{F,-},A_j^{F,+}]〉,$$

$$\bigcap _{j\in J}^2{A}_j=〈\bigcap _{j\in J}[A_j^{T,-},A_j^{T,+}],\bigcup _{j\in J}[A_j^{I,-},A_j^{I,+}],\bigcup _{j\in J}[A_j^{F,-},A_j^{F,+}]〉.$$

(ii) 

The union of A and B, denoted by $A{\cup }^{i}B$ ($i=1,2$), is an IVNCS in X defined by:

$A{\cup }^{1}B=<[A^{T,-},A^{T,+}]\cup [B^{T,-},B^{T,+}],[A^{I,-},A^{I,+}]\cup [B^{I,-},B^{I,+}],$

$[A^{F,-},A^{F,+}]\cap [B^{F,-},B^{F,+}]>,$

$A{\cup }^{2}B=<[A^{T,-},A^{T,+}]\cup [B^{T,-},B^{T,+}],[A^{I,-},A^{I,+}]\cap [B^{I,-},B^{I,+}],$

$[A^{F,-},A^{F,+}]\cap [B^{F,-},B^{F,+}]>.$

(ii’) 

The union of ${\left(A_j\right)}_{j\in J}$, denoted by ${\bigcup }_{j\in J}^i{A}_j$ ($i=1,2$), is an IVNCS in X defined by:

$$\bigcup _{j\in J}^1{A}_j=〈\bigcup _{j\in J}[A_j^{T,-},A_j^{T,+}],\bigcup _{j\in J}[A_j^{I,-},A_j^{I,+}],\bigcap _{j\in J}[A_j^{F,-},A_j^{F,+}]〉,$$

$$\bigcup _{j\in J}^2{A}_j=〈\bigcup _{j\in J}[A_j^{T,-},A_j^{T,+}],\bigcap _{j\in J}[A_j^{I,-},A_j^{I,+}],\bigcap _{j\in J}[A_j^{F,-},A_j^{F,+}]〉.$$

(iii) 

$\left[\right]A=〈[A^{T,-},A^{T,+}],[A^{I,-},A^{I,+}],{[A^{T,-},A^{T,+}]}^c〉$.

(iv) 

$<>A=〈{[A^{F,-},A^{F,+}]}^c,[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉$.

From Definitions 10–13, we get similar results from Propositions 3.5 and 3.6 in [30].

Proposition 4.

Let $A,B,C\in IVNCS\left(X\right)$, $i=1,2$. Then,

(1) 

If $A{\subset }_{i}B$ and $B{\subset }_{i}C$, then $A{\subset }_{i}C$,

(2) 

$A{\subset }_{i}A{\cup }^{i}B$ and $B{\subset }_{i}A{\cup }^{i}B$,

(3) 

$A{\cap }^{i}B{\subset }_{i}A$ and $A{\cap }^{i}B{\subset }_{i}B$,

(4) 

$A{\subset }_{i}B$ if and only if $A{\cap }^{i}B=A$,

(5) 

$A{\subset }_{i}B$ if and only if $A{\cup }^{i}B=B$.

Proposition 5.

Let X$A,B,C\in IVNCS\left(X\right)$, ${\left(A_j\right)}_{j\in J}\subset IVNCS\left(X\right)$, and let $i=1,2$; $k=1,2,3$. Then

(1) 

(Idempotent laws) $A{\cup }^{i}A=A,A{\cap }^{i}A=A,$

(2) 

(Commutative laws) $A{\cup }^{i}B=B{\cup }^{i}A,A{\cap }^{i}B=B{\cap }^{i}A,$

(3) 

(Associative laws) $A{\cup }^i\left(B{\cup }^{i}C\right)=\left(A{\cup }^{i}B\right){\cup }^{i}C,A{\cap }^i\left(B{\cap }^{i}C\right)=\left(A{\cap }^{i}B\right){\cap }^{i}C$,

(4) 

(Distributive laws) $A{\cup }^i\left(B{\cap }^{i}C\right)=\left(A{\cup }^{i}B\right){\cap }^i\left(A{\cup }^{i}C\right),$

$A{\cap }^i\left(B{\cup }^{i}C\right)=\left(A{\cap }^{i}B\right){\cup }^i\left(A{\cap }^{i}C\right),$

(4’) 

(Generalized distributive laws) $\left({\bigcap }_{j\in J}^i{A}_j\right){\cup }^{i}A={\bigcap }_{j\in J}^i\left(A_j{\cup }^{i}A\right),$

$\left({\bigcup }_{j\in J}^i{A}_j\right){\cap }^{i}A={\bigcup }_{j\in J}^i\left(A_j{\cap }^{i}A\right),$

(5) 

(Absorption laws) $A{\cup }^i\left(A{\cap }^{i}B\right)=A,A{\cap }^i\left(A{\cup }^{i}B\right)=A,$

(6) 

(DeMorgan’s laws):  ${\left(A{\cup }^{i}B\right)}^{k,c}=A^{k,c}{\cap }^i{B}^{k,c},{\left(A{\cap }^{i}B\right)}^{k,c}=A^{k,c}{\cup }^i{B}^{k,c},$

(6’) 

(Generalized DeMorgan’s laws) ${\left({\bigcup }_{j\in J}^i{A}_j\right)}^{k,c}={\bigcap }_{j\in J}^i{A}_j^{k,c},$

(7) 

${\left(A^{k,c}\right)}^{k,c}=A$,

(8) (8a)

$A{\cup }^i{\mathsf{\varnothing }}_{i,IVN}=A,A{\cap }^i{\mathsf{\varnothing }}_{i,IVN}={\mathsf{\varnothing }}_{i,IVN},$

  (8b)

$A{\cup }^i{X}_{i,IVN}=X_{i,IVN},A{\cap }^i{X}_{i,IVN}=A,$

  (8c)

${X_{1,IVN}}^{1,c}={\mathsf{\varnothing }}_{1,IVN},{X_{1,IVN}}^{2,c}={\mathsf{\varnothing }}_{2,IVN},{X_{1,IVN}}^{3,c}={\mathsf{\varnothing }}_{1,IVN},$

${X_{2,IVN}}^{1,c}={\mathsf{\varnothing }}_{2,IVN},{X_{2,IVN}}^{2,c}={\mathsf{\varnothing }}_{1,IVN},{X_{2,IVN}}^{3,c}={\mathsf{\varnothing }}_{2,IVN},$

${X_{3,IVN}}^{1,c}={\mathsf{\varnothing }}_{3,IVN},{X_{3,IVN}}^{2,c}=X_{3,IVN},{X_{3,IVN}}^{3,c}=X_{4,IVN},$

${X_{4,IVN}}^{1,c}={\mathsf{\varnothing }}_{4,IVN},{X_{4,IVN}}^{2,c}=X_{4,IVN},{X_{4,IVN}}^{3,c}=X_{3,IVN},$

${{\mathsf{\varnothing }}_{1,IVN}}^{1,c}=X_{1,IVN},{{\mathsf{\varnothing }}_{1,IVN}}^{2,c}=X_{2,IVN},{{\mathsf{\varnothing }}_{1,IVN}}^{3,c}=X_{1,IVN},$

${{\mathsf{\varnothing }}_{2,IVN}}^{1,c}=X_{2,IVN},{{\mathsf{\varnothing }}_{2,IVN}}^{2,c}=X_{1,IVN},{{\mathsf{\varnothing }}_{2,IVN}}^{3,c}=X_{2,IVN},$

${{\mathsf{\varnothing }}_{3,IVN}}^{1,c}=X_{3,IVN},{{\mathsf{\varnothing }}_{3,IVN}}^{2,c}={\mathsf{\varnothing }}_{3,IVN},{{\mathsf{\varnothing }}_{3,IVN}}^{3,c}={\mathsf{\varnothing }}_{4,IVN},$

${{\mathsf{\varnothing }}_{4,IVN}}^{1,c}=X_{4,IVN},{{\mathsf{\varnothing }}_{4,IVN}}^{2,c}={\mathsf{\varnothing }}_{4,IVN},{{\mathsf{\varnothing }}_{4,IVN}}^{3,c}={\mathsf{\varnothing }}_{3,IVN},$

  (8d)

$A{\cup }^i{A}^{k,c}\ne X_{j,IVN},A{\cap }^i{A}^{k,c}\ne {\mathsf{\varnothing }}_{j,IVN}$ in general (see Example 5),

where $j=1,2,3,4$.

Example 5.

Consider the IVNCS A in X given in Example 4. Then,

$A{\cap }^1{A}^{1,c}$

$=〈\left[\right\{a,b,c\},\{a,b,c,d\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉$

${\cap }^1<[\{e,f,g,h,i\},\{d,e,f,g,h,i\}],[\{a,b,c,d,g,h,i\},\{a,b,c,d,f,g,h,i\}],$

$\left[\right\{a,b,c,d,e,f\},\{a,b,c,d,e,f,i\left\}\right]>$

$=〈[\mathsf{\varnothing },\{d\left\}\right],[\mathsf{\varnothing },\{f\left\}\right],\left[\right\{a,b,c,d,e,f,g,h\},X\}]〉$

$\ne {\mathsf{\varnothing }}_{j,IVN}.$

Similarly, we can check that:

$$A{\cup }^1{A}^{1,c}\ne X_{j,IVN},A{\cap }^1{A}^{2,c}\ne {\mathsf{\varnothing }}_{j,IVN},A{\cup }^1{A}^{2,c}\ne X_{j,IVN}.$$

Additionally, we can easily check the remainders.

A neighborhood system of a point is very important in a classical topology. Then we propose an interval-valued neutrosophic crisp point to define the concept of an interval-valued neutrosophic crisp neighborhood. Moreover, when we deal with separation axioms in an interval-valued neutrosophic crisp topology, the notion of interval-valued neutrosophic crisp points is used. Then we define it below.

Definition 14.

Let $a\in X$, $A\in IVNCS\left(X\right)$. Then the form $〈[\left\{a\right\},\left\{a\right\}],\tilde{\mathsf{\varnothing }},[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$ [resp. $〈\tilde{\mathsf{\varnothing }},[\left\{a\right\},\left\{a\right\}],[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$] is called an interval-valued neutrosophic [resp. vanishing] point in X and denoted by $a_{{}_{IVN}}$ [resp. $a_{{}_{IVNV}}$]. We will denote the set of all interval-valued neutrosophic points in X as $IV{N}_P\left(X\right)$.

(i) 

We say that $a_{{}_{IVN}}$ belongs to A, denoted by $a_{{}_{IVN}}\in A$, if $a\in A^{T,+}$.

(ii) 

We say that $a_{{}_{IVNV}}$ belongs to A, denoted by $a_{{}_{IVNV}}\in A$, if $a\notin A^{F,+}$.

Proposition 6.

Let $A\in IVNCS\left(X\right)$. Then $A=A_{IVN}{\cup }^1{A}_{IVNV},$

where $A_{IVN}={\bigcup }_{a_{{}_{IVN}}\in A}^1{a}_{{}_{IVN}},A_{IVNV}={\bigcup }_{a_{{}_{IVNV}}\in A}^1{a}_{{}_{IVNV}}.$

In fact,

$$A_{IVN}=〈[A^{T,-},A^{T,+}],\tilde{\mathsf{\varnothing }},{[A^{T,-},A^{T,+}]}^c〉$$

and

$$A_{IVNV}=〈\tilde{\mathsf{\varnothing }},[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉.$$

Proof. 

$A_{IVN}={\bigcup }_{a_{{}_{IVN}}\in A}^1{a}_{{}_{IVN}}={\bigcup }_{a_{{}_{IVN}}\in A}^1〈[\left\{a\right\},\left\{a\right\}],\tilde{\mathsf{\varnothing }},[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$

$=〈{\bigcup }_{a_{{}_{IVN}}\in A}[\left\{a\right\},\left\{a\right\}],{\bigcup }_{a_{{}_{IVN}}\in A}\tilde{\mathsf{\varnothing }},{\bigcap }_{a_{{}_{IVN}}\in A}[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$

$=〈[{\bigcup }_{a\in A^{T,-}}\left\{a\right\},{\bigcup }_{a\in A^{T,+}}\left\{a\right\}],\tilde{\mathsf{\varnothing }},[{\bigcap }_{a\in A^{T,+}}{\left\{a\right\}}^c,{\bigcap }_{a\in A^{T,-}}{\left\{a\right\}}^c]〉$

$=〈[A^{T,-},A^{T,+}],\tilde{\mathsf{\varnothing }},[{A^{T,+}}^c,{A^{T,-}}^c]〉$

$=〈[A^{T,-},A^{T,+}],\tilde{\mathsf{\varnothing }},{[A^{T,-},A^{T,+}]}^c〉,$

$A_{IVNV}={\bigcup }_{a_{{}_{IVNN}}\in A}^1{a}_{{}_{IVNV}}={\bigcup }_{a_{{}_{IVNV}}\in A}^1〈\tilde{\mathsf{\varnothing }},[\left\{a\right\},\left\{a\right\}],[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$

$=〈{\bigcup }_{a_{{}_{IVNV}}\in A}\tilde{\mathsf{\varnothing }},{\bigcup }_{a_{{}_{IVNV}}\in A}[\left\{a\right\},\left\{a\right\}],{\bigcap }_{a_{{}_{IVNV}}\in A}[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$

$=〈\tilde{\mathsf{\varnothing }},[{\bigcup }_{a\in A^{I,-}}\left\{a\right\},{\bigcup }_{a\in A^{I,+}}\left\{a\right\},[{\bigcap }_{a\notin A^{F,+}}{\left\{a\right\}}^c,{\bigcap }_{a\in A^{F,-}}{\left\{a\right\}}^c]〉$

$=〈\tilde{\mathsf{\varnothing }},[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉.$

Then we have,

$A_{IVN}{\cup }^1{A}_{IVNV}=〈[A^{T,-},A^{T,+}],\tilde{\mathsf{\varnothing }},{[A^{T,-},A^{T,+}]}^c〉{\cup }^1〈\tilde{\mathsf{\varnothing }},[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉$

$=〈[A^{T,-},A^{T,+}]\cup \tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}\cup [A^{I,-},A^{I,+}],{[A^{T,-},A^{T,+}]}^c\cap [A^{F,-},A^{F,+}]〉$

$=〈[A^{T,-},A^{T,+}],[A^{I,-},A^{I,+}],[{A^{T,+}}^c\cap A^{F,-},{A^{T,-}}^c\cap A^{F,+}〉$

$=〈[A^{T,-},A^{T,+}],[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}〉$

$=A.$

This completes the proof. ‎‎□‎‎

Example 6.

Let $X=\{a,b,c,d,e,f,g,h,i\}$ and consider the IVNCS in X given by:

$$A=〈\left[\right\{a,b\},\{a,b,c\left\}\right],\left[\right\{d\},\{d,e\left\}\right],\left[\right\{f,g\},\{f,g,h\left\}\right]〉.$$

Then clearly, we have:

$A_{IVN}$

$={\bigcup }_{a_{{}_{IVI}}\in A}^1〈[\left\{a\right\},\left\{a\right\}],\tilde{\mathsf{\varnothing }},[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$

$=〈[\{a,b\},\{a,b,c\}],\tilde{\mathsf{\varnothing }},[{\left\{a\right\}}^c\cap {\left\{b\right\}}^c\cap {\left\{c\right\}}^c,{\left\{a\right\}}^c\cap {\left\{b\right\}}^c]〉$

$=〈[\{a,b\},\{a,b,c\}],\tilde{\mathsf{\varnothing }},[\{d,e,f,g,h,i\},\{c,d,e,f,g,h,i\}]〉$

$=〈[A^{T,-},A^{T,+}],\tilde{\mathsf{\varnothing }},{[A^{T,-},A^{T,+}]}^c〉,$

$A_{IVNV}$

$={\bigcup }_{a_{{}_{IVNV}}\in A}^1〈\tilde{\mathsf{\varnothing }},[\left\{a\right\},\left\{a\right\}],[{\left\{a\right\}}^c,{\left\{a\right\}}^c]〉$

$=<\tilde{\mathsf{\varnothing }}{,[\left\{d\right\},\{d,e\}],[\left\{a\right\}}^c\cap {\left\{b\right\}}^c\cap {\left\{c\right\}}^c\cap {\left\{d\right\}}^c\cap {\left\{e\right\}}^c\cap {\left\{h\right\}}^c\cap {\left\{i\right\}}^c,$

${\left\{a\right\}}^c\cap {\left\{b\right\}}^c\cap {\left\{c\right\}}^c\cap {\left\{d\right\}}^c\cap {\left\{e\right\}}^c\cap {\left\{i\right\}}^c]>$

$=〈\tilde{\mathsf{\varnothing }},[\left\{d\right\},\{d,e\}],[\{f,g\},\{f,g,h\}]〉$

$=〈\tilde{\mathsf{\varnothing }},[A^{I,-},A^{I,+}],[A^{F,-},A^{F,+}]〉$.

Thus $A_{IVN}{\cup }^1{A}_{IVNV}=〈\left[\right\{a,b\},\{a,b,c\left\}\right],\left[\right\{d\},\{d,e\left\}\right],\left[\right\{f,g\},\{f,g,h\left\}\right]〉=A.$ So we can confirm that Proposition 6 holds.

Proposition 7.

Let ${\left(A_j\right)}_{j\in J}\subset IVNCS\left(X\right)$ and let $a\in X$.

(1) $a_{{}_{IVN}}\in {\bigcap }_{j\in J}^1{A}_j$ [resp. $a_{{}_{IVNV}}\in {\bigcap }_{j\in J}^1{A}_j$] ⇔$a_{{}_{IVN}}\in A_j$ [resp. $a_{{}_{IVNV}}\in A_j$] for each $j\in J$.

(2) $a_{{}_{IVN}}\in {\bigcup }_{j\in J}^1{A}_j$ [resp. $a_{{}_{IVNV}}\in {\bigcup }_{j\in J}^1{A}_j$] ⇔ there exists $j\in J$ such that $a_{{}_{IVN}}\in A_j$ [resp. $a_{{}_{IVNV}}\in A_j$.

Proof. 

(1) Suppose $a_{{}_{IVN}}\in {\bigcap }_{j\in J}^1{A}_j$ and let $A={\bigcap }_{j\in J}^1{A}_j$. Since $A^{T,+}={\bigcap }_{j\in J}{A}_j^{T,+}$, $a\in {\bigcap }_{j\in J}{A}_j^{T,+}$. Then $a\in A_j^{T,+}$ for each $j\in J$. Thus $a_{{}_{IVN}}\in A_j$ for each $j\in J$. The converse is proved similarly. The proof of the second part is omitted.

(2) Suppose $a_{{}_{IVNV}}\in {\bigcup }_{j\in J}^1{A}_j$ and let $A={\bigcup }_{j\in J}^1{A}_j$. Since $A^{F,+}={\bigcap }_{j\in J}{A}_j^{T,+}$, $a\notin {\bigcap }_{j\in J}{A}_j^{T,+}$. Then $a\notin A_j^{T,+}$ for some $j\in J$. Thus $a_{{}_{IVNV}}\in A_j$ for some $j\in J$. The converse is shown similarly. The proof of the first part is omitted. ‎‎□‎‎

Proposition 8.

Let $A,B\in IVNCS\left(X\right)$. Then,

(1) 

$A{\subset }_{1}B$ if and only if $a_{{}_{IVN}}\in A\Rightarrow a_{{}_{IVN}}\in B$ [resp. $a_{{}_{IVNV}}\in A\Rightarrow a_{{}_{IVNV}}\in B$] for each $a\in X$.

(2) 

$A=B$ if and only if $a_{{}_{IVN}}\in A\iff a_{{}_{IVN}}\in B$ [resp. $a_{{}_{IVNV}}\in A\iff a_{{}_{IVNV}}\in B$] for each $a\in X$.

Proof. 

Straightforward. ‎‎□‎‎

When we discuss with continuities in a classical topology, the concepts of the preimage and image of a classical subset under a mapping are used. Then we define ones of an IVNCS under a mapping as follows.

Definition 15.

Let $f:X\to Y$ be a mapping, $A\in IVNCS\left(X\right),B\in IVNCS\left(Y\right)$.

(i) 

The image of A under f, denoted by $f\left(A\right)$, is an IVNCS in Y defined as:

$$f\left(A\right)=〈[f\left(A^{T,-}\right),f\left(A^{T,+}\right)],[f\left(A^{I,-}\right),f\left(A^{I,+}\right)],[f\left(A^{F,-}\right),f\left(A^{F,+}\right)]〉.$$

(ii) 

The preimage of B under f, denoted by $f^{-1}\left(B\right)$, is an interval set in X defined as:

$$f^{-1}\left(B\right)=〈[f^{-1}\left(B^{T,-}\right),f^{-1}\left(B^{T,+}\right)],[f^{-1}\left(B^{I,-}\right),f^{-1}\left(B^{I,+}\right)],[f^{-1}\left(B^{F,-}\right),f^{-1}\left(B^{F,+}\right)]〉.$$

It is clear that $f\left(a_{{}_{IVN}}\right)=f{\left(a\right)}_{{}_{IVN}}$ and $f\left(a_{{}_{IVNV}}\right)=f{\left(a\right)}_{{}_{IVNV}}$ for each $a\in X$.

From the above definition, we have similar results of the image and the preimage of classical subsets under a mapping.

Proposition 9.

Let $f:X\to Y$ be a mapping, $A,A_1,A_2\in IVNCS\left(X\right),{\left(A_j\right)}_{j\in J}\subset IVNCS\left(X\right)$ and let $B,B_1,B_2\in IVNCS\left(Y\right),{\left(A_j\right)}_{j\in J}\subset IVNCS\left(Y\right)$. Let $i=1,2$; $k=1,2,3$; $l=1,2,3,4$. Then,

(1) 

If $A_1{\subset }_i{A}_2$, then $f\left(A_1\right){\subset }_{i}f\left(A_2\right)$,

(2) 

If $B_1{\subset }_i{B}_2$, then $f^{-1}\left(B_1\right){\subset }_i{f}^{-1}\left(B_1\right)$,

(3) 

$A{\subset }_i{f}^{-1}\left(f\left(A\right)\right)$ and if f is injective, then $A=f^{-1}\left(f\left(A\right)\right)$,

(4) 

$f\left(f^{-1}\left(B\right)\right){\subset }_{i}B$ and if f is surjective, $f\left(f^{-1}\left(B\right)\right)=B$,

(5) 

$f^{-1}\left({\bigcup }_{j\in J}^i{B}_j\right)={\bigcup }_{j\in J}^i{f}^{-1}\left(B_j\right)$,

(6) 

$f^{-1}\left({\bigcap }_{j\in J}^i{B}_j\right)={\bigcap }_{j\in J}^i{f}^{-1}\left(B_j\right)$,

(7) 

$f{\left({\bigcup }_{j\in J}^i{A}_j\right)}_i{\subset }_i{\bigcup }_{j\in J}^{i}f\left(A_j\right)$ and if f is surjective, then $f{\left({\bigcup }_{j\in J}^i{A}_j\right)}_i={\bigcup }_{j\in J}^{i}f\left(A_j\right)$,

(8) 

$f\left({\bigcap }_{j\in J}^i{A}_j\right){\subset }_i{\bigcap }_{j\in J}^{i}f\left(A_j\right)$ and if f is injective, then $f\left({\bigcap }_{j\in J}^i{A}_j\right)={\bigcap }_{j\in J}^{i}f\left(A_j\right)$,

(9) 

If f is surjective, then $f{\left(A\right)}^{k,c}{\subset }_{i}f\left(A^{k,c}\right)$,

(10) 

$f^{-1}\left(B^{k,c}\right)=f^{-1}{\left(B\right)}^{k,c}$,

(11) 

$f^{-1}\left({\mathsf{\varnothing }}_{l,IVN}\right)={\mathsf{\varnothing }}_{l,IVN}$, $f^{-1}\left(X_{l,IVN}\right)=X_{l,IVN}$,

(12) 

$f\left({\mathsf{\varnothing }}_{l,IVN}\right)={\mathsf{\varnothing }}_{l,IVN}$ and if f is surjective, then $f\left(X_{l,IVN}\right)=X_{l,IVN}$,

(13) 

If $g:Y\to Z$ is a mapping, then ${(g\circ f)}^{-1}\left(C\right)=f^{-1}\left(g^{-1}\left(C\right)\right)$, for each $C\in \left[Z\right].$

Proof. 

The proofs are straightforward. ‎‎□‎‎

4. Interval-Valued Topological Spaces

In this section, we define an interval-valued neutrosophic crisp topology on X and study some of its properties, and give some examples. We also introduce the concepts of an interval-valued neutrosophic crisp base and subbase, and a family of IVNCSs gets the necessary and sufficient conditions to become IVNCB and gives some examples.

From this section to the rest sections, ${\subset }_1$, ${\cup }^1$, ${\cap }^1$, ${}^{3,c}$, ${\mathsf{\varnothing }}_{1,IVN}$, and $X_{1,IVN}$ are denoted by ⊂, ∩, ∪, ${}^c$, ${\mathsf{\varnothing }}_{IVN}$, and $X_{IVN}$, respectively.

Definition 16.

Let $\mathsf{\varnothing }\ne \tau \subset IVNCS\left(X\right)$. Then τ is called an interval-valued neutrosophic crisp topology (briefly, IVNCT) on X, if it satisfies the following axioms:

(IVNCO)

${\mathsf{\varnothing }}_{IVN},X_{IVN}\in \tau$,

(IVNCO)

$A\cap B\in \tau$ for any $A,B\in \tau$,

(IVNCO)

${\bigcup }_{j\in J}{A}_j\in \tau$ for any family ${\left(A_j\right)}_{j\in J}$ of members of τ.

In this case, the pair $(X,\tau )$ is called an interval-valued neutrosophic crisp topological space (briefly, IVNCTS) and each member of τ is called an interval-valued neutrosophic crisp open set (briefly, IVNCOS) in X. An IVNCS A is called an interval-valued neutrosophic crisp closed set (briefly, IVNCCS) in X, if $A^c\in \tau$.

It is obvious that $\{{\mathsf{\varnothing }}_{IVN},X_{IVN}\}$ [resp. $IVNC\left(X\right)$] is an IVNCT on X, and called the interval-valued neutrosophic crisp indiscrete topology (briefly, IVNCIT) [resp. the interval-valued neutrosophic crisp discrete topology (briefly, IVNCDT)] on X. The pair $(X,{\tau }_{{}_{IVN,0}})$ [resp. $(X,{\tau }_{{}_{IVN,1}})$] is called an interval-valued neutrosophic crisp indiscrete [resp. discrete] space (briefly, IVNCITS) [resp. (briefly, IVNCDTS)].

$IVNCT\left(X\right)$ represents the set of all IVNCTs on X. For an IVNCTS X, the set of all IVNCOs [resp. IVNCCSs] in X is denoted by $IVNCO\left(X\right)$ [resp. $IVNCC\left(X\right)$].

Remark 2.

(1) For each $\tau \in IVNCT\left(X\right)$, consider three families of IVSs in X:

$${\tau }^T=\{[A^{T,-},A^{T,+}]\in IVS\left(X\right):A\in \tau \},{\tau }^I=\{[A^{I,-},A^{I,+}]\in IVS\left(X\right):A\in \tau \},$$

$${\tau }^F=\{[{A^{F,+}}^c,{A^{F,-}}^c]\in IVS\left(X\right):A\in \tau \}.$$

Then we can easily check that ${\tau }^T$, ${\tau }^I$ and ${\tau }^F$ are IVTs on X.

In this case, ${\tau }^T$ [resp. ${\tau }^I$ and ${\tau }^F$] is called the membership [resp. indeterminacy and non-membership] topology of τ and we write $\tau =〈{\tau }^T,{\tau }^I,{\tau }^F〉$. In fact, we can consider $(X,{\tau }^T,{\tau }^I,{\tau }^F)$ as an interval-valued tri-topological space on X (see the concept of bitopology introduced by Kelly [39]).

Furthermore, we can consider three intuitionistic topology on X proposed by cCoker [14]:

$${\tau }_{{}_T}=\{(A^{T,-},{A^{T,+}}^c)\in IS\left(X\right):A\in \tau \},{\tau }_{{}_I}=\{(A^{I,-},{A^{I,+}}^c]\in IS\left(X\right):A\in \tau \},$$

$${\tau }_{{}_F}=\{{A^{F,+}}^c,A^{F,-})\in IS\left(X\right):A\in \tau \}.$$

Let us also consider six families of ordinary subsets of X:

$${\tau }^{T,-}=\{A^{T,-}\subset X:A\in \tau \},{\tau }^{T,+}=\{A^{T,+}\subset X:A\in \tau \},$$

$${\tau }^{I,-}=\{A^{I,-}\subset X:A\in \tau \},{\tau }^{I,+}=\{A^{I,+}\subset X:A\in \tau \},$$

$${\tau }^{F,-}=\{{A^{T,+}}^c\subset X:A\in \tau \},{\tau }^{F,+}=\{{A^{I,-}}^c\subset X:A\in \tau \}.$$

Then clearly, ${\tau }^{T,-},{\tau }^{T,+},{\tau }^{I,+},{\tau }^{I,-},{\tau }^{F,-},{\tau }^{F,+}$ are ordinary topologies on X.

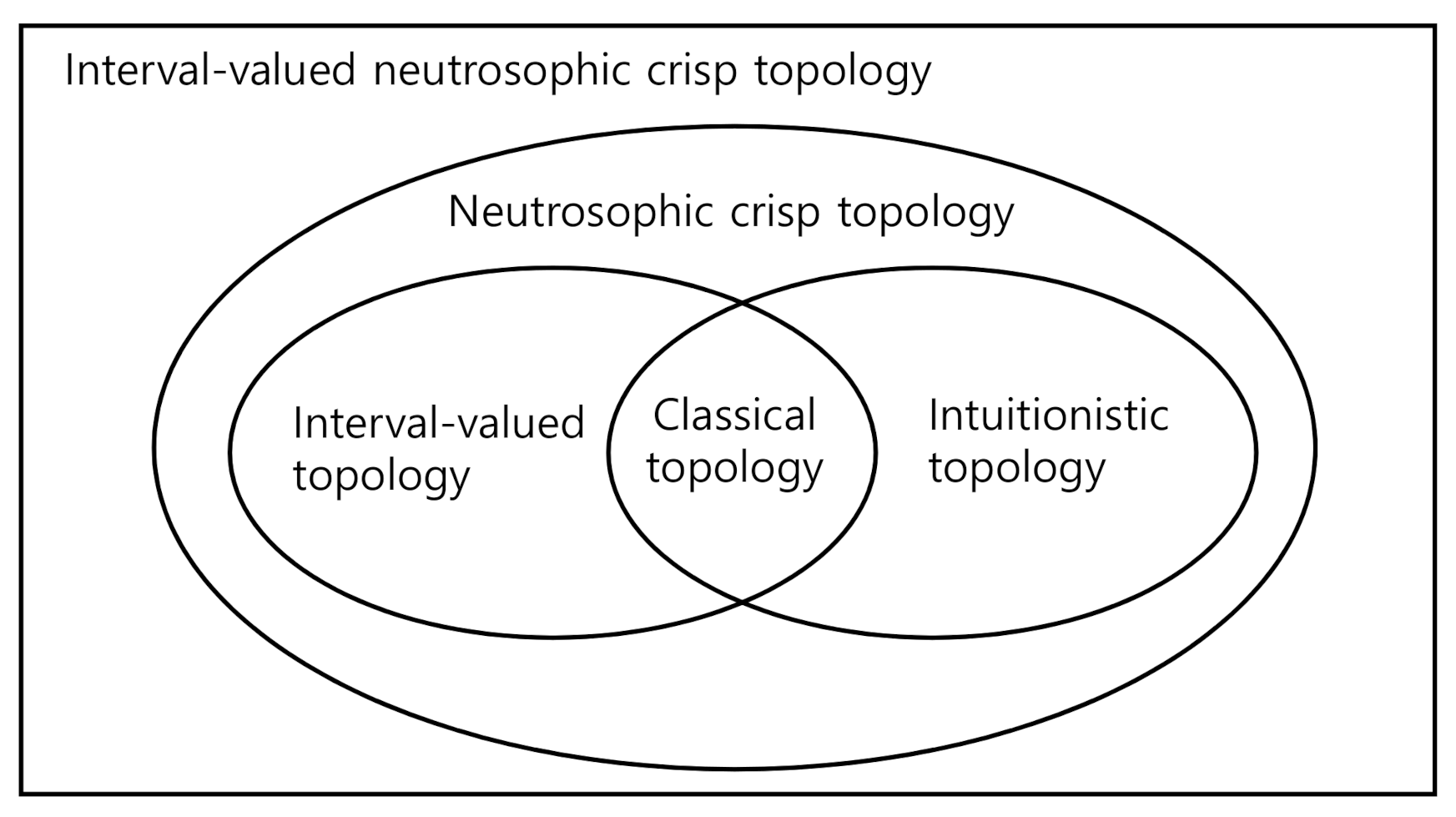
(2) Let $(X,{\tau }_o)$ be an ordinary topological space. Then there are four IVNCTs on X given by:

$${\tau }^1=\left\{\begin{array}{c}\{〈[G,G],\tilde{\mathsf{\varnothing }},[G^c,G^c]〉\in IVNC\left(X\right):G\in {\tau }_o\}ifG\ne X\hfill \\ \{{\mathsf{\varnothing }}_{IVN},X_{IVN}\}ifG=X,\hfill \end{array}\right.$$

$${\tau }^2=\left\{\begin{array}{c}\{〈[G,G],\tilde{X},[G^c,G^c]〉\in IVNC\left(X\right):G\in {\tau }_o\}ifG\ne X\hfill \\ \{{\mathsf{\varnothing }}_{IVN},X_{IVN}\}ifG=X,\hfill \end{array}\right.$$

$${\tau }^3=\left\{\begin{array}{c}\{〈[\mathsf{\varnothing },G],\tilde{\mathsf{\varnothing }},[\mathsf{\varnothing },G^c]〉\in IVNC\left(X\right):G\in {\tau }_o\}ifG\ne \mathsf{\varnothing }\hfill \\ \{{\mathsf{\varnothing }}_{IVN},X_{IVN}\}ifG=\mathsf{\varnothing },\hfill \end{array}\right.$$

$${\tau }^4=\left\{\begin{array}{c}\{〈[\mathsf{\varnothing },G],\tilde{X},[\mathsf{\varnothing },G^c]〉\in IVNC\left(X\right):G\in {\tau }_o\}ifG\ne \mathsf{\varnothing }\hfill \\ \{{\mathsf{\varnothing }}_{IVN},X_{IVN}\}ifG=\mathsf{\varnothing }.\hfill \end{array}\right.$$

(3) Let $(X,{\tau }_{{}_{IV}})$ be an IVTS introduced by Kim et al. [30]. Then clearly,

$$\tau =\{〈[A^{-},A^{+}],\tilde{\mathsf{\varnothing }},[{A^{+}}^c,{A^{-}}^c]〉\in IVNC\left(X\right):A\in {\tau }_{{}_{IV}}\}\in IVNCT\left(X\right).$$

(4) Let $(X,{\tau }_{{}_I})$ be an ITS introduced by cCoker [14]. Then clearly,

$$\tau =\{〈[A^{\in },{A^{\notin }}^c],\tilde{\mathsf{\varnothing }},[A^{\notin },{A^{\in }}^c]〉\in IVNC\left(X\right):A\in {\tau }_{{}_I}\}\in IVNCT\left(X\right).$$

(5) Let $(X,{\tau }_{{}_{NC}})$ be a neutrosophic crisp topological space introduced by Salama and Smarandache [34]. Then clearly,

$$\tau =\{〈[A^T,A^T],[A^I,A^I],[A^F,A^F]〉\in IV{N}^{*}\left(X\right)):A\in {\tau }_{{}_{NC}}\}\in IVNCT\left(X\right).$$

From Remark 2, we can easily see that an IVNCT is a generalization of a classical topology, an IVT, an IT, and neutrosophic crisp topology. Then we have the following Figure 1:

Example. 7.

(1) Let $X=\{a,b\}$. Then we can easily check that:

${\tau }_{{}_{IVN,1}}=\{{\mathsf{\varnothing }}_{IVN},a_{{}_{IVN}},b_{{}_{IVN}},a_{{}_{IVNV}},b_{{}_{IVNV}},〈\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }},[\left\{b\right\},\left\{b\right\}]〉,$

$〈\left[\right\{a\},\{a\left\}\right],\left[\right\{a\},\{a\left\}\right],\left[\right\{b\},\{b\left\}\right]〉,X_{IVN}\}.$

(2) Let $A\in IVNCS\left(X\right)$. Then A is said to be finite, if $A^{T,+},A^{I,+}$, and $A^{F,+}$ are finite. Consider the family

$$\tau =\{U\in IVNCS\left(X\right):U={\mathsf{\varnothing }}_{IVN}or{U}^c\mathrm{is}\mathrm{finite}\}.$$

Then we can easily prove that $\tau \in IVNCT\left(X\right).$

In this case, τ is called an interval-valued neutrosiophic crisp cofinite topology (briefly, IVNCCFT) on X.

(3) Let $A\in IVNCS\left(X\right)$. Then A is said to be countable, if $A^{T,+},A^{I,+}$, and $A^{F,+}$ are countable. Consider the family:

$$\tau =\{U\in IVNCS\left(X\right):U={\mathsf{\varnothing }}_{IVN}\mathrm{or}{U}^c\mathrm{is}\mathrm{countable}\}.$$

Then we can easily show that $\tau \in IVNCT\left(X\right).$

In this case, τ is called an interval-valued neutrosiophic crisp cocountable topology (briefly, IVNCCCT) on X.

(4) Let $X=\{a,b,c,d,e,f,g,h,i\}$ and the family τ of IVNCSs on X given by:

$$\tau =\{{\mathsf{\varnothing }}_{IVN},A_1,A_2,A_3,A_4,X_{IVN}\},$$

where $A_1=〈\left[\right\{a,b\},\{a,b,c\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g,i\left\}\right]〉,$

$A_2=〈\left[\right\{a,d\},\{a,c,d\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉,$

$A_3=〈\left[\right\{a\},\{a,c\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉,$

$A_4=〈\left[\right\{a,b,d\},\{a,b,c,d\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g,i\left\}\right]〉.$Then we can easily check that $\tau \in IVNCT\left(X\right)$.

(5) Let $X=\{0,1\}.$ Consider the family τ of IVNCSs on X given by:

$$\tau =\{{\mathsf{\varnothing }}_{IVN},〈[\left\{0\right\},\left\{0\right\}],\tilde{\mathsf{\varnothing }},[\left\{1\right\},\left\{1\right\}]〉,X_{IVN}\}.$$

Then we can easily prove that $\tau \in IVNCT\left(X\right)$. In this case, $(X,\tau )$ is called the interval-valued neutrosophic crisp Sierpin${}^{{}^{\prime }}$ski space.

From Definition 16, we have the following.

Proposition 10.

Let X be an IVNCTS. Then:

(1) 

${\mathsf{\varnothing }}_{IVN},X_{IVN}\in IVNCC\left(X\right)$,

(2) 

$A\cup B\in IVNCC\left(X\right)$ for any $A,B\in IVNCC\left(X\right)$,

(3) 

${\bigcap }_{j\in J}{A}_j\in IVNCC\left(X\right)$ for any ${\left(A_j\right)}_{j\in J}\subset IVNCC\left(X\right)$.

To discuss $IVNCT\left(X\right)$ with a view-point of lattice theory, we define an order between two IVCTs.

Definition 17.

Let ${\tau }_1,{\tau }_2\in IVNCT\left(X\right)$. Then we say that ${\tau }_1$ is contained in ${\tau }_2$ or ${\tau }_1$ is coarser than ${\tau }_2$ or ${\tau }_2$ is finer than ${\tau }_1$, if ${\tau }_1\subset {\tau }_2,$ i.e., $A\in {\tau }_2$ for each $A\in {\tau }_1$.

For each $\tau \in IVNCT\left(X\right)$, ${\tau }_{{}_{IVN,0}}\subset \tau \subset {\tau }_{{}_{IVN,1}}$ is clear.

From Definitions 14 and 16, we get the following.

Proposition 11.

Let ${\left({\tau }_j\right)}_{j\in J}\subset IVNCT\left(X\right)$. Then ${\bigcap }_{j\in J}{\tau }_j\in IVNCT\left(X\right)$.

In fact, ${\bigcap }_{j\in J}{\tau }_j$ is the coarsest IVNCT on X containing each ${\tau }_j$.

Proposition 12.

Let $\tau ,\gamma \in IVNCT\left(X\right)$. We define $\tau \wedge \gamma$ and $\tau \vee \gamma$ as follows:

$$\tau \wedge \gamma =\{W:W\in \tau ,W\in \gamma \},$$

$$\tau \vee \gamma =\{W:W=U\cup V,U\in \tau ,V\in \gamma \}.$$

Then we have:

(1) 

$\tau \wedge \gamma$ is an IVNCT on X which is the finest IVNCT coarser than both τ and γ,

(2) 

$\tau \vee \gamma$ is an IVNCT on X which is the coarsest IVNCT finer than both τ and γ,

Proof. 

(1) Clearly, $\tau \wedge \gamma \in IVNCT\left(X\right).$ Let $\eta$ be any IVNCT on X which is coarser than both $\tau$ and $\gamma$, and let $W\in \eta$. Then $W\in \tau$ and $W\in \gamma$. Thus $W\in \tau \wedge \gamma$. So $\eta$ is coarser than $\tau \wedge \gamma$.

(2) The proof is similar to (1). ‎‎□‎‎

From Definition 17, Propositions 11 and 12, we can easily see that $\left(IVNCT\right(X),\subset )$ forms a complete lattice with the least element ${\tau }_{{}_{IVN,0}}$ and the greatest element ${\tau }_{{}_{IVN,1}}$.

A topology on a set can be a complicated collection of subsets of subsets of a set, and it can be difficult to describe the entire collection. In most cases, one describes a subcollection (called a base and a subbase) that “generates” the topology. Then we define a base and a subbase in an IVNCT. Moreover, we introduce the various intervals via IVNCSs in real line $\mathbb{R}$.

Definition 18.

Let $(X,\tau )$ be an IVNCTS.

(i) A subfamily β of τ is called an interval-valued neutrosophic crisp base (briefly, IVNCB) for τ, if for each $A\in \tau$, $A={\mathsf{\varnothing }}_{IVN}$ or there is ${\beta }^{{}^{\prime }}\subset \beta$ such that $A=\bigcup {\beta }^{{}^{\prime }}$.

(ii) A subfamily σ of τ is called an interval-valued neutrosophic crisp subbase (briefly, IVNCSB) for τ, if the family $\beta =\{\bigcap {\sigma }^{{}^{\prime }}:{\sigma }^{{}^{\prime }}\mathrm{is}\mathrm{a}\mathrm{finite}\mathrm{subset}\mathrm{of}\sigma \}$ is an IVNCB for τ.

Remark 3.

(1) Let β be an IVNCB for an IVNCT τ on a non-empty set X and consider three families of IVSs in X:

$${\beta }^T=\{[A^{T,-},A^{T,+}]\in IVS\left(X\right):A\in \beta \},{\beta }^I=\{[A^{I,-},A^{I,-}]\in IVS\left(X\right):A\in \beta \},$$

$${\beta }^F=\{[{A^{F,+}}^c,{A^{F,-}}^c]\in IVS\left(X\right):A\in \beta \}.$$

Then we can easily see that ${\beta }^T$, ${\beta }^I$, and ${\beta }^F$ are an interval-valued base (see [30]) for ${\tau }^T$, ${\tau }^I$, and ${\tau }^F$, respectively.

Furthermore, we can consider three intuitionistic base on X defined by cCoker [14]:

$${\beta }_{{}_T}=\{(A^{T,-},{A^{T,+}}^c)\in IS\left(X\right):A\in \beta \},{\beta }_{{}_I}=\{(A^{I,-},{A^{I,+}}^c]\in IS\left(X\right):A\in \beta \},$$

$${\beta }_{{}_F}=\{{A^{F,+}}^c,A^{F,-})\in IS\left(X\right):A\in \beta \}.$$

Let also us consider six families of ordinary subsets of X:

$${\beta }^{T,-}=\{A^{T,-}\subset X:A\in \beta \},{\beta }^{T,+}=\{A^{T,+}\subset X:A\in \beta \},$$

$${\beta }^{I,-}=\{A^{I,-}\subset X:A\in \beta \},{\beta }^{I,+}=\{A^{I,+}\subset X:A\in \beta \},$$

$${\beta }^{F,-}=\{{A^{T,+}}^c\subset X:A\in \beta \},{\beta }^{F,+}=\{{A^{I,-}}^c\subset X:A\in \beta \}.$$

Then clearly, ${\beta }^{T,-},{\beta }^{T,+},{\beta }^{I,+},{\beta }^{I,-},{\beta }^{F,-},{\beta }^{F,+}$ are ordinary bases for ordinary topologies ${\tau }^{T,-},{\tau }^{T,+},{\tau }^{I,+},{\tau }^{I,-},{\tau }^{F,-},{\tau }^{F,+}$ on X, respectively.

(2) Let σ be an IVNCSB for an IVNCT τ on a non-empty set X and consider three families of IVSs in X:

$${\sigma }^T=\{[A^{T,-},A^{T,+}]\in IVS\left(X\right):A\in \sigma \},{\sigma }^I=\{[A^{I,+},A^{I,-}]\in IVS\left(X\right):A\in \sigma \},$$

$${\sigma }^F=\{[{A^{F,+}}^c,{A^{F,-}}^c]\in IVS\left(X\right):A\in \sigma \}.$$

Then we can easily see that ${\sigma }^T$, ${\sigma }^I$, and ${\sigma }^F$ are an interval-valued subbases (see [30]) for ${\tau }^T$, ${\tau }^I$, and ${\tau }^F$, respectively.

Furthermore, we can consider three intuitionistic base on X defined by cCoker [14]:

$${\sigma }_T=\{(A^{T,-},{A^{T,+}}^c)\in IS\left(X\right):A\in \sigma \},{\sigma }_I=\{(A^{I,-},{A^{I,+}}^c]\in IS\left(X\right):A\in \sigma \},$$

$${\sigma }_F=\{{A^{F,+}}^c,A^{F,-})\in IS\left(X\right):A\in \sigma \}.$$

Let also us consider six families of ordinary subsets of X:

$${\sigma }^{T,-}=\{A^{T,-}\subset X:A\in \sigma \},{\sigma }^{T,+}=\{A^{T,+}\subset X:A\in \sigma \},$$

$${\sigma }^{I,-}=\{A^{I,-}\subset X:A\in \sigma \},{\sigma }^{I,+}=\{A^{I,+}\subset X:A\in \sigma \},$$

$${\sigma }^{F,-}=\{{A^{T,+}}^c\subset X:A\in \sigma \},{\sigma }^{F,+}=\{{A^{F,-}}^c\subset X:A\in \sigma \}.$$

Then clearly, ${\sigma }^{T,-},{\sigma }^{T,+},{\sigma }^{I,+},{\sigma }^{I,-},{\sigma }^{F,-},{\sigma }^{F,+}$ are ordinary subbases for ordinary topologies ${\tau }^{T,-},{\tau }^{T,+},{\tau }^{I,+},{\tau }^{I,-},{\tau }^{F,-},{\tau }^{F,+}$ on X, respectively.

Example 8.

(1) Let $\sigma =\{〈\left[\right(a,b),(a,\infty \left)\right],[\mathsf{\varnothing },\mathsf{\varnothing }],[\mathsf{\varnothing },(-\infty ,a\left]\right]〉:a,b\in \mathbb{R}\}$ be the family of IVNCs in $\mathbb{R}$. Then σ generates an IVNCT τ on $\mathbb{R}$ which is called the “usual left interval-valued neutrosophic crisp topology (briefly, ULIVNCT)” on $\mathbb{R}$. In fact, the IVNCB β for τ can be written in the form:

$$\beta =\left\{{\mathbb{R}}_{IVN}\right\}\cup \{{\cap }_{\gamma \in \mathsf{\Gamma }}{S}_{\gamma }:S_{\gamma }\in \sigma ,\mathsf{\Gamma }\mathrm{is}\mathrm{finite}\}$$

and τ consists of the following IVNCSs in $\mathbb{R}$:

$$\tau =\{{\mathsf{\varnothing }}_{IVN},{\mathbb{R}}_{IVN}\}\cup \left\{〈[\cup (a_j,b_j),(c,\infty )],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉\right\}$$

or

$$\tau =\{{\mathsf{\varnothing }}_{IVN},{\mathbb{R}}_{IVN}\}\cup \left\{〈[\cup (a_k,b_k),\mathbb{R}],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉\right\},$$

where $a_j,b_j,c\in \mathbb{R}$, $\{a_j:j\in J\}$ is bounded from below, $c<inf\{a_j:j\in J\}$ and $a_k,b_k\in \mathbb{R}$, $\{a_k:k\in K\}$ is not bounded from below.

Similarly, one can define the “usual right interval-valued neutrosophic crisp topology (briefly, URIVNCT)” on $\mathbb{R}$ using an analogue construction.

(2) Consider the family σ of IVNCSs in $\mathbb{R}$:

$\sigma =\{〈[(a,b),(a_1,\infty )\cap (-\infty ,b_1)],\tilde{\mathsf{\varnothing }},[\mathsf{\varnothing },(-\infty ,a_1]\cup [b_1,\infty ]〉$

$:a,b,a_1,b_1\in \mathbb{R},a_1\le a,b_1\ge b\}.$Then σ generates an IVNCT τ on $\mathbb{R}$ which is called the “usual interval-valued neutrosophic crisp topology (briefly, UIVNCT)” on $\mathbb{R}$. In fact, the IVNCB β for τ can be written in the form:

$$\beta =\left\{{\mathbb{R}}_{IVN}\right\}\cup \{{\cap }_{\gamma \in \mathsf{\Gamma }}{S}_{\gamma }:S_{\gamma }\in \sigma ,\mathsf{\Gamma }\mathrm{is}\mathrm{finite}\}$$

and the elements of τ can be easily written down as in (1).

(3) Consider the family ${\sigma }_{[0,1]}$ of IVNCSs in $\mathbb{R}$:

${\sigma }_{[0,1]}=\{〈[[a,b],[a,\infty )\cap (-\infty ,b]],\tilde{\mathsf{\varnothing }},[\mathsf{\varnothing },(-\infty ,a]\cup [b,\infty ]〉$

$:a,b\in \mathbb{R}\mathrm{and}0\le a\le b\le 1\}.$Then ${\sigma }_{[0,1]}$ generates an IVNCT ${\tau }_{[0,1]}$ on $\mathbb{R}$ which is called the “usual unit closed interval interval-valued neutrosophic crisp topology” on $\mathbb{R}$. In fact, the IVNCB ${\beta }_{[0,1]}$ for ${\tau }_{[0,1]}$ can be written in the form:

$${\beta }_{[0,1]}=\left\{{\mathbb{R}}_{IVN}\right\}\cup \{{\cap }_{\gamma \in \mathsf{\Gamma }}{S}_{\gamma }:S_{\gamma }\in \sigma {}_{[0,1]},\mathsf{\Gamma }\mathrm{is}\mathrm{finite}\}$$

and the elements of τ can be easily written down as in (1).

In this case, $([0,1],{\tau }_{[0,1]})$ is called the “interval-valued neutrosophic crisp nusual unit closed interval” and denoted by ${[0,1]}_{IVNCI}$. In fact,

$${[0,1]}_{IVNCI}=〈[[0,1],[0,\infty )\cup (-\infty ,1]],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉.$$

(4) Let $\beta =\{a_{{}_{IVN}}:a\in X\}\cup \{a_{{}_{IVNV}}:a\in X\}$. Then β is an IVNCB for the interval-valued neutrosophic crisp discrete topology ${\tau }_1$ on X.

(5) Let $X=\{a,b,c,d,e,f,g,h,i\}$ and consider the family β of IVNCSs in X given by:

$$\beta =\{A,B,X_{IVN}\},$$

where $A=〈\left[\right\{a,b\},\{a,b,c\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g,i\left\}\right]〉,$

$B=〈\left[\right\{a,d\},\{a,c,d\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉.$

Assume that β is an IVNCB for an IVNCT τ on X. Then by the definition of base, $\beta \subset \tau$. Thus $A,B\in \tau$. So $A\cap B=〈\left[\right\{a\},\{a,c\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉\in \tau$. However for any ${\beta }^{{}^{\prime }}\subset \beta$, $A\cap B\ne \bigcup {\beta }^{{}^{\prime }}$. Hence β is not an IVNCB for an IVNCT on X.

From (1), (2), and (3) in Example 8, we can define interval-valued neutrosophic crisp intervals as following.

Definition 19.

Let $a,b\in \mathbb{R}$ such that $a\le b$. Then:

(i) 

(The closed interval) ${[a,b]}_{IVNCI}=〈[[a,b],[a,-\infty )\cap (-\infty ,b]],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉$,

(ii) 

(The open interval) ${(a,b)}_{IVNCI}=〈[(a,b),(a,-\infty )\cap (-\infty ,b)],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉$,

(iii) 

(The half open interval or the half closed interval)

$${(a,b]}_{IVNCI}=〈[(a,b],(a,-\infty )\cap (-\infty ,b]],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$$

$${[a,b)}_{IVI}=〈[[a,b),[a,-\infty )\cap (-\infty ,b)],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$$

(iv) 

(The half interval-valued real line)

$${(-\infty ,a]}_{IVNCI}=〈[(-\infty ,a],(-\infty ,a]],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$$

$${(-\infty ,a)}_{IVNCI}=〈[(-\infty ,a),(-\infty ,a)],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$$

$${[a,\infty )}_{IVNCI}=〈[[a,\infty ),[a,\infty )],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$$

$${(a,\infty )}_{IVNCI}=〈[(a,\infty ),(a,\infty )],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉,$$

(v) 

(The interval-valued real line)

$${(-\infty ,\infty )}_{IVMCI}=〈[(-\infty ,\infty ),(-\infty ,\infty )],\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }}〉={\mathbb{R}}_{IVN}.$$

The following provide a necessary and sufficient condition which a collection of IVNCSs in a set X is an IVNCB for some IVNCT on X.

Theorem 1.

Let $\beta \subset IVNCS\left(X\right)$. Then β is an IVNCB for an IVNCT τ on X if and only if it satisfies the following properties:

(1) 

$X_{IVN}=\bigcup \beta$,

(2) 

If $B_1,B_2\in \beta$ and $a_{{}_{IVN}}\in B_1\cap B_2$ [resp. $a_{{}_{IVNV}}\in B_1\cap B_2$], then there exists $B\in \beta$ such that $a_{{}_{IVN}}\in B\subset B_1\cap B_2$ [resp. $a_{{}_{IVNV}}\in B\subset B_1\cap B_2$].

Proof. 

The proof is the same as one in classical topological spaces. ‎‎□‎‎

Example 9.

Let $X=\{a,b,c\}$ and consider the family of IVNCSs in X given by:

$$\beta =\{A_1,A_2,A_3,A_3\},$$

where $A_1=〈\left[\right\{b\},\{a,b\left\}\right],\left[\right\{b\},\{b\left\}\right],\left[\right\{c\},\{c\left\}\right]〉,$

$A_2=〈[\{b,c\},\{b,c\}],[\left\{a\right\},\left\{a\right\}],\tilde{\mathsf{\varnothing }}〉,$

$A_3=〈\left[\right\{a\},\{a\left\}\right],\left[\right\{c\},\{c\left\}\right],\left[\right\{b\},\{b\left\}\right]〉,$

$A_4=〈[\left\{b\right\},\tilde{\mathsf{\varnothing }},[\left\{c\right\},\left\{c\right\}]〉,$

Then clearly, β satisfies two conditions of Theorem 1. Thus β is an IVNCB for an IVNCT τ on X. In fact, we have:

$$\tau =\{{\mathsf{\varnothing }}_{IVN},A_1,A_2,A_3,A_4,A_5,A_6,A_7,X_{IVN}\},$$

where $A_5=〈[\{b,c\},X],[\{a,b\},\{a,b\}],\tilde{\mathsf{\varnothing }}〉,$

$A_6=〈[\{a,b\},\{a,b\}],[\{b,c\},\{b,c\}],\tilde{\mathsf{\varnothing }}〉,$

$A_7=〈\tilde{X},[\{a,c\},\{a,c\}],\tilde{\mathsf{\varnothing }}〉.$

The following provide a sufficient condition which a collection of IVNCSs in a set X is an IVNCB for some IVNCT on X.

Proposition 13.

Let $\sigma \subset IVNCS\left(X\right)$ such that $X_{IVN}=\bigcup \sigma$. Then there exists a unique IVNCT τ on X such that σ is an IVNCSB for τ.

Proof. 

Let $\beta =\{B\in IVNCS\left(X\right):B={\bigcap }_{i=1}^n{S}_i\mathrm{and}{S}_i\in \sigma \}$. Let $\tau =\{U\in IVNCS\left(X\right):U=\tilde{\mathsf{\varnothing }}\text{or there is a subcollection}{\beta }^{{}^{\prime }}\mathrm{of}\beta \text{such that}U=\bigcup {\beta }^{{}^{\prime }}\}$. Then we can show that $\tau$ is the unique IVNCT on X such that $\sigma$ is an IVNCSB for $\tau$. ‎‎□‎‎

In Proposition 13, $\tau$ is called the IVNCT on X generated by $\sigma$.

Example 10.

Let $X=\{a,b,c,d,e\}$ and consider the family σ of IVNCSs in X given by:

$$\sigma =\{A_1,A_2,A_3,A_4\},$$

where $A_1=〈\left[\right\{a\},\{a\left\}\right],\left[\right\{b\},\{b\left\}\right],\left[\right\{c,d\},\{c,d\left\}\right]〉,$

$A_2=〈\left[\right\{a,b,c\},\{a,b,c\left\}\right],\left[\right\{b,d\},\{b,d\left\}\right],\left[\right\{e\},\{e\left\}\right]〉,$

$A_3=〈\left[\right\{b,c,e\},\{b,c,e\left\}\right],\left[\right\{c,e\},\{c,d,e\left\}\right],\left[\right\{d\},\{d\left\}\right]〉,$

$A_4=〈\left[\right\{c,d\},\{c,d\left\}\right],\left[\right\{a,c\},\{a,c\left\}\right],\left[\right\{a,b\},\{a,b\left\}\right]〉.$

Then clearly, $\bigcup \sigma =X_{IVN}$. Let β be the collection of all finite intersections of members of σ. Then we have:

$$\beta =\{A_1,A_2,A_3,A_4,A_5,A_6,A_7,A_8,A_9,A_{10},A_{11},A_{12}\},$$

where $A_5=〈\left[\right\{a\},\{a\left\}\right],\left[\right\{b\},\{b\left\}\right],\left[\right\{c,d,e\},\{c,d,e\left\}\right]〉,$

$A_6=〈\tilde{\mathsf{\varnothing }},[\left\{b\right\},\left\{b\right\}],[\{c,d\},\{c,d\}]〉,$

$A_7=〈\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }},[\{a,b,c,d\},\{a,b,c,d\}]〉,$

$A_8=〈\left[\right\{b,c\},\{b,c\left\}\right],[\mathsf{\varnothing },\{d\left\}\right],\left[\right\{d,e\},\{d,e\left\}\right]〉,$

$A_9=〈[\left\{c\right\},\left\{c\right\}],\tilde{\mathsf{\varnothing }},[\{a,b,e\},\{a,b,e\}]〉,$

$A_{10}=〈\left[\right\{c\},\{c\left\}\right],\left[\right\{c\},\{c\left\}\right],\left[\right\{a,b,d\},\{a,b,d\left\}\right]〉,$

$A_{11}=〈\tilde{\mathsf{\varnothing }},\tilde{\mathsf{\varnothing }},[\{c,d,e\},\{c,d,e\}]〉,$

$A_{12}=〈[\left\{c\right\},\left\{c\right\}],\tilde{\mathsf{\varnothing }},[\{a,b,d,e\},\{a,b,d,e\}]〉.$

Thus we have the generated IVNCT τ by σ:

$\tau =\{{\mathsf{\varnothing }}_{IVN},A_1,A_2,A_3,A_4,A_5,A_6,A_7,A_8,A_9,A_{10},A_{11},A_{12},A_{13},A_{14},A_{15},A_{16},A_{17},A_{18},X_{IVN}\},$

where $A_{13}=〈[\{a,b,c\},\{a,b,c\}],[\{b,d\},\{b,d\}],\tilde{\mathsf{\varnothing }}〉,$

$A_{14}=〈\left[\right\{a,b,c,e\},\{a,b,c,e\left\}\right],\left[\right\{b,c,e\},\{b,c,d,e\left\}\right],\left[\right\{d\},\{d\left\}\right]〉,$

$A_{15}=〈[\{a,c,d\},\{a,c,d\}],[\{a,b,c\},\{a,b,c\}],\tilde{\mathsf{\varnothing }}〉,$

$A_{16}=〈[\{a,b,c,e\},\{a,b,c,e\}],[\{b,c,d,e\},\{b,c,d,e\}],\tilde{\mathsf{\varnothing }}〉,$

$A_{17}=〈[\{a,b,c,d\},\{a,b,c,d\}],[\{a,b,c,d\},\{a,b,c,d\}],\tilde{\mathsf{\varnothing }}〉,$

$A_{18}=〈\tilde{X},[\{a,c,e\},\{a,c,e\}],\tilde{\mathsf{\varnothing }}〉.$

Remark 4.

By using “${\subset }_2,{\cup }_2,{\cap }_2,{}^{i,c}(i=1,2,3),{\mathsf{\varnothing }}_{2,IN},X_{2,IN}$, and $INC\left(X\right)$, we can have the definitions corresponding to Definitions 16 and 18, respectively.

5. Interval-Valued Neutrosophic Crisp Neighborhoods

In this section, we introduce the concept of interval-valued neutrosophic crisp neighborhoods of IVNPs of two types, and find their various properties and give some examples.

Definition 20.

Let X be an IVNCTS, $a\in X$, $N\in IVNCS\left(X\right)$. Then:

(i) N is called an interval-valued neutrosophic crisp neighborhood (briefly, IVNCN) of $a_{{}_{IVN}}$, if there exists a $U\in IVNCO\left(X\right)$ such that:

$$a_{{}_{IVN}}\in U\subset N,i.e.,a\in U^{T,-}\subset N^{T,-},$$

(ii) N is called an interval-valued neutrosophic crisp vanishing neighborhood (briefly, IVNCVN) of $a_{{}_{IVNV}}$, if there exists a $U\in IVNCO\left(X\right)$ such that:

$$a_{{}_{IVNV}}\in U\subset N,i.e.,a\notin N^{F,+}\subset U^{F,+}.$$

The set of all IVNCNs [resp. IVNCVNs] of $a_{{}_{IVN}}$ [resp. $a_{{}_{IVNV}}$] is denoted by $N\left(a_{{}_{IVN}}\right)$ [resp. $N{(}_{{}_{IVNV}})$] and will be called an IVNC neighborhood system of $a_{{}_{IVN}}$ [resp. $a_{{}_{IVNV}}$].

Example 11.

Let $X=\{a,b,c,d,e,f,g,h,i\}$ and let τ be the IVNCT on X given in Example 7 (4). Consider the IVNCS $N=〈\left[\right\{a,b,d\},\{a,b,c,d\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g\},\{g\left\}\right]〉$ in X. Then we can easily check that:

$N\in N\left(a_{{}_{IVN}}\right)\cap N\left(a_{{}_{IVNV}}\right),N\in N\left(b_{{}_{IVN}}\right)\cap N\left(b_{{}_{IVNV}}\right),$

$N\in N\left(d_{{}_{IVN}}\right)\cap N\left(d_{{}_{IVNV}}\right),N\in N\left(c_{{}_{IVNV}}\right).$

An IVNC neighborhood system of $a_{{}_{IVN}}$ has a similar property for a neighborhood system of a point in a classical topological space.

Proposition 14.

Let X be an IVNCTS, $a\in X$.

[IVNCN1]

If $N\in N\left(a_{{}_{IVN}}\right)$, then $a_{{}_{IVN}}\in N$.

[IVNCN2]

If $N\in N\left(a_{{}_{IVN}}\right)$ and $N\subset M$, then $M\in N\left(a_{{}_{IVN}}\right)$.

[IVNCN3]

If $N,M\in N\left(a_{{}_{IVN}}\right)$, then $N\cap M\in N\left(a_{{}_{IVN}}\right)$.

[IVNCN4]

If $N\in N\left(a_{{}_{IVN}}\right)$, then there exists $M\in N\left(a_{{}_{IVN}}\right)$ such that $N\in N\left(b_{IVN}\right)$ for each $b_{IVN}\in M$.

Proof. 

The proofs of [IVNCN1], [IVNCN2], and [IVNCN4] are easy.

[IVNCN3] Suppose $N,M\in N\left(a_{{}_{IVN}}\right)$. Then there are $U,V\in IVNCO\left(X\right)$ such that $a_{{}_{IVN}}\in U\subset Nand{a}_{{}_{IVN}}\in V\subset M.$ Let $W=U\cap V$. Then clearly, $W\in IVNCO\left(X\right)$ and $a_{{}_{IVN}}\in W\subset N\cap M$. Thus $N\cap M\in N\left(a_{{}_{IVN}}\right)$. ‎‎□‎‎

In addition, an IVNC neighborhood system of $a_{{}_{IVNV}}$ has the similar property.

Proposition 15.

Let X be an IVNCTS, $a\in X$.

[IVNCVN1]

If $N\in N\left(a_{{}_{IVNV}}\right)$, then $a_{{}_{IVNV}}\in N$.

[IVNCVN2]

If $N\in N\left(a_{{}_{IVNV}}\right)$ and $N\subset M$, then $M\in N\left(a_{{}_{IVNV}}\right)$.

[IVNCVN3]

If $N,M\in N\left(a_{{}_{IVNV}}\right)$, then $N\cap M\in N\left(a_{{}_{IVNV}}\right)$.

[IVNCVN4]

If $N\in N\left(a_{{}_{IVNV}}\right)$, then there exists $M\in N\left(a_{{}_{IVNV}}\right)$ such that $N\in N\left(b_{{}_{IVNV}}\right)$ for each $b_{{}_{IVNV}}\in M$.

Proof. 

The proof is similar to one of Proposition 15. ‎‎□‎‎

From Definition 20, we have two IVNCTs containing a given IVNCT.

Proposition 16.

Let $(X,\tau )$ be an IVNCTS and let us define two families:

$${\tau }_{{}_{IVN}}=\{U\in IVNCS\left(X\right):U\in N\left(a_{{}_{IVN}}\right)foreach{a}_{{}_{IVN}}\in U\}$$

and

$${\tau }_{{}_{IVNV}}=\{U\in IVNCS\left(X\right):U\in N\left(a_{{}_{IVNV}}\right)foreach{a}_{{}_{IVNV}}\in U\}.$$

Then we have:

(1)${\tau }_{{}_{IVN}},{\tau }_{{}_{IVNV}}\in IVNCT\left(X\right)$,

(2)$\tau \subset {\tau }_{{}_{IVN}}$ and $\tau \subset {\tau }_{{}_{IVNV}}$.

Proof. 

(1) We only prove that ${\tau }_{{}_{IVNV}}\in IVNCT\left(X\right)$.

(IVNCO${}_1$) From the definition of ${\tau }_{{}_{IVNV}}$, we have ${\mathsf{\varnothing }}_{IVN},X_{IVN}\in {\tau }_{{}_{IVNV}}.$

(IVNCO${}_2$) Let $U,V\in IV{N}^{*}\left(X\right)$ such that $U,V\in {\tau }_{{}_{IVNV}}$ and let $a_{{}_{IVNV}}\in U\cap V.$ Then clearly, $U,V\in N\left(a_{{}_{IVNV}}\right)$. Thus by [IVNCVN3], $U\cap V\in N\left(a_{{}_{IVNV}}\right).$ So $U\cap V\in {\tau }_{{}_{IVNV}}$.

(IVNCO${}_3$) Let ${\left(U_j\right)}_{j\in J}$ be any family of IVNCSs in ${\tau }_{{}_{IVNV}}$, let $U={\bigcup }_{j\in J}{U}_j$ and let $a_{{}_{IVNV}}\in U$. Then by Proposition 7 (2), there is $j_0\in J$ such that $a_{{}_{IVNV}}\in U_{j_0}$. Since $U_{j_0}\in {\tau }_{{}_{IVNV}}$, $U_{j_0}\in N\left(a_{{}_{IVNV}}\right)$ by the definition of ${\tau }_{{}_{IVNV}}$. Since $U_{j_0}\subset U$, $U\in N\left(a_{{}_{IVNV}}\right)$ by [IVNCVN2]. So by the definition of ${\tau }_{{}_{IVNV}}$, $U\in {\tau }_{{}_{IVNV}}$.

(2) Let $U\in \tau$. Then clearly, $U\in N\left(a_{{}_{IVN}}\right)$ and $U\in N\left(a_{{}_{IVNV}}\right)$ for each $a_{{}_{IVN}}\in G$ and $a_{{}_{IVNV}}\in G$, respectively. Thus $U\in {\tau }_{{}_{IVN}}$ and $U\in {\tau }_{{}_{IVNV}}$. So the results hold. ‎‎□‎‎

Remark 5.

(1) From the definitions of ${\tau }_{IVN}$ and ${\tau }_{IVNV}$, we can easily have:

$${\tau }_{{}_{IVN}}=\tau \cup \{U\in IVNCS\left(X\right):V^{T,-}\subset U^{T,-},V\in \tau \}$$

and

$${\tau }_{{}_{IVNV}}=\tau \cup \{U\in IVNCS\left(X\right):U^{F,+}\subset V^{F,+},V\in \tau \}.$$

(2) For any IVNCT τ on a set X, we can have six IVTs on X given by:

$${\tau }_{{}_{IVN}}^T=\{[U^{T,-},U^{T,+}]\in IVS\left(X\right):U\in {\tau }_{{}_{IVN}}\},$$

$${\tau }_{{}_{IVN}}^I=\{[U^{I,-},U^{I,+}]\in IVS\left(X\right):U\in {\tau }_{{}_{IVN}}$$

$${\tau }_{{}_{IVN}}^F=\{[{U^{F,+}}^c,{U^{F,-}}^c]\in IVS\left(X\right):U\in {\tau }_{{}_{IVN}}\},$$

$${\tau }_{{}_{IVNV}}^T=\{[U^{T,-},U^{T,-}]\in IVS\left(X\right):U\in {\tau }_{{}_{IVNV}}\},$$

$${\tau }_{{}_{IVNV}}^I=\{[U^{I,-},U^{I,+}]\in IVS\left(X\right):U\in {\tau }_{{}_{IVNV}}\},$$

$${\tau }_{{}_{IVNV}}^F=\{[{U^{F,+}}^c,U^{F,+}]\in IVS\left(X\right):U\in {\tau }_{{}_{IVNV}}\}.$$

Furthermore, we have 12 ordinary topologies on X:

$${\tau }_{{}_{IVN}}^{T,-}=\{U^{T,-}\subset X:U\in {\tau }_{{}_{IVN}}\},{\tau }_{{}_{IVN}}^{T,+}=\left\{U^{T,+}\right]\subset X:U\in {\tau }_{{}_{IVN}}\},$$

$${\tau }_{{}_{IVN}}^{I,-}=\{U^{I,-}\subset X:U\in {\tau }_{{}_{IVN}}\},{\tau }_{{}_{IVN}}^{I,+}=\left\{U^{I,+}\right]\subset X:U\in {\tau }_{{}_{IVN}}\},$$

$${\tau }_{{}_{IVN}}^{F,-}=\{{U^{F,+}}^c\subset X:U\in {\tau }_{{}_{IVN}}\},{\tau }_{{}_{IVN}}^{F,+}=\{{U^{F,-}}^c\subset X:U\in {\tau }_{{}_{IVN}}\},$$

$${\tau }_{{}_{IVNV}}^{T,-}=\{U^{T,-}\subset X:U\in {\tau }_{{}_{IVNV}}\},{\tau }_{{}_{IVNV}}^{T,+}=\{U^{T,-}\subset X:U\in {\tau }_{{}_{IVNV}}\},$$

$${\tau }_{{}_{IVNV}}^{I,-}=\{U^{I,-}\subset X:U\in {\tau }_{{}_{IVNV}}\},{\tau }_{{}_{IVNV}}^{I,+}=\{U^{I,+}\subset X:U\in {\tau }_{{}_{IVNV}}\},$$

$${\tau }_{{}_{IVNV}}^{F,-}=\{{U^{F,+}}^c\subset X:U\in {\tau }_{{}_{IVNV}}\},{\tau }_{{}_{IVNV}}^{F,+}=\{U^{F,+}\subset X:U\in {\tau }_{{}_{IVNV}}\}.$$

Example 12.

Let $X=\{a,b,c,d,e,f,g,h,i\}$ and consider IVNCT τ on X given in Example 7 (4). Then from Remark 5 ((1), we have:

$${\tau }_{{}_{IVN}}=\tau \cup \{A_5,A_6,A_7\},$$

where $A_5=〈\left[\right\{a,b,c\},\{a,b,c\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g,i\left\}\right]〉,$

$A_6=〈\left[\right\{a,c,d\},\{a,c,d\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g,h\},\{g,h,i\left\}\right]〉,$

$A_7=〈\left[\right\{a,b,c,d\},\{a,b,c,d\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g,i\left\}\right]〉.$

Additionally, we have:

$${\tau }_{{}_{IVNV}}=\tau \cup \{A_8,A_9,A_{10},A_{11}\},$$

where $A_8=〈\left[\right\{a,b\},\{a,b,c\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g\left\}\right]〉,$

$A_9=〈\left[\right\{a,d\},\{a,c,d\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g,h\},\{g,h\left\}\right]〉,$

$A_{10}=〈\left[\right\{a\},\{a,c\left\}\right],\left[\right\{e\},\{e\left\}\right],\left[\right\{g\},\{g,h\left\}\right]〉,$

$A_{11}=〈\left[\right\{a,b,d\},\{a,b,c,d\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g\left\}\right]〉.$

So we can confirm that Proposition 16 holds.

Furthermore, we can obtain six IVTs on X for τ:

$${\tau }_{{}_{IVN}}^T,{\tau }_{{}_{IVN}}^I,{\tau }_{{}_{IVN}}^F,{\tau }_{{}_{IVNV}}^T,{\tau }_{{}_{IVNV}}^I,{\tau }_{{}_{IVNV}}^F.$$

Additionally, we have 12 ordinary topologies on X:

$${\tau }_{{}_{IVN}}^{T,-},{\tau }_{{}_{IVN}}^{T,+},{\tau }_{{}_{IVN}}^{I,-},{\tau }_{{}_{IVN}}^{I,+},{\tau }_{{}_{IVN}}^{F,-},{\tau }_{{}_{IVN}}^{F,+},$$

$${\tau }_{{}_{IVNV}}^{T,-},{\tau }_{{}_{IVNV}}^{T,+},{\tau }_{{}_{IVNV}}^{I,-},{\tau }_{{}_{IVNV}}^{I,+},{\tau }_{{}_{IVNV}}^{F,-},{\tau }_{{}_{IVNV}}^{F,+}.$$

The following is the immediate result of Proposition 16 (2).

Corollary 1.

Let $(X,\tau )$ be an IVNCTS and let $IVNC{C}_{\tau }$ [resp. $IVNC{C}_{{\tau }_{{}_{IVN}}}$ and $IVNC{C}_{{\tau }_{{}_{IVNV}}}$] be the set of all IVNCCSs w.r.t. τ [resp. ${\tau }_{{}_{IVN}}$ and ${\tau }_{{}_{IVNV}}$]. Then,

$$IVNC{C}_{\tau }\subset IVNC{C}_{{\tau }_{{}_{IVN}}},\mathrm{and}IVNC{C}_{\tau }\subset IVNC{C}_{{\tau }_{{}_{IVNV}}}.$$

Example 13.

Let $(X,\tau )$ be the IVNCTS given in Example 12. Then we have:

$IVNC{C}_{\tau }=\{{\mathsf{\varnothing }}_{IVN},X_{IVN},A_1^c,A_2^c,A_3^c,A_4^c\},$

$IVNC{C}_{{\tau }_{{}_{IVN}}}=IVNC{C}_{\tau }\cup \{A_5^c,A_6^c,A_7^c\},$

$IV{C}_{{\tau }_{{}_{IVNV}}}=IV{C}_{\tau }\cup \{A_8^c,A_9^c,A_{10}^c,A_{11}^c\},$

where $A_1^c=〈\left[\right\{g\},\{g,i\left\}\right],\left[\right\{a,b,c,d,h\},\{a,b,c,d,f,h\left\}\right],\left[\right\{a,b\},\{a,b,c\left\}\right]〉,$

$A_2^c=〈\left[\right\{g,h\},\{g,h,i\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a,d\},\{a,c,d\left\}\right]〉,$

$A_3^c=〈\left[\right\{g,h\},\{g,h,i\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a\},\{a,c\left\}\right]〉,$

$A_4^c=〈\left[\right\{g\},\{g,i\left\}\right],\left[\right\{a,b,c,d,h\},\{a,b,c,d,f,h\left\}\right],\left[\right\{a,b,d\},\{a,b,c,d\left\}\right]〉,$

$A_5^c=〈\left[\right\{g\},\{g,i\left\}\right],\left[\right\{a,b,c,d,h\},\{a,b,c,d,f,h\left\}\right],\left[\right\{a,b,c\},\{a,b,c\left\}\right]〉,$

$A_6^c=〈\left[\right\{g,h\},\{g,h,i\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a,c,d\},\{a,c,d\left\}\right]〉,$

$A_7^c=〈\left[\right\{g\},\{g,i\left\}\right],\left[\right\{a,b,c,d,h\},\{a,b,c,d,f,h\left\}\right],\left[\right\{a,b,c,d\},\{a,b,c,d\left\}\right]〉,$

$A_8^c=〈\left[\right\{g\},\{g\left\}\right],\left[\right\{a,b,c,d,h\},\{a,b,c,d,f,h\left\}\right],\left[\right\{a,b\},\{a,b,c\left\}\right]〉,$

$A_9^c=〈\left[\right\{g,h\},\{g,h\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a,d\},\{a,c,d\left\}\right]〉,$

$A_{10}^c=〈\left[\right\{g\},\{g,h\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a\},\{a,c\left\}\right]〉,$

$A_{11}^c=〈\left[\right\{g\},\{g\left\}\right],\left[\right\{a,b,c,d,h\},\{a,b,c,d,f,h\left\}\right],\left[\right\{a,b,d\},\{a,b,c,d\left\}\right]〉.$

Thus we can confirm that Corollary 1 holds.

Now let us consider the converses of Propositions 14 and 15.

Proposition 17.

Suppose to each $a\in X$, there corresponds a set $N^{*}\left(a_{{}_{IVNV}}\right)$ of IVNCSs in X satisfying the conditions [IVNCVN1], [IVNCVN2], [IVNCVN3], and [IVNCVN4] in Proposition 15. Then there is an IVNCT on X such that $N^{*}\left(a_{{}_{IVNV}}\right)$ is the set of all IVNCVNs of $a_{{}_{IVNV}}$ in this IVNCT for each $a\in X$.

Proof. 

Let,

$${\tau }_{{}_{IVNV}}=\{U\in IVNCS\left(X\right):U\in N\left(a_{{}_{IVNV}}\right)\mathrm{for}\mathrm{each}{a}_{{}_{IVNV}}\in U\},$$

where $N\left(a_{{}_{IVNV}}\right)$ denotes the set of all IVNCVNs in $\tau$.

Then clearly, ${\tau }_{{}_{IVNV}}\in IVNCT\left(X\right)$ by Proposition 16. We will prove that $N^{*}\left(a_{{}_{IVNV}}\right)$ is the set of all IVNCVNs of $a_{{}_{IVNV)}}$ in ${\tau }_{{}_{IVNV}}$ for each $a\in X$.

Let $V\in IV{N}^{*}\left(X\right)$ such that $V\in N^{*}\left(a_{{}_{IVNV}}\right)$ and let U be the union of all the IVNCVPs $b_{{}_{IVNV}}$ in X such that $U\in N^{*}\left(a_{{}_{IVNV}}\right)$. If we can prove that:

$$a_{{}_{IVNV}}\in U\subset V\mathrm{and}U\in {\tau }_{{}_{IVNV}},$$

then the proof will be complete.

Since $V\in N_{*}\left(a_{{}_{IVNV}}\right)$, $a_{{}_{IVNV}}\in U$ by the definition of U. Moreover, $U\subset V$. Suppose $b_{{}_{IVNV}}\in U$. Then by [IVNCVN4], there is an IVNCS $W\in N^{*}\left(b_{{}_{IVNV}}\right)$ such that $V\in N^{*}\left(c_{{}_{IVNV)}}\right)$ for each $c_{{}_{IVNV}}\in W$. Thus $c_{{}_{IVNV}}\in U$. By Proposition 9, $W\subset U$. So by [IVNCVN2], $U\in N^{*}\left(b_{{}_{IVNV}}\right)$ for each $b_{{}_{IVNV}}\in U$. Hence by the definition of ${\tau }_{{}_{IVNV}}$, $U\in {\tau }_{{}_{IVNV}}$. This completes the proof. ‎‎□‎‎

Proposition 18.

Suppose to each $a\in X$, there corresponds a set $N^{*}\left(a_{{}_{IVN}}\right)$ of IVNCSs in X satisfying the conditions [IVNCN1], [IVNCN2], [IVNCN3], and [IVNCN4] in Proposition 14. Then there is an IVNCT on X such that $N^{*}\left(a_{{}_{IVN}}\right)$ is the set of all IVNCNs of $a_{{}_{IVN)}}$ in this IVNCT for each $a\in X$.

Proof. 

The proof is similar to Proposition 17. ‎‎□‎‎

The following provide a necessary and sufficient condition which an IVNCSs is an IVNCOS in an IVNCTS.

Theorem 2.

Let $(X,\tau )$ be an IVNCTS, $A\in IVNCS\left(X\right)$. Then $A\in \tau$ if and only if $A\in N\left(a_{{}_{IVN}}\right)$ and $A\in N\left(a_{{}_{IVNV}}\right)$ for each $a_{{}_{IVN}},a_{{}_{IVNV}}\in A$.

Proof. 

Suppose $A\in N\left(a_{{}_{IVN}}\right)$ and $A\in N\left(a_{{}_{IVNV}}\right)$ for each $a_{{}_{IVN}},a_{{}_{IVNV}}\in A$. Then there are $U_{a_{{}_{IVN}}},V_{a_{{}_{IVNV}}}\in \tau$ such that $a_{{}_{IVN}}\in U_{a_{{}_{IVN}}}\subset A$ and $a_{{}_{IVNV}}\in V_{a_{{}_{IVNV}}}\subset A$. Thus,

$$A=\left(\bigcup _{a_{{}_{IVN}}\in A}{a}_{{}_{IVN}}\right)\cup \left(\bigcup _{a_{{}_{IVNV}}\in A}{a}_{{}_{IVNV}}\right)\subset \left(\bigcup _{a_{{}_{IVN}}\in A}{U}_{a_{{}_{IVN}}}\right)\cup \left(\bigcup _{a_{{}_{IVNV}}\in A}{V}_{a_{{}_{IVNV}}}\right)\subset A.$$

So $A=\left({\bigcup }_{a_{{}_{IVN}}\in A}{U}_{a_{{}_{IVN}}}\right)\cup \left({\bigcup }_{a_{{}_{IVNV}}\in A}{V}_{a_{{}_{IVNV}}}\right).$ Since $U_{a_{{}_{IVN}}},V_{a_{{}_{IVNV}}}\in \tau$, $A\in \tau$.

The proof of the necessary condition is easy. ‎‎□‎‎

Now we will give the relation among three IVNCTs, $\tau$, ${\tau }_{{}_{IVN}}$ and ${\tau }_{{}_{IVNV}}$.

Proposition 19.

$\tau ={\tau }_{{}_{IVN}}\cap {\tau }_{{}_{IVNV}}.$

Proof. 

From Proposition 16 (2), it is clear that $\tau \subset {\tau }_{{}_{IVN}}\cap {\tau }_{{}_{IVNV}}.$

Conversely, let $U\in {\tau }_{{}_{IVN}}\cap {\tau }_{{}_{IVNV}}.$ Then clearly, $U\in {\tau }_{{}_{IVN}}$ and $U\in {\tau }_{{}_{IVNV}}.$ Thus U is an IVNCN of each of its IVNCPs $a_{{}_{IVN}}$ and an IVNCVN of each of its IVNCVPs $a_{{}_{IVNV}}$. Thus, there are $U_{a_{{}_{IVN}}},U_{a_{{}_{IVNV}}}\in \tau$ such that $a_{{}_{IVN}}\in U_{a_{{}_{IVN}}}\subset U$ and $a_{{}_{IVNV}}\in U_{a_{{}_{IVNV}}}\subset U$. So we have:

$$U_{IVN}=\bigcup _{a_{{}_{IVN}}\in U}{a}_{{}_{IVN}}\subset \bigcup _{a_{{}_{IVN}}\in U}{U}_{a_{{}_{IVN}}}\subset U$$

and

$$U_{IVNV}=\bigcup _{a_{{}_{IVNV}}\in U}{a}_{{}_{IVNV}}\subset \bigcup _{a_{{}_{IVNV}}\in U}{U}_{a_{{}_{IVNV}}}\subset U.$$

By Proposition 5, we get:

$$U=U_{IVN}\cup U_{IVNV}\subset \left(\bigcup _{a_{{}_{IVN}}\in U}{U}_{a_{{}_{IVN}}}\right)\cup \left(\bigcup _{a_{{}_{IVNV}}\in U}{U}_{a_{{}_{IVNV}}}\right)\subset U,i.e.,$$

$$U=\left(\bigcup _{a_{{}_{IVN}}\in U}{U}_{a_{{}_{IVN}}}\right)\cup \left(\bigcup _{a_{{}_{IVNV}}\in U}{U}_{a_{{}_{IVNV}}}\right).$$

It is obvious that $\left({\bigcup }_{a_{{}_{IVN}}\in U}{U}_{a_{{}_{IVN}}}\right)\cup \left({\bigcup }_{a_{{}_{IVNV}}\in U}{U}_{a_{{}_{IVNV}}}\right)\in \tau .$ Hence $U\in \tau .$ Therefore ${\tau }_{{}_{IVN}}\cap {\tau }_{{}_{IVNV}}\subset \tau .$ This completes the proof. ‎‎□‎‎

From Proposition 19, we get the following.

Corollary 2.

Let $(X,\tau )$ be an IVNCTS. Then,

$$IVNC{C}_{\tau }=IVNC{C}_{{\tau }_{{}_{IVN}}}\cap IVNC{C}_{{\tau }_{{}_{IVNV}}}.$$

Example 14.

In Example 12, we can easily check that Corollary 2 holds.

6. Interiors and Closures of IVNCSs

In this section, we define interval-valued neutrosophic crisp interiors and closures, and investigate some of their properties and give some examples. In particular, we will show that there is a unique IVNCT on a set X from the interval-valued neutrosophic crisp closure [resp. interior] operator.

In an IVNCTS, we can define a closure and an interior as well as two other types of closures and interiors by Proposition 16.

Definition 21.

Let $(X,\tau )$ be an IVNCTS, $A\in IVNCS\left(X\right)$.

(i) 

The interval-valued neutrosophic crisp closure of A w.r.t. τ, denoted by $IVNcl\left(A\right)$, is an IVNCS in X defined as:

$$IVNcl\left(A\right)=\bigcap \{K:K^c\in \tau \mathrm{and}A\subset K\}.$$

(ii) 

The interval-valued neutrosophic crisp interior of A w.r.t. τ, denoted by $IVNint\left(A\right)$, is an IVS in X defined as:

$$IVNint\left(A\right)=\bigcup \{G:G\in \tau \mathrm{and}G\subset A\}.$$

(iii) 

The interval-valued neutrosophic crisp closure of A w.r.t. ${\tau }_{{}_{IVN}}$, denoted by $c{l}_{{}_{IVN}}\left(A\right)$, is an IVNCS in X defined as:

$$c{l}_{{}_{IVN}}\left(A\right)=\bigcap \{K:K^c\in {\tau }_{{}_{IVN}}\mathrm{and}A\subset K\}.$$

(iv) 

The interval-valued neutrosophic crisp interior of A w.r.t. ${\tau }_{{}_{IVN}}$, denoted by $in{t}_{{}_{IVN}}\left(A\right)$, is an IVS in X defined as:

$$in{t}_{{}_{IVN}}\left(A\right)=\bigcup \{G:G\in {\tau }_{{}_{IVN}}\mathrm{and}G\subset A\}.$$

(v) 

The interval-valued neutrosophic crisp closure of A w.r.t. ${\tau }_{{}_{IVNV}}$, denoted by $c{l}_{{}_{IVNV}}\left(A\right)$, is an IVNCS in X defined as:

$$c{l}_{{}_{IVNV}}\left(A\right)=\bigcap \{K:K^c\in {\tau }_{{}_{IVNV}}\mathrm{and}A\subset K\}.$$

(vi) 

The interval-valued neutrosophic crisp interior of A w.r.t. ${\tau }_{{}_{IVNV}}$, denoted by $in{t}_{{}_{IVNV}}\left(A\right)$, is an IVNCS in X defined as:

$$in{t}_{{}_{IVNV}}(A=\bigcup \{G:G\in {\tau }_{{}_{IVNV}}\mathrm{and}G\subset A\}.$$

Remark 6.

From the above definition, it is obvious that the followings hold:

$$IVNint\left(A\right)\subset in{t}_{{}_{IVN}}\left(A\right),IVNint\left(A\right)\subset in{t}_{{}_{IVNV}}\left(A\right)$$

and

$$c{l}_{{}_{IVN}}\left(A\right)\subset IVNcl\left(A\right),c{l}_{{}_{IVNV}}\left(A\right)\subset IVNcl\left(A\right).$$

Example 15.

Let $(X,\tau )$ be the IVNCTS given in Examples 12 and 13. Consider two IVNCSs in X:

$$A=〈\left[\right\{a,b,c\},\{a,b,c,d\left\}\right],\left[\right\{a,e\},\{a,e,f\left\}\right],\left[\right\{g\},\{g\left\}\right]〉,$$

$$B=〈\left[\right\{g,h\},\{g,h,i\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,e,f\left\}\right],\left[\right\{a\},\{a,c\left\}\right]〉.$$

Then,

$IVNint\left(A\right)=\bigcup \{G\in \tau :G\subset A\}=A_1\cup A_3=〈\left[\right\{a,b\},\{a,b,c\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g,i\left\}\right]〉,$

$in{t}_{{}_{IVN}}\left(A\right)=\bigcup \{G\in {\tau }_{{}_{IVN}}:G\subset A\}=A_1\cup A_3\cup A_5$

$=〈\left[\right\{a,b,c\},\{a,b,c\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g,i\left\}\right]〉,$

$in{t}_{{}_{IVNV}}\left(A\right)=\bigcup \{G\in {\tau }_{{}_{IVNV}}:G\subset A\}=A_1\cup A_3\cup A_8\cup A_{10}$

$=〈\left[\right\{a,b\},\{a,b,c\left\}\right],\left[\right\{e\},\{e,f\left\}\right],\left[\right\{g\},\{g\left\}\right]〉$

and

$IVNcl\left(B\right)=\bigcap \{F:F^c\in \tau ,B\subset F\}=A_2^c\cap A_3^c$

$=〈\left[\right\{g,h\},\{g,h,i\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a,d\},\{a,c,d\left\}\right]〉,$

$c{l}_{{}_{IVN}}\left(B\right)=\bigcap \{F:F^c\in {\tau }_{{}_{IVN}},B\subset F\}=A_2^c\cap A_3^c\cap A_6^c\cap A_{10}^c$

$=〈\left[\right\{g,h\},\{g,h,i\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a,c,d\},\{a,c,d\left\}\right]〉,$

$c{l}_{IVNV}\left(B\right)=\bigcap \{F:F^c\in {\tau }_{IVNV},B\subset F\}=A_2^c\cap A_3^c\cap A_9^c\cap A_{10}^c$

$=〈\left[\right\{g\},\{g,h\left\}\right],\left[\right\{a,b,c,d,f\},\{a,b,c,d,f\left\}\right],\left[\right\{a,d\},\{a,c,d\left\}\right]〉.$

Thus we can confirm that Remark 6 holds.

Proposition 20.

Let $(X,\tau )$ be an IVNCTS, $A\in IVNCS\left(X\right)$. Then,

$$IVNint\left(A^c\right)={\left(IVNcl\left(A\right)\right)}^{c}andIVNcl\left(A^c\right)={\left(IVNint\left(A\right)\right)}^c.$$

Proof. 

$IVNint\left(A^c\right)=\bigcup \{U\in \tau :U\subset A^c\}=\bigcup \{U\in \tau :U\subset 〈A^F,{A^I}^c,A^T〉\}$

$=\bigcup \{U\in \tau :U^T\subset A^F,U^I\subset {A^I}^c,U^F\supset A^T\}$

$=\bigcup \{U\in \tau :U^T\subset A^F,{U^I}^c\subset A^I,U^F\supset A^T\}$

$={(\bigcap \{U^c:U\in \tau ,A\subset U^c\})}^c$

$={\left(IVNcl\left(A\right)\right)}^c.$

Similarly, we can show that $IVNcl\left(A^c\right)={\left(IVNint\left(A\right)\right)}^c.$ ‎‎□‎‎

Proposition 21.

Let $(X,\tau )$ be an IVNCTS, $A\in IVNCS\left(X\right)$. Then,

$$IVNint\left(A\right)=in{t}_{{}_{IVN}}\left(A\right)\cap in{t}_{{}_{IVNV}}\left(A\right).$$

Proof. 

The proof is straightforward from Proposition 19 and Definition 21. ‎‎□‎‎

The following is the immediate result of Definition 21, and Propositions 20 and 21.

Corollary 3.

Let $(X,\tau )$ be an IVNCTS and let $A\in IVNCS\left(X\right)$. Then,

$$IVNcl\left(A\right)=c{l}_{{}_{IVN}}\left(A\right)\cup c{l}_{{}_{IVNV}}\left(A\right).$$

Example 16.

Let A and B be two IVNCSs in X given in Example 15. Then we can easily check that:

$$in{t}_{IVN}\left(A\right)\cap in{t}_{IVNV}\left(A\right)=IVNint\left(A\right),c{l}_{IVN}\left(B\right)\cup c{l}_{IVNV}\left(B\right)=IVNcl\left(B\right).$$

Theorem 3.

Let X be an IVNCTS, $A\in IVNCS\left(X\right)$. Then:

(1) 

$A\in IVNCC\left(X\right)$⇔ if $A=IVNcl\left(A\right)$,

(2) 

$A\in IVNCO\left(X\right)$⇔$A=IVNint\left(A\right)$.

Proof. 

Straightforward. ‎‎□‎‎

Proposition 22

(Kuratowski Closure Axioms). Let X be an IVNCTS, $A,B\in IVNCS\left(X\right)$. Then,

[IVNCK0]

If $A\subset B$, then $IVNcl\left(A\right)\subset IVNcl\left(B\right)$,

[IVNCK1]

$IVNcl\left({\mathsf{\varnothing }}_{IVN}\right)={\mathsf{\varnothing }}_{IVN},$

[IVNCK2]

$A\subset IVNcl\left(A\right),$

[IVNCK3]

$IVNcl\left(IVNcl\right(A\left)\right)=IVNcl\left(A\right),$

[IVNCK4]

$IVcl(A\cup B)=IVNcl\left(A\right)\cup IVNcl\left(A\right)$.

Proof. 

Straightforward. ‎‎□‎‎

Let $IVNc{l}^{*}:IVNCS\left(X\right)\to IVNCS\left(X\right)$ be the mapping satisfying the properties [IVNCK1], [IVNCK2], [IVNCK3], and [IVNCK4]. Then the mapping $IVc{l}^{*}$ is called the interval-valued neutrosophic crisp closure operator (briefly, IVNCCO) on X.

Proposition 23.

Let $IVNc{l}^{*}$ be the IVNCCO on X. Then there exists a unique IVNCT τ on X such that $IVNc{l}^{*}\left(A\right)=IVNcl\left(A\right)$, for each $A\in IVNCS\left(X\right)$, where $IVNcl\left(A\right)$ denotes the interval-valued neutrosophic crisp closure of A in the IVNCTS $(X,\tau )$. In fact,

$$\tau =\{A^c\in IVNCS\left(X\right):IVNc{l}^{*}\left(A\right)=A\}.$$

Proof. 

The proof is almost similar to the case of classical topological spaces. ‎‎□‎‎

Proposition 24.

⇔Let X be an IVNCTS, $A,B\in IVNCS\left(X\right)$. Then,

[IVNCI0]

If $A\subset B$, then $IVNint\left(A\right)\subset IVNint\left(B\right)$,

[IVNCI1]

$IVNint\left(X_{IVN}\right)=X_{IVN},$

[IVNCI2]

$IVNint\left(A\right)\subset A,$

[IVNCI3]

$IVNint\left(IVNint\right(A\left)\right)=IVNint\left(A\right),$

[IVNCI4]

$IVNint(A\cap B)=IVNint\left(A\right)\cap IVNint\left(A\right)$.

Proof. 

Straightforward. ‎‎□‎‎

Let $IVNin{t}^{*}:IVNCS\left(X\right)\to IVNCS\left(X\right)$ be the mapping satisfying the properties [IVNCI1], [IVNCI2], [IVNCI3], and [IVNCI4]. Then the mapping $IVNin{t}^{*}$ is called the interval-valued neutrosophic crisp interior operator (briefly, IVNCIO) on X.

Proposition 25.

Let $IVNin{t}^{*}$ be the IVNCIO on X. Then there exists a unique IVNCT τ on X such that $IVNin{t}^{*}\left(A\right)=IVNint\left(A\right)$ for each $A\in IVNCS\left(X\right)$, where $IVNint\left(A\right)$ denotes the interval-valued neutrosophic crisp interior of A in the IVNCTS $(X,\tau )$. In fact,

$$\tau =\{A\in IVNCS\left(X\right):IVNin{t}^{*}\left(A\right)=A\}.$$

Proof. 

The proof is similar to one of Proposition 23. ‎‎□‎‎

7. Interval-Valued Neutrosophic Crisp Continuous Mappings

In this section, we define an interval-valued neutrosophic crisp continuity and quotient topology, and study some of their properties.

Definition 22.

Let $X,\tau ),(Y,\delta )$ be two IVTSs proposed in [30]. Then a mapping $f:X\to Y$ is said to be interval-valued continuous, if $f^{-1}\left(V\right)\in \tau$ for each $V\in \delta$.

Definition 23.

Let $X,\tau ),(Y,\delta )$ be two IVNCTSs. Then a mapping $f:X\to Y$ is said to be interval-valued neutrosophic crisp continuous, if $f^{-1}\left(V\right)\in \tau$ for each $V\in \delta$.

From Remark 2 (1), and Definitions 22 and 23, we can easily have the following.

Theorem 4.

Let $(X,\tau ),(Y,\delta )$ be two IVNCTSs and let $f:X\to Y$ be a mapping. Then f is interval-valued neutrosophic crisp continuous if and only if $f:(X,{\tau }^T)\to (Y,{\delta }^T)$, $f:(X,{\tau }^I)\to (Y,{\delta }^I)$, and $f:(X,{\tau }^F)\to (Y,{\delta }^F)$ are interval-valued continuous, respectively.

The followings are immediate results of Proposition 9 (13) and Definition 23.

Proposition 26.

Let $X,Y,Z$ be IVNCTSs.

(1) 

The identity mapping $id:X\to X$ is continuous.

(2) 

If $f:X\to Y$ and $g:Y\to Z$ are continuous, then $g\circ f:X\to Z$ is continuous.

Remark 7.

From Proposition 26, we can easily see that the class of all IVNCTSs and continuous mappings, denoted byIVNCTop, forms a concrete category.

The followings are immediate results of Definition 23.

Proposition 27.

Let $X,Y$ be INCTSs.

(1) 

If X is an IVNCDTS, the $f:X\to Y$ is continuous,

(2) 

If Y is an IVNCITS, then $f:X\to Y$ is continuous.

Theorem 5.

Let $X,Y$ be IVNCTSs and let $f:X\to Y$ be a mapping. Then the followings are equivalent:

(1) 

f is continuous,

(2) 

$f^{-1}\left(C\right)\in IVNCC\left(X\right)$ for each $C\in IVNCC\left(Y\right)$,

(3) 

$f^{-1}\left(S\right)\in IVNCO\left(X\right)$ for each member S of the subbase for the IVNCT on Y,

(4) 

$IVNcl\left(f^{-1}\left(B\right)\right)\subset f^{-1}\left(IVNcl\left(B\right)\right)$ for each $B\in IVNC\left(Y\right)$,

(5) 

$f\left(IVNcl\right(A\left)\right)\subset IVNcl\left(f\right(A\left)\right)$ for each $A\in IVNC\left(X\right)$.

Proof. 

The proofs of (1)⇒(2)⇒(3)⇒(1) are obvious.

(2)⇒(4): Suppose the condition (2) holds and let $B\in INC\left(Y\right)$. By Proposition 22 [IVNCK2], $B\subset IVNcl\left(B\right)$. Then by Proposition 9 (2), $f^{-1}\left(B\right)\subset f^{-1}\left(IVNcl\left(B\right)\right)$. Thus by Proposition 22 [INCK0],

$$IVNcl\left(f^{-1}\left(B\right)\right)\subset IVNcl\left(f^{-1}\left(IVNcl\left(B\right)\right)\right).$$

Since $IVNcl\left(B\right)\in IVNCC\left(Y\right)$, $f^{-1}\left(IVNcl\left(B\right)\right)\in IVNCC\left(X\right)$ by the condition (2). So by Theorem 3 (1), $IVNcl\left(f^{-1}\left(IVNcl\left(B\right)\right)\right)=f^{-1}\left(IVNcl\left(B\right)\right).$ Hence $IVNcl\left(f^{-1}\left(B\right)\right)\subset f^{-1}\left(IVNcl\left(B\right)\right).$

(4)⇒(5): Suppose the condition (4) holds and let $B=f\left(A\right)$ for each $A\in IVNC\left(X\right)$. Then we have $IVNcl\left(f^{-1}\left(f\left(A\right)\right)\right)\subset f^{-1}\left(IVNcl\left(f\left(A\right)\right)\right)$. Thus by Proposition 9 (3), $IVNcl\left(A\right)\subset f^{-1}\left(IVNcl\left(f\left(A\right)\right)\right)$. So by Proposition 9 (1) and (4), $f\left(IVNcl\right(A\left)\right)\subset IVNcl\left(f\right(A\left)\right)$.

(5)⇒(4): The proof is similar to (4)⇒(5). ‎‎□‎‎

Theorem 6.

Let $X,Y$ be IVNCTSs and let $f:X\to Y$ be a mapping. Then f is continuous if and only if $f^{-1}\left(IVNint\left(B\right)\right)\subset IVNint\left(f^{-1}\left(B\right)\right)$ for each $B\in INC\left(Y\right).$

Proof. 

The proof is straightforward. ‎‎□‎‎

Definition 24.

Let $(X,\tau ),(Y,\delta )$ be two IVNCTSs. Then a mapping $f:X\to Y$ is said to be:

(i) 

Interval-valued neutrosophic crisp open, if $f\left(U\right)\in \delta$ for each $U\in \tau$,

(ii) 

Interval-valued neutrosophic crisp closed, if $f\left(C\right)\in IVNCC\left(Y\right)$ for each $C\in IVNCC\left(X\right).$

Proposition 28.

Let $X,Y,Z$ be IVNCTSs, let $f:X\to Y$ and $g:Y\to Z$ be mappings. If $f,g$ are open [resp. closed], then $g\circ g$ is open [resp. closed].

Proof. 

The proof is straightforward. ‎‎□‎‎

Theorem 7.

Let $X,Y$ be IVNCTSs and let $f:X\to Y$ be a mapping. Then f is open if and only if $IVNint\left(f\right(A\left)\right)\subset f\left(IVNint\right(A\left)\right)$ for each $A\in IVNC\left(X\right).$

Proof. 

The proof is straightforward. ‎‎□‎‎

Proposition 29.

Let $X,Y$ be IVNCTSs and let $f:X\to Y$ be injective. If f is continuous, then $f\left(IVNint\right(A\left)\right)\subset IVNint\left(f\right(A\left)\right)$ for each $A\in IVNC\left(X\right).$

Proof. 

The proof is straightforward. ‎‎□‎‎

The following is the immediate result of Theorem 7 and Proposition 29.

Corollary 4.

Let $X,Y$ be IVNCTSs and let $f:X\to Y$ be continuous, open, and injective. Then $f\left(IVNint\right(A\left)\right)=IVNint\left(f\right(A\left)\right)$ for each $A\in IVNC\left(X\right).$

Theorem 8.

Let $X,Y$ be IVNCTSs and let $f:X\to Y$ be a mapping. Then f is close if and only if $IVNcl\left(f\right(A\left)\right)\subset f\left(IVNcl\right(A\left)\right)$ for each $A\in IVNC\left(X\right).$

Proof. 

The proof is straightforward. ‎‎□‎‎

The following is the immediate result of Theorems 5 and 8.

Corollary 5.

Let $X,Y$ be IVNCTSs and let $f:X\to Y$ be a mapping. Then f is continuous and closed if and only if $f\left(VINcl\right(A\left)\right)=IVNcl\left(f\right(A\left)\right)$ for each $A\in IVNC\left(X\right).$

Definition 25.

Let $(X,\tau ),(Y,\delta )$ be two IVNCTSs. Then a mapping $f:X\to Y$ is called an interval-valued neutrosophic crisp homeomorphism, if f is bijective, continuous, and open.

Theorem 9.

Let $X,Y$ be IVNCDTSs and let $f:X\to Y$ be a mapping. Then f is a homeomorphism if and only if f is bijective.

Proof. 

The proof is straightforward. ‎‎□‎‎

Definition 26.

Let $(X,\tau )$ be an IVNCTS, let Y be a set and let $f:X\to Y$ be a surjective mapping. Let δ be the family of IVNCSs in Y given by:

$$\delta =\{B\in IVNC\left(Y\right):f^{-1}\left(B\right)\in \tau \}.$$

Then δ is called the interval-valued neutrosophic crisp quotient topology (briefly, IVNCQT) on Y.

It can easily be seen that $\delta \in IVNCT\left(Y\right)$. It is also obvious that for each $B\in IVNC\left(Y\right)$, B is closed in δ if and only if $f^{-1}\left(B\right)$ is closed in X.

Proposition 30.

Let $(X,\tau ),(Y,\delta )$ be two IVNCTSs, where δ is the IVNCQT on Y. Then a surjection $f:X\to Y$ is continuous and open. Moreover, δ is the finest topology on Y which f is continuous.

Proof. 

The proof is similar to the classical case. ‎‎□‎‎

The following is the immediate result of Proposition 30.

Corollary 6.

Let $(X,\tau ),(Y,\delta )$ be two IVNCTSs. If a mapping $f:X\to Y$ is continuous, open, and sujective, then δ is the IVNCQT on Y. But the converse does not hold in general(See Example 17).

Example 17.

Let $\left(\right[0,1],\tau )$ be an IVNCTS and let $A=[{\displaystyle \frac{1}{2}},1]$. Consider the characteristic function ${\chi }_{{}_A}:[0,1]\to \{0,1\}$, where $\{0,1\}$ is the interval-valued neutrosophic crisp Sierpin${}^{{}^{\prime }}$ski space (see Example 7 (5)). Then we can easily see that the topology on $\{0,1\}$ is the IVNCQT. On the other hand, ${({\displaystyle \frac{1}{2}},1)}_{IVNCI}\in \tau$ but ${\chi }_{{}_A}\left({({\displaystyle \frac{1}{2}},1)}_{IVNCI}\right)$ is not open in $\{0,1\}$. Thus ${\chi }_{{}_A}$ is not an open mapping.

Theorem 10.

Let $(X,\tau ),(Y,\delta ),(Z,\sigma )$ be IVNCTSs, where δ is the IVNCQT on Y. Let $f:X\to Y$ and $g:Y\to Z$ be mappings. Then g is continuous if and only if $g\circ f$ is continuous.

Proof. 

The proof is similar to the classical case. ‎‎□‎‎

8. Conclusions

We obtained various properties of IVNCSs and discussed with IVNCTSs which can be considered as an interval-valued tri-opological space. Moreover, we defined an interval-valued neutrosophic crisp base and subbase and proved the characterization of an interval-valued neutrosophic crisp base. Next, we introduced the concept of interval-valued neutrosophic crisp neighborhoods and obtained some similar properties to classical neighborhoods. Furthermore, we defined interval-valued neutrosophic crisp closures and interiors, and found some properties. We also introduced the concept of interval-valued neutrosophic crisp continuities and obtained its various properties.

In future, we expect that one can apply the concept of IVNCSs to group and ring theory, $BCK$-algebra, and category theory, etc. We also expect that one can define the notions of interval-valued soft sets and interval-valued neutrosophic crisp soft sets. Besides, the theorems developed in this manuscript will promote future studies on the geometry calibration for multi-cameras.