A Bounded Exhaustive Search Technique for Optimal Phasor Measurement Unit Placement in Power Grids

Abstract

This paper proposes a technique to determine the possible optimal placement of the phasor measurement unit (PMU) in power grids for normal operating conditions. All possible combinations of PMU placement, including infeasible combinations, are typically considered in finding the optimal solution, which could be a massive search space. An integer search algorithm called the bounded search technique is introduced to reduce the search space in solving a minimum number of PMU allocations whilst maintaining full system observability. The proposed technique is based on connectivity and symmetry constraints that can be derived from the observability matrix. As the technique is coupled with the exhaustive technique, the technique is called the bounded exhaustive search (BES) technique. Several IEEE test systems, namely, IEEE 9-bus, IEEE 14-bus, IEEE 24-bus and IEEE 30-bus, are considered to showcase the performance of the proposed technique. An initial Monte Carlo simulation was carried out to evaluate the capability of the bounded search technique in providing a smaller feasible search space. The effectiveness of the BES technique in terms of computational time is compared with the existing exhaustive technique. Results demonstrate that the search space can be reduced tremendously, and the computational burden can be eased, when finding the optimal PMU placement in power grids.

1. Introduction

Power grids are vulnerable to fault occurrences that are subject to more frequent power system failures, resulting in financial and production losses. Therefore, monitoring power grid conditions over a wide area is important to ensure more reliable power system operation. Phasor measurement units (PMUs) with global positioning systems (GPSs) are installed in power grids to provide synchronised data measurements at substations or system buses. The first prototype of PMU was developed in 1980s by Virginia Tech, and currently, there are a number of PMU technologies being deployed all over the world to get precise power system state measurements [1]. The data collected from PMUs can be used to identify fault location [2], detect power quality events [3] and evaluate power system stability [4]. PMUs are suggested to be installed at all buses to ensure full system observability. However, this solution is not cost-effective, and a direct estimation can be carried out to determine the state vector of adjacent buses. In other words, it is not necessary to install PMUs at all buses, and therefore, the number of PMU installations can be reduced. This issue attracted many researchers to come up with a new method for determining the optimal placements of PMUs in power grids in previous decades [5].

The determination of optimal PMU placement has been solved using different approaches that can be divided into analytical and heuristic. Integer linear programming (ILP) is one of the commonly used analytical approaches to solve the optimal PMU placement problem [6,7,8,9,10]. In [6], a numerical implementation of ILP is used to identify optimal PMU placement without non-linear power flow formulation. Instead of dealing with non-linear equations separately, equivalent linear terms are used in [7] to tackle the non-linearity issues and solve the problem using an exhaustive search technique. The exhaustive search technique is another analytical approach to overcome the shortcoming of ILP, especially in obtaining the global optimal solution, as suggested in [8]. Recently in [9], a hybrid approach using ILP and exhaustive search was proposed to overcome time-consuming nature of exhaustive search. However, exhaustive search helps find any missing optimal solution. This work was further extended in [10] to improve the distribution of redundancy measurements from allocated PMUs. Instead of combining methods with exhaustive search, the authors in [11] used two analytical approaches, namely, mixed integer linear programming (MILP) and nonlinear programming (NLP), to solve the optimal PMU placement problem. NLP is used to explore possible local minima solutions, whereas the MILP is used to ensure a global optima solution can be obtained.

Apart from the analytical approach, a heuristic technique based on natural behaviour was used in [12,13,14,15,16,17,18] to overcome the problem of being trapped in local minima and released them from the computational burden of solving the optimal PMU placement problem. A heuristic rule called tabu search is used in [12] to accelerate optimisation in solving the combinatorial problem of PMU placement as an alternative to the complicated matrix analysis of the analytical approach. In [13], the particle swarm optimisation-based method is used to find the minimum number of PMUs whilst maintaining full network observability at the maximum measurement redundancy. The genetic algorithm was used in [14] for another monitoring device placement that uses a concept similar to the PMU placement. Topology was incorporated into the observability concept to address the issue with installation in radial systems. This work was extended in [15] using a combination of three different techniques, namely, the artificial immune system, quantum computing and the gravitational search algorithm, which is called the adaptive quantum-inspired gravitational search algorithm. Using the same observability concept, the firefly algorithm is used in [16]. Similarly, the optimisation technique was improved in [17] by adopting quantum computing in the firefly algorithm to solve combinatorial problems. Recently, a hybrid algorithm of the genetic algorithm and minimum spanning tree was suggested in [18] to find an optimal allocation of PMUs in power grids. In this case, the genetic algorithm was used to repair any unobservable buses of the allocated PMUs.

Although the aforementioned works have improved the computational time in solving the optimal PMU placement, the optimiser still needs to explore all combinations, including unfulfilled observability constraints, and they are penalised or modified to obtain feasible solutions. Alternatively, the observability constraints can be used directly to confine the search and reduce the infeasible combinations. Furthermore, the observability matrix in the PMU placement problem is used to establish the observability constraints in forms of symmetry. Thus, the PMU placement will end up with the same combinations at several points in the search. This situation can be avoided to help reduce the search space. Therefore, this work aims to develop a bounded search by incorporating connectivity and symmetry constraints in a search algorithm. The heuristic-based search algorithm is not suitable for showcasing the effectiveness of the proposed approach because the obtained optimal solution highly depends on random initialisation. An exhaustive technique is used as the search algorithm for a more consistent performance.

This paper is organised as follows. An overview of the existing concept of system observability is provided in Section 2. This concept is used to establish the proposed bounded search technique. The development of bounded search using the features of the connectivity and symmetry constraints is explained in Section 3. Optimal PMU placement formulation using a bounded exhaustive search technique is presented in Section 4. The effectiveness of the proposed technique was tested on several test systems, namely, IEEE 9-bus, IEEE 14-bus, IEEE 24-bus and IEEE 30-bus, and the results are discussed in Section 5. Finally, a conclusion is drawn in Section 6.

2. Concept of System Observability

In the context of PMU placement, the system observability refers to the capability of the allocated PMUs in power grids to provide sufficient information including estimation required information of the uninstalled buses if necessary for monitoring the whole power systems. The assessments of system observability can be classified into numerical and topological approaches [7]. In the numerical approach, the observability of PMU is based on power flow calculation, and electrical quantities are used to define PMU observability. By contrast, the topological approach is based on the connectivity of system buses, and full system observability can be achieved when at least one PMU is connected to each bus in the power network. In this work, topological approach is considered because it has less computational burden compared with the numerical approach, and it is commonly used in solving the optimal PMU placement problem [7]. The following topological rules are applied [13]:

• All buses that are installed with PMU can be directly observed. The voltage phasor of the bus and the current phasor of all connected branches to the installed bus can be obtained directly without additional calculation, which is known as direct measurement.
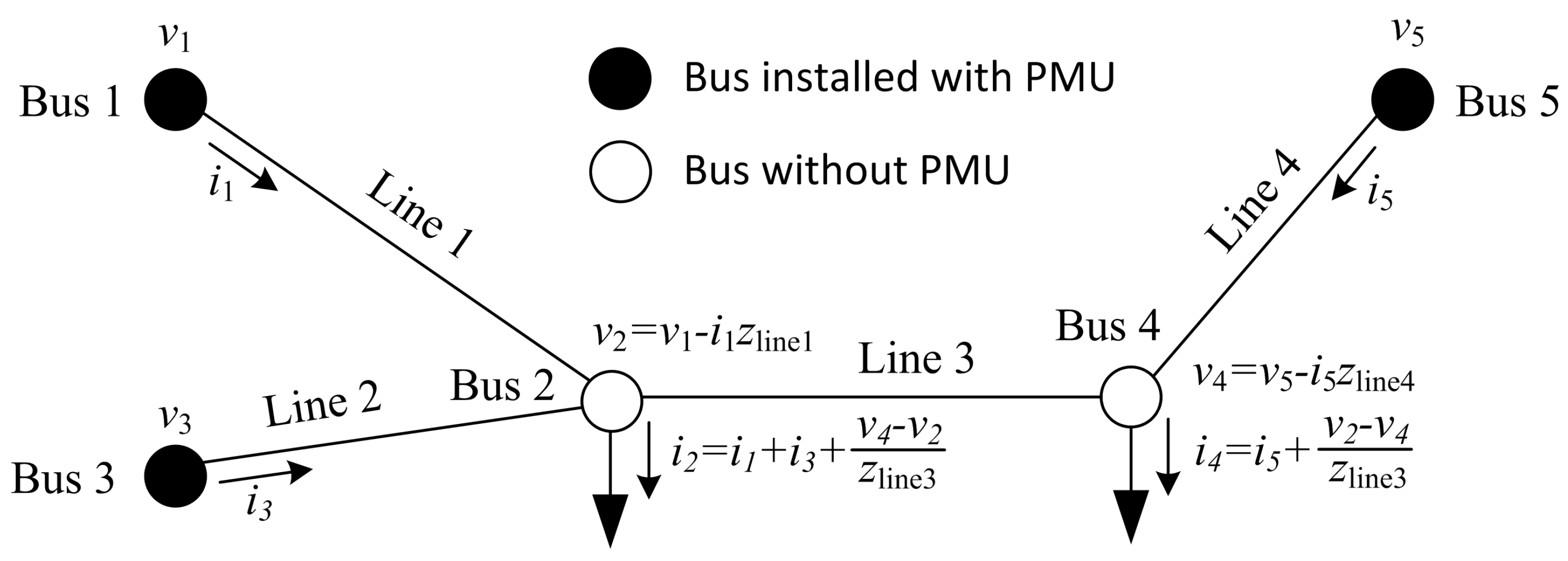
• Buses adjacent to installed buses are also observable. Referring to Figure 1, the voltage phasor of the adjacent bus can be calculated using the interconnected line impedance, the voltage and current phasors at the installed buses based on Kirchhoff’s voltage law (KVL). The leaving or entering current phasor (i.e., load or generator) at the adjacent bus can also be obtained from the measured current phasors of the connected branches using Kirchhoff’s current law (KCL) which is known as pseudo measurement.
• All buses that do not comply the two conditions above are considered unobservable.

A binary observability matrix, A, can be constructed using the above rules to assess system observability. Row of matrix A (j) represents the observable buses, whereas its column (k) represents the PMU installation buses. It provides information as to which buses are observable when the PMU is installed at a certain bus. The element of observability matrix, A, can be defined using the following expression:

$$a_{jk}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j=k\hfill \\ 1,\hfill & \mathrm{if}\mathrm{bus}j\mathrm{is}\mathrm{connected}\mathrm{to}\mathrm{bus}k\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

The entry “1” indicates that bus j can be observed by PMU installed at bus k; otherwise, the entry “0” is used. Apart from the observability matrix, a binary vector of PMU placement, X, is also required to evaluate system observability. The placement vector, X, indicates where the PMU should be installed. The element of the placement vector can be defined as follows:

$$x_j=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{PMU}\mathrm{is}\mathrm{installed}\mathrm{at}\mathrm{bus}j\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(2)

Multiplication of observability matrix, A, and placement vector, X, provides the number of PMUs that are responsible for monitoring or observing at each bus. At least one PMU is required to observe each bus in a power grid to ensure full system observability. However, more than one PMU is suggested in several circumstances [10]. Therefore, a coefficient, b, is used to set the minimum number of PMU that are needed to observe at each bus. On that premise, the observability constraints can be defined as follows:

$$A·X\ge W$$

(3)

where W is a vector whose elements are all b values. Let each bus is observed by at least one PMU ($b=1$), and the observability constraints in Equation (3) for the five-bus grid structure in Figure 1 can be written as follows:

$$A·X=\left\{\begin{array}{cc}{x}_1+x_2\hfill & \ge 1\hfill \\ x_1+x_2+x_3+x_4\hfill & \ge 1\hfill \\ x_2+x_3\hfill & \ge 1\hfill \\ x_2+x_4+x_5\hfill & \ge 1\hfill \\ x_4+x_5\hfill & \ge 1\hfill \end{array}\right.$$

(4)

In this case, full system observability of the five-bus power grid can be achieved with a minimum of two PMUs that are installed either at buses 2 and 4 or buses 2 and 5. The first four constraints in Equation (4) are fulfilled when a PMU is placed at bus 2 and the last constraint is fulfilled when a PMU is installed either at bus 4 or 5. This concept will be used to establish the proposed bounded search technique.

3. Bounded Search Technique

In our previous work [19], we found that the combinations of PMU placement with higher redundancy provide lower deviations in their measurements. Instead, the higher deviations could provide more useful information of the system operation. Although the redundancy is good for monitoring system backup, the significance of measured data should not be sacrificed, and the system backup can be easily achieved by properly setting the b coefficient. Therefore, this paper suggests a search technique that identifies PMU placement with lesser redundancy in its measurement. This can be achieved by removing possible candidates for PMU installation when a PMU is installed at a certain bus subject to the redundancy requirement. By doing this, the size of search space can be reduced, and the PMU combinations are bounded to the feasible solutions only. This approach is called bounded search, and it is based on two constraints, namely, connectivity and symmetry that will be explained in more detail in the following subsections.

3.1. Connectivity Constraints

A combination of PMUs in this work is generated using an integer to represent the bus location for PMU placement instead of a binary number that is commonly used by other researchers in the literature. The integer used is easier to interpret and requires less space to generate a combination compared with the binary number. This technique is discussed by using the exemplar five-bus power grid as depicted in Figure 1.

In this work, a PMU placement is constructed bit by bit until all buses are observed. A temporary vector of possible buses for PMU installation is required and denoted as AL. Several buses will be removed from vector AL when a PMU is placed in the power grid. As discussed earlier, system buses have two types, namely, direct measurement and pseudo measurement. The direct measurement bus can be removed first, and the pseudo-measurement bus will be removed when the redundancy requirement is fulfilled. For that reason, another vector to count the number of PMUs that are observing the respective bus is introduced and denoted as RC. The elements of RC will be removed when the redundancy requirement is achieved. Whenever the size of RC is shrunk, the size of AL will be reduced accordingly. Initially, all buses are available for PMU installation, and no bus is observed by any PMU. Hence, the initial conditions for AL and RC of the exemplar grid are set as AL = [1 2 3 4 5] and RC = [0 0 0 0 0].

This technique is not a standalone approach, and it requires a search operator to select a suitable bus in each bit. The implementation with exhaustive technique will be discussed in Section 4. Therefore, the first candidate will always be selected in this example. Coefficient b is set to 1, and the following procedure is applied to generate a bit-by-bit combination of PMU placement:

• Select a bus location for PMU installation from AL. Assume that bus 1 is selected.
• Identify the direct and pseudo-measurement buses with respect to the selected bus. This step can be done by finding entry “1” from the corresponding row of matrix A. Store all pseudo-measurement buses in a vector denoted as SL. Bus 1 becomes a direct measurement bus, and only bus 2 can be identified as a pseudo-measurement bus (SL = [2]).
• Update RC by adding 1 to its elements that correspond to the identified buses. RC becomes [1 1 0 0 0].
• Check values at the direct measurement bus in RC. Remove the corresponding element of RC if the redundancy requirement is fulfilled, and update AL accordingly. Otherwise, select another bus to be installed with PMU for the next subsequence bit from the identified pseudo-measurement buses, SL. Repeat steps (2) to (4) until the direct measurement bus can be removed. AL = [2 3 4 5], and RC = [1 0 0 0] because $b=1$ is used.
• Check for other values in RC that are equal to b and eliminate the corresponding element of AL and RC. Skip this step if the condition is not satisfied. Now, AL = [3 4 5], and RC = [0 0 0].
• Repeat steps (1) to (5) for the next bits until AL is empty.

At this point, a combination of buses 1, 3 and 4 is generated for a possible PMU placement in the five-bus grid. If the first bit starts with bus 2, a combination of buses 2 and 5 is then generated. However, the combination of buses 2 and 4 as mentioned in the previous section will not be generated due to observation redundancy between them. If redundancy is required, coefficient b can be set to 2. In this example, a combination of buses 1, 2, 3, 4 and 5 will be generated. However, at least one PMU to observe each bus is sufficient, and this condition is used in this work.

3.2. Symmetry Constraints

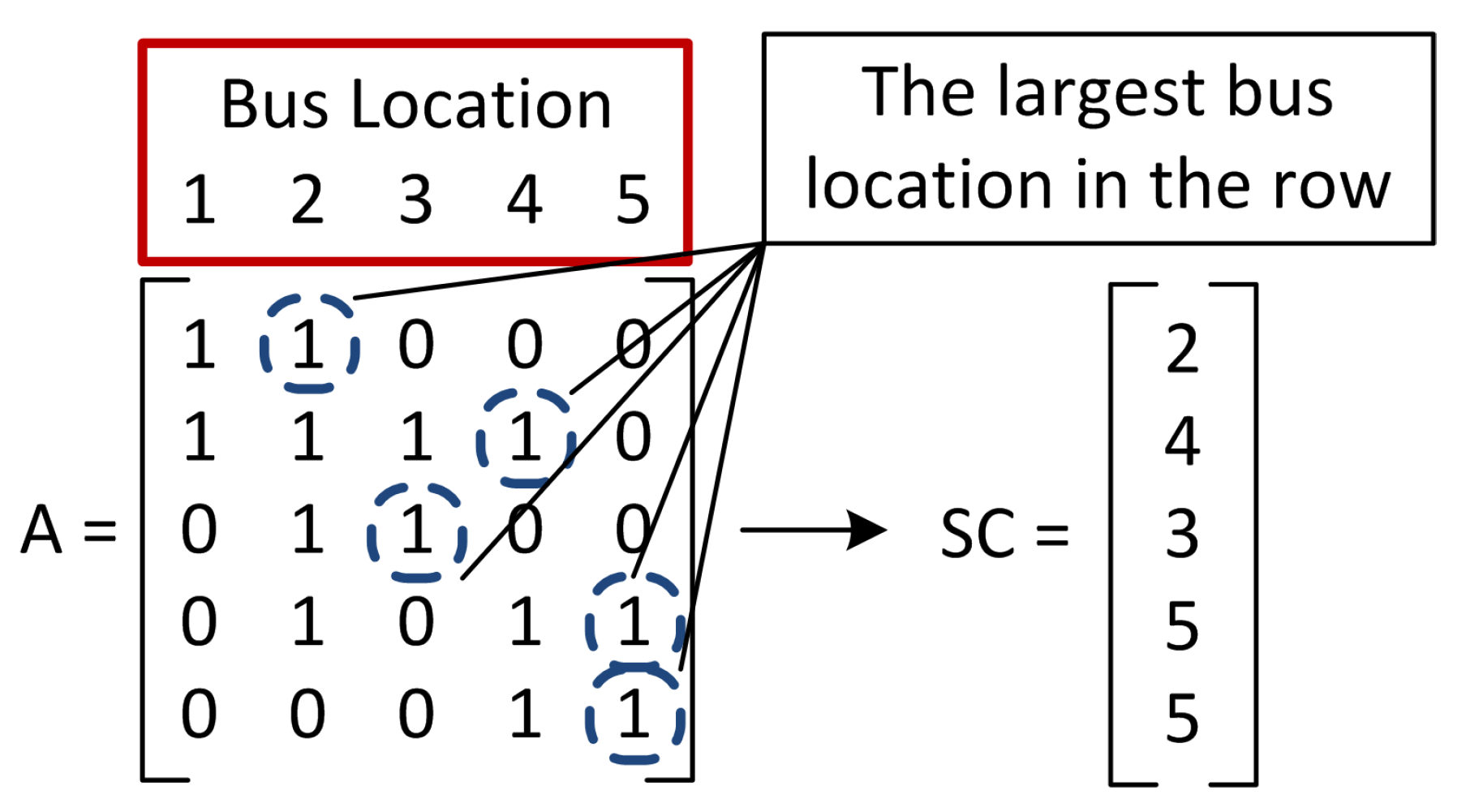
At several points in the previous operation, similar combinations of PMU placement or duplications will be produced due to the symmetry feature of system observability. For example, a combination of buses 3, 1 and 5 similar to the previous one will be produced when bus 3 is selected at the first bit. This issue can be addressed by applying the symmetry constraints to the PMU placement. A vector, SC with the same size as AL and RC, is required, and it works as an indicator to avoid duplications in the PMU placement. The SC vector can be constructed before the search is carried out or during the construction of observability matrix, A because it depends on the grid structure. Figure 2 illustrates how to construct an SC vector for a given matrix A. The entry for the j-th element of SC can be defined as the largest number of bus location (as indicated by a red box in the figure) with entry “1” in the j-th row of matrix A. The values in SC will be used as the largest bus location can be assigned for a particular bit in generating the PMU combination.

After the SC vector is established, it can be implemented to limit the selection of possible candidates for the PMU placement. Before the procedure in Section 3.1 is carried out, the largest bus location, h for a particular bit n, is set to a minimum value of elements in SC, as expressed in Equation (5). Using the five-bus grid as an example, the largest bus location that can be assigned to the first bit is bus 2, and selection for PMU placement after bus 2 in that particular bit is not allowed. Then, the corresponding elements of SC will be eliminated according to AL and RC when the procedure in Section 3.1 is carried out. If bus 1 is selected for the first bit, the largest bus location that can be assigned to the second bit becomes bus 3 where SC = [3,5,5] after removing buses 1 and 2 in AL; that is, bus 3 must be selected if bus 1 is chosen at the first bit. This step is carried out together with the procedure in Section 3.1 until AL is empty. By applying this step, combinations such as [3,1,4], [3,1,5], [4,1,3], [4,3,1], [5,1,3], [5,2] and [5,3,1] can be avoided as they are duplication or symmetrical to the combinations of [1,3,4], [1,3,5] and [2,5].

$$h_n=min(SC)$$

(5)

As a result, this technique helps reduce the search space tremendously. In the exemplar five-bus grid, it reduces the 31 combinations to only three feasible combinations. However, this technique depends on the numbering system that is used to label substations or buses in power grids. The numbering of interconnected buses should be in a sequence as long as possible with high interconnections to make the proposed technique works more effectively. Then, small numbering should be assigned to the longest path, and a larger numbering should be assigned for a shorter path.

4. Optimal PMU Placement Formulation

As mentioned earlier, the bounded search is incorporated with the exhaustive technique and called bounded exhaustive search (BES) technique. The BES technique is implemented to obtain optimal PMU placement at a minimum number of PMUs for monitoring the whole system. An objective function of the optimisation problem can be expressed in Equation (6) as to achieve the ultimate goal of minimising PMU installation cost. The reason is that most of the installation cost comes from deployment process of the PMU installations and therefore, the number of substations or buses for PMU installations must be minimised [20]. The observability constraints in Equation (3) can be relaxed because the search procedure is based on the bounded search technique. 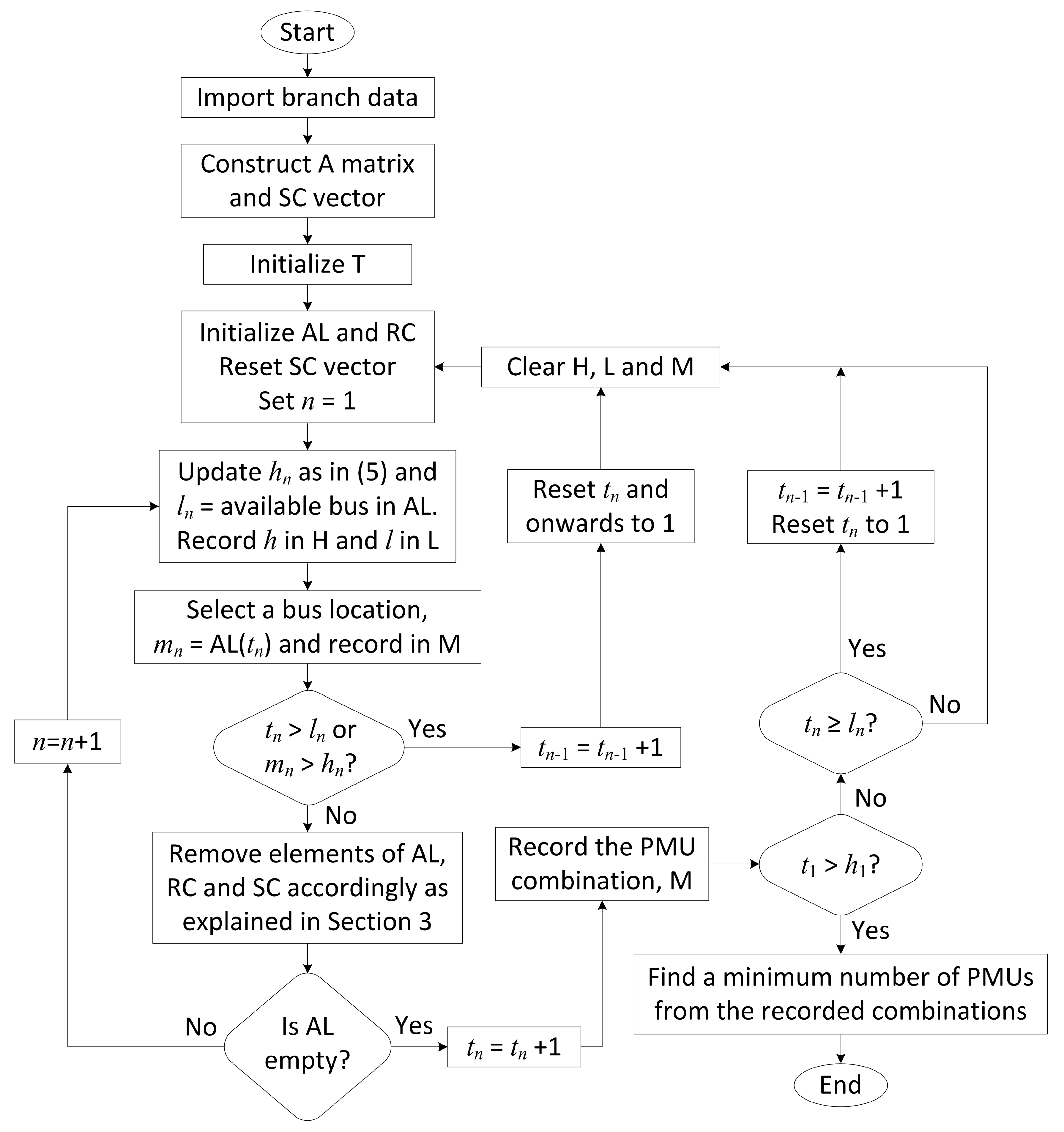Figure 3 shows the overall BES implementation to solve the optimal PMU placement problem by considering at least one PMU to observe each bus (b = 1).

$$f=min(\sum _{j=1}^N{x}_j)$$

(6)

In the figure, a set of control variables, t is given by a vector T and used to select a bus location for the PMU placement. In exhaustive search, all elements of T are initially set to 1 and start counting from the right hand side (i.e., the least significance bit). The length of PMU placement combination varies depending on the bus selection in an early stage. The length of T can be set to the total number of buses in the considered power grid, but the last bit can be determined when vector AL is empty. The last bit keeps counting up and updates the next bit when it reaches the limit. In other circumstances when it violates the designed symmetry constraints, the counting will skip and jump to the next combination. This process will continue until the stopping criterion is fulfilled, as shown in Figure 3.

The procedure based on the objective function in Equation (6), however, will produce multiple solutions. An index can be used to rank the multiple solutions and an optimal solution is selected according to the highest rank. This approach is applied in [9] using an index called system observability redundancy index (SORI) but it does not solve the multiple solutions in certain power grids. Therefore, another index based on voltage magnitude deviations as suggested in [19] is used as indicator to select the optimal solution. The voltage magnitude deviation index can be constructed using fault analysis to indicate the critical buses in power grids. The voltage magnitude deviation index at bus j is denoted as ${\sigma }_j^v$. More detail explanation on how to establish the index can be found in [19]. An optimal solution can be selected from the highest of the total voltage magnitude deviation index that corresponds to the PMU placement combination using the following indicator:

$$\eta =\sum _{j=1}^N{\sigma }_j^v{x}_j$$

(7)

5. Results and Discussion

The performance of the proposed technique was evaluated using several IEEE test systems, namely, IEEE 9-bus [21], IEEE 24-bus [22], IEEE 14-bus and IEEE 30-bus [23] to represent power grids for solving the optimal PMU placement problem. A comparison between the IEEE test systems in terms of system topology is provided in

Table 1. A system topology comparison of the used IEEE test systems.

Item	Test System
	IEEE 9-Bus	IEEE 14-Bus	IEEE 24-Bus	IEEE 30-Bus
Number of generator buses	3	5	11	6
Number of load buses	3	8	13	24
Number of transmission lines	9	20	38	41
Maximum number of	3	5	5	7
connected lines to a bus
Reference bus location	1	1	13	1
Level of complexity	Simple mesh	Weakly mesh	Heavily mesh	Heavily mesh

for better understanding. The problem was developed within the MATLAB environment and solved using a PC of 2.9 GHz and 12 GB RAM.

A Monte Carlo analysis was carried out to showcase the effectiveness of bounded search in avoiding infeasible PMU combinations.

Table 2. Infeasibility check using Monte Carlo analysis.

Test System	Number of Infeasible Combinations		Probability for Infeasible Combination (%)
	Conventional	Bounded Search	Conventional	Bounded Search
IEEE 9-bus	31,715	0	63.43	0
IEEE 14-bus	31,193	0	62.39	0
IEEE 24-bus	39,625	0	79.25	0
IEEE 30-bus	45,118	0	90.24	0

shows a comparison of infeasibility check based on constraints in Equation (3) between the conventional and the proposed search space described in Section 3 using different t input settings from a Monte Carlo simulation for 50,000 runs. It clearly shows that the infeasible region of search space increases with the size of power grid, thereby reducing the probability of obtaining a feasible PMU combination, especially when considering the same sampling size. This finding is essential for heuristic approach settings. After the proposed bounded search technique is applied, only the feasible region will be explored where not a single combination is counted as an infeasible combination, as shown in Table 2. Thus, the search space is successfully reduced into the feasible region by using the bounded search technique.

The reduced sizes of search space in the test systems using the proposed bounded search technique are compared with the original size used in the conventional technique, as tabulated in

Table 3. Size reduction of search space using different bus numbering systems.

Test System	Original Size	Standard Numbering		Alternative Numbering		Reduced Size without Duplications
		Reduced Size	Number of Duplications	Reduced Size	Number of Duplications
IEEE 9-bus	511	92	84	12	4	8
IEEE 14-bus	16,383	93	55	59	21	38
IEEE 24-bus	16,777,215	140,500	140,108	3560	3168	392
IEEE 30-bus	1,073,741,823	36,022	33,846	18,060	15,884	2176

. The sizes are reduced tremendously after applying the proposed technique, but the standard bus numbering system used in the provided data causes high duplications of PMU combinations, especially in the IEEE-24 bus. The duplications refer to different combinations that result to the same placement. For instance, combinations of [1,3,2], [2,1,3], [2,3,1], [3,1,2] and [3,2,1] are duplications to a combination of [1,2,3]. Unlike other test systems, buses in the IEEE 24-bus are labelled in a very bad sequence, in which only two interconnected buses can be identified as the longest path in a sequence. As mentioned in Section 3.2, the symmetry constraints can be addressed more effectively if the buses are labelled in a more appropriate sequence. The results for alternative numbering in Table 3 are based on the numbering in

Table 4. Alternative numbering used for test systems.

Test System	Bus Re-Numbering as Referred to the Standard Numbering
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
IEEE 9-bus	1	9	8	2	3	4	5	6	7
IEEE 14-bus	1	2	3	4	5	6	13	14	10	11	12	7	8	9
IEEE 24-bus	1	5	8	6	2	4	23	22	7	3	16	24	15	17	10
IEEE 30-bus	1	2	13	12	22	3	23	14	24	4	25	11	30	10	9
Test System	Bus Re-Numbering as Referred to the Standard Numbering
	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
IEEE 24-bus	11	18	19	12	13	20	21	14	9
IEEE 30-bus	29	28	19	20	21	5	6	8	7	26	27	16	15	17	18

. The alternative bus numbering in Table 4 is just an option to show the effect of using a different bus numbering used and might not be the best option. Table 3 shows that the size of search space is further reduced when less similar combinations or duplications are generated using the alternative numbering. Although the size is reduced, the possible combinations without duplications remain the same, which clearly shows that the search space can be reduced if the symmetry constraints are addressed properly. However, the reduced size without duplications is difficult to achieve due to the mesh grid structure of the test systems used.

Table 5. Performance comparison between the proposed and existing techniques.

Test System	Optimum Number		Computational Time (s)
	Exhaustive Search [8]	Proposed BES	Exhaustive Search [8]	Proposed BES
IEEE 9-bus	3	3	0.108	0.024
IEEE 14-bus	4	4	1.781	0.031
IEEE 24-bus	7	7	1862.65	0.963
IEEE 30-bus	10	10	N/A	7.547

shows a performance comparison between the proposed BES and the existing exhaustive technique presented in [8]. For a fair comparison, the exhaustive technique in [8] is developed and implemented in the same environment. However, the IEEE 30-bus takes a long time to compute the existing exhaustive technique; thus, it is not carried out in this work. The optimum number of PMUs for the IEEE 30-bus is taken from reference [8]. The results show that the proposed BES technique can provide the same optimum number of PMUs compared with the existing technique. Furthermore, the BES requires much less computational time in which less than 8 seconds is taken to solve the optimal PMU placement problem in the IEEE 30-bus because a smaller search space needs to be explored, as discussed earlier. This part is the key point of this work where the search space to solve the optimal PMU placement problem can be reduced using the connectivity and symmetry constraints.

Table 6. PMU placement combinations obtained from the BES technique.

Test System	Number of PMUs	PMU Placement (Bus)	Indicator $\mathit{\eta }$
IEEE 9-bus	3	1, 7, 9	3.3522
		2, 4, 9	3.3463
		3, 4, 7	3.3459
		4, 7, 9	3.4993
IEEE 14-bus	4	2, 6, 8, 9	5.7892
		2, 7, 10, 13	7.0128
		2, 7, 11, 13	6.9629
		2, 8, 10, 13	6.3104
IEEE 24-bus	7	2, 3, 7, 10, 16, 21, 23	9.5087
		3, 4, 7, 10, 16, 21, 23	9.7302

shows all possible combinations of optimal PMU placement in the standard numbering system that are obtained from the BES technique. A total of 84 combinations are possible with a minimum of 10 PMUs in the IEEE 30-bus; therefore, they are not presented here. Selection indicator $\eta$ in the table can be calculated from the obtained voltage magnitude deviation index as given in Appendix A using Equation (7). It is used to indicate the most suitable combination for PMU installations. The highest value of $\eta$ is selected because PMUs at these locations give the most significant deviations in their measurements for different events in the power grids. Hence, an optimal PMU placement can be selected from the possible PMU combinations in the used IEEE test systems based on the highest value of $\eta$ (bolded) and they are presented in

Table 7. Optimal PMU placement in the used IEEE test systems.

Test System	Optimal PMU Placement (Bus)
IEEE 9-bus	1, 7, 9
IEEE 14-bus	2, 7, 10, 13
IEEE 24-bus	3, 4, 7, 10, 16, 21, 23
IEEE 30-bus	1, 7, 10, 11, 12, 19, 24, 26, 28, 29

. As a result, the ultimate goal to minimise the involvement substations or buses will not be jeopardised in determining a single optimal PMU placement solution.

The proposed technique can also be applied to provide monitoring system backup during contingencies by resetting the b coefficient.

Table 8. Optimal PMU placement in the used IEEE test systems when $b=2$.

Test System	Number of PMUs	Optimal PMU Placement (Bus)
IEEE 9-bus	6	1,2,3,4,7,9
IEEE 14-bus	9	2,3,5,6,7,8,9,10,13
IEEE 24-bus	14	1,2,4,7,8,10,11,15,16,17,20,21,23,24
IEEE 30-bus	21	1,3,5,7,8,9,10,11,12,13,15,17,18,19,22,24,25,26,28,29,30

shows optimal PMU placement in the used IEEE test systems when b is set to 2 using the same procedure as in the previous setting. In this case, an uninstalled PMU bus can still be monitored by another PMU adjacent to the bus during contingencies such as outage of a transmission line or loss of a PMU operation. In normal condition if a transmission line between installed and uninstalled PMU buses is outage, PMU at the installed bus is not able to make a direct estimation of the uninstalled bus due to loss of connection. Although this setting helps to provide backup during contingencies, the number of buses for PMU installations becomes double or more as can be observed from the table. Furthermore, the contingency conditions occur only sometimes and mostly temporary. Therefore, a case study based on normal operating conditions gives a fair solution and further analysis can be carried out to find a trade-off between the probability of the contingency cases and the investment cost for additional PMU installations.

6. Conclusions

A new bounded search technique is introduced in this paper to address the issue with maintaining full observability of power grids at a minimum number of PMUs. The technique is mainly based on the use of connectivity and symmetry constraints. The technique was implemented together with the exhaustive technique—making the BES technique—to solve the optimisation problem. Several IEEE test systems, namely, IEEE 9-bus, IEEE 14-bus, IEEE 24-bus and IEEE 30-bus were considered to represent power grids and showcase the performance of the proposed technique. A tremendous search space reduction can be achieved using the introduced bounded search technique; it was able reach up to 97.65%, 99.64%, 99.98% and 99.99% reductions from the original search size of IEEE 9-bus, IEEE 14-bus, IEEE 24-bus and IEEE 30-bus test systems, respectively. Furthermore, the reduced space in this work was proven to always be within a feasible region. This technique leads to a low computational time when it is coupled with the exhaustive technique in solving the optimal PMU placement problem. The coupled technique or BES technique was validated and compared with the existing exhaustive technique and provided the same optimum number of PMUs in all test systems but with far shorter computational times. The computational times to solve PMU placement using the BES technique in IEEE 9-bus, IEEE 14-bus and IEEE 24-bus test systems became 4.5, 57.5 and 1934.2 times, respectively, faster than full exhaustive technique that was used in the previous works. The proposed technique, however, is highly dependent on the system topology; any changes to the structure of a power grid will require another bus renumbering process, and the computational time increases exponentially with the size of power grid. Nonetheless, the bounded search technique is not limited to the exhaustive technique, and it can be implemented with other techniques to expedite the computation in solving the optimal PMU placement problem.