A Ring Signature Based Anonymity Authentication Scheme for Group Medical Consultation

Abstract

Due to the rapid development of physiological monitoring devices, internet of things (IoT) and communication technology, telecare medical information systems (TMIS) are getting more and more important in assisting doctors in completing medical work nowadays. Because of the open nature of wireless networks, a secure TMIS which offers authentication, anonymity and privacy features is required. There are many schemes protecting TMIS that have been proposed recently. Unfortunately, they cannot guarantee both patient’s and doctor’s privacy and security at the same time. This paper proposes a ring signature-based TMIS authentication scheme for a group consultation environment. In our proposed scheme, a patient can inquire about their symptoms without revealing their identity, and a doctor can also keep their own identity confidential when making a diagnosis. In view of the increasing number of serious patient–physician disputes, our proposed scheme can have a practical application. Compared to other related work, our scheme achieves improved security properties and higher efficiency.

1. Introduction

A new clinical service called telecare medical information systems (TMIS) has appeared because of the development of wireless sensor network (WSN) technology and various applications supported by the internet of things (IoT). Compared with traditional clinical services, patients can communicate with doctors or specialists through the internet by text, voice or video, instead of going to the hospitals directly. Through sensor technology, the patients’ health status data, such as heart rhythm, blood pressure and sugar levels, can be transmitted to doctors through the internet. Doctors or specialists can then make an evaluation by analyzing these data.

Though TMIS services bring new convenience, they suffer from some security problems. One of the most important issues is privacy. A patient’s health data are sensitive information; however, due to the open nature of wireless networks, they are easy to be captured by others. To handle these issues, a secure TMIS is essential to ensure data integrity, confidentiality and availability. In 2012, an efficient remote user authentication scheme for TMIS was proposed by Wu et al. [1]. In the same year, He et al. [2] pointed out that Wu et al.’s scheme was vulnerable to impersonation attack and insider attack, and they proposed another authentication scheme for TMIS. Immediately after, Wei et al. [3] criticized that the schemes mentioned were unable to achieve secure two-factor authentication and presented an enhanced secure authentication protocol. In Ref. [4], Zhu considered that the schemes in Ref. [5] could not defend against off-line password guessing attacks and proposed an RSA-based authentication scheme for TMIS. Nevertheless, none of these schemes in Ref. [1,2,3,4] can protect patient privacy secretly. In Ref. [5], Pu et al. protected patient identity privacy by transforming a one-factor authentication protocol to a two-factor anonymous authentication protocol. However, Pu et al.’s scheme involves high communication costs, computation costs and storage costs. Later, Chen et al. proposed an ID-based authentication scheme in Ref. [6] to overcome the defect of Khan et al.’s scheme [7], which does not protect the user’s anonymity. Based on the reduced computation of the hash function and XOR (exclusive or operation), this scheme is suitable for a telecare medical information system. In 2013, Cao et al. [8], Xie et al. [9], Lin [10] and Jiang et al. [11] all pointed out that Chen et al.’s scheme had several security flaws, such as being susceptible to an off-line password guessing attack, privacy leakage, etc. Later in 2013, Liu et al. proposed certificateless remote anonymous authentication schemes [12] based on elliptic curve cryptography (ECC). Their ECC is based on the computational Diffie–Hellman problem (CDHP). Liu et al.’s schemes not only achieve mutual authentication, but also are relatively cost-effective compared with existing schemes [11,12,13,14,15,16,17,18]. In 2014, Giri et al. applied RSA to design an anonymous authentication scheme for TMIS [17]. In their scheme, Giri et al. stored the digest of patient’s passwords and a random number in the smart card first, and assumed that all secret parameters regarding the patient and server were completely sealed. Then, by combining RSA, one-way hash function and nonce, they tried to build up a secure authentication scheme between patient and server. With such detailed arrangements, they proved that their authentication scheme withstands insider attack, user impersonation attack, and so on. Although the security of Giri et al.’s authentication scheme was proven, its computation cost on the receiver side is significantly higher than that on the sender side. In the same year, Zhao applied ECC to design an anonymous authentication scheme [18]. In his scheme, the ECC is also based on CDHP. Zhao successfully protected the patient’s identity privacy and out-performed Liu et al. [16] in terms of the computation costs on the sender’s and receiver’s sides. This is because a module exponentiation operation is excluded from Zhao’s scheme. In 2019, Arezou et al. applied ECC to design their robust and efficient mutual authentication scheme [19]. To achieve mutual authentication, a mobile device is held by the patient instead of a smart card. The patient’s identity is never transmitted over the unreliable channels and the adversary cannot access it from the encrypted form. They claimed that the anonymity of the patient is guaranteed. Their computation analysis also confirmed that the computation costs on the sender and receiver sides are similar to those proposed by Liu et al. [12] in 2013.

Although researchers have continuously attempted to design authentication schemes for protecting patient identity privacy, there is another issue that should also be addressed, which is the medical dispute. When a medical accident occurs, revealing the identity of a certain doctor or specialist can also be a safety concern for medical workers. For example, many diagnoses are conducted with the involvement of several doctors, and doctors who perform treatment later will usually refer to the treatment of the previous doctorand; as such, it is unfair to only reveal one doctor’s identity. Therefore, in the context of TMIS, the privacy of the identities of both the patient and the doctor is very important, especially when there is a patient–doctor medical care dispute.

Luckily, ring signatures enable a user to sign a message in such a way that the receiver knows the signature comes from a group, but does not directly reveal the signer’s identity. This idea was first proposed by Rivest et al. [20]. Typically, a ring signature scheme contains M signers to form a ring. If a signer in the ring wants to sign a received message, s/he can generate a ring signature with his/her secret key. After that, users or verifiers cannot identify the signer, but only verify the validation of the signature with the public key of the ring. Subsequently, there have been extensive studies into ring signatures [21,22,23,24,25]. Ring signatures are similar, but are not comparable, to group signatures [26,27,28]. Group signatures have a feature that includes the traceability of a signer’s identity that can be traced by a group manager served by an additional entity. The main duty of the group manager is to reveal the identity of the real signer when a dispute occurs. Compared to a group signature, ring signatures do not require coordination among the various users or a group manager. Both ring signature and group signature are useful in applications, such as e-government or e-voting, when the signer’s anonymity needs to be ensured [20,25]. However, the ring signature is more suitable for the treatment scenario between multiple doctors and a single patient.

In this paper, we propose a ring signature-based authentication scheme for TMIS in a group consultation environment. Due to the anonymity feature of the ring signature, the group member, such as a doctor or a patient, can preserve their identity information. The remaining part of this paper is arranged as follows: Section 2 provides preliminaries that introduce bilinear maps, elliptic curve cryptosystems and ECDLP; Section 3 briefly introduces Shim’s ring signature scheme, which will be used in our TMIS authentication scheme; Section 4 discusses security and possible attacks; Section 5 compares our proposal with five other approaches in terms of security and efficiency; Section 6 implements our protocol with a MIRACL (Multiprecision Integer and Rational Arithmetic) cryptographic library and tests the time cost for different group sizes and message amounts; and lastly, Section 7 gives a brief conclusion.

2. Related Work

We briefly introduce Shim’s ring signature scheme RSCP (Received Signal Code Power) [29] in this section. In our group medical consultation scheme, we will use Shim’s ring signature to achieve the goal of anonymous authentication. Compared to other ring signature schemes, Shim’s ring signature scheme is based on bilinear pairings and the ECC cryptographic system. Therefore, it requires less computation cost and is more secure [29]. Four algorithms are included in RSCP: System setup, KeyGen, RSign and RVfy. System parameters are generated in the System setup part, the user’s public/secret key pair is generated in the KeyGen part, ring signature is generated by the RSign algorithm, and the RVfy algorithm is used for signature verification. A notation list is given in

Table 1. Notations List.

Notations	Descriptions	Notations	Descriptions
Ui	A user i	Pi	A patient
Di	A doctor	G1	An additive cyclic group of prime order q
G2	A multiplicative cyclic group of same order q	P	A random point of group G1
Q	A random point of group G1	PKZ	The public key of user Z
SKZ	The master secret key of user Z	e	A bilinear map, e: G1 × G1 → G2
H	A secure one-way hash function, where G1 × M × G1n→ Zq*	EX	Encryption algorithm with public key X

.

System setup: The system manager chooses two multiplicative cyclic groups G₁, G₂.

With the same prime order q. Generate a bilinear map e: G₁ × G₁ → G₂ and a secure one-way hash function H: G₁ × M × G₁ⁿ → Z_q^*. Choose two random points P, Q ∈ G₁.

Then the system manager publishes system parameters {G₁, G₂, P, Q, e, q, H}.

KeyGen. For a user U_i, pick a random s_i ∈ Z_q^* as U_i’s private key and compute public key of U_i: PK_i = s_i·P.

RSign. Given the group of users’ public keys set {PK₁, PK₂…, PK_n}, a public key PK_j ∈ {PK₁, PK₂…, PK_n} and the corresponding private key s_j, as well as a message m ∈ {0,1} *, the ring signature is generated as below:

Step 1: Choose n-1 points A_i ∈ G₁ for I ∈ [1, n], i ≠ j;

Step 2: Compute h_i = H (A_i, m, PK₁, PK₂…, PK_n ) for I ∈ [1, n], i ≠ j;

Step 3: Choose a random number t ∈ Z_q^* and compute A_j = t·P-${\displaystyle \sum }_{i\ne j}^n$ (h_i·PK_i + A_i), h_j = H (A_j, m, PK₁, PK₂…, PK_n), B = (t + h_j·s_j)·Q;

Step 4: Output the ring signature S= {A₁, A₂…, A_n, B}.

RVfy. Given a set of public keys {PK₁, PK₂…, PK_n}, signature S can be verified through the steps below:

Step 1: Compute h_i = H (A_i, m, PK₁, PK₂…, PK_n) for I ∈ [1, n];

Step 2: Verify the signature as equation e (P, B)? =e (${\displaystyle \sum }_{i=1}^n$ (h_i ⋅ PK_i + A_i) + h_j ⋅ PK_j + B, Q).

If the equation holds, the signature is verified successfully; otherwise, reject the message m.

3. Preliminaries

This section introduces some preliminaries used in our scheme.

3.1. Bilinear Maps

Given a cyclic multiplicative group G order q, the generator of group G is g, given another multiplicative cyclic group G_T with the same order q. A bilinear pairing refers to a map e; G × G → G_T should satisfy the following properties:

(1)

Bilinearity: For all P, Q ∈ _R G and a, b ∈ _R Z_q*, e (aP, bQ) = e (P, Q)^ab;

(2)

Non-degeneracy: There exist g₁, g₂ ∈_R G such that e (aP, bQ) ≠ 1G_T;

(3)

Computability: For all P, Q ∈ _R G, there is an efficient algorithm to compute e (aP, bQ).

3.2. Elliptic Curve Cryptosystem

An elliptic curve cryptosystem (ECC) is an asymmetrical cryptosystem. Such a system was independently proposed by Miller [30] and Koblitz [31] in 1985 and 1987, respectively. Compared to RSA, ECC can achieve the same security requirements with a shorter key-length [32]. As such, it has recently been widely used in many cryptographic schemes.

An elliptic curve [33,34] is defined over a finite field F_p by equation E_p (a, b): y² = x³ + ax + b, where p is a large prime and 4a³ + 27b² = 0 mod p. The points on this elliptic curve form a cyclic group. Addition in this group is defined as points P, Q, R ∈ E_p(a,b) on one line, then P + Q + R = O (O is the infinite point). Given an integer s ∈ F_p^* and a point P ∈ E_p(a, b), the multiplication operation s·P over E_p(a,b) is defined as P + P + … + P in s times. If P is symmetrical with P′ on the X axis, then P + P’ = O. Furthermore, point P is a base point with an order n if and only if n·P = O.

3.3. Elliptic Curve Discrete Logarithm Problem

Every cryptosystem has its own challenging particulars, such as the integer factorization used in RSA. The most important challenge in ECC is the elliptic curve discrete logarithm problem (ECDLP) [29]. Based on ECDLP, many other difficult problems can be addressed, such as the computational Diffie–Hellman problem (CDHP) and the elliptic curve factorization problem (ECFP). In our proposed scheme described in Section 4, we will use ECDLP.

Definition—elliptic curve discrete logarithm problem (ECDLP): Given two points P and O over E_p (a, b), it is very hard to find an integer s ∈ E_p* such that Q = sP.

4. Our Proposed Group Consultation Authentication Scheme

Sometimes patient’s treatments are conducted by a group of consultants, which includes doctors and specialist therapists, such as rehabilitation therapists. In such a treatment case, in which multiple doctors/specialist therapists and a single patient are involved, it is necessary to protect the doctors’ identities and the patient’s identity at the same time. If there is a medical care dispute, the treatment evaluation should be conducted in advance before revealing the doctors’ identities. With the feature of ring signature, no verifier can link the signed message and signer.

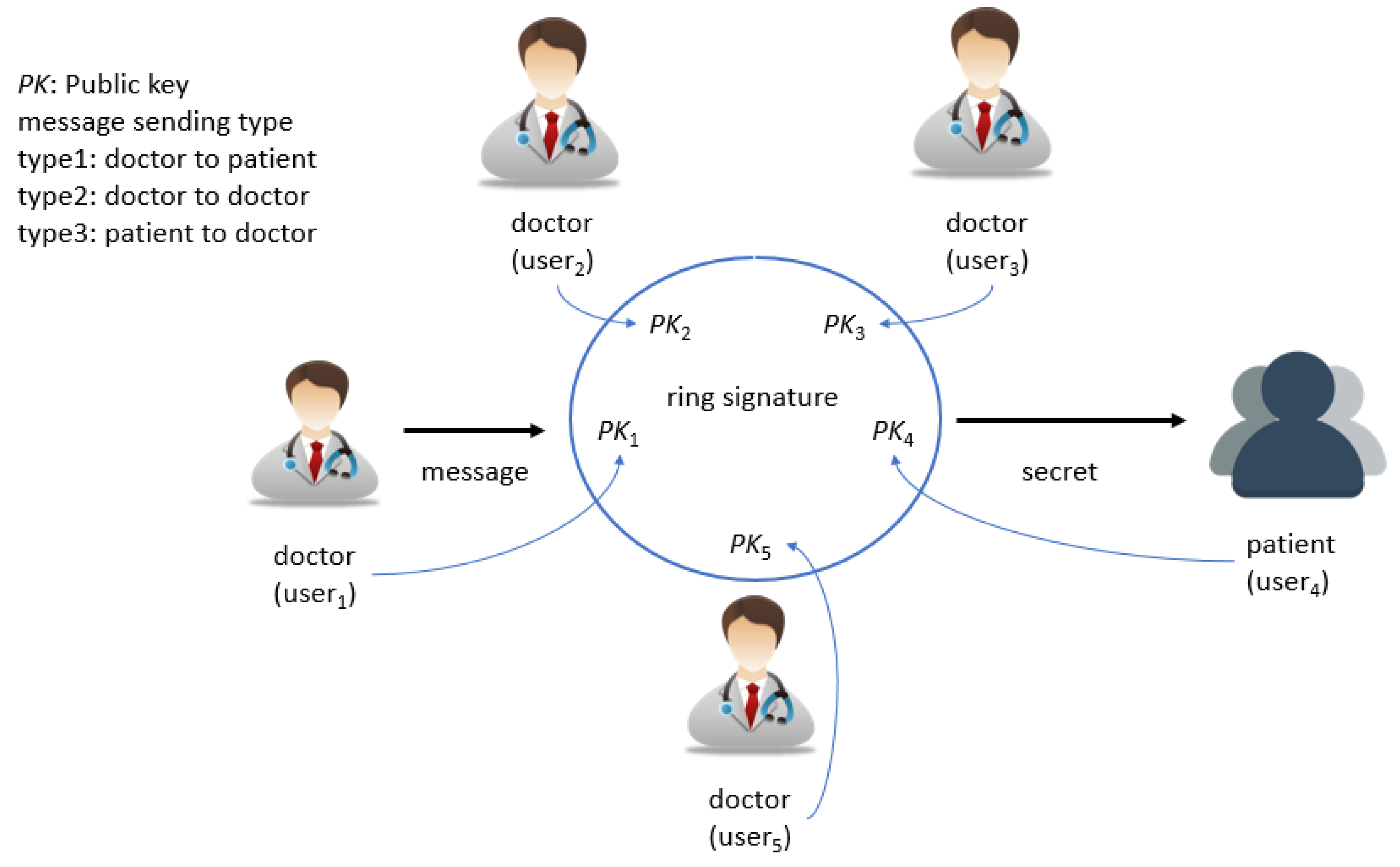
To meet the above requirements, there are three types of message-sending models defined according to the corresponding sender and receiver in our proposed group consultation authentication scheme, as shown in Figure 1. Type 1 is sent from doctor to patient when a doctor wants to send the patient’s diagnostic information to him or her. Type 2 is when the message is sent from a doctor to the other doctor when a doctor wants to send diagnostic information of a given patient to the other doctor for the following treatments. The last type is sent from patient to doctor when a patient wants to send the state of their illness to the doctor.

Six algorithms compose the mechanism: System setup, KeyGen, D-sign, P-sign, D-verify and P-verify. D-sign and P-sign are the signing phase for a doctor and patient, respectively. Similarly, D-verify and P-verify are for the verification phase for a doctor and patient, respectively. A notation list is given below.

System setup: The system manager chooses two multiplicative cyclic groups G₁, G₂ with the same prime order q. Generate a bilinear map e: G₁ × G₁ → G₂ and a secure one-way hash function H: G₁ × M × G₁ⁿ → Z_q^*. Choose two random points P, Q ∈ G₁. Then the system manager publishes the system parameters {G₁, G₂, P, Q, e, q, H}.

KeyGen: A user U_i (doctor or patient) first randomly generates a random s_i ∈ Z_q^* as U_i’s private key by using a random number generator and then computes their public key U_i: PK_i = s_i·P.

D-sign: Before one doctor U_D wants to send diagnostic information m to other doctors or the diagnosed patient U_P, the doctor first collects the other doctors’/patient’s public keys PK₁, PK₂…, PK_n. Then, they input the diagnostic information m ∈ {0,1} *, the doctor’s secret key s_D and {PK₁, PK₂…, PK_n} in the below steps to generate the ring signature:

Step 1: Choose n-1 points A_D ∈ G₁ for I ∈ [1, n], i ≠ D;

Step 2: Compute h_i = H (A_i, m, PK₁, PK₂…, PK_n) for i ∈ [1, n], i ≠ D;

Step 3: Choose a random number t∈Z_q^* and compute A_D = t·P-${\displaystyle \sum }_{ i\ne D}^n$ (h_i·PK_i + A_i),

h_D = H (A_D, m, PK₁, PK₂…, PK_n), B = (t + h_D·s_D) ·Q;

Step 4: Output the ring signature S = {A₁, A₂…, A_n, B};

Step 5: Send {S, E_PKX (m, γ)} to U_P.

It is noted that the diagnostic information m not only contains the diagnostic information, but also contains the treatment information, drug information, and timestamp. Such an arrangement is intended to make sure two different blocks produce signatures that would not appear to be the same.

P-sign: Similar to D-sign, before one patient U_p wants to send the state of illness m to other doctors, the current doctor collects the following doctors’ public keys PK₁, PK₂…, PK_n first. They then input the message m ∈ {0,1} *, the patient secret key s_P and {PK₁, PK₂…, PK_n} into the below steps to generate the ring signature:

Step 1: Choose n-1 points A_P ∈ G₁ for i ∈ [1, n], i ≠ P;

Step 2: Compute h_i = H (A_i, m, PK₁, PK₂…, PK_n) for i ∈ [1, n], i ≠ P;

Step 3: Choose a random number t∈Z^* and compute A_P = t·P-${\displaystyle \sum }_{ i\ne P}^n$(h_i·PK_i + A_i), h_P = H (A_P, m, PK₁, PK₂…, PK_n), B = (t + h_P·s_P)·Q;

Step 4: Output the ring signature S = {A₁, A₂…, A_n, B};

Step 5: Send {S, E_PKX (m, γ)} to U_D.

D-verify: If the following doctors in the consultation group received the message and its signature, they can check the ring signature with the result of whether this message comes from this consultation group:

Step 1: Decrypt the message with sk_D and check the validation of γ, and ignore the message if γ is invalid; otherwise, continue to Step 2;

Step 2: Collect public keys {PK₁, PK₂…, PK_n} of this consultation group;

Step 3: Compute h_i = H (A_i, m, PK₁, PK₂…, PK_n) for i ∈ [1, n];

Step 4: Verify the signature as equation e (P, B)? = e (${\displaystyle \sum }_{ i\ne P}^n$(h_i·PK_i + A_i), Q).

If the equation holds, the signature is verified successfully and comes from a legal consultation group; otherwise, this message is from a sender outside of this consultation group, so one should reject message m.

P-verify: Similar to D-verify, if a patient in a consultation group receives a message and its signature, the patient can check the ring signature with the result of whether this message comes from this consultation group:

Step 1: Decrypt the message with sk_P and check the validation of γ, and ignore the message if γ is invalid; otherwise, continue to Step 2;

Step 2: Collect the public keys {PK₁, PK₂…, PK_n} of this consultation group;

Step 3: Compute h_i = H (A_i, m, PK₁, PK₂…, PK_n) for i ∈ [1, n];

Step 4: Verify the signature as equation e (P, B)? = e (${\displaystyle \sum }_{ i\ne D}^n$(h_i·PK_i + A_i), Q).

If the equation holds, the signature is verified successfully and comes from a legal consultation group; otherwise, this message is coming from a sender outside of this consultation group, so one should reject message m.

The overall flowchart of our proposed ring signature mechanism is summarized and shown in Figure 2.

5. Discussions about Possible Attacks

In this section, we prove that our scheme can resist possible attacks, through means such as identity privacy preservation (anonymity authentication), confidentiality, and replay attack [17,18,33,35,36]. As mentioned previously, medical disputes are a significant problem. If a medical accident happens, it may harm the safety of medical workers when a doctor’s or specialist’s identity is illegally revealed. Therefore, it is also an important part of the information security process to ensure identity privacy in TMIS. Moreover, confidentiality is an integral part of patient health care data.

Identity privacy preservation: In our group consultation scheme, the signature with a set of public keys PK₁, PK₂, …, PK_n is generated in advance. Due to the privacy preservation property of a ring signature, the receiver cannot know any identity information about the message sender. Additionally, all user communication history cannot be traced because a random number is changed in each round.

Preserving patient privacy: In our scheme, the sender encrypts the message with the receiver’s public key before the data transfer. Therefore, the patient’s privacy is preserved with the confidentiality of message m. As our signing phase is based on an elliptic curve cryptosystem, an ECC encryption algorithm can be chosen as the encryption algorithm. The ECC encryption is based on ECDLP. If we use ECC encryption as E, then we can use the public key and private key generated in the setup phase directly.

Replay Attack: We embed a timestamp into the ciphertext in each transmitted message. The freshness of a timestamp will be checked before the receiver validates the signature. If an attacker intercepted a legal user’s message and resends this message to the receiver, it will be rejected because the timestamp check will not be passed.

Forging a signature: In our scheme, the final signature is S = {A₁, A₂…, A_n, B}, B = (t + h_j·s_j)·Q. The attacker cannot forge a signature because he does not have the private key s_j. Besides, given another signature S′= {A₁′, A₂′…, A_n′_, B′}, the attacker cannot calculate the private key s_j based on the security property of the ECDLP and paring. Therefore, our scheme can resist a signature-forging attack.

6. Security and Efficiency Comparisons

In this section, we present the performance assessment of our proposal and another five medical information system schemes—Islam et al. [36], Li [37], Liu et al. [12], Zhao et al. [17], and Guo et al. [38].

Table 2. Security comparison of our scheme with other similar schemes.

Islam et al.		Li	Liu et al.	Zhao	Guo et al.	Our Scheme
Identity privacy preservation	×	×	×	×	×	√
Preserving patient privacy	√	√	√	√	√	√
Replay attack	√	√	√	√	√	√
Signature forging	√	√	√	√	√	√
Provision of provable security	×	×	×	×	√	√

shows a comparison of the security properties with the other five schemes. From the comparison we can see that our proposed scheme has the best security compared to the others, in terms of identity privacy preservation, preserving patient privacy, and replay attack and signature forging security, as previously proven. Provision of provable security can be found in the literature [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38].

The notations T_e, T_h, T_p, T_m, T_i and T_s represent module exponentiation, one-way hash function, pairing operation, point multiplication of ECC, modular inversion and symmetric encryption/decryption, respectively. The n in our scheme means the group size (number of members in the consultation group). Since the number of doctors in a consultation group is limited, the value of n will not be too large. From

Table 3. Efficiency comparison of our proposal with similar schemes.

	Islam et al.	Li	Liu et al.	Zhao	Guo et al.	Our Scheme
Sender	8Tm + 2Ts + 5Th	10Tm + 2Ts + 5Th	Te + 4Tp + 3Th	3Tp + 4Th + Tm + Ts	8Th + 2Tm + Tp	(n + 1)Tm + nTh
Receiver	4Tp + 5Tm + 2Ts + 5Th	4Tp + 5Tm + 2Ts + 5Th	Te + Tp + 3Th + Ti + 2Tm	6Tp + 5Th +Ts	4Th + 2Ts + Tp + 3Tm	2TP + nTM + nTh

, we can see that our ring signature-based medical information system is more efficient than other schemes.

7. Experimental Results

To evaluate the effectiveness of our group consultation scheme, we conducted two experiments (sign phase and verify phase) on a computer with a 3.6 GHz processor and 8 G RAM, running a Windows 7 operation system, which is similar to previous setups in the literature [16,17]. We used the cryptographic library MIRACL to implement the protocol. The key length was set as 512 bits and Tate Paring was used. As is known, point multiplication costs less time than a paring operation. From Figure 3 and Figure 4, we can see that the verification phase needs more time than the sign phase because of paring operations. Comparing our scheme with other existing schemes, it can be noted that our proposed scheme needs the least time in the sign phase while maintaining satisfying result in the verification phase. Given that our proposed scheme achieves better security characteristics, it can be concluded that our proposed scheme provides maximum benefit in both aspects of efficiency and security. In each experiment, we considered two group size conditions: two and five. Considering the practical situation of a group consultation, we did not setup an excessively large group size. From the experimental results, we can see that the time cost increases with an increase in group size. When there are more members in a group, more operations (point multiplication) are needed. Additionally, if group size is fixed, the more messages that are signed/verified, the more time is needed with linear complexity O(n).

8. Conclusions

In this paper we propose a new ring signature-based anonymity authentication scheme, designed for a group medical consultation environment that protects both doctor and patient privacy. Compared with other schemes, our proposed scheme needs less time, but has more security features, such as anonymity for both doctor and patient. According to the experiments, satisfactory efficiency is achieved for both sides in terms of verification and sign in. Thus, our proposed scheme achieves an optimal balance between security and efficiency when compared with all current TMIS authentication schemes. With the current results, in the future, we will explore the extended group medical consultation scenarios involving various IoT devices, since physiological information pre-collected by IoT devices will be an important reference for doctors in order to diagnose patients.