Lorentz Violation at the Level of Undergraduate Classical Mechanics
Abstract
1. Introduction
2. General Theory
2.1. Transformations and Symmetries
Key Idea 1: In the Standard-Model Extension, the vacuum is not symmetrical under rotations. It has a directionality to it.
- In the flat-spacetime limit of the SME, momentum and energy are conserved. This implies that the background vector field cannot be a force field; a background force field would generate momentum (and kinetic energy) from nothing. Instead, the background fields that appear in the SME are more abstract.It is reasonable to instead imagine a background torque field, i.e., a field that encourages everything in the universe to rotate around a particular axis. Such effects do occur in the SME, but they are not directly relevant to this work;
- The background field we’ll be studying in this work is a matrix (a 2nd-rank tensor) rather than a vector. Details of its behavior appear later in this section;
- The full SME has many fields: A torque-producing field that acts on electrons, a torque-producing field that acts on protons, and so on. The fields that act on different particles do not necessarily point in the same direction or have the same magnitude.Moreover, there are other effects that cannot be cleanly represented as torques: a vector field that behaves in many ways, like the electromagnetic vector potential, a matrix field that causes a particle’s kinetic energy to depend on the direction of its velocity, and so on. The fundamental goal of the SME is to include all effects that violate Lorentz symmetry while respecting most other important aspects of the Standard Model; this leads to a broad smorgasbord of effects.
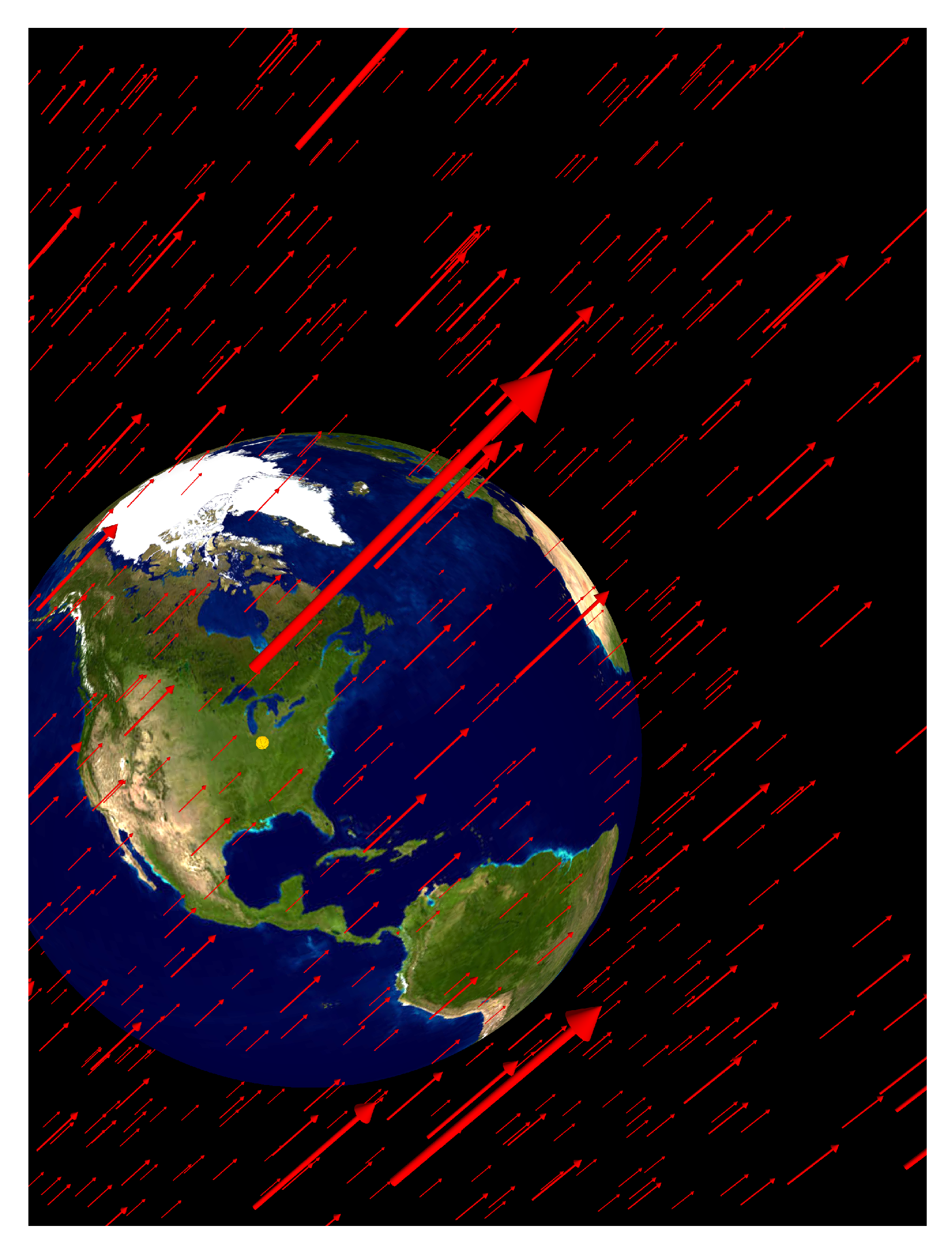
Key Idea 2: An important technique for searching for Lorentz violation is to create a system, such as an atomic clock, that should keep ticking at a constant rate according to conventional physics. We then watch it very carefully as it rotates with Earth through the background field.
Key Idea 3: Since Lorentz-violating effects are correlated to the background vacuum, they are correlated to sidereal days.
2.2. Lagrangian, Momentum, and Newton’s 2nd Law
3. Example Systems
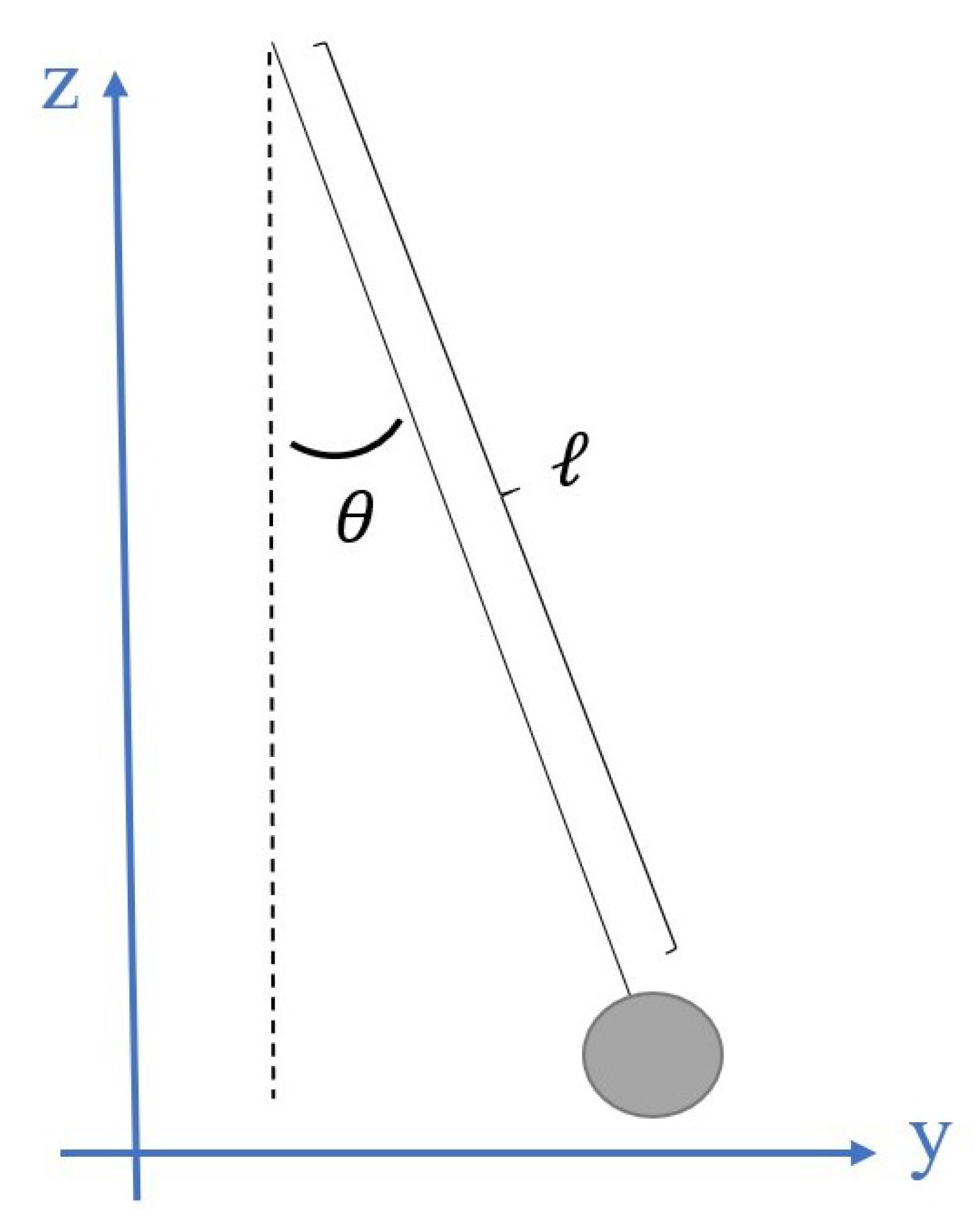
3.1. Simple Pendulum
3.1.1. Theory: Period
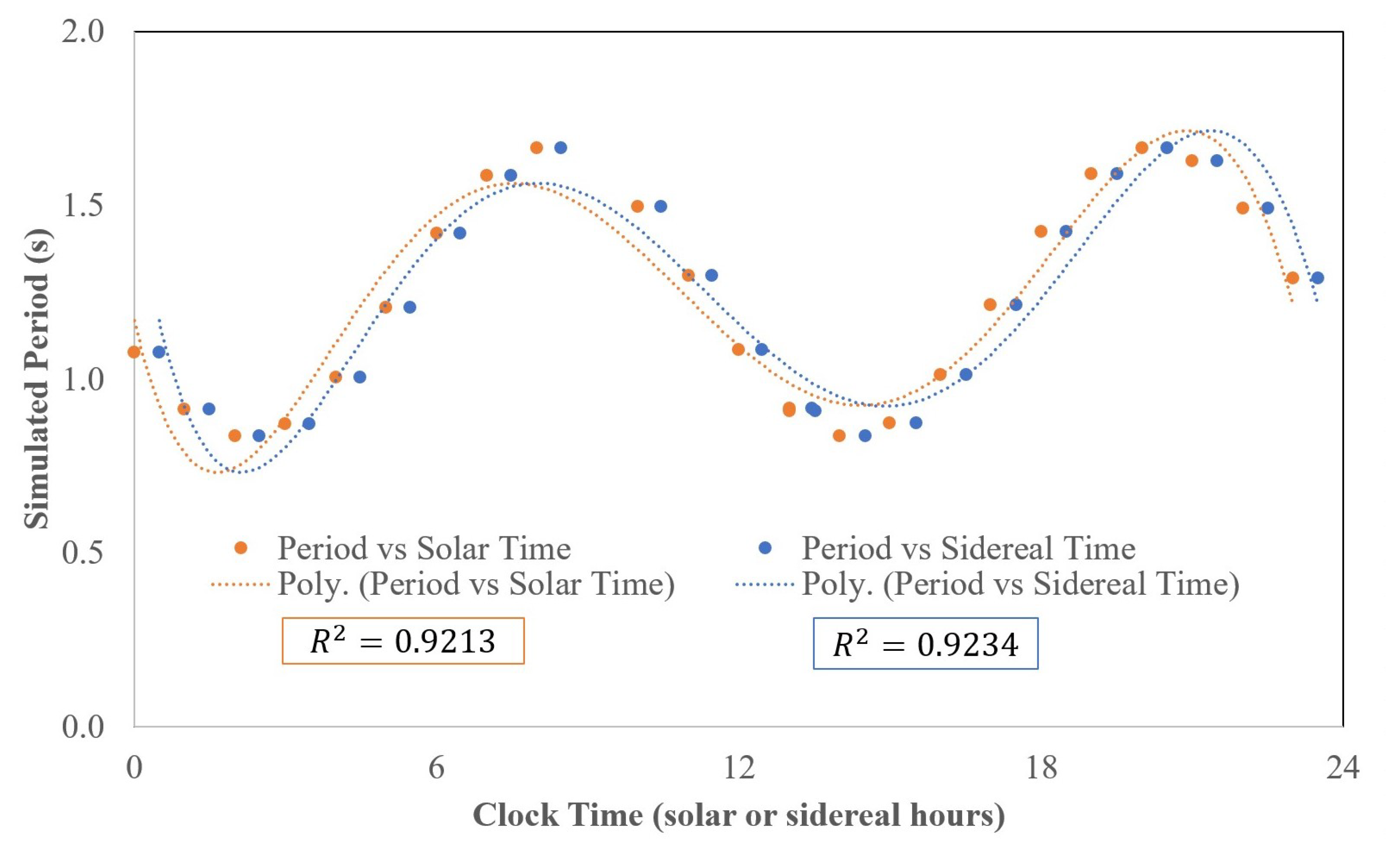
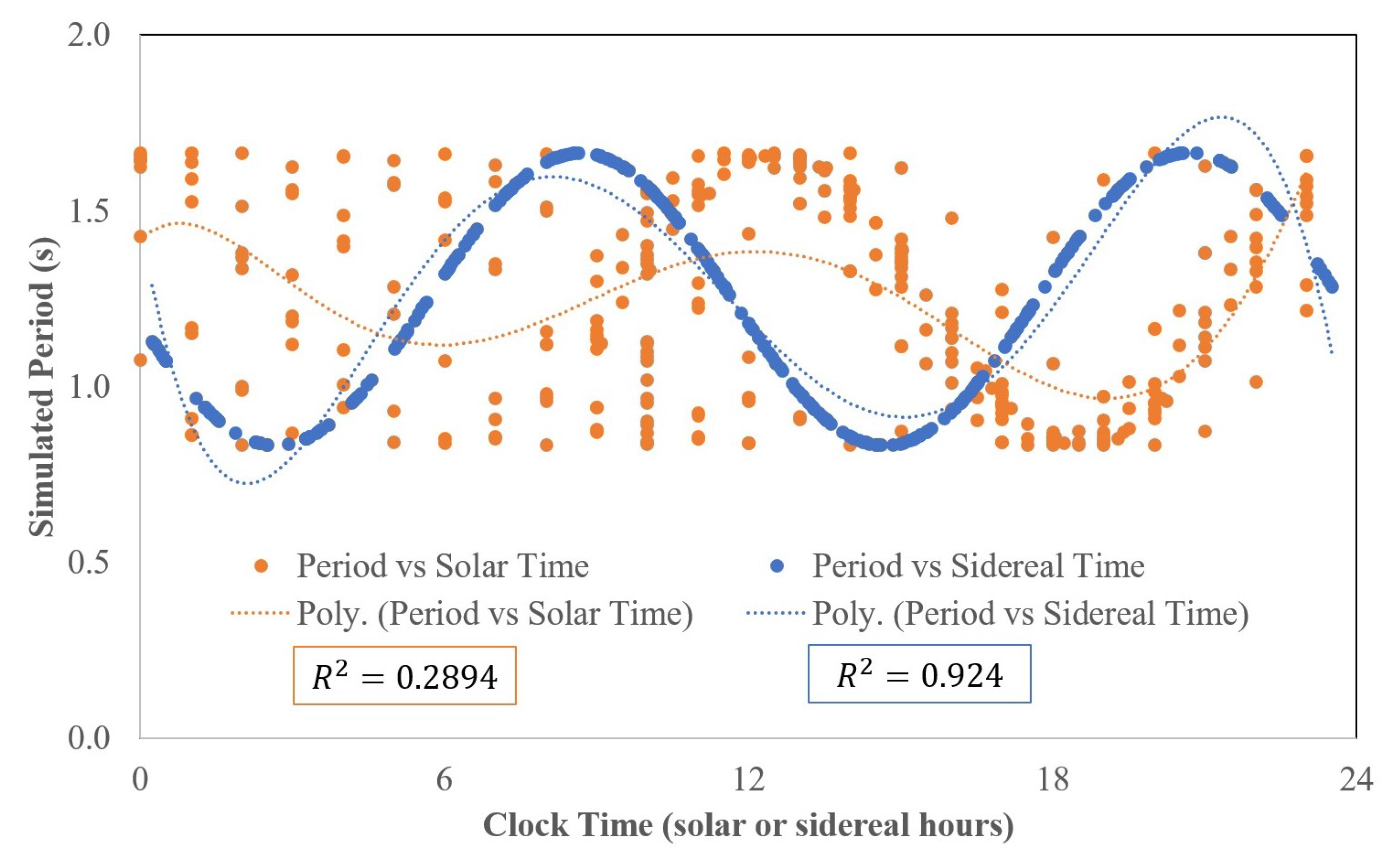
3.1.2. Simulated Data
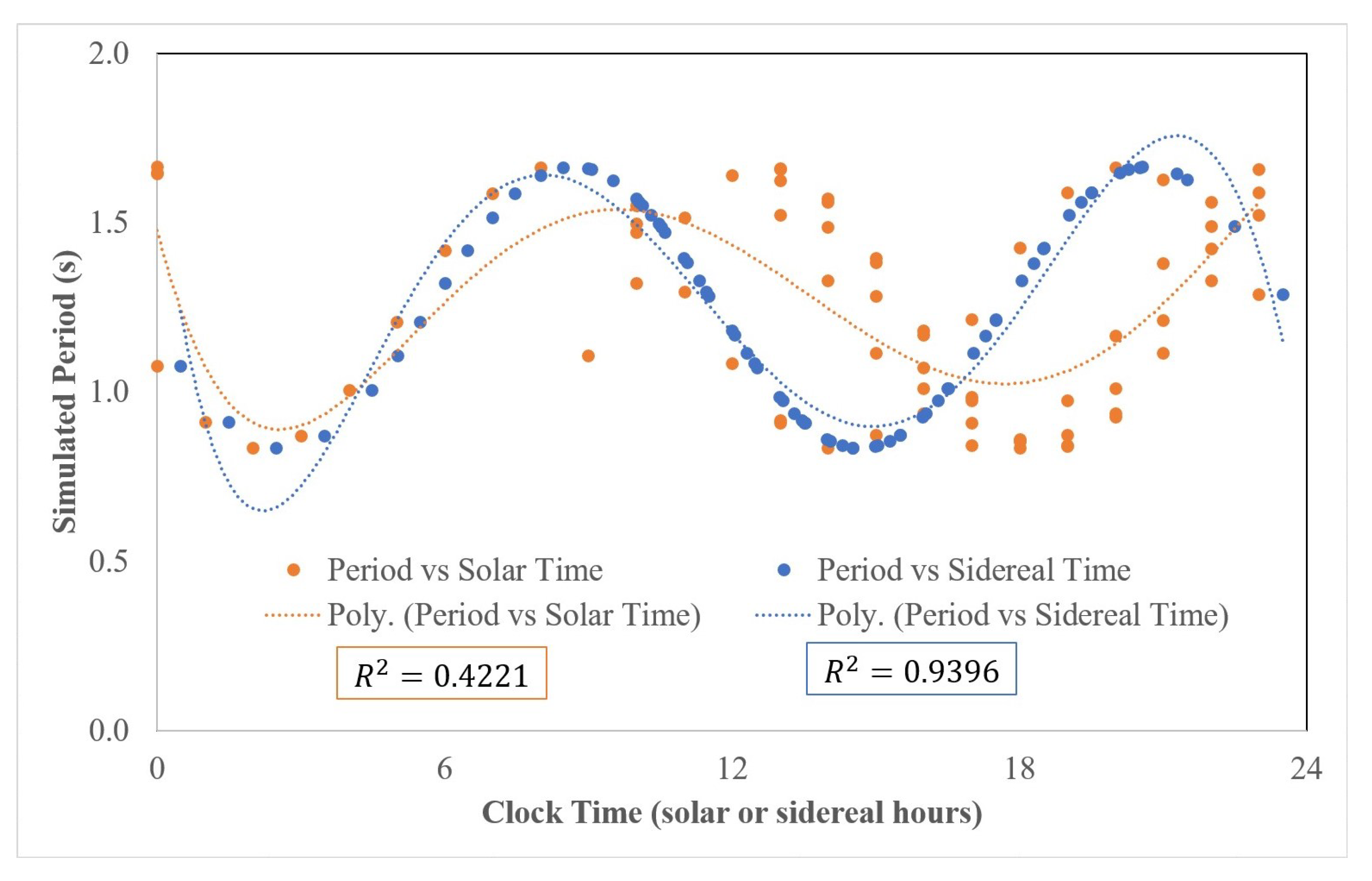
3.1.3. Pendulum Experiment
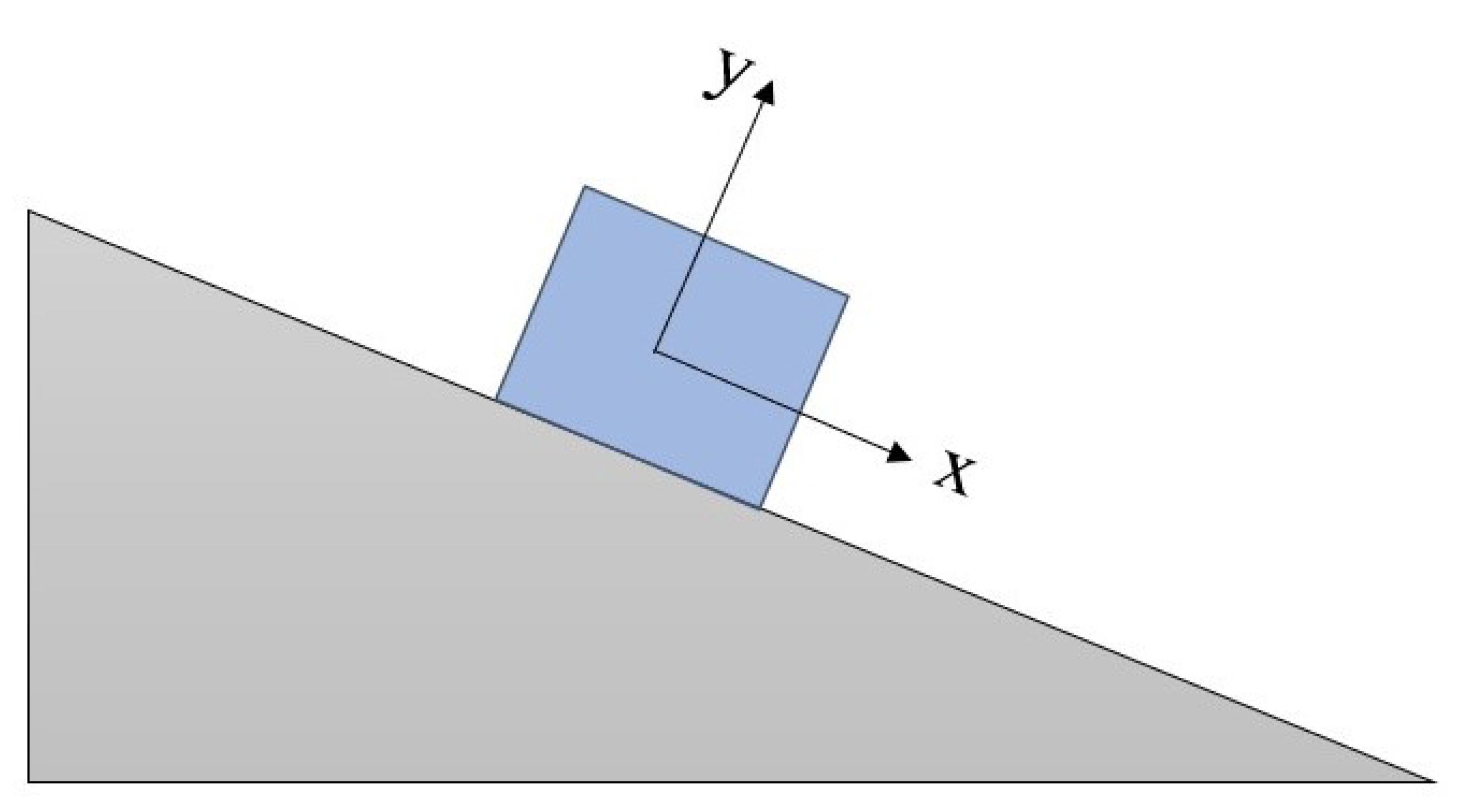
3.2. Block on Inclined Plane
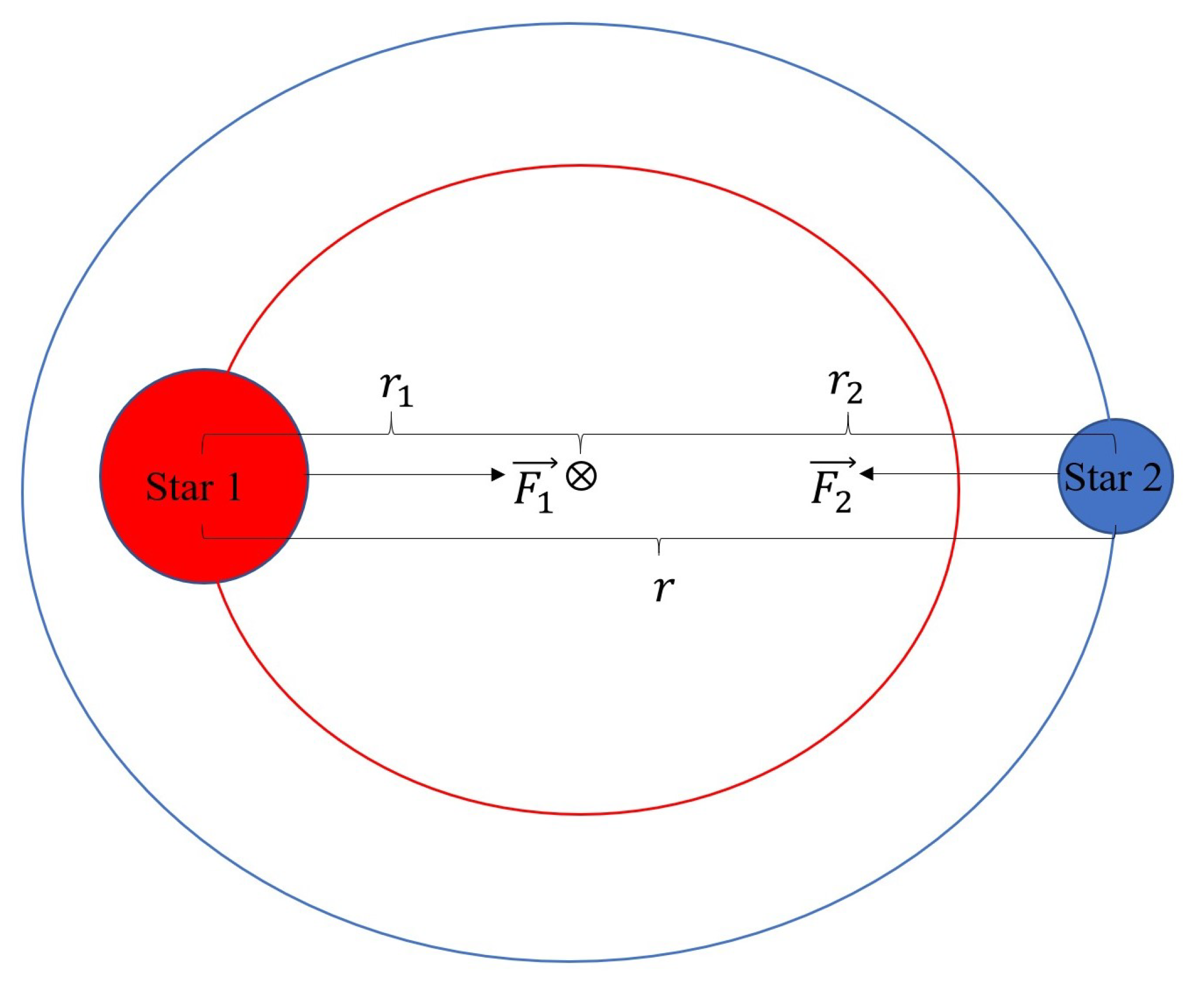
3.3. Binary Star System
3.3.1. Theory: Equations of Motion
3.3.2. Theory: Energy
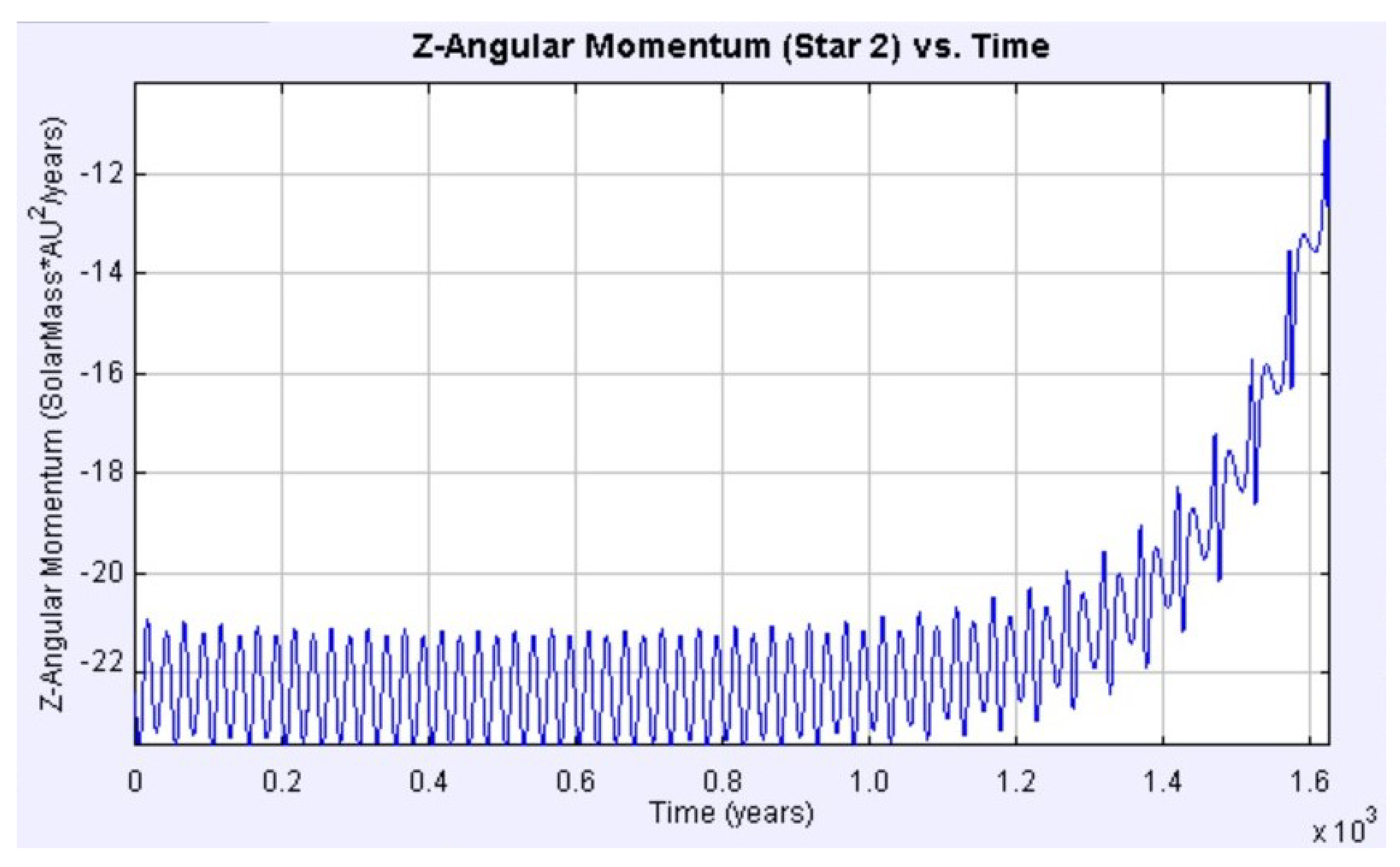
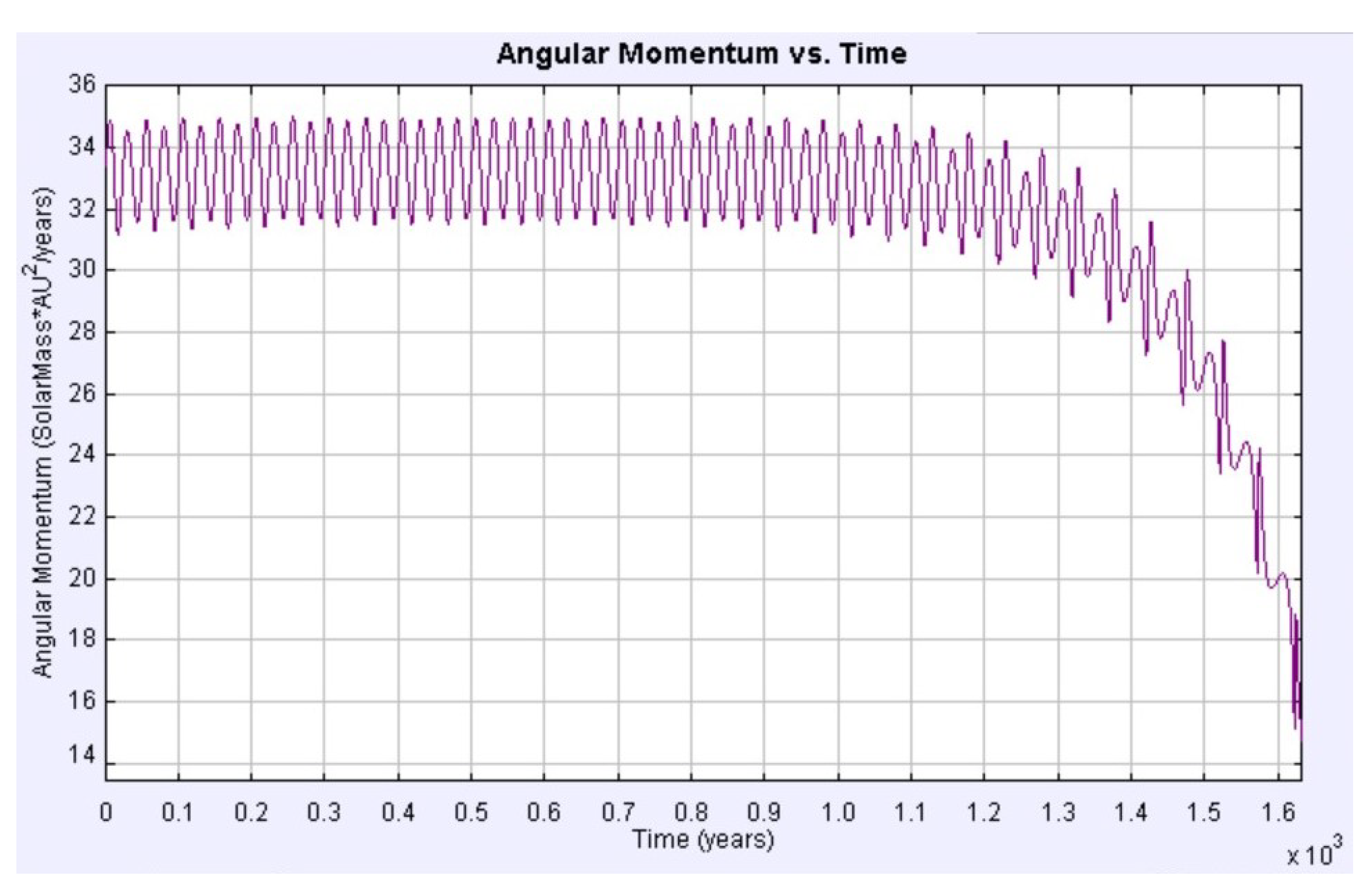
3.3.3. Theory: Angular Momentum
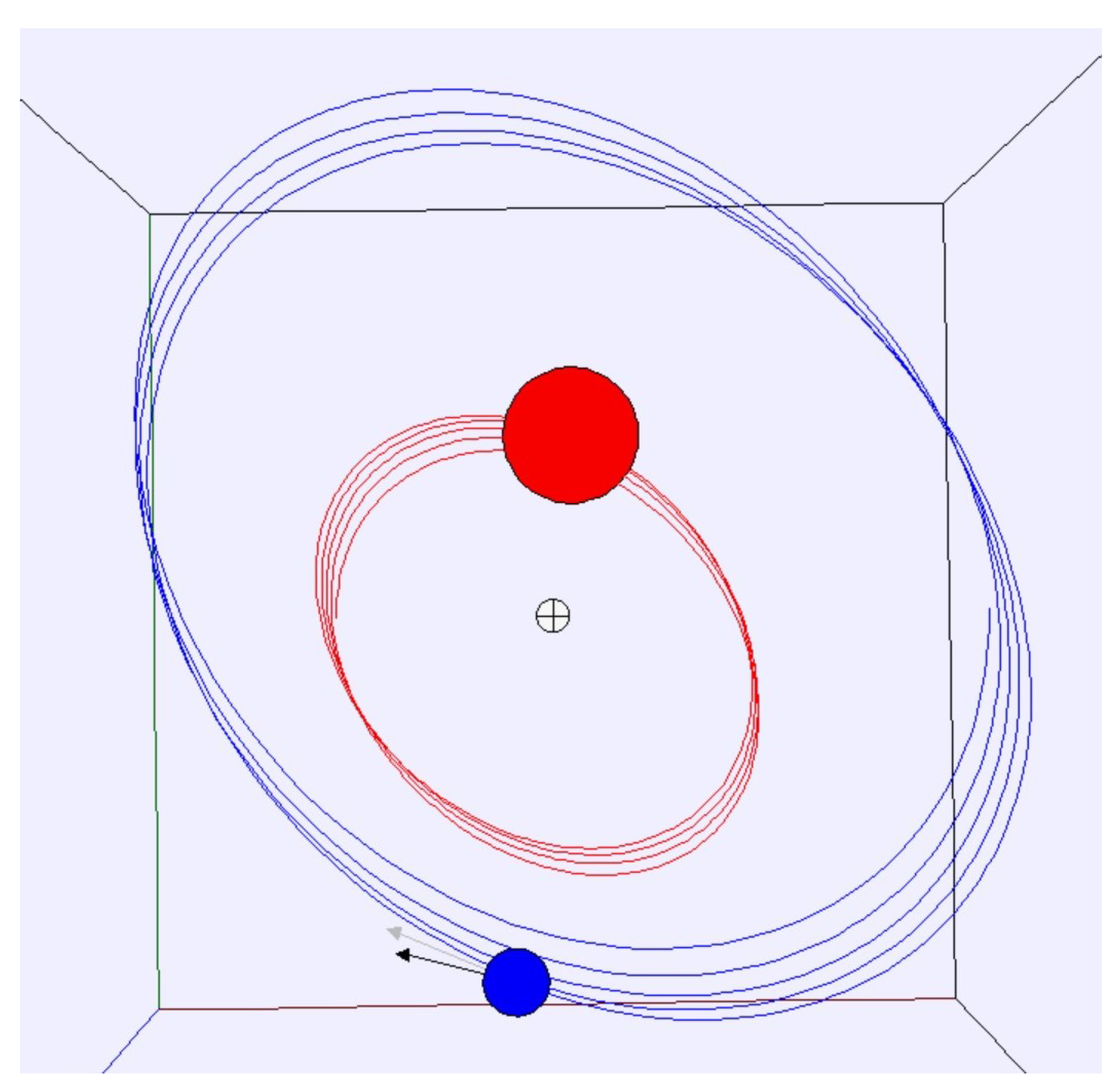
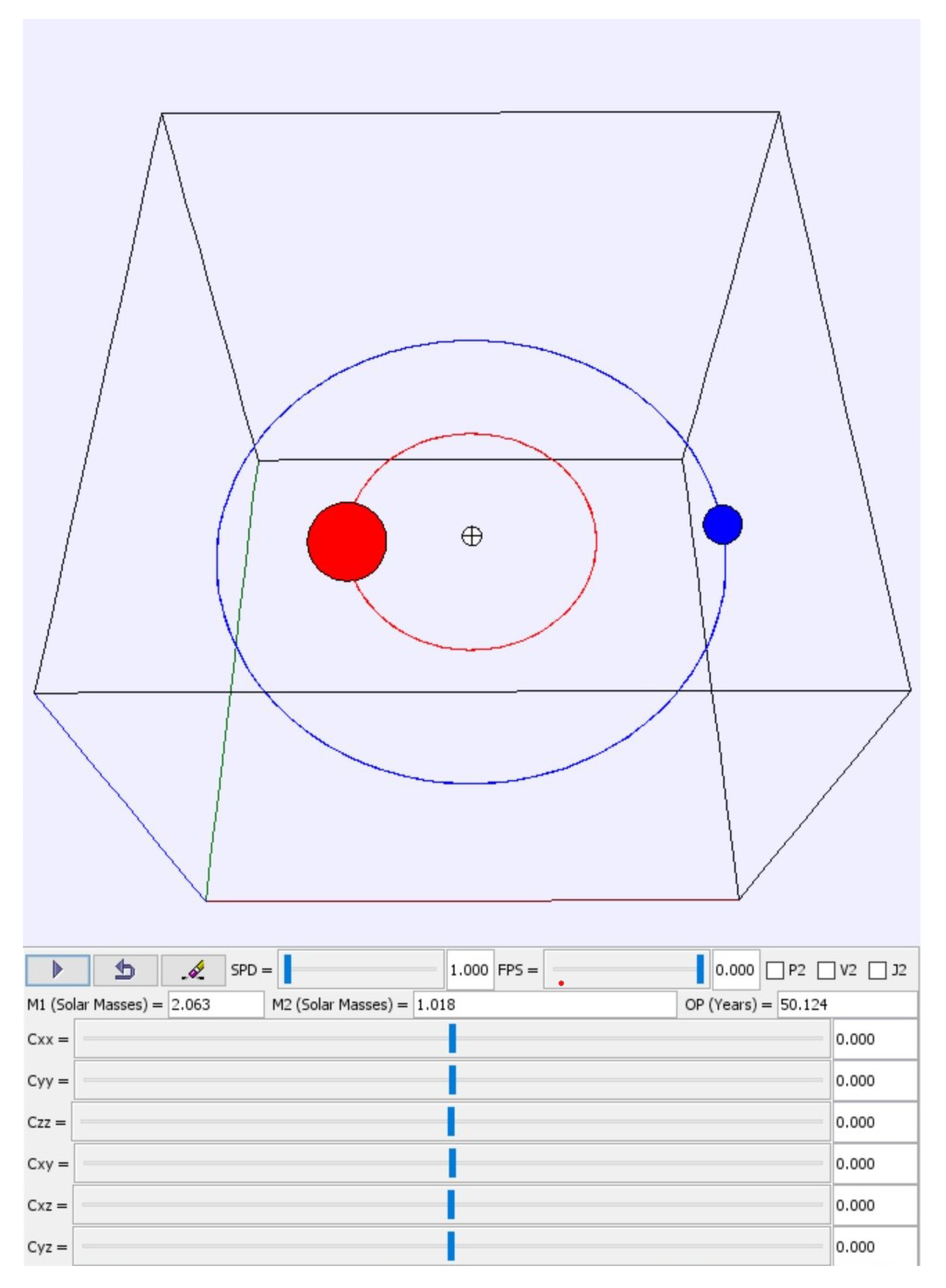
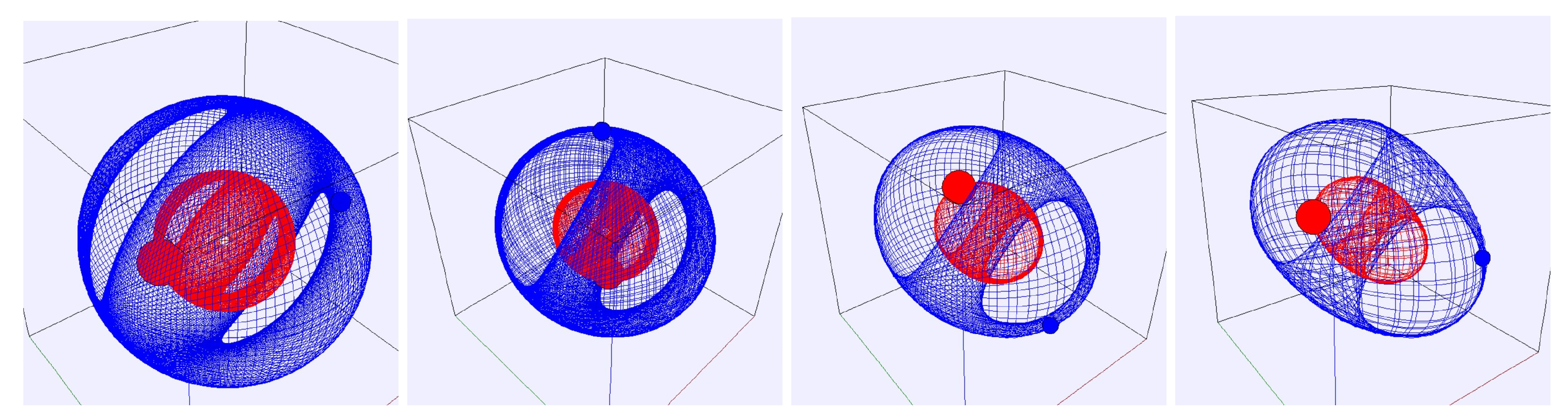
3.3.4. Binary Star System Computational Simulation
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SME | Standard-Model Extenshion |
| EJS | Easy Java Simulation |
References
- Kostelecky, V.; Samuel, S. Spontaneous Breaking of Lorentz Symmetry in String Theory. Phys. Rev. D 1989, 39, 683. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.; Potting, R. CPT and strings. Nucl. Phys. B 1991, 359, 545–570. [Google Scholar] [CrossRef]
- Connes, A. Noncommutative Geometry; Springer: San Diego, CA, USA, 1994. [Google Scholar]
- Carroll, S.M.; Harvey, J.A.; Kostelecky, V.A.; Lane, C.D.; Okamoto, T. Noncommutative field theory and Lorentz violation. Phys. Rev. Lett. 2001, 87, 141601. [Google Scholar] [CrossRef] [PubMed]
- Colladay, D.; Kostelecky, V. Lorentz violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Kostelecky, V. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. Rev. Mod. Phys. 2011, 83, 11–31. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Lane, C.D. Constraints on Lorentz violation from clock comparison experiments. Phys. Rev. 1999, D60, 116010. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Vargas, A.J. Lorentz and CPT Tests with Clock-Comparison Experiments. Phys. Rev. D 2018, 98, 036003. [Google Scholar] [CrossRef]
- Safronova, M.; Budker, D.; De Mille, D.; Kimball, D.F.J.; Derevianko, A.; Clark, C. Search for New Physics with Atoms and Molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Lane, C.D. Using Comparisons of Clock Frequencies and Sidereal Variation to Probe Lorentz Violation. Symmetry 2017, 9, 245. [Google Scholar] [CrossRef]
- Bailey, Q.G.; Kostelecky, V. Signals for Lorentz violation in post-Newtonian gravity. Phys. Rev. D 2006, 74, 045001. [Google Scholar] [CrossRef]
- Kostelecky, A.V.; Tasson, J.D. Matter-gravity couplings and Lorentz violation. Phys. Rev. D 2011, 83, 016013. [Google Scholar] [CrossRef]
- Kostelecky, A.V.; Russell, N. Classical kinematics for Lorentz violation. Phys. Lett. B 2010, 693, 443–447. [Google Scholar] [CrossRef]
- Bertschinger, T.; Flowers, N.A.; Moseley, S.; Pfeifer, C.R.; Tasson, J.D.; Yang, S. Spacetime Symmetries and Classical Mechanics. Symmetry 2018, 11, 22. [Google Scholar] [CrossRef]
- Jansky, K.G. Electrical Disturbances Apparently of Extraterrestrial Origin. Proc. Inst. Radio Eng. 1982, 21, 1387–1398. [Google Scholar]
- Kostelecky, V.; Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 2002, 66, 056005. [Google Scholar] [CrossRef]
- Pihan-Le Bars, H.; Guerlin, C.; Lasseri, R.; Ebran, J.; Bailey, Q.; Bize, S.; Khan, E.; Wolf, P. Lorentz-symmetry test at Planck-scale suppression with nucleons in a spin-polarized 133Cs cold atom clock. Phys. Rev. D 2017, 95, 075026. [Google Scholar] [CrossRef]
- Mittleman, R.; Ioannou, I.; Dehmelt, H.; Russell, N. Bound on CPT and Lorentz symmetry with a trapped electron. Phys. Rev. Lett. 1999, 83, 2116–2119. [Google Scholar] [CrossRef]
- Mittleman, R.K.; (University of Washington, Seattle, WA, USA). Personal communication, 1999.
- PASCO Smart Gate PS-2180. Available online: www.pasco.com (accessed on 20 February 2020).
- Clyburn, M. Binary Star System with Lorentz Symmetry Violating Effects. 2020. Available online: https://www.compadre.org/OSP/items/Detail.cfm?ID=15555 (accessed on 10 September 2020).



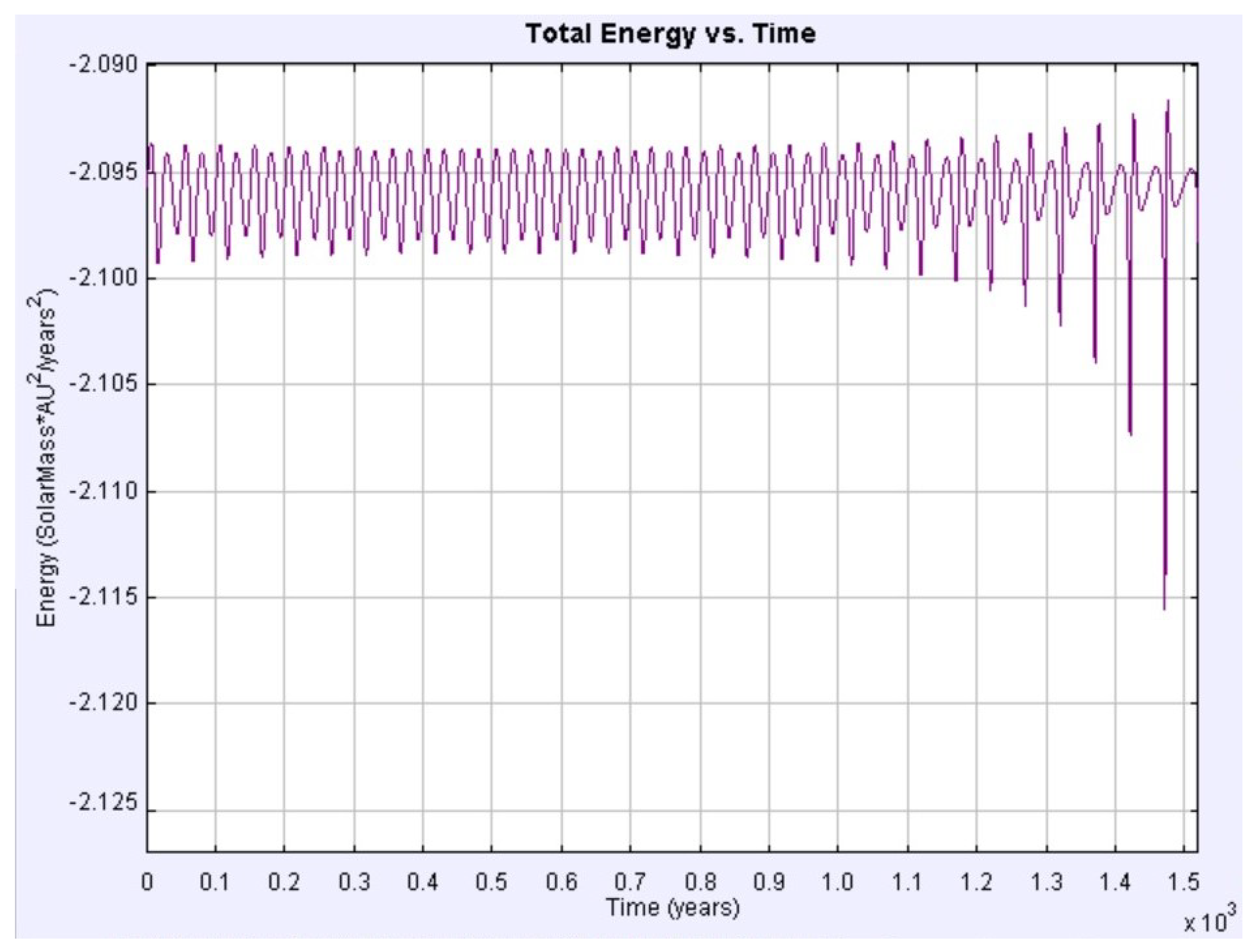
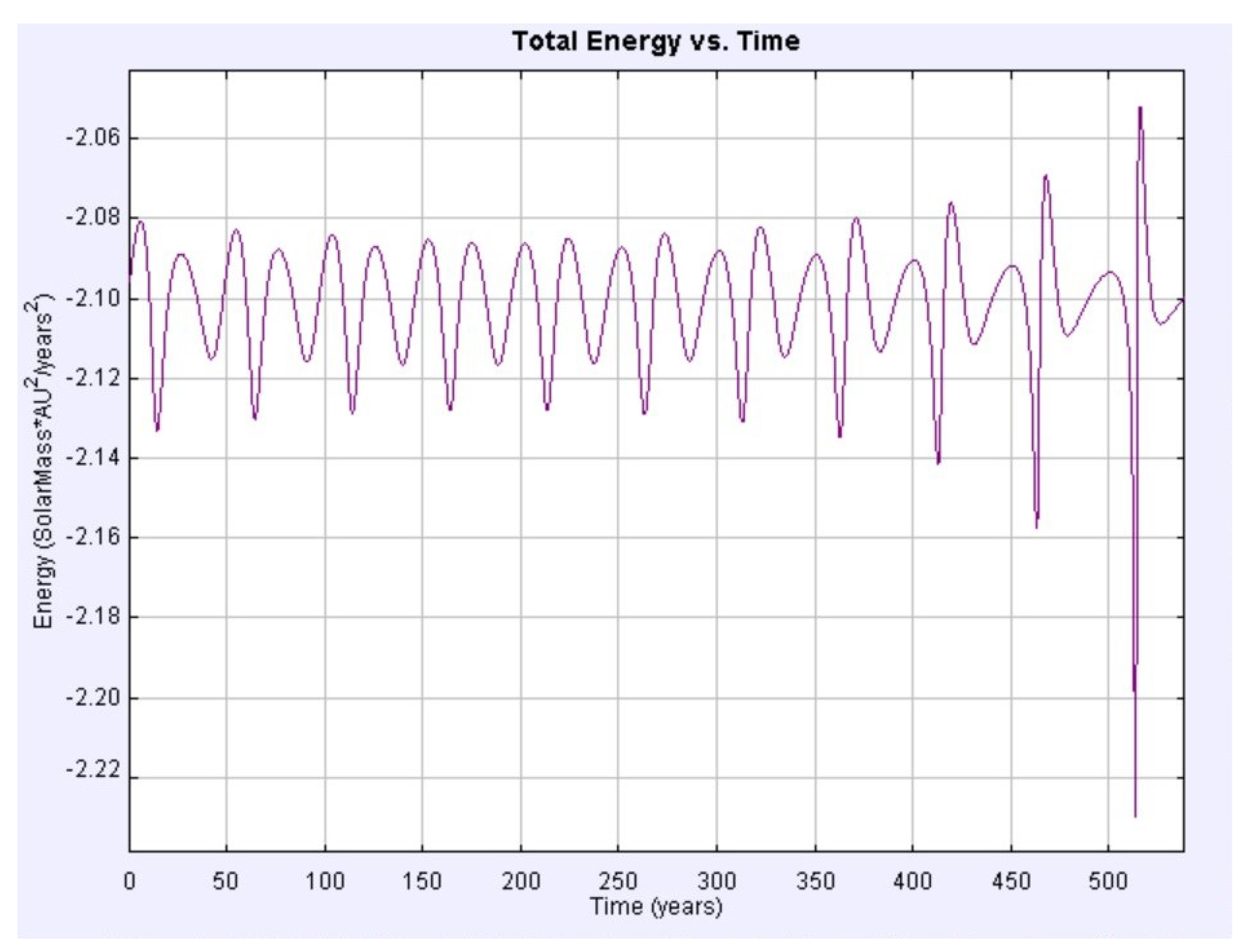
| Constants | Value | Uncertainty |
|---|---|---|
| Mass m | 0.1 kg | ±0.01 kg |
| Length ℓ | 0.47 m | ±0.01 m |
| Initial Angle | 25 | |
| Co-latitude | 0.9724 rad | ±0.0005 rad |
| SME Coefficient | Value | Uncertainty |
|---|---|---|
| −0.00012 | ±0.00079 | |
| −0.00058 | ±0.00066 | |
| 0.00014 | ±0.00081 |
| Parameter | Value |
|---|---|
| 2.063 M | |
| 1.018 M | |
| 50.124 years | |
| (−6.536, 0, 0) AU | |
| (13.246, 0, 0) AU | |
| (0, 0.819,0) AU/years | |
| (0, −1.66,0) AU/years |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clyburn, M.; Lane, C.D. Lorentz Violation at the Level of Undergraduate Classical Mechanics. Symmetry 2020, 12, 1734. https://doi.org/10.3390/sym12101734
Clyburn M, Lane CD. Lorentz Violation at the Level of Undergraduate Classical Mechanics. Symmetry. 2020; 12(10):1734. https://doi.org/10.3390/sym12101734
Chicago/Turabian StyleClyburn, Madeline, and Charles D. Lane. 2020. "Lorentz Violation at the Level of Undergraduate Classical Mechanics" Symmetry 12, no. 10: 1734. https://doi.org/10.3390/sym12101734
APA StyleClyburn, M., & Lane, C. D. (2020). Lorentz Violation at the Level of Undergraduate Classical Mechanics. Symmetry, 12(10), 1734. https://doi.org/10.3390/sym12101734





