Optimal and Nonoptimal Gronwall Lemmas

Abstract

In this paper, we study some optimal inequalities of the Riccati type and of the Bihari type. We also consider nonoptimal inequalities of the Wendorf type. At the same time, we get a partial answer to Problems 5 and 9, formulated by I. A. Rus. This paper is also motivated by the fact that, in many inequalities, the upper bound is not an optimal one.

1. Introduction

Generally, inequalities have an important role in the development of all branches of mathematics—for instance, in differential and integral equations theory, partial differential equations theory, in the qualitative theory of differential equations, and stability theory. Many inequalities appear in modern science, in economical theory, in engineering, etc.

In what follows, we will consider some concrete optimal and nonoptimal Gronwall lemmas for differential equations and integral equations.

We will study inequalities of the form

$$x\le A\left(x\right),$$

(1)

where $A:X\to X$ is a Picard operator and $\left(X,\to ,\le \right)$ is an ordered L-space.

We first recall some notions and notations used in the paper. Let $F_A=\left\{x\in X\mid A\left(x\right)=x\right\}$ be the fixed points set of A. Let $A_0:=1_X,A^1:=A,\dots ,A^{n+1}:=A\circ A^n,n\in \mathbb{N}.$

Definition 1

([1]). Let X be a nonempty set. Let $s\left(X\right):=\left\{{\left(x_n\right)}_{n\in \mathbb{N}}\right|x_n\in X,n\in \mathbb{N}\}$. Let $c\left(X\right)$ be a subset of $s\left(X\right)$ and $Lim:c\left(X\right)\to X$ be an operator. The triple $(X,c(X),Lim)$ is called an L-space (denoted by $(X,\to )$) if the following conditions are satisfied:

(i) 

if $x_n=x$ for all $n\in \mathbb{N}$, then ${\left(x_n\right)}_{n\in \mathbb{N}}\in c\left(X\right)$ and $Lim{\left(x_n\right)}_{n\in \mathbb{N}}=x$;

(ii) 

if ${\left(x_n\right)}_{n\in \mathbb{N}}\in c\left(X\right)$ and $Lim{\left(x_n\right)}_{n\in \mathbb{N}}=x$, then, for all subsequences ${\left(x_{n_i}\right)}_{i\in \mathbb{N}}$ of ${\left(x_n\right)}_{n\in \mathbb{N}}$, we have that ${\left(x_{n_i}\right)}_{i\in \mathbb{N}}\in c\left(X\right)$ and $Lim{\left(x_{n_i}\right)}_{i\in \mathbb{N}}=x$.

An element of $c(X$) is called a convergent sequence and $x=Lim{\left(x_n\right)}_{n\in \mathbb{N}}$ is the limit of this sequence. We write ${\left(x_n\right)}_{n\in \mathbb{N}}\to x$ or $x_n\to x$ as $n\to \infty .$

Definition 2

([2]). Let X be a nonempty set. $(X,\to ,\le )$ is called an ordered L-space if:

(i) 

$(X,\to )$ is an L-space;

(ii) 

$(X,\le )$ is a partially ordered set;

(iii) 

if ${\left(x_n\right)}_{n\in \mathbb{N}}\to x,{\left(y_n\right)}_{n\in \mathbb{N}}\to y$ and $x_n\le y_n$ for each $n\in \mathbb{N},$ then $x\le y$.

Definition 3

([3]). Let $\left(X,\to ,\le \right)$ be an ordered L-space. An operator $A:X⟶X$ is called a Picard operator if there exists $x_A^{*}\in X$ such that $F_A=\left\{x_A^{*}\right\}$ and $A^n\left(x\right)⟶x_A^{*}$ as $n⟶\infty$ for all $x\in X.$

Now, we present Lemmas 1 and 2 in order to define the notion of optimal and nonoptimal lemmas. We follow the terminology and notation from [3,4,5].

Lemma 1. 

(Abstract Gronwall Lemma [4,6]) (AGL). Let $\left(X,\to ,\le \right)$ be an ordered L-space and $A:X\to X$ an operator. We suppose that:

(i) 

A is a Picard operator;

(ii) 

A is an increasing operator.

If we denote by $x_A^{*}$ the unique fixed point of $A,$ then we have:

$$x\in X,x\le A\left(x\right)\Rightarrow x\le x_A^{*}.$$

(2)

Lemma 2. 

(Abstract Gronwall Comparison Lemma [7]). Let $\left(X,\to ,\le \right)$ be an ordered L-space and $A,B:X\to X$ two operators. We suppose that:

(i) 

A and B are Picard operators;

(ii) 

A is an increasing operator;

(iii) 

$A\le B$.

If we denote by $x_A^{*}$ the unique fixed point of A and by $x_B^{*}$ the unique fixed point of $B,$ then

$$x\le A\left(x\right)\Rightarrow x\le x_A^{*}\le x_B^{*}.$$

We can conclude, from Lemma 1, that $x_A^{*}$ is the upper optimal bound for the solutions of the inequality (1).

So, if we can determine the explicit form for $x_A^{*}$, then we have a bound for the solutions of the inequality (1) and $x_A^{*}$ is the optimal bound. If the optimal bound $x_A^{*}$ cannot be derived explicitly or can not be found, then we apply Lemma 2 and the bound $x_B^{*}$ is not optimal but it is useful for applications. One of the most interesting nonoptimal inequalities is the Wendorff inequality (see Example 3).

In the paper [8], I. A. Rus proposed ten open problems regarding the theory of Gronwall lemmas. In this paper, we present some partial responses to Problems 5 and 9. We recall these problems bellow.

Problem 5. In which Gronwall lemmas are the upper bounds fixed points of the operator A?

Problem 9. Give new concrete and abstract Gronwall lemmas.

These problems were also studied by Craciun and Lungu in [4], Lungu and Rus [7], and Lungu and Ciplea [9].

2. Optimal Gronwall Lemmas

In this section, we consider some optimal lemmas, which are consequences of the Abstract Gronwall Lemma (AGL).

2.1. Optimal Riccati Type Inequality

In what follows, we present an upper bound of the solutions of the Riccati type inequality, which is the fixed point of the corresponding operator. Hence, we have an optimal Gronwall lemma.

In $C\left(\left[a,b\right],\mathbb{R}\right)$ we consider the Bielecki norm:

$${∥u∥}_{\tau }:=\underset{x\in [a,b]}{max}\left(\left|u\left(x\right)\right|e^{-\tau \left(x-a\right)}\right),\tau \in {\mathbb{R}}_{+}^{*}.$$

For $R\in {\mathbb{R}}_{+}$, let

$$\overline{B}\left(c,R\right)=\left\{u\in C\left(\left[a,b\right],R_{+}\right),\underset{x\in \left[a,b\right]}{max}\left|u\left(x\right)-c\right|e^{-\tau \left(x-a\right)}\le R\right\}.$$

We consider $\left(X,\to ,\le \right):=\left(\overline{B}\left(c,R\right),\stackrel{{∥·∥}_{\tau }}{\to },\le \right).$

Lemma 3.

We assume that:

(i) 

$u\in \overline{B}\left(c,R\right),\alpha \in C\left(\left[a,b\right],{\mathbb{R}}_{+}\right);$

(ii) 

$c,p,q,r\in {\mathbb{R}}_{+}$ and $q^2\le 4pr;$

(iii) 

$\left[pM{\left(R+c\right)}^2+qM\left(R+c\right)+rM\right]\left(b-a\right)\le R$, where $M,R$ are such that:

$$\left|\alpha \left(x\right)\right|\le M,\forall x\in \left[a,b\right].$$

Then:

(a) 

there exists a unique solution $u^{*}\in \overline{B}\left(c,R\right)$ of the equation (Riccati type equation):

$$u\left(x\right)=c+{\int }_a^x\left[p\alpha \left(s\right)u^2\left(s\right)+q\alpha \left(s\right)u\left(s\right)+r\alpha \left(s\right)\right]ds,x\in \left[a,b\right];$$

(3)

(b) 

if $u\in \overline{B}\left(c,R\right)$ satisfies the inequality

$$u\left(x\right)\le c+{\int }_a^x\left[p\alpha \left(s\right)u^2\left(s\right)+q\alpha \left(s\right)u\left(s\right)+r\alpha \left(s\right)\right]ds,x\in \left[a,b\right],$$

(4)

then

$$u\left(x\right)\le u_A^{*}\left(x\right),$$

where

$$\begin{array}{cc}\hfill & u_A^{*}\left(x\right)=y_1\left(x\right)\hfill \\ \hfill & +exp{\int }_a^x\left(2p\alpha \left(s\right)y_1\left(s\right)+q\alpha \left(s\right)\right)ds·{\left[c-{\int }_a^{x}p\alpha \left(s\right)exp\left({\int }_a^s\left(2p\alpha \left(\tau \right)y_1\left(\tau \right)+q\alpha \left(\tau \right)\right)d\tau \right)ds\right]}^{-1}\hfill \end{array}$$

(5)

in the interval where

$$c-{\int }_a^{x}p\alpha \left(s\right)exp\left({\int }_a^s\left(2p\alpha \left(\tau \right)y_1\left(\tau \right)+q\alpha \left(\tau \right)\right)d\tau \right)ds\ne 0,$$

and $y_1\left(x\right)$ is a particular solution of the Riccati type equation

$$y^{\prime }\left(x\right)=p\alpha \left(x\right)y^2\left(x\right)+q\alpha \left(x\right)y\left(x\right)+r\alpha \left(x\right).$$

Proof. 

(a) Let $A:X\to X$ be the operator defined by:

$$A\left(u\right)\left(x\right)=c+{\int }_a^x\left[p\alpha \left(s\right)u^2\left(s\right)+q\alpha \left(s\right)u\left(s\right)+r\alpha \left(s\right)\right]ds,x\in \left[a,b\right].$$

From (iii), we have that $A\left(\overline{B}\left(c,R\right)\right)\subset \overline{B}\left(c,R\right)$, so the operator A is well defined.

The operator is increasing, by the assumption of (ii). Using conditions (i)–(iii), it follows that

$${∥A\left(u\right)-A\left(v\right)∥}_{\tau }\le \frac{M\left[2p\left(R+c\right)+q\right]}{\tau }{∥u-v∥}_{\tau },\mathrm{for}\mathrm{all}u,v\in \overline{B}\left(c,R\right),\tau >0.$$

Indeed, we have

$$\begin{array}{cc}\hfill & \left|A\left(u\left(x\right)\right)-A\left(v\left(x\right)\right)\right|\le {\int }_a^x\left[p\alpha \left(s\right)\left(u\left(s\right)+v\left(s\right)\right)+q\alpha \left(s\right)\right]\left|u\left(s\right)-v\left(s\right)\right|ds\hfill \\ \hfill & ={\int }_a^x\left[p\alpha \left(s\right)\left(u\left(s\right)+v\left(s\right)\right)+q\alpha \left(s\right)\right]\left|u\left(s\right)-v\left(s\right)\right|e^{-\tau \left(s-a\right)}{e}^{\tau \left(s-a\right)}ds\hfill \\ \hfill & \le {\int }_a^x\left[p\alpha \left(s\right)\left(u\left(s\right)+v\left(s\right)\right)+q\alpha \left(s\right)\right]e^{\tau \left(s-a\right)}{∥u-v∥}_{\tau }ds\hfill \\ \hfill & \le M\left[2p\left(R+c\right)+q\right]{∥u-v∥}_{\tau }{\int }_a^x{e}^{\tau \left(s-a\right)}ds\hfill \\ \hfill & \le M\left[2p\left(R+c\right)+q\right]{∥u-v∥}_{\tau }\frac{e^{\tau \left(x-a\right)}}{\tau }.\hfill \end{array}$$

Hence

$${∥A\left(u\right)-A\left(v\right)∥}_{\tau }\le \frac{M\left[2p\left(R+c\right)+q\right]}{\tau }{∥u-v∥}_{\tau }.$$

We chose $\tau >0$ such that

$$\frac{M\left[2p\left(R+c\right)+q\right]}{\tau }<1;$$

thus, the operator A is a contraction, which implies that A is a Picard operator. Hence, there exists a unique solution $u^{*}\in \overline{B}\left(c,R\right)$ to Equation (3).

(b) We determine the fixed point of the operator $A,$ which is a solution of the equation $u\left(x\right)=A\left(u\right)\left(x\right)$ for all $x\in \left[a,b\right].$ This equation is equivalent to the following Cauchy problem:

$$\left\{\begin{array}{c}{u}^{\prime }\left(x\right)=p\alpha \left(x\right)u^2\left(x\right)+q\alpha \left(x\right)u\left(x\right)+r\alpha \left(x\right)\hfill \\ u\left(a\right)=c\hfill \end{array}.\right.$$

(6)

If $y_1$ is a solution of the Riccati Equation (3), then the solution of the Cauchy problem (6) $u_A^{*}\left(x\right)$ is given in (5), and it is the optimal solution of inequality (4). Therefore, Lemma 3 is an AGL consequence and it is an optimal Gronwall lemma. ☐

Example 1.

We consider $u\in C\left(\left[0,0.5\right],{\mathbb{R}}_{+}\right)$. If $u\in \overline{B}\left(0,1\right)$ satisfies the inequality

$$u\left(x\right)\le {\int }_0^x\left[s{u}^2\left(s\right)+2su\left(s\right)+s\right]ds,x\in \left[0,0.5\right],$$

(7)

then

$$u\left(x\right)\le u_A^{*}\left(x\right),$$

where

$$u_A^{*}\left(x\right)=-1-\frac{2}{x^2-2}$$

is the solution of the Cauchy problem

$$\left\{\begin{array}{c}{u}^{\prime }\left(x\right)=x{u}^2\left(x\right)+2xu\left(x\right)+x\hfill \\ u\left(0\right)=0\hfill \end{array}.\right.$$

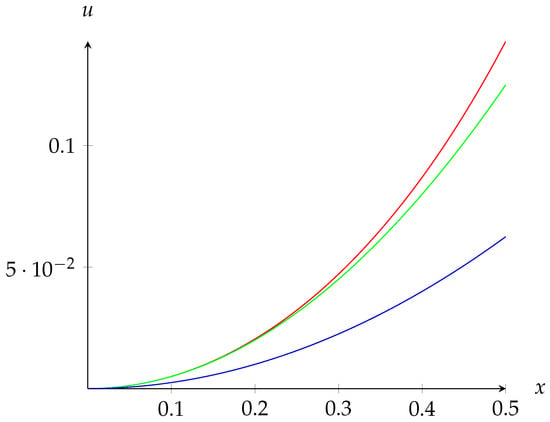
For example, $u_1\left(x\right)=x^2/2$ and $u_2\left(x\right)=x^2/4$ satisfy inequality (7) and, geometrically, if we represent the functions $u_1,u_2$ and $u_A^{*}$, we have that the graphs of $u_1,u_2$ are below $u_A^{*}$ (see Figure 1).

Figure 1. Representation of the curves $u_A^{*}=-1-\frac{2}{x^2-2}$, which is the optimal solution (red color), $u_1=x^2/2$ (green color), $u_2=x^2/4$ (blue color), together on $\left[0,0.5\right]$.

2.2. Optimal Bihari Type Inequality

In [4], an upper bound of the solutions of the Bihari inequality has been given, which is the fixed point of the corresponding operator.

Here, we will show that Lemma 2.2 from [4] is an optimal one. If we consider the inequality

$$y\left(x\right)\le c+{\int }_a^{x}p\left(s\right)V\left(y\left(s\right)\right)ds,c>0,x\in \left[a,b\right],$$

where $p\in C\left(\left[a,b\right],{\mathbb{R}}_{+}\right),V$ is continuous, positive, increasing and the Lipschitz function, then

$$y\left(x\right)\le y^{*}\left(x\right),y^{*}\left(x\right)=F^{-1}\left(\varphi \left(x\right)+F\left(c\right)\right),$$

where

$$F\left(y\right)={\int }_a^y\frac{dy}{V\left(y\right)},\varphi \left(x\right)={\int }_a^{x}p\left(s\right)ds\mathrm{and}{F}^{-1}\mathrm{is}\mathrm{the}\mathrm{inverse}\mathrm{of}F.$$

If we consider $\left(X,\to ,\le \right):=\left(C\left[a,b\right],\stackrel{{∥·∥}_{\tau }}{\to },\le \right),$ where ${∥·∥}_{\tau }$ is the Bielecki norm and $A:X\to X$, $A\left(y\right)\left(x\right)=c+{\int }_a^{x}p\left(s\right)V\left(y\left(s\right)\right)ds,x\in \left[a,b\right],$ the fixed point of the operator A is

$$y^{*}\left(x\right)=F^{-1}\left(\varphi \left(x\right)+F\left(c\right)\right).$$

Hence, the Bihari inequality is an optimal one.

Example 2.

We consider $y\in C\left(\left[\frac{\pi }{6},\frac{\pi }{3}\right],{\mathbb{R}}_{+}\right)$. If y satisfies the inequality

$$y\left(x\right)\le \sqrt{e}+{\int }_{\frac{\pi }{6}}^x\frac{y\left(s\right)lny\left(s\right)}{tans}ds,x\in \left[\frac{\pi }{6},\frac{\pi }{3}\right]$$

(8)

then

$$y\left(x\right)\le y^{*}\left(x\right),$$

where

$$y^{*}\left(x\right)=e^{sinx}$$

is the solution of the Cauchy problem

$$\left\{\begin{array}{c}{y}^{\prime }=\frac{ylny}{tanx}\hfill \\ y\left(\frac{\pi }{6}\right)=\sqrt{e}\hfill \end{array}.\right.$$

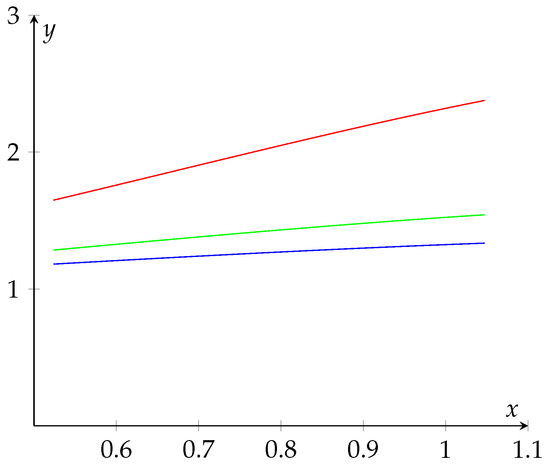
For example, $y_1\left(x\right)=e^{\frac{sinx}{2}}$ and $y_2\left(x\right)=e^{\frac{sinx}{3}}$ satisfy inequality (8) and, geometrically, we have that the graphs of $y_1,y_2$ are below $y^{*}$ (see Figure 2).

Figure 2. Representation of the curves $y^{*}\left(x\right)=e^{sinx}$, which is the optimal solution (red color), $y_1\left(x\right)=e^{\frac{sinx}{2}}$ (green color), $y_2\left(x\right)=e^{\frac{sinx}{3}}$ (blue color), together on $\left[\frac{\pi }{6},\frac{\pi }{3}\right]$.

3. Nonoptimal Gronwall Lemmas

In some concrete Gronwall lemmas, only the following implication holds:

$$x\le A\left(x\right)\Rightarrow x\le y^{*}\ne x_A^{*}.$$

In this part we consider consequences of Lemma 2. We consider $\left(X,\to ,\le \right):=\left(C\left(D\right),\stackrel{{∥·∥}_{\tau }}{\to },\le \right),$ where $D=$$\left[0,a\right]\times \left[0,b\right]$ and ${∥·∥}_{\tau }$ is the Bielecki norm on $C\left(D\right):$

$${∥u∥}_{\tau }:=\underset{D}{max}\left(\left|u\left(x,y\right)\right|e^{-\tau \left(x+y\right)}\right),\tau \in {\mathbb{R}}_{+}^{*}.$$

Lemma 4. 

(Wendorff type inequality) ([10,11,12,13,14]).

We assume that

(i) 

$v\in C\left(\left[0,a\right]\times \left[0,b\right],{\mathbb{R}}_{+}\right),c\in {\mathbb{R}}_{+};$

(ii) 

v is increasing.

If $u\in C\left(\left[0,a\right]\times \left[0,b\right],{\mathbb{R}}_{+}\right)$ satisfies

$$u\left(x,y\right)\le c+{\int }_0^x{\int }_0^{y}v\left(s,t\right)u\left(s,t\right)dsdt,x\in \left[0,a\right],y\in \left[0,b\right],$$

then

$$u\left(x,y\right)\le cexp\left({\int }_0^x{\int }_0^{y}v\left(s,t\right)dsdt\right).$$

(9)

We consider the operator $A:X\to X,$

$$A\left(u\right)\left(x,y\right):=c+{\int }_0^x{\int }_0^{y}v\left(s,t\right)u\left(s,t\right)dsdt,\left(x,y\right)\in D.$$

This operator is an increasing Picard operator, but the function $u\left(x,y\right)=cexp\left({\int }_0^x{\int }_0^{y}v\left(s,t\right)dsdt\right)$ is not a fixed point of operator $A.$

Remark 1.

The right side of (9) is not a fixed point of operator A, so the concrete Lemma 4 is not a consequence of the abstract Gronwall Lemma 1.

Example 3.

We consider $v\left(x,y\right)=2x$ in the Wendorff inequality.

Let $\alpha =1.$ If $u\in C\left(\left[0,2\right]\times \left[0,1\right],{\mathbb{R}}_{+}\right)$ satisfies

$$u\left(x,y\right)\le 1+{\int }_0^x{\int }_0^{y}2su\left(s,t\right)dsdt,x\in \left[0,2\right],y\in \left[0,1\right],$$

(10)

with conditions

$$u\left(x,0\right)=u\left(0,y\right)=1,$$

then

$$u\left(x,y\right)\le exp\left(x^{2}y\right).$$

In this case, the corresponding operator $A:X\to X$ is

$$A\left(u\right)\left(x,y\right):=1+{\int }_0^x{\int }_0^{y}2su\left(s,t\right)dsdt$$

and the function $exp\left(x^{2}y\right)$ is not a fixed point of operator $A.$ However, we remark that $exp\left(x^{2}y\right)$ is a fixed point of operator

$$B\left(u\right)\left(x,y\right):=1+{\int }_0^x{\int }_0^y\left[2su\left(s,t\right)+2s^{3}tu\left(s,t\right)\right]dsdt;$$

hence, here, Lemma 2 is applied. We have

$$u\left(x,y\right)\le A\left(u\right)\left(x,y\right)\Rightarrow u\left(x,y\right)\le u_A^{*}\left(x,y\right)\le u_B^{*}\left(x,y\right),$$

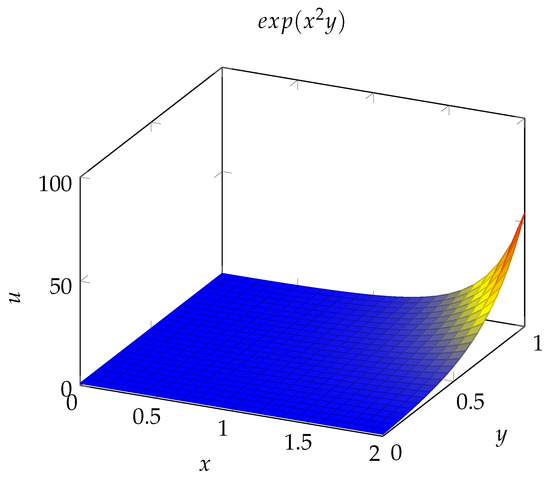
where $u_B^{*}\left(x,y\right)=exp\left(x^{2}y\right)$ and $u_A^{*}\left(x,y\right)$ is the fixed point of operator A. Geometrically, the surface $u_B^{*}\left(x,y\right)=exp\left(x^{2}y\right)$, represented in Figure 3, is above the surface corresponding to the optimal solution $u_A^{*}$, which cannot be explicitly derived.

Figure 3. Representation of the surface $u=exp\left(x^{2}y\right)$ on $[0,2]\times [0,1]$.

Example 4.

We consider the inequality (see [15])

$$u\left(x\right)\le c+{\int }_a^{x}K\left(x,s\right)u\left(s\right)ds,$$

(11)

where u is a continuous and positive function for all $x\ge a$ and K is of $C^1$ class after x and continuous after $s,$$K\left(x,s\right)\ge 0$ for $x\ge s\ge a$ and $c>0.$

Then,

$$u\left(x\right)\le cexp\left\{{\int }_a^x\left[K\left(x,s\right)+{\int }_a^s\frac{\partial K\left(s,\sigma \right)}{\partial s}d\sigma \right]ds\right\},x\ge a.$$

In this case, operator A is

$$A\left(u\right)\left(x\right):=c+{\int }_a^{x}K\left(x,s\right)u\left(s\right)ds.$$

We remark that the function

$$\overline{u}\left(x\right)=cexp\left\{{\int }_a^x\left[K\left(x,s\right)+{\int }_a^s\frac{\partial K\left(s,\sigma \right)}{\partial s}d\sigma \right]ds\right\},x\ge a$$

is not the fixed point of operator A; therefore, inequality (11) is nonoptimal.

Remark 2.

For other examples in this direction, see [15,16,17,18,19,20,21,22,23,24].

4. Conclusions

In this paper, we studied concrete optimal Gronwall lemmas corresponding to Riccati and Bihari type inequalities and nonoptimal Gronwall lemmas corresponding to Wendorf type inequalities. Moreover, we obtained a partial response to Problems 5 and 9, formulated by I. A. Rus in [8]. Some geometrical meanings were also given. In the case containing the functions of one variable, where optimal Gronwall lemmas were applied, the curve corresponding to every solution of the given inequality was below the curve corresponding to the optimal solution. In the case containing the functions of two variables, the surface corresponding to each solution of the given inequality was below the surface of the corresponding optimal solution.