Lorentz Forces Effects on the Interactions of Nanoparticles in Emerging Mechanisms with Innovative Approach
Abstract
1. Introduction
2. Methods
3. Entropy Generation
4. Results and Discussion
Solution Validation
5. Conclusions
- (1)
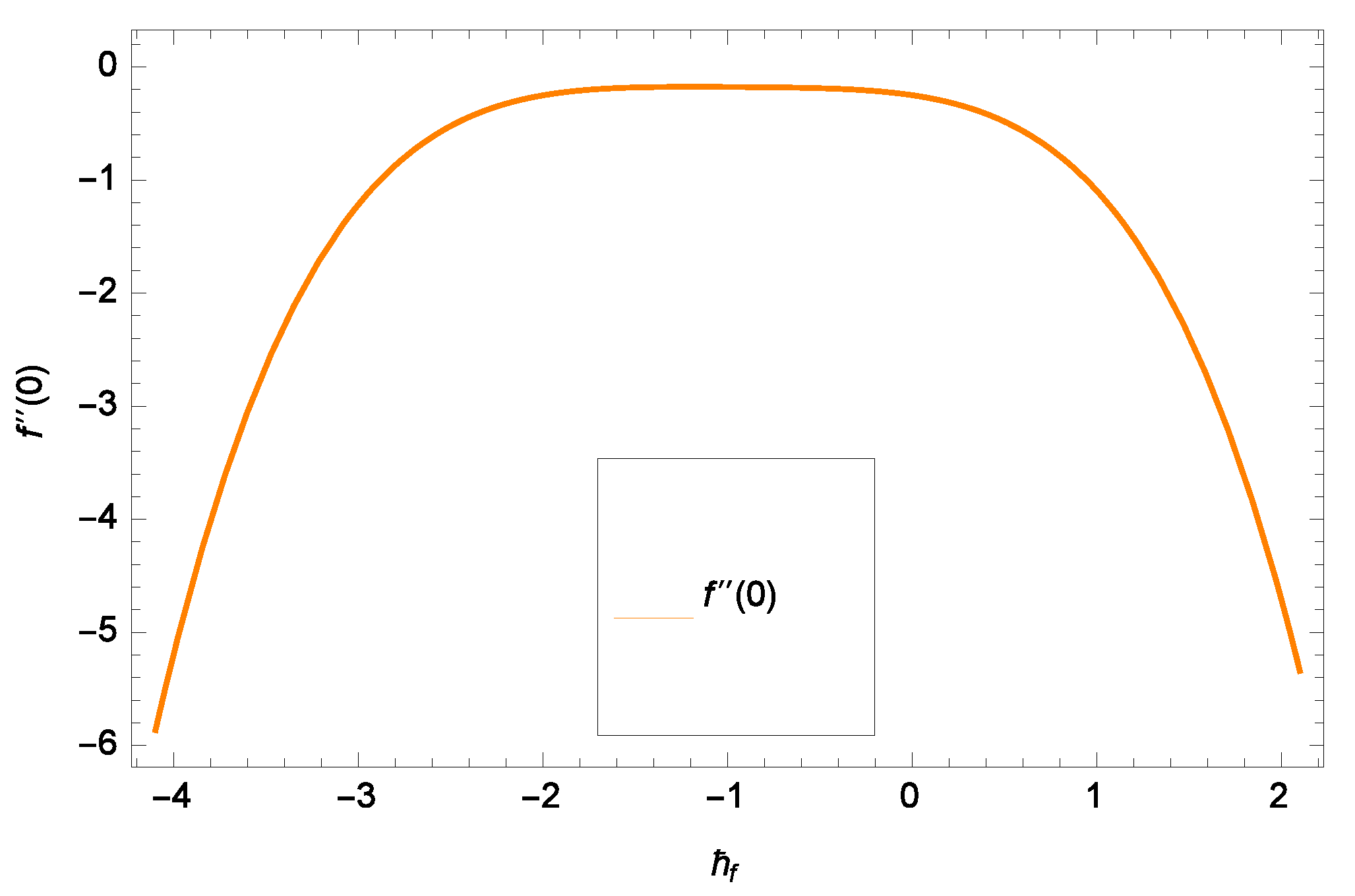
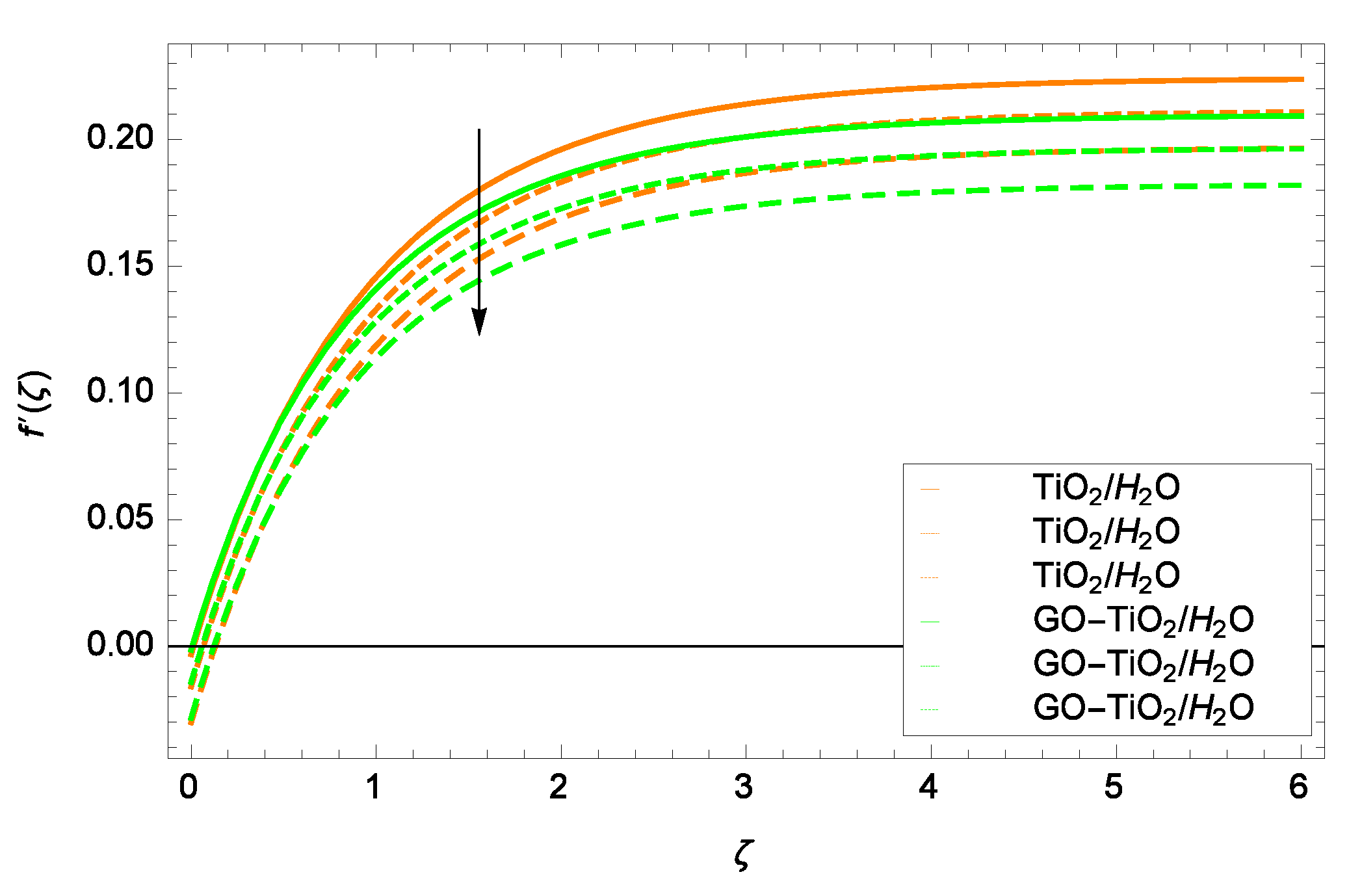
- Velocity decreases with increasing the parameters M, f, and increases with increasing the parameter .
- (2)
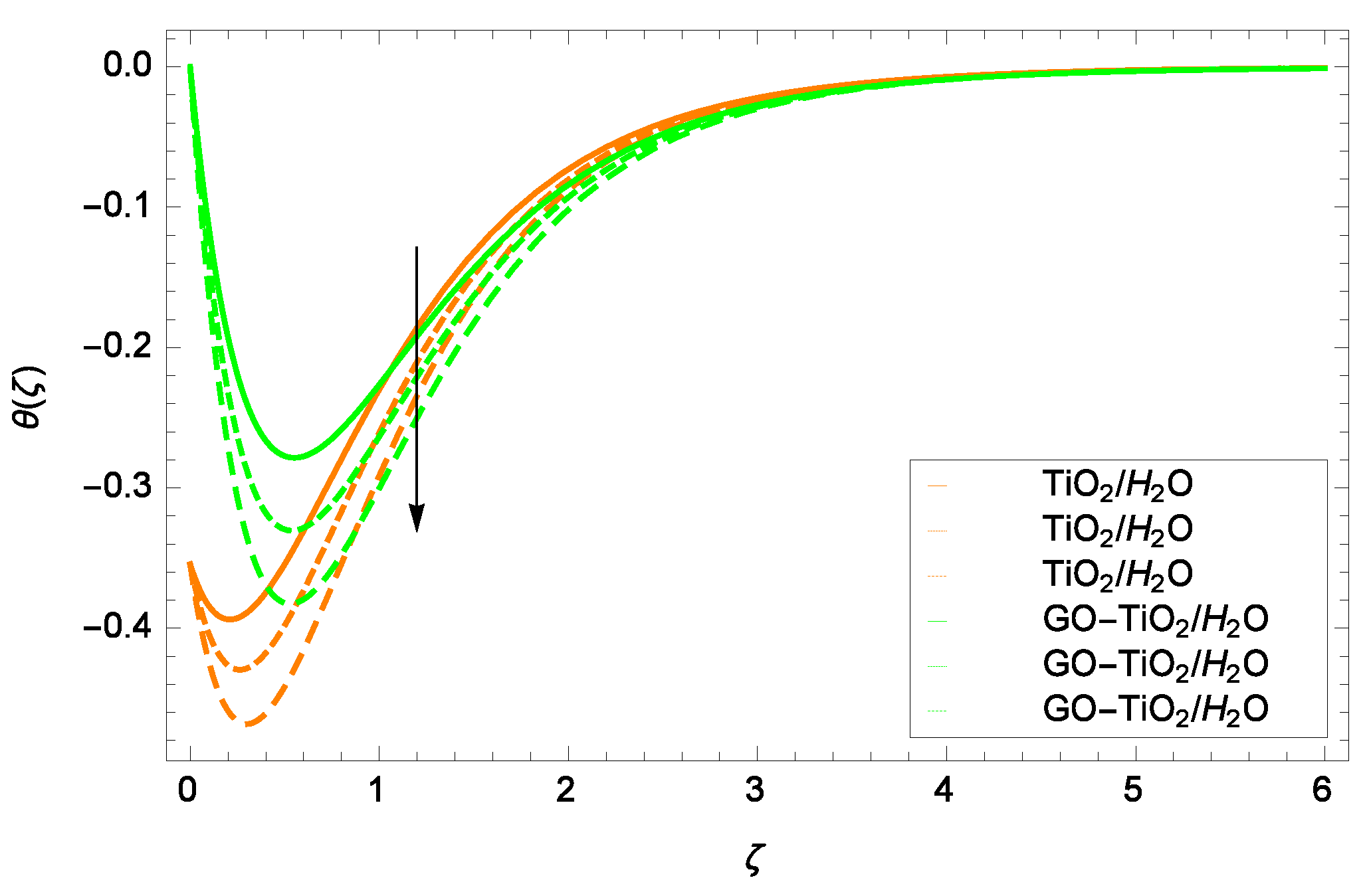
- Temperature decreases with increasing the parameters Pr, , f.
- (3)
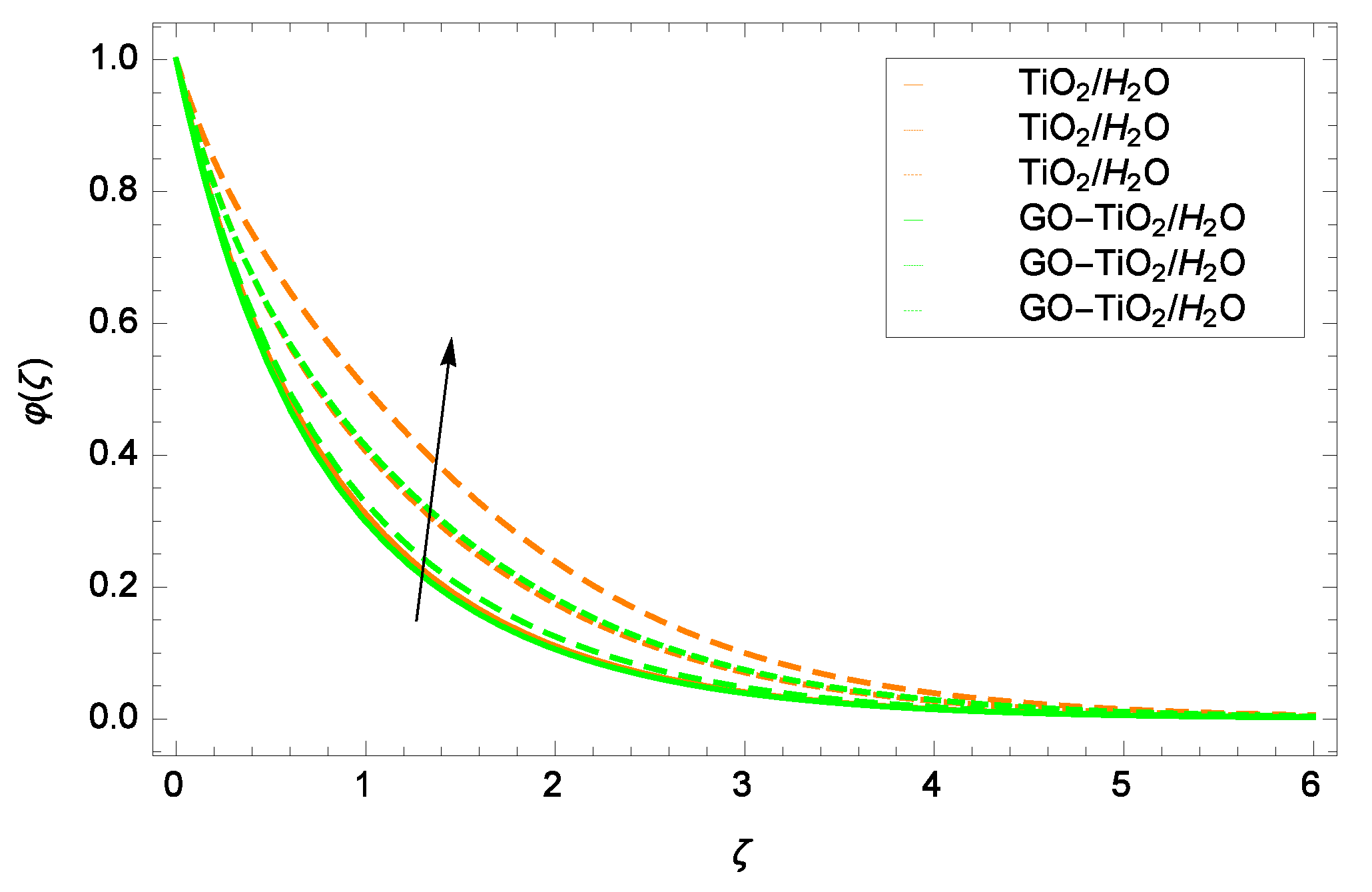
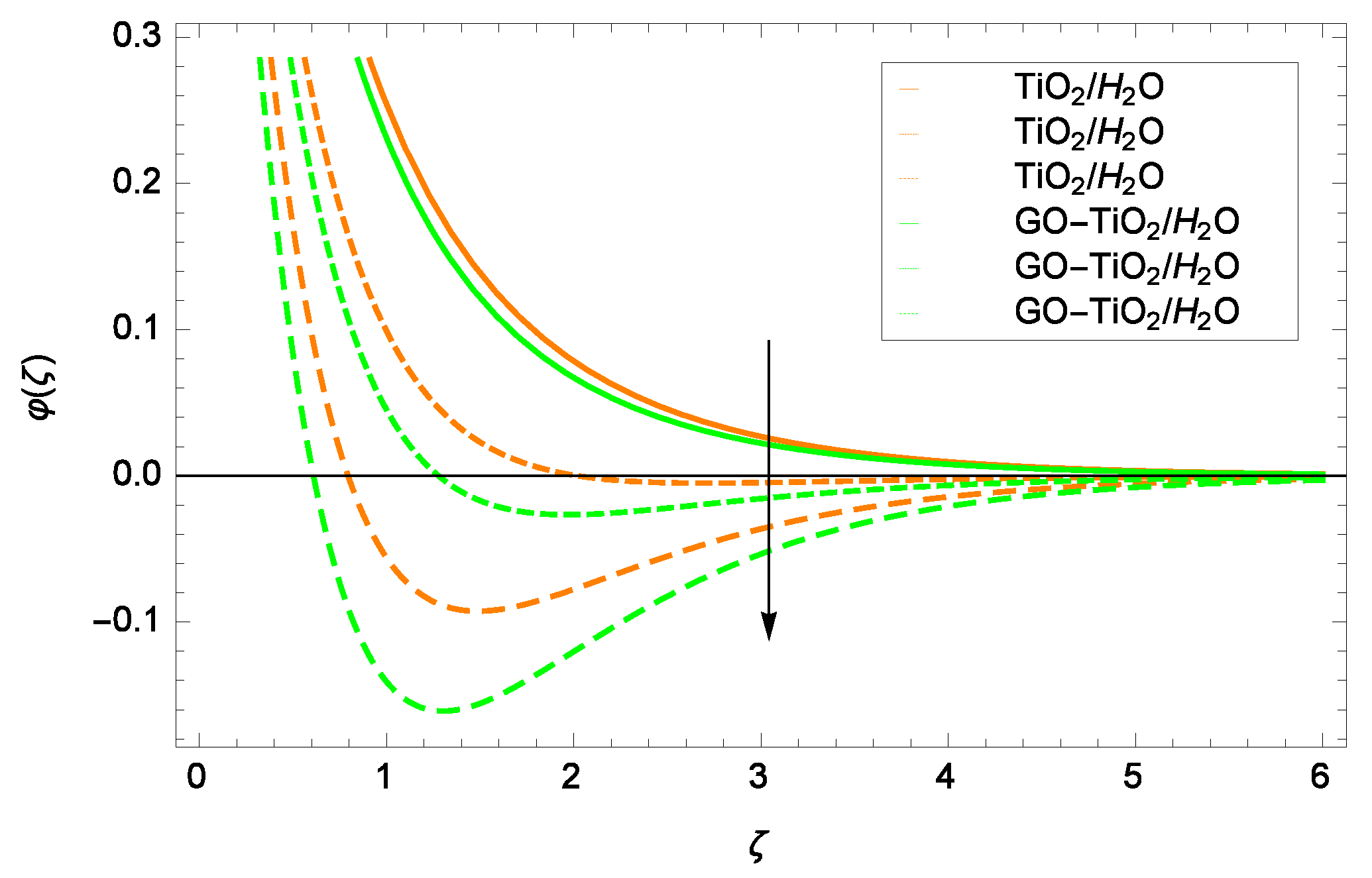
- Nanoparticles concentration decreases with increasing the parameter f and increases with increasing the parameter Sc.
- (4)
- Entropy generation increases with increasing the parameters Re and Br.
- (5)
- Both the velocity components decrease with the Hall effect parameter m.
- (6)
- Streamlines show that the trapping increases at the left side of the surface for the parameter m.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shatey, S.; Mosta, S. Variable viscosity on magnetohydrodynamic fluid flow and heat transfer over an unsteady stretching surface with Hall effect. Bound. Value Probl. 2010, 2010, 257568. [Google Scholar] [CrossRef]
- Hayat, T.; Awais, M.; Nawaz, M.; Iram, S.; Alsaedi, A. Mixed convection three-dimensional flow with Hall and ion-slip effects. Int. J. Nonlinear Sci. Numer. Simul. 2013, 14, 167–177. [Google Scholar] [CrossRef]
- Ahmed, S.; Zueco, J. Modeling of heat and mass transfer in a rotating vertical porous channel with Hall current. Chem. Eng. Commun. 2011, 198, 1294–1308. [Google Scholar] [CrossRef]
- Gaffar, S.A.; Prasad, V.R.; Reddy, E.K. MHD free convection flow of Eyring-Powell fluid from vertical surface in porous media with Hall/ionslip currents and Ohnic dissipation. Alex. Eng. J. 2016, 55, 875–905. [Google Scholar] [CrossRef]
- El-Aziz, M.A. Effects of Hall current on the flow and heat transfer of a nanofluid over a stretching sheet with partial slip. Int. J. Mod. Phys. C 2013, 24, 1350044. [Google Scholar] [CrossRef]
- Hayat, T.; Iqbal, M.; Yasmin, H.; Alsaadi, F. Hall Hall effects on peristaltic flow of couple stress fluid in an inclined asymmetric channel. Int. J. Biomath. 2014, 7, 1450057. [Google Scholar] [CrossRef]
- Khan, N.S. Bioconvection in second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Braz. J. Phys. 2018, 43, 227–241. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Graphene family nanofluids: A critical review and future research directions. Energy Convers. Manag. 2019, 196, 1222–1256. [Google Scholar] [CrossRef]
- Briffa, S.M.; Lynch, I.; Hapiuk, D.; Valsami-Jones, E. Physical and chemical transformations of zirconium doped ceria nanoparticles in the presence of phosphate: Increasing realism in environmental fate and behaviour experiments. Environ. Pollut. 2019, 252, 974–981. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Khan, M.A.; Bonyah, E.; Islam, S. Mixed convection in gravity-driven thin film non-Newtonian nanofluids flow with gyrotactic microorganisms. Results Phys. 2017, 7, 4033–4049. [Google Scholar] [CrossRef]
- Bahiraei, M. Particle migration in nanofluids: A critical review. Int. J. Therm. Sci. 2016, 109, 90–113. [Google Scholar] [CrossRef]
- Saba, F.; Ahmed, N.; Khan, U.; Mohyud-Din, S.T. A novel coupling of (CNT-Fe3O4/H2O) hybrid nanofluid for improvements in heat transfer for flow in an asymmetric channel with dilating/squeezing walls. Int. J. Heat Mass Transf. 2019, 136, 186–195. [Google Scholar] [CrossRef]
- Bahiraei, M.; Rahmani, R.; Yaghoobi, A.; Khodabandeh, E.; Mashayekhi, R.; Amani, M. Recent research contributions concerning use of nanofluids in heat exchangers: A critical review. Appl. Therm. Eng. 2018, 133, 137–159. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Bahiraei, M.; Heshmatian, S. Electronic cooling with nanofluids: A critical review. Energy Convers. Manag. 2018, 172, 438–456. [Google Scholar] [CrossRef]
- Gulzar, O.; Qayoum, A.; Gupta, R. Experimental study on stability and rheological behaviour of hybrid Al2O3-TiO2 Therminol-55 nanofluids for considering solar collectors. Powder Technol. 2019, 352, 436–444. [Google Scholar] [CrossRef]
- Dalkilic, A.S.; Turk, O.A.; Mercan, H.; Nakkaew, S. An experimental investigation on heat transfer characteristics of graphite-SiO2/water hybrid nanofluid flow in horizontal tube with various quad-channel twisted tape inserts. Int. Commun. Heat Mass Transf. 2019, 107, 1–13. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, I.; Alqahtani, A.M.; Alshomrani, A.S. Magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer. J. Appl. Sci. 2017, 7, 271. [Google Scholar] [CrossRef]
- Rosca, N.C.; Pop, I. Unsteady boundary layer flow of a nanofluid past a moving surface in an external uniform free stream using Buongiorno’s model. Comput. Fluids 2014, 95, 49–55. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Khan, M.A.; Islam, S.; Khan, W.; Bonyah, E. Flow and heat transfer in water based liquid film fluids dispensed with graphene nanoparticles. Results Phys. 2018, 8, 1143–1157. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, W. Thermophoresis and thermal radiation with heat and mass transfer in a magnetohydrodynamic thin film second-grade fluid of variable properties past a stretching sheet. Eur. Phys. J. Plus 2017, 132, 11. [Google Scholar] [CrossRef]
- Palwasha, Z.; Khan, N.S.; Shah, Z.; Islam, S.; Bonyah, E. Study of two dimensional boundary layer thin film fluid flow with variable thermo-physical properties in three dimensions space. AIP Adv. 2018, 8, 105318. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, A.; Shah, Z. Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. J. Nanofluids 2017, 6, 812–829. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv. 2019, 8, 115302. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Kumam, P.; Shah, Z.; Islam, S.; Khan, W.; Zuhra, S.; Sohail, A. Influence of inclined magnetic field on Carreau nanoliquid thin film flow and heat transfer with graphene nanoparticles. Energies 2019, 12, 1459. [Google Scholar] [CrossRef]
- Khan, N.S. Study of two dimensional boundary layer flow of a thin film second grade fluid with variable thermo-physical properties in three dimensions space. Filomat 2019, 33, 5387–5405. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S. Boundary layer unsteady flow and heat transfer in a second grade thin film nanoliquid embedded with graphene nanoparticles past a stretching sheet. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, W.; Khan, I.; Ali, L. Thin film flow of a second-grade fluid in a porous medium past a stretching sheet with heat transfer. Alex. Eng. J. 2017, 57, 1019–1031. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Alam, A.; Islam, S.; Khan, A. Buoyancy effects on nanoliquids film flow through a porous medium with gyrotactic microorganisms and cubic autocatalysis chemical reaction. Adv. Mech. Eng. 2020, 12, 1–17. [Google Scholar] [CrossRef]
- Palwasha, Z.; Islam, S.; Khan, N.S.; Ayaz, H. Non-Newtonian nanoliquids thin film flow through a porous medium with magnetotactic microorganisms. Appl. Nanosci. 2018, 8, 1523–1544. [Google Scholar] [CrossRef]
- Khan, N.S. Mixed convection in MHD second grade nanofluid flow through a porous medium containing nanoparticles and gyrotactic microorganisms with chemical reaction. Filomat 2019, 33, 4627–4653. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Shah, Z.; Islam, Z.; Bonyah, E. Simulation of bioconvection in the suspension of second grade nanofluid containing nanoparticles and gyrotactic microorganisms. AIP Adv. 2018, 8, 105210. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Z.; Shutaywi, M.; Kumam, P.; Thounthong, P. A comprehensive study to the assessment of Arrhenius activation energy and binary chemical reaction in swirling flow. Sci. Rep. 2020, 10, 7868. [Google Scholar] [CrossRef] [PubMed]
- Zuhra, S.; Khan, N.S.; Islam, S. Magnetohydrodynamic second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comput. Appl. Math. 2018, 37, 6332–6358. [Google Scholar] [CrossRef]
- Zuhra, S.; Khan, N.S.; Islam, S.; Nawaz, R. Complexiton solutions for complex KdV equation by optimal homotopy asymptotic method. Filomat 2020, 33, 6195–6211. [Google Scholar] [CrossRef]
- Zahra, A.; Mahanthesh, B.; Basir, M.F.M.; Imtiaz, M.; Mackolil, J.; Khan, N.S.; Nabwey, H.A.; Tlili, I. Mixed radiated magneto Casson fluid flow with Arrhenius activation energy and Newtonian heating effects: Flow and sensitivity analysis. Alex. Eng. J. 2020, 57, 1019–1031. [Google Scholar]
- Liaqat, A.; Asifa, T.; Ali, R.; Islam, S.; Gul, T.; Kumam, P.; Mukhtar, S.; Khan, N.S.; Thounthong, P. A new analytical approach for the research of thin-film flow of magneto hydrodynamic fluid in the presence of thermal conductivity and variable viscosity. ZAMM J. Appl. Math. Mech. Z. Angewwandte Math. Mech. 2020, 1–13. [Google Scholar] [CrossRef]
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. [Google Scholar] [CrossRef]
- Ahmad, S.; Nadeem, S. Flow analysis by Cattaneo-Christov heat flux in the presence of Thomson and Troian slip condition. Appl. Nanosci. 2020. [Google Scholar] [CrossRef]
- Khan, N.; Riaz, I.; Hashmi, M.S.; Musmar, S.A.; Khan, S.U.; Abdelmalek, Z.; Tlili, I. Aspects of chemical entropy generation in flow of Casson nanofluid between radiative stretching disks. Entropy 2020, 22, 495. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S.; Shah, Q. Entropy generation in two phase model for simulating flow and heat transfer of carbon nanotubes between rotating stretchable disks with cubic autocatalysis chemical reaction. Appl. Nanosci. 2019, 9, 1797–1822. [Google Scholar] [CrossRef]
- Zaib, A.; Khan, U.; Shah, Z.; Kumam, P.; Thounthong, P. Optimization of entropy generation in flow of micrpolar mixed convective magnetite (Fe3O4) ferroparticle over a vertical plate. Alex. Eng. J. 2019, 58, 1461–1470. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Z.; Islam, S.; Khan, I.; Alkanhal, T.A.; Tlili, I. Entropy generation in MHD mixed convection non-Newtonian second-grade nanoliquid thin film flow through a porous medium with chemical reaction and stratification. Entropy 2019, 21, 139. [Google Scholar] [CrossRef]
- Shahsavar, A.; Baseri, M.M.; Al-Rashed, A.A.A.A.; Afrand, M. Numerical investigation of forced convection heat transfer and flow irreversibility in a novel heat sink with helical microchannels working with biologically synthesized water-silver nano-fluid. Int. Commun. Heat Mass Transf. 2019, 108, 104324. [Google Scholar] [CrossRef]
- Khan, N.S.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S.; Khan, A. Hall current and thermophoresis effects on magnetohydrodynamic mixed convective heat and mass transfer thin film flow. J. Phys. Commun. 2019, 3, 035009. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R.; Abdelsalam, S.I. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Phys. Scr. 2019, 95, 045206. [Google Scholar] [CrossRef]
- Shah, Z.; Kumam, P.; Deebani, W. Radiative MHD Casson nanofluid flow with activation energy and chemical reaction over nonlinear stretching surface through entropy generation. Sci. Rep. 2020, 10, 4402. [Google Scholar] [CrossRef]
- Khan, N.S.; Kumam, P.; Thounthong, P. Renewable energy technology for the sustainable development of thermal system with entropy measures. Int. J. Heat Mass Transf. 2019, 145, 118713. [Google Scholar] [CrossRef]
- Khan, N.S.; Kumam, P.; Thounthong, P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluid flow. Sci. Rep. 2020, 10, 1226. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Q.; Bhaumik, A.; Kumam, P.; Thounthong, P.; Amiri, I. Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Sci. Rep. 2020, 10, 4448. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Q.; Sohail, A. Dynamics with Cattaneo-Christov heat and mass flux theory of bioconvection Oldroyd-B nanofluid. Adv. Mech. Eng. 2020. [Google Scholar] [CrossRef]
- Rahila, N.; Noor, M.; Shah, Z.; Sohail, M.; Kumam, P.; Thounthong, P. Entropy generation optimization in MHD pseudoplastic fluid comprising motile microorganisms with stratification effect. Alex. Eng. J. 2020, 59, 485–496. [Google Scholar]
- Liao, S.J. Homotopy Analysis Method in Nonlinear Differential Equations; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
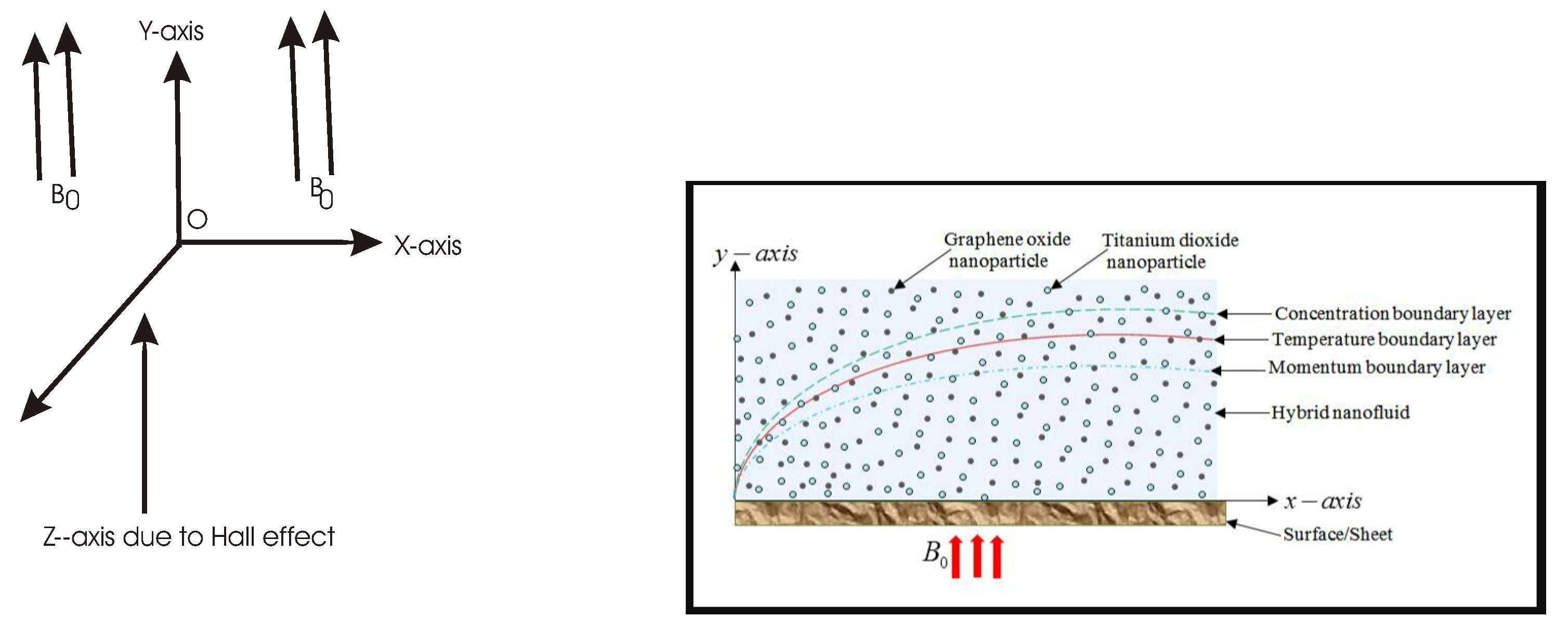

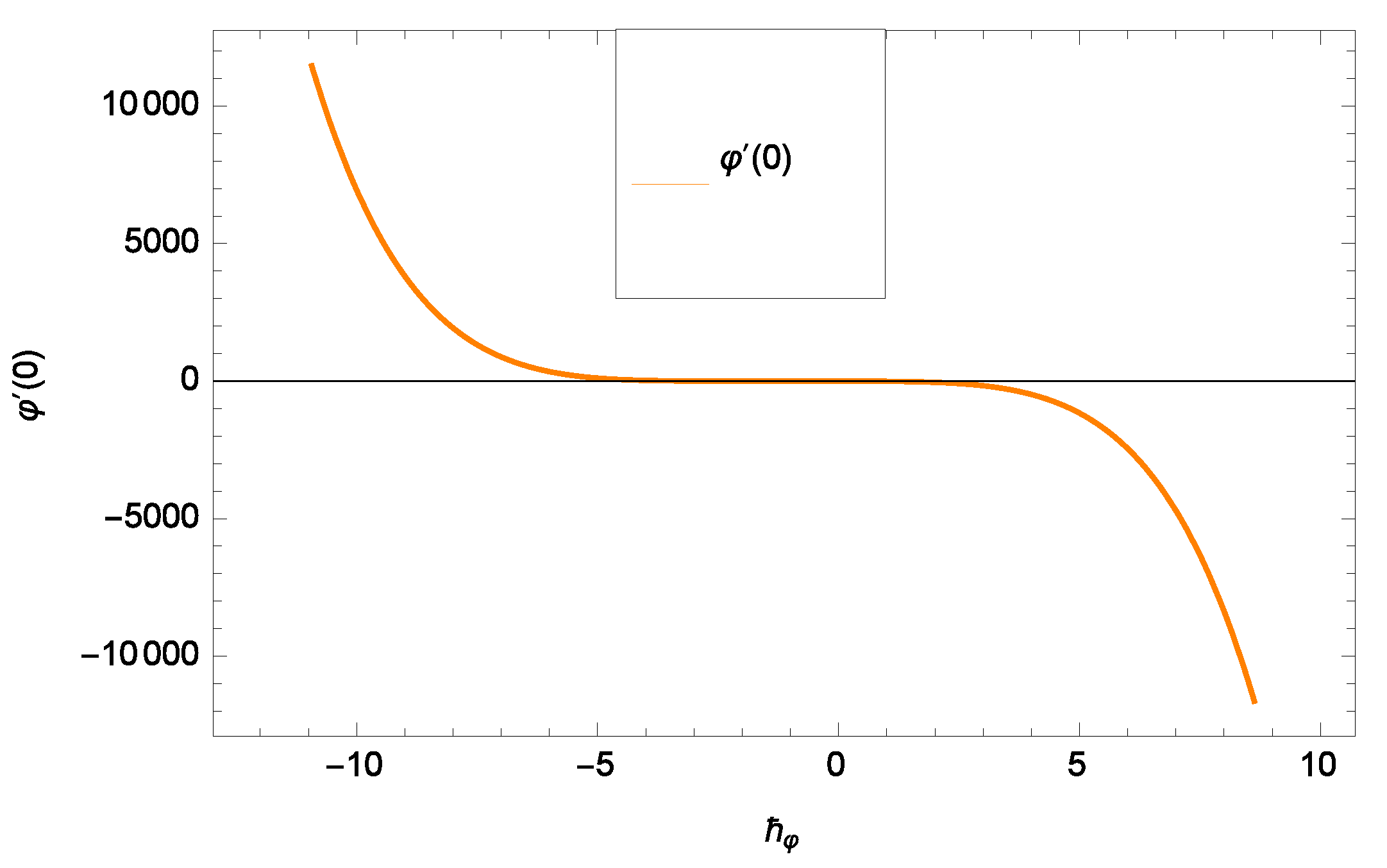






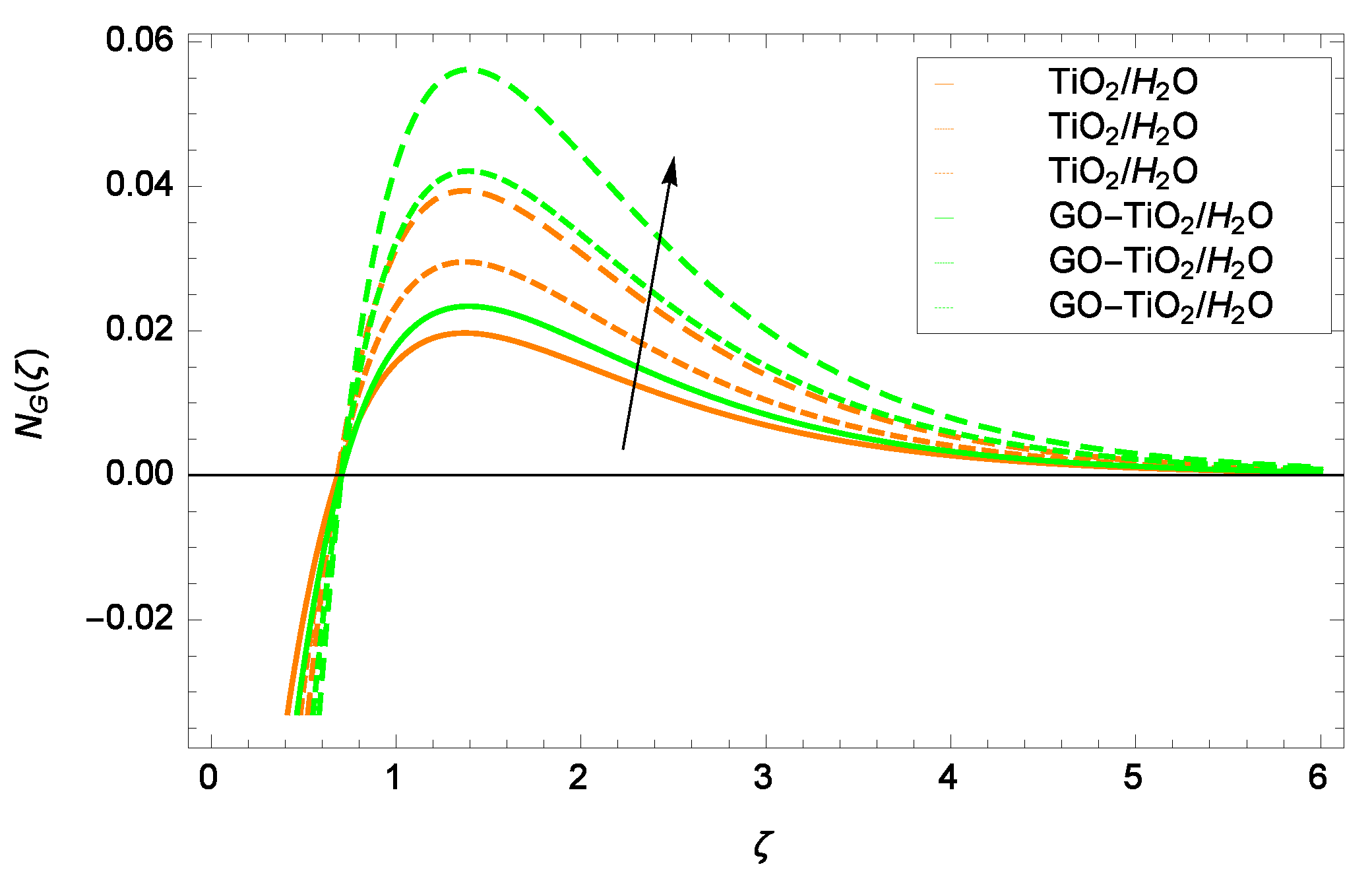

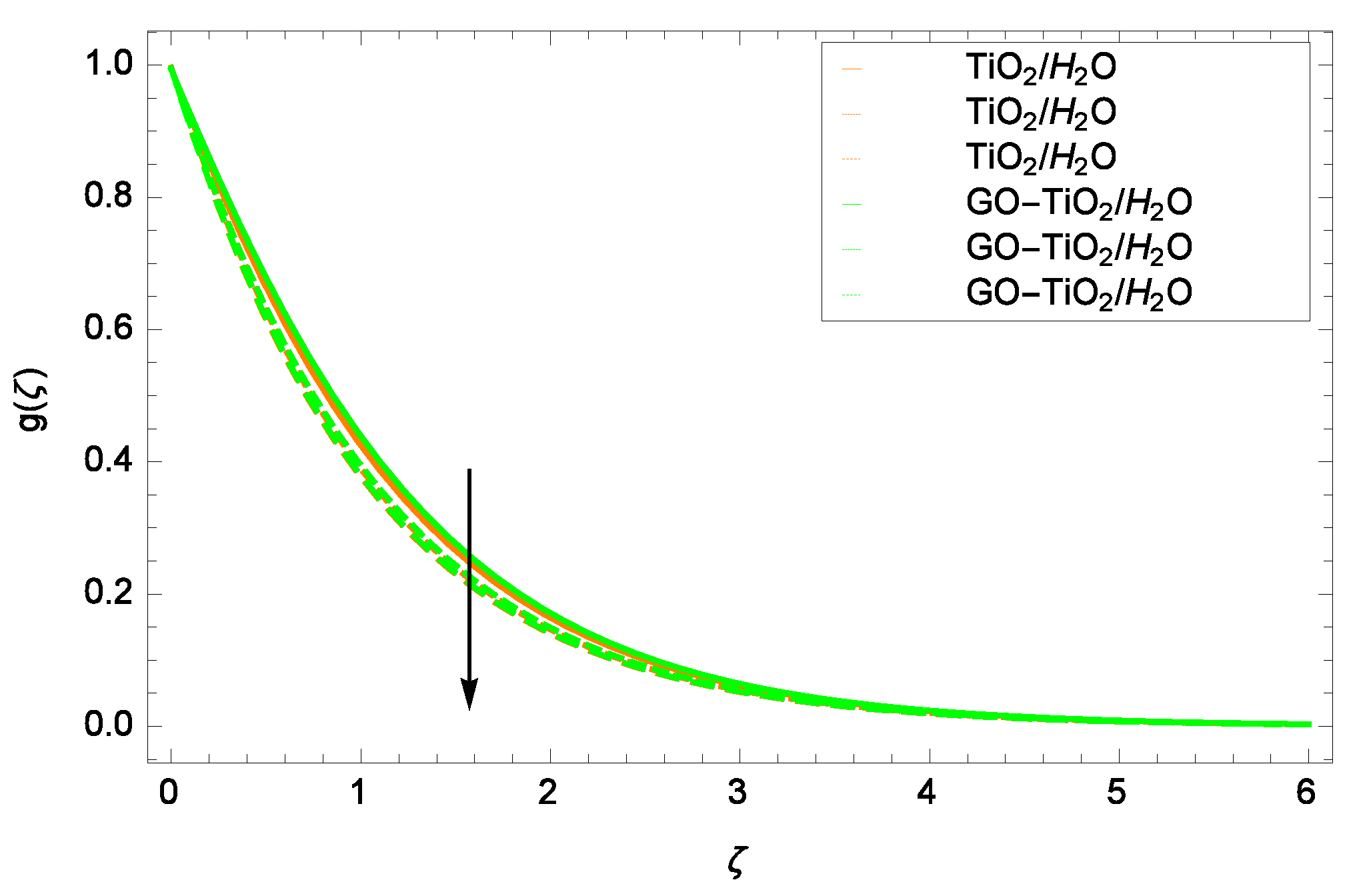
| Thermophysical Properties | HO | TiO (Titania) | GO (Graphene Oxide) |
|---|---|---|---|
| (Density) (kg/m) | = 997.1 | = 4250 | = 1800 |
| c (Heat capacity) (J/kg K) | (c) = 4179 | (c) = 686.2 | (c) = 717 |
| k (Thermal conductivity) (W/m K) | k = 0.613 | k = 8.9538 | k = 5000 |
| (Electrical conductivity) (Um) | = 0.05 | = 2.38 × 10 | = 1.1 × 10 |
| Properties | Nanofluid (TiO/HO) |
|---|---|
| Density () | = (1 − ) + |
| Heat capacity (c) | (c) = (1 − )(c) + (c) |
| Dynamic viscosity () | = |
| Thermal conductivity (k) | = |
| Electrical conductivity () | = 1 + , where = |
| Properties | Hybrid nanofluid (GO-TiO/HO) |
| Density () | = (1 − ( + )) + + |
| Heat capacity (c) | (c) = (1 − ( + ))(c) + (c) + (c) |
| Dynamic viscosity () | = |
| Thermal conductivity (k) | = |
| Electrical conductivity () | = 1 + |
| Published Paper [19] | Present Work | Error | |
|---|---|---|---|
| 0 | 5.6418 × 10 | 5.6417 × 10 | 0.0001 × 10 |
| (15/2) | 5.7501 × 10 | 5.7500 × 10 | 0.0001 × 10 |
| 15 | 5.8072 × 10 | 5.8071 × 10 | 0.0001 × 10 |
| 30 | 5.7700 × 10 | 5.7700 × 10 | 0.0000 × 10 |
| 45 | 5.52287 × 10 | 5.52285 × 10 | 0.0002 × 10 |
| 60 | 5.0721 × 10 | 5.0720 × 10 | 0.0001 × 10 |
| 75 | 4.3686 × 10 | 4.3684 × 10 | 0.0002 × 10 |
| (165/2) | 3.8999 × 10 | 3.8998 × 10 | 0.0001 × 10 |
| 90 | 3.3205 × 10 | 3.3205 × 10 | 0.0000 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, N.S.; Shah, Q.; Sohail, A.; Kumam, P.; Thounthong, P.; Bhaumik, A.; Ullah, Z. Lorentz Forces Effects on the Interactions of Nanoparticles in Emerging Mechanisms with Innovative Approach. Symmetry 2020, 12, 1700. https://doi.org/10.3390/sym12101700
Khan NS, Shah Q, Sohail A, Kumam P, Thounthong P, Bhaumik A, Ullah Z. Lorentz Forces Effects on the Interactions of Nanoparticles in Emerging Mechanisms with Innovative Approach. Symmetry. 2020; 12(10):1700. https://doi.org/10.3390/sym12101700
Chicago/Turabian StyleKhan, Noor Saeed, Qayyum Shah, Arif Sohail, Poom Kumam, Phatiphat Thounthong, Amiya Bhaumik, and Zafar Ullah. 2020. "Lorentz Forces Effects on the Interactions of Nanoparticles in Emerging Mechanisms with Innovative Approach" Symmetry 12, no. 10: 1700. https://doi.org/10.3390/sym12101700
APA StyleKhan, N. S., Shah, Q., Sohail, A., Kumam, P., Thounthong, P., Bhaumik, A., & Ullah, Z. (2020). Lorentz Forces Effects on the Interactions of Nanoparticles in Emerging Mechanisms with Innovative Approach. Symmetry, 12(10), 1700. https://doi.org/10.3390/sym12101700