Abstract
To provide an available diagnostic model for diagnosing coronary atherosclerotic heart disease to provide an auxiliary function for doctors, we proposed a new evolutionary classification model in this paper. The core of the prediction model is a kernel extreme learning machine (KELM) optimized by an improved salp swarm algorithm (SSA). To get a better subset of parameters and features, the space transformation mechanism is introduced in the optimization core to improve SSA for obtaining an optimal KELM model. The KELM model for the diagnosis of coronary atherosclerotic heart disease (STSSA-KELM) is developed based on the optimal parameters and a subset of features. In the experiment, STSSA-KELM is compared with some widely adopted machine learning methods (MLM) in coronary atherosclerotic heart disease prediction. The experimental results show that STSSA-KELM can realize excellent classification performance and more robust stability under four indications. We also compare the convergence of STSSA-KELM with other MLM; the STSSA-KELM model has demonstrated a higher classification performance. Therefore, the STSSA-KELM model can effectively help doctors to diagnose coronary heart disease.
1. Introduction
Coronary atherosclerotic heart disease (CHD), coronary heart disease, is a common cardiovascular disease (CVD) [1]. CHD is caused by abnormal lipid metabolism. The abnormal deposition of lipids and other substances in the blood in the coronary artery can gradually develop into atherosclerotic plaques and cause stenosis and occlusion in the vascular lumen, leading to ischemia, hypoxia, or necrosis of cardiomyocytes in the corresponding blood supply area, and then cause clinical symptoms such as chest tightness and chest pain. In the past decades, the incidence of CVD has been increasing annually and became the biggest threat to human health. Studies have shown that the prevalence of cardiovascular diseases is still on the rise. According to an American Heart Association (AHA) report, ~17.8 million deaths were attributed to CVD globally in 2017, which had an increase of 21.1% compared to the number in 2007. The age-adjusted death rate per 100,000 population was 233.1 in 2017, which decreased by 10.3% from 2007. Overall, the crude prevalence of the cardiovascular disease in 2017 was 485.6 million, an increase of 28.5% over 2007 [2]. It is expected that the mortality rate of CVD will continue to rise in the next 5–10 years. Therefore, the prevention and control of CVD are in urgent need, and various approaches need to be developed to deal with this public health problem.
In fact, this problem can be effectively addressed if CHD can be diagnosed early and effectively, so as to start a timely intervention. Invasive coronary angiography has long been the gold standard for the diagnosis of coronary heart disease. This operation relies on the support of percutaneous catheterization technology. It is an invasive operation, which has the risk of vascular injury, iatrogenic infection, and other related risks. Therefore, researchers began to develop a non-invasive and efficient diagnostic tool for CHD. Through the health system, a large amount of health data can be collected, including medical history, auxiliary examination, and laboratory examination data [3,4,5]. This message can be used to establish risk prediction models that can help to predict and prevent future CHD occurrence. Several well-known risk prediction models have been established, including the Framingham risk scores (FRS), the risk of atherosclerotic cardiovascular disease (ASCVD), and diabetes cardiovascular risk assessment in the UK prospective diabetes study (UKPDS). The above model predicts the occurrence of disease through traditional statistical methods, which require that the tested objects must meet the preconditions of the model, such as using the time series model, logistic regression model, and other methods to evaluate the incidence of disease [6,7]. It is generally accepted that current risk prediction models are flawed in assessing CVD risk in specific populations (i.e., young adults and female subjects [8], patients with inflammatory diseases [9], sedentary central obese patients, asymptomatic atherosclerosis patients, chronic kidney disease patients, etc.) and in high-risk populations. Therefore, it is particularly important to develop more effective risk prediction models and to discover more potential risk factors associated with the occurrence of CHD, thereby more effectively predicting the occurrence of CHD.
Diagnosing CHD by machine learning (ML) algorithms are receiving more and more attention from researchers [10]. Artificial neural networks (ANN), decision tree (DT), random forest (RF), and support vector machine (SVM) are the most widely adopted ML methods for CVD research. It applies to almost all data sets reported in the literature with good performance, ease of use, and low computational burden [11]. Dogan et al. developed a CHD risk prediction model by combining single nucleotide polymorphism (SNP) and genome-wide methylation (DNAm) data from 1180 individuals in the training set, using an RF algorithm to predict the risk of symptomatic CHD within five years. The sensitivity and specificity of the test were 0.70 and 0.74, respectively [12]. Donghee Han et al. compared the individual coronary artery calcium score risk prediction model constructed by a boosted ensemble algorithm (LogitBoost) with a traditional risk prediction method, and the result showed that the AUC value in the ML model was obviously more excellent than other models in the test set [13]. The advantage of ML attracts the attention of many researchers in the cardiovascular field. In this study, a new prediction model of CHD is constructed based on the cardiovascular risk factors, and try to incorporate glomerular filtration rate and thyrotropin into the learning model, in order to improve the prediction accuracy further.
In this study, we introduce a space transformation mechanism into salp swarm algorithm (STSSA) [14,15,16,17] to optimize the kernel extreme learning machine (KELM) model, and verify that STSSA-KELM can effectively diagnose coronary heart disease. The SSA is one of the metaheuristic methods; hence, it depends on two interactive searching cores [18,19]. In the proposed model (STSSA-KELM), the space transformation mechanism is embedded in SSA to balance exploration and development capabilities further. The improved SSA is used to train an optimal KELM model to predict coronary heart disease. In the experiment, STSSA-KELM was compared with other machine learning algorithms for predicting coronary heart disease. The results show that STSSA-KELM can obtain better sorting results and outstanding stability by observing these four indicators.
The primary contribution of this study can be summarized as follows:
- (a)
- A spatial transformation improved SSA (STSSA) is applied to KELM training.
- (b)
- The established STSSA effectively tackled the parameter turning for KELM in an excellent manner.
- (c)
- The developed STSSA-KELM model is mainly applied to predict coronary heart disease.
The rest of the paper is structured as follows. A brief description of the data is given in Section 2. Section 3 provides a detailed description of the proposed STSSA-KELM. An analysis of the STSSA-KELM on the relevant dataset is presented in Section 4. Section 5 gives some discussions. Conclusions and suggestions for future work are presented in Section 5.
2. Materials and Methods
2.1. DATA Collection
This study collected data from 443 patients who underwent selective coronary angiography during hospitalization, in the Affiliated Hospital of Medical School, Ningbo University, including age, sex, height, weight, history of hypertension, history of hyperlipidemia, history of diabetes, smoking, glomerular filtration rate (eGFR), thyroid-stimulating hormone (TSH). All patients have signed informed consent for coronary angiography. The particulars of the data are shown in Table 1. The data were divided into coronary artery disease group (219 cases) and normal group (224 cases), according to the results of coronary angiography.

Table 1.
Illustration of 34 attributes.
The interpretation of the results was performed jointly by two interventional physicians, and if the results were different, the analysis would be made by the third physician. Through the radial artery selective left and right coronary angiography examination, according to the Judkin’s method of multi-position radiation, through the “diameter method” for coronary stenosis degree interpretation: coronary angiography left the main trunk, left anterior descending branch, left circumflex branch, right coronary artery or its main branch of the stenosis rate ≥50%, defined as CHD.
2.2. Proposed Stssa-Kelm Method
The proposed STSSA-KELM method consists of four parts: data normalization, KELM parameter optimization, feature selection, and classification. First, standardize the collected data and scale the data to [−1,1]. Then, the two critical parameters (C and γ) of KELM are optimized by the continuous STSSA, and at the same time, the binary STSSA algorithm is used to search for the best feature subset of the CHD data. At last, the test data set is classified using the tuned KELM and the best feature subset. The use of K-fold cross-validation is a common approach when dividing data into training and test sets. Therefore, this paper uses 10-fold cross-validation for data partitioning. The flowchart of STSSA-KELM is shown in Figure 1.
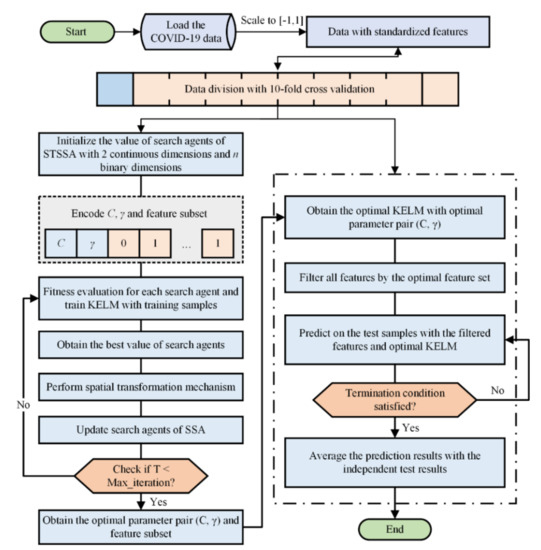
Figure 1.
Flow chart of STSSA-based KELM model (STSSA-KELM).
2.2.1. Parameter Optimization and Feature Selection by Continuous and Binary STSSA
This research developed a hybrid classification model STSSA-KELM based on STSSA and KELM to predict the CHD data. The parametric optimization of KELM uses continuous STSSA, while binary STSSA is used in the feature selection process. From the original thesis, it is known that the original STSSA is all tested on continuous problems and can be used for constrained or non-constrained problems. In order to use continuous STSSA and discrete STSSA to optimize the KELM parameters and data feature subsets at the same time, a search agent, including continuous variables and discrete variables, is adopted.
2.2.2. Classification Based on KELM
The KELM is a machine learning model established on the basis of ELM and inspired by the kernel function in SVM. The stability and generalization of KELM are better than the traditional extreme learning machine [20,21,22,23,24,25,26,27,28].
The traditional extreme learning machine is similar to feedforward neuron network (FNN). For an ELM with L hidden layer nodes, its prediction model is as follows:
where is the weight matrix between the hidden layer and output layer, is the penalty factor, is the training error, N is the size of training samples .
Unlike FNN, the weight matrix between the hidden layer and output layer is obtained by solving pseudo inverse:
where represents the diagonal matrix, is the hidden layer output matrix, and denotes the target output target matrix.
Based on ELM, KELM improves the stability and generalization of the model, by introducing kernel functions. The random mappings in the ELM are replaced by nuclear mapping. Since the kernel function takes the form of the inner product, it is not essential to either know the feature mapping function of the hidden layer node or set the number of hidden layer nodes. When solving the model output, it is only necessary to know the specific form of the kernel function.
The following equation can define the kernel matrix in KELM:
where uses RBF kernel function, its expression with kernel parameter is:
Finally, KELM can be expressed by the following formula:
2.2.3. Detailed Procedure of STSSA-KELM
Two parameters in KELM were tuned using STSSA, in order to improve the stability and generalization performance of KELM fully. The selection of CHD features was performed while optimizing these two parameters. The detailed process for parameter optimization and feature selection through STSSA is as follows:
- Step 1:
- Initialize the parameters of STSSA: the maximum number of iterations T, the number of search agents N.
- Step 2:
- Initialize the search agents of STSSA. Use random numbers generated in the solution space to initialize continuous variables in the search agent, and use random 0 or 1 to initialize discrete variables.
- Step 3:
- Calculate the fitness value of each search agent, according to the following formula:
- Step 4:
- Perform spatial transformation mechanism and select the highest fitness N search agent updates the current population.
- Step 5:
- Update parameter c, according to Equation (2).
- Step 6:
- Update the value of the search agents.
- Step 7:
- If the maximum iterations are satisfied, output the best search agent where the first two dimensions represent (C, γ), and the binary values of the other dimensions are used to filter out the selected features. Otherwise, jump to Step 4.
- Step 8:
- Optimize the obtained optimal parameters and optimal feature subsets with the KELM prediction model, and use the optimal model to predict the test set.
- Step 9:
- If the termination condition is met, output the average result. Otherwise, jump to Step 8.
3. Results
The experiment was done with the MATLAB R2018 software. The data are normalized into [−1,1], before processing the classification task. 10-fold cross-validation (CV) was employed to split the date, in which nine parts were used for training data and the last one for the testing phase. STSSA, SSA, PSO, and GWO were implemented from scratch. Regarding the random forest (RF), KELM, and SVM, the related codes shared in public websites (http://www3.ntu.edu.sg/home/egbhuang, https://www.csie.ntu.edu.tw/~cjlin/libsvm/, and https://code.google.com/archive/p/randomforest-matlab) were adopted. Moreover, the trial and error method is used to set parameters. The search range of the two parameters of SVM and KELM were set the same in the [2−10, 210]. For RF, the default setting was used.
In this experiment, we estimated the effectiveness of the STSSA-KELM model. The detailed results are shown in Table 2. From the table, we can see that the classification accuracy obtained by STSSA-KELM is 84.40%, Matthews correlation coefficient is 69.20%, sensitivity is 87.30%, specificity is 81.70%, and the variance is 0.058, 0.0118, 0.074, and 0.065, respectively. In addition, what we can observe in the experiment is that the STSSA algorithm can automatically obtain the optimal parameters of KELM, which shows that the addition of spatial transformation mechanism makes the new STSSA algorithm have more substantial search capability and accuracy.

Table 2.
Classification performance of STSSA-KELM, in terms of ACC (Accuracy), MCC (Matthews correlation coefficient), sensitivity, and specificity.
To validate the usability of this approach, we present a comparative study with five other effectiveness machine learning models, including SSA-KELM, PSO-KELM, GWO-KELM, SVM, and RF. The comparison results of the six methods are shown in Figure 2. The results show that the STSSA-KELM model is superior to the other five models in four evaluation indexes. This signifies that the STSSA-KELM model obtains better performance and stability by adding a spatial conversion mechanism. In the ACC evaluation index, the STSSA-KELM model has the best evaluation effect, which is 1.80 percentage points higher than GWO-KELM. SSA-KELM, RF, and PSO-KELM are in the second place, SSA-KELM is 2.00 percentage points lower than STSSA-KELM, the effect of SVM is the worst, GWO-KELM variance is the largest, 0.079. In the MCC evaluation index, the STSSA-KELM model still acquired the best results, followed by GWO-KELM. GWO-KELM was 3.80% lower than STSSA-KELM, SSA-KELM, RF, and PSO-KELM were behind, SSA-KELM was 4.00% lower than STSSA-KELM, SVM effect was the worst; GWO-KELM variance was the largest, 0.158. From the perspective of sensitivity evaluation indexes, the STSSA-KELM model gets the best evaluation effect, followed by the SSA-KELM model, with a difference of only 2.00 percentage points, followed by RF, GWO-KELM, and SVM. PSO-KELM model has the worst effect and the largest variance, reaching 0.089. The results of STSSA-KELM and GWO-KELM were the best. PSO-KELM, RF, and SSA-KELM are the second, in which the difference between SSA-KELM and STSSA-KELM is only 2.30 percentage points; the worst is SVM, and the variance of PSO-KELM is the largest, reaching 0.109.
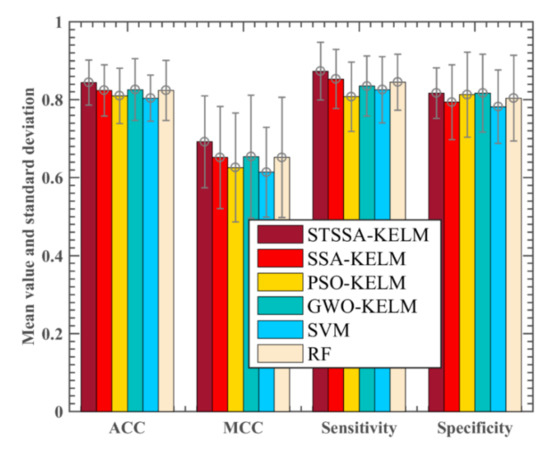
Figure 2.
Classification performance of five models, in terms of ACC, MCC, sensitivity, and specificity.
We have conducted the Friedman test to validate the significance of the proposed STSSA-KELM as shown in Table 3. As shown in Figure 2, the results show that STSSA-KELM has the best performance, and SSA-KELM is the second. From the table, we can see that the mean level of STSSA-KELM is 1 higher than that of the second SSA-KELM, which further proves the effectiveness of STSSA-KELM.

Table 3.
Comparison results of STSSA and other five models, based on the Friedman test.
To characterize the convergence of the proposed STSSA-KELM model, we also record the tendency that the accuracy of three kinds of KELM models, which are based on swarm intelligence algorithm, changes with population iteration. It is revealed in Figure 3 that after many iterations, the STSSA-KELM model can quickly and continuously jump out of the local optimum to reach the optimal accuracy, indicating that the STSSA-KELM method has strong local search ability and global search ability. The main reason is that the spatial transformation mechanism enhances the local search ability and global search ability of the SSA, and makes the hybrid algorithm better balanced between the exploration and the exploration. By observing the curve in Figure 3, it is found that the SSA-KELM model needs more iterations to converge, and the accuracy is not as high as STSSA-KELM. GWO-KELM has the second-highest accuracy, which can continuously jump out of the local optimum, and the improvement with iteration accuracy is not apparent. PSO-KELM has the lowest accuracy among all algorithms, far less than the STSSA-KELM model, and the improvement with iteration accuracy is not apparent, so it is easy to sink into the local optimum.
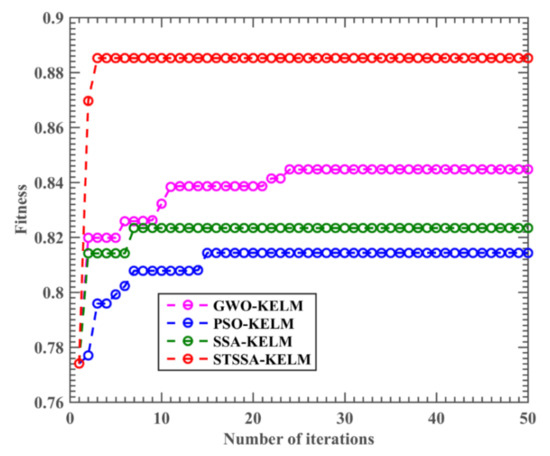
Figure 3.
Relationship between training accuracy of STSSA-KELM, GWO-KELM, SSA-KELM, and PSO-KELM and the number of iterations.
In this procedure, STSSA not only achieves the best setting of KELM, but also chooses the best feature set. We used ten times of CV technology. Figure 4 illustrates the frequency of the main characteristics identified by the STSSA-KELM during the 10-fold CV procedure. As shown in the figure, F33 (thyrotropin) and F26 (estimated glomerular filtration rate) are the two characteristics with the highest frequency, 10 and 9 times, respectively. Other clinically widely validated indicators, such as F1 (age), F3 (gender), F4 (weight), F5 (height), F9 (hypertension), F10 (hyperlipidemia), F11 (diabetes mellitus), F16 (smoking history), also showed a higher frequency.
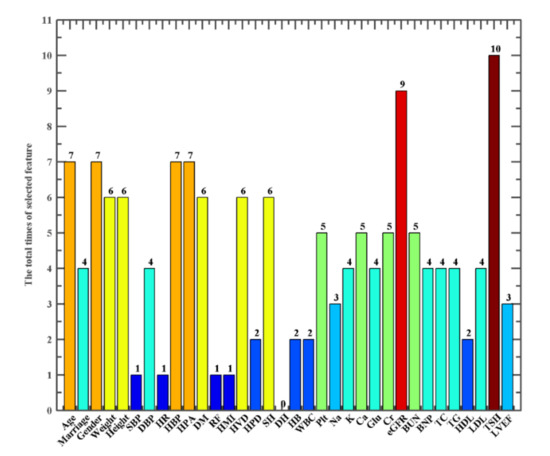
Figure 4.
Frequency of the features selected by STSSA-KELM via the 10-fold CV scheme.
4. Discussion
According to the 2019 Guidelines for Primary Prevention of Cardiovascular Diseases issued by ACC/AHA, hypertension, smoking, dyslipidemia, diabetes mellitus, overweight and obesity, inadequate physical activity, unreasonable diet, metabolic syndrome and air pollution are nine crucial risk factors for CVD [29]. Since the 1970s, many countries and regions have carried out large-scale studies on cardiovascular risk factors, and have successively introduced a variety of cardiovascular risk assessment methods, such as the FRS [30], ASCVD [31], UKPDS [32], and so on. Many clinical researchers have recognized the established traditional risk factors of CVD and its risk prediction model. However, it cannot wholly and accurately predict CHD. Therefore, researchers are also committed to exploring new predictors and biomarkers to help better predict the risk of CHD.
Studies have found that patients with chronic kidney disease have a high incidence of cardiovascular events [33]. Potential mechanisms include the accumulation of harmful biological factors due to endothelial function, decreased renal clearance, activation of the renin-angiotensin system, oxidative stress, disorders of lipid metabolism, chronic inflammation caused by the accumulation of inflammatory factors, etc. [34]. Tonelli et al. compared the incidence of cardiovascular events between patients with chronic kidney disease and those without chronic kidney disease through a population cohort study. They found that the incidence of cardiovascular events in patients with chronic kidney disease was significantly higher than that in the latter, revealing that chronic kidney disease may be a potential cardiovascular risk factor [35]. Matsushita et al. explored the independent association of changes in eGFR with CHD and all-cause death, and the results showed that changes in eGFR were related to a higher risk of CHD and all-cause death [36].
TSH is a hormone secreted by the adenohypophysis, which promotes the proliferation of thyroid follicular epithelial cells and the synthesis and release of thyroid hormones. TSH responds significantly and accurately to small changes in thyroid hormone concentrations in circulating blood. Besides, there is increasing evidence that thyrotropin has extrathyroid effects [37]. Studies have shown that hypothyroidism is associated with an increased incidence of CHD, with potential mechanisms including changes in lipid profiles caused by thyroid hormones, and abnormal lipid metabolism (increased levels of total cholesterol and low-density lipoprotein cholesterol), leading to atherosclerosis [37]. Onat et al. studied the correlation between serum TSH level and the risk of CHD in the normal range, and the results showed that the TSH level might be associated with the incidence of CHD [38]. A prospective study conducted by Li et al. explored the effect of TSH on the risk of CHD in patients with normal thyroid function, and analyzed the correlation and potential value of TSH in predicting CHD. The results showed that TSH could be used as a biomarker for predicting CHD [39].
Based on the above analysis results, in addition to the traditional risk factors of CHD, such as age, sex, height, weight, history of hypertension, history of hyperlipidemia, history of diabetes mellitus, and smoking history, we also incorporated TSH and eGFR into the proposed ML model. According to the experimental results, we can find that the accuracy can be improved significantly after incorporating the factors of eGFR and TSH, compared with the model constructed by traditional risk factors of CHD.
It should be noted that there are also some deficiencies in this study. Firstly, in the original data, we tried to count the symptoms of patients with CHD. However, in the end, because the clinical manifestations of patients with CHD are too complex to make statistics more complicated, we removed these data; there are also different degrees of missing sample values in the data set, among which the missing laboratory test indicators are more serious. More missing data are BNP, which may lead to a decline in the actual diagnostic performance of the model because the BNP value filled with the mean is lower than the BNP level in patients with heart failure, which is considered as a possible complication of CHD. In addition, traditional risk scores such as FRS and ASCVD are largely derived from data from non-Spanish and American African populations, while our data are derived from Asian populations, and there is some racial interference in the comparison of the results.
In conclusion, in this research, we put forward a new diagnostic model of CHD based on electronic health data using a machine learning algorithm. The model has certain risk assessment ability, which can provide a personalized reference for risk assessment of CHD in the clinic, and help to reduce the workload of clinicians and provide a new method for the clinical diagnosis of CHD.
5. Conclusions and Future Perspectives
In this study, an efficacious STSSA-KELM model was developed to predict coronary heart disease. The main originality of this method is to introduce the space transformation mechanism into SSA, which is used to better balance the global search capability and the local search capability. STSSA-KELM has superior prediction accuracy and a more consistent performance than other machine learning algorithms in the diagnosis of coronary heart disease.
In the future, it is our goal to utilize the STSSA-KELM model to diagnose other diseases, such as pleural effusion, diabetes, appendicitis, and so on. Additionally, the core method STSSA can also be used for parameter tuning for the artificial intelligence models, such as support vector machines [40,41,42,43,44], and convolutional neural networks [45,46,47,48,49]. Moreover, it can also be applied to tackle the feature selection problems [28,41,50,51]. Other problems including social evolution modelling [52], video coding optimization [53], parameter estimation of solar cell [54,55,56,57], and others [58,59,60,61,62] are also interesting topics that are worthy of investigation in the near future.
Author Contributions
W.H. and Y.X. conceived and designed the experiments; M.W. performed the experiments; H.L. and H.C. analyzed the data; H.C. contributed reagents/materials/analysis tools; W.H. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We acknowledge the efforts of Ali Asghar Heidari (http://aliasgharheidari.com) during this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, K.F.; Wang, Y.M.; Zhu, J.Z.; Zhou, Q.Y.; Wang, N.F. National prevalence of coronary heart disease and its relationship with human development index: A systematic review. Eur. J. Prev. Cardiol. 2016, 23, 530–543. [Google Scholar] [CrossRef] [PubMed]
- Virani, S.S.; Alonso, A.; Benjamin, E.J.; Bittencourt, M.S.; Callaway, C.W.; Carson, A.P.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Delling, F.N.; et al. Heart Disease and Stroke Statistics-2020 Update: A Report From the American Heart Association. Circulation 2020, 141, e139–e596. [Google Scholar] [CrossRef] [PubMed]
- Wen, D.; Zhang, X.; Liu, X.; Lei, J. Evaluating the consistency of current mainstream wearable devices in health monitoring: A comparison under free-living conditions. J. Med. Internet Res. 2017, 19, e68. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Wen, D.; Liang, L.; Jia, Y.; Gao, L.; Lei, J. Evaluating the validity of current mainstream wearable devices in fitness tracking under various physical activities: Comparative study. JMIR mHealth uHealth 2018, 6, e94. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Sun, J.; Li, J.; Zhang, J.; Asundi, A.; Chen, Q. High-resolution transport-of-intensity quantitative phase microscopy with annular illumination. Sci. Rep. 2017, 7, 1–22. [Google Scholar] [CrossRef]
- Calvert, J.S.; Price, D.A.; Chettipally, U.K.; Barton, C.W.; Feldman, M.D.; Hoffman, J.L.; Jay, M.; Das, R. A computational approach to early sepsis detection. Comput. Biol. Med. 2016, 74, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Kuijpers, J.M.; Koolbergen, D.R.; Groenink, M.; Peels, K.C.H.; Reichert, C.L.A.; Post, M.C.; Bosker, H.A.; Wajon, E.; Zwinderman, A.H.; Mulder, B.J.M.; et al. Incidence, risk factors, and predictors of infective endocarditis in adult congenital heart disease: Focus on the use of prosthetic material. Eur. Heart J. 2017, 38, 2048–2056. [Google Scholar] [CrossRef]
- Shashikumar, S.P.; Stanley, M.D.; Sadiq, I.; Li, Q.; Holder, A.; Clifford, G.D.; Nemati, S. Early sepsis detection in critical care patients using multiscale blood pressure and heart rate dynamics. J. Electrocardiol. 2017, 50, 739–743. [Google Scholar] [CrossRef]
- Chung, C.P.; Oeser, A.; Avalos, I.; Raggi, P.; Stein, C.M. Cardiovascular risk scores and the presence of subclinical coronary artery atherosclerosis in women with systemic lupus erythematosus. Lupus 2006, 15, 562–569. [Google Scholar] [CrossRef]
- Jiang, Q.; Shao, F.; Gao, W.; Chen, Z.; Jiang, G.; Ho, Y.-S. Unified no-reference quality assessment of singly and multiply distorted stereoscopic images. IEEE Trans. Image Process. 2018, 28, 1866–1881. [Google Scholar] [CrossRef]
- Abdar, M.; Ksiazek, W.; Acharya, U.R.; Tan, R.S.; Makarenkov, V.; Plawiak, P. A new machine learning technique for an accurate diagnosis of coronary artery disease. Comput. Methods Programs Biomed. 2019, 179, 104992. [Google Scholar] [CrossRef] [PubMed]
- Dogan, M.; Beach, S.; Simons, R.; Lendasse, A.; Penaluna, B.; Philibert, R. Blood-Based Biomarkers for Predicting the Risk for Five-Year Incident Coronary Heart Disease in the Framingham Heart Study via Machine Learning. Genes 2018, 9, 641. [Google Scholar] [CrossRef] [PubMed]
- Han, D.; Kolli, K.K.; Gransar, H.; Lee, J.H.; Choi, S.Y.; Chun, E.J.; Han, H.W.; Park, S.H.; Sung, J.; Jung, H.O.; et al. Machine learning based risk prediction model for asymptomatic individuals who underwent coronary artery calcium score: Comparison with traditional risk prediction approaches. J. Cardiovasc. Comput. Tomogr. 2019, 14, 168–176. [Google Scholar] [CrossRef] [PubMed]
- Panda, N.; Majhi, S.K. Improved spotted hyena optimizer with space transformational search for training pi-sigma higher order neural network. Comput. Intell. 2020, 36, 320–350. [Google Scholar] [CrossRef]
- Panda, N.; Majhi, S.K. Improved Salp Swarm Algorithm with Space Transformation Search for Training Neural Network. Arabian J. Sci. Eng. 2020, 45, 2743–2761. [Google Scholar] [CrossRef]
- Naidu, Y.R.; Ojha, A.K. A space transformational invasive weed optimization for solving fixed-point problems. Appl. Intell. 2018, 48, 942–952. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z. Quantum-behaved particle swarm optimization with generalized space transformation search. Soft Comput. 2020, 1–17. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C.; Wu, G.; Wang, X. A novel differential search algorithm and applications for structure design. Appl. Math. Comput. 2015, 268, 246–269. [Google Scholar] [CrossRef]
- Sun, G.; Yang, B.; Yang, Z.; Xu, G. An adaptive differential evolution with combined strategy for global numerical optimization. Soft Comput. 2019, 24, 6277–6296. [Google Scholar] [CrossRef]
- Chen, H.; Yang, B.; Liu, D.; Liu, W.; Liu, Y.; Zhang, X.; Hu, L. Using blood indexes to predict overweight statuses: An extreme learning machine-based approach. PLoS ONE 2015, 10, e0143003. [Google Scholar] [CrossRef]
- Hu, L.; Hong, G.; Ma, J.; Wang, X.; Chen, H. An efficient machine learning approach for diagnosis of paraquat-poisoned patients. Comput. Biol. Med. 2015, 59, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Hu, L.; Ma, C.; Wang, Z.-Y.; Chen, H.-L. A fast approach for detection of erythemato-squamous diseases based on extreme learning machine with maximum relevance minimum redundancy feature selection. Int. J. Syst. Sci. 2015, 46, 919–931. [Google Scholar] [CrossRef]
- Xia, J.; Chen, H.; Li, Q.; Zhou, M.; Chen, L.; Cai, Z.; Fang, Y.; Zhou, H. Ultrasound-based differentiation of malignant and benign thyroid Nodules: An extreme learning machine approach. Comput. Methods Programs Biomed. 2017, 147, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhao, H.; Han, T.; Zhou, H.; Li, C. A grey wolf optimizer using Gaussian estimation of distribution and its application in the multi-UAV multi-target urban tracking problem. Appl. Soft Comput. J. 2019, 78, 240–260. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, C.; Wei, Y.; Yu, F.; Wang, M.; Chen, H. An Effective Computational Model for Bankruptcy Prediction Using Kernel Extreme Learning Machine Approach. Comput. Econ. 2017, 49, 325–341. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Q.; Luo, J.; Xu, Y.; Zhang, X. An enhanced Bacterial Foraging Optimization and its application for training kernel extreme learning machine. Appl. Soft Comput. 2020, 86, 105884. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Li, H.; Cai, Z.; Zhao, X.; Tong, C.; Li, J.; Xu, X. Grey wolf optimization evolving kernel extreme learning machine: Application to bankruptcy prediction. Eng. Appl. Artif. Intell. 2017, 63, 54–68. [Google Scholar] [CrossRef]
- Qiang, L.; Huiling, C.; Hui, H.; Xuehua, Z.; ZhenNao, C.; Changfei, T.; Wenbin, L.; Xin, T. An Enhanced Grey Wolf Optimization Based Feature Selection Wrapped Kernel Extreme Learning Machine for Medical Diagnosis. Comput. Math. Methods Med. 2017, 2017, 1–15. [Google Scholar]
- Arnett, D.K.; Blumenthal, R.S.; Albert, M.A.; Buroker, A.B.; Goldberger, Z.D.; Hahn, E.J.; Himmelfarb, C.D.; Khera, A.; Lloyd-Jones, D.; McEvoy, J.W.; et al. 2019 ACC/AHA Guideline on the Primary Prevention of Cardiovascular Disease: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation 2019, 140, e596–e646. [Google Scholar] [CrossRef]
- D’Agostino, R.B., Sr.; Vasan, R.S.; Pencina, M.J.; Wolf, P.A.; Cobain, M.; Massaro, J.M.; Kannel, W.B. General cardiovascular risk profile for use in primary care: The Framingham Heart Study. Circulation 2008, 117, 743–753. [Google Scholar] [CrossRef]
- Goff, D.C., Jr.; Lloyd-Jones, D.M.; Bennett, G.; Coady, S.; D’Agostino, R.B.; Gibbons, R.; Greenland, P.; Lackland, D.T.; Levy, D.; O’Donnell, C.J.; et al. 2013 ACC/AHA guideline on the assessment of cardiovascular risk: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation 2014, 129, S49–S73. [Google Scholar] [CrossRef] [PubMed]
- Danner, O.K.; Hendren, S.; Santiago, E.; Nye, B.; Abraham, P. Physiologically-based, predictive analytics using the heart-rate-to-Systolic-Ratio significantly improves the timeliness and accuracy of sepsis prediction compared to SIRS. Am. J. Surg. 2017, 213, 617–621. [Google Scholar] [CrossRef] [PubMed]
- Association of estimated glomerular filtration rate and albuminuria with all-cause and cardiovascular mortality in general population cohorts: A collaborative meta-analysis. Lancet 2010, 375, 2073–2081. [CrossRef]
- Schiffrin, E.L.; Lipman, M.L.; Mann, J.F. Chronic kidney disease: Effects on the cardiovascular system. Circulation 2007, 116, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Tonelli, M.; Muntner, P.; Lloyd, A.; Manns, B.J.; Klarenbach, S.; Pannu, N.; James, M.T.; Hemmelgarn, B.R. Risk of coronary events in people with chronic kidney disease compared with those with diabetes: A population-level cohort study. Lancet 2012, 380, 807–814. [Google Scholar] [CrossRef]
- Matsushita, K.; Selvin, E.; Bash, L.D.; Franceschini, N.; Astor, B.C.; Coresh, J. Change in estimated GFR associates with coronary heart disease and mortality. J. Am. Soc. Nephrol. 2009, 20, 2617–2624. [Google Scholar] [CrossRef]
- Back, J.S.; Jin, Y.; Jin, T.; Lee, S.M. Development and Validation of an Automated Sepsis Risk Assessment System. Res. Nurs. Health 2016, 39, 317–327. [Google Scholar] [CrossRef]
- Onat, A.; Aydin, M.; Can, G.; Celik, E.; Altay, S.; Karagoz, A.; Ademoglu, E. Normal thyroid-stimulating hormone levels, autoimmune activation, and coronary heart disease risk. Endocrine 2015, 48, 218–226. [Google Scholar] [CrossRef]
- Li, H.; Cui, Y.; Zhu, Y.; Yan, H.; Xu, W. Association of high normal HbA1c and TSH levels with the risk of CHD: A 10-year cohort study and SVM analysis. Sci. Rep. 2017, 7, 45406. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H. Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Appl. Soft Comput. 2020, 88, 105946. [Google Scholar] [CrossRef]
- Huang, H.; Feng, X.; Zhou, S.; Jiang, J.; Chen, H.; Li, Y.; Li, C. A new fruit fly optimization algorithm enhanced support vector machine for diagnosis of breast cancer based on high-level features. BMC Bioinform. 2019, 20, 290. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Hou, L.; Sharma, B.Y.; Li, H.; Chen, C.; Li, Y.; Zhao, X.; Huang, H.; Cai, Z.; Chen, H. Developing a new intelligent system for the diagnosis of tuberculous pleural effusion. Comput. Methods Programs Biomed. 2018, 153, 211–225. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Hu, L.; Li, H.; Hong, G.; Zhang, T.; Ma, J.; Lu, Z. An Effective Machine Learning Approach for Prognosis of Paraquat Poisoning Patients Using Blood Routine Indexes. Basic Clin. Pharmacol. Toxicol. 2017, 120, 86–96. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Chen, H.; Yu, Z.; Kang, W.; Zhang, B.; Li, H.; Yang, B.; Liu, D. Evolving support vector machines using fruit fly optimization for medical data classification. Knowl.-Based Syst. 2016, 96, 61–75. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, T.; Wang, J.; Tang, G.; Zhao, L. Pyramid Channel-based Feature Attention Network for image dehazing. Comput. Vis. Image Underst. 2020, 197–198, 103003. [Google Scholar] [CrossRef]
- Li, Y.; Cui, W.-G.; Huang, H.; Guo, Y.-Z.; Li, K.; Tan, T. Epileptic seizure detection in EEG signals using sparse multiscale radial basis function networks and the Fisher vector approach. Knowl.-Based Syst. 2019, 164, 96–106. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Tang, Z.; Lei, B. Deep Spatial-Temporal Feature Fusion from Adaptive Dynamic Functional Connectivity for MCI Identification. IEEE Trans. Med. Imaging 2020. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Evolving Deep Convolutional Neural Networks for Image Classification. IEEE Trans. Evolut. Comput. 2020, 24, 394–407. [Google Scholar] [CrossRef]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G.; Lv, J. Automatically Designing CNN Architectures Using the Genetic Algorithm for Image Classification. IEEE Trans. Cybern. 2020. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, M.; Wang, D.; Zhou, P.; Tao, D. Top-k Feature Selection Framework Using Robust 0-1 Integer Programming. IEEE Trans. Neural Netw. Learn. Syst. 2020. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, R.; Wang, X.; Chen, H.; Li, C. Boosted binary Harris hawks optimizer and feature selection. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Xue, X.; Wang, S.F.; Zhan, L.J.; Feng, Z.Y.; Guo, Y.D. Social Learning Evolution (SLE): Computational Experiment-Based Modeling Framework of Social Manufacturing. IEEE Trans. Ind. Inform. 2019, 15, 3343–3355. [Google Scholar] [CrossRef]
- Zhou, Y.; Tian, L.; Zhu, C.; Jin, X.; Sun, Y. Video Coding Optimization for Virtual Reality 360-Degree Source. IEEE J. Sel. Top. Signal Process. 2020, 14, 118–129. [Google Scholar] [CrossRef]
- Jiao, S.; Chong, G.; Huang, C.; Hu, H.; Wang, M.; Heidari, A.A.; Chen, H.; Zhao, X. Orthogonally adapted Harris hawks optimization for parameter estimation of photovoltaic models. Energy 2020, 203, 117804. [Google Scholar] [CrossRef]
- Zhang, H.; Heidari, A.A.; Wang, M.; Zhang, L.; Chen, H.; Li, C. Orthogonal Nelder-Mead moth flame method for parameters identification of photovoltaic modules. Energy Convers. Manag. 2020, 211, 112764. [Google Scholar] [CrossRef]
- Ridha, H.M.; Heidari, A.A.; Wang, M.; Chen, H. Boosted mutation-based Harris hawks optimizer for parameters identification of single-diode solar cell models. Energy Convers. Manag. 2020, 209, 112660. [Google Scholar] [CrossRef]
- Abbassi, A.; Abbassi, R.; Heidari, A.A.; Oliva, D.; Chen, H.; Habib, A.; Jemli, M.; Wang, M. Parameters identification of photovoltaic cell models using enhanced exploratory salp chains-based approach. Energy 2020, 198, 117333. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Zhao, H. An Improved Ant Colony Optimization Algorithm Based on Hybrid Strategies for Scheduling Problem. IEEE Access 2019, 7, 20281–20292. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Zou, L.; Li, G.; Yang, X.; Wu, D. A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput. 2017, 21, 4387–4398. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, J.; Deng, W.; Song, Y. Semi-Supervised Broad Learning System Based on Manifold Regularization and Broad Network. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 983–994. [Google Scholar] [CrossRef]
- Deng, W.; Liu, H.; Xu, J.; Zhao, H.; Song, Y. An Improved Quantum-Inspired Differential Evolution Algorithm for Deep Belief Network. IEEE Trans. Instrum. Meas. 2020. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Xu, J.; Deng, W. Performance Prediction Using High-Order Differential Mathematical Morphology Gradient Spectrum Entropy and Extreme Learning Machine. IEEE Trans. Instrum. Meas. 2019. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).