Abstract
The main purpose of this study is to investigate the multislip effects on the magneto-hydrodynamic (MHD) mixed convection unsteady flow of micropolar nano-fluids over a stretching/shrinking sheet along with radiation in the presence of a heat source. The consequences of multislip and buoyancy conditions have been integrated. By using the suitable similarity variables are used to solve the governing non-linear partial differential equations into a system of coupled non-linear ordinary differential equations. The transformed equations are solved numerically by using Runge–Kutta fourth-order method with shooting technique. The impacts of the several parameters on the velocity, temperature, micro-rotation, and concentration profiles as well as on the skin friction coefficient, Sherwood number, and Nusselt number are discussed with the help of graphs and tables.
1. Introduction
Nanofluids played an important role in recent years due to their vast variety and complex applications, such as in the medical applications, the petroleum industry, and food processing. Many researchers attracted by convective heat transfer using suspensions of nano-sized particles also the temperature of the base fluid increases by nano-particles which is the main source in the heat transfer performance [1,2]. The mixture of base fluids and nano-particles called nano-fluid and is the advanced category of heat transfer. Nano-fluid is created by the distribution of solid particles with no dimensions. The heat transfer capabilities are limited due to low thermal conductivity, such as water, engine oil, and ethylene glycol. On the other hand, metals have very high thermal conductivity. This is the most appropriate method for increasing the heat transfer coefficient. Choi and Eastman [3] firstly gave the concept of nano-fluid. They described that the thermal conductivity would increase after adding a small number of nanoparticles. Unsteady magneto-hydrodynamic (MHD) flow of Casson nanofluid over a moving vertical semi-infinite plate was numerically studied by Babu [4]. Ali et al. [5] investigated the effects of multiple slips with the presence of chemical reaction. Mohyud-Din et al. [6] examined the behavior of a flowing nano-fluid over a flat moving plate. They also described that when nano-particle increases in numbers thermal conductivity also increases. The same behavior of nano-particles was examined by Akbari et al. [7] and Hayat et al. [8]. Kamal et al. [9] investigated the MHD stagnation point flow of nano-fluid in the presence of a chemical reaction. The unsteady nano-fluid flow through the previous medium was analyzed by Kumar et al. [10].
In recent years, the theory of micro-fluids has found great attention, as traditional Newtonian fluids cannot properly identify the characteristic of liquids with suspended particles. A micropolar fluid assumes the key equations of the non-Newtonian fluid model. In the micropolar fluid model, a micro-rotation vector and a coupling parameter are gathered to analyze the kinematics of micro-transformation. Such types of fluid models can be applied to give the details of the flow of colloidal solutions, liquid crystals, liquids with additives, suspension solutions, animal blood, etc., A microscopic fluid is a fluid with internal structures during which the pairing between the spin and macroscopic velocity field of each particle is considered. It is a hydro-dynamic framework acceptable for angular systems because of macroscopic shaped particles. Mabood and Shateyi [11] studied the effects of multislip on the unsteady hydro-magnetic flow of heat transfer and mass transfer impact by radiation in a porous frame of reference. Magnetohydrodynamic boundary layer flow of incompressible fluid within the moving vertical plate involving heat source and the chemical reaction was investigated by Das and Dorjee [12]. Jena [13] and his coworkers studied the thermo effects on MHD viscoelastic fluid flow. They described that additional parameters rise by this phenomenon. Malarselvi et al. [14] accomplished the investigation on time-dependent MHD flow for several parameters over a flat surface. Nandeppanavar et al. [15] investigated that no stagnation point flow consisting of viscous fluid and heat transfer along with velocity due to the moving surface. Baag [16] and his coworkers described the flow analysis and heat transfer analysis past a porous medium in the presence of heat source. Imtiaz et al. [17] studied the unsteady MHD flow of a curved surface. Kempannagari et al. [18] analyzed the impact of heat transfer on MHD ferrofluid flow.
Pordanjani et al. [19] the effect of the presence of radiation on the convection heat transfer rate and the nano-fluid entropy generation within a diagonal rectangular chamber is investigated numerically in the presence of a magnetic field. Malvandi et al. [20] investigates the effects of nano-particle migration on hydromagnetic (MHD) mixed convection of alumina/water nano-fluid inside a vertical annular pipe. Karimipour et al. [21] simulate the nano-fluid flow in a micro-channel in the presence of a magnetic field. Abdollahzadeh et al. [22] investigates the effect of MHD forces on a two-phase boiling flow in a vertical path with nano-particles. Mishra et al. [23] examined the influence of the various physical parameters and the inertia effect of micropolar fluids. Sohaib et al. [24] analyzed the various effects of radiation on MHD flow of micropolar fluid due to the porous medium. Subba et al. [25] explained that the mixed convection entrenched in a porous medium. Liaqat et al. [26] investigated the impact of multiple slips on MHD unsteady Casson nano-fluid flow, heat, and mass transfer in the presence of heat source with thermo-diffusion effect over a stretching/shrinking sheet. Shahid Ali et al. [27] examined the multiple slips on hydromagnetics axisymmetric nano-fluid steady flow, heat and mass transfer influenced by radiation, buoyancy and chemical effect in a permeable frame of reference. Ilyas Khan et al. [28] focused on the MHD channel flow of electrically conducting nano-fluid in a porous medium with the suction and injection effect influence of a transverse magnetic field. Liaqat et al. [29] investigated the impact of multi-slip and solutal boundary conditions on MHD unsteady bioconvective micropolar nano-fluid restraining gyrotactic microorganism, heat and mass transfer effect over a stretching/shrinking sheet. Hayat et al. [30] studied that the velocity profile reduces as the values of the suction and stretching and the wall thickness parameters increase largely also the volume fraction and porosity parameters rises. In several manufacturing processes slip condition on stretching surfaces is important, the slip boundary condition is compulsory when the flow pressure is low. Slip conditions were used by Malarselvi et ai. [31]. Mozaffari et al. [32] investigated the effects of aging and S/B ratio on rheological properties of diluted bitumen and find the solutions at concentrations above and below the critical S/B. Darjani et al. [33] discussed an alternative approach for deriving the equation of state for a two-dimensional lattice gas which is based on arguments similar to those used in the derivation of the Langmuir–Szyszkowski equation of state for localized adsorption. Darjani et al. [34] investigated the possible mechanisms leading to the focusing and defocusing of colloidal nano-particle size distribution during the synthesis. Also, by using the in situ SAXS to measure the evolution of size, size distribution and concentration of Pd colloidal nano-particles during synthesis and population balance modeling (PBM). Li et al. [35] developed a methodology and a trimer-monomer ITC model to obtain the Gibbs free energy, enthalpy, and entropy for toluene and quantify the monomer content. Mozaffari et al. [36] focused on using continuum calculations to simulate the Stokes flow movement of (neutral) self-diffusiophoretically driven, spherical, and catalytic Janus locomotors in the vicinity of a planar wall to understand the fundamentals of boundary guidance. Mozaffari et al. [37] scrutinized that the characterizing of oil film rheology below and above critical S/B ratio at a length scale comparable to the film thickness where oil film separating two water droplets stops draining. Liu et al. [38] showed that all experimental features of the dilatational rheology of asphaltenes laden interfaces be qualitatively explained by diffusional relaxation models provided that the mixture nature of asphaltenes. Lok et al. [39] studied the unsteady flow of micropolar fluid. The impacts of an external magnetic field were numerically described by Sharma et al. [40]. Elahi et al. [41] numerically examined the solution of mixed convection heat transfer over a stretching sheet. The multiple solutions of MHD heat transfer flow with viscous dissipation were conducted by Dhanai et ai. [42].
In earlier research, several researchers revealed the effects of different operative parameters distinctly/collectively such as the Reynolds number, nano-particles volume fraction and slip effects. According to the author’s best knowledge, a numerical investigation of multi-slips effects on hydro-magnetic mixed convection unsteady flow of micropolar nano-fluid with radiation in the presence of heat source has not yet been considered. Numerical solutions are examined for some special cases, while the overall physical interpretation for the various parameters is investigated with the help of graphs. The main purpose of the present study was to extend the recently published work of Mabood and Shateyi [11]. The governing nonlinear PDEs are transformed into a set of particularly nonlinear odes with the support of appropriate similarity transformations and the nonlinear coupled odes are solved numerically with the R-K shooting technique. The impacts of the several physical parameters on the fluid velocity, temperature, solutal, and nano-particle volume fraction functions are examined in detail for some special cases. An exact solution of flow velocity, skin friction coefficient, and Nusselt number is compared with the numerical solution obtained by the R-K shooting method and also with numerical results available in the literature.
2. Mathematical Formulation
An unsteady two dimensional MHD flow of incompressible nano-fluid in the presence of thermal radiation over an electrically conducted shrinking/stretching sheet has been considered for investigation. The x-axis is chosen along the sheet and y-axis is normal to it as shown in Figure 1. The sheet is moving with non-uniform velocity , where a is the stretching/shrinking rate along x-axis and is positive constant with property . The transverse magnetic field is with , where is the strength of magnetic field. The ambient temperature, ambient solutal concentration and ambient nano-particle concentration are , , and respectively. The temperature of the sheet, concentration, and the nano-particle volume fraction are , and at the surface respectively.
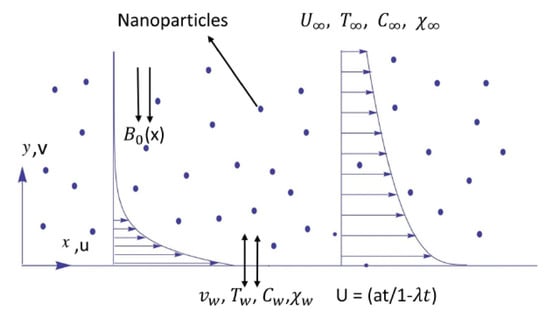
Figure 1.
Physical configuration and coordinate system.
The , , and assumed as of the following form (see [11]):
where , and are the reference temperature, reference solutal concentration and reference nano-particle concentration, respectively, such that , and . The expressions only valid if .
By using the above assumptions, the governing boundary layer equations for the flow problem are as follows (see [8,9,43,44]):
and the boundary conditions are (see [11,44]):
where u is the velocity component along x and v is the velocity component along y, respectively; is dynamic viscosity, k is vortex viscosity, is fluid density, N is micro-rotation vector, is the electrical conductivity, is thermal diffusivity, is spin gradient viscosity, g is gravity acceleration. Further , and are thermal expansion coefficient, solutal concentration expansion coefficient and nano-particle concentration expansion coefficient. T is the temperature, C is the solutal concentration, is the nano-particle concentration. , , , , are the molecular diffusivity, thermal diffusivity, Brownian diffusivity, Soret diffusivity and Dufour diffusivity. is the Stefan–Boltzmann constant, is the mean absorption coefficient, Q is the chemical reaction.
Generally, the stream function which is defined as and . By using the following similarity transformations to convert Equations (1)–(6) into system of ordinary differential equations [31,44].
By using similarity transformation Equation (9), the nonlinear partial differential Equations (1)–(6) transform into the system of nonlinear ODE’s:
and the transformed boundary conditions Equations (7) and (8) are:
The parameters in Equations (10)–(16) are defined as: , , , , , , , , , , , , , , , , , , where M is the magnetic parameter, is material parameter, is the unsteadiness parameter, , and are buoyancy parameters, is the Brownian motion parameter, is the Prandtl number, is the thermophoresis parameter, is the Lewis number, R is the thermal radiation parameter, is the Dufour parameter, is the Soret parameter, is the Schmidt number, is the chemical reaction parameter, and is Suction/injection parameter.
3. Implementation of Method
By using the shooting method, numerically solve the system of ordinary differential Equations (10)–(14) with the boundary conditions (15) and (16). The Runge–Kutta method is more capable and proficient than other numerical methods as HPM, FDM, HPM, etc. Furthermore, it is seen that the Runge–Kutta method is employed in commercial software, such as ANSYS, ABAQUS, ADINA, and MATLAB. For the transformation of Equations (10)–(14) into a system of the first-order ordinary differential equations, introduce the new variables,
The corresponding dimensionless boundary conditions are:
To explain the system of first-order ordinary differential equations with the help of the shooting technique, eleven initial conditions are required. Hence, we guess five unknown initial conditions , , , , . The appropriate guesses for these five missing unknown conditions are chosen such that the five known boundary conditions are nearly satisfied for . To develop the correctness of the missing initial conditions, Newton’s iterative structure is applied until the required approximation is seen. The calculations have been completed for the several developing parameters and for the suitable bounded domain instead of where is the positive real number and is chosen such that no significant variations appeared in the results for the values greater than . The criteria for stopping the iteration process is
where is real number which is positive and very small.
4. Results and Discussion
Our main goal is to examine the unsteadiness effects on the nano-fluid flow quantities. We consider the analysis of the thermo-diffusion and multislip effects on MHD mixed convection unsteady flow of micropolar nano-fluid over a shrinking/stretching sheet with radiation in the presence of a heat source. Table 1 shows the comparison between the results of heat transfer which are obtained by R-K shooting technique and the previous studied numerical results [11,29,45,46] and exact solution of Ishak et al. [47]. There is 4 decimal accuracy between the results under special cases (, , , , , , , , , , , , ). Table 2 shows the comparison of the skin friction coefficient with available numerical and exact results are done. In Table 2, we present a comparison between our results and the numerical results of Gireesha et al. [48], Bagh et al. [5] and the exact solution of Mudassar et al. [49] is done under the special cases (, , , , , , , , ). The comparison of the results of local skin friction and couple stress with already published research work by Eldabe et al. [50] and Hsiao et al. [51] by using R-K shooting technique are shown in Table 3.

Table 1.
Comparison of for various values of .

Table 2.
Comparison of for various values of M.

Table 3.
Comparison of and with our results.
The effect on velocity function of M without hydro-dynamic slip and with hydro-dynamic slip is shown in Figure 2. In both cases the component of velocity decreases as well as M increases. Physically the motion of the fluid slowed when M produced Lorentz force. However, the velocity boundary layer decreases in the presence of hydro-dynamic slip. The momentum boundary layer thickness reduced by as shown in Figure 2. The velocity profiles for different values of K as shown in Figure 3. As K increases the velocity profile increases in both cases. The velocity increases when the value of the buoyancy parameter increases without and with as shown in Figure 4. The growth of velocity depends on buoyancy parameters. It is noticed that the velocity profile enhanced when the radiation parameter R increased. Figure 5 shows that the velocity, boundary layer thickness increases with the increasing values of buoyancy parameter and R without existence and existence of slip.
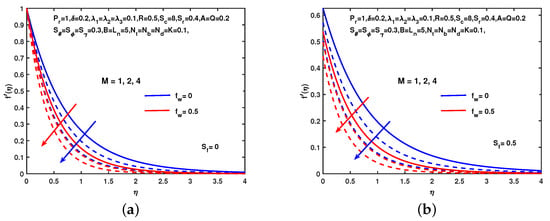
Figure 2.
Influence of M and on . (a) No slip. (b) With slip.
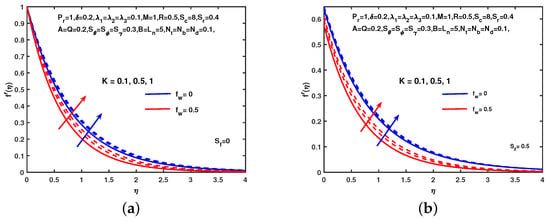
Figure 3.
Influence of K and on . (a) No hydrodynamic slip. (b) With hydrodynamic slip.
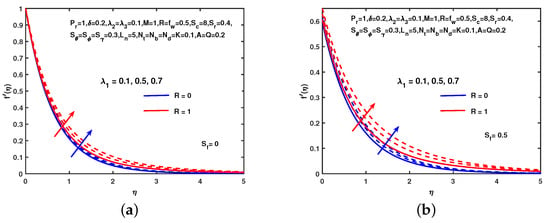
Figure 4.
Influence of and R on . (a) No slip. (b) With slip.
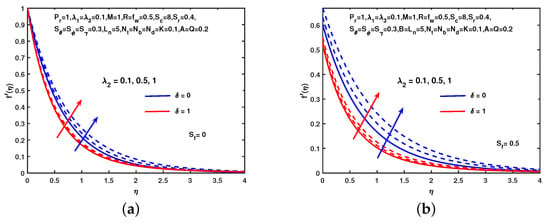
Figure 5.
Influence of and on . (a) No slip. (b) With slip.
The influence of M on temperature with and without thermal slip shows in Figure 6. This shows that the temperature increases as the value of M increases. Physically warms up the liquid by applying the magnetic field. Thermal boundary layer thickness decreases due to and , see Figure 6. It is observed that the behavior of is the same as the temperature profile see Figure 7. For small size nano-particles, will be more prominent and have large values. It is also observed that temperature has the same behavior when unsteady parameter increases. Similarly, the behavior of on thermal profile is shown in Figure 8. Clearly we can see that the increment in causes the increase in the thermal slip boundary layer and observed the behavior of is similar in Figure 8.
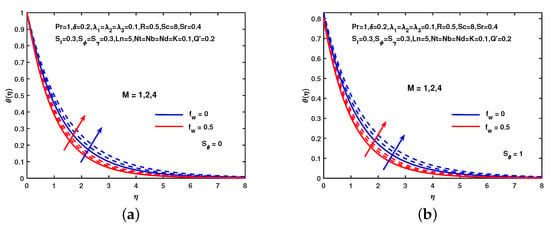
Figure 6.
Influence of M and on . (a) No slip. (b) With slip.
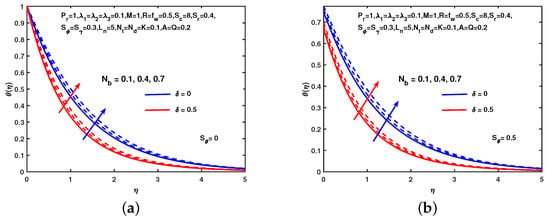
Figure 7.
Influence of and on . (a) No slip. (b) With slip.
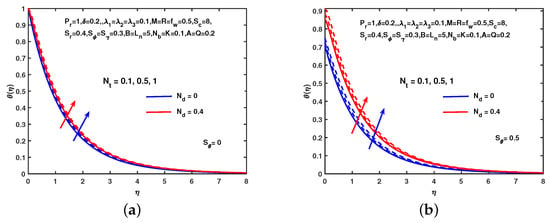
Figure 8.
Influence of and on . (a) No slip. (b) With slip.
In Figure 9, the effect of soret parameter, , on the solutal profile is examined, and several interesting interpretations of solutal distribution are seen. It is also clear from the figure that the solutal profile increases without and with solutal slip. Also, the solutal profile enhances with the escalating values of . Figure 10 reveals that the impact of M on the solutal profile without and with solutal slip. Figure 10 shows that the solutal profile enhances with the increasing values of M in each case. Also, see the impact of on the solutal profile which is scrutinized that the solutal concentration enhances with the increment in . Figure 11 explains the consequences of on the nano-particle volume fraction profile without and with concentration slip. The figure represents that the nano-particle volume fraction profile reduces with the increasing values of in each case. Also, it observes the effects of on the nano-particle volume fraction profile. It is clear that the nano-particle volume fraction profile reduces with increment in values. Figure 12 reveals that the impact of M on the nano-particle profile without and with concentration slip. Figure 12 describes that the nano-particle profile enhances with the increasing values of M in each case. Also, see the impact of on the nano-particle profile which is scrutinized that the nano-particle volume fraction profile enhances with the increment in .
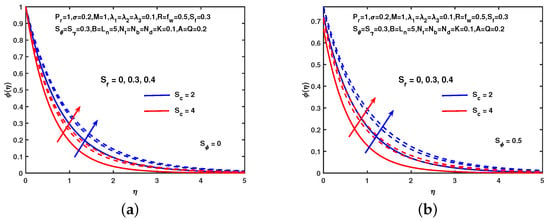
Figure 9.
Influence of and on . (a) No slip. (b) With slip.
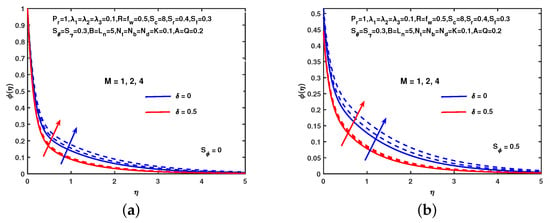
Figure 10.
Influence of M and on . (a) No hydrodynamic slip. (b) With hydrodynamic slip.
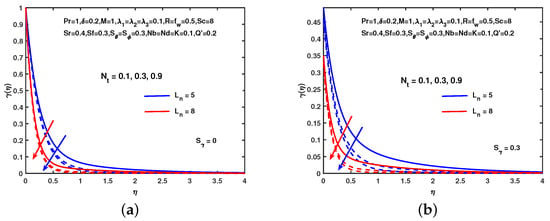
Figure 11.
Influence of and on . (a) No slip. (b) With slip.
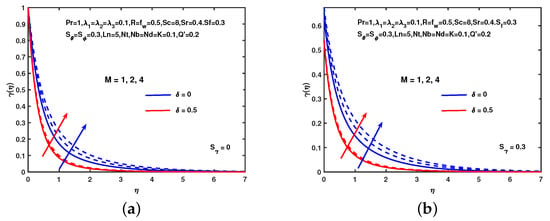
Figure 12.
Influence of M and on . (a) No slip. (b) With slip.
Figure 13 shows the effect of M on g without and with hydro-dynamic slip. It is observed in both cases that the micro-rotation decreases as the value of M increases. Influence of K and without and with hydro-dynamic slip-on g describes in Figure 14. The micro-rotation profile increases as an increase in the value of K. Figure 15 depicts the impact of M on g without and with thermal slip. It is observed in both cases that the micro-rotation decreases as the value of M increases. A similar effect of is observed.
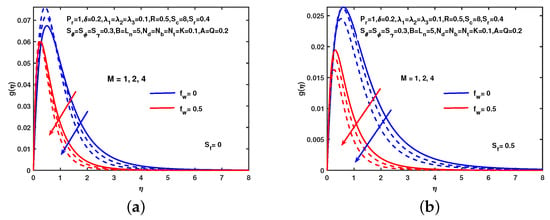
Figure 13.
Influence of M and on g. (a) No slip. (b) With slip.
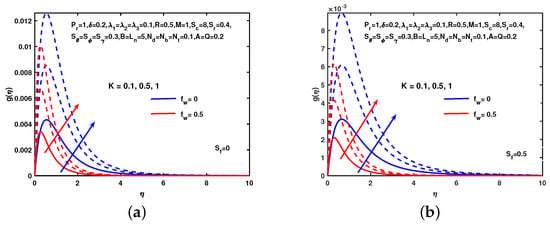
Figure 14.
Influence of K and on g. (a) No slip. (b) With slip.
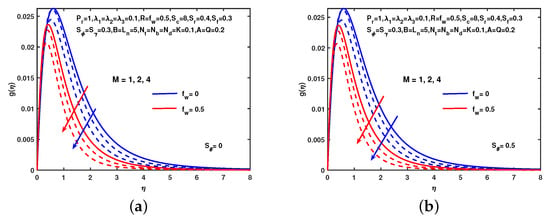
Figure 15.
Influence of M and on g. (a) No slip. (b) With slip.
Figure 16 shows the result of magnetic, unsteadiness, slip velocity on the skin friction coefficient. We see in this figure that the skin friction coefficient decreases along with increasing values of slip velocity and unsteady parameter . However, it increases along with the increasing values of slip velocity and buoyancy parameter . Figure 17 represents the consequences of R, , , concentration, and thermal slips on local Nusselt number. It is perceived that the local Nusselt number reduces on increasing R, , and with and without slip effects. Figure 18 depicts the impacts of M, and on Sherwood number. It is perceived that the mass transfer rate enhances as M and enhances without and with the concentration slip and suction/injection parameter.
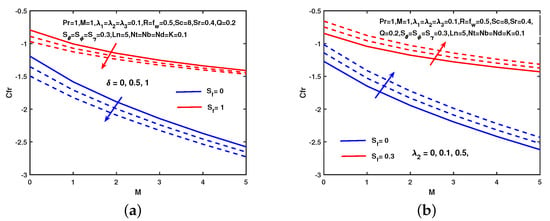
Figure 16.
Influence of and on . (a) No slip. (b) With slip.
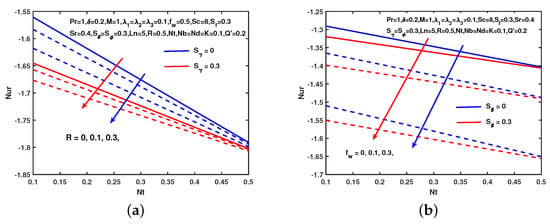
Figure 17.
Influence of R and on . (a) No slip. (b) With slip.
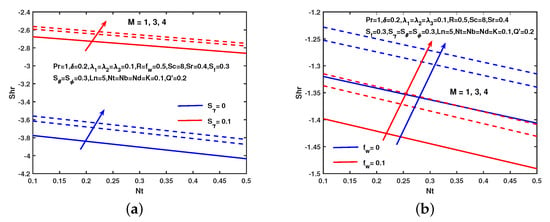
Figure 18.
Influence of M on . (a) No slip. (b) With slip.
Table 4 illustrates the variation of physical parameters M, , , , , with (, , , , , , , on the local skin friction , couple stress , heat transfer coefficient and Sherwood number coefficient .

Table 4.
Numerical values for different physical constraints M, , , , , , , , , .
The following results are obtained from Table 4.
(i) Local skin friction and couple stress are increasing, while and are decreasing at the increasing values of M. (ii) The increment in the values of buoyancy parameters , , , causes the declining in values of and while the values of and are increasing. (iii) For increasing values of the values of , and are increasing and the value of is decreasing. (iv) The values of , , and increasing at the increment in values of .
5. Conclusions
The present study investigates an unsteady magnetohydrodynamic micropolar nano-fluid flow and the heat transfer over a permeable stretching sheet with radiation in the presence of heat source. The study was conducted to investigate the multi-slip effects on magnetohydrodynamic micropolar nano-fluid flow over a stretching sheet. The mathematical model system of equations has been solved by using the Runge–Kutta method with shooting technique. The computations have been performed for velocity, temperature, micro-rotation, and nano-fluid volume fraction functions for the different values of physical parameters. For the given problem, the existing results in Table 1 show the accuracy of up to four decimal places. Moreover, the comparison of the existing results of the given model with previous studies has been discussed. A parametric study has been made to explore the effects of various parameters on the velocity, temperature, micro-rotation, concentration profiles, the skin friction coefficient, Sherwood number, and Nusselt number. Furthermore, the local skin friction, couple stress, Nusselt number, and Sherwood number are inspected graphically. The main findings from the present work are stated as,
- The fluid velocity, temperature solutal and nano-particle profile are seen to increase with an increment in unsteadiness parameter.
- The fluid velocity and micro-rotation declines while temperature shows opposite behavior with the enhancement in magnetic parameter, suction, hydro-dynamic, and thermal slips.
- The skin-friction coefficient decline with the increment of slip parameters, magnetic and unsteadiness parameter but shows the opposite effect for increasing values of hydrodynamic slip and thermal buoyancy.
- The reduced Nusselt number decreases with the enhancement in suction, radiation, thermophoresis parameter, thermal, and solutal slips.
- The Sherwood number increases with an increase in magnetic parameter, suction parameter, and hydro-dynamic slip.
- The fluid velocity and micro-rotation increase with the increment in K, , and .
- Temperature and solutal concentration increase with the increment in thermophoresis parameter, Schmidt number, Brownian motion parameter, Soret parameter, and thermal slip while the nano-particle concentration declines as the values of thermophoresis parameter, lewis number, and nano-particle slip increase.
Author Contributions
S.A. modeled the problem and wrote the manuscript and thoroughly checked the mathematical modeling and English corrections. B.A. helped in MATLAB coding. S.Y., and A.M. writing—review and editing. L.A. help in editing. S.A. contributed to the results and discussions. All authors finalized the manuscript after its internal evaluation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| M | Magnetic parameter |
| Material parameter | |
| Radiation parameter | |
| Unsteadiness parameter | |
| Buoyancy parameter | |
| Brownian motion parameter | |
| Thermo-phoresis parameter | |
| Prandtl number | |
| Lewis number | |
| R | Thermal radiation parameter |
| Dufour parameter | |
| Soret parameter | |
| Schmidt number | |
| Q | Chemical reaction |
| Suction/Injection parameter | |
| N | Microrotation vector |
| Electrical conductivity | |
| Thermal diffusivity | |
| Spin gradient viscosity | |
| g | Gravity |
| Mean absorption coefficient | |
| Stefan-Boltzmann constant | |
| T | Temperature |
| Sheet temperature | |
| Ambient temperature | |
| Reference temperature | |
| Solutal concentration | |
| Ambient solutal concentration | |
| Velocity of sheet | |
| Reference solutal concentration | |
| Nanoparticle volume fraction | |
| Ambient nanoparticle concentration | |
| Reference nanoparticle concentration | |
| Thermal diffusivity | |
| Molecular diffusivity | |
| Brownian diffusivity | |
| Soret diffusivity | |
| Dufour diffusivity | |
| Dynamic viscosity | |
| k | Vortex viscosity |
| Fluid density | |
| Velocity components | |
| Cartesian coordinates | |
| Reduced skin friction co-efficient | |
| Local Nusselt number | |
| Reduced Sherwood number |
References
- Özerinç, S.; Kakaç, S.; Yazıcıoğlu, A.G. Enhanced thermal conductivity of nanofluids: A state-of-the-art review. Microfluid. Nanofluidics 2010, 8, 145–170. [Google Scholar] [CrossRef]
- Godson, L.; Raja, B.; Lal, D.M.; Wongwises, S. Enhancement of heat transfer using nanofluids—an overview. Renew. Sustain. Energy Rev. 2010, 14, 629–641. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Laboratory: Argonne, IL, USA, 1995. [Google Scholar]
- Babu, D.V. Unsteady MHD Free Convection flow in a Casson Nano Fluid Through Porous Medium with Suction and Heat Source. Int. J. Eng. Sci. Math. 2019, 8, 62–75. [Google Scholar]
- Ali, B.; Nie, Y.; Khan, S.A.; Sadiq, M.T.; Tariq, M. Finite Element Simulation of Multiple Slip Effects on MHD Unsteady Maxwell Nanofluid Flow over a Permeable Stretching Sheet with Radiation and Thermo-Diffusion in the Presence of Chemical Reaction. Processes 2019, 7, 628. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Khan, U.; Ahmed, N.; Rashidi, M.M. A study of heat and mass transfer on magnetohydrodynamic (MHD) flow of nanoparticles. Propuls. Power Res. 2018, 7, 72–77. [Google Scholar] [CrossRef]
- Akbari, O.A.; Toghraie, D.; Karimipour, A.; Marzban, A.; Ahmadi, G.R. The effect of velocity and dimension of solid nanoparticles on heat transfer in non-Newtonian nanofluid. Phys. Low-Dimensional Syst. Nanostruct. 2017, 86, 68–75. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. Simulation of ferromagnetic nanomaterial flow of Maxwell fluid. Results Phys. 2018, 8, 34–40. [Google Scholar] [CrossRef]
- Kamal, F.; Zaimi, K.; Ishak, A.; Pop, I. Stability analysis of MHD stagnation-point flow towards a permeable stretching/shrinking sheet in a nanofluid with chemical reactions effect. Sains Malays. 2019, 48, 243–250. [Google Scholar] [CrossRef]
- VMSS Kiran Kumar, R.; Vindo Kumar, G.; Verma, S. Unsteady Magnetohydrodynamic Stagnation Point Flow of a Nanofluid over a Slendering Stretching Sheet Using Buongiorno’s Model. Int. J. Res. Ind. Eng. 2018, 7, 84–105. [Google Scholar]
- Mabood, F.; Shateyi, S. Multiple Slip Effects on MHD Unsteady Flow Heat and Mass Transfer Impinging on Permeable Stretching Sheet with Radiation. Model. Simul. Eng. 2019, 2019, 11. [Google Scholar] [CrossRef]
- Das, U.J.; Dorjee, S. Magnetohydrodynamic Boundary Layer Flow with Soret/Dufour effects in presence of Heat source and Chemical Reaction. Int. J. Appl. Eng. Res. 2019, 14, 485–490. [Google Scholar]
- Jena, S.; Dash, G.; Mishra, S. Chemical reaction effect on MHD viscoelastic fluid flow over a vertical stretching sheet with heat source/sink. Ain Shams Eng. J. 2016. [Google Scholar] [CrossRef]
- Malarselvi, A.; Bhuvaneswari, M.; Sivasankaran, S.; Ganga, B.; Hakeem, A.A. Impacts of chemical reaction on MHD double diffusive flow with suction/blowing and slip. J. Phys. Conf. Ser. Iop Publ. 2018, 1139, 012089. [Google Scholar] [CrossRef]
- Nandeppanavar, M.M.; Kemparaju, M.; Shakunthala, S. MHD stagnation point slip flow due to a non-linearly moving surface with effect of non-uniform heat source. Nonlinear Eng. 2019, 8, 270–282. [Google Scholar] [CrossRef]
- Baag, S.; Mishra, S.; Hoque, M.M.; Anika, N.N. Magnetohydrodynamic boundary layer flow over an exponentially stretching sheet past a porous medium with uniform heat source. J. Nanofluids 2018, 7, 570–576. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Alsaedi, A.; Hobiny, A. Homogeneous-heterogeneous reactions in MHD flow due to an unsteady curved stretching surface. J. Mol. Liq. 2016, 221, 245–253. [Google Scholar] [CrossRef]
- Kempannagari, A.K.; Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Impact of frictional heating on MHD radiative ferrofluid past a convective shrinking surface. Defect and diffusion forum. Trans. Tech. Publ. 2017, 378, 157–174. [Google Scholar]
- Pordanjani, A.H.; Aghakhani, S.; Karimipour, A.; Afrand, M.; Goodarzi, M. Investigation of free convection heat transfer and entropy generation of nanofluid flow inside a cavity affected by magnetic field and thermal radiation. J. Therm. Anal. Calorim. 2019, 137, 997–1019. [Google Scholar] [CrossRef]
- Malvandi, A.; Safaei, M.; Kaffash, M.; Ganji, D. MHD mixed convection in a vertical annulus filled with Al2O3–water nanofluid considering nanoparticle migration. J. Magn. Magn. Mater. 2015, 382, 296–306. [Google Scholar] [CrossRef]
- Karimipour, A.; D’Orazio, A.; Shadloo, M.S. The effects of different nano particles of Al2O3 and Ag on the MHD nano fluid flow and heat transfer in a microchannel including slip velocity and temperature jump. Phys. Low-Dimensional Syst. Nanostruct. 2017, 86, 146–153. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.Y.; Ghasemi, M.; Alamian, R.; Wongwises, S.; Afrand, M.; Shadloo, M.S. Modeling of Subcooled Flow Boiling with Nanoparticles under the Influence of a Magnetic Field. Symmetry 2019, 11, 1275. [Google Scholar] [CrossRef]
- Mishra, S.; Hoque, M.M.; Mohanty, B.; Anika, N. Heat transfer effect on MHD flow of a micropolar fluid through porous medium with uniform heat source and radiation. Nonlinear Eng. 2019, 8, 65–73. [Google Scholar] [CrossRef]
- Hydromagnetic Stagnation Point Flow of Micropolar Fluids due to a Porous Stretching Surface with Radiation and Viscous Dissipation Effects. Sci. Int. (Lahore) 2015, 27, 3965–3971.
- Subba, R.G.R.; Jawad, C.A.; Rashad, A. Mixed convection from a vertical surface embedded in a porous medium saturated with a non-Newtonian nanofluid. J. Appl. Fluid Mech. 2013, 6, 301–309. [Google Scholar]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite Element Analysis of Thermo-Diffusion and Multi-Slip Effects on MHD Unsteady Flow of Casson Nano-Fluid over a Shrinking/Stretching Sheet with Radiation and Heat Source. Appl. Sci. 2019, 9, 5217. [Google Scholar] [CrossRef]
- Khan, S.A.; Nie, Y.; Ali, B. Multiple Slip Effects on Magnetohydrodynamic Axisymmetric Buoyant Nanofluid Flow above a Stretching Sheet with Radiation and Chemical Reaction. Symmetry 2019, 11, 1171. [Google Scholar] [CrossRef]
- Khan, I.; Alqahtani, A.M. MHD Nanofluids in a Permeable Channel with Porosity. Symmetry 2019, 11, 378. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Mujeed, S.; Abdal, S. Finite Element Simulation of Multi-Slip Effects on Unsteady MHD Bioconvective Micropolar nanofluid Flow Over a Sheet with Solutal and Thermal Convective Boundary Conditions. Coatings 2019, 9, 842. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Alsaedi, A. MHD convective flow of magnetite-Fe3O4 nanoparticles by curved stretching sheet. Results Phys. 2017, 7, 3107–3115. [Google Scholar] [CrossRef]
- Malarselvi, A.; Bhuvaneswari, M.; Sivasankaran, S.; Ganga, B.; Hakeem, A.A. Effect of Slip and Convective Heating on Unsteady MHD Chemically Reacting Flow Over a Porous Surface with Suction. In Applied Mathematics and Scientific Computing; Springer: Berlin/Heidelberg, Germany, 2019; pp. 357–365. [Google Scholar]
- Mozaffari, S.; Tchoukov, P.; Atias, J.; Czarnecki, J.; Nazemifard, N. Effect of asphaltene aggregation on rheological properties of diluted athabasca bitumen. Energy Fuels 2015, 29, 5595–5599. [Google Scholar] [CrossRef]
- Darjani, S.; Koplik, J.; Pauchard, V. Extracting the equation of state of lattice gases from random sequential adsorption simulations by means of the Gibbs adsorption isotherm. Phys. Rev. 2017, 96, 052803. [Google Scholar] [CrossRef] [PubMed]
- Mozaffari, S.; Li, W.; Dixit, M.; Seifert, S.; Lee, B.; Kovarik, L.; Mpourmpakis, G.; Karim, A.M. The role of nanoparticle size and ligand coverage in size focusing of colloidal metal nanoparticles. Nanoscale Adv. 2019, 1, 4052–4066. [Google Scholar] [CrossRef]
- Li, W.; Ivanov, S.; Mozaffari, S.; Shanaiah, N.; Karim, A.M. Palladium Acetate Trimer: Understanding Its Ligand-Induced Dissociation Thermochemistry Using Isothermal Titration Calorimetry, X-ray Absorption Fine Structure, and 31P Nuclear Magnetic Resonance. Organometallics 2018, 38, 451–460. [Google Scholar] [CrossRef]
- Mozaffari, A.; Sharifi-Mood, N.; Koplik, J.; Maldarelli, C. Self-diffusiophoretic colloidal propulsion near a solid boundary. Phys. Fluids 2016, 28, 053107. [Google Scholar] [CrossRef]
- Mozaffari, S.; Tchoukov, P.; Mozaffari, A.; Atias, J.; Czarnecki, J.; Nazemifard, N. Capillary driven flow in nanochannels–Application to heavy oil rheology studies. Colloids Surfaces Physicochem. Eng. Asp. 2017, 513, 178–187. [Google Scholar] [CrossRef]
- Liu, F.; Darjani, S.; Akhmetkhanova, N.; Maldarelli, C.; Banerjee, S.; Pauchard, V. Mixture effect on the dilatation rheology of asphaltenes-laden interfaces. Langmuir 2017, 33, 1927–1942. [Google Scholar] [CrossRef]
- Lok, Y.; Amin, N.; Pop, I. Unsteady mixed convection flow of a micropolar fluid near the stagnation point on a vertical surface. Int. J. Therm. Sci. 2006, 45, 1149–1157. [Google Scholar] [CrossRef]
- Sharma, P.; Sinha, S.; Yadav, R.; Filippov, A.N. MHD mixed convective stagnation point flow along a vertical stretching sheet with heat source/sink. Int. J. Heat Mass Transf. 2018, 117, 780–786. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Shehzad, N.; Alamri, S.Z. Structural impact of Kerosene-Al2O3 nanoliquid on MHD Poiseuille flow with variable thermal conductivity: Application of cooling process. J. Mol. Liq. 2018, 264, 607–615. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. Critical values in slip flow and heat transfer analysis of non-Newtonian nanofluid utilizing heat source/sink and variable magnetic field: Multiple solutions. J. Taiwan Inst. Chem. Eng. 2016, 58, 155–164. [Google Scholar] [CrossRef]
- Ashraf, M.; Bashir, S. Numerical simulation of MHD stagnation point flow and heat transfer of a micropolar fluid towards a heated shrinking sheet. Int. J. Numer. Methods Fluids 2012, 69, 384–398. [Google Scholar] [CrossRef]
- Abdul Latiff, N.A.; Uddin, M.J.; Bég, O.A.; Ismail, A.I. Unsteady forced bioconvection slip flow of a micropolar nanofluid from a stretching/shrinking sheet. Proc. Inst. Mech. Eng. Part J. Nanomater. Nanoeng. Nanosyst. 2016, 230, 177–187. [Google Scholar] [CrossRef]
- Pal, D. Combined effects of non-uniform heat source/sink and thermal radiation on heat transfer over an unsteady stretching permeable surface. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1890–1904. [Google Scholar] [CrossRef]
- Haile, E.; Shankar, B. Heat and mass transfer in the boundary layer of unsteady viscous nanofluid along a vertical stretching sheet. J. Comput. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over an unsteady stretching vertical surface. Meccanica 2009, 44, 369–375. [Google Scholar] [CrossRef]
- Gireesha, B.; Ramesh, G.; Bagewadi, C. Heat transfer in MHD flow of a dusty fluid over a stretching sheet with viscous dissipation. J. Appl. Sci. Res. 2012, 3, 2392–2401. [Google Scholar]
- Jalil, M.; Asghar, S.; Yasmeen, S. An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface. Math. Probl. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Ouaf, M.E. Chebyshev finite difference method for heat and mass transfer in a hydromagnetic flow of a micropolar fluid past a stretching surface with Ohmic heating and viscous dissipation. Appl. Math. Comput. 2006, 177, 561–571. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).