Efficient C2 Continuous Surface Creation Technique Based on Ordinary Differential Equation
Abstract
1. Introduction
2. Related Work
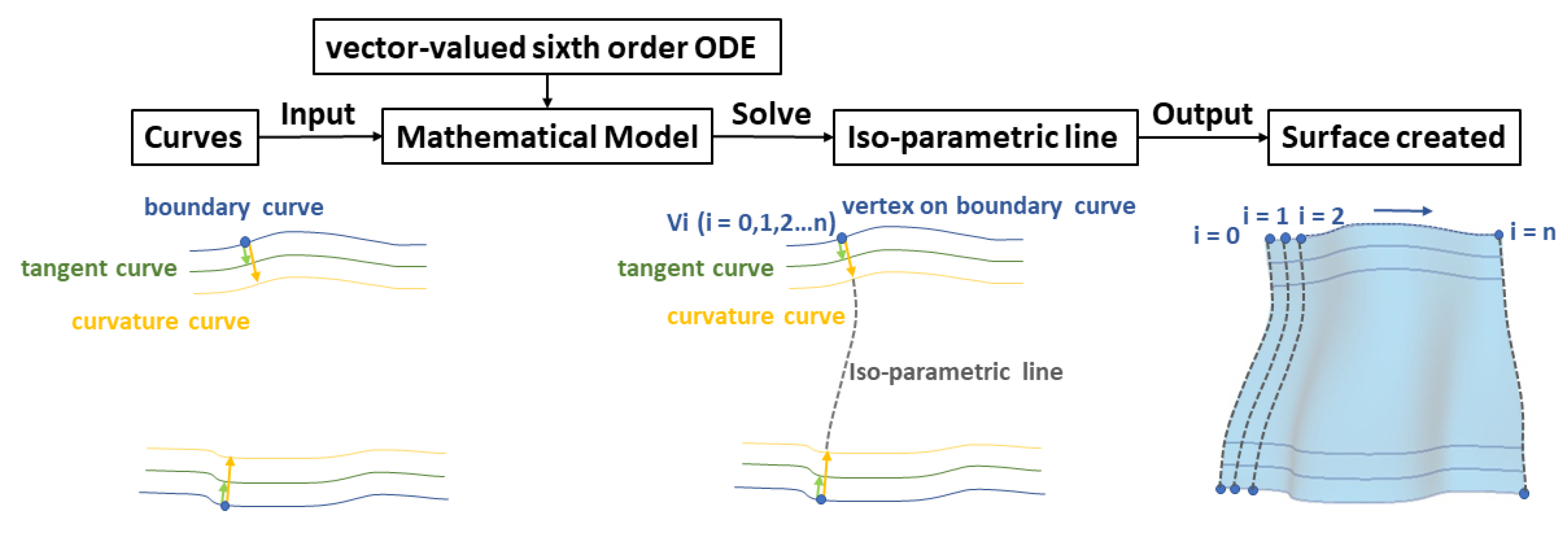
3. Mathematical Model
4. Closed Form Complementary Solution
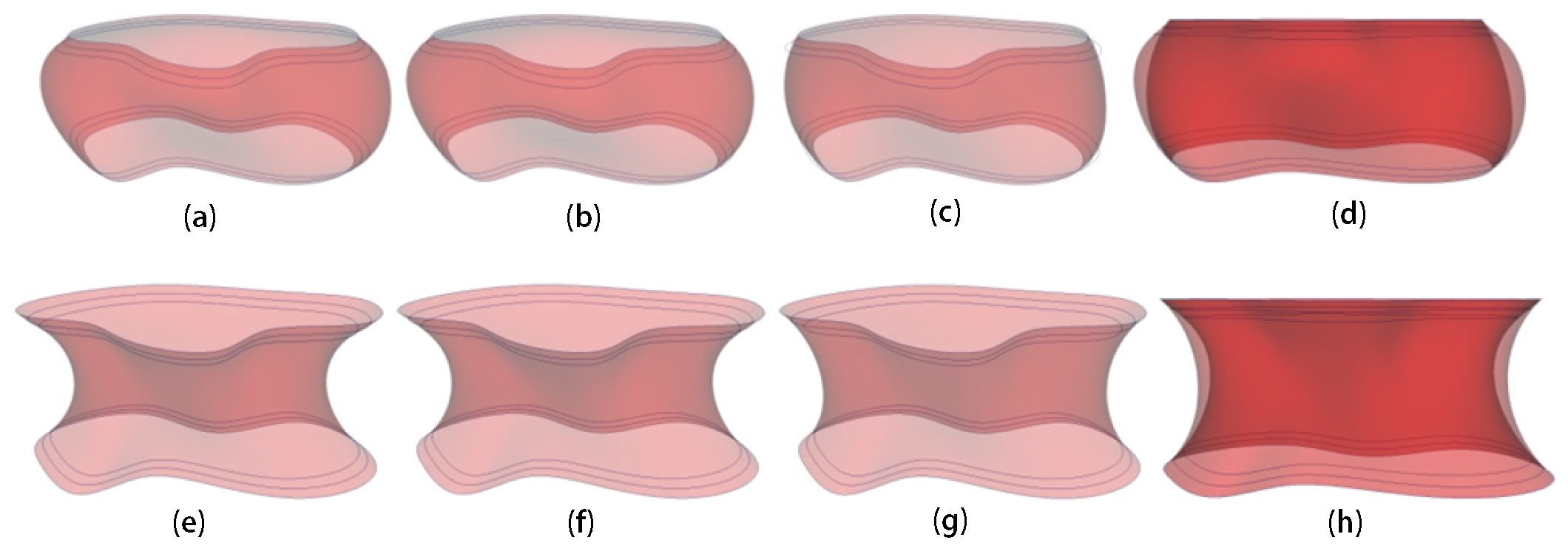
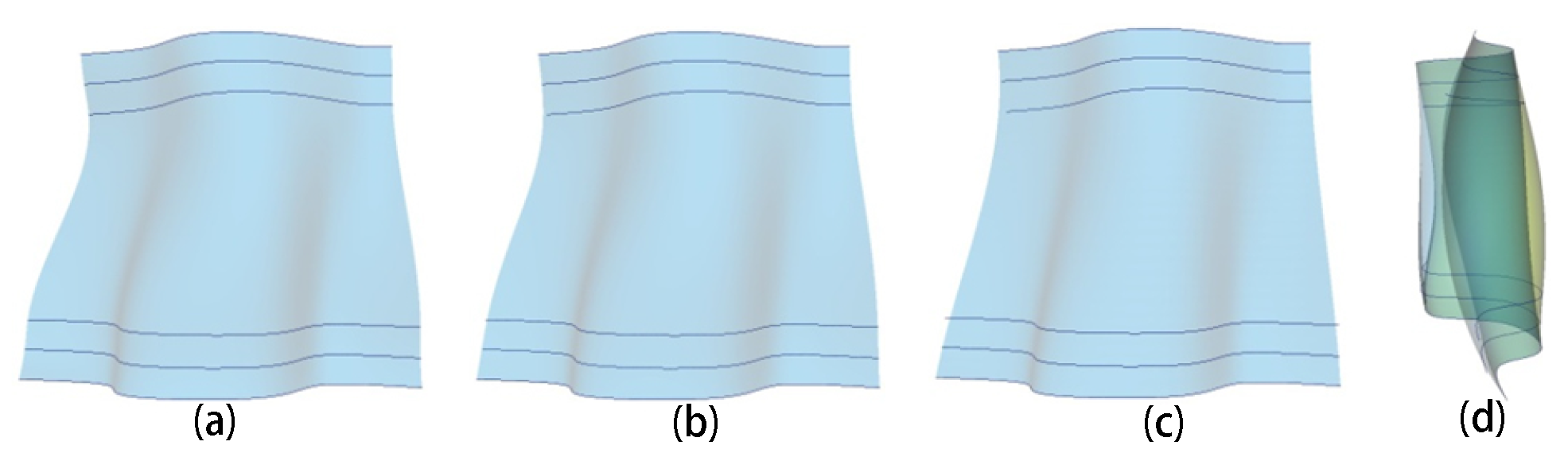
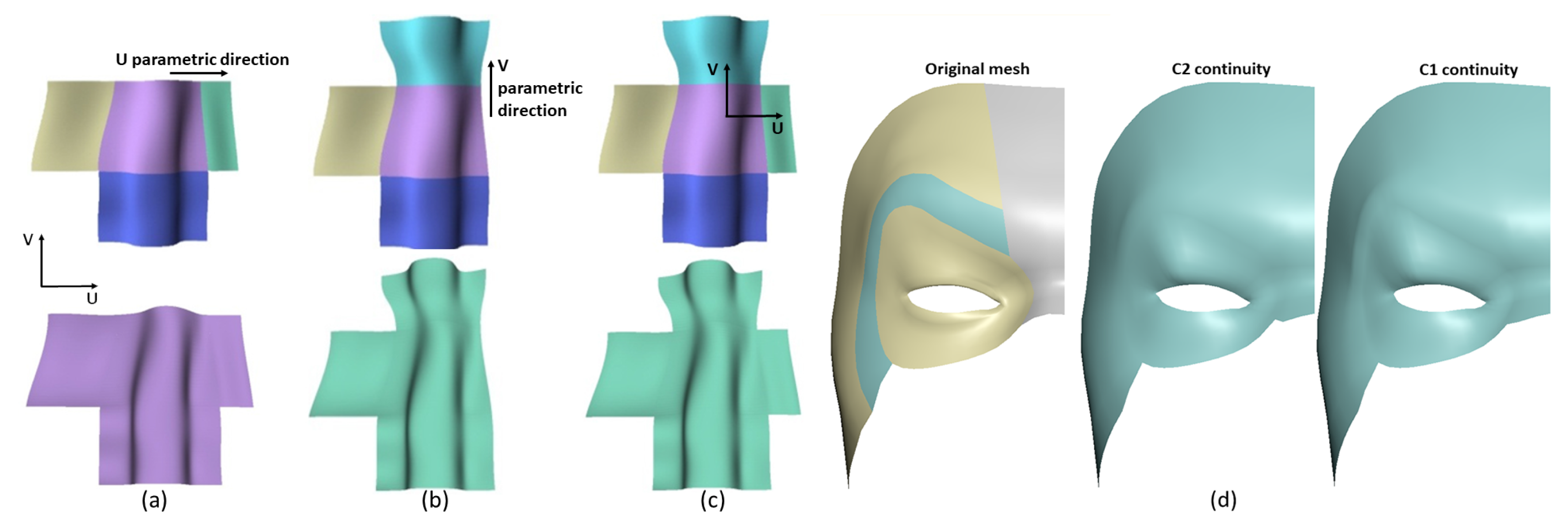
5. Continuity between Adjacent Surface Patches
5.1. Continuity in Parametric Direction U
5.2. Continuity in Parametric Direction V
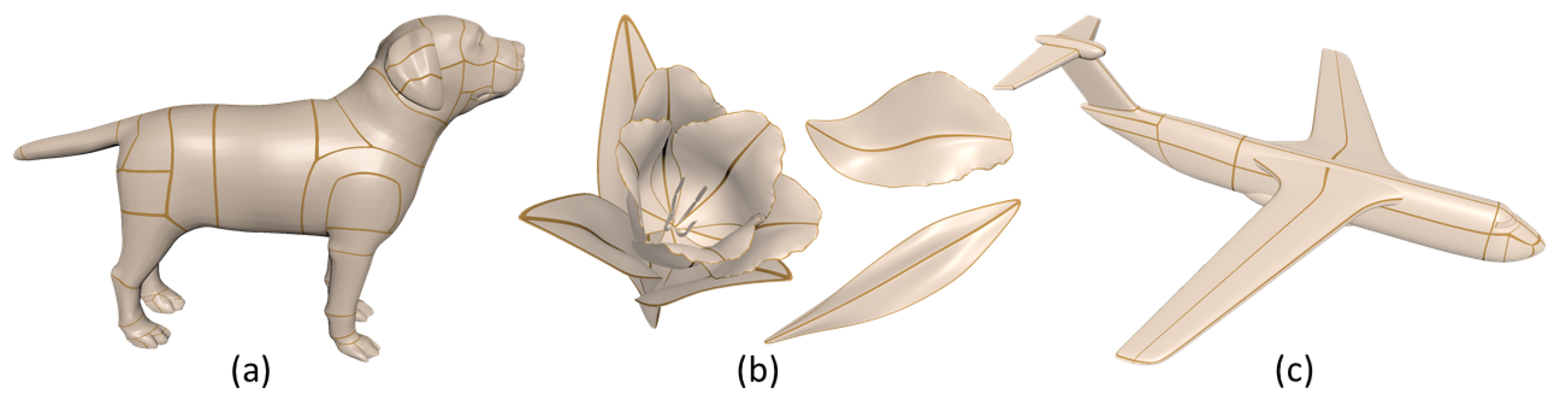
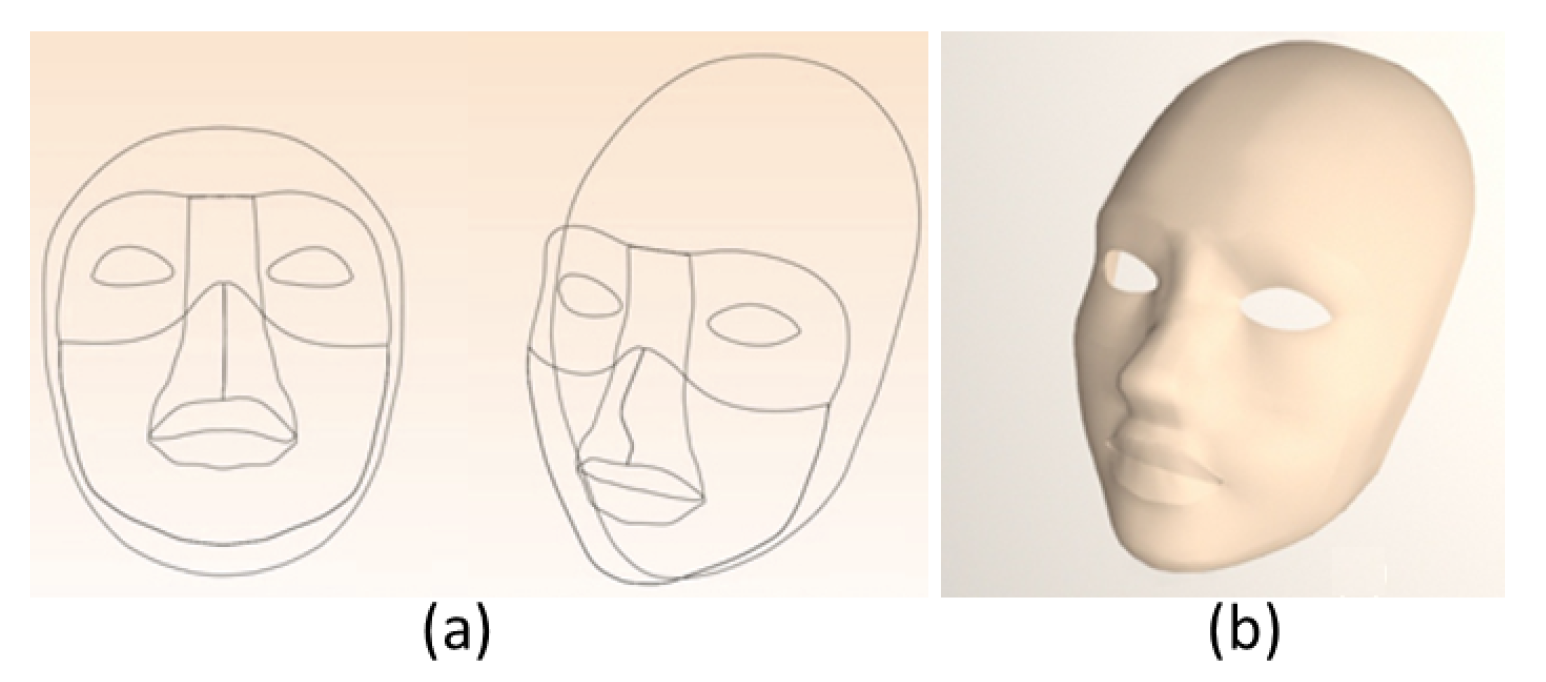
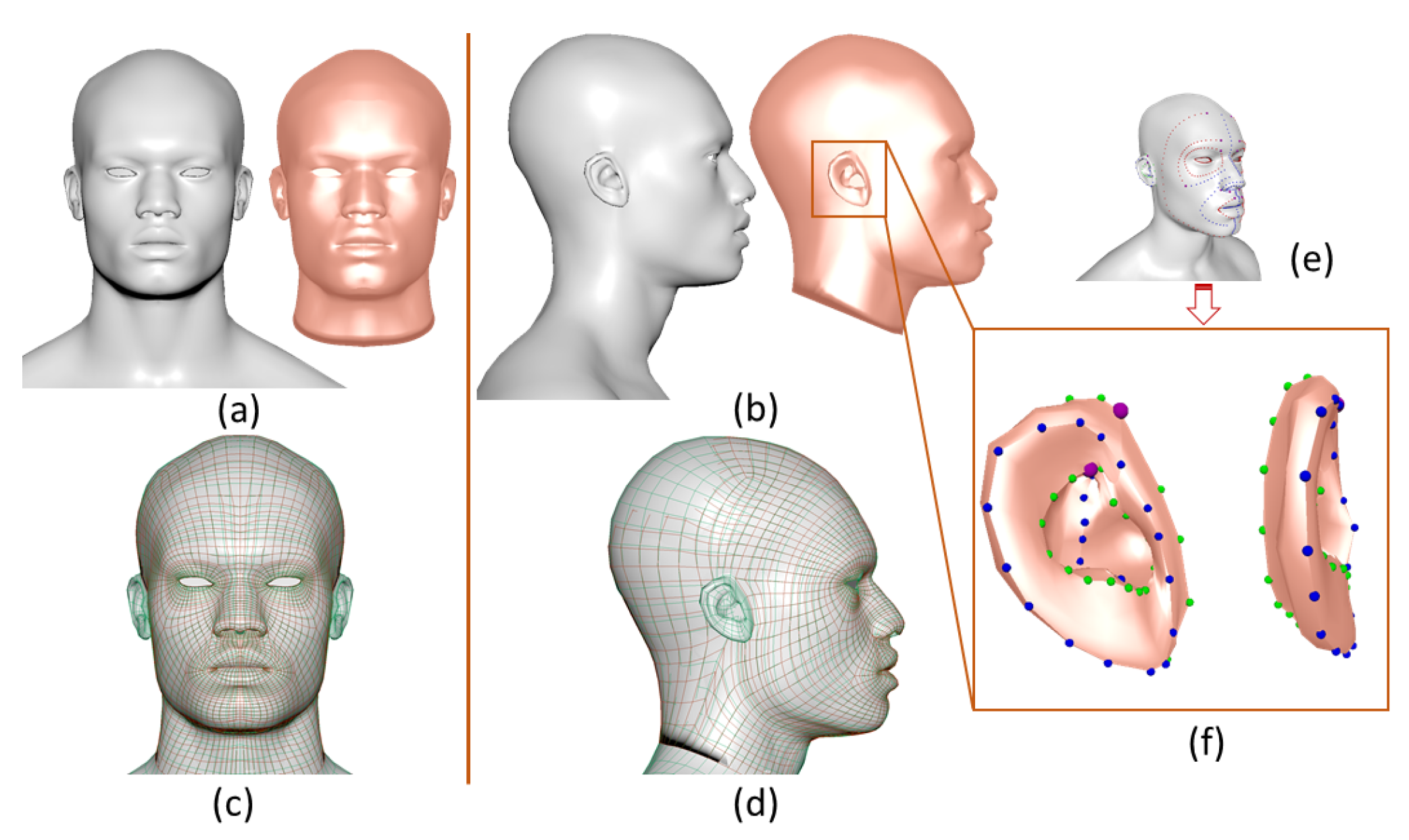
6. Experiments and Application
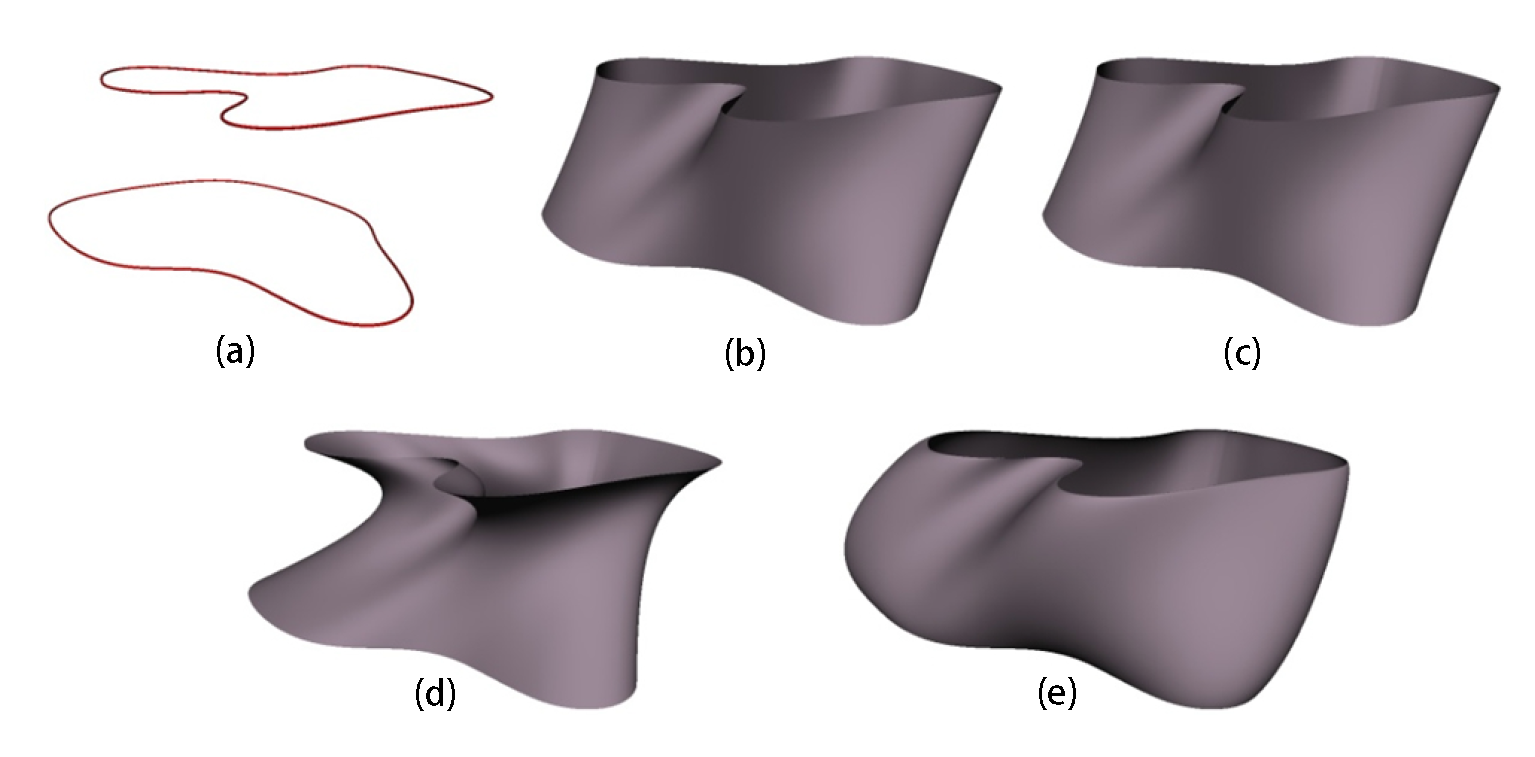
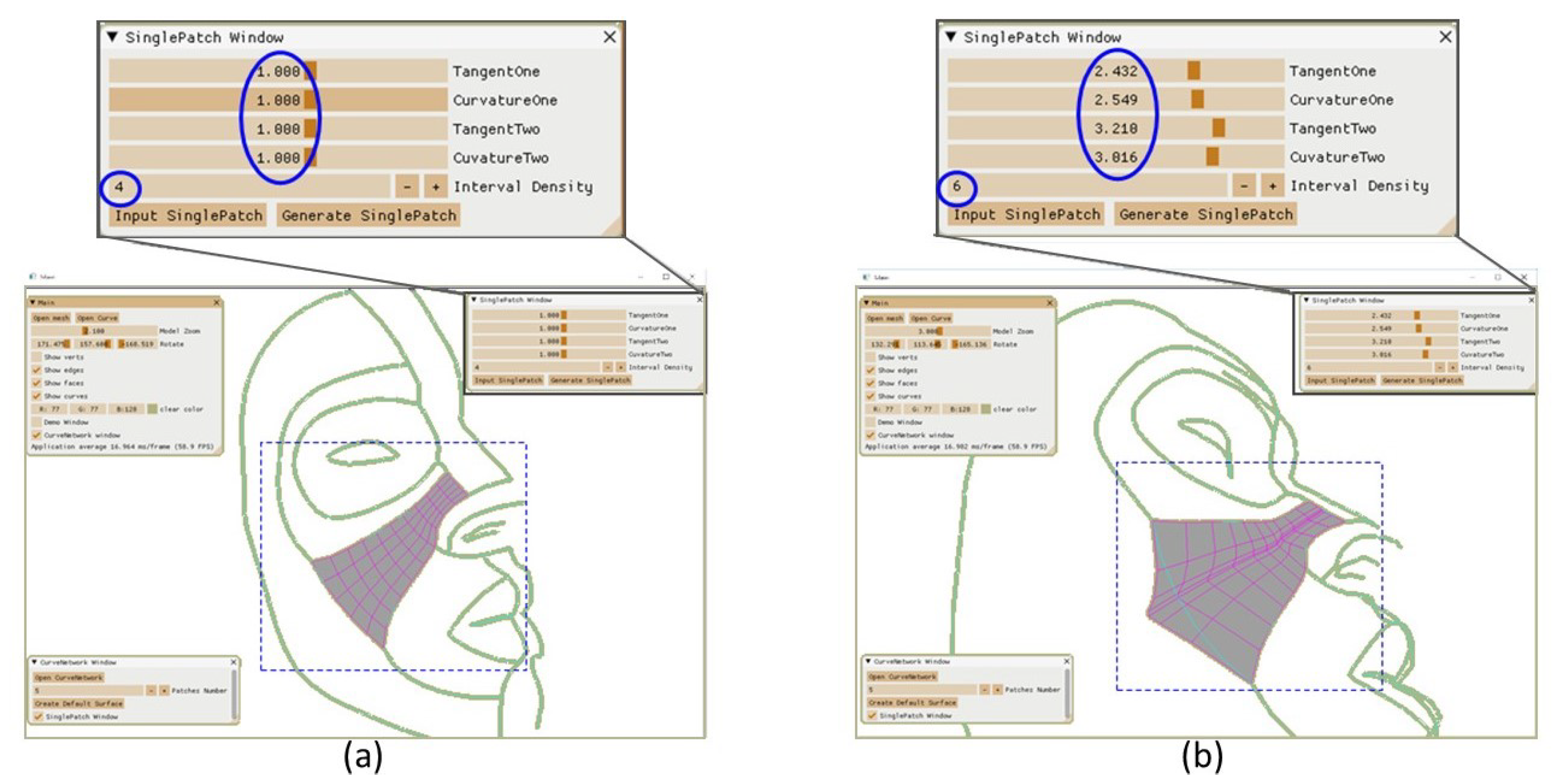
6.1. Creation of Single Surface
6.2. Creation of Complicated Objects
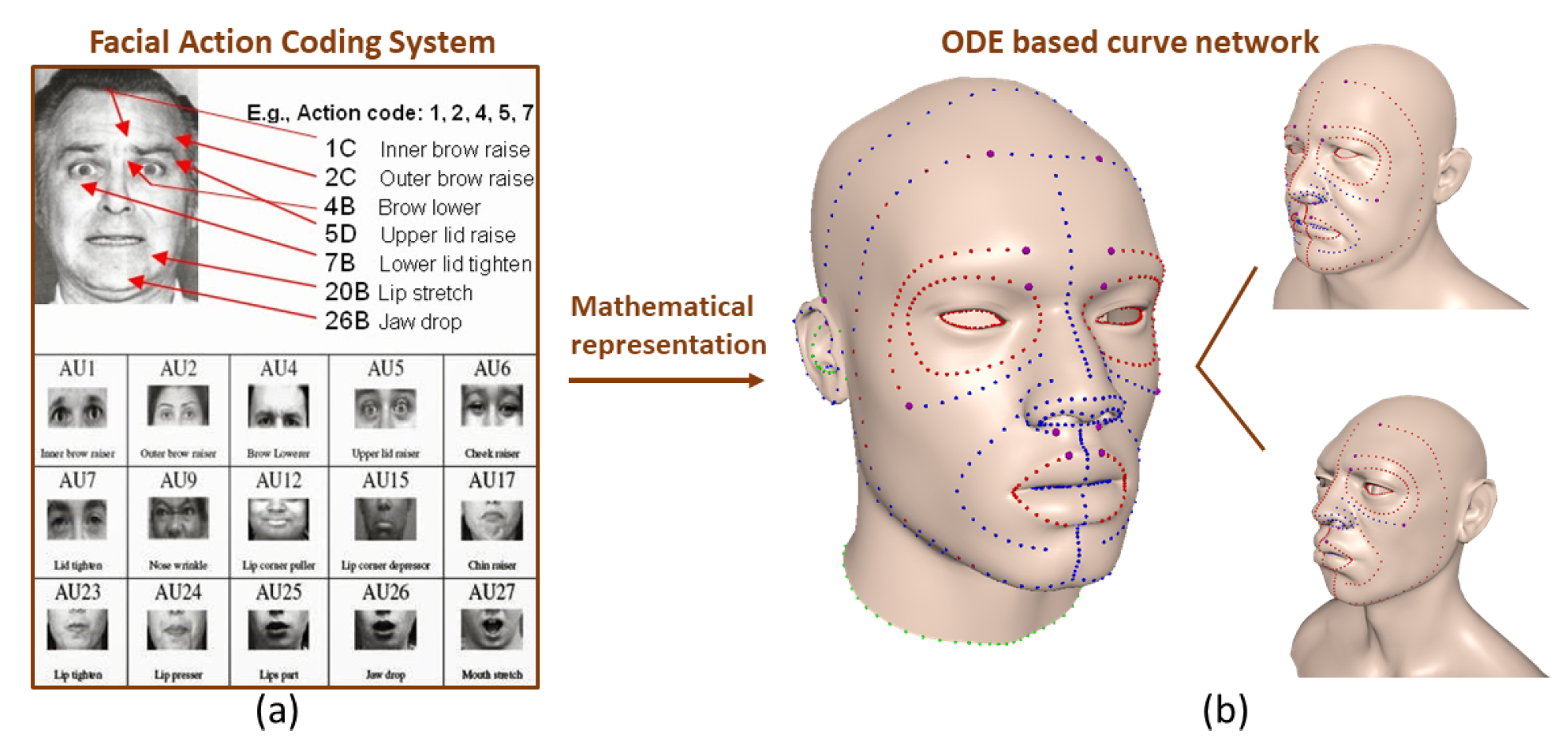
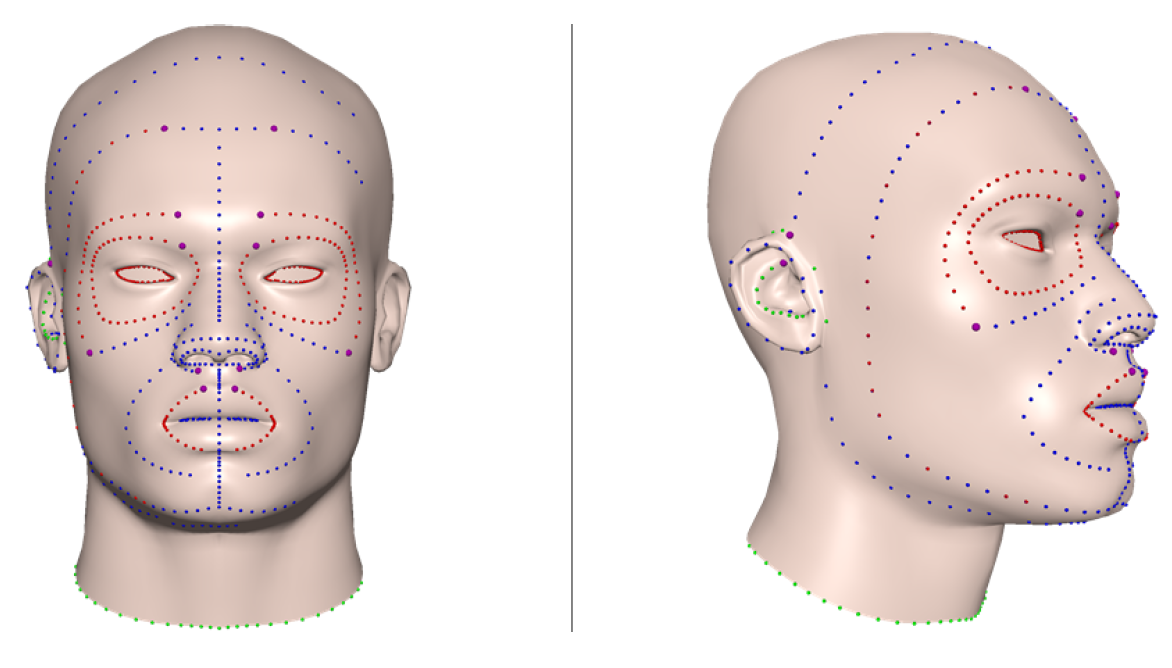
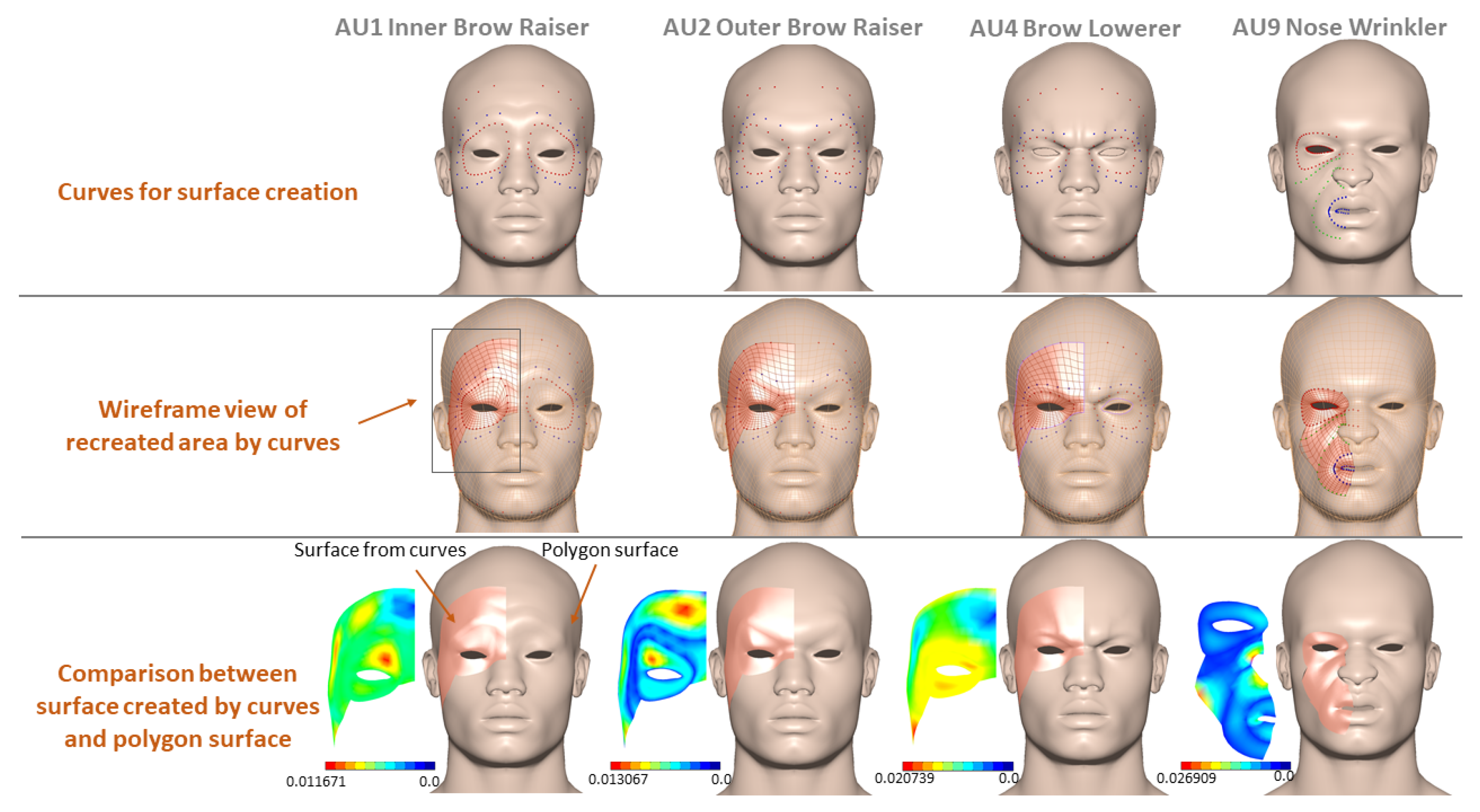
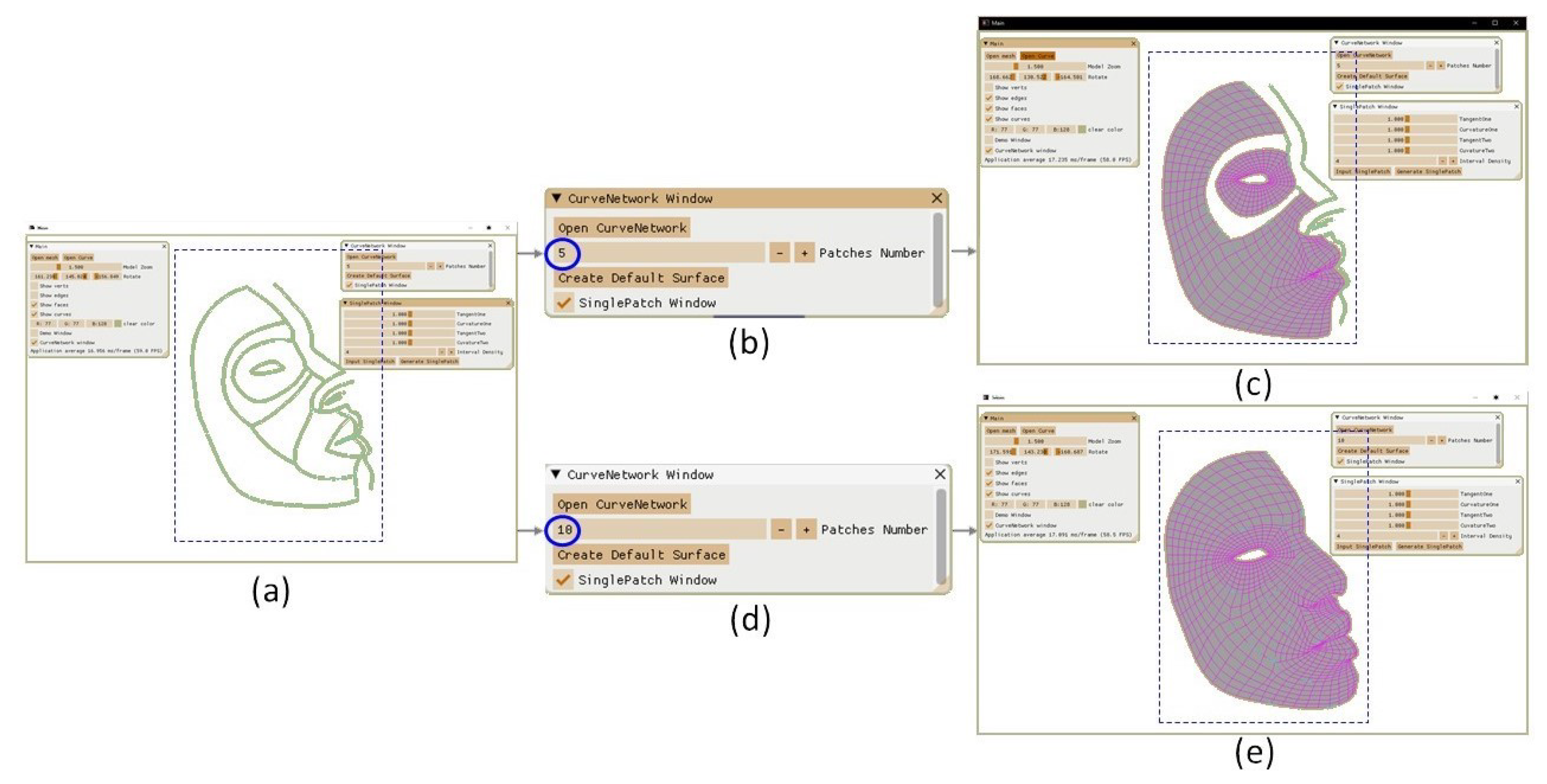
6.3. One Application of C2 Curve Network for Face Modeling
7. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Russo, M. Polygonal Modeling: Basic and Advanced Techniques; Jones & Bartlett Learning: Burlington, MA, USA, 2006. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Farin, G. Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Stam, J. Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 19–24 July 1998; ACM: New York, NY, USA, 1998; pp. 395–404. [Google Scholar]
- DeRose, T.; Kass, M.; Truong, T. Subdivision surfaces in character animation. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 19–24 July 1998; ACM: New York, NY, USA, 1998; pp. 85–94. [Google Scholar]
- Warren, J.; Weimer, H. Subdivision Methods for Geometric Design: A Constructive Approach; Morgan Kaufmann: Burlington, MA, USA, 2001. [Google Scholar]
- Cashman, T.J.; Augsdörfer, U.H.; Dodgson, N.A.; Sabin, M.A. NURBS with extraordinary points: high-degree, non-uniform, rational subdivision schemes. In ACM Transactions on Graphics (TOG); ACM: New York, NY, USA, 2009; Volume 28, p. 46. [Google Scholar]
- Várady, T.; Salvi, P.; Rockwood, A. Transfinite surface interpolation with interior control. Graph. Model. 2012, 74, 311–320. [Google Scholar] [CrossRef]
- Nealen, A.; Müller, M.; Keiser, R.; Boxerman, E.; Carlson, M. Physically Based Deformable Models in Computer Graphics. Computer Graphics Forum; Wiley: Hoboken, NJ, USA, 2006; Volume 25, pp. 809–836. [Google Scholar]
- Chaudhry, E.; Bian, S.; Ugail, H.; Jin, X.; You, L.; Zhang, J.J. Dynamic skin deformation using finite difference solutions for character animation. Comput. Graph. 2015, 46, 294–305. [Google Scholar] [CrossRef]
- You, L.; Yang, X.; Pachulski, M.; Zhang, J.J. Boundary Constrained Swept Surfaces for Modelling and Animation. Computer Graphics Forum; Wiley: Hoboken, NJ, USA, 2007; Volume 26, pp. 313–322. [Google Scholar]
- You, L.; Yang, X.; You, X.Y.; Jin, X.; Zhang, J.J. Shape manipulation using physically based wire deformations. Comput. Animat. Virtual Worlds 2010, 21, 297–309. [Google Scholar] [CrossRef]
- Chaudhry, E.; You, L.; Jin, X.; Yang, X.; Zhang, J.J. Shape modeling for animated characters using ordinary differential equations. Comput. Graph. 2013, 37, 638–644. [Google Scholar] [CrossRef]
- You, L.; Ugail, H.; Tang, B.; Jin, X.; You, X.Y.; Zhang, J.J. Blending using ODE swept surfaces with shape control and C1 continuity. Vis. Comput. 2014, 30, 625–636. [Google Scholar] [CrossRef]
- Li, Z.C. Boundary penalty finite element methods for blending surfaces, I basic theory. J. Comput. Math. 1998, 110, 457–480. [Google Scholar]
- Li, Z.C.; Chang, C.S. Boundary penalty finite element methods for blending surfaces, III. Superconvergence and stability and examples. J. Comput. Appl. Math. 1999, 110, 241–270. [Google Scholar] [CrossRef]
- Cheng, S.; Bloor, M.I.; Saia, A.; Wilson, M.J. Blending between quadric surfaces using partial differential equations. Adv. Des. Autom. 1990, 1, 257–263. [Google Scholar]
- Bloor, M.I.; Wilson, M.J. Representing PDE surfaces in terms of B-splines. Comput. Aided Des. 1990, 22, 324–331. [Google Scholar] [CrossRef]
- Bloor, I.M.; Wilson, M.J. Spectral approximations to PDE surfaces. Comput. Aided Des. 1996, 28, 145–152. [Google Scholar] [CrossRef]
- Bian, S.; Deng, Z.; Chaudhry, E.; You, L.; Yang, X.; Guo, L.; Ugail, H.; Jin, X.; Xiao, Z.; Zhang, J.J. Efficient and realistic character animation through analytical physics-based skin deformation. Graph. Models 2019, 104, 101035. [Google Scholar] [CrossRef]
- Paul, E.; Wallace, F.V.; Joseph, H.C. Facial Action Coding System. The Manual on CD ROM; A Human Face: Salt Lake City, UT, USA, 2002. [Google Scholar]
- Hamm, J.; Kohler, C.G.; Gur, R.C.; Verma, R. Automated facial action coding system for dynamic analysis of facial expressions in neuropsychiatric disorders. J. Neurosci. Methods 2011, 200, 237–256. [Google Scholar] [CrossRef] [PubMed]
- Freitas-Magalhães, A. The Face of Lies; Leya: Amadora, Portugal, 2013. [Google Scholar]

| Models | Male Face | Flower | Petal | Leaf | Dog | Plane |
|---|---|---|---|---|---|---|
| Polygon Verts | 4081 | 37,584 | 6594 | 1538 | 148,450 | 19,042 |
| Curve Variables | 1467 | 6462 | 1132 | 298 | 24,066 | 4526 |
| Data Size Comparison | 36% | 17% | 17% | 19% | 16% | 23% |
| Proportion of Data Compression | 64% | 83% | 83% | 81% | 84% | 77% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, S.; Maguire, G.; Kokke, W.; You, L.; Zhang, J.J. Efficient C2 Continuous Surface Creation Technique Based on Ordinary Differential Equation. Symmetry 2020, 12, 38. https://doi.org/10.3390/sym12010038
Bian S, Maguire G, Kokke W, You L, Zhang JJ. Efficient C2 Continuous Surface Creation Technique Based on Ordinary Differential Equation. Symmetry. 2020; 12(1):38. https://doi.org/10.3390/sym12010038
Chicago/Turabian StyleBian, Shaojun, Greg Maguire, Willem Kokke, Lihua You, and Jian J. Zhang. 2020. "Efficient C2 Continuous Surface Creation Technique Based on Ordinary Differential Equation" Symmetry 12, no. 1: 38. https://doi.org/10.3390/sym12010038
APA StyleBian, S., Maguire, G., Kokke, W., You, L., & Zhang, J. J. (2020). Efficient C2 Continuous Surface Creation Technique Based on Ordinary Differential Equation. Symmetry, 12(1), 38. https://doi.org/10.3390/sym12010038






