A Structured Table of Graphs with Symmetries and Other Special Properties
Abstract
1. Introduction
2. Criteria and Optimal Graphs
2.1. Criteria
2.1.1. Diameter and MPL of a Regular Graph
2.1.2. Bisection Bandwidth
2.1.3. Automorphism Group Size
2.2. Optimal Graphs
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barnes, G.; Brown, R.; Kato, M.; Kuck, D.; Slotnick, D.; Stokes, R. The ILLIAC IV Computer. IEEE Trans. Comput. 1968, C-17, 746–757. [Google Scholar] [CrossRef]
- Dally, W.J.; Seitz, C.L. The torus routing chip. Distrib. Comput. 1986, 1, 187–196. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M. Topological properties of hypercubes. IEEE Trans. Comput. 1988, 37, 867–872. [Google Scholar] [CrossRef]
- Tripathy, C.; Mahapatra, R.; Misra, R. Reliability analysis of hypercube multicomputers. Microelectron. Reliab. 1997, 37, 885–891. [Google Scholar] [CrossRef]
- Lai, P.L.; Hsu, H.C.; Tsai, C.H.; Stewart, I.A. A class of hierarchical graphs as topologies for interconnection networks. Theor. Comput. Sci. 2010, 411, 2912–2924. [Google Scholar] [CrossRef][Green Version]
- Guo, D.; Chen, T.; Li, D.; Liu, Y.; Liu, X.; Chen, G. BCN: Expansible network structures for data centers using hierarchical compound graphs. In Proceedings of the 2011 IEEE INFOCOM, Shanghai, China, 10–15 April 2011. [Google Scholar] [CrossRef]
- Jung, S.; Kim, S.; Kahng, B. Geometric fractal growth model for scale-free networks. Phys. Rev. E 2002, 65, 056101. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.L.; Feng, T.Y. On a Class of Multistage Interconnection Networks. IEEE Trans. Comput. C 1980, 29, 694–702. [Google Scholar] [CrossRef]
- Malluhi, Q.; Bayoumi, M. The hierarchical hypercube: a new interconnection topology for massively parallel systems. IEEE Trans. Parallel Distrib. Syst. 1994, 5, 17–30. [Google Scholar] [CrossRef]
- Hammack, R.; Imrich, W.; Klavzar, S. Handbook of Product Graphs (Discrete Mathematics and Its Applications); CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Deng, Y.; Guo, M.; Ramos, A.F.; Huang, X.; Xu, Z.; Liu, W. Optimal Low-Latency Network Topologies for Cluster Performance Enhancement. arXiv 2019, arXiv:1904.00513. [Google Scholar]
- Xu, Z.; Deng, Y. Optimal Routing for a Family of Scalable Interconnection Networks. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis (SC’19 Poster), Denver, CO, USA, 17–22 November 2019. [Google Scholar]
- Xu, Z.; Huang, X.; Jimenez, F.; Deng, Y. A New Record of Graph Enumeration Enabled by Parallel Processing. Mathematics 2019, 7, 1214. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Ruzzenenti, F.; Basosi, R. Complex Networks and Symmetry I: A Review. Symmetry 2010, 2, 1683–1709. [Google Scholar] [CrossRef]
- Garrido, A. Symmetry in Complex Networks. Symmetry 2011, 3, 1–15. [Google Scholar] [CrossRef]
- Conder, M. Marston Conder Web. Available online: https://www.math.auckland.ac.nz/~conder/ (accessed on 6 October 2019).
- Balasubramanian, K. Computational Techniques for the Automorphism Groups of Graphs. J. Chem. Inf. Model. 1994, 34, 621–626. [Google Scholar] [CrossRef]
- Razinger, M.; Balasubramanian, K.; Munk, M.E. Graph automorphism perception algorithms in computer-enhanced structure elucidation. J. Chem. Inf. Model. 1993, 33, 197–201. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, K. Computational Enumeration of Colorings of Hyperplanes of Hypercubes for all Irreducible Representations and Applications. J. Math. Sci. Model. 2018, 1, 158–180. [Google Scholar] [CrossRef]
- Bapat, R.B. Graphs and Matrices; Springer: London, UK, 2014. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Singleton, R.R. On Moore Graphs with Diameters 2 and 3. In Selected Papers of Alan J Hoffman; World Scientific: Singapore, 2003; pp. 377–384. [Google Scholar] [CrossRef]
- Cerf, V.G.; Cowan, D.D.; Mullin, R.C.; Stanton, R.G. A lower bound on the average shortest path length in regular graphs. Networks 1974, 4, 335–342. [Google Scholar] [CrossRef]
- Dally, W.; Towles, B. Principles and Practices of Interconnection Networks; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2003. [Google Scholar]
- MacArthur, B.D.; Sánchez-García, R.J.; Anderson, J.W. Symmetry in complex networks. Discret. Appl. Math. 2008, 156, 3525–3531. [Google Scholar] [CrossRef]
- Sanders, P.; Schulz, C. Think locally, act globally: Highly balanced graph partitioning. In International Symposium on Experimental Algorithms; Springer: Berlin, Germany, 2013; pp. 164–175. [Google Scholar]
- The Sage Developers. SageMath, The Sage Mathematics Software System (Version 8.8). Available online: https://www.sagemath.org (accessed on 6 October 2019).
- Tange, O. GNU Parallel 2018; Lulu.com: Morrisville, NC, USA, 2018. [Google Scholar]
- Dummit, D.S.; Foote, R.M. Abstract Algebra; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- The GAP Group. GAP—Groups, Algorithms, and Programming, Version 4.10.2. 2019. Available online: https://www.gap-system.org (accessed on 6 October 2019).
- Dokchitser, T. GroupNames. Available online: https://people.maths.bris.ac.uk/~matyd/GroupNames/index.html (accessed on 6 October 2019).
- Wolfram Research. “GraphData” from Wolfram Mathematica. Available online: https://reference.wolfram.com/language/ref/GraphData.html (accessed on 6 October 2019).
- Pegg, E., Jr.; Exoo, G. Crossing number graphs. Math. J. 2009, 11, 161–170. [Google Scholar] [CrossRef]
- Exoo, G.; Jajcay, R. Dynamic cage survey. Electron. J. Combin 2008, 15, 4. [Google Scholar]
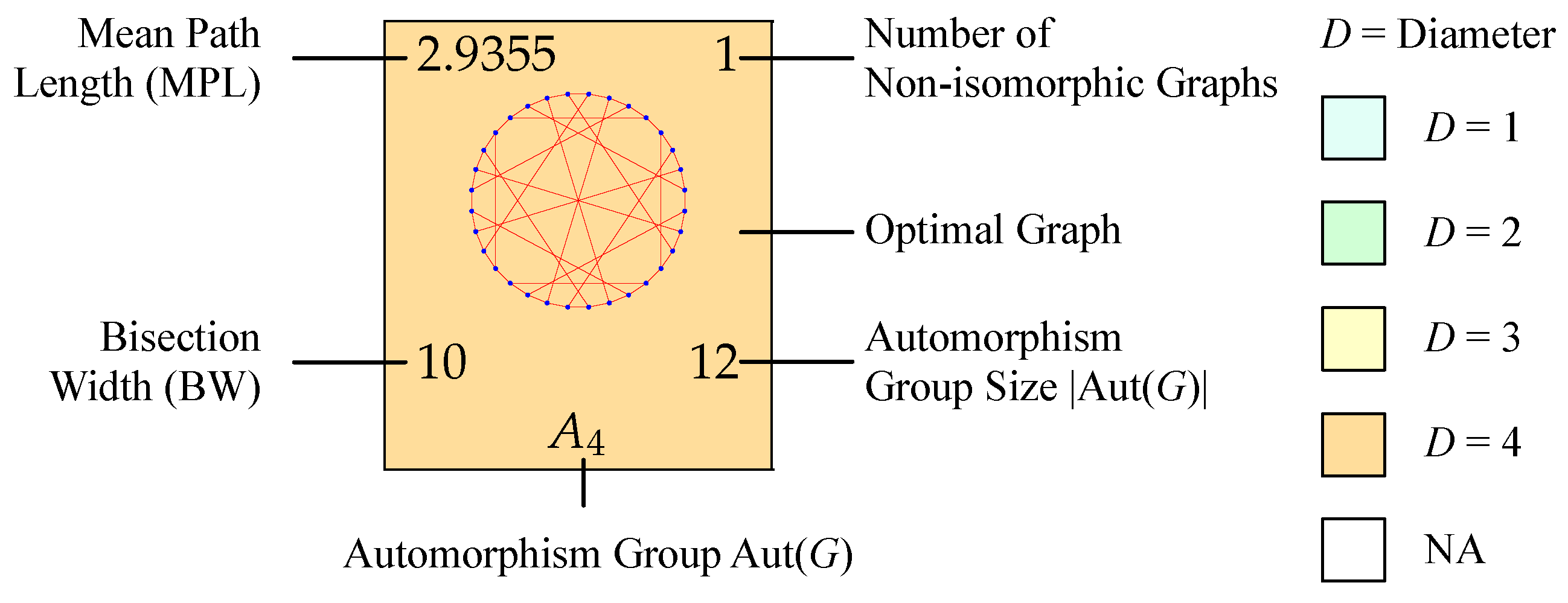
| Symbol | Description |
|---|---|
| Alternating group on a set of length n | |
| Cyclic group of order n | |
| Dihedral group of order | |
| General linear group of degree n over finite field | |
| Projective general linear group obtained from | |
| Symmetric group on a set of length n | |
| Automorphism group of group H | |
| Holomorph of group H | |
| Direct product of groups K and H | |
| Direct product of m copies of group H | |
| Semidirect product of groups K and H (In this manuscript, H acting faithfully on K) | |
| Wreath product of groups K and H, H acting on (n is ommited when or ) |
| k | 3 | 4 | 5 | 6 | 7 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | |||||||||||
| 4 | 1.0000 | 1 | |||||||||
 | |||||||||||
| 4 | 24 | ||||||||||
| 5 | 1.0000 | 1 | |||||||||
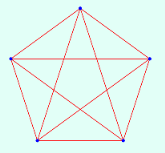 | |||||||||||
| 6 | 120 | ||||||||||
| 6 | 1.4000 | 1 | 1.2000 | 1 | 1.0000 | 1 | |||||
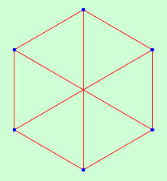 |  | 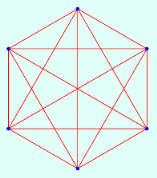 | |||||||||
| 5 | 72 | 6 | 48 | 9 | 720 | ||||||
| 7 | 1.3333 | 1 | 1.0000 | 1 | |||||||
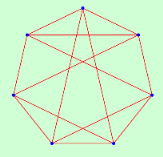 |  | ||||||||||
| 6 | 48 | 12 | 5040 | ||||||||
| 8 | 1.5714 | 1 | 1.4286 | 1 | 1.2857 | 1 | 1.1429 | 1 | 1.0000 | 1 | |
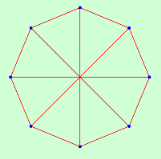 |  | 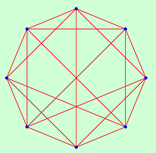 | 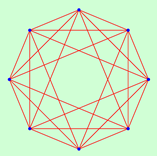 |  | |||||||
| 4 | 16 | 8 | 1152 | 10 | 60 | 12 | 384 | 16 | 40320 | ||
| 9 | 1.5000 | 1 | 1.2500 | 1 | |||||||
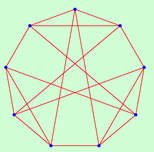 |  | ||||||||||
| 8 | 72 | 14 | 1296 | ||||||||
| 10 | 1.6667 | 1 | 1.5556 | 1 | 1.4444 | 1 | 1.3333 | 1 | 1.2222 | 1 | |
 | 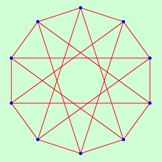 | 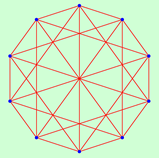 | 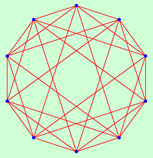 |  | |||||||
| 5 | 120 | 8 | 320 | 13 | 28800 | 14 | 288 | 17 | 576 | ||
| 11 | 1.6000 | 1 | 1.4000 | 1 | |||||||
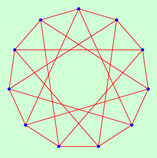 |  | ||||||||||
| 8 | 22 | 16 | 5760 | ||||||||
| 12 | 1.9091 | 1 | 1.6364 | 1 | 1.5455 | 1 | 1.4545 | 1 | 1.3636 | 1 | |
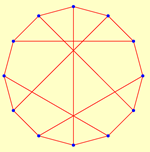 | 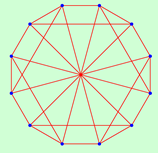 | 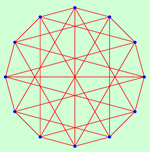 |  |  | |||||||
| 6 | 18 | 10 | 48 | 12 | 576 | 18 | 1036800 | 20 | 4608 | ||
| k | 3 | k | 4 | ||||
|---|---|---|---|---|---|---|---|
| N | N | ||||||
| 14 | 2.0769 | 1 | 13 | 1.6667 | 1 | ||
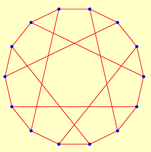 | 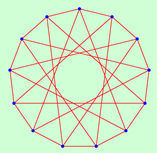 | ||||||
| 7 | 336 | 10 | 52 | ||||
| 16 | 2.2000 | 2 | 14 | 1.6923 | 1 | ||
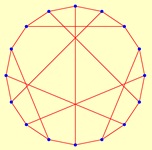 |  | ||||||
| 6 | 6 | 10 | 96 | ||||
| 18 | 2.2941 | 1 | 15 | 1.7143 | 1 | ||
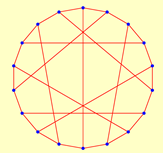 | 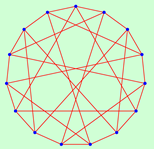 | ||||||
| 7 | 8 | 10 | 12 | ||||
| 20 | 2.3684 | 1 | 16 | 1.7500* | 1 | ||
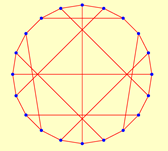 | 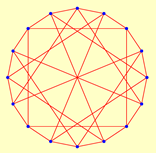 | ||||||
| 8 | 20 | 12 | 32 | ||||
| 22 | 2.4805* | 1 | 17 | 1.8162* | 1 | ||
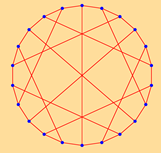 | 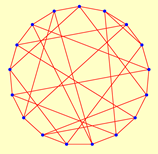 | ||||||
| 9 | 16 | 12 | 36 | ||||
| 24 | 2.5652 | 1 | 18 | 1.8627* | 1 | ||
 | 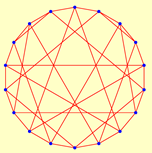 | ||||||
| 8 | 32 | 12 | 12 | ||||
| 26 | 2.6800 | 1 | 19 | 1.8889 | 1 | ||
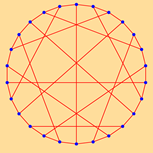 | 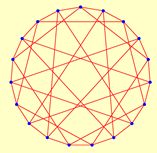 | ||||||
| 9 | 52 | 12 | 24 | ||||
| 28 | 2.7778 | 1 | 20 | 1.9474 | 1 | ||
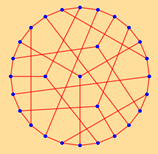 | 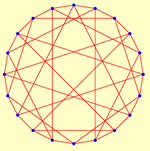 | ||||||
| 10 | 336 | 14 | 96 | ||||
| 30 | 2.8621 | 1 | 21 | 2.0000 | 2 | ||
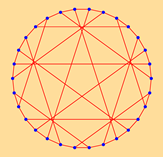 | 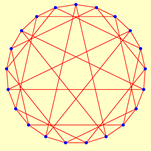 | ||||||
| 9 | 1440 | 14 | 14 | ||||
| 32 | 2.9355 | 1 | 32 | 2.3548 | 3 | ||
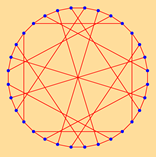 | 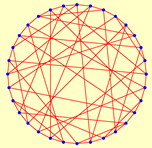 | ||||||
| 10 | 12 | 18 | 3 | ||||
| 2.2000 | 2 | 2.0000 | 2 | 2.3548 | 3 | 2.3548 | 3 |
 | 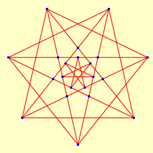 |  | 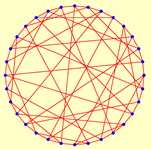 | ||||
| 6 | 6 | 14 | 14 | 18 | 3 | 18 | 3 |
| Semidirect Product Group | Finite Presentation | |
|---|---|---|
| (26,3) | ||
| (13,4) | ||
| (20,4) | ||
| k | N | Named Graphs |
| 4 | Tetrahedral graph; Complete; Distance-transitive; Strongly regular; Cayley; (3,3)-Cage; Circulant; Planar; Smallest cubic crossing number-0 | |
| 6 | Thomsen graph; Complete bipartite; Distance-transitive; Strongly regular; Cayley; (3,4)-Cage; Circulant; Smallest cubic crossing number-1 | |
| 8 | Wagner graph; Vertex-transitive; Cayley; Circulant; tripartite | |
| 10 | Petersen graph; Nonhamiltonian; Distance-transitive; Strongly regular; (3,5)-Cage; Smallest cubic crossing number-2; tripartite | |
| 3 | 14 | Heawood graph; Bipartite; Distance-transitive; Cayley; (3,6)-Cage; Smallest cubic crossing number-3 |
| 22 | Smallest cubic crossing number-7; tripartite | |
| 24 | McGee graph; (3,7)-Cage; Smallest cubic crossing number-8; tripartite | |
| 26 | Generalized Petersen-(13,5); Vertex-transitive; Smallest cubic crossing number-9; tripartite | |
| 28 | Coxeter graph; Nonhamiltonian; Distance-transitive; Smallest cubic crossing number-11; tripartite | |
| 30 | Levi graph; Bipartite; Distance-transitive; (3,8)-Cage; Smallest cubic crossing number-13 (to be proved) | |
| 5 | Pentatope graph; Complete; Distance-transitive; Strongly regular; Cayley; (4,3)-Cage; Circulant | |
| 6 | Octahedral graph; Complete tripartite; Distance-transitive; Strongly regular; Cayley; Planar; Circulant | |
| 8 | Complete bipartite; Distance-transitive; Strongly regular; Cayley; (4,4)-Cage; Circulant | |
| 4 | 9 | Generalized quadrangle-(2,1); (2, 3)-Hamming graph; (3, 3)-rook graph; 9-Paley graph; Distance-transitive; Strongly regular; Cayley; tripartite |
| 10 | Arc-transitive; Cayley; Circulant; tripartite | |
| 11 | 4-Andrásfai graph; Vertex-transitive; Cayley; Circulant; tripartite | |
| 12 | Vertex-transitive; Cayley; Circulant; tripartite | |
| 13 | 13-Cyclotomic graph; Arc-transitive; Cayley; Circulant; 4-partite | |
| 19 | Robertson graph; (4,5)-cage; tripartite | |
| 21 | Brinkmann graph; 4-partite (Table 4) | |
| 6 | Complete; Distance-transitive; Strongly regular; Cayley; (5,3)-Cage; Circulant | |
| 5 | 8 | (5,3)-Cone graph; 4-partite |
| 10 | Complete bipartite; Distance-transitive; Strongly regular; Cayley; (5,4)-Cage; Circulant | |
| 7 | Complete; Distance-transitive; Strongly regular; Cayley; (6,3)-Cage; Circulant | |
| 8 | 16-Cell; Complete 4-partite; Distance-transitive; Strongly regular; Cayley; Circulant | |
| 6 | 9 | Complete tripartite; Distance-transitive; Strongly regular; Cayley; Circulant |
| 10 | (6,4)-Cone graph; tripartite | |
| 12 | Complete bipartite; Distance-transitive; Strongly regular; Cayley; (6,4)-Cage; Circulant | |
| 7 | 8 | Complete; Distance-transitive; Strongly regular; Cayley; (7,3)-Cage; Circulant |
| 12 | Vertex-transitive; Cayley; Circulant; 4-partite |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Huang, X.; Xu, Z.; Deng, Y. A Structured Table of Graphs with Symmetries and Other Special Properties. Symmetry 2020, 12, 2. https://doi.org/10.3390/sym12010002
Zhang Y, Huang X, Xu Z, Deng Y. A Structured Table of Graphs with Symmetries and Other Special Properties. Symmetry. 2020; 12(1):2. https://doi.org/10.3390/sym12010002
Chicago/Turabian StyleZhang, Yidan, Xiaolong Huang, Zhipeng Xu, and Yuefan Deng. 2020. "A Structured Table of Graphs with Symmetries and Other Special Properties" Symmetry 12, no. 1: 2. https://doi.org/10.3390/sym12010002
APA StyleZhang, Y., Huang, X., Xu, Z., & Deng, Y. (2020). A Structured Table of Graphs with Symmetries and Other Special Properties. Symmetry, 12(1), 2. https://doi.org/10.3390/sym12010002






