Abstract
In a real-time system, a series of jobs invoked by each task should finish its execution before its deadline, and EDF (Earliest Deadline First) is one of the most popular scheduling algorithms to meet such timing constraints of a set of given tasks. However, EDF is known to be ineffective in meeting timing constraints for non-preemptive tasks (which disallow any preemption) when the system does not know the future job release patterns of the tasks. In this paper, we develop a scheduling algorithm for a real-time system with a symmetry multiprocessor platform, which requires only limited information about the future job release patterns of a set of non-preemptive tasks, called LCEDF. We then derive its schedulability analysis that provides timing guarantees of the non-preemptive task set on a symmetry multiprocessor platform. Via simulations, we demonstrate the proposed schedulability analysis for LCEDF significantly improves the schedulability performance in meeting timing constraints of a set of non-preemptive tasks up to 20.16%, compared to vanilla non-preemptive EDF.
1. Introduction
Real-time systems have been widely deployed as emerging systems (e.g., autonomous vehicles) need stringent timing requirements [1,2]. One of the most important issues for real-time systems is to design scheduling algorithms that are favorable to satisfying timing constraints of all jobs invoked by a given set of tasks and to develop their schedulability analysis that gives offline guarantees on satisfaction of the timing constraints. Many studies have aimed at addressing the issue, and EDF (Earliest Deadline First) is one of the most popular and effective scheduling algorithms [3].
However, EDF is known to have poor performance in meeting job deadlines of non-preemptive tasks (which disallow any preemption) when the system does not know the future release pattern of jobs invoked by the tasks [4]. This is because, vanilla non-preemptive EDF has inherent limitations in meeting deadlines of non-preemptive tasks without information for the future job release patterns. For example, suppose that there are two jobs, whose release time is and deadline is , and whose release time is and deadline is ; also, the execution time of and are 3 and 1, respectively. Under vanilla non-preemptive EDF, if , executes for , which yields a deadline miss for . One may argue that if delays its execution until finishes its execution, we can avoid the deadline of . However, this prevents a deadline miss only when we know the value of x in advance. That is, if delays its execution until finishes its execution when x is larger than 7 (without knowing x in advance), cannot finish its execution until , yielding its deadline miss. Therefore, without knowing x, there exists a situation where vanilla non-preemptive EDF yields a deadline miss.
To address the inherent limitation of vanilla non-preemptive EDF, Ekelin developed a new EDF scheduling algorithm, called CEDF (Clairvoyant non-preemptive EDF) [5]. The assumption of this algorithm is that the system knows the future release patterns of all jobs. Using the information for the future job release patterns, CEDF is successfully able to schedule many non-preemptive task sets without any job deadline miss, which is difficult for vanilla non-preemptive EDF. However, the information is not available for many real-time systems; this necessitates a new non-preemptive scheduling algorithm, which requires only limited information for the future job release patterns but yields better performance than vanilla non-preemptive EDF in terms of meeting deadlines of all jobs invoked by a set of given non-preemptive tasks.
In this paper, we develop a scheduling algorithm for a real-time system with a symmetry multiprocessor platform, which requires limited information about the future job release patterns of a set of non-preemptive tasks, called LCEDF. While each task invokes a series of jobs, we assume to know the release time of each task’s the next job only (to be detailed in Section 3). LCEDF classifies a given set of non-preemptive tasks into two: and . If a task cannot be schedulable (i.e., cannot meet its jobs deadlines) without knowing the future job release patterns of tasks (to be detailed in Section 4), the task belongs to the former; otherwise, the task belongs to the latter. Then, we develop a processor idling mechanism for jobs of tasks in when the execution of jobs of tasks in results in a deadline miss of tasks in . We explain details of LCEDF in Section 4.
We next derive a schedulability analysis for LCEDF. Based on the schedulability analysis for vanilla non-preemptive EDF, we investigate the effect of the processor idling on tasks in and those in in terms of meeting their job deadlines. According to the scheduling policy of LCEDF, the interference from other tasks on a task in decreases, compared to vanilla non-preemptive EDF, while that in increases. By carefully calculating how much the interference is decreased and increases, we complete the schedulability analysis for LCEDF, to be detailed in Section 5.
To evaluate the schedulability performance by LCEDF, we generate a number of task sets, and measure how many task sets are schedulable by LCEDF as opposed to vanilla non-preemptive EDF. The simulation results show that the LCEDF schedulability analysis finds a number of additional schedulable task sets, which cannot be deemed schedulable by the vanilla EDF schedulability analysis; the amount of improvement in terms of the number of schedulable task sets by LCEDF is up to 20.16%.
In summary, this paper makes the following contributions.
- We raise a problem for developing a non-preemptive scheduling algorithm that requires only limited information for the future job release patterns of a set of non-preemptive tasks.
- We develop a new non-preemptive scheduling algorithm, LCEDF, which enforces processor idling.
- We derive a schedulability analysis for LCEDF, by addressing the properties of LCEDF.
- We demonstrate the effectiveness of LCEDF in terms of schedulability performance, via simulations.
The rest of this paper is organized as follows. Section 2 discusses literature review. Section 3 explains the system model, assumptions and notations. Section 4 develops the LCEDF scheduling algorithm, and Section 5 derives its schedulability analysis. Section 6 evaluates the schedulability performance of LCEDF, and Section 7 discusses and concludes the paper.
2. Literature Review
2.1. Clairvoyant Scheduling
The most relevant paper to our study is the study proposed by Ekelin [5]. In the paper, the assumption is that the system knows release patterns of all future jobs. Using the information, the study predicts job deadline misses without processor idling, and therefore calculates when we should idle the processor to avoid job deadline misses. The paper is different from our study in that the paper assumes clairvoyance (while ours assumes limited clairvoyance), and the paper works with a uniprocessor platform only (while ours works with a multiprocessor platform as well).
Note that there are several studies which deal with scheduling for the job scheduling area [6,7]. However, their system model is different from ours and the study by Ekelin [5], in that their system model consists of (Job, Constraint, Query), which cannot be applied to the system model of our study.
2.2. Schedulability Analysis for Vanilla EDF
There have been several attempts to develop schedulability analyses for vanilla (global non-preemptive) EDF on a multiprocessor platform. After Baruah initiated the analysis [8], two different schedulability analyses were presented in 2008 [9,10]. Also, Lee et al. proposed a new schedulability analysis [11,12] using the well-known schedulability analysis technique for preemptive scheduling algorithms, called RTA (Response Time Analysis). This analysis becomes a basis for not only the schedulability analysis of LCEDF as explained in Section 5, but also the schedulability analysis of other non-preemptive scheduling algorithm, e.g., non-preemptive fixed-priority scheduling [12,13]. However, there has been no study that develops a schedulability analysis for scheduling algorithms that exploit clairvoyance or limited clairvoyance. This is because the study proposed by Ekelin [5] does not need any schedulability analysis as the algorithm knows every future schedule, and there has been no attempt to develop scheduling algorithms utilizing limited clairvoyance.
3. System Model, Assumptions and Notations
We target a set of sporadic real-time tasks [14], executed on a multiprocessor platform consisting of m symmetric processors. A task is specified as where is the minimum separation (or the period), is the worst-case execution time, and is the relative deadline. A task invokes a series of jobs, and the job of is denoted by . Let , , and denote the release time of , the execution time of (which is the same as ), and the absolute deadline of (which is the same as ), respectively. The release time between two consecutive jobs of (e.g., and ) should be no smaller than . Also, once is released, it should finish its execution for up to () time units no later than (). We summarize notations for task and job parameters in Table 1. In this paper, we use a critical time instant of a job , which is . The physical meaning of is as follows: if the job does not start its execution until , the job misses its deadline. A job cannot be executed more than one processor at the same time. We assume a quantum-based time unit; without loss of generality, the quantum length equals 1. Therefore, all task and job parameters are natural numbers.

Table 1.
Notations for task and job parameters.
We assume limited clairvoyance for future job release patterns. That is, let future jobs at t imply jobs whose execution has not been finished until t, and then at t we assume that for every we know the release time of the future job whose release time is the earliest among all future jobs of at t.
In this paper, we consider global non-preemptive scheduling. Under global scheduling, each task (as well as each job) can be executed in any processor, and under non-preemptive scheduling, a job does not pause its execution once it starts to execute. In the rest of this paper, we omit the term “global non-preemptive”; for example, EDF refers global non-preemptive EDF. As notations, let LHS and RHS denote the left-hand side and the right-hand side, respectively.
4. Methodology: Design of the LCEDF Scheduling Algorithm
In this section, we first discuss limitation of vanilla EDF in meeting non-preemptive tasks’ job deadlines without the information about the future job release patterns of tasks. We then explain design principles for LCEDF, and finally develop the LCEDF scheduling algorithm.
4.1. Limitation of Vanilla EDF
In this subsection, we discuss limitation of vanilla EDF. To this end, we first explain the scheduling algorithm of vanilla (global non-preemptive) EDF. Vanilla EDF manages a ready queue, in which jobs are sorted such that a job with an earlier deadline has a higher priority. Whenever there exists an unoccupied processor, the highest-priority job in the ready queue starts its execution on the processor; once a job starts its execution, the job cannot be preempted by any other job until the job finishes its execution.
As many studies pointed out [5], non-preemptive EDF is not effective in meeting job deadlines, if the information about the future job release patterns is not available (i.e., the system is non-clairvoyant). The following example demonstrates such ineffectiveness of EDF in meeting job deadlines.
Example 1.
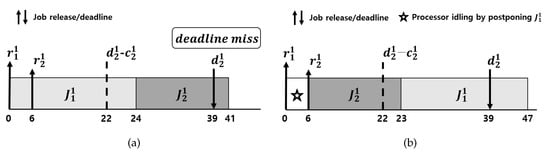
Consider a task set τ with the following two tasks is executed on a uniprocessor platform: , , . Consider the following scenario: (i) the interval of interest is ; and (ii) is released at and is released at . We show the schedule under vanilla EDF. At , vanilla EDF schedules , because any job of is not released at ; then, occupies the processor . Suppose that is released at ; then, misses its deadline without having any chance to compete for an unoccupied processor until as shown in Figure 1a. What if we know at that will be released at ? Then, by idling the processor in , we can make and schedulable as shown in Figure 1b. However, without the information of the future release time of , we cannot idle the processor. This is because, if is not released until , eventually misses its deadline. Note that the task set is schedulable by LCEDF, to be presented in Example 3 in Section 4.3.

Figure 1.
Schedule of of and of . (a) Schedule by vanilla EDF; (b) Schedule by processor idling.
The similar phenomenon occurs on a symmetry multiprocessor platform, as demonstrated in the following example.
Example 2.
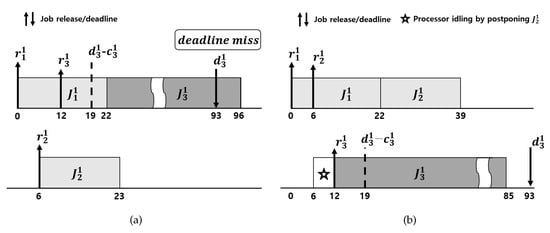
Consider a task set τ with the following three tasks on a two-processor platform: , and . Consider the following scenario: (i) the interval of interest is ; (ii) is released at , and and is released at and , respectively. We show the schedule under vanilla EDF. At , vanilla EDF schedules , because and are not released at ; then, occupies the processor . Suppose that and are released at and , respectively; then, misses its deadline without having any chance to compete for unoccupied processors until as shown in Figure 2a. If we know that and will be released at and , respectively, we can make schedulable by idling a processor in as shown in Figure 2b. However, without the information of the future release time of , we cannot idle the processor; this is because, if is not released until , eventually misses its deadline. Note that the task set is schedulable by LCEDF, to be presented in Example 4 in Section 4.3.

Figure 2.
Schedule of of , of , and of . (a) Schedule by vanilla EDF; (b) Schedule by processor idling.
As shown in Examples 1 and 2, there may exist a release pattern that yields a deadline miss of a job of of interest under vanilla EDF, if of is smaller than the worst-case execution time of some other tasks (i.e., ). The following observation records this property formally. (Observation 1 is already implicitly incorporated into the existing schedulability analysis for vanilla EDF [11,12].)
Observation 1.
Suppose that we do not know any future job release pattern. Then, there exists a release pattern that yields a deadline miss of a job of of interest, if there exist at least m tasks whose worst-case execution time (i.e., ) is larger than .
The observation holds as follows. Suppose that jobs of m tasks whose worst-case execution time is larger than are released at . We consider the following situation. Suppose that the m jobs start their execution at . In this case, if a job of is released at , the job of misses its deadline. In addition, if any of the m jobs do not start its execution forever, the jobs eventually miss their deadlines. Therefore, the observation holds.
The observation is important because if there exists such a task , the task set including is unschedulable by vanilla EDF. Therefore, we design LCEDF so as to carefully handle such a task in Observation 1, which is detailed in the next subsection.
4.2. Design Principle for LCEDF
Motivated by Observation 1, we would like to avoid job deadline misses of tasks which belong to in Observation 1, by using the limited information about the future job release patterns. To this end, we classify tasks offline as follows:
- , a set of tasks which satisfy that there exist at least m other tasks whose execution time (i.e., ) is larger than , and
- , a set of tasks which do not belong to .
We would like to avoid the deadline miss situations shown in Figure 1a and Figure 2a, in which a job of a task in misses its deadline without having any chance to compete for an unoccupied processor until , which is the last time instant each job should start its execution to avoid its deadline miss. As we explained in Figure 1b and Figure 2b, the situations can be avoided using knowledge of future job release patterns. In this paper, we aim at developing a systematic way to avoid such deadline miss situations with only a limited information for future job release patterns (explained in Section 3). To this end, we manage a critical queue CQ, in which jobs of tasks in are sorted by their , which is the last time instant each job should start its execution to avoid its deadline miss. Whenever a job of a task in is able to start its execution, we check whether executing the job of a task in will jeopardize timely execution of jobs in CQ by experiencing the deadline miss situations such as Figure 1a and Figure 2a. If so, the job of a task in will be postponed by idling a processor where the job is supposed to execute under vanilla EDF. Note that although we assume to know the next job’s release time of all tasks in Section 3, we actually need to know the next job’s release time of tasks in only.
As we mentioned, the LCEDF algorithm avoids the deadline miss situations of jobs of tasks in shown in Figure 1a and Figure 2a, by postponing jobs of tasks in . Then, the main problem is when jobs of tasks in should postpone their executions for timely execution of jobs of tasks in . The more postponing yields the higher and lower chance for timely execution of jobs of tasks in and , respectively; on the other hand, the less postponing results in the lower and higher chance for timely execution of jobs of tasks in and , respectively. Therefore, we need to minimize postponing the execution of jobs of tasks in while guaranteeing timely execution of jobs of tasks in . We may classify the situations where a job of in has and does not have at least a chance to compete for unoccupied processors until , into four situations as shown in Figure 3.
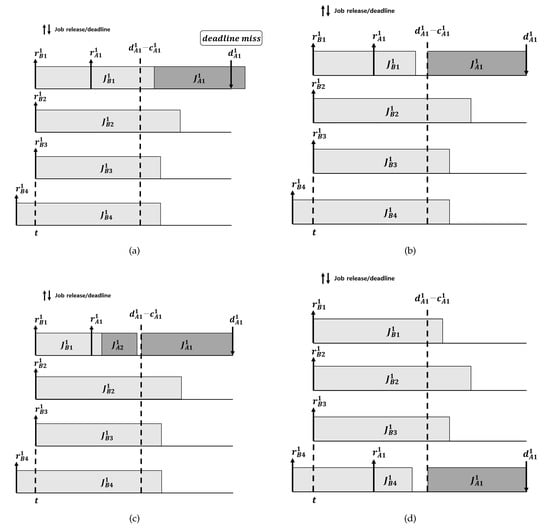
Figure 3.
Four cases where a job of has and does not have at least a chance to compete for unoccupied processors until . (a) The case where the timely execution of of cannot be guaranteed at t; (b) The case where the timely execution of of is guaranteed at t, due to a job of a task in which starts its execution at t but finishes its execution until ; (c) The case where the timely execution of of is guaranteed at t, due to a job of a task in which starts its execution at t but finishes its execution until ; (d) The case where the timely execution of of is guaranteed at t, due to a job of a task in which starts its execution before t but finishes it execution until .
We now discuss the four situations at t in Figure 3. Suppose that at t, there are three unoccupied processors out of the four processors in the system. And, three jobs (, and ) of tasks belonging to start their executions at t, while one job () of a task belonging to keeps its execution started before t. Now we are interested in the timely execution of of a task in . If all the four jobs (i.e., , , and ) finish their execution after , misses its deadline without having any chance to compete for unoccupied processors, as shown in Figure 3a. However, if at least one job among the three jobs (, and ) which start its execution at t finish their execution no later than , then does not miss its deadline as shown in Figure 3b. Similarly, although there is another job of a task in , does not miss its deadline as long as finishes its execution before , which is shown in Figure 3c. We have another case where does not miss its deadline; that is the case where the job of which keeps its execution started before t finishes its execution before , as shown in Figure 3d.
Therefore, if the current situation does not belong to one of situations illustrated in Figure 3b–d, we judge that there exists a job deadline miss. Once we judge such a deadline-miss situation, we choose the lowest-priority job among the jobs of tasks in which is supposed to start their execution at t, and avoid the lowest-priority job’s execution, by idling a processor intentionally.
4.3. Algorithm Details and Examples
Based on the design principle explained in Section 4.2, we detail the LCEDF algorithm using pseudo code and examples in this subsection.
As shown in Algorithm 1, the input components of LCEDF at t are the ready queue RQ, the critical queue CQ, the number of unoccupied processors , and the running job set RJ. Here, RQ is a set of ready jobs at t, and CQ is a set of jobs which will be released after t, invoked by .
| Algorithm 1 The LCEDF algorithm |
Input: the ready queueRQ, the critical queueCQ, the number of unoccupied processors , and the running job setRJ, at t
|
Step 1 in Algorithm 1 assigns jobs of tasks in belonging to RQ, to unoccupied processors. Since we postpone the execution of jobs of tasks in in order for timely execution of jobs of tasks in , the highest-priority jobs of tasks in belonging to RQ can be executed, which is the same as that under vanilla EDF. To this end, we first find jobs of tasks in belonging to RQ, whose execution is started at t in unoccupied processors (Lines 2–3). Such a job starts its execution and it removed from RQ (Line 4). Also, whenever a job starts its execution on an unoccupied processor, we decrease the number of unoccupied processors by 1 (Line 4). Then, we update the release information of a task which invokes the job starting its execution (Line 5).
In Step 1 we start the execution of higher-priority jobs of tasks in belonging to RQ, and therefore we are ready to start the execution of higher-priority jobs of tasks in belonging to RQ in the remaining unoccupied processors. In Step 2, we decide whether each job of a task in belonging to RQ starts or postpones its execution, according to whether it is possible to guarantee the timely execution of jobs of tasks in belonging to CQ. First, we investigate whether it is possible to guarantee the schedulability of each job of tasks in belonging to CQ (Line 9). If the number of jobs in RQ is strictly smaller than , we can assign an unoccupied processor to even though all jobs in RQ start their execution in unoccupied processors. Since we reserve an unoccupied processors for , we decrease the number of unoccupied processors by 1; then continue the for statement (Lines 10–11). If there is no more unoccupied processor, we stop this process because we cannot start any job execution (Lines 13–15). We set IsFeasible as CASE-0 (Line 16), and investigate whether the current situation belongs one of the three cases in Figure 3b–d where the timely execution of a job of a task in is guaranteed; based on the cases, we change IsFeasible to either CASE-1, CASE-2 or CASE-3 (Lines 17–36).
The for statement in Lines 17–22 aims at checking whether execution of the highest-priority jobs in RQ compromises the schedulability of any job of tasks in in CQ. We assume to assign the highest-priority job of a task in to an unoccupied processor (Line 17). If the finishing time of the job’s execution (i.e., ) is no later than that is the last instant at which in CQ starts its execution without its deadline miss, we set IsFeasible as Case-1 (Line 19), which corresponds to Figure 3b.
The for statements respectively in Lines 24–29 and Lines 30–35 are performed only when IsFeasible is equal to Case-0, which means the timely execution of the job in CQ is not guaranteed yet. In the for statement in Lines 24–29, we check the finishing time of a job in CQ (i.e., ) is no later than , which corresponds to Figure 3c; since cannot start its execution until t because is later than t, we calculate the earliest finishing time of the job by (Line 25). If so, we set IsFeasible as Case-2 (Line 26). In the for statement Lines 30–35, we check the finishing time of a job in RJ which starts its execution before t (i.e., ) is no later than , which corresponds to Figure 3d, where denotes the remaining execution time of at t; this is because, starts its execution before t (Line 31). If so, we set IsFeasible as Case-3 (Line 32).
In Lines 37–43, if IsFeasible is set to Case-1, we remove the highest-priority job in RQ that satisfies and start to execute the job; also, we decrease the number of unoccupied processors by 1 (Line 38). If IsFeasible is set to Case-2 or Case-3, we remove the highest-priority job in RQ and start to execute the job; also, we decrease the number of unoccupied processors by 1 (Line 40). Otherwise (meaning that IsFeasible equals to Case-0), we just decrease the number of unoccupied processors by 1, meaning that we postpone a job of a task in belonging to RQ (Line 42).
In Steps 1 and 2, we already guarantee the timely execution of jobs of tasks belonging to in CQ, meaning that the remaining unoccupied processors can serve for jobs of tasks in in RQ. Therefore, in Step 3 we start to execute highest-priority jobs in RQ (Lines 46–48).
In the following examples, we show that the task sets associated with the processor platforms in Examples 1 and 2 can be schedulable by the LCEDF algorithms.
Example 3.
Consider the task set with the processor platform shown in Example 1; that is, and are scheduled on a uniprocessor platform. We first categorize each task into or . When we calculate of , we get 17; since there is one task whose execution time is larger than 17 (which is ), belongs to . Similarly, of is 79, which is no smaller than ; therefore, belongs to .
Consider the following scenario which is the same as that of Example 1: (i) the interval of interest is ; and (ii) is released at and is released at . Since we categorized as , we know that at , will release at . At , there is only in the ready queue; according to Step 2 we examine if there is an unoccupied processor for in the critical queue to be executed. This can be done by checking resulting , which is wrong. We conclude that there is no unoccupied processor for to be executed after . Hence we postpone and execute at ; this yields that the task set is schedulable by LCEDF.
Example 4.
Consider the task set with the processor platform shown in Example 2; that is, , , and are scheduled on a two-processor platform. We first categorize each task into or . If we calculate of , we get 8; since there are two tasks whose execution time is larger than 8 (which is and ), belongs to . Similarly, and belong to .
Consider the following scenario which is the same as that of Example 2: (i) the interval of interest is ; and (ii) is released at , and and is released at and , respectively. Since we categorized as , we know that at , will release at . At , there is only in the ready queue; according to Step 2 we examine if there is an unoccupied processor for in the critical queue to be executed. Since there are two unoccupied processors and there is only one job in the ready queue, we do not postpone the execution of . At the , there is only in the ready queue; according to Step 2 we examine if there is an unoccupied processor for in the critical queue to be executed. This can be done by checking resulting , which is wrong. We conclude that there is no unoccupied processor for to be executed after . Hence we postpone and execute at ; this yields that the task set is schedulable by LCEDF.
We now discuss time-complexity of the LCEDF algorithm itself. Algorithm 1 takes , where the number of tasks in is n. That is, the number of jobs in is upper-bounded by n (See the number of iterations in Line 10), and the number of iterations for Lines 17, 24 and 30 are also upper-bounded by n. Also, it takes to sort jobs according to EDF. Therefore, . Note that LCEDF performs Algorithm 1 only when there is job release, job completion or processor idling.
5. Methodology: Schedulability Analysis for LCEDF
In the previous section, we succeed to develop a new scheduling algorithm, LCEDF, which potentially improves vanilla EDF using limited information for the future job release pattern. However, the algorithm becomes useful, only if we can provide offline timing guarantees of a given set of tasks under the algorithm. In this section, we develop a schedulability analysis for LCEDF, which offers such offline timing guarantees. We first investigate the existing schedulability analysis for vanilla EDF, which is a basis for that for LCEDF. We then derive effects of postponing jobs and idling processors on schedulability. Finally, we incorporate the effects to the existing schedulability analysis technique, yielding a new schedulability analysis for LCEDF.
5.1. Existing Schedulability Analysis for Vanilla EDF
As a basis for the schedulability analysis for LCEDF to be developed, we choose to use one of the most popular schedulability analysis techniques, called RTA (Response Time Analysis) for non-preemptive scheduling [11,12]. Let denote the length of cumulative intervals in where a job of of interest cannot execute due to other jobs’ execution. By the definition of , at least one unit of execution is performed in if the following inequality holds [11,12]:
Under non-preemptive scheduling, a job continues its execution once it starts to execute. Therefore, if Equation (1) holds, the job of finishes its execution no later than [11,12]. That is, since at least one unit of execution of the job of of interest is performed in , the remaining execution of the job of of interest at is as much as at most .
Then, the remaining issue is how to calculate . To this end, the existing studies calculate an upper-bound of under the target scheduling algorithm. Considering a job of of interest cannot execute in a time slot only if there are m other jobs executed in the time slot, the existing studies calculate an upper bound of the length of cumulative intervals where the job of of interest cannot execute while jobs of execute in .
For vanilla EDF, the existing studies consider two upper bounds. The first upper-bound is the maximum length of cumulative intervals where jobs of execute in [15]. Figure 4a illustrates the job release and execution pattern that maximizes the amount of execution of jobs of in an interval of length ℓ. The job release and execution pattern is as follows: the first and last jobs of execute as late and early as possible, respectively, and the interval of interest starts at the beginning of the first job’s execution. Here, denote the slack value of , meaning that every job of finishes its execution no later than its absolute deadline ahead of time units. We will explain how to calculate and use for RTA. Under the job release and execution pattern in Figure 4a, the number of jobs whose absolute deadlines are within the interval of interest can be calculated by [15] where
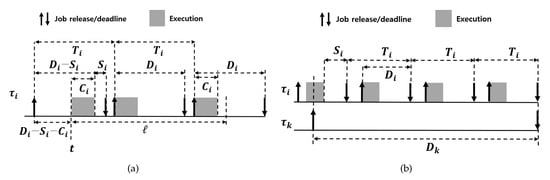
Figure 4.
Two upper bounds for . (a) The maximum length of cumulative intervals where jobs of execute in ; (b) The maximum length of cumulative intervals where jobs of have a higher priority than the job of of interest in under EDF.
Then, the amount of execution in the figure can be calculated by [15] where
After executing jobs of in an interval of length ℓ, at most one job of can be (partially) executed. Then, is the maximum length of the job’s execution. Since a job of ’s execution cannot be larger than , we take the minimum between and , yielding Equation (3).
To calculate the second upper-bound, the existing studies focus on the execution window of the job of , meaning that the interval between the job’s release time and absolute deadline, whose length is . They then calculate the maximum length cumulative intervals where jobs of have a higher-priority than the job of of interest in the interval of length . Under vanilla EDF, a job of can have a higher priority than a job of only if the job of has an earlier absolute deadline than the job of . Figure 4b illustrates the situation for the second upper-bound. Similar to , we can calculate , the number of jobs of that have a higher priority than the job of , whose release times are within the interval of interest of length (i.e., the job of ’s execution window), as follows [15]:
The, the amount of execution in the figure can be calculated by [15] where
Then, and operate as an upper bound of the amount of higher-priority execution of jobs of (than the job of ) in the interval of interest. Since we focus on non-preemptive scheduling, it is possible for a lower-priority job of to prevent the job of ’s execution. This happens only when a job of starts its execution before the release time of the job of of interest. In this case, the job of can block the execution of the job of of interest during at most .
Considering a job of of interest cannot execute in a time slot only if there are m other jobs executed in the time slot, can be upper-bounded as follows [11,12].
Since we calculate the two upper-bounds and and the interval length is ℓ, the amount of higher-priority execution of (than the job of of interest) in is . Also, if a job of starts its execution before the release of the job of of interest, the job of can interfere with the job of during at most . Since there exist at most m blocking jobs, we add for all tasks , and add the m largest difference between and if the difference is positive. Finally, we divide the sum by m, because the job of cannot be executed only when m other jobs execute, yielding Equation (6).
Using the above equations, RTA for vanilla EDF operates as follows. With for every , the following procedure is performed. For each , we set and check Equation (1) by replacing as the RHS of Equation (6). If Equation (1) does not hold, we repeat to set ℓ as the RHS of Equation (1). If Equation (1) holds with , is schedulable; otherwise, is unschedulable. Then, if every task is schedulable, the task set is schedulable; otherwise, we update the slack values, and repeat the procedure with the updated slack values until every task is schedulable (schedulable task set) or there is no more slack update (unschedulable task set). Note that slack updates are performed as follows: for each schedulable task , we set as , which is explained in [11,12].
5.2. Schedulability Analysis for LCEDF
The most prominent characteristic of LCEDF is to postpone jobs of tasks in and to idle processors for tasks in . In this subsection, we calculate upper-bounds of for tasks in and , which are different from those under vanilla EDF. Compared to the upper-bounds under vanialla EDF, an upper-bound of for should be no larger, and that for should be no smaller. The former holds because some jobs of tasks in cannot execute even though their priorities are higher than jobs of tasks in . This, in turn, makes the latter holds.
We first calculate an upper-bound of for . Recall that is a set of tasks which satisfy that there exist at least m other tasks whose execution time is larger than . Suppose that a job of a task in is ready to execute by having the highest priority among jobs in the ready queue at , and the earliest time instant for a job of a task in (which does not start its execution until ) to encounter an unoccupied processor after is . Then, the job of cannot start its execution, if holds and other processors are occupied until . Since we do not know which job of a task in is ready to execute and when other processors are occupied, the LCEDF schedulability analysis to be developed should capture such situations offline.
To derive the schedulability analysis for LCEDF, we utilize the following property for LCEDF.
Lemma 1.
Under LCEDF, the number of tasks which fully interfere with the execution of a job of (of interest) during is at most .
Proof.
According to LCEDF, a job of a task in can start its execution only if every job of a task in has at least one chance to compete for unoccupied processors until . If not (i.e., at least one job of a task in cannot have any chance if the job of the task in starts its execution), we postpone the execution of the job of the task in . Therefore, of cannot experience more than fully interfering jobs during . □
Using the lemma, we derive for as follows.
Lemma 2.
Let denote , meaning that is ’s term in the numerator of the RHS of Equation (6). Under LCEDF, for is upper-bounded as follows:
where α denotes the largest value of among ; if the value is negative, α is set to 0.
Proof.
We show that in Lemma 2 there are at most tasks that fully interfere with the execution of of in . Therefore, the largest value of (among ) cannot be larger than . We take the minimum between and for the task with largest value of , which is implemented by subtraction of . □
If compare the RHS of Equation (6) and that of Equation (7), the latter is no larger than the former; their difference is equal to . This means that a task which is not schedulable by vanilla EDF can be schedulable by LCEDF.
Next, we calculate an upper-bound of for . Recall that is a set of tasks which do not belong to . In addition to interference and blocking calculated in Equation (6), a job of a task cannot be executed due to processor idling by the LCEDF algorithm. Therefore, we need to calculate how long a job of a task can experience processor idling due to jobs of a task , which is denoted by .
If there are more than two tasks in the task set, it is possible for a job of a task in to be postponed by jobs of different tasks in . Therefore, we need to calculate how long jobs of a task incur processor idling that disallows a job of to perform its execution. Suppose that a job of starts its execution at , and and the earliest time instant for a job of a task (which does not start its execution until ) to encounter an unoccupied processor after is . Then, to trigger processor idling for , should be satisfied, and in this case, the processor idling duration is as shown in Figure 5. Considering jobs of can postpone the job of , the following lemma holds.
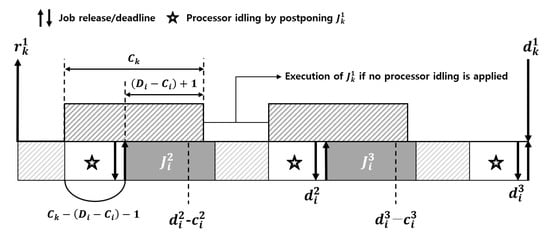
Figure 5.
The maximum cumulative length where the execution of a job of of interest is postponed by jobs of in .
Lemma 3.
The processor idling duration by in the execution window of a job of (i.e., for ) is at most where
Proof.
A job of can be postponed by a job of , only when the finishing time of ’s execution is later than . Therefore, can trigger postponing the execution of by processor idling during at most . Also, in , there can be jobs of that fully trigger postponing the execution of by processor idling, and there can be additional at most one job of that does partially. Therefore, similar to calculation of and , we can calculate the processor idling duration by , as . □
Then, we can derive for under LCEDF, by adding to Equation (6), which is recorded in the following lemma.
Lemma 4.
Under LCEDF, for is upper-bounded as follows:
Proof.
Then, how to apply RTA with for LCEDF is the same as that for vanilla EDF, which is explained in the last paragraph of Section 5.1.
Now, we discuss time-complexity of the proposed schedulability analysis. Since the schedulability analysis’ basis is RTA, the time-complexity is the same as that of RTA for vanilla EDF. That is, to test the schedulability of a task with given ℓ, we need to calculate all other tasks’ interference, yielding time-complexity, where n is the number of tasks in . Considering each task has at most choices for ℓ and there are n tasks in , it takes to determine the schedulability of all tasks without slack reclamation. The slack reclamation repeats to test schedulablity without slack reclamation, at most times, yielding time-complexity, which is the same as RTA for vanilla EDF.
6. Experiment and Results
In this section, we evaluate the schedulability performance of LCEDF. To this end, we first explain the task set generation strategy. Using a number of task sets generated by the strategy, we evaluate how many task sets are schedulable (i.e., meet all job deadlines are guaranteed) by the schedulability analysis for LCEDF and vanilla EDF.
6.1. Generation of Task Sets
We deploy a widely used task set generation method for real-time systems [16,17,18]. We have two input parameters: (a) the number of processors ( and 8), and (b) task utilization () distributions (bimodal with parameters 0.1, 0.3, 0.5, 0.7 or 0.9, or exponential with parameter 0.1, 0.3, 0.5, 0.7 or 0.9). Then, each task’s parameters are determined as follows: is uniformly distributed in , is determined by (b), and is set to . For every pair of (a) and (b), we generate 10,000,000 task sets with the following procedure, yielding 10,000,000 · 4 · 10 = 400,000,000 task sets in total.
- S1.
- We generate a set of tasks; note that a set of no more than m tasks are trivially schedulable by a m-processor platform.
- S2.
- We check whether the generated task set passes the necessary feasibility condition [19].
- S3.
- If it fails to pass the condition, we discard the generated task set (because it is unschedulable by every scheduling algorithm) and go to S1. If it passes, we include the generated task set as a tested task set of interest, and then we add one task to the generated task set and go to S2.
6.2. Evaluation Results
Using a number of generated task sets, we calculate the ratio of the number of task sets schedulable by LCEDF (and vanilla EDF) among the number of generated task sets, called schedulability ratio. Different from general-purpose systems, hard real-time systems do not allow any single job deadline miss; therefore, schedulability ratio has been used as a typical metric for evaluating hard real-time scheduling. Figure 6 targets a specific m, and shows the ratio, where the x-axis means the task set utilization, i.e., . We can check the schedulability improvement trend by LCEDF, for given m in the figure. On the other hand, Figure 7 targets a specific pair of m and task utilization (i.e., ) distribution, and shows the ratio. Among ten distributions, we choose to show the results for bimodal with 0.9, exponential with 0.9, and that with 0.1 in the figure, because they yields task sets each of whose average number of tasks is the smallest, medium, and the largest. We can check the schedulability improvement trend for given task utilization distribution in the figure.
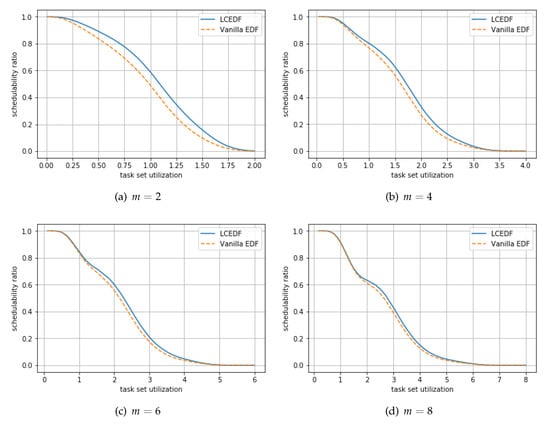
Figure 6.
The ratio of the number of task sets schedulable by LCEDF (and vanilla EDF) among the number of generated task sets, for given m.
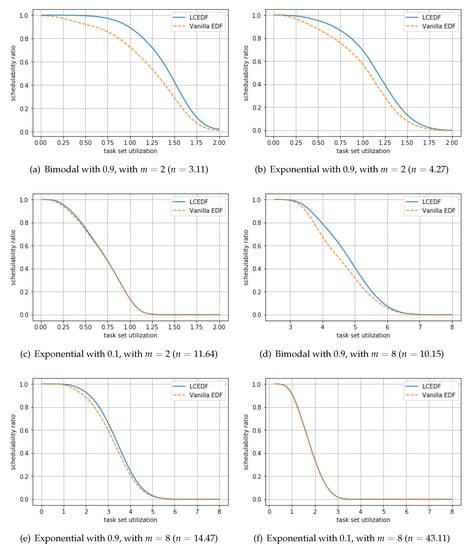
Figure 7.
The ratio of the number of task sets schedulable by LCEDF (and vanilla EDF) among the number of generated task sets, for given m and task utilization distribution, where n denotes the average number of tasks in each task set.
- O1.
- According to Figure 6, the schedulability performance of LCEDF under every m is superior to that of vanilla EDF.
- O2.
- According to Figure 6, the schedulability improvement by LCEDF is more significant with smaller m.
- O3.
- According to Figure 6, the difference between the ratio by LCEDF and that by EDF becomes larger until some point of task set utilization, but becomes smaller after the point.
- O4.
- According to Figure 7, the schedulability improvement by LCEDF is significant with task sets each of whose number of tasks are small (i.e., task sets generated by bimodal distribution with 0.9).
O1 shows that the LCEDF schedulability analysis finds additional task sets that are schedulable by LCEDF but unschedulable by EDF, regardless of the number of processors. The schedulability improvement by LCEDF comes from proper decisions for applying postponing jobs and idling processors. As a result, the LCEDF schedulability analysis deems a task set schedulable, if the vanilla EDF schedulability analysis does; in addition, the LCEDF schedulability analysis deems some additiona task sets schedulable, which cannot be deemed schedulable by the vanilla EDF schedulability analysis, by reducing interference on jobs of tasks in at the expense of increasing interference on jobs of tasks in . Compared to the vanilla EDF schedulability analysis, the LCEDF schedulability analysis deems additional , , , and task sets schedulable on average, respectively for and 8. Also, for task sets with similar task set utilization (i.e., for given x-axis in Figure 6, the LCEDF schedulability analysis improves schedulability up to , , , and , respectively for and 8.
When it comes to O2, the superiority of LCEDF over vanilla EDF in terms of schedulability performance decreases as the number of processors increases, as we mentioned in the quantitative improvement according to different m. This is because, the number of tasks in that interfere with jobs of tasks in increases as the number of processors increases while the advantage of LCEDF by applying idling processors remains the same regardless of the number of processors. Therefore, as the number of processors increases, the advantage of LCEDF in terms of schedulability becomes smaller.
O3 represents the correlation between task set utilization and the results for O1. The schedulability of LCEDF is similar to that of vanilla EDF, with low task set utilization. This is because, many task sets with low task set utilization are schedulable by vanilla EDF, and they have a few tasks which belong to . As task set utilization increases, the number of task sets unschedulable by EDF increases and the number of tasks belonging to in each task set also increases; this yields the schedulability difference between LCEDF and EDF. However, if the task set utilization is larger than some point, it is apt to have at least one unschedulable task due to large interference from other tasks. Therefore, the schedulability difference between LCEDF and EDF gradually decreases after some point of task set utilization.
O4 represents the schedulability results according to the number of tasks in each task set. As shown in Figure 7, the schedulability difference between LCEDF and EDF is significant when the number of tasks in each task set is small (i.e., generated by bimodal distribution with 0.9); in particular, the difference is up to 20.16% with and 12.97% with . On the other hand, there is a little improvement when the number of tasks in each task set is large (i.e., generated by exponential distribution with 0.1); in this case, the difference is up to 1.92% with and 0.53% with .
In summary, LCEDF improves schedulability, compared to EDF. The improvement is maximized when (i) the number of tasks in each task set is small, (ii) the number of processors is small, and (iii) the task set utilization is moderate.
7. Discussion and Conclusions
In this paper, we propose a new non-preemptive scheduling algorithm, LCEDF, which utilizes the limited information of future job release patterns. By investigating the limitations of vanilla EDF in terms of meeting job deadlines of non-preemptive tasks, we design LCEDF by classifying tasks into two types and handling them differently. We then develop a schedulability analysis for LCEDF, by analyzing the interference increment/decrement for the two types of tasks. The simulation results show that LCEDF improves schedulability performance of non-preemptive task sets, compared to vanilla EDF. Due to the high schedulability performance of the LCEDF schedulability analysis, we expect that the LCEDF algorithm is potentially employed in actual systems that require real-time guarantees, e.g., autonomous vehicles. This requires addressing some practical issues such as how to know and manage information of the future job release pattern. Once the LCEDF algorithm is employed in the actual system, it improves schedulability performance, meaning that the actual system can accommodate more tasks under the same hardware.
While we found a number of additional task sets which are not deemed schedulable by vanilla EDF but deemed schedulable by LCEDF, we believe that there still exist some task sets which are actually schedulable by LCEDF, but not deemed schedulable by the LCEDF schedulability analysis. This necessitates additional research on how to tightly upper-bound the interference calculation under LCEDF. Also, LCEDF requires the information of future job release patterns although the information is limited. In the future we need to figure out how to reduce the required information for LCEDF.
Author Contributions
Conceptualization, H.L. and J.L.; Software, H.L.; data curation, H.L. and J.L.; writing-original draft preparation, H.L. and J.L.; writing-review and editing, J.L.; Supervision, J.L.; project administration, J.L.; funding acquisition J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2019R1A2B5B02001794, 2017H1D8A2031628). The work was also supported by the MSIT(Ministry of Science and ICT), Korea, under the ICT Consilience Creative program(IITP-2019-2015-0-00742) supervised by the IITP(Institute for Information & communications Technology Planning & Evaluation).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baek, J.; Baek, J.; Yoo, J.; Baek, H. An N-Modular Redundancy Framework Incorporating Response-Time Analysis on Multiprocessor Platforms. Symmetry 2019, 11, 960. [Google Scholar] [CrossRef]
- Baek, H.; Lee, J. Task-Level Re-execution Framework for Improving Fault-Tolerance on Symmetry Multiprocessors. Symmetry 2019, 11, 651. [Google Scholar] [CrossRef]
- Liu, C.; Layland, J. Scheduling Algorithms for Multi-programming in A Hard-Real-Time Environment. J. ACM 1973, 20, 46–61. [Google Scholar] [CrossRef]
- Buttazzo, G.; Bertogna, M.; Yao, G. Limited Preemptive Scheduling for Real-Time Systems: A Survey. IEEE Trans. Ind. Inf. 2013, 9, 3–15. [Google Scholar] [CrossRef]
- Ekelin, C. Clairvoyant Non-Preemptive EDF Scheduling. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Dresden, Germany, 5–7 July 2006; pp. 23–32. [Google Scholar]
- Subramani, K. A specification framework for real-time scheduling. In Proceedings of the International Conference on Current Trends in Theory and Practice of Computer Science (SOFSEM), Milovy, Czech Republic, 22–29 November 2002; pp. 195–207. [Google Scholar]
- Subramani, K. An Analysis of Partially Clairvoyant Scheduling. J. Math. Model. Algorithms (JMMA) 2003, 2, 97–119. [Google Scholar] [CrossRef]
- Baruah, S. The non-preemptive scheduling of periodic tasks upon multiprocessors. Real-Time Syst. 2006, 32, 9–20. [Google Scholar] [CrossRef]
- Guan, N.; Yi, W.; Gu, Z.; Deng, Q.; Yu, G. New schedulability test conditions for non-preemptive scheduling on multiprocessor platforms. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Barcelona, Spain, 30 November–3 December 2008; pp. 137–146. [Google Scholar]
- Leontyev, H.; Anderson, J.H. A Hierarchical Multiprocessor Bandwidth Reservation Scheme with Timing Guarantees. In Proceedings of the Euromicro Conference on Real-Time Systems (ECRTS), Prague, Czech Republic, 2–4 July 2008; pp. 191–200. [Google Scholar]
- Lee, J.; Shin, K.G. Controlling Preemption for Better Schedulability in Multi-Core Systems. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), San Juan, PR, USA, 4–7 December 2012; pp. 29–38. [Google Scholar]
- Lee, J.; Shin, K.G. Improvement of Real-Time Multi-Core Schedulability with Forced Non-Preemption. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1233–1243. [Google Scholar] [CrossRef]
- Lee, J. Improved Schedulability Analysis Using Carry-in Limitation for Non-Preemptive Fixed-Priority Multiprocessor Scheduling. IEEE Trans. Comput. 2017, 66, 1816–1823. [Google Scholar] [CrossRef]
- Mok, A. Fundamental Design Problems of Distributed Systems for the Hard-Real-Time Environment. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1983. [Google Scholar]
- Bertogna, M.; Cirinei, M. Response-Time Analysis for globally scheduled Symmetric Multiprocessor Platforms. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Tucson, AZ, USA, 3–6 December 2007. [Google Scholar]
- Baruah, S.K.; Bletsas, K.; Andersson, B. Scheduling Arbitrary-Deadline Sporadic Tasks on Multiprocessors. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Barcelona, Spain, 30 November–3 December 2008. [Google Scholar]
- Bertogna, M.; Cirinei, M.; Lipari, G. Schedulability Analysis of Global Scheduling Algorithms on Multiprocessor Platforms. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 553–566. [Google Scholar] [CrossRef]
- Baker, T. An Analysis of EDF Schedulability on a Multiprocessor. IEEE Trans. Parallel Distrib. Syst. 2005, 16, 760–768. [Google Scholar] [CrossRef]
- Baker, T.P.; Cirinei, M. A Necessary and Sometimes Sufficient Condition for the Feasibility of Sets of Sporadic Hard-deadline Tasks. In Proceedings of the IEEE Real-Time Systems Symposium (RTSS), Rio de Janeiro, Brazil, 5–8 December 2006; pp. 178–190. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).