CARS Algorithm-Based Detection of Wheat Moisture Content before Harvest
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Design and Sample Collection
2.2. Data Processing and Analysis
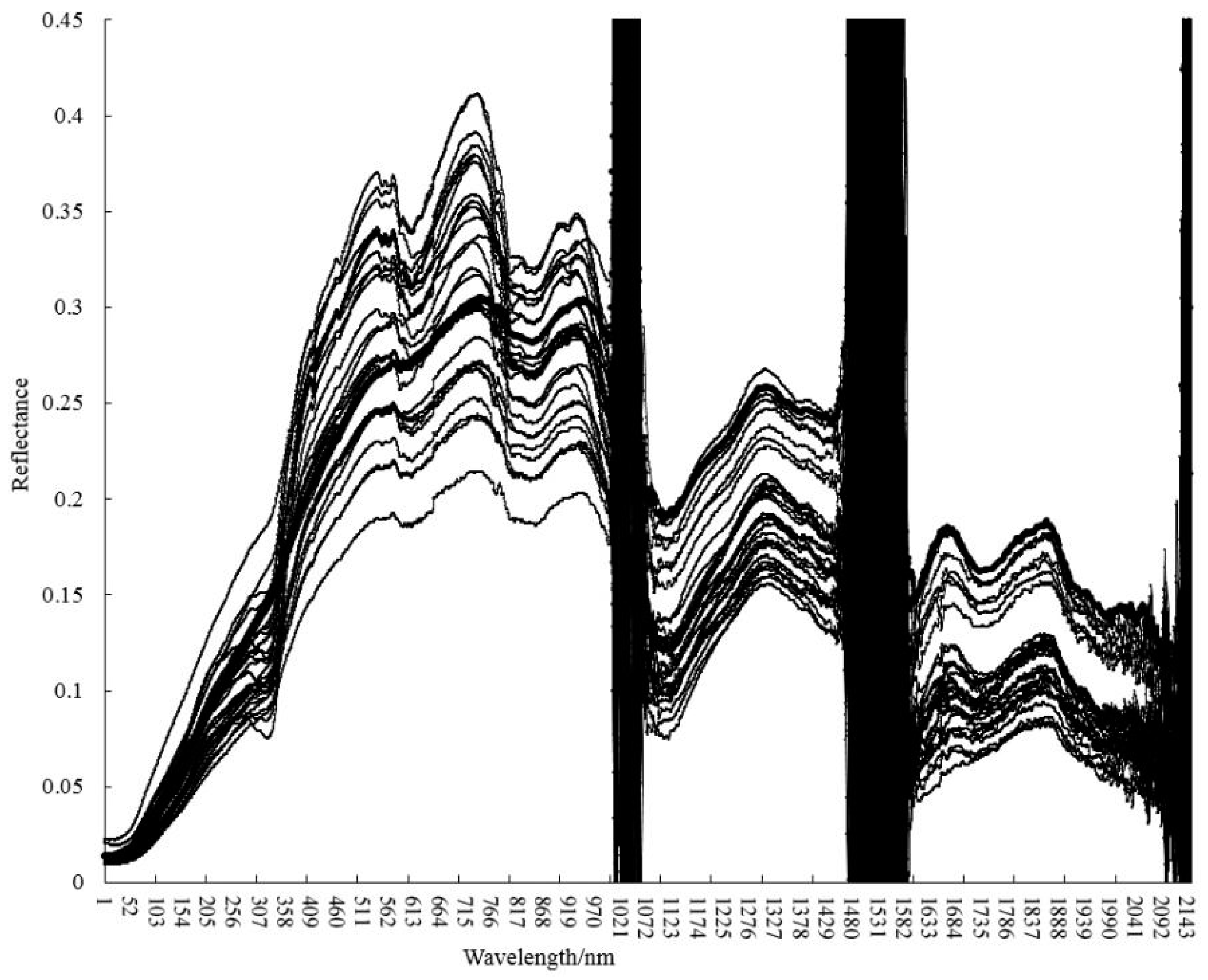
2.2.1. Spectra Pretreatment
2.2.2. Competitive Adaptive Reweighted Sampling (CARS)
2.2.3. Establishment and Calibration of PLSR Model
3. Results and Analysis
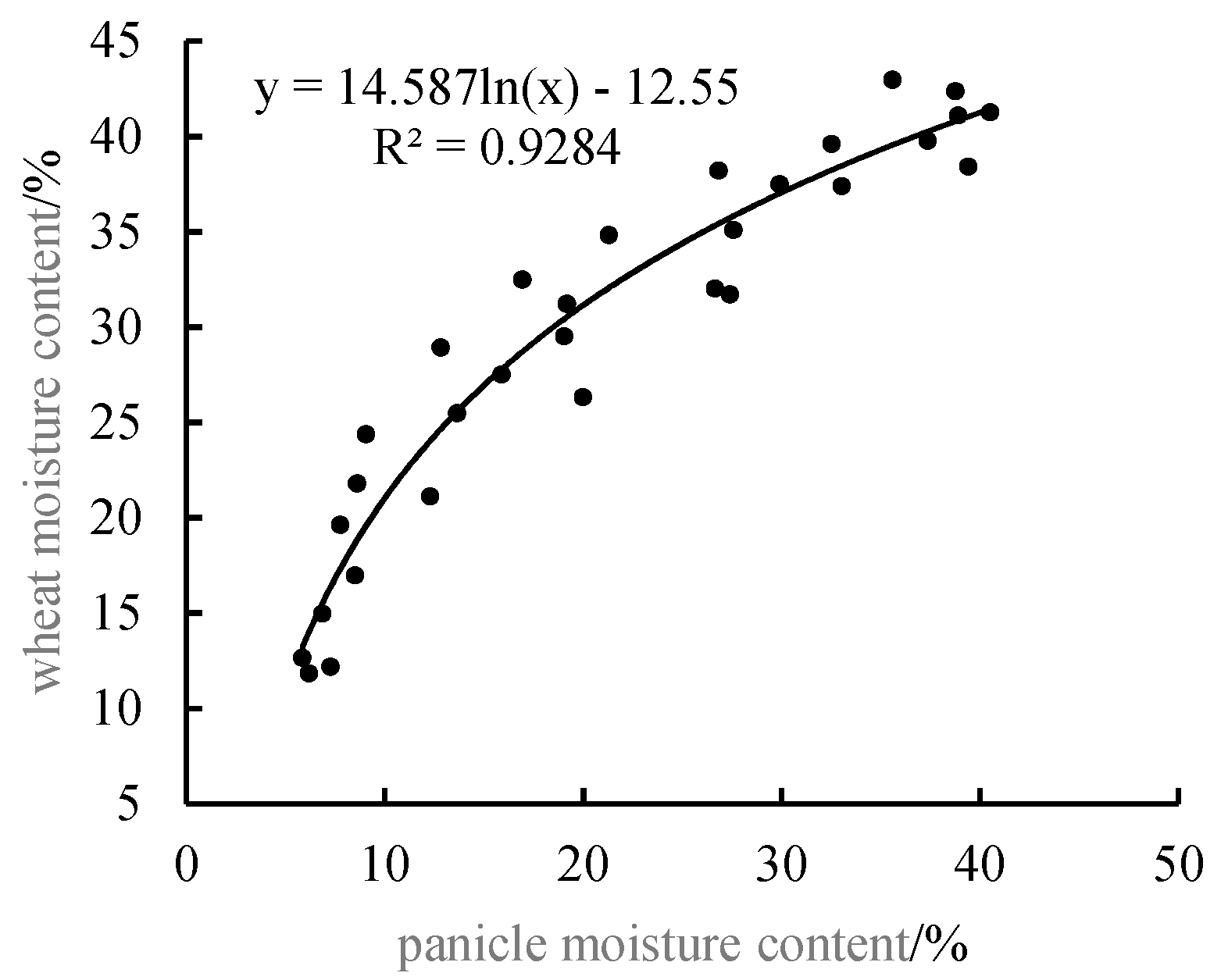
3.1. Changes in Moisture Content of Wheat and Panicle Samples
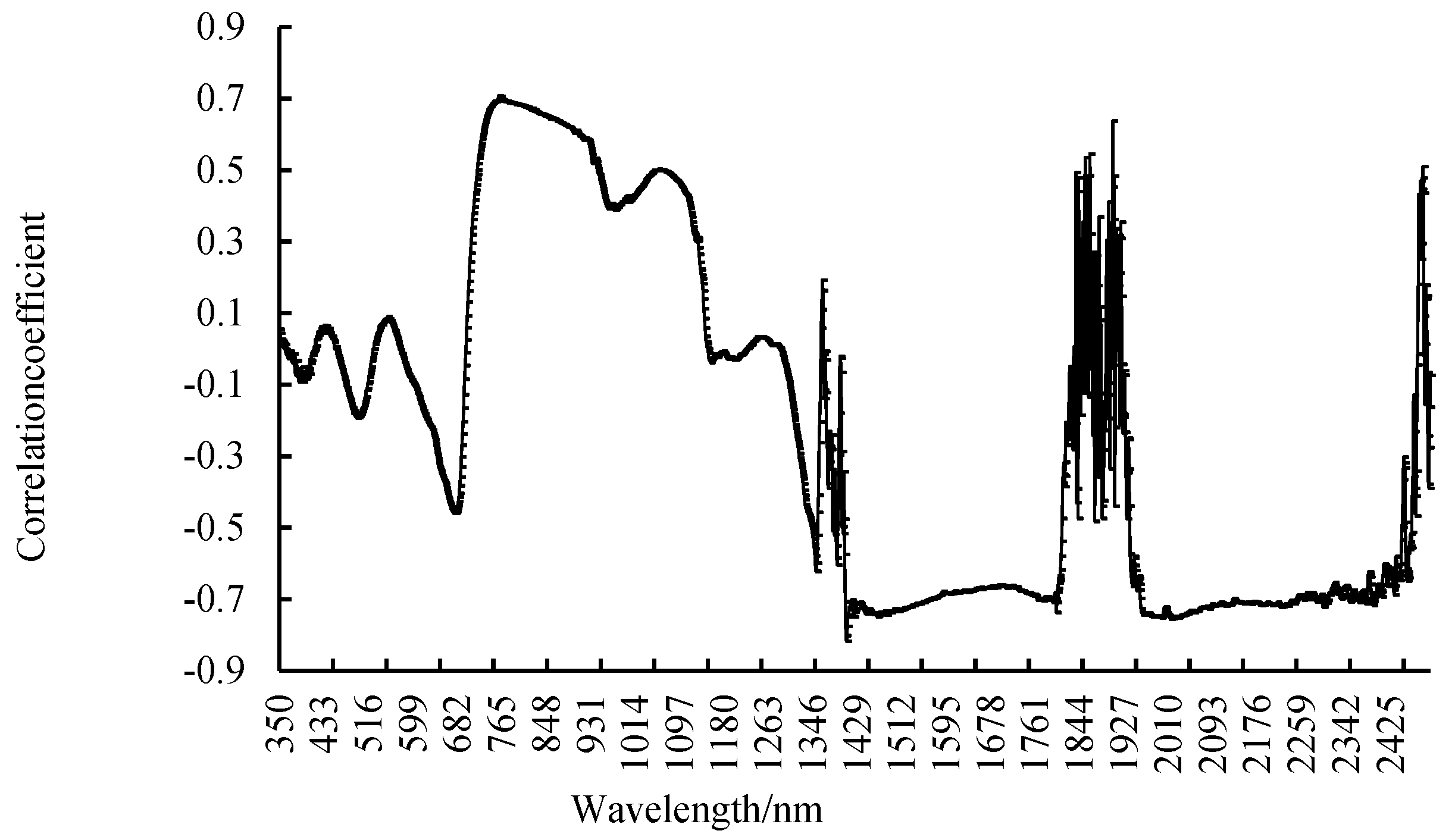
3.2. Correlation Analysis
3.3. Selection of Spectral Sensitive Bands of PMC
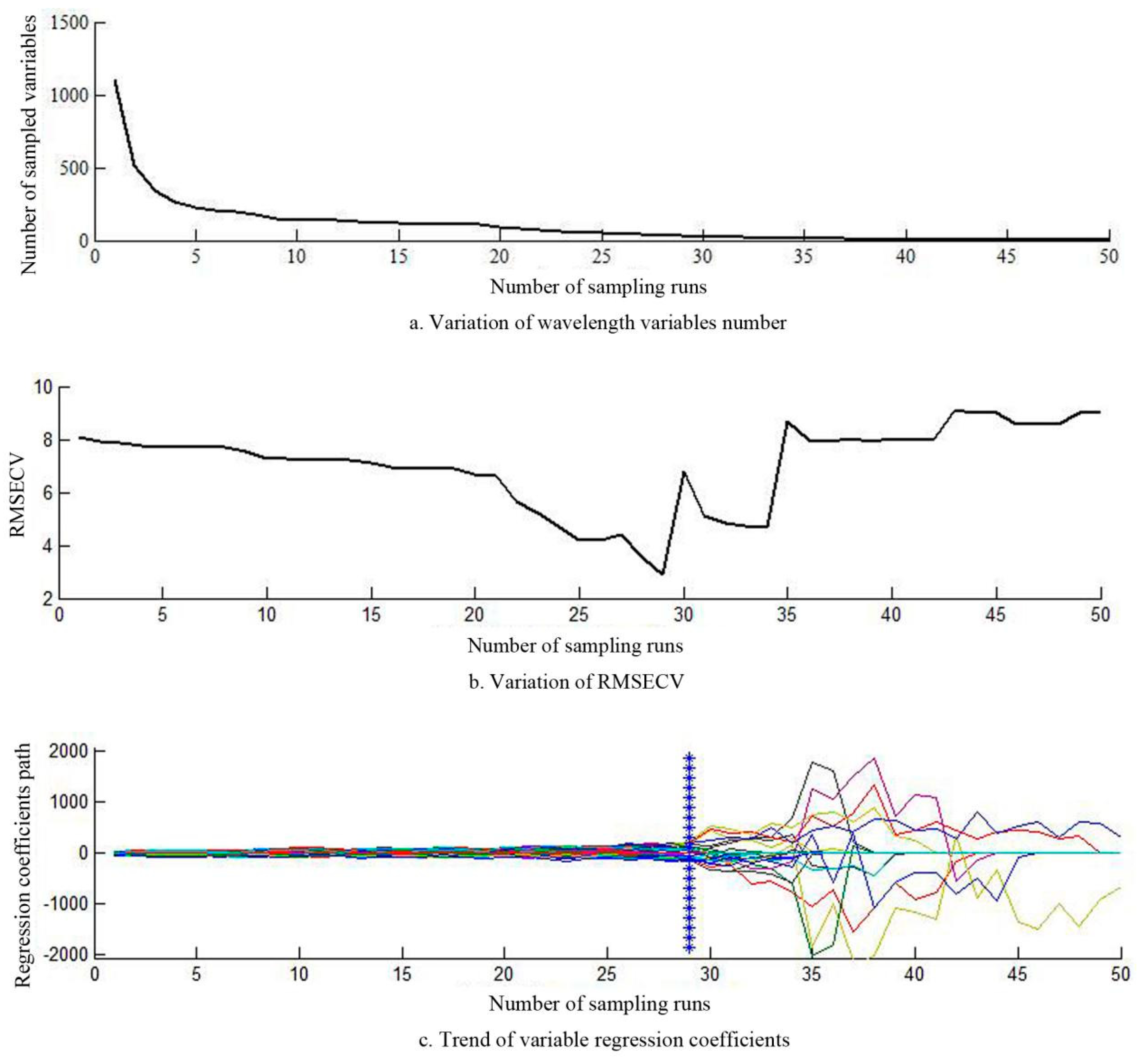
3.4. Variable Optimization by CARS Algorithm
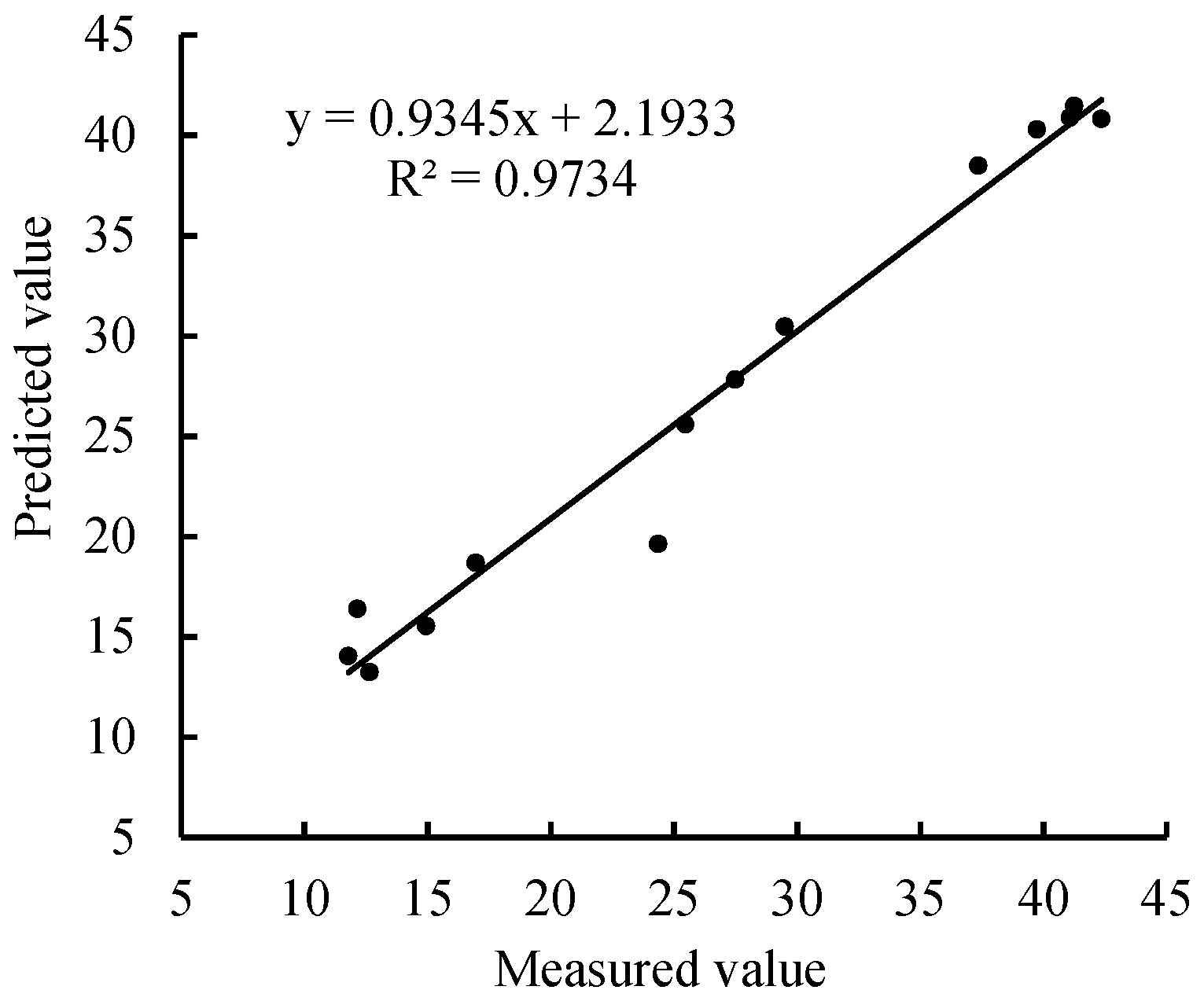
3.5. The Establishment and Verification of Optimal-Variable-Based PLSR Model
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cao, F.F.; Huang, D.; Zhu, J.F.; Wu, L.P. The Wheat Harvest Loss and its Main Determinants in China: An Empirical Analysis Based on Survey Data from 1135 Households. J. China Rural Surv. 2018, 2, 75–87. [Google Scholar]
- Cao, F.; Zhu, J.F.; Guo, Y.; Liu, J.P.; Wu, L.P. Wheat harvest loss in China: Based on experiments and surveys in 5 cities of 4 provinces. J. Arid Land Resour. Environ. 2018, 32, 7–14. [Google Scholar]
- Yan, Y.L. Foundation and Application of Near Infrared Spectroscopy; China Light Industry Press: Beijing, China, 2005. [Google Scholar]
- Xue, Z.C.; Gao, H.Y.; Liu, J. Monitoring growth and grain yield of wheat in fields with different soil fertility levels and different fertilizer application using spectral reflectance technique. J. Triticeae Crop. 2011, 31, 136–142. [Google Scholar]
- Yuan, L. Identification and Differentiation of Wheat Diseases and Insects with Multi-Sourse and Multi-Scale Remote Sensing Data. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2015. [Google Scholar]
- Li, C.J. Study on the Technology of Monitoring Winter Wheat Grain Protein Content on Regional Scale by Remote Sensing. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2005. [Google Scholar]
- Huan, K.W.; Liu, X.X.; Zheng, F.; Cai, X.; Yu, S.; Shi, X. Variable selection of near-infrared spectroscopy for measuring wheat protein based on MC-LPG. Trans. CSAE 2013, 29, 266–271. [Google Scholar]
- Sun, J.; Cong, S.L.; Mao, H.P.; Wu, X.; Zhang, X.; Wang, P. CARS-ABC-SVR model for predicting leaf moisture of leaf-used lettuce based on hyperspectral. Trans. CSAE 2017, 33, 178–184. [Google Scholar]
- Li, Q.B. Study on Several Key Techniques of Near-Infrared Spectroscopy Analysis. Ph.D. Thesis, Tianjin University, Tianjin, China, 2002. [Google Scholar]
- Lu, C.X.; Jiang, X.P.; Zhang, Y.Q.; Zhang, X. Variable selection based near infrared spectroscopic quantitative analysis on wheat crude protein content. Trans. Chin. Soc. Agric. Mach. 2016, 47 (Suppl. S1), 340–346. [Google Scholar]
- Cai, L.H.; Ding, J.L. Wavelet transformation coupled with CARS algorithm improving prediction accuracy of soil moisture content based on hyperspectral reflectance. Trans. CSAE 2017, 33, 144–151. [Google Scholar]
- Li, J.B.; Peng, Y.K.; Chen, L.P.; Huang, W.Q. Near-Infrared hyperspectral imaging combined with CARS Algorithm to quantitatively determine soluble solids content in “Ya” pear. Spectrosc. Spectr. Anal. 2014, 34, 1264–1269. [Google Scholar]
- Sudhakar, S.; Francis, S.; Balaji, V. Odd Mean Labeling for Two Star Graph. Appl. Math. Nonlinear Sci. 2017, 2, 195–200. [Google Scholar] [CrossRef]
- Mi, C.; Shen, Y.; Mi, W.J.; Huang, Y.F. Ship Identification Algorithm Based on 3D Point Cloud for Automated Ship Loaders. J. Coast. Res. 2015, 73, 28–34. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Zhan, B.S.; Ni, J.H.; Li, J. Hyperspectral technology combined with CARS algorithm to quantitatively determine the SSC in Korla Fragrant Pear. Spectrosc. Spectr. Anal. 2014, 34, 2752–2757. [Google Scholar]
- Sun, T.; Xu, W.L.; Lin, J.L.; Liu, M.H.; He, X.W. Determination of soluble solids content in navel oranges by Vis/NIR diffuse transmission spectra combined with CARS method. Spectrosc. Spectr. Anal. 2012, 32, 3229–3233. [Google Scholar]
- Yu, L.; Zhu, Y.X.; Hong, Y.S.; Xia, T.; Liu, M.; Zhou, Y. Determination of soil moisture content by hyperspectral technology with CARS algorithm. Trans. CSAE 2016, 32, 138–145. [Google Scholar]
- Wu, J.Z.; Xu, Y. NIR quantitative model optimization of fatty acid inedible oil based on CARS-PLS. Trans. Chin. Soc. Agric. Mach. 2011, 42, 162–166. [Google Scholar]
- Yu, L.; Hong, Y.S.; Geng, L.; Zhou, Y.; Zhu, Q.; Cao, J.; Nie, Y. Hyperspectral estimation of soil organic matter content based on partial least squares regression. Trans. CSAE 2015, 31, 103–109. [Google Scholar]
- Liu, X.Y. Monitoring Models of Physiological Parameters of Corn and Farmland Soil Information Based on Hyper-Spectral Reflectance. Ph.D. Thesis, Northwest A&F University, Yangling, China, 2016. [Google Scholar]
- Butanda, J.A.; Málaga, C.; Plaza, R.G. On the Stabilizing Effect of Chemotaxis on Bacterial Aggregation Patterns. Appl. Math. Nonlinear Sci. 2017, 2, 157–172. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.Y.; Li, P.W.; Wang, W.; Zhou, W.; Zhang, J. Determination of moisture in chestnuts using near infrared spectroscopy. Trans. CSAE 2010, 26, 338–341. [Google Scholar]
- Jin, H.; Li, L.; Cheng, J. Rapid and non-destructive determination of moisture content of peanut kernels using hyperspectral imaging technique. Food Anal. Methods 2015, 8, 1–9. [Google Scholar] [CrossRef]
- Gao, W.; Wang, W.F. The Fifth Geometric-Arithmetic Index of Bridge Graph and Carbon Nanocones. J. Differ. Equ. Appl. 2017, 23, 100–109. [Google Scholar] [CrossRef]
- Xiong, X.M.; Wang, X.M.; Zhang, W.T.; Nie, J.Y.; Tang, Y.W. Design of wheat moisture content detection system based on three-wavelength near-infrared method. Jiangsu Agric. Sci. 2016, 44, 390–393. [Google Scholar]
- He, H.J.; Wang, Y.L.; Qiao, H.; Ou, H.Q.; Liu, H.; Wang, H.; Zhu, Y.D.; Jiang, S.Q. Rapid non-contact evaluation of wheat grain moisture content based on long-wave near-infrared spectroscopy. J. Hainan Norm. Univ. 2019, 32, 26–32. [Google Scholar]

| Sample Set | Sample Size | Wheat Moisture Content/% | Panicle Moisture Content/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Minimum Value | Maximum Value | Average Vaule | Standard Deviation | Minimum Value | Maximumvalue | Average Vaule | Standard Deviation | ||
| Modeling set | 30 | 11.82 | 42.95 | 29.62 | 9.72 | 5.85 | 40.52 | 21.53 | 11.82 |
| Testing set | 14 | 11.79 | 42.35 | 26.94 | 11.85 | 5.85 | 40.52 | 20.07 | 14.25 |
| Model | Regression Equation | Modeling Set | Validation Set | |||
|---|---|---|---|---|---|---|
| R² | F | R2v | RMSEv | REv/% | ||
| Exponentiol | y = 14.839e0.0291x | 0.7704 | 93.969 | 0.942 | 20.342 | 20.466 |
| Logarithm | y = 14.587ln(x) − 12.55 | 0.9284 | 362.957 | 0.987 | 3.859 | 7.532 |
| Linear | y = 0.766x + 13.134 | 0.8677 | 183.576 | 0.963 | 12.198 | 17.365 |
| Polynomial | y = −0.0201x2 + 1.6769x + 5.5504 | 0.9158 | 146.884 | 0.982 | 5.426 | 9.972 |
| Power | y = 5.2698x0.5746 | 0.8876 | 221.178 | 0.977 | 6.946 | 11.102 |
| Variable Selection Methods | Variable Number | Calibration Sets | Prediction Sets | |||
|---|---|---|---|---|---|---|
| RMSEC | R2c | RMSEP | R2p | RPD | ||
| sensitive band -PLSR | 1103 | 7.612 | 0.668 | 9.803 | 0.843 | 1.140 |
| sensitive band -CARS-PLRS | 30 | 0.9301 | 0.995 | 2.676 | 0.945 | 3.362 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, H.; Wang, W.; Chong, D.; Zhang, B. CARS Algorithm-Based Detection of Wheat Moisture Content before Harvest. Symmetry 2020, 12, 115. https://doi.org/10.3390/sym12010115
Ji H, Wang W, Chong D, Zhang B. CARS Algorithm-Based Detection of Wheat Moisture Content before Harvest. Symmetry. 2020; 12(1):115. https://doi.org/10.3390/sym12010115
Chicago/Turabian StyleJi, Hong, Wanzhang Wang, Dongfeng Chong, and Boyang Zhang. 2020. "CARS Algorithm-Based Detection of Wheat Moisture Content before Harvest" Symmetry 12, no. 1: 115. https://doi.org/10.3390/sym12010115
APA StyleJi, H., Wang, W., Chong, D., & Zhang, B. (2020). CARS Algorithm-Based Detection of Wheat Moisture Content before Harvest. Symmetry, 12(1), 115. https://doi.org/10.3390/sym12010115




