Involutory Quandles and Dichromatic Links
Abstract
1. Introduction
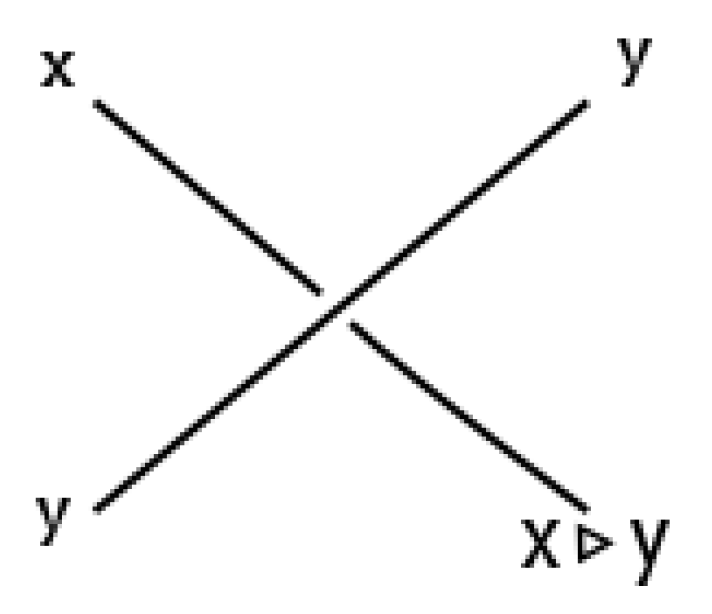
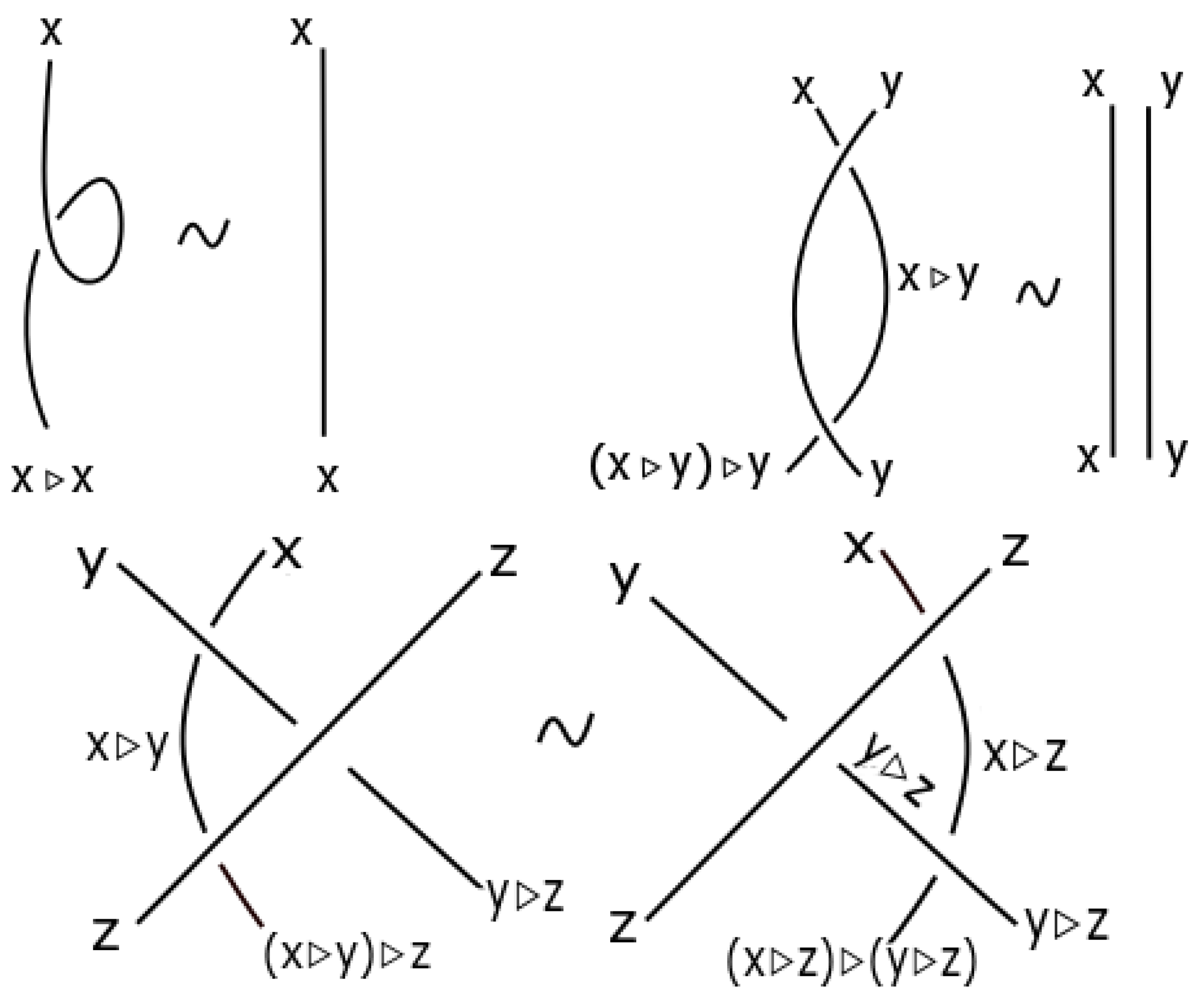
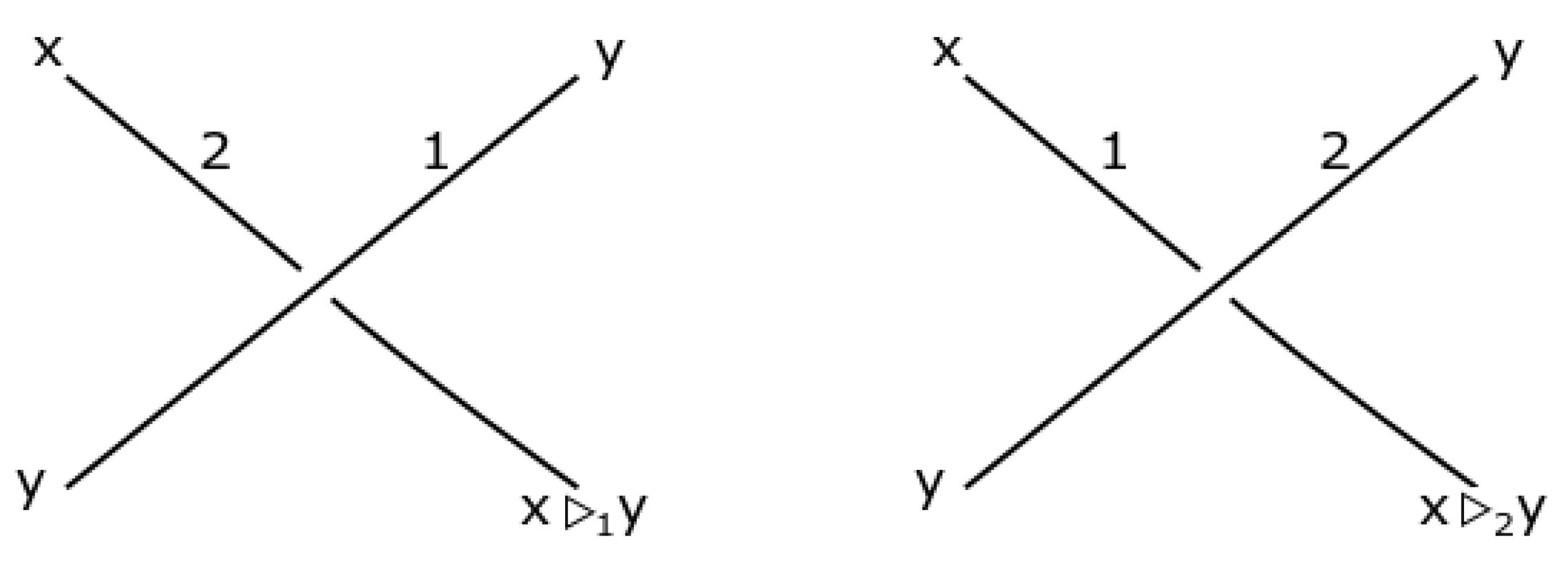
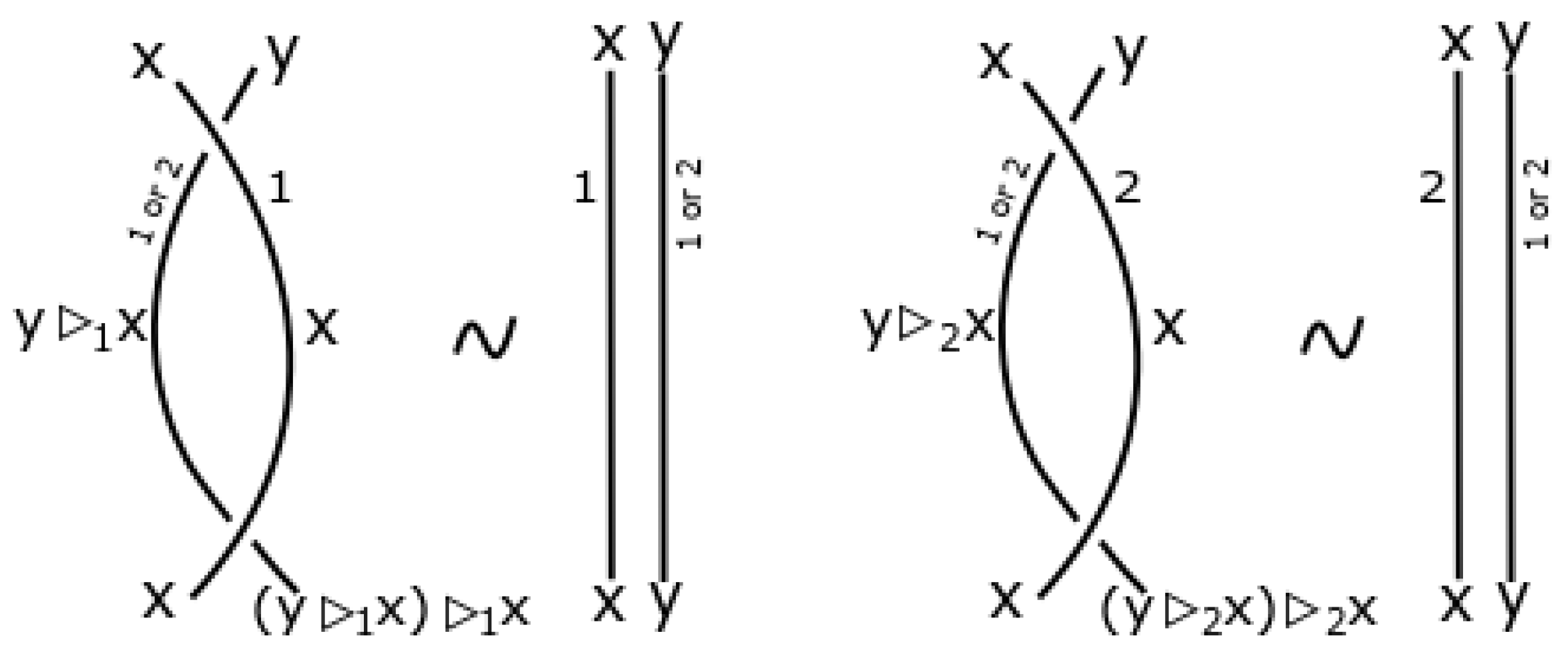
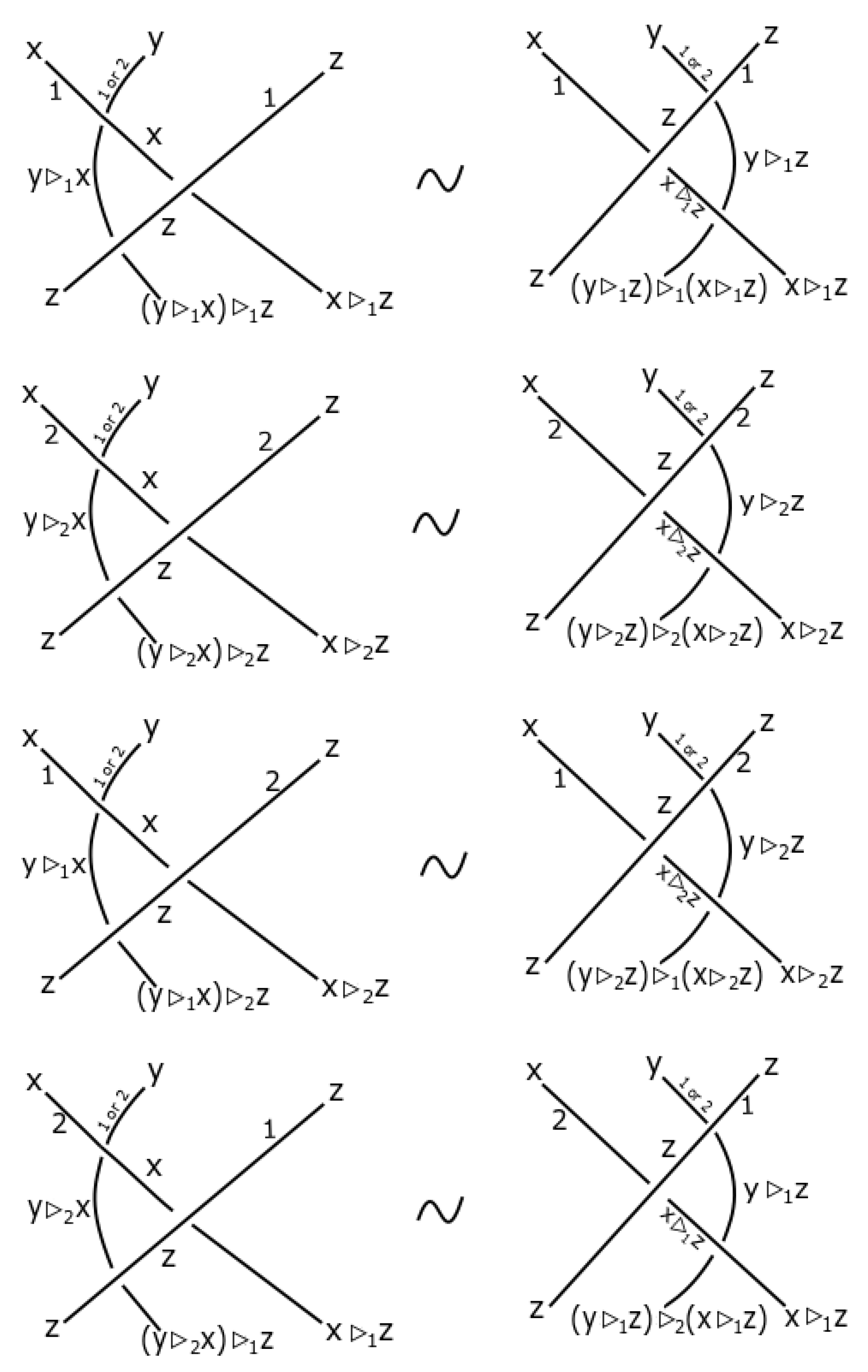
2. Basic Concepts and Terminology
- 1.
- , for all .
- 2.
- , for all .
- 3.
- , for all .
- Any non-empty set X with operation , for all is a kei. It is called the trivial kei.
- Let be a symmetric bi-linear form on . Let X be the subset of consisting of vectors such that . Then, the operationdefines a kei structure on X. This kei is called a Coxeter kei.
- A set with operation , for all is a kei.
- A group with operation is a kei. It is called the core kei of the group G.
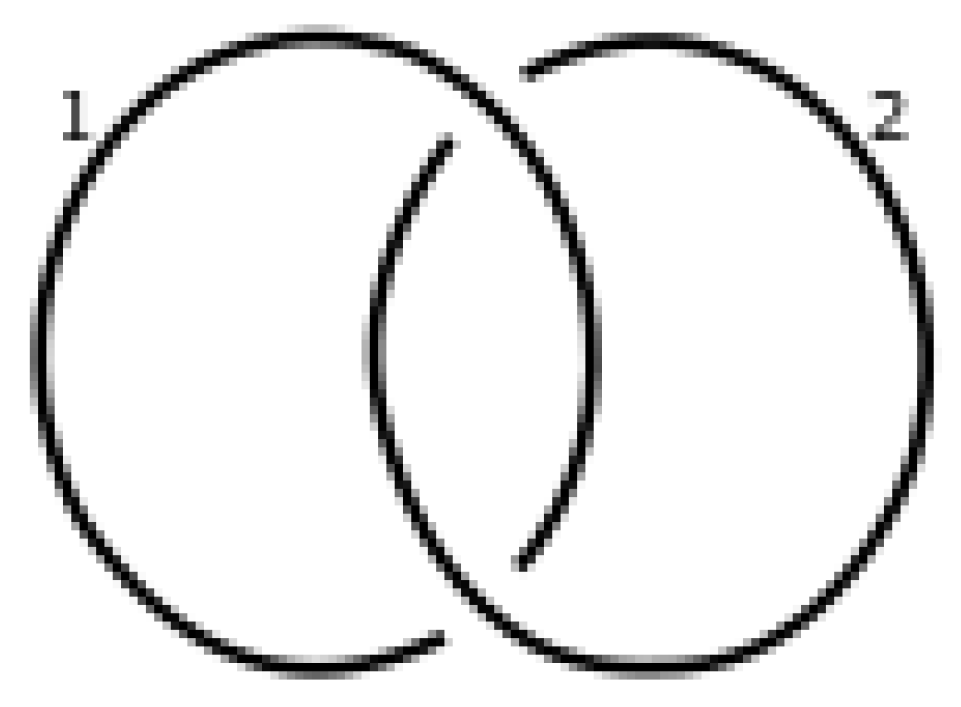
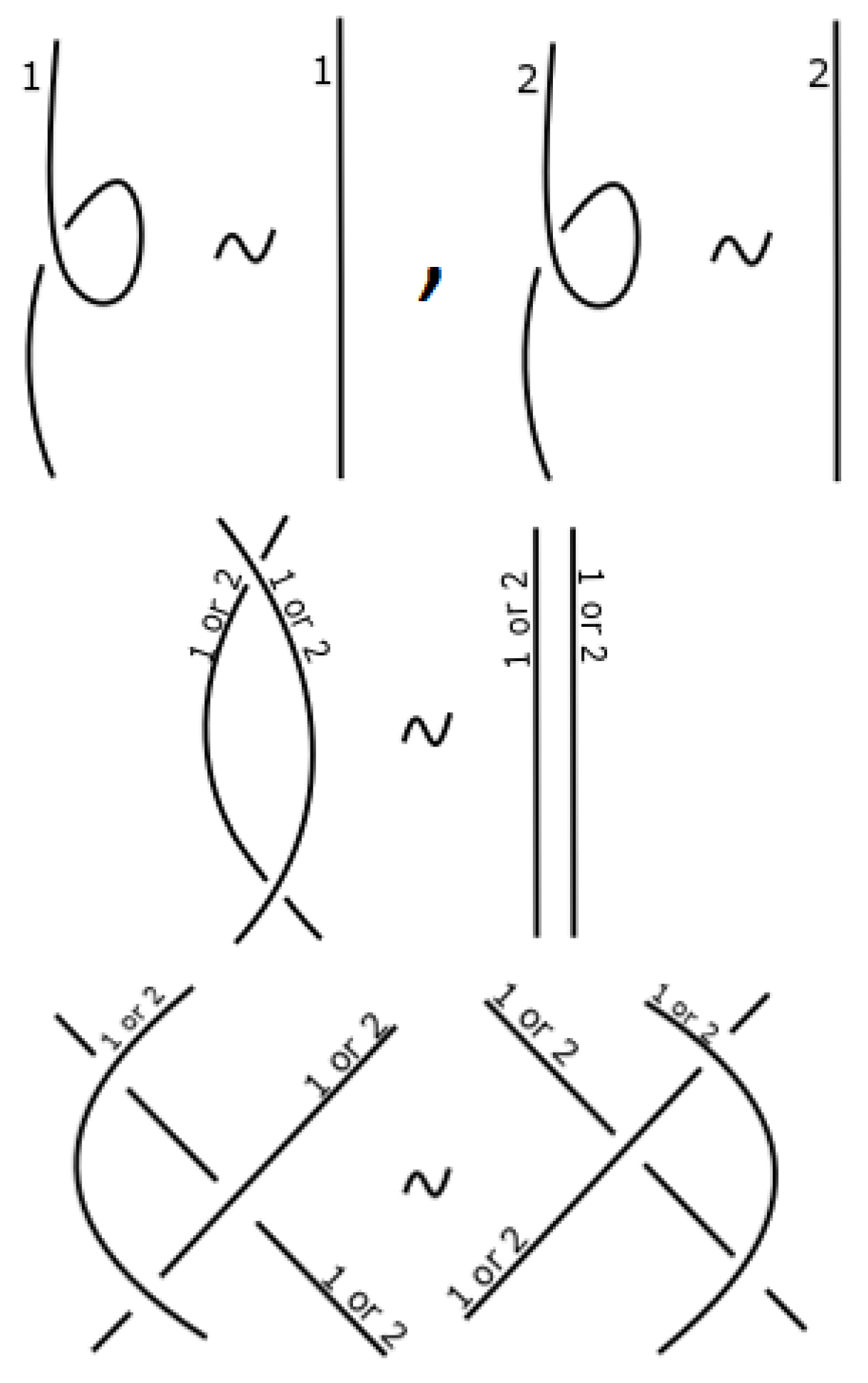
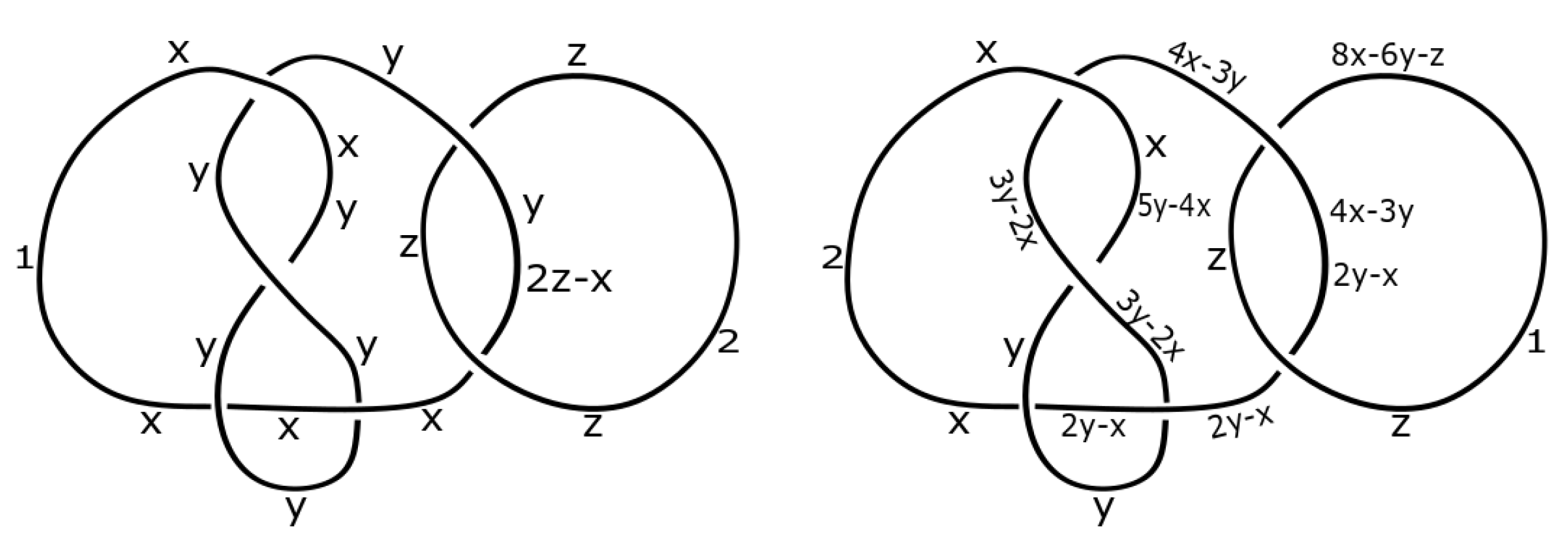
3. Construction of Dikei
4. Applications
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bataineh, K. On the skein theory of dichromatic links and invariants of finite type. J. Knot Theory Its Ramif. 2017, 26, 1750092. [Google Scholar] [CrossRef]
- Hoste, J.; Kidwell, M.E. Dichromatic link invariants. Trans. Am. Math. Soc. 1990, 321, 197–229. [Google Scholar] [CrossRef]
- Hoste, J.; Przytycki, J.H. An invariant of dichromatic link. Proc. Am. Math. Soc. 1989, 105, 1003–1007. [Google Scholar] [CrossRef]
- Bataineh, K.; Elhamdadi, M.; Hajij, M.; Youmans, W. Generating sets of Reidemeister moves of oriented singular links and quandles. J. Knot Theory Its Ramif. 2018, 27, 1850064. [Google Scholar] [CrossRef]
- Carter, J.S.; Silver, D.S.; Williams, S.G.; Elhamdadi, M.; Saito, M. Virtual knot invariants from group biquandles and their cocycles. J. Knot Theory Its Ramif. 2009, 18, 957–972. [Google Scholar] [CrossRef]
- Chien, J.; Nelson, S. Virtual Links with Finite Medial Bikei. J. Symb. Comput. 2019, 92, 211–221. [Google Scholar] [CrossRef]
- Churchill, I.R.; Elhamdadi, M.; Hajij, M.; Nelson, S. Singular knots and involutive quandles. J. Knot Theory Its Ramif. 2017, 26, 1750099. [Google Scholar] [CrossRef]
- Clark, W.E.; Elhamdadi, M.; Saito, M.; Yeatman, T. Quandle colorings of knots and applications. J. Knot Theory Its Ramif. 2014, 23, 1450035. [Google Scholar] [CrossRef] [PubMed]
- Elhamdadi, M.; Nelson, S. Quandles; American Mathematical Soc.: Providence, RI, USA, 2015; p. 47. [Google Scholar]
- Henrich, A.; Nelson, S. Semiquandles and flat virtual knots. Pac. J. Math. 2010, 248, 155–170. [Google Scholar] [CrossRef][Green Version]
- Joyce, D. A classifying invariant of knots, the knot quandle. J. Pure Appl. Algebra 1982, 23, 37–65. [Google Scholar] [CrossRef]
- Kauffman, L.H. Invariants of graphs in three-space. Trans. Am. Math. Soc. 1989, 311, 697–710. [Google Scholar] [CrossRef]
- Nelson, S.; Rivera, P. Bikei invariants and gauss diagrams for virtual knotted surfaces. J. Knot Theory Its Ramif. 2016, 25, 1640008. [Google Scholar] [CrossRef]
- Przytycki, J. 3-coloring and other elementary invariants of knots. Banach Cent. Publ. 1998, 42, 275–295. [Google Scholar] [CrossRef]
- Stanovský, D. The origins of involutory quandles. arXiv 2015, arXiv:1506.02389. [Google Scholar]
- Wada, M. Group invariants of links. Topology 1992, 31, 399–406. [Google Scholar] [CrossRef]
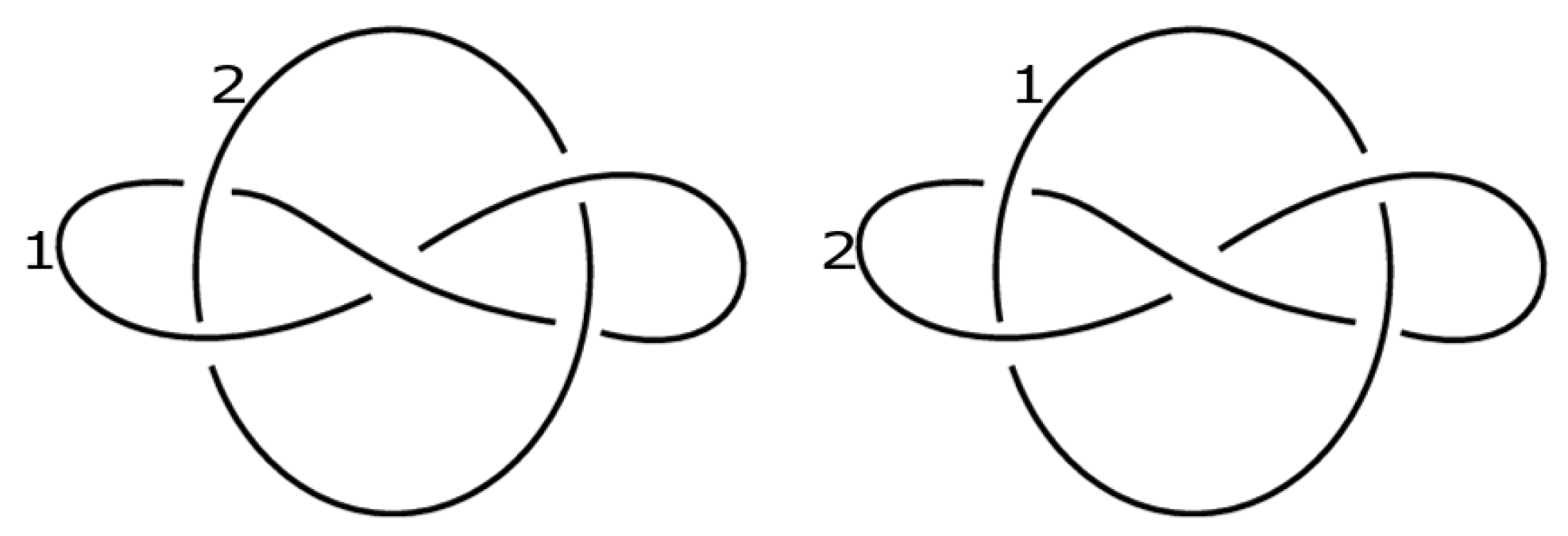
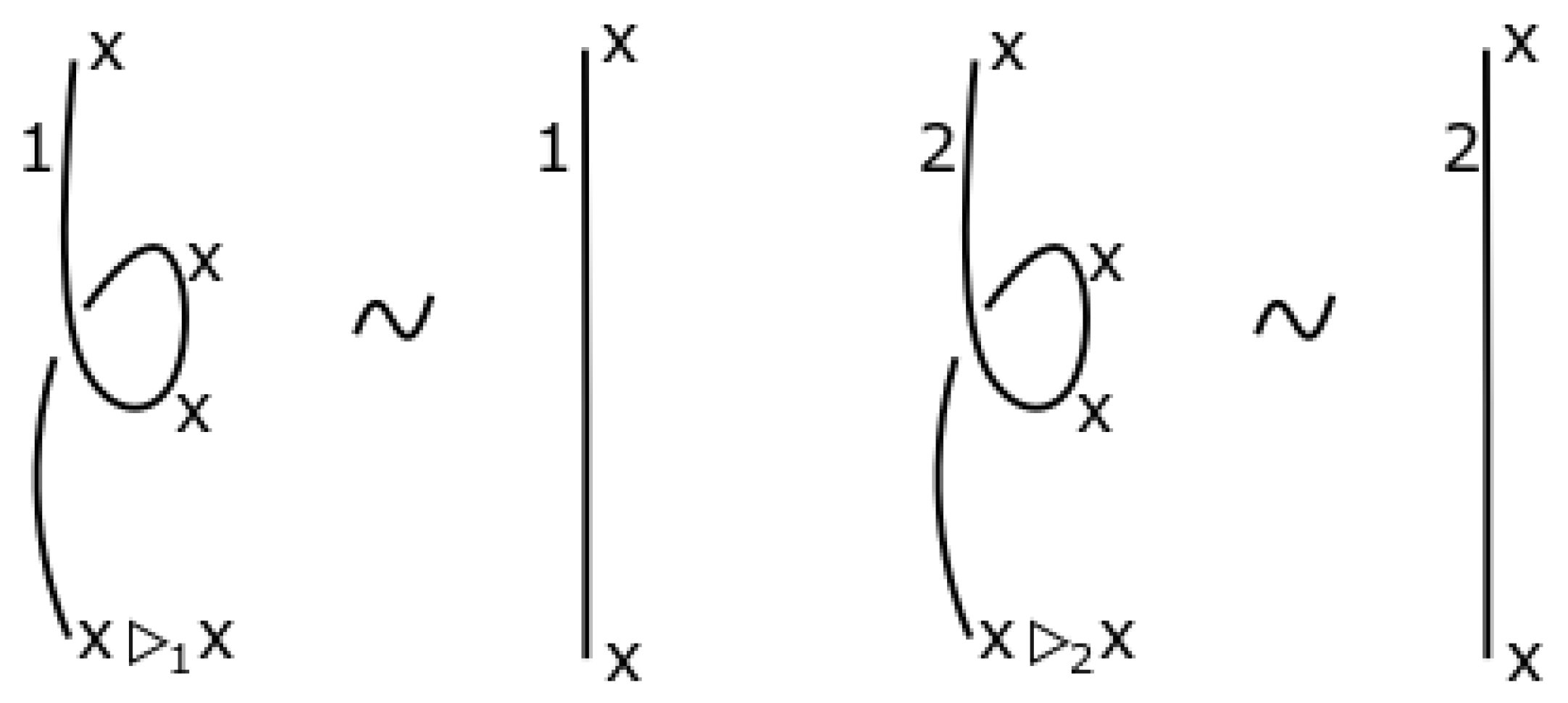
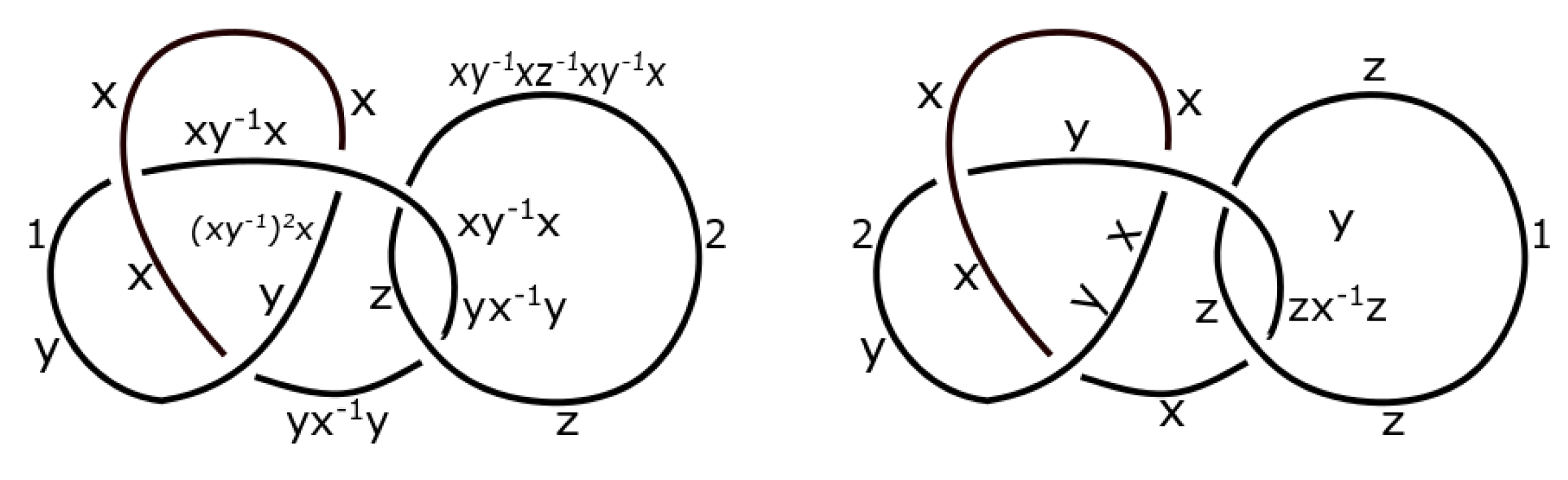
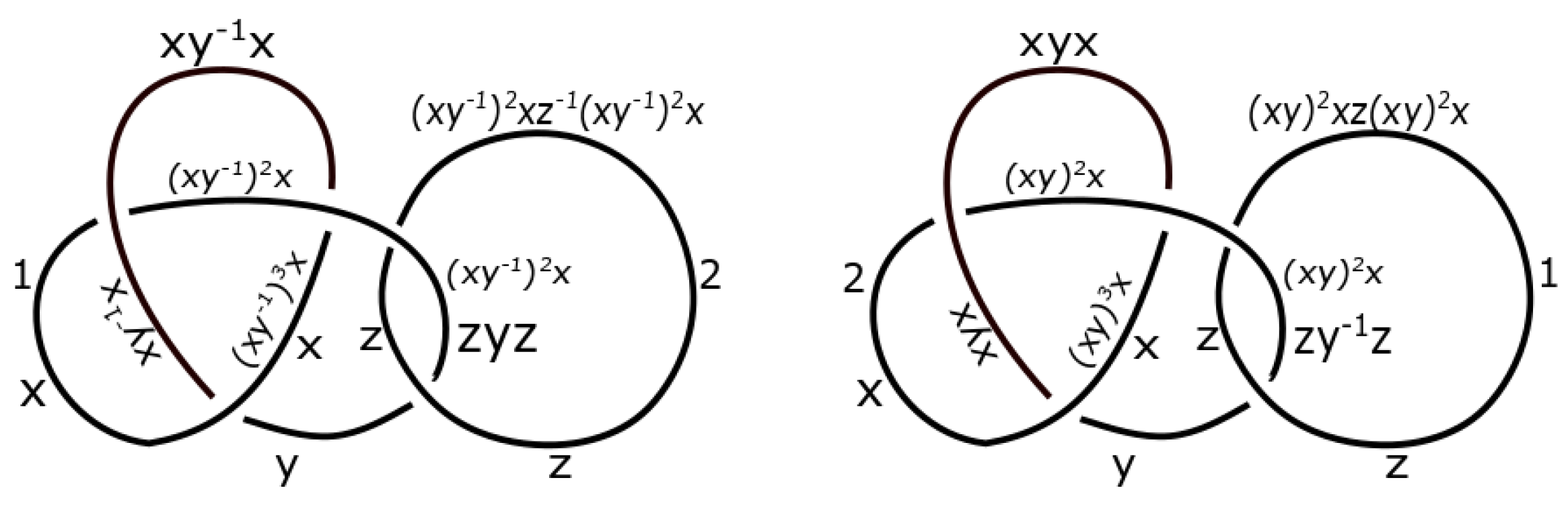
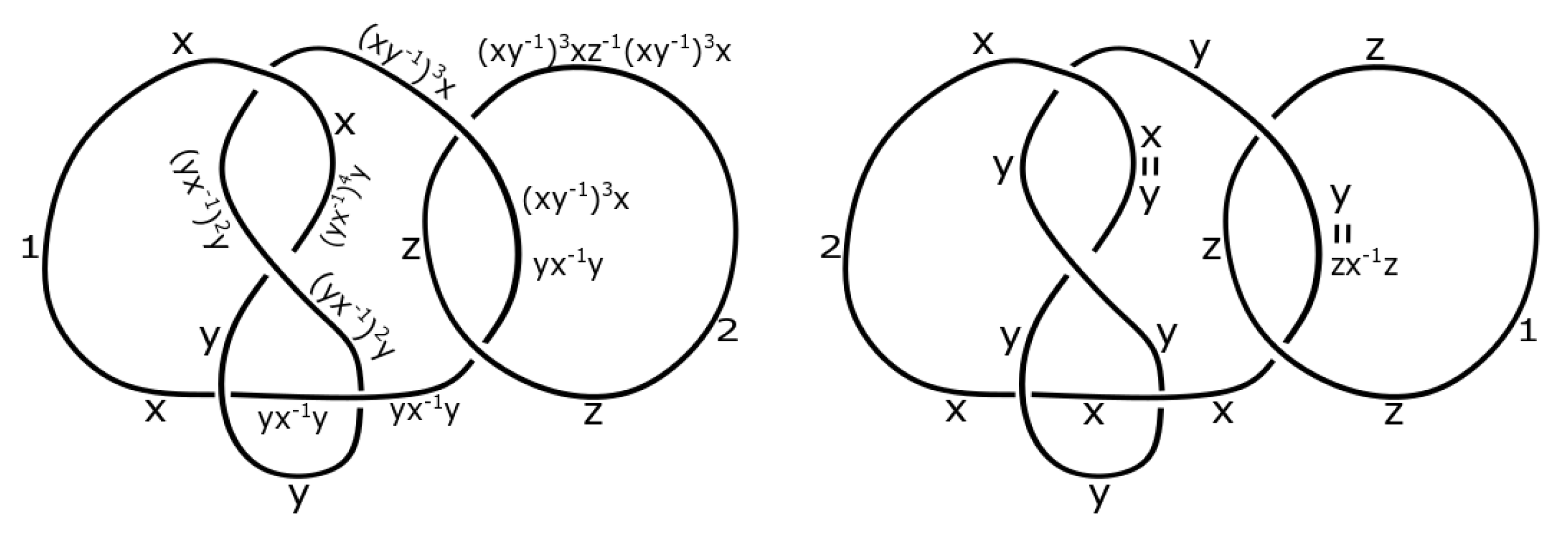
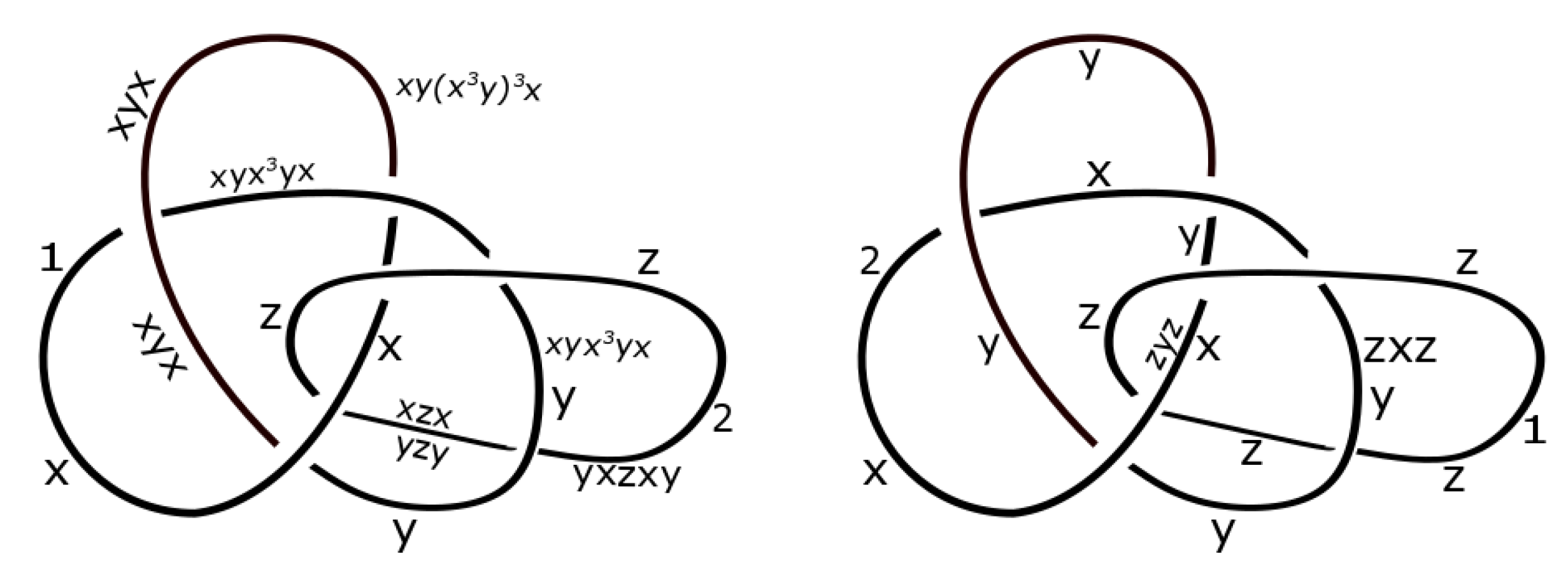
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bataineh, K.; Saidi, I. Involutory Quandles and Dichromatic Links. Symmetry 2020, 12, 111. https://doi.org/10.3390/sym12010111
Bataineh K, Saidi I. Involutory Quandles and Dichromatic Links. Symmetry. 2020; 12(1):111. https://doi.org/10.3390/sym12010111
Chicago/Turabian StyleBataineh, Khaled, and Ilham Saidi. 2020. "Involutory Quandles and Dichromatic Links" Symmetry 12, no. 1: 111. https://doi.org/10.3390/sym12010111
APA StyleBataineh, K., & Saidi, I. (2020). Involutory Quandles and Dichromatic Links. Symmetry, 12(1), 111. https://doi.org/10.3390/sym12010111



