A Modified Equation for Thickness of the Film Fabricated by Spin Coating

Abstract

According to the equation for Newtonian fluids, the film thickness after spin coating is determined by five parameters: angular velocity, spin coating time, viscosity, density of the coating material, and initial thickness of the material before spin coating. The spin coating process is commonly controlled by adjusting only the angular velocity parameter and the coating time in the Newtonian expression. However, the measured coating thickness obtained is then compared to the theoretical thickness calculated from the Newtonian fluid equation. The measured coating thickness usually varies somewhat from the theoretical thickness; further details are described in Section 1. Thus, the Newtonian fluid equation must be modified to better represent the actual film thickness. In this paper, we derive a new formula for the spin coating film thickness, which is based on the equation for Newtonian fluids, but modified to better represent film thicknesses obtained experimentally. The statistical analysis is performed to verify our modifications.

1. Introduction

In Ref. [1], Emslie, Bonner and Peck proposed differential equations in cylindrical polar coordinates to calculate the thickness of Newtonian liquid on a rotating disk. They took cylindrecal polar coordinates $(r,\theta ,z)$ rotating with the spinning disk at angular velocity W. The z dependence of the radial velocity v of the liquid at any point $(r,\theta ,z)$ can be found by equating the viscous and centrifugal forces per unit volume:

$$-\eta \frac{{\partial }^{2}v}{\partial z^2}=\rho W^{2}r,$$

(1)

where $\eta$ is the viscosity and $\rho$ the density of the liquid. Equation (1) may be integrated employing the boundary conditions that $v=0$ at the surface of the disk $(z=0)$ and $\partial v/\partial z=0$ at the free surface of the liquid $(z=h)$, where the shearing force must vanish. Hence,

$$v=\frac{1}{\eta }(-\frac{1}{2}\rho W^{2}r{z}^2+\rho W^{2}rhz).$$

(2)

The radial flow q per unit length of circumference is

$$q={\int }_0^{h}vdz=\frac{\rho W^{2}r{h}^3}{3\eta }.$$

(3)

In order to obtain a differential equation for h we apply the equation of continuity,

$$r\frac{\partial h}{\partial t}=-\frac{\partial \left(rq\right)}{\partial r}.$$

(4)

Thus, via Equation (3),

$$\frac{\partial h}{\partial t}=-K\frac{1}{r}\frac{\partial }{\partial r}\left(r^2{h}^3\right),$$

(5)

where $K=\frac{\rho W^2}{3\mu }$.

They obtained the solution which depends only on t. In this case, we have

$$\frac{dh}{dt}=-2K{h}^3.$$

(6)

Hence, they obtained the general solution (7), the equation for thickness of the film fabricated by spin coating, describes the film thickness obtained after the spin coating process

$$h=\frac{h_0}{\sqrt{1+\frac{4\rho W^2{h}_0^{2}t}{3\mu }}},$$

(7)

where $h_0$ is the initial thickness of the coating material [1,2,3,4]. Note that the final thickness of the film is affected more by the angular velocity and time than by the other factors. Given that $W=\frac{\pi }{30}\times \omega$, where $\omega$ is the number of revolutions per minute (RPM), the final thickness h of the film can be treated as a two-variable function of t and $\omega$ [1,2,3,4,5,6,7,8,9,10,11,12].

Spin coating technology is useful in modern industrial society. However, it still relies on Formula (7), which was introduced in the 1950s, to determine spin coating film thickness. Many companies that deal with spin coating processes do not actually use the equation for thickness of the film fabricated by spin coating (7) to determine spin coating thickness, due to the considerable discrepancy between the theoretical and actual thickness values. Because of these differences in the spin coating process, the traditional equation for thickness of the film fabricated by spin coating (7) was not used, but rather the repetitive empirical formula has been used. Currently, many scholars are trying to reduce these differences [13,14]. The disadvantages of our approach is that the empirical formula must be refreshed whenever the experimental environment changes; additionally, this process tends to be costly and time-consuming. Thus, a new mathematical formula is needed to describe the spin coating process and resulting film thickness. In order to verify this, we are going to conduct an experiment to measure the final thickness in the spin coating process. The experimental environment is given as follows:

(a)

The viscous PDMS (Polydimethylsiloxane) coated on the glass (Sylagard 184, Dowcoaning) is using the spin coating material.

(b)

The substrate of size $2\times 2{\mathrm{cm}}^2$ is used to measure the film thickness at the center of the substrate, and the substrate of size $3\times 3{\mathrm{cm}}^2$ is used to measure the overall thickness distribution of the PDMS film.

(c)

We fix the viscosity, density of coating material, initial thickness at $4000\mathrm{cP}$, $965\mathrm{kg}/{\mathrm{m}}^3$ and $0.105\mathrm{cm}$. Then, the rotation time is fixed at 300 s and the experiment is performed in 500 RPM units from 500 to 6000 RPM.

(d)

The spin coating is performed by Spin coater ACE-200 (DongAh Trade Corp, Seoul, South Korea).

(e)

Finally, we measure all samples thickness and thickness distribution to step measurement by surface profiler DektakXT (Bruker, Karlsruhe, Germany).

(f)

Thickness measurement is performed by measuring the thickness when the stylus of the DektakXT passed through the coated film from the uncoated section of the substrate.

(g)

We focus on a coating thickness range of 4 to $20$ $\mathsf{\mu }$m using experimental limits of $\omega =1000,2000$ and 3000 and $t=300,450$ and 600 s. In these experimental conditions, the equation for thickness of the film fabricated by spin coating is given by the formula:

$$h\left(\omega \right)=\frac{1050}{\sqrt{1+0.00116671{\omega }^2}}\left(\mathsf{\mu }\mathrm{m}\right),$$

where $\mathsf{\mu }$m is the micro meter, i.e., 1 $\mathsf{\mu }$m = 10${}^{-6}$$\mathsf{\mu }$m.

Remark 1.

PDMS is a non-Newtonian fluid and, in [15], the authors pointed out that a study on the realistic flow for flattening of thickness through spin coating using non-Newtonian fluids. However, in [16], experiments were conducted with non-Newtonian fluids to study the applicability of non-Newtonian fluids to Newtonian fluid law. In this paper, the experiments were carried out using the most basic theory about the thickness of films made by the spin coating and non-Newtonian fluids. Based on the results, Equation (7) was used to modify the new equation.

After conducting the experiment, we can find that the measured thickness (MT) is slightly different from the theoretical thickness (TT). These differences are given by the Table 1 below.

Table 1. The thickness profile at each RPM and fixed time as 300 s.

RPM	TT ($\mathsf{\mu }$m)	MT ($\mathsf{\mu }$m)
500	$61.38$	$52.99$
1000	$30.73$	$25.09$
1500	$20.49$	$15.36$
2000	$15.37$	$11.16$
2500	$12.30$	$8.53$
3000	$10.25$	$6.60$
3500	$8.78$	$5.30$
4000	$7.68$	$4.26$
4500	$6.83$	$3.92$
5000	$6.15$	$3.54$
5500	$5.59$	$2.80$
6000	$5.12$	$2.72$

The existing equation for Newtonian fluids has five parameters: viscosity and density of material, spin coating speed and time, and initial height of the material before spin starting. Due to these various parameters, there is a difference in thickness to apply the existing equation to actual experiments. Equation (7) is an ideal equation containing at least five variables. However, it does not include variables such as the surface tension of the substrate. These variables and experimental conditions affect the difference between the theoretical thickness and the actual thickness.

This paper introduces a modified equation for thickness of the film fabricated by spin coating like Equation (7) that is based on curve estimation and polyhedron approximation. The mathematical accuracy of the proposed formula is examined through a statistical analysis of thickness [17,18]. Finally, the modified Newtonian fluid formula is used to construct an Excel-based thickness calculator for spin coating applications. Here, we use the Statistical Package for Social Science (SPSS software, IBM Corp., Armonk, NY, USA) to estimate the curve and the polyhedron that best matches the experimental data.

2. A Modified Equation for Thickness of the Film Fabricated by Spin Coating via the Curve Estimation

In this section, we establish the modified equation for thickness of the film fabricated by spin coating in the spin coating process as a curve estimated function, and begin by referring to Table 1 above. From Table 1 in Section 1, the thickness calculated using the conventional theoretical equation and the thickness obtained using a repetitive empirical formula differ considerably. Thus, the theoretical equation must be modified with a curve estimated function to provide a more accurate calculated film thickness.

2.1. Fixed Time at 300 s

The estimation method is carried out through three steps. We shall explain this step by step.

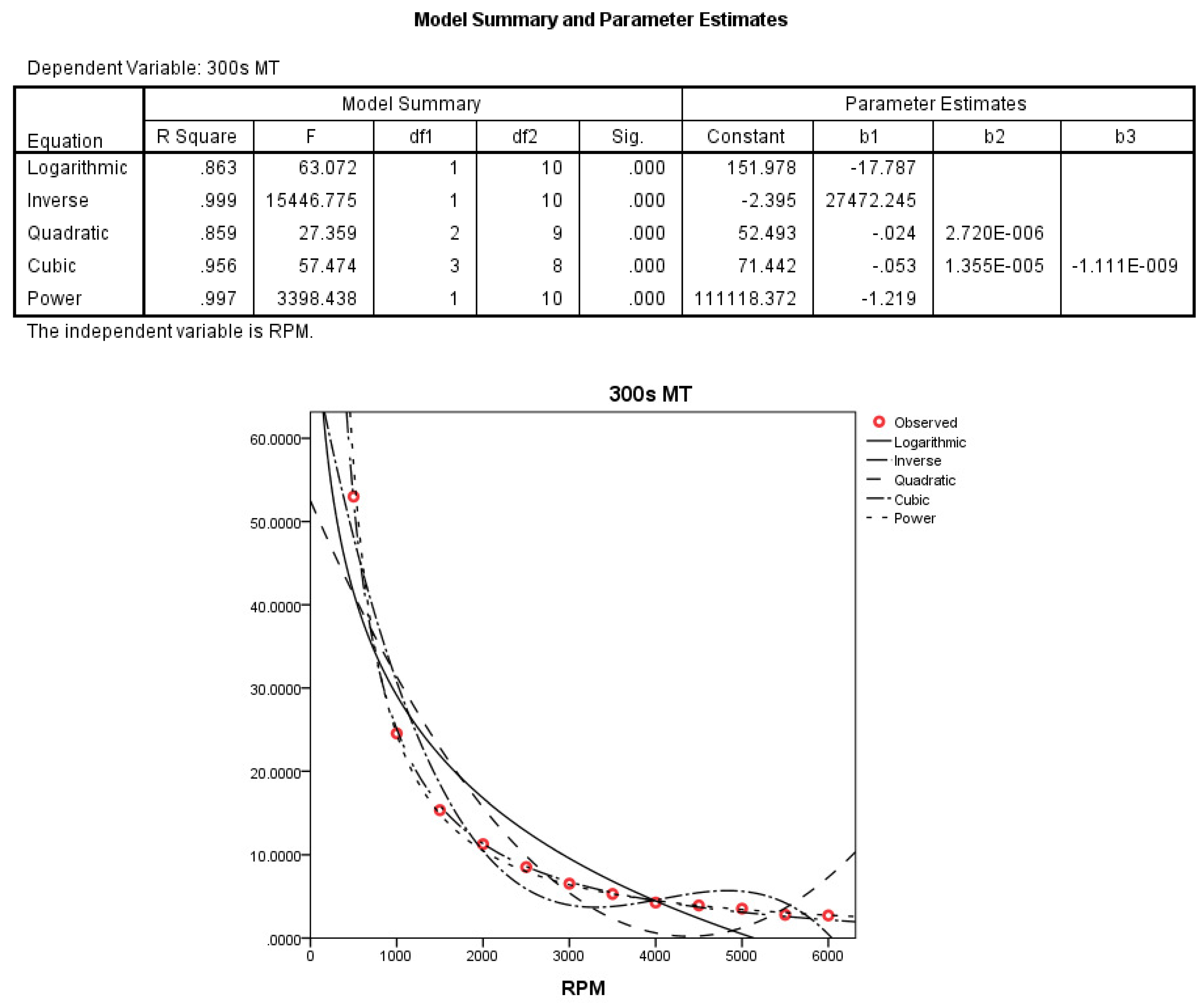
Step 1. We use the Curve Estimation of the regression analysis from the SPSS to make a curve estimate for the MT value of Table 1 above. There are 11 models available in the curve estimation menu. Among these, we select five models with the possibility of being suitable for MT data. They are Logarithmic, Inverse, Quadratic, Cubic and Power models. The results of the analysis are as follows (Figure 1).

Figure 1. Curve estimation for 300 s MT.

As shown in Figure 1 above, we can choose the power model and the inverse model based on the value of the coefficient of determination. The estimated functions are given by the formulas

$$\mathrm{power}:h_{power}\left(\omega \right)=111118.372{\omega }^{-1.2193}$$

and

$$\mathrm{inverse}:h_{inverse}\left(\omega \right)=-2.3948+\frac{27472.2453}{\omega }.$$

Both estimated functions are suitable for reducing the difference in film thickness mentioned above. It is also possible to select and use what is applicable to each company. Then, we obtain Table 2 involving the estimated function value and $R^2$ (coefficient of determination) value with respect to the MT value.

Table 2. Estimated function value and $R^2$ value for the MT value.

RPM	TT	MT	${\mathit{h}}_{\mathit{inverse}}$	${\mathit{h}}_{\mathit{power}}$
500	$61.375$	$52.991$	$52.550$	$56.876$
1000	$30.727$	$24.541$	$25.077$	$24.428$
1500	$20.490$	$15.357$	$15.920$	$14.900$
2000	$15.368$	$11.280$	$11.341$	$10.492$
2500	$12.295$	$8.528$	$8.594$	$7.992$
3000	$10.246$	$6.530$	$6.763$	$6.399$
3500	$8.783$	$5.301$	$5.454$	$5.303$
4000	$7.685$	$4.264$	$4.473$	$4.506$
4500	$6.831$	$3.920$	$3.710$	$3.903$
5000	$6.148$	$3.536$	$3.100$	$3.433$
5500	$5.589$	$2.801$	$2.600$	$3.056$
6000	$5.123$	$2.718$	$2.184$	$2.748$
$R^2$			0.999	0.997

As shown in Table 2 above, MT value and estimated function value are each somewhat different. To compensate for this, we implement the next step.

Step 2. Let $E_{300}$ denote the difference of the TT value and the MT value. That is to say, let $E_{300}$ = TT −MT. Then, we obtain Table 3 below.

Table 3. Estimated $E_{300}$ value.

RPM	TT	MT	${\mathit{E}}_{300}$
500	$61.375$	$52.991$	$8.384$
1000	$30.727$	$24.541$	$6.186$
1500	$20.490$	$15.357$	$5.133$
2000	$15.368$	$11.280$	$4.089$
2500	$12.295$	$8.528$	$3.767$
3000	$10.246$	$6.530$	$3.716$
3500	$8.783$	$5.301$	$3.481$
4000	$7.685$	$4.264$	$3.421$
4500	$6.831$	$3.920$	$2.911$
5000	$6.148$	$3.536$	$2.612$
5500	$5.589$	$2.801$	$2.788$
6000	$5.123$	$2.718$	$2.406$

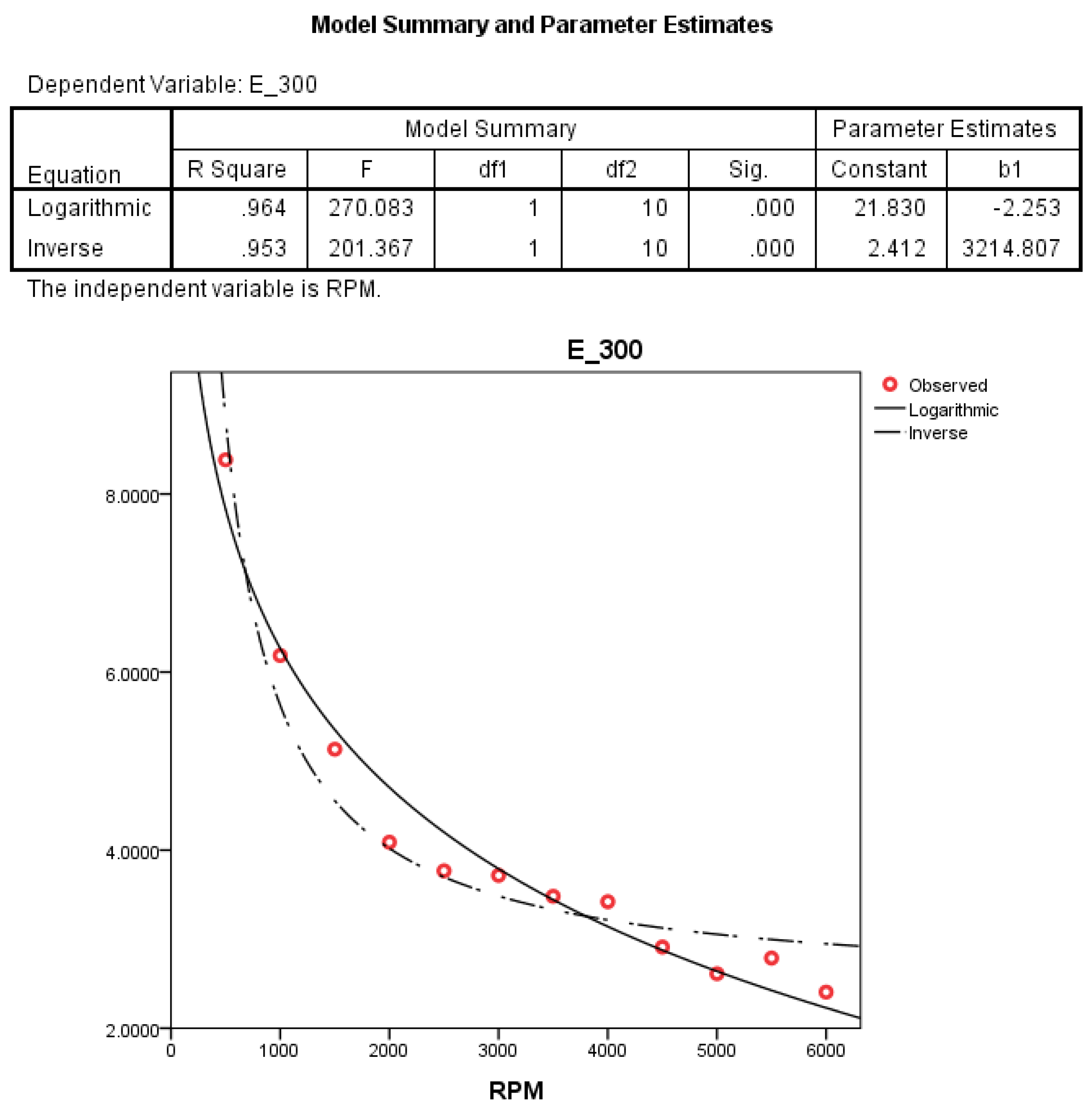
We then perform the curve estimate for the $E_{300}$ value by using the SPSS. We will use the Logarithmic model and the Inverse model as selected in Step 1. The results of the analysis are as follows (Figure 2).

Figure 2. Curve estimation for $E_{300}$.

Thus, the estimated functions are given by the formulas

$$\mathrm{Logarithmic}:h\left(\omega \right)=21.83-2.253ln\left(\omega \right)$$

and

$$\mathrm{Inverse}:h\left(\omega \right)=2.41182+\frac{3214.8068}{\omega }.$$

By using these functions, the estimated functions are given by the formulas

$$h_{log}\left(\omega \right)=\frac{1050}{\sqrt{1+0.00116671w^2}}-21.83+2.253ln\left(\omega \right)$$

and

$$h_{inv}\left(\omega \right)=\frac{1050}{\sqrt{1+0.00116671w^2}}-2.41182-\frac{3214.8068}{\omega }.$$

All four estimated functions given are suitable for reducing time and cost in the spin-coating process. To reduce the difference further, the following comparisons are made. The data obtained by each functions are given by the following Table 4 below.

Table 4. Data obtained by each estimated functions.

RPM	TT	MT	${\mathit{h}}_{\mathit{log}}$	${\mathit{h}}_{\mathit{inv}}$
500	$61.375$	$52.991$	$53.538$	$52.534$
1000	$30.727$	$24.541$	$24.462$	$25.100$
1500	$20.490$	$15.357$	$15.138$	$15.935$
2000	$15.368$	$11.280$	$10.665$	$11.349$
2500	$12.295$	$8.528$	$8.095$	$8.598$
3000	$10.246$	$6.530$	$6.456$	$6.763$
3500	$8.783$	$5.301$	$5.340$	$5.452$
4000	$7.685$	$4.264$	$4.543$	$4.469$
4500	$6.831$	$3.920$	$3.955$	$3.705$
5000	$6.148$	$3.536$	$3.510$	$3.093$
5500	$5.589$	$2.801$	$3.165$	$2.593$
6000	$5.123$	$2.718$	$2.895$	$2.176$
$R^2$			0.964	0.953

The function that the best describes the measured thickness (MT) value among the functions derived in Steps 1 and 2 undergo several iterations until the smallest error (see Table 5) is achieved. Here, the sum of squares error (SSE) is given. The red value for each RPM represents the smallest difference.

Table 5. The smallest error.

RPM	MT-${\mathit{h}}_{\mathit{inverse}}$	MT-${\mathit{h}}_{\mathit{power}}$	MT-${\mathit{h}}_{\mathit{log}}$	MT-${\mathit{h}}_{\mathit{inv}}$
500	$0.442$	$-3.885$	$-0.557$	$0.457$
1000	$-0.537$	$0.113$	$0.079$	$-0.560$
1500	$-0.563$	$0.457$	$0.219$	$-0.578$
2000	$-0.061$	$0.788$	$0.615$	$-0.069$
2500	$-0.066$	$0.536$	$0.434$	$-0.069$
3000	$-0.233$	$0.131$	$0.073$	$-0.233$
3500	$-0.153$	$-0.001$	$-0.039$	$-0.151$
4000	$-0.210$	$-0.243$	$-0.280$	$-0.206$
4500	$0.210$	$0.017$	$-0.035$	$0.215$
5000	$0.437$	$0.104$	$0.027$	$0.443$
5500	$0.201$	$-0.255$	$-0.364$	$0.208$
6000	$0.534$	$-0.031$	$-0.178$	$0.542$
SSE	$1.490$	$16.375$	$1.181$	$1.565$

To test compliance, we decide to use function with the smallest SSE value to approximate MT value. It is

$$h_{t=300}\left(\omega \right)\equiv h_{log}\left(\omega \right)=\frac{1050}{\sqrt{1+0.00116671w^2}}-21.83+2.253ln\left(\omega \right).$$

(8)

Step 3. We now establish the following hypothesis to test the function $h_{log}$ and the consistency of MT value. Let ${\mu }_{MT}$ and ${\mu }_h$ be population means of MT values and the estimated function $h_{log}$, respectively. Then, we formulate the following research hypothesis.

$$H_0:{\mu }_{MT}={\mu }_h,$$

$$H_1:{\mu }_{MT}\ne {\mu }_h.$$

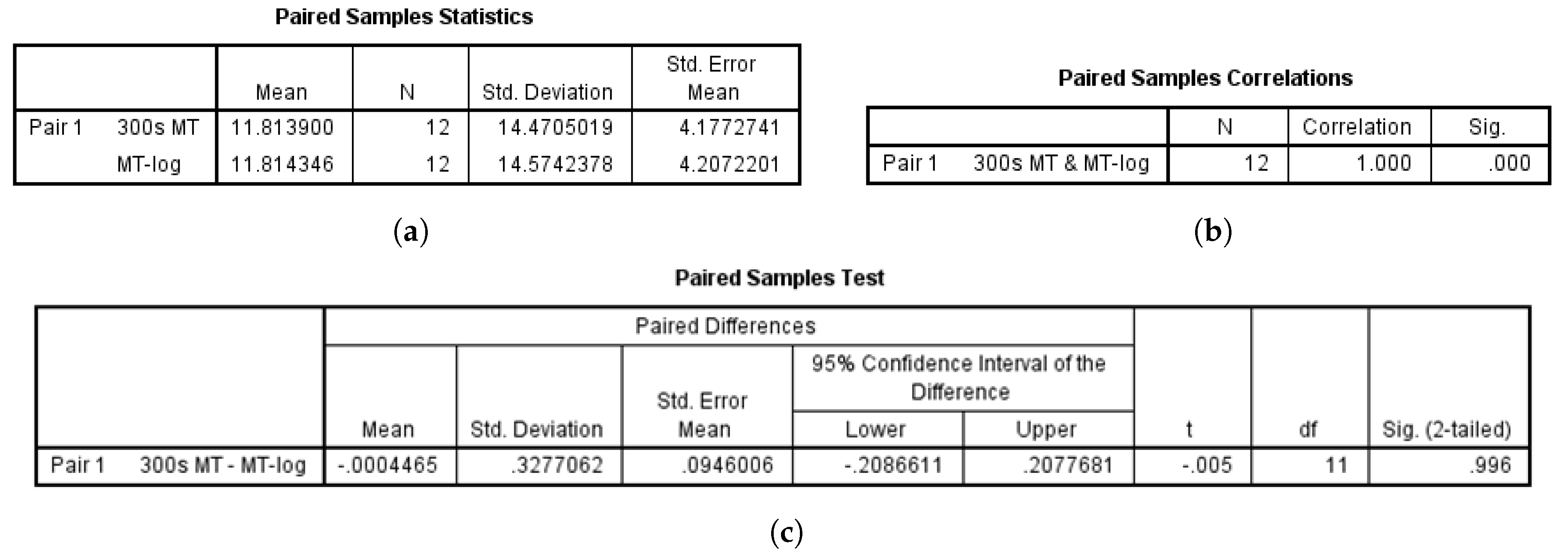
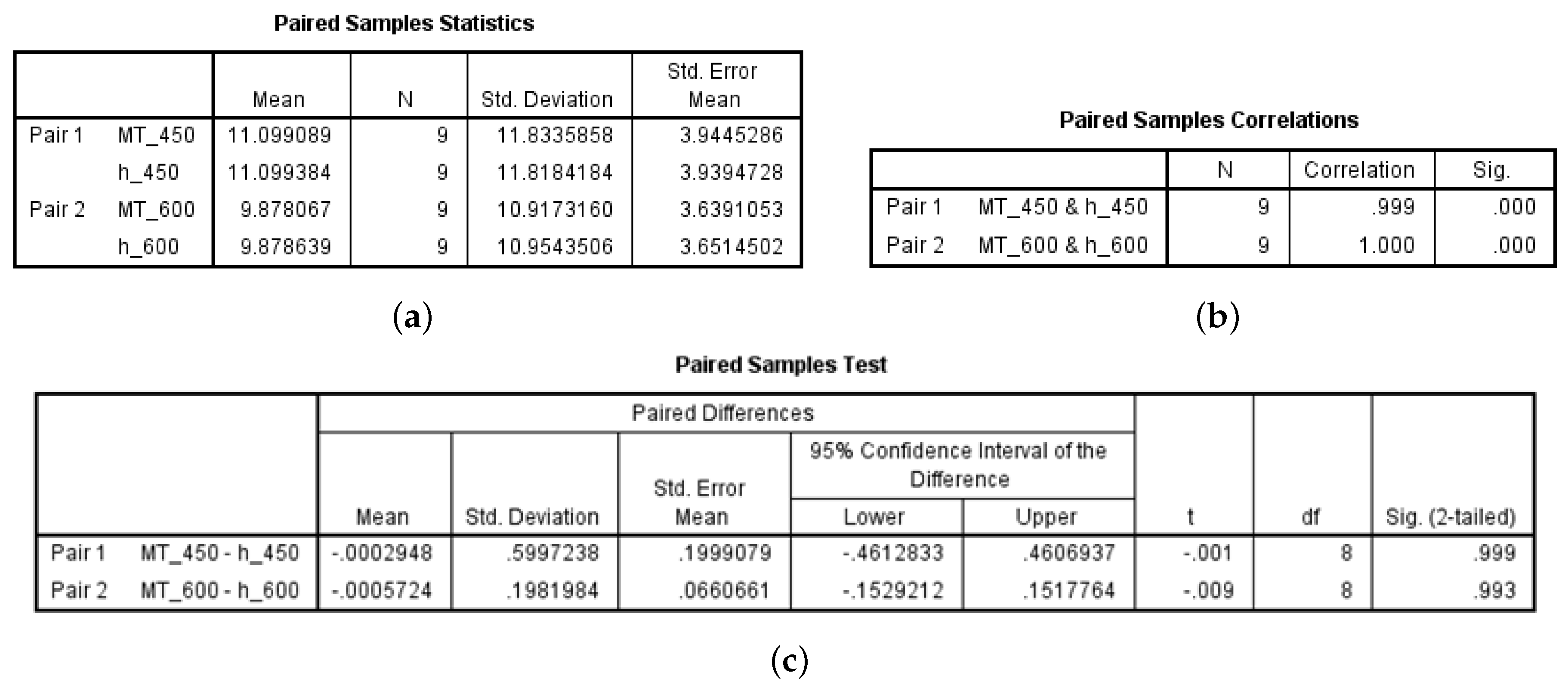
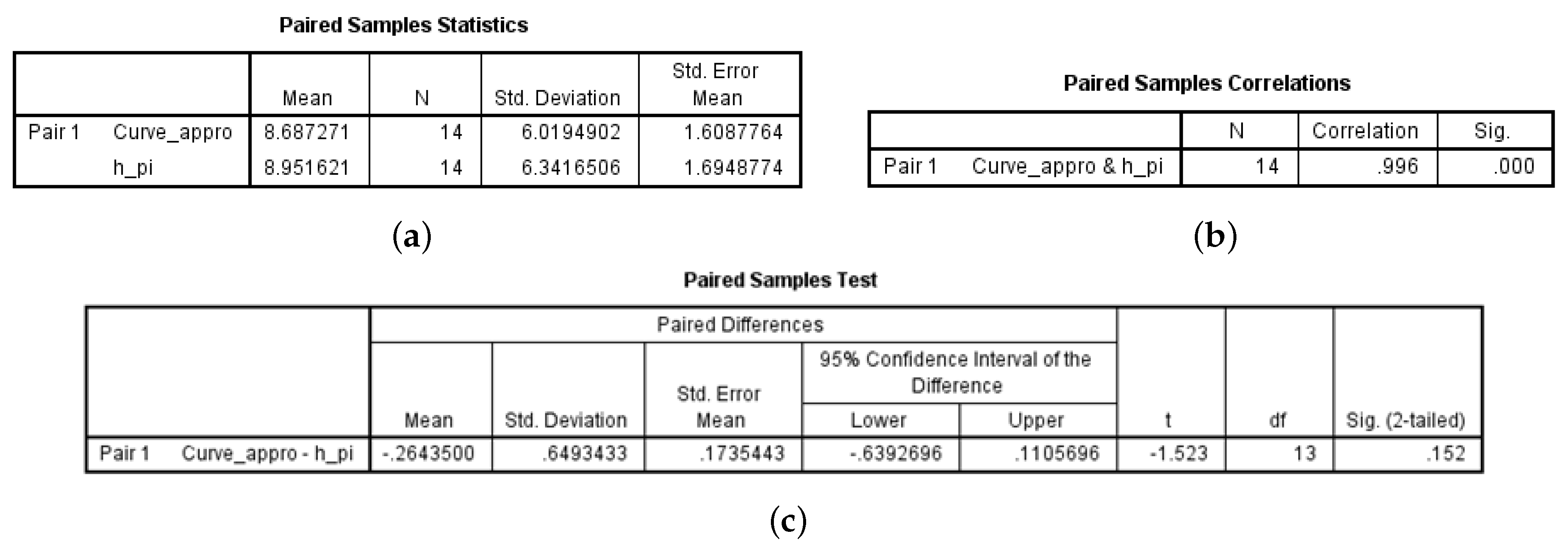
To test this hypothesis, the results of the paired Samples t-test at a significant level $\alpha =5\%$ are as follows (Figure 3).

Figure 3. t-test.

Therefore, we accept the null hypothesis ($H_0$) to obtain the statistical basis for estimating $h_{log}$ as an approximation of the MT value. From Steps 1 through 3, the best-estimated function corresponds to a fixed time of 300 s; i.e., the function given by Equation (8) is the best curve estimate for a fixed time of 300 s.

2.2. Fixed RPM at 1000

By the similar method as in Section 2.1, we can obtain the estimated function of the following case of fixed RPM at 1000. Then, the estimated function is given by the formula

$$h_{\omega =1000}\left(t\right)=\frac{1050}{\sqrt{1+3.889t}}-22.2524+2.69ln\left(t\right).$$

We also can compare the TT value, the MT value and the estimated function value as the following Table 6.

Table 6. Compared values when there is fixed RPM 1000.

TIME	TT	MT	${\mathit{h}}_{\mathit{w}=1000}$
100	$53.176$	$43.269$	$43.311$
200	$37.625$	$29.576$	$29.625$
300	$30.727$	$24.541$	$23.818$
400	$26.613$	$19.710$	$20.478$
500	$23.905$	$18.192$	$18.270$
600	$21.731$	$16.591$	$16.687$
700	$20.121$	$15.948$	$15.490$
800	$18.822$	$14.431$	$14.551$

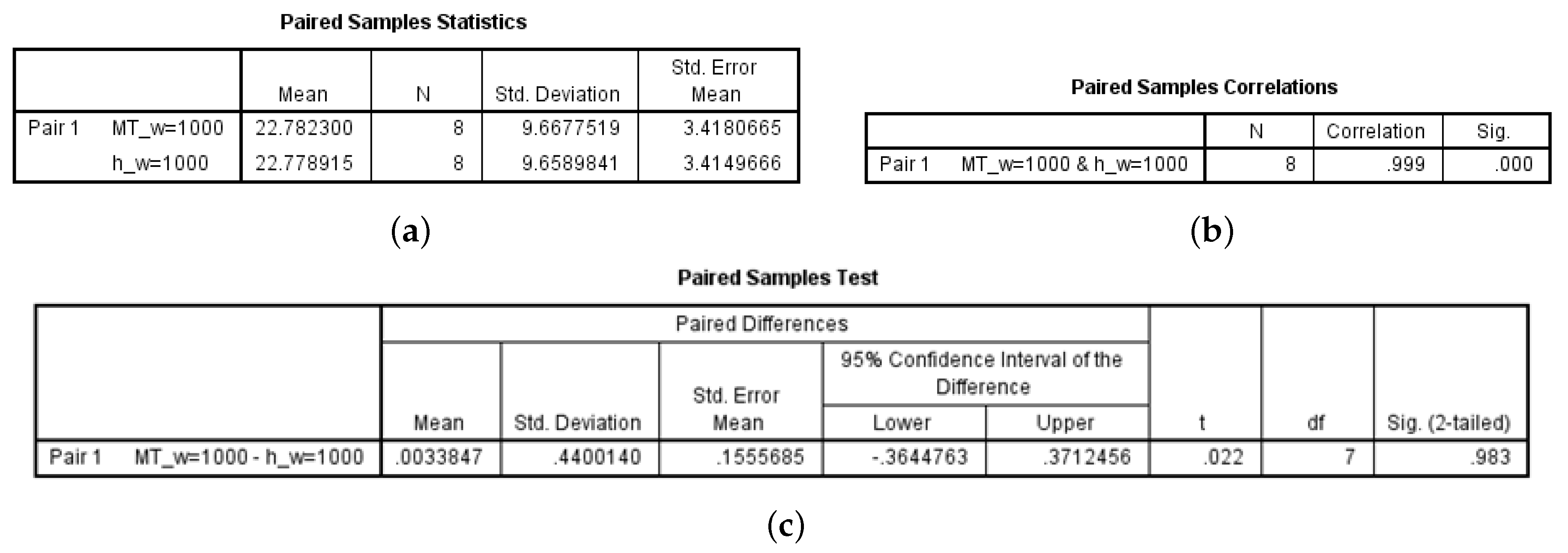
The statistical hypothesis test of the estimated function $h_{\omega =1000}\left(t\right)$ is as follows. The results of the paired Sample t-test to verify the homogeneity of the two groups, as shown in Step 3 of Section 2.1, are as follows (Figure 4).

Figure 4. t-test.

Therefore, we have a statistical basis to conclude that populations in both sample spaces are equal to each other at a significant level $\alpha =5\%$.

2.3. Other Cases

Through the process same as in cases $2.1$ and $2.2$ above, we obtain estimated functions for the time fixed at 450 and 600 s and the RPM fixed at 2000 and 3000. First, when the time is fixed at 450 and 600, we obtain estimated functions by setting the RPM as a variable as follows:

$$\begin{array}{cc}\hfill & h_{t=450}\left(\omega \right)=\frac{1050}{\sqrt{1+0.00175{\omega }^2}}-1.9398-\frac{4346.44}{\omega }\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & h_{t=600}\left(\omega \right)=\frac{1050}{\sqrt{1+0.00233342{\omega }^2}}-19.8476+2.104ln\left(\omega \right).\hfill \end{array}$$

Table 7 is about the value of MT${}_{t=450}$ and MT${}_{t=600}$, and estimated function values.

Table 7. The thickness profile at $t=450$ and $t=600$.

RPM	MT${}_{\mathit{t}=450}$	${\mathit{h}}_{\mathit{t}=450}$	MT${}_{\mathit{t}=600}$	${\mathit{h}}_{\mathit{t}=600}$
500	$38.969$	$39.510$	$36.454$	$36.664$
1000	$20.242$	$18.806$	$16.591$	$16.418$
1500	$11.639$	$11.894$	$10.177$	$10.029$
2000	$8.309$	$8.436$	$7.133$	$7.012$
2500	$6.134$	$6.361$	$4.996$	$5.309$
3000	$5.216$	$4.978$	$4.493$	$4.243$
3500	$4.199$	$3.990$	$3.580$	$3.532$
4000	$2.989$	$3.248$	$3.002$	$3.037$
4500	$2.199$	$2.672$	$2.478$	$2.681$

Results of the t-test for estimated function values and MT values are as follows (in Figure 5), respectively.

Figure 5. t-test.

Therefore, we see that the mean of populations of estimated functions and MT values are the same at a significant level $\alpha =5\%$.

Next, when the RPM is fixed, we obtain estimated functions for the time parameter

$$\begin{array}{c}\hfill h_{\omega =2000}\left(t\right)=\frac{1050}{\sqrt{1+15.5561t}}-3.2594-\frac{333.83446}{t}\end{array}$$

and

$$\begin{array}{c}\hfill h_{\omega =3000}\left(t\right)=\frac{1050}{\sqrt{1+35.00132t}}-12.8084+1.60735ln\left(t\right).\end{array}$$

We get MT${}_{\omega =2000}$, MT${}_{\omega =3000}$ and estimated values as shown in Table 8.

Table 8. The thickness profile at $\omega =2000$ and $\omega =3000$.

TIME	MT${}_{\mathit{\omega }=2000}$	${\mathit{h}}_{\mathit{\omega }=2000}$	MT${}_{\mathit{\omega }=3000}$	${\mathit{h}}_{\mathit{\omega }=3000}$
100	$19.908$	$20.015$	$12.224$	$12.340$
200	$13.986$	$13.893$	$8.493$	$8.257$
300	$11.280$	$10.996$	$6.530$	$6.606$
400	$9.240$	$9.206$	$5.662$	$5.695$
500	$7.977$	$7.978$	$5.265$	$5.118$
600	$7.133$	$7.052$	$4.493$	$4.719$
700	$5.984$	$6.325$	$4.472$	$4.430$
800	$5.703$	$5.735$	$4.235$	$4.210$

The results of the t-test are as follows (in Figure 6):

Figure 6. t-test.

In addition, we see that the mean of populations of estimated functions and MT values are the same at a significant level $\alpha =5\%$.

2.4. Summary of Section 2

From Section 2.1, Section 2.2 and Section 2.3, we derived a curve-estimated function for each case. Figure 7 shows that all functions provided an estimate that was statistically equivalent to the MT values. These results suggest that the estimated function can be induced for other RPMs and times.

Figure 7. Six curve estimated functions.

3. A Modified Equation for Thickness of the Film Fabricated by Spin Coating via the Polyhedron Approximation

In Section 2, we obtained six estimated functions regarding t and $\omega$. In this section, we are going to establish the polyhedron approximation with respect to the modified equation for thickness of the film fabricated by spin coating.

3.1. Polyhedron Approximation

We first take 13 points from $a_1$ to $a_{13}$ via the estimated functions obtained in Section 2. Using these points, we can divide into 13 areas of the domain $D=\left\{\right(t,\omega \left)\right|300\le t<\infty ,1000\le \omega <\infty \}$ as follows (Figure 8):

Figure 8. Separated domain.

Now, let $D_{i,j,k}$ be the sub-area of D with $a_i$, $a_j$ and $a_k$ as the vertex. Then, each area can be expressed in Table 9:

Table 9. Each sub-area of domain.

Sub-Area	Domain
$D_{1,2,3}$	$\left\{(t,\omega )\right|300\le t<450,1000\le \omega <4000-\frac{20}{3}t\}$
$D_{2,3,5}$	$\left\{(t,\omega )\right|300\le t<450,4000-\frac{20}{3}t\le \omega <2000\}$
$D_{2,4,5}$	$\left\{(t,\omega )\right|450\le t<600,1000\le \omega <5000-\frac{20}{3}t\}$
$D_{3,5,6}$	$\left\{(t,\omega )\right|300\le t<450,2000\le \omega <5000-\frac{20}{3}t\}$
$D_{4,5,7}$	$\left\{(t,\omega )\right|450\le t<600,5000-\frac{20}{3}t\le \omega <2000\}$
$D_{5,6,8}$	$\left\{(t,\omega )\right|300\le t<450,5000-\frac{20}{3}t\le \omega <3000\}$
$D_{5,7,8}$	$\left\{(t,\omega )\right|450\le t<600,2000\le \omega <6000-\frac{20}{3}t\}$
$D_{7,8,9}$	$\left\{(t,\omega )\right|450\le t<600,6000-\frac{20}{3}t\le \omega <3000\}$
$D_{4,7,10}$	$\left\{\right(t,\omega \left)\right|600\le t<\infty ,1000\le \omega <2000\}$
$D_{7,9,11}$	$\left\{\right(t,\omega \left)\right|600\le t<\infty ,2000\le \omega <3000\}$
$D_{9,11,12}$	$\left\{\right(t,\omega \left)\right|600\le t<\infty ,3000\le \omega <\infty \}$
$D_{8,9,12}$	$\left\{\right(t,\omega \left)\right|450\le t<600,3000\le \omega <\infty \}$
$D_{8,9,13}$	$\left\{\right(t,\omega \left)\right|300\le t<450,3000\le \omega <\infty \}$

Let $A_i$ be the intersection of the function values of $a_i$ for functions obtained in Section 2. We then split the graph of the two-parameter function into a plane passing through three points as shown below (Figure 9).

Figure 9. Planes.

Let ${\Pi }_{i,j,k}$ be the equation of plane passing through three points $A_i$, $A_j$ and $A_k$. Then, all equations of the plane are as follows (Table 10).

Table 10. Equation of planes.

Plane	Equation
${\Pi }_{1,2,3}$	$t+0.391529\omega +29.4118h-1401.53=0$
${\Pi }_{2,3,5}$	$t+0.677312\omega +64.2123h-2349.91=0$
${\Pi }_{2,4,5}$	$t+0.635932\omega +60.2894h-2238.84=0$
${\Pi }_{3,5,6}$	$t+0.295985\omega +64.2123h-1547.26=0$
${\Pi }_{4,5,7}$	$t+0.977515\omega +102.669h-3276.9=0$
${\Pi }_{5,6,8}$	$t+0.36767\omega +110.947h-2127.51=0$
${\Pi }_{5,7,8}$	$t+0.340246\omega +102.669h-2002.36=0$
${\Pi }_{7,8,9}$	$t+0.548209\omega +214.9h-3207.38=0$
${\Pi }_{4,7,10}$	$t+1.46929\omega +154.321h-4623.61=0$
${\Pi }_{7,9,11}$	$t+1.89665\omega +743.49h-9620.82=0$
${\Pi }_{9,11,12}$	$t+1.07435\omega +743.494h-7153.9=0$
${\Pi }_{8,9,12}$	$t+0.31053\omega +214.9h-2494.34=0$
${\Pi }_{6,8,13}$	$t+0.214127\omega +110.947h-1666.86=0$

Let $h_{{\Pi }_{i,j,k}}(t,\omega )$ denote the new expression of plane with respect to t and $\omega$. For example,

$$h_{{\Pi }_{1,2,3}}(t,\omega )=47.652-0.0133\omega -0.034t$$

and

$$h_{{\Pi }_{3,5,6}}(t,\omega )=24.096-0.0043\omega -0.0156t.$$

Using these, we obtain an approximate polyhedron function of the modified. Let

$$\begin{array}{c}\hfill h_{\Pi }(t,\omega )=\sum _{i,j,k}{h}_{{\Pi }_{i,j,k}}(t,\omega ){\chi }_{D_{i,j,k}},\end{array}$$

(9)

where ${\sum }_{i,j,k}$ means adding all the possible circumstances in Table 10 above. The function $h_{\Pi }(t,\omega )$ is the polyhedron approximation of the equation for thickness of the film fabricated by spin coating.

3.2. Verification of the Polyhedron Approximation

In this section, we try to perform statistical verification of the polyhedron approximation obtained in Section 3.1. In order to do this, we first choose 14 points except $a_j$’s, denoted by $b_j$’s, in Figure 10. These points $b_j$ are in the six curve estimation functions in Section 2. We are going to use these points to determine if the polyhedron function $h_{\Pi }(t,\omega )$ is an extension function with curve estimation functions.

Figure 10. Add Points for the verification.

We then obtain the following Table 11 below.

Table 11. Compared values.

${\mathit{b}}_{\mathit{i}}$	Coordinates	${\mathit{Curve}}_{\mathit{appro}}$	${\mathbf{\Pi }}_{\mathit{i},\mathit{j},\mathit{k}}$	${\mathit{h}}_{\mathbf{\Pi }}\left({\mathit{b}}_{\mathit{i}}\right)$
$b_1$	$(400,1000)$	$20.4781$	${\Pi }_{1,2,3}$	$20.7520$
$b_2$	$(300,1500)$	$15.1329$	${\Pi }_{1,2,3}$	$17.5020$
$b_3$	$(500,1000)$	$18.2702$	${\Pi }_{2,4,5}$	$18.3349$
$b_4$	$(300,2500)$	$8.0908$	${\Pi }_{3,5,6}$	$8.6660$
$b_5$	$(700,1000)$	$15.4906$	${\Pi }_{4,7,10}$	$15.9110$
$b_6$	$(500,2000)$	$7.9778$	${\Pi }_{5,7,8}$	$8.0531$
$b_7$	$(400,3000)$	$5.6956$	${\Pi }_{6,8,13}$	$5.7239$
$b_8$	$(700,2000)$	$6.3254$	${\Pi }_{4,7,10}$	$6.8300$
$b_9$	$(600,2500)$	$5.3086$	${\Pi }_{7,9,11}$	$5.6600$
$b_{10}$	$(500,3000)$	$5.1175$	${\Pi }_{8,9,12}$	$5.0570$
$b_{11}$	$(300,4500)$	$3.9517$	${\Pi }_{6,8,13}$	$3.7739$
$b_{12}$	$(700,3000)$	$4.4294$	${\Pi }_{9,11,12}$	$4.5120$
$b_{13}$	$(450,4500)$	$2.6720$	${\Pi }_{6,8,13}$	$2.4239$
$b_{14}$	$(600,4500)$	$2.6812$	${\Pi }_{9,11,12}$	$2.5420$

We can perform the statistical analysis to see whether the polyhedron approximation is correct. The results of the analysis are as follows (Figure 11):

Figure 11. t-test.

This shows that the significance value $0.152$ is greater than the significance level value $0.05$. Therefore, we can not reject the null hypothesis $h_0:{\mu }_{Curv{e}_{appro}}={\mu }_{h_{\Pi }}$. This means that values of $Curv{e}_{appro}$ are statistically equal to values of $h_{\Pi }$.

3.3. Summary of Section 3

We took points from $a_1$ to $a_{13}$ in the domain of $f_{\Pi }(t,\omega )$ using the six curves described in Section 2 to find the approximate function for the binary function $f(t,\omega )$. The domain was then divided into sub-areas $D_{i,j,k}$, passing through three points, $a_i,a_j$, and $a_k$. We obtained equations of planes ${\Pi }_{i,j,k}$ passing through $A_i,A_j$, and $A_k$, corresponding to the MT values of $a_i,a_j$, and $a_k$ at each vertex of $D_{i,j,k}$, respectively. We then estimated the polyhedron approximation, $h_{\Pi }(t,\omega )$, as shown in Equation (9). To assess the suitability of the polyhedron approximation $h_{\Pi }$, we set 14 points of $b_1,\cdots ,b_{14}$ in the domain D. The values listed in Table 12 were determined by substituting ${\mathit{Curve}}_{\mathit{a}}\mathit{ppro}$ and $h_{\Pi }$. Then, a paired sample t-test was performed between ${\mathit{Curve}}_{\mathit{a}}\mathit{ppro}$ and $h_{\Pi }$ values, i.e., the curve approximation data from Section 2 and the data obtained by substituting the equation of polyhedron $h_{\Pi }$, respectively, to determine whether the mean was statistically identical within $5\%$ of the significance level. Our results revealed that the polyhedron approximation $h_{\Pi }$ contained six of the curves from Section 2; thus, our function provides a good approximation of the binary function $f(t,w)$.

Table 12. Compared values.

$\mathit{h}\left(\mathsf{\mu }\mathbf{m}\right)$	$\mathit{\omega }$	t	t	$\mathit{\omega }$
4	1000 2000 3000	- 1251 925	300 450 600	4453 3493 3150
5	1000 2000 3000	- 956 526	300 450 600	3692 2990 2623
6	1000 2000 3000	- 752 360	300 450 600	3181 2613 2265
7	1000 2000 3000	- 606 269	300 450 600	2809 2321 2002
8	1000 2000 3000	6194 498 211	300 450 600	2522 2087 1799
9	1000 2000 3000	3007 415 171	300 450 600	2294 1896 1637
10	1000 2000 3000	2062 350 143	300 450 600	2106 1737 1503
15	1000 2000 3000	749 174 71	300 450 600	1511 1224 1078
20	1000 2000 3000	418 100 44	300 450 600	1187 945 846

4. Application: Target Verification

In this section, we try the target verification. We first set the target thickness and thus obtain the required time or RPM for each cases. Finally, we again conduct an experiment. The maximum rotation time for the Spin Coater ACE-200 is 999 s. Thus, the likelihood of error in the coating thickness estimations below $4\mathsf{\mu }\mathrm{m}$ and above $20\mathsf{\mu }\mathrm{m}$ is high.

The following table shows the results obtained by using the curve estimation function obtained in Section 2 when the RPM is fixed at $\omega =1000,2000$ and 3000, and the rotation time t is fixed at $t=300,450$ and 600, respectively (see Table 12).

With regard to Table 12, we discuss the thickness value for the parameters specified. When the RPM is fixed, there is no value at $\omega =1000$, as shown in the table. Because the function $h_{w=1000}\left(t\right)=\frac{1050}{\sqrt{1+3.889t}}-22.2524+2.69ln\left(t\right)$ has a local minimum value $7.847$ at $t=9793.59$, there is no value from $4\mathsf{\mu }\mathrm{m}$ to $7\mathsf{\mu }\mathrm{m}$. Therefore, when a thickness of $4\mathsf{\mu }\mathrm{m}$ to $7\mathsf{\mu }\mathrm{m}$ is desired, a speed higher than 1000 RPM is required. Additionally, because the ACE-200 system has a maximum spin time of 999 s, it cannot provide a thickness in the desired range of $8\mathsf{\mu }\mathrm{m}$ to $10\mathsf{\mu }\mathrm{m}$ when $\omega =1000$. We give the following summary in Table 13:

Table 13. Suitable RPM with fixed rotation time.

Target Thickness $\left(\mathsf{\mu }\mathbf{m}\right)$	Suitable RPM
11–20	less than 1000
7–10	1000–3000
4–6	more than 3000

In another experiment, the rotation time t is held fixed at $t=300,450$ and 600 s. To obtain the desired thickness, as shown in Table 12, the RPM could be adjusted for the fixed time frame. In contrast to the previous case in which the RPM was fixed, here we are able to adjust the RPM to produce the desired thickness within the allowable range, given a fixed rotation time. Therefore, it appears to be more effective to fix the rotation time t to obtain the target film thickness in spin coating processes.

Table 14 lists the thicknesses determined by substituting RPM for the rotation time t for each coating thickness into $h_{\Pi }$ from Section 3. To compare these values with MT values, we prepare three samples in which the rotation time is fixed at 450 s. The MT${}_{t=450}$ values in the following table represent the average values of the raw data of the three samples.

Table 14. RPMs for the target thickness, polyhedron values and MT value.

$\mathit{h}\left(\mathsf{\mu }\mathbf{m}\right)$	t	$\mathit{\omega }$	${\mathit{h}}_{\mathbf{\Pi }}\left(\mathsf{\mu }\mathbf{m}\right)$	MT${}_{\mathit{t}=450}\left(\mathsf{\mu }\mathbf{m}\right)$
4	300 450 600	4453 3493 3150	$3.863$ $4.602$ $4.432$	3.777
5	300 450 600	3692 2990 2623	$5.309$ $5.271$ $5.340$	4.956
6	300 450 600	3181 2613 2265	$6.280$ $6.515$ $6.271$	6.058
7	300 450 600	2809 2321 2002	$7.337$ $7.479$ $6.955$	6.390
8	300 450 600	2522 2087 1799	$8.571$ $8.251$ $8.981$	7.481
9	300 450 600	2294 1896 1637	$9.552$ $9.757$ $10.510$	8.587
10	300 450 600	2106 1737 1503	$10.360$ $11.426$ $11.783$	9.723
15	300 450 600	1511 1224 1078	$17.356$ $16.813$ $15.820$	15.163
20	300 450 600	1187 945 846	$21.665$ − −	21.872

Actually, this result indicates that the results in Section 2 and Section 3 and the values observed by the experiment are the same within the margin of error.

5. Conclusions

5.1. Importance of Results and Formulas in This Paper

Spin coating technology is useful in modern industrial society. However, it still relies on Formula (7), which was introduced in the 1950s, to determine spin coating film thickness. This conventional approach requires extensive time and experimentation to obtain the desired coating thickness, which increases costs. Here, we propose an alternative to this conventional approach. Using the function $h_{\Pi }$, we can estimate the desired coating thickness given the rotation time and RPM, according to the conditions of the coating device. The coating thicknesses achieved using the proposed approach were within the error range expected. In an example described in Section 4, we were able to obtain the coating thickness based on a fixed rotation time and RPM, using the six functions developed in Section 2. Additionally, the binary function $h_{\Pi }(t,\omega )$ estimated in Section 3 allows users to simulate the desired thickness without having to perform an actual experiment. As a result, many spin coating companies will save time and money using the method implemented in this study.

5.2. Another Approach

Our original goal was to express the equation for thickness of the film fabricated by spin coating as a new binary function. In Section 2, curved estimates were determined for each fixed variable, and, in Section 3.1, an approximation of the polyhedron function was acquired through the plane approximation method. In the next research work, we will attempt to obtain an approximation of the equation for thickness of the film fabricated by spin coating as a binary function of the curved estimate and polyhedron function. In Section 3, we split the domain D using points $a_1$ through $a_{13}$. Using a similar method, we obtained the function $h_{{\Pi }_n}$ with n-splitting points. Then, $h_{\Pi }\equiv h_{{\Pi }_{13}}$. By adding more splitting points, we can derive the function $f(t,\omega )$ as the limit of $h_{{\Pi }_n}(t,\omega )$. That is,

$$h(t,w)=\underset{n\to \infty }{lim}{h}_{{\Pi }_n}(t,\omega ).$$

5.3. Expected Results

In this study, we estimated the bivariate function $h(t,\omega )$ by assuming rotation time and RPM as independent variables, while the other factors remained fixed. However, the factors affecting the actual coating thickness are $h_0$, $\rho$, and $\mu$. Thus, the addition of other variables to the function formula should improve the accuracy of the spin coating thickness prediction. Considering all of the factors that affect thickness would make the formula too complex, but given that spin coating companies use fixed coating materials, $\rho$ and $\mu$ can be considered constants.

Therefore, in future studies, we will attempt to estimate a three-variable function $h(t,\omega ,h_0)$ by setting the independent variables t, $\omega$, and $h_0$.

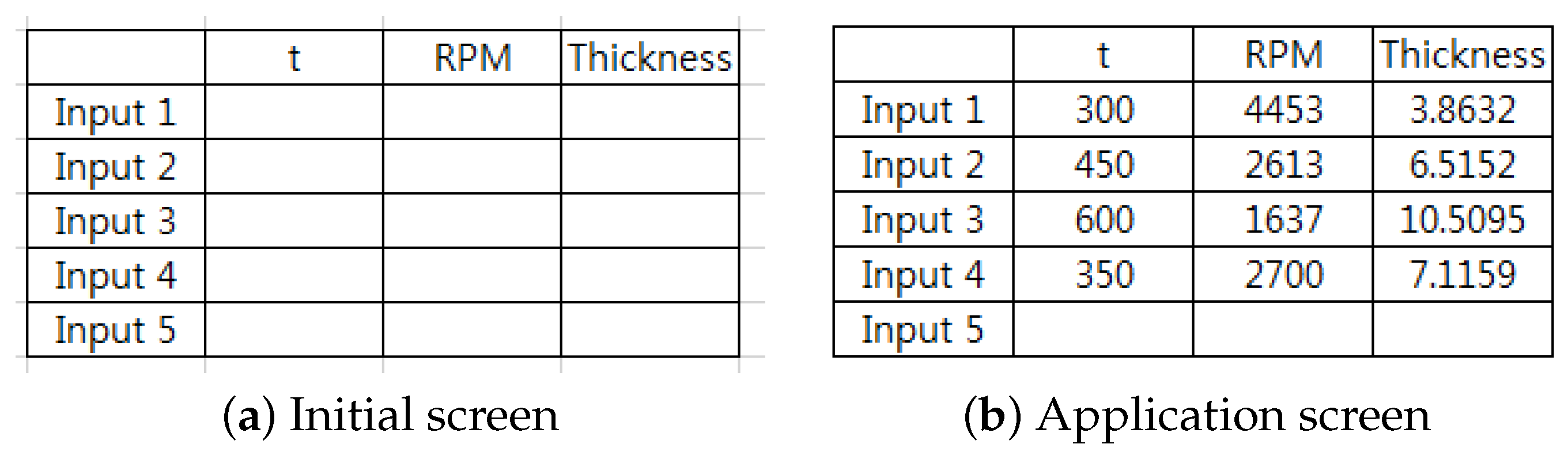
5.4. Capture of the Thickness Calculator by the Excel Program

Based on the results of this study, we developed a thickness calculator using the Microsoft Office Excel program (Microsoft Corp., Redmond, WA, USA). Here, we show screen shots of the initial screen and application screen of the calculator. This calculator can predict the thickness without actual experimentation. As you can see in Figure 12, Figure 13 and Figure 14 below, they are shown for $t=150$ and $\omega =2700$. We will supply our calculator to companies free of charge, in order to help them achieve the desired coating thickness in spin coating processes.

Figure 12. Calculator for t and RPM.

Figure 13. Calculator for RPM.

Figure 14. Calculator for t.

We finish this paper by giving a remark.

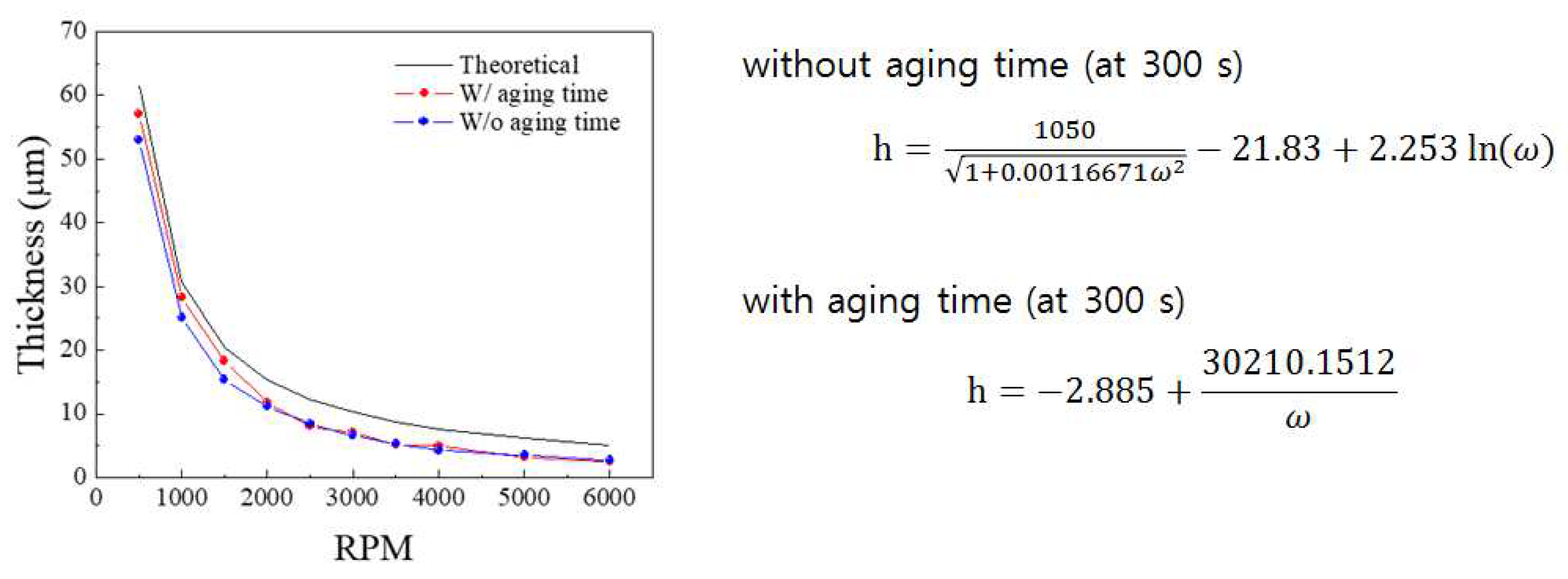
Remark 2.

We are working on data at fixed conditions of 300 s, as well as different times or fixed RPM conditions, and we will do further research. As shown in Figure 15 below, the experiment was conducted under different conditions, and it was confirmed that the thickness was changed due to the parameters that were not considered in the existing equation. For example, when the aging time is given after spin coating for a fixed condition of 300 s, the thickness changes as shown in the attached figure and the equation, and the equation obtained through curve estimation also changes. In addition, it is expected that process conditions for the manufacture of the desired thickness can be derived simply. In addition, it will be possible to apply to other materials, and further experiments are planned.

Figure 15. Further research.