An Image Style Transfer Network Using Multilevel Noise Encoding and Its Application in Coverless Steganography
Abstract
1. Introduction
- Diversity loss is used to prevent the network from falling into local optimization and allows the network to generate diversity image style transfer results.
- Residual learning is introduced to improve the network training speed significantly.
- Coverless steganography and image style transfer are combined, a coverless steganography scheme is presented. The performance of our coverless steganography scheme is good in steganographic capacity, anti-steganalysis, security, and robustness.
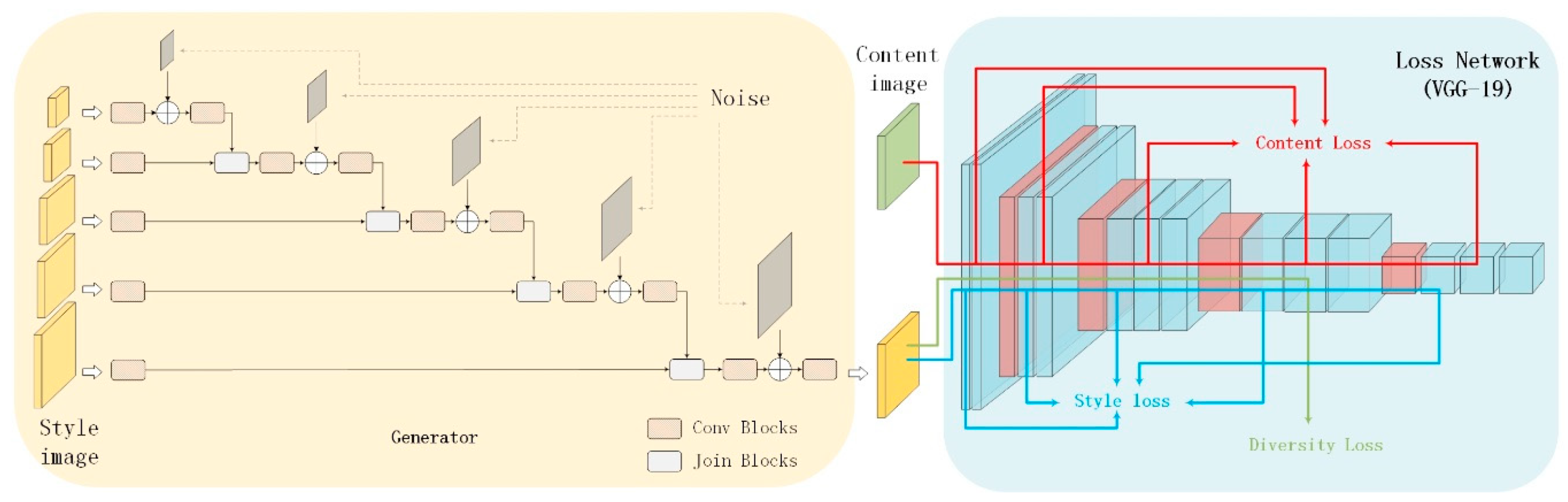
2. MNE-Style: Image Style Transfer Network Using Multilevel Noise Encoding
2.1. Generator using Multilevel Noise Encoding
2.2. Loss Function
2.2.1. Content Loss
2.2.2. Style Loss
2.2.3. Diversity Loss
2.2.4. Total Loss
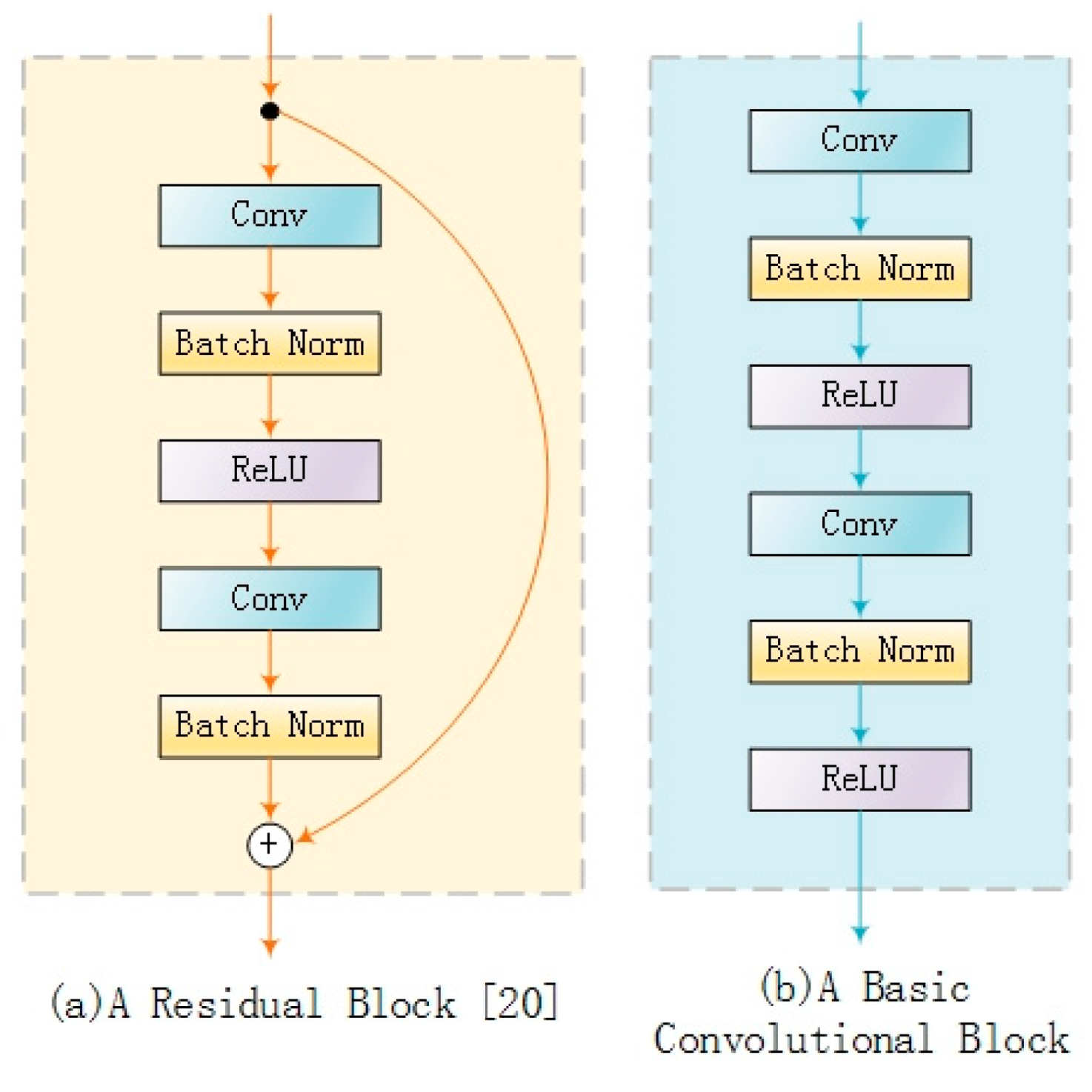
2.3. Residual Learning
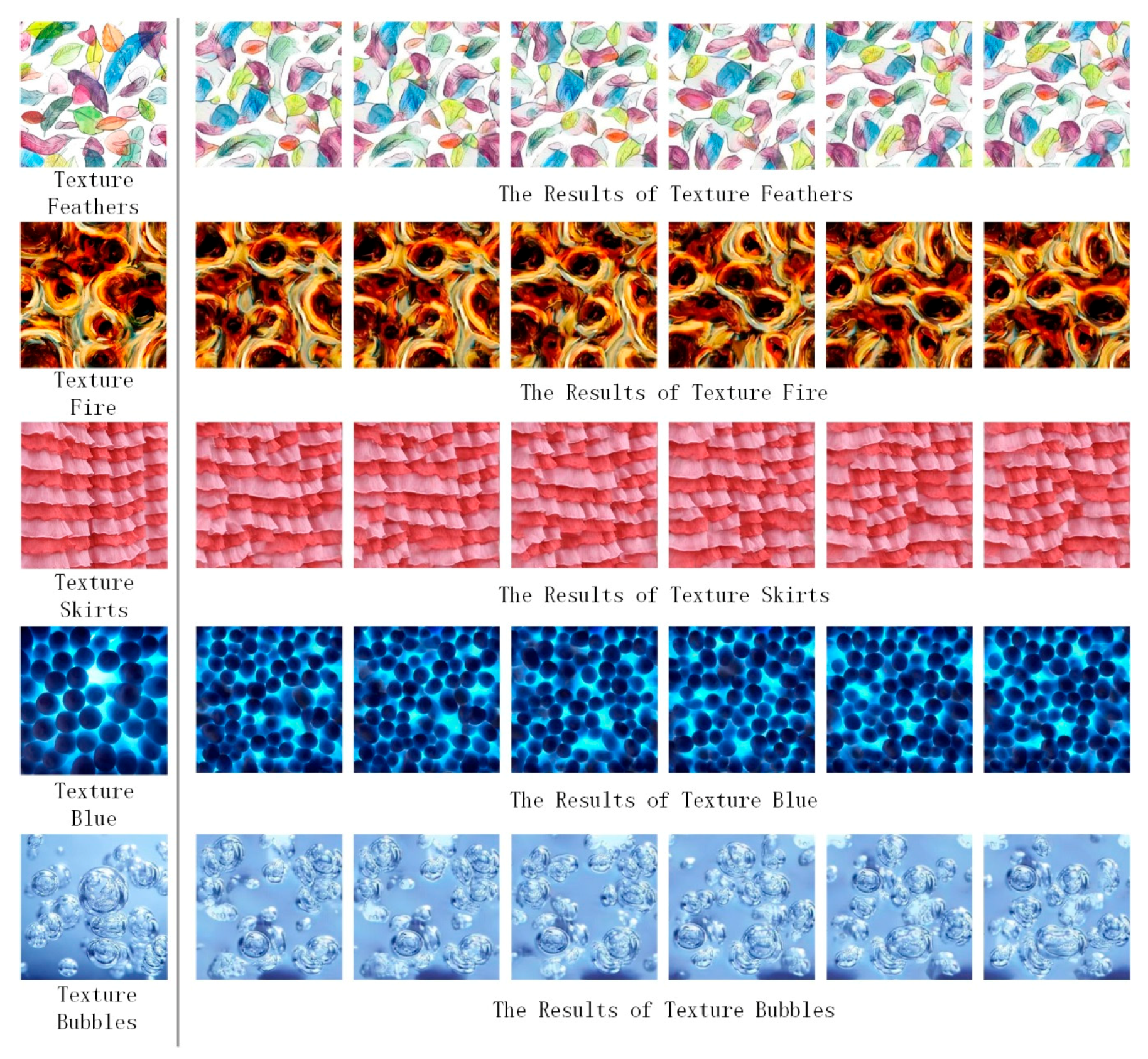
2.4. Diversified Texture Synthesis
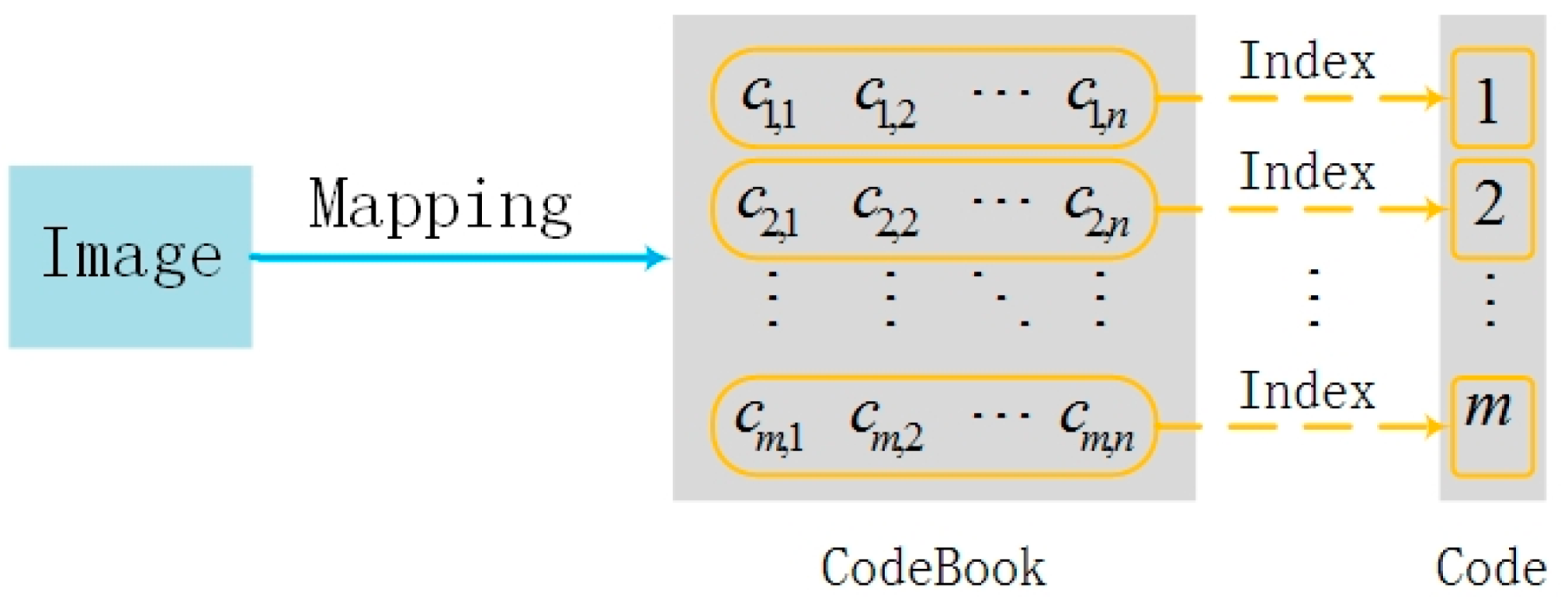
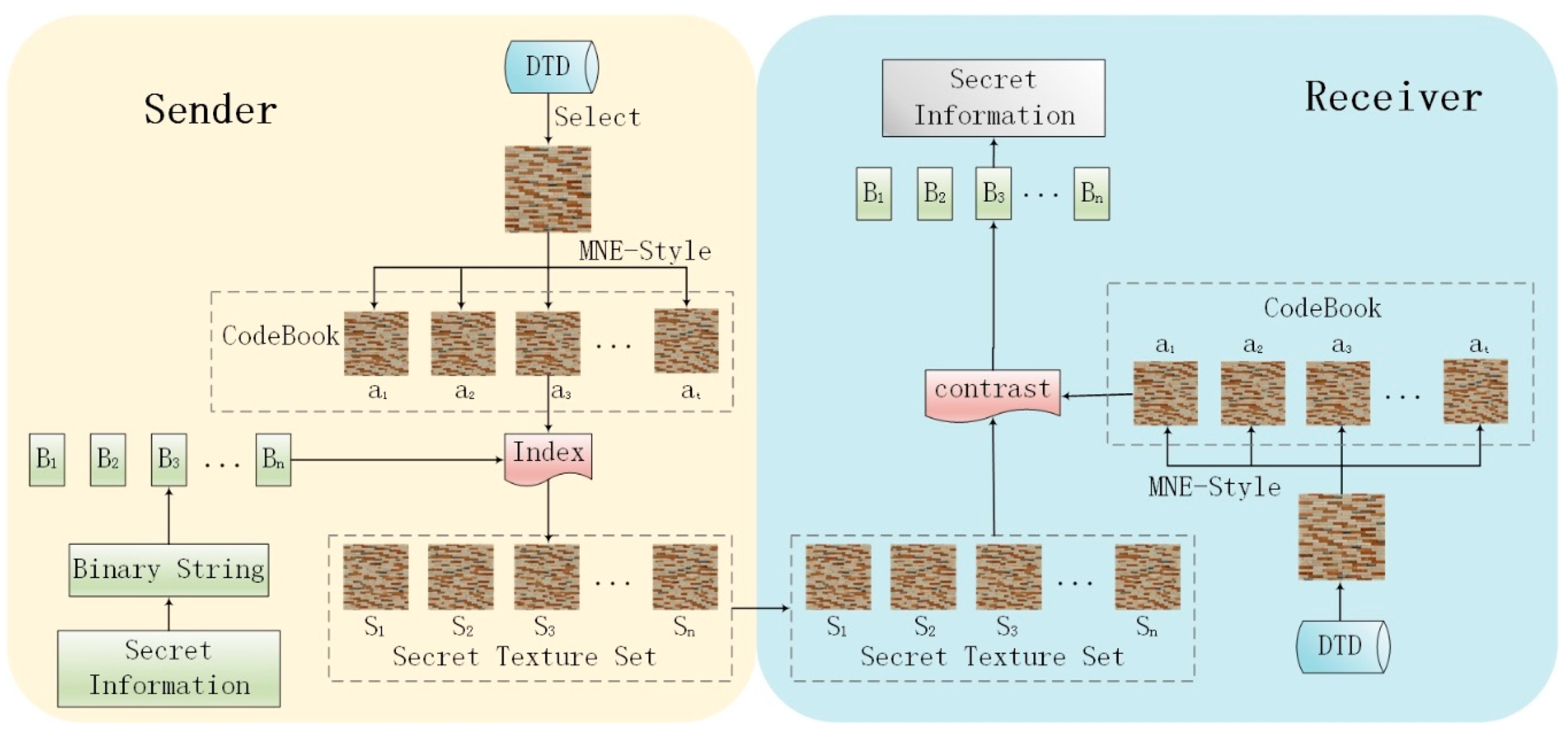
3. The Integration Scheme of Coverless Steganography
3.1. Hiding Method
- Step 1.
- One texture image from the public DTD dataset is selected and input into the MNE-Style network. The image step size of diversity loss , diversity loss weight , and style loss weight are specified. The diversify texture synthesis is performed. The collection of these diverse texture synthesis results is used as a codebook.
- Step 2.
- According to the step size of diversity loss, the various texture synthesis results generated by the MNE-Style are numbered in order. For example, , the diversity texture synthesis result is sequentially marked as 0000 0000, 0000 0001, 0000 0010, 0000 0011, ..., 1111 1111 according to the output numbers 1, 2, 3, 4, ..., 256. These 8-bit code streams are mapped to codes corresponding to the codebook.
- Step 3.
- The secret information is segmented according to the codeword number in codeword book. The segmentation results are B1, B2, ..., Bn, the corresponding image set is found in the codeword book according to the results of B1, B2, ..., Bn. In the order of B1 to Bn, the to-be-transmitted information hiding codeword set constitutes.
3.2. Extraction Method
- Step 1.
- The closest original texture image is selected in the DTD according to the received image information of the secret texture image set.
- Step 2.
- The selected DTD texture image is used as an input of the MNE-Style network, and the coverless steganography codeword book is synthesized via network according to received network parameters. Network parameters include the image step size of diversity loss , diversity loss weight , and style loss weight .
- Step 3.
- The various texture synthesis results generated by the MNE-Style network are numbered in order according to the image diversity generation step size.
- Step 4.
- The peak signal to noise ratio (PSNR) of each image in the secret texture image set and each image in the codeword book are calculated. The image is considered to correspond to the secret information represented by the current image of the codeword book when the value is the largest (or infinite). All secret information segments are connected in order to obtain the hidden texts.
4. Experimental Results
4.1. Diversity of Image Style Transfer Results
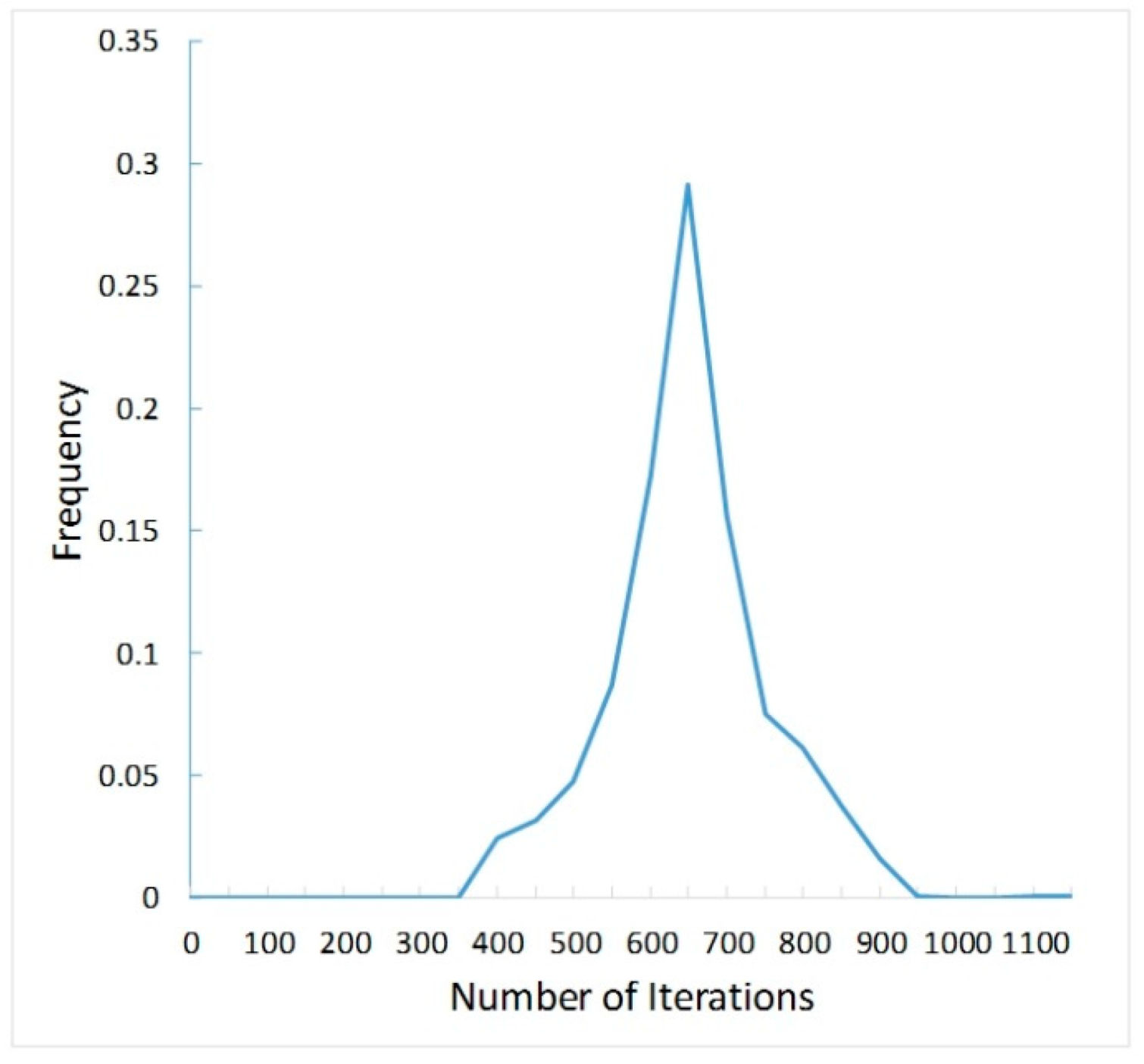
4.2. Network Speed
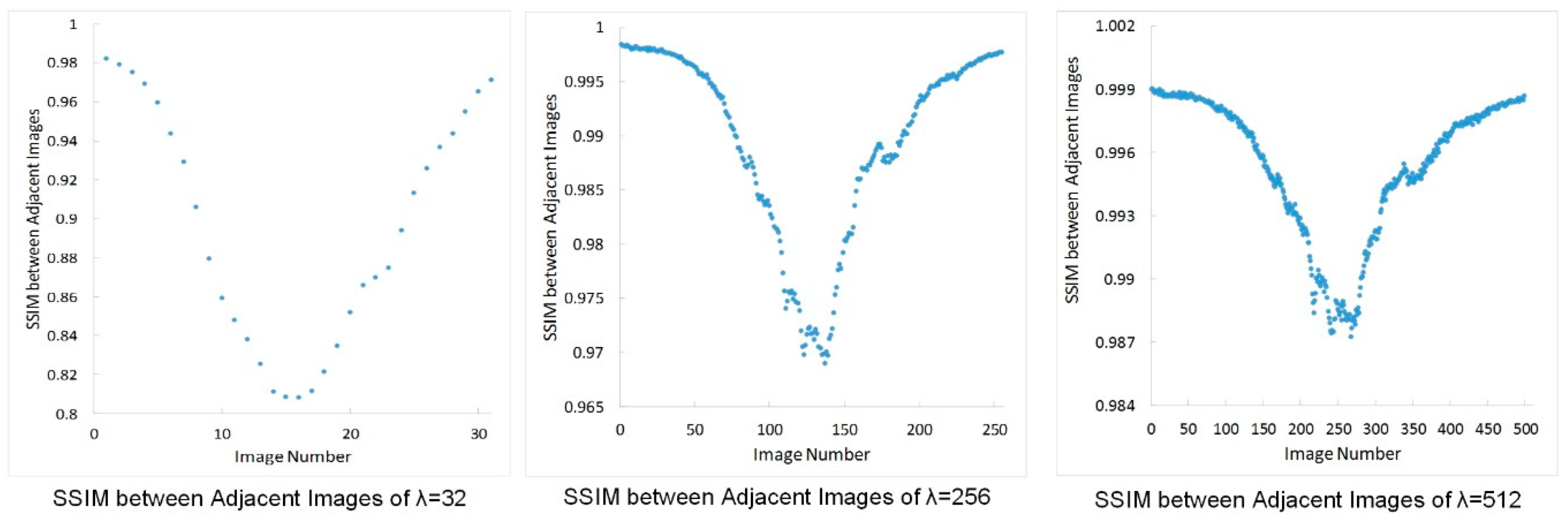
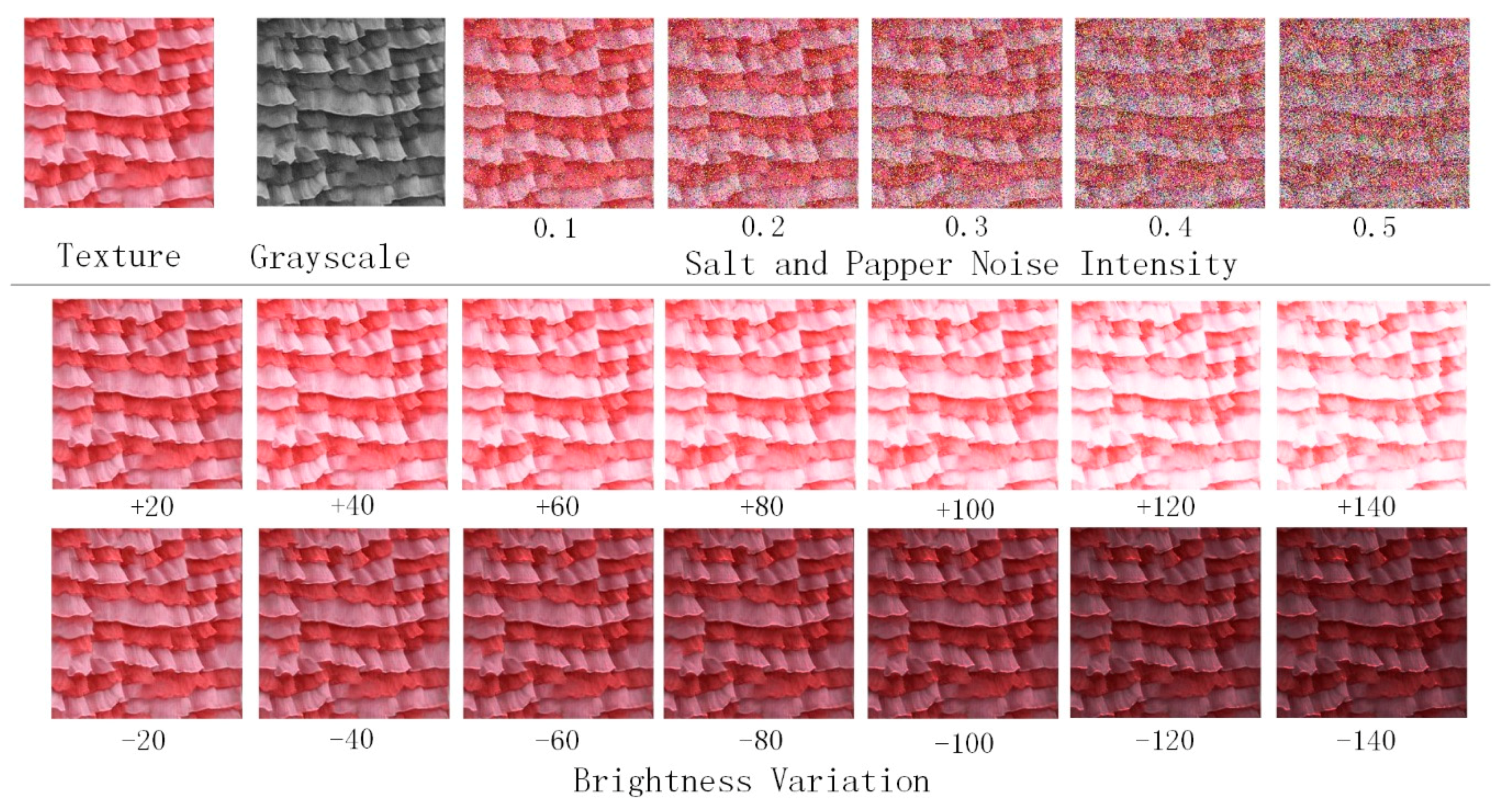
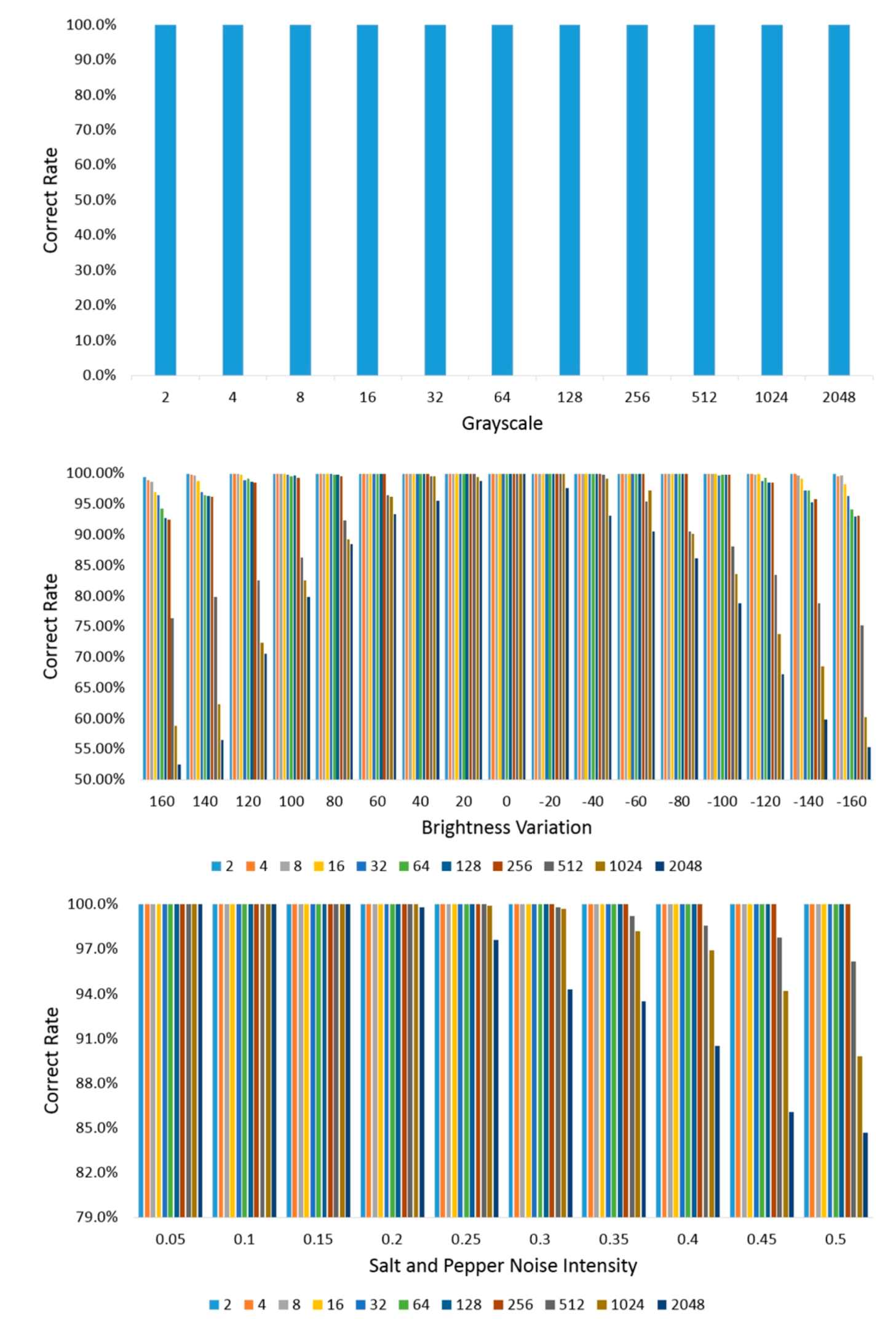
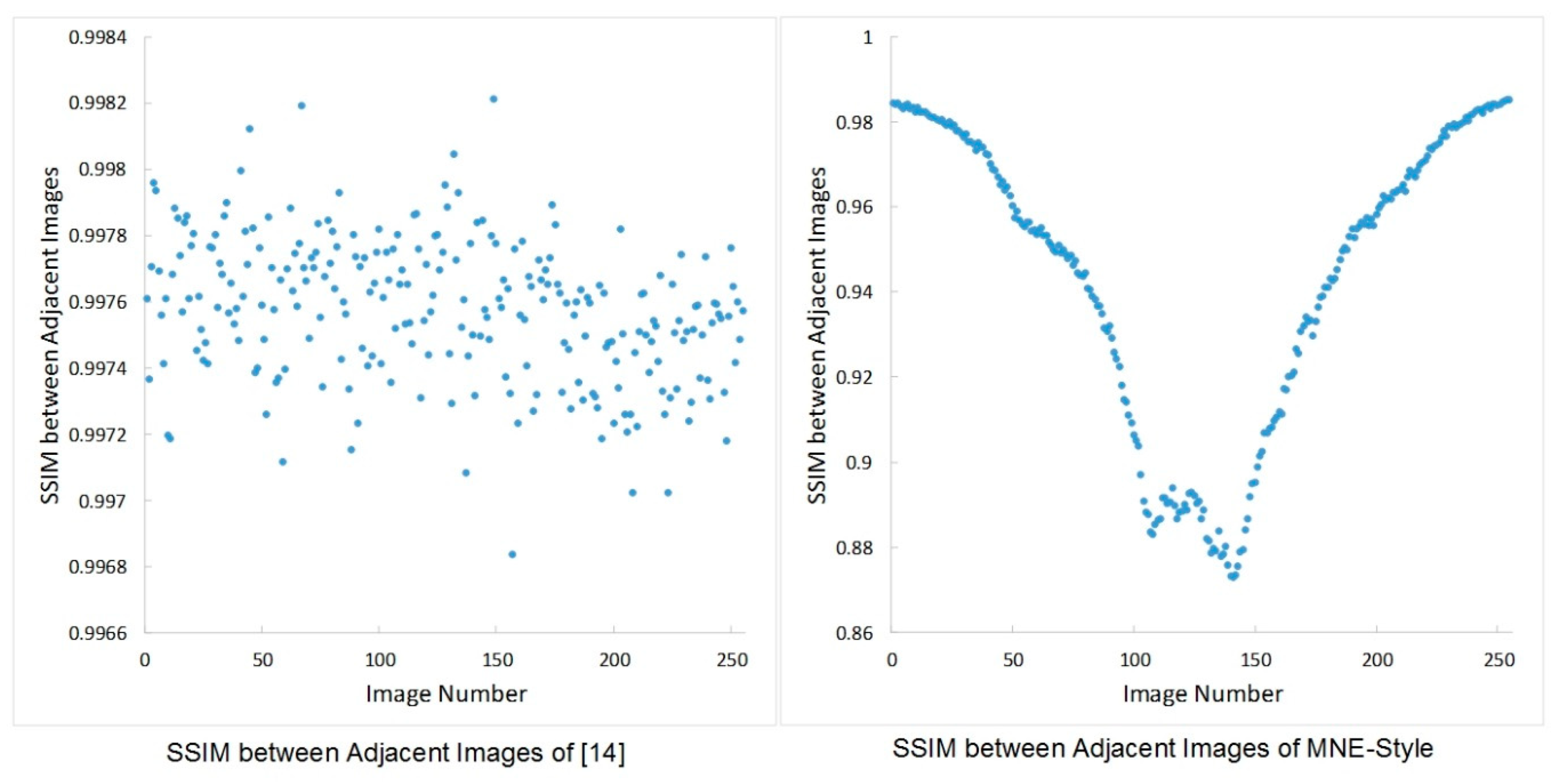
4.3. Diversity Texture Synthesis Results and Robustness of Steganography
4.4. The Capacity of Coverless Steganography
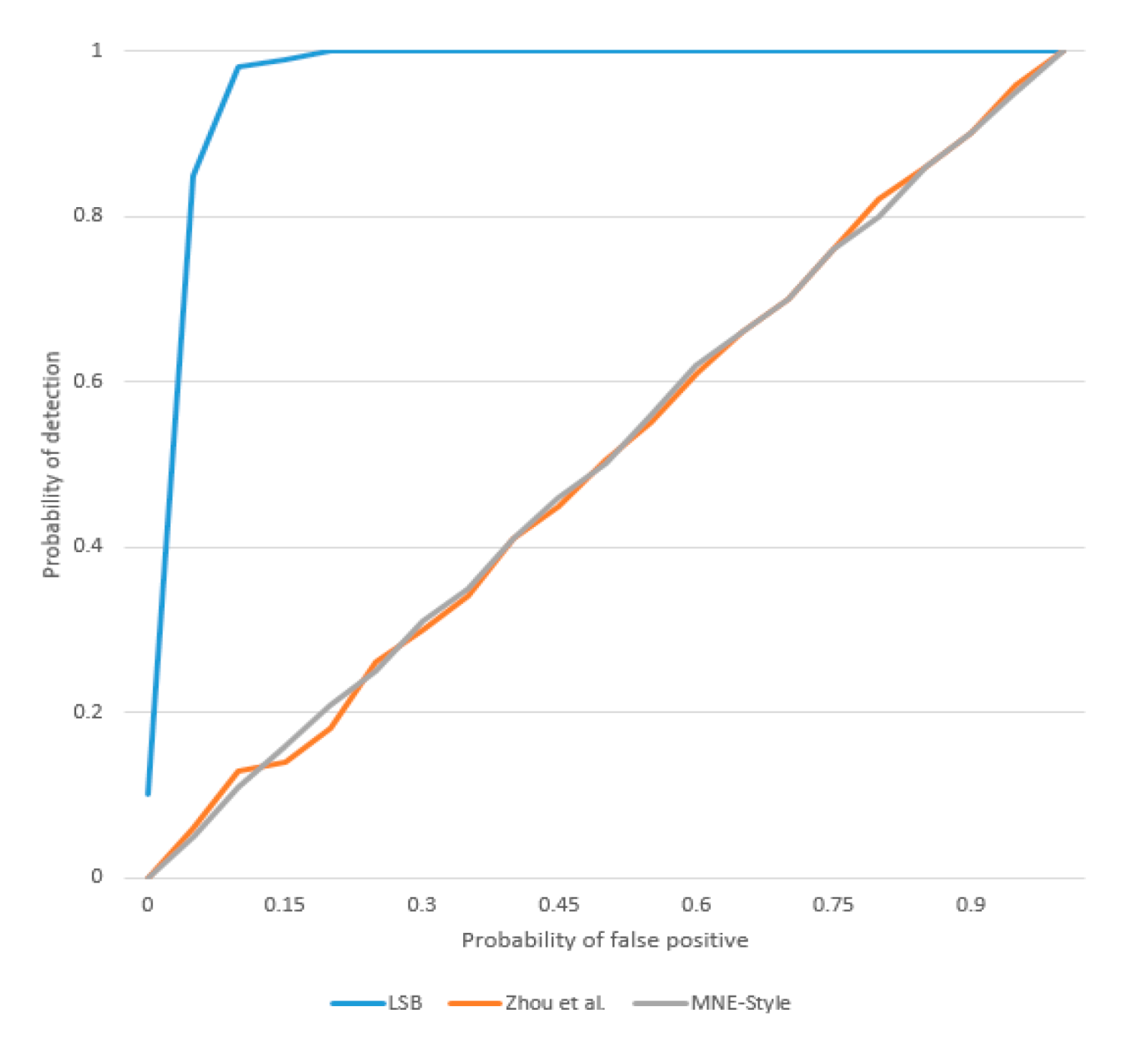
4.5. Anti-Steganalysis and Security
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, C.; Zhang, H.; Feng, D.; Cao, Z.; Huang, J. Survey of information security. Sci. China Ser. F Inf. Sci. 2007, 50, 273–298. [Google Scholar] [CrossRef]
- Wu, H.C.; Wu, N.I.; Tsai, C.S.; Hwang, M.S. Image steganographic scheme based on pixel-value differencing and LSB replacement methods. IEE Proc. Vis. Image Signal Process. 2005, 152, 611–615. [Google Scholar] [CrossRef]
- Zakaria, A.; Hussain, M.; Wahab, A.; Idris, M.; Abdullah, N.; Jung, K.H. High-Capacity Image Steganography with Minimum Modified Bits Based on Data Mapping and LSB Substitution. Appl. Sci. 2018, 8, 2199. [Google Scholar] [CrossRef]
- Bender, W.; Gruhl, D.; Morimoto, N.; Lu, A. Techniques for data hiding. IBM Syst. J. 1996, 35, 313–336. [Google Scholar] [CrossRef]
- Ni, Z.; Shi, Y.Q.; Ansari, N.; Su, W. Reversible data hiding. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 354–362. [Google Scholar]
- Li, X.; Wang, J. A steganographic method based upon JPEG and particle swarm optimization algorithm. Inf. Sci. 2007, 177, 3099–3109. [Google Scholar] [CrossRef]
- Mckeon, R.T. Strange fourier steganography in movies. In Proceedings of the IEEE International Conference on Electro/information Technology, Chicago, IL, USA, 17–20 May 2007. [Google Scholar]
- Chen, W.Y. Color image steganography scheme using set partitioning in hierarchical trees coding, digital Fourier transform and adaptive phase modulation. Appl. Math. Comput. 2007, 185, 432–448. [Google Scholar] [CrossRef]
- Zhang, X.; Qian, Z.; Li, S. Prospect of Digital Steganography Research. J. Appl. Sci. 2016, 34, 475–489. [Google Scholar]
- Zhou, Z.; Cao, Y.; Sun, X. Coverless Information Hiding Based on Bag-of-WordsModel of Image. J. Appl. Sci. 2016, 34, 527–536. [Google Scholar]
- Otori, H.; Kuriyama, S. Texture Synthesis for Mobile Data Communications. IEEE Comput. Graph. Appl. 2009, 29, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.C.; Wang, C.M. Steganography using reversible texture synthesis. IEEE Trans. Image Process. 2014, 24, 130–139. [Google Scholar] [PubMed]
- Liu, M.M.; Zhang, M.Q.; Liu, J.; Zhang, Y.N.; Ke, Y. Coverless Information Hiding Based on Generative Adversarial Networks. arXiv 2017, arXiv:1712.06951. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. A Neural Algorithm of Artistic Style. arXiv 2015, arXiv:1508.06576. [Google Scholar] [CrossRef]
- Li, Y.; Fang, C.; Yang, J.; Wang, Z.; Lu, X.; Yang, M.H. Universal Style Transfer via Feature Transforms. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Li, Y.; Fang, C.; Yang, J.; Wang, Z.; Lu, X.; Yang, M.H. Diversified Texture Synthesis with Feed-Forward Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; pp. 2672–2680. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Texture Synthesis Using Convolutional Neural Networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar] [CrossRef]
- Ulyanov, D.; Lebedev, V.; Vedaldi, A.; Lempitsky, V.S. Texture Networks: Feed-forward Synthesis of Textures and Stylized Images. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A Style-Based Generator Architecture for Generative Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–21 June 2019. [Google Scholar]
- Aly, H.A.; Dubois, E. Image up-sampling using total-variation regularization with a new observation model. IEEE Trans. Image Process. 2005, 14, 1647–1659. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Proceedings of the European conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar] [CrossRef]
- Mahendran, A.; Vedaldi, A. Understanding Deep Image Representations by Inverting Them. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar] [CrossRef]
- Chen, T.Q.; Schmidt, M. Fast Patch-based Style Transfer of Arbitrary Style. arXiv 2016, arXiv:1612.04337. [Google Scholar]
- Yi, C.; Zhou, Z.; Yang, C.N.; Leqi, J.; Chengsheng, Y.; Xingming, S. Coverless information hiding based on Faster R-CNN. In Proceedings of the International Conference on Security with Intelligent Computing and Big-Data Services, Guilin, China, 14–16 December 2018. [Google Scholar]
- Zhou, Z.; Sun, H.; Harit, R.; Chen, X.; Sun, X. Coverless Image Steganography Without Embedding. In Proceedings of the International Conference on Cloud Computing and Security, Nanjing, China, 13–15 August 2015. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Liu, J. Cross-domain image steganography based on GANs. In Proceedings of the International Conference on Security with Intelligent Computing and Big-Data Services, Guilin, China, 14–16 December 2018. [Google Scholar]
- Ker, A.D. Improved Detection of LSB Steganography in Grayscale Images. In Proceedings of the 6th International Conference on Information Hiding, Toronto, ON, Canada, 23–25 May 2004. [Google Scholar]



| Method | Time (min) |
|---|---|
| MNE-Style | 24 |
| MNE-Style without residual learning | 53 |
| Method | N.Iters | Time/Iter. (min) | Time (min) |
|---|---|---|---|
| Gatys et al. [14] | 10,000 | 0.099 | 990 |
| Johnson et al. [22] | 2000 | 0.126 | 252 |
| Li et al. [16] | 1000 | 0.078 | 78 |
| MNE-Style | 1000 | 0.024 | 24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Su, S.; Li, L.; Zhou, Q.; Lu, J.; Chang, C.-C. An Image Style Transfer Network Using Multilevel Noise Encoding and Its Application in Coverless Steganography. Symmetry 2019, 11, 1152. https://doi.org/10.3390/sym11091152
Zhang S, Su S, Li L, Zhou Q, Lu J, Chang C-C. An Image Style Transfer Network Using Multilevel Noise Encoding and Its Application in Coverless Steganography. Symmetry. 2019; 11(9):1152. https://doi.org/10.3390/sym11091152
Chicago/Turabian StyleZhang, Shanqing, Shengqi Su, Li Li, Qili Zhou, Jianfeng Lu, and Chin-Chen Chang. 2019. "An Image Style Transfer Network Using Multilevel Noise Encoding and Its Application in Coverless Steganography" Symmetry 11, no. 9: 1152. https://doi.org/10.3390/sym11091152
APA StyleZhang, S., Su, S., Li, L., Zhou, Q., Lu, J., & Chang, C.-C. (2019). An Image Style Transfer Network Using Multilevel Noise Encoding and Its Application in Coverless Steganography. Symmetry, 11(9), 1152. https://doi.org/10.3390/sym11091152




