Study on a Surrounding Rock Pressure Calculation Method for Super-Large Section Highway Tunnels
Abstract
:1. Introduction
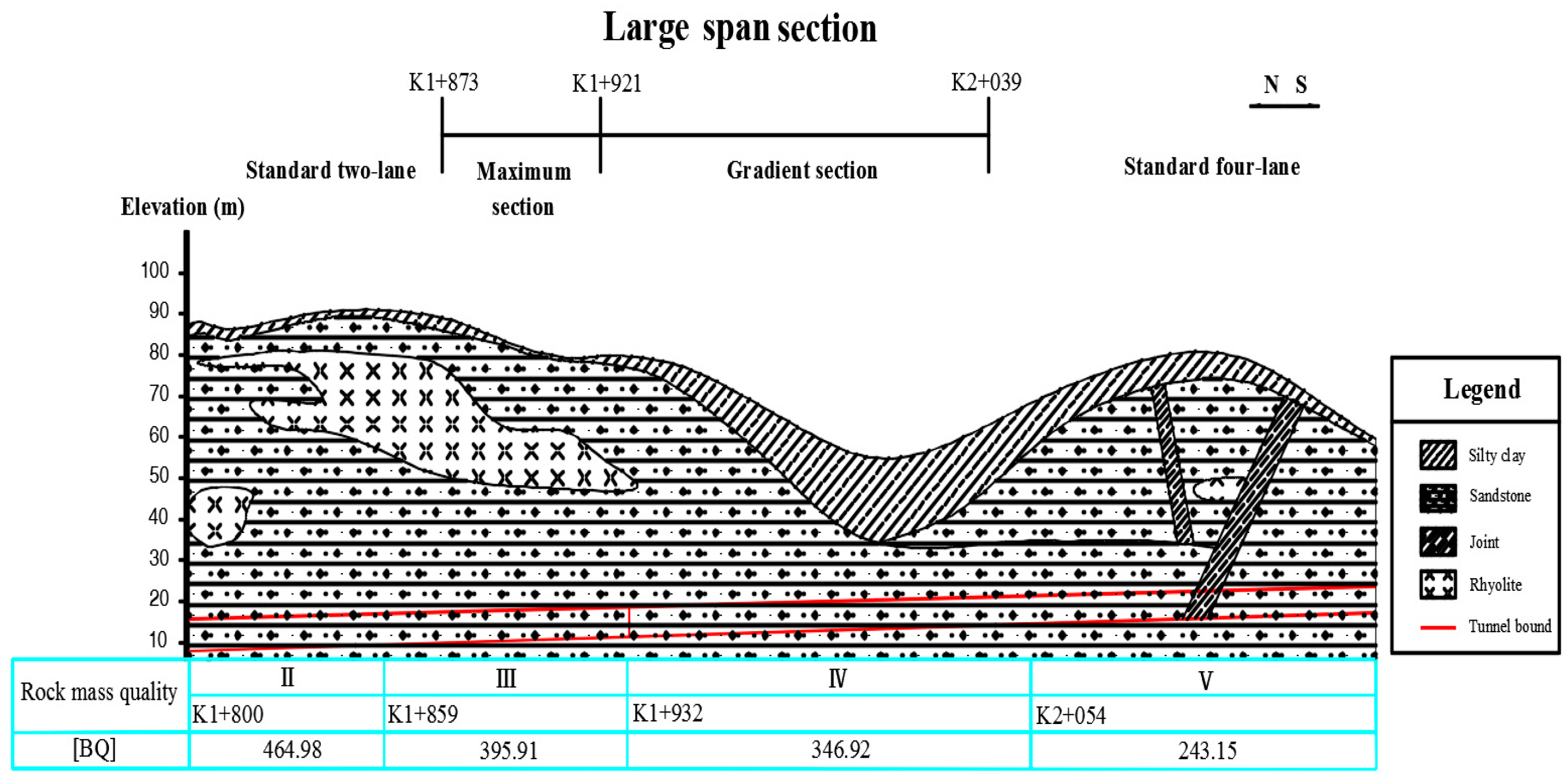
2. Project Overview
3. Applicability Analysis of Various Traditional Methods of Calculating the Surrounding Rock Pressure for Super-Large Section Tunnel
- 1)
- Traditional theories: including Protodyakonov’s theory, Terzaghi theory, and the Caquot correlation.
- 2)
- Industry recommended standards: Code for Design of Railway Tunnel (TB10003-2016), Guidelines for Design of Highway Tunnel (JTG D70-2010) and Specification for design of hydraulic tunnel (DLT_5195-2004).
- 3)
- Surrounding rock pressure correlations based on rock mass classification system: including correlations based on the Q system proposed by Grimstad and Barton [15] and by Bhasin and Grimstad [19]. Geol [20] proposed a correlation based on rock mass number N, while Unal [21] proposed a correlation based on RMR classification system.
3.1. Comparison of the Common-Applied Calculation Methods for Surrounding Rock Pressure
- γ—Rock mass bulk density; h1 = d1/f; d1 = 0.5d + htan(45°–0.5ϕ); d—Tunnel span; h—Tunnel height; ϕ—Internal friction; f—Rigidity coefficient.
- c—Cohesion; λ—Lateral pressure coefficient. The other parameters are the same as above.
- h* = h{0.45×2s−1×[1+i(B−5)]}; S—Surrounding rock grade; B—Tunnel span; i—Surrounding rock pressure change rate. The other parameters are the same as above.
- k1 and k2, calculation coefficients; r—Approximate radius. The other parameters are the same as above.
- ; RQD—Rock quality index; Jn—Joint group coefficient; Jr—Joint roughness coefficient; Ja—Joint alteration value; Jw—Water cut reduction coefficient of joints; SRF—Initial stress reduction coefficient. P1 is the same as P2 when Jn = 9, P1 is greater than P2 when Jn < 9 and P1 is less than P2 when Jn > 9.
- . α is a correction factor, usually 0.5~2.0. The other parameters are the same as above.
- The parameters are the same as in Correlation 5
- RMR76 is the hierarchical value of the RMR system.
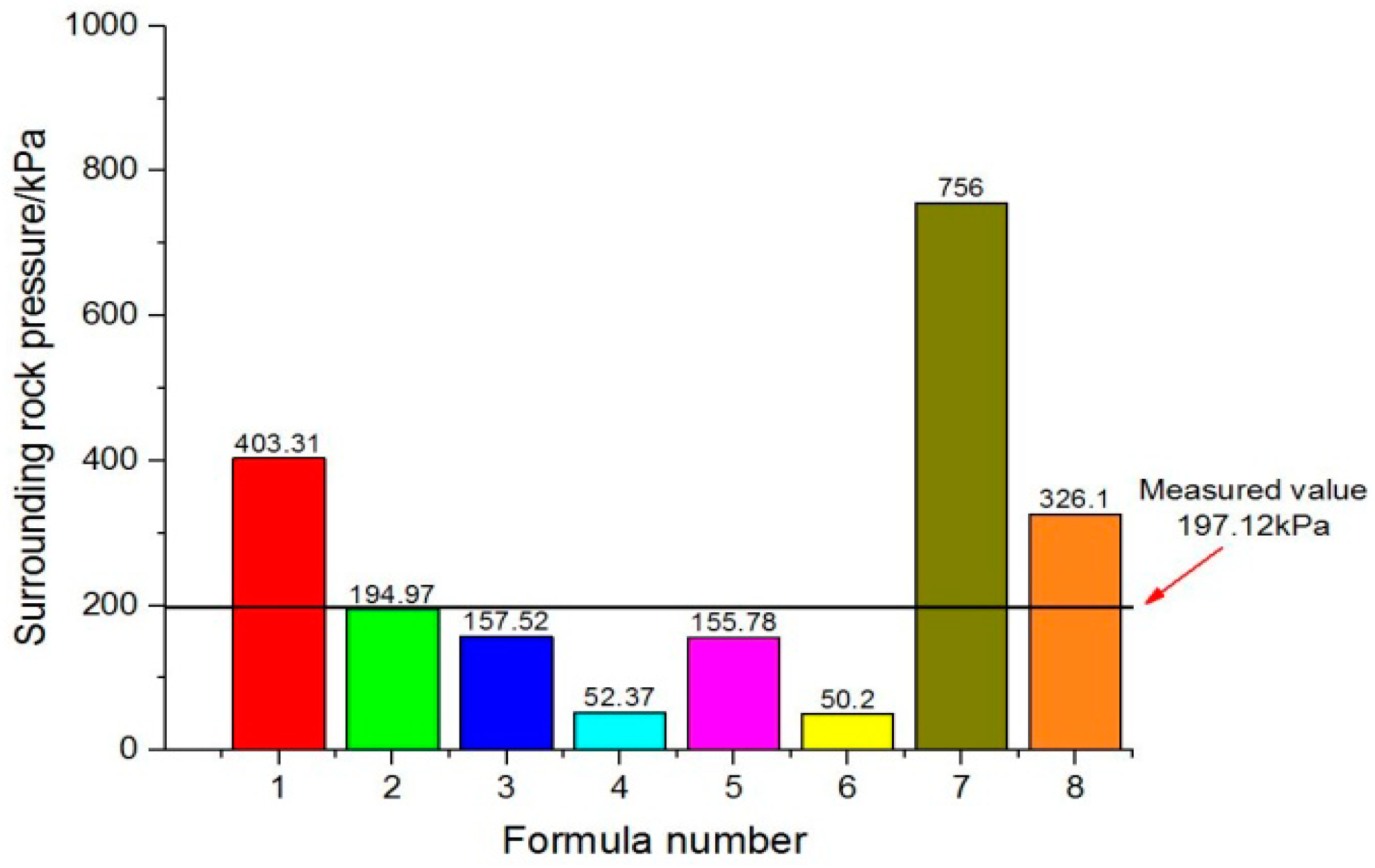
3.2. Analysis of Different Surrounding Rock Pressure Calculation Methods for the Large-Span Section of the Liantang Tunnel
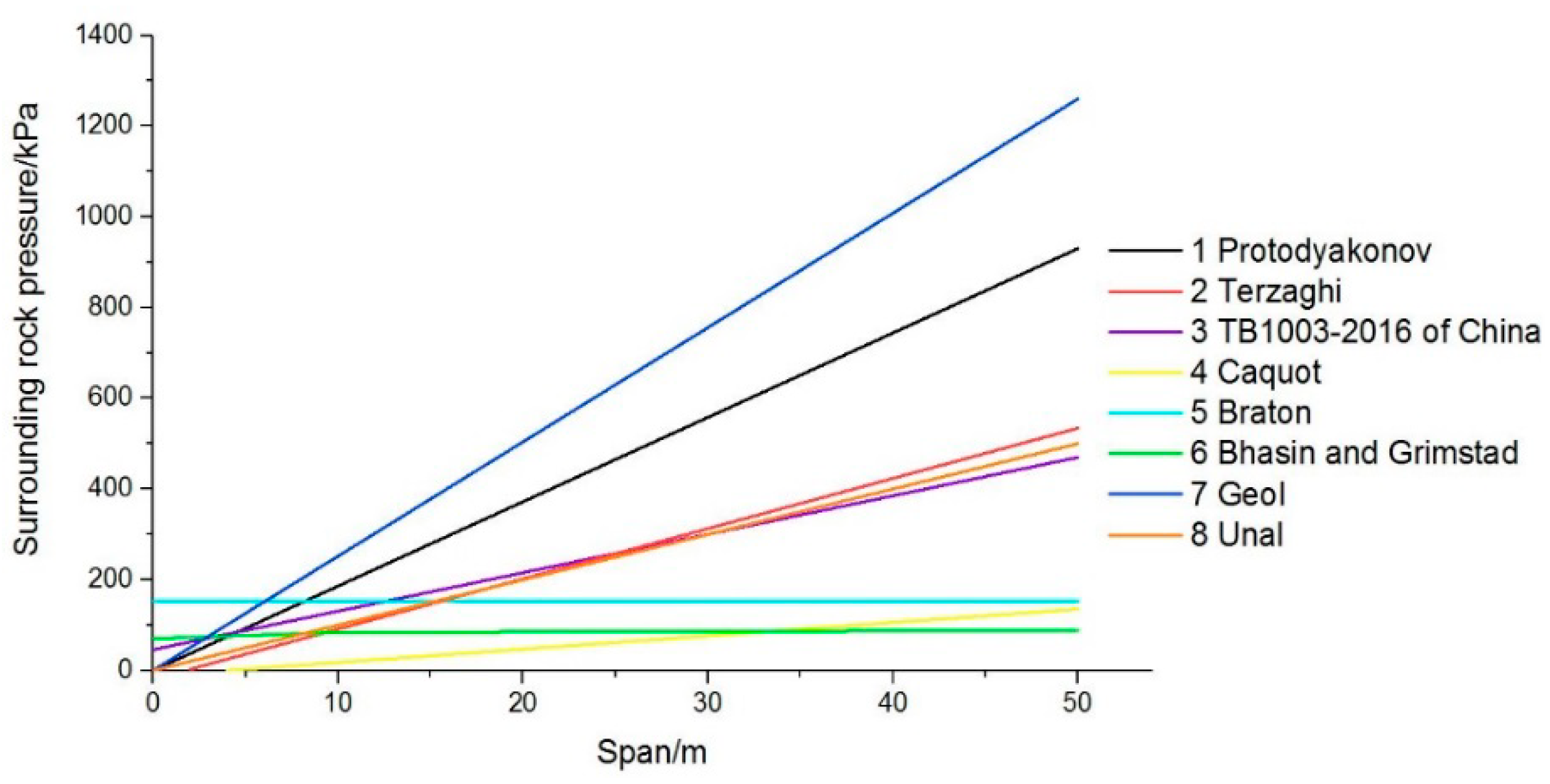
3.3. Influence of Span on the Calculation Methods of Surrounding Rock Pressure
4. Study on Surrounding Rock Pressure under Different Spans and Different Q Values
4.1. Numerical Model
4.2. Selection of Parameters and Calculation Conditions
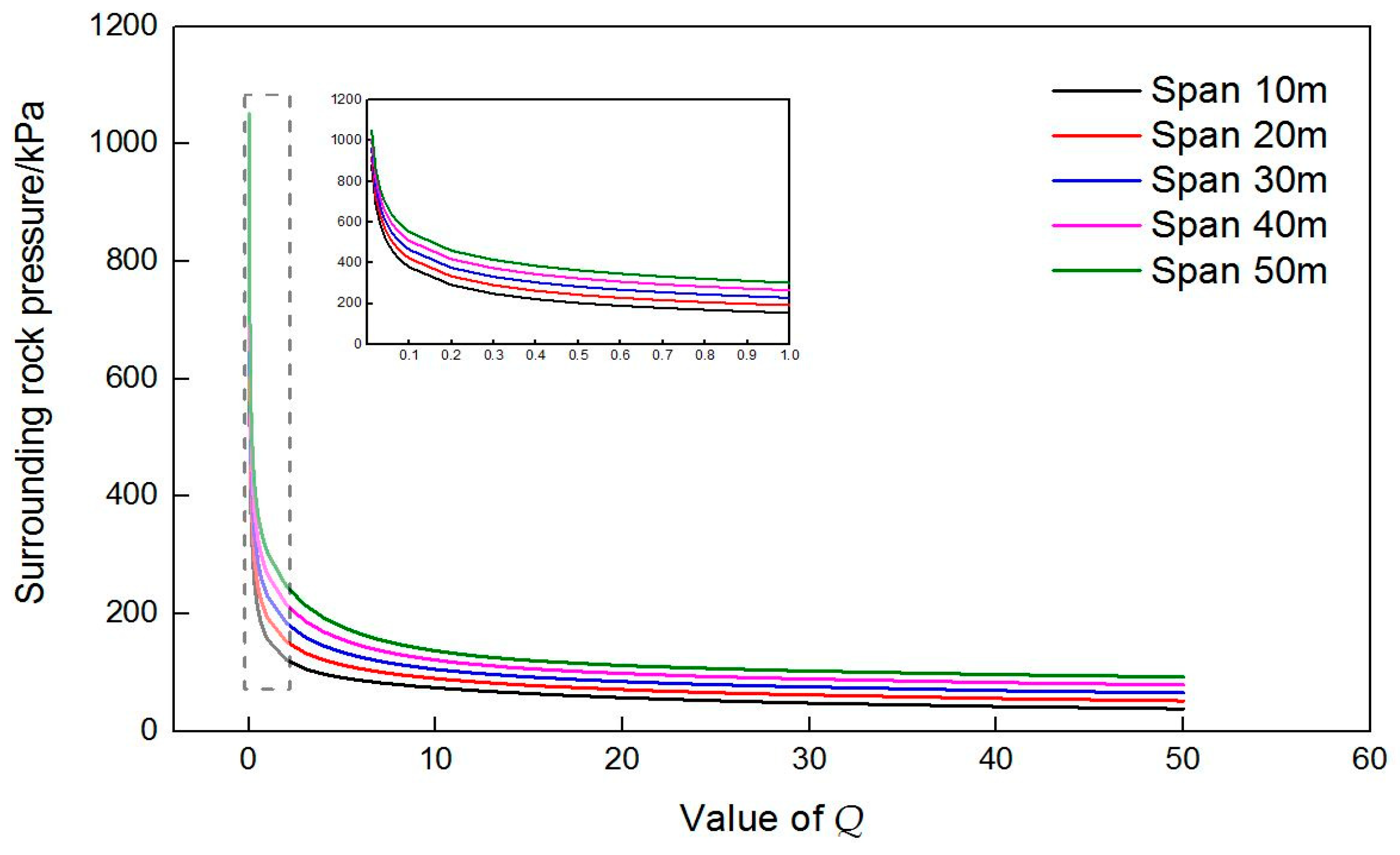
4.3. Analysis of the Calculated Results
- 1)
- Under the same span, the surrounding rock pressure decreases with the increase in Q value.
- 2)
- Under the same Q value, the pressure increases with the increase in tunnel span. However, as the Q value increases, the increase in pressure gradually decreases.
5. Estimation of the Surrounding Rock Pressure Based on Q System and Span
5.1. Establishment of the Estimation Correlation
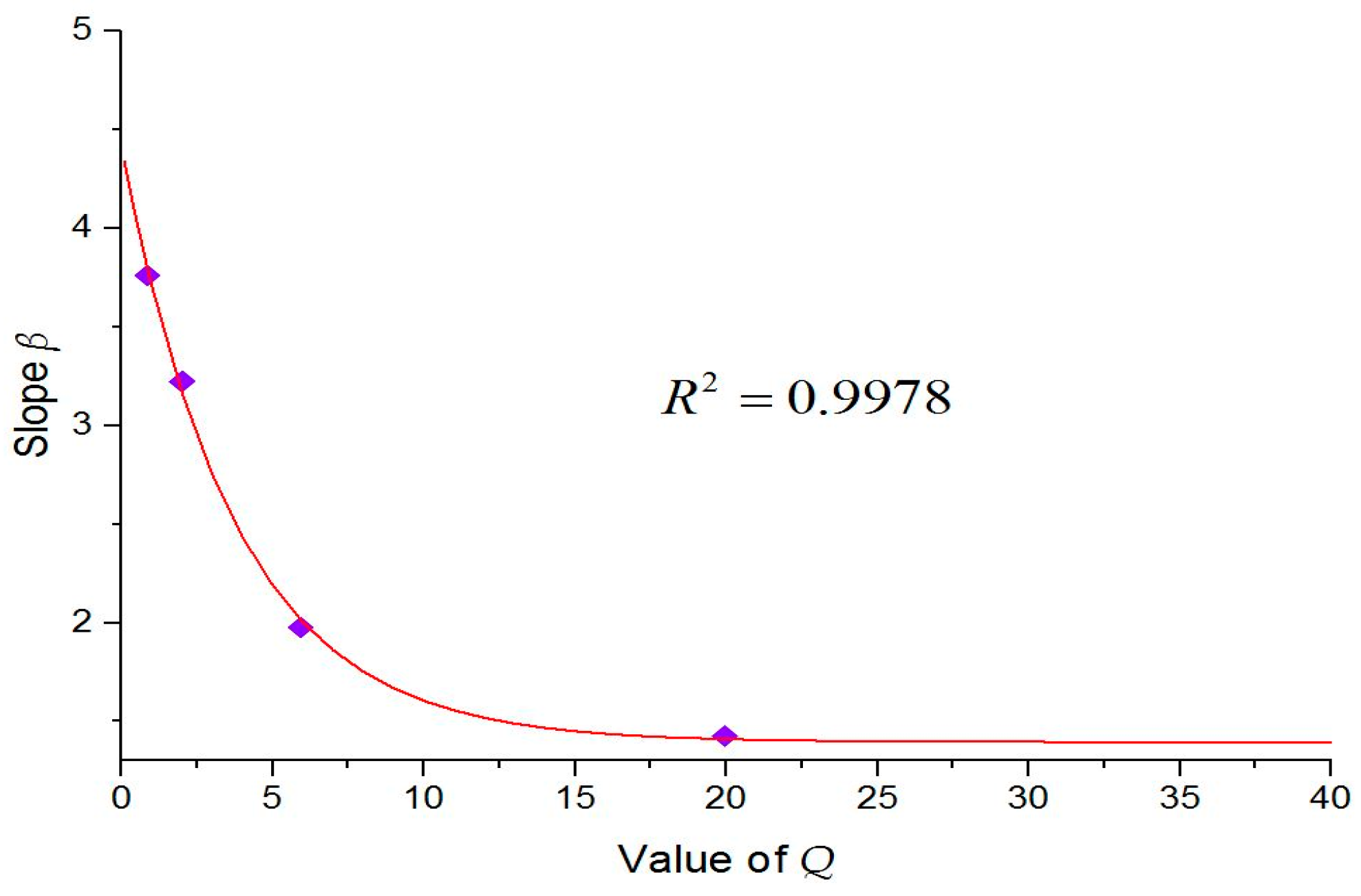
- 1)
- Under the same span, with the increase in Q value, the quality of surrounding rock increases. Furthermore, the surrounding rock pressure of the vault gradually decreases and tends to stabilize.
- 2)
- Under the same Q value, as the span increases, the surrounding rock pressure of the vault gradually becomes larger.
- 3)
- According to the local graph, when Q value is between 0 and 1, the slope of surrounding rock pressure curve increases rapidly with the decrease in Q value for the same span. This means a worse quality of surrounding rock results in a greater increase in the surrounding rock pressure.
- 4)
- As shown in the local graph, smaller the Q value, worse is the quality of surrounding rock, and more obvious is the influence of span on the surrounding rock pressure.
- 1)
- The relationship between the slope β and Q value is based on the calculation model of lateral pressure coefficient λ = 2 and height-to-span ratio of 0.6. Therefore, the correlations are applicable to caverns, whose product of the lateral pressure coefficient and height-to-span ratio is close to 1.
- 2)
- The correlations are derived on the basis of Q system, so they are similar to the correlation based on Q system. They represent the calculation of surrounding rock pressure under deep burial conditions.
- 3)
- The surrounding rock pressure of underground structure with a span greater than 10 m is analyzed statistically in the process of deriving the correlation. Therefore, the calculation correlations for the surrounding rock pressure are more suitable for underground structures with large span.
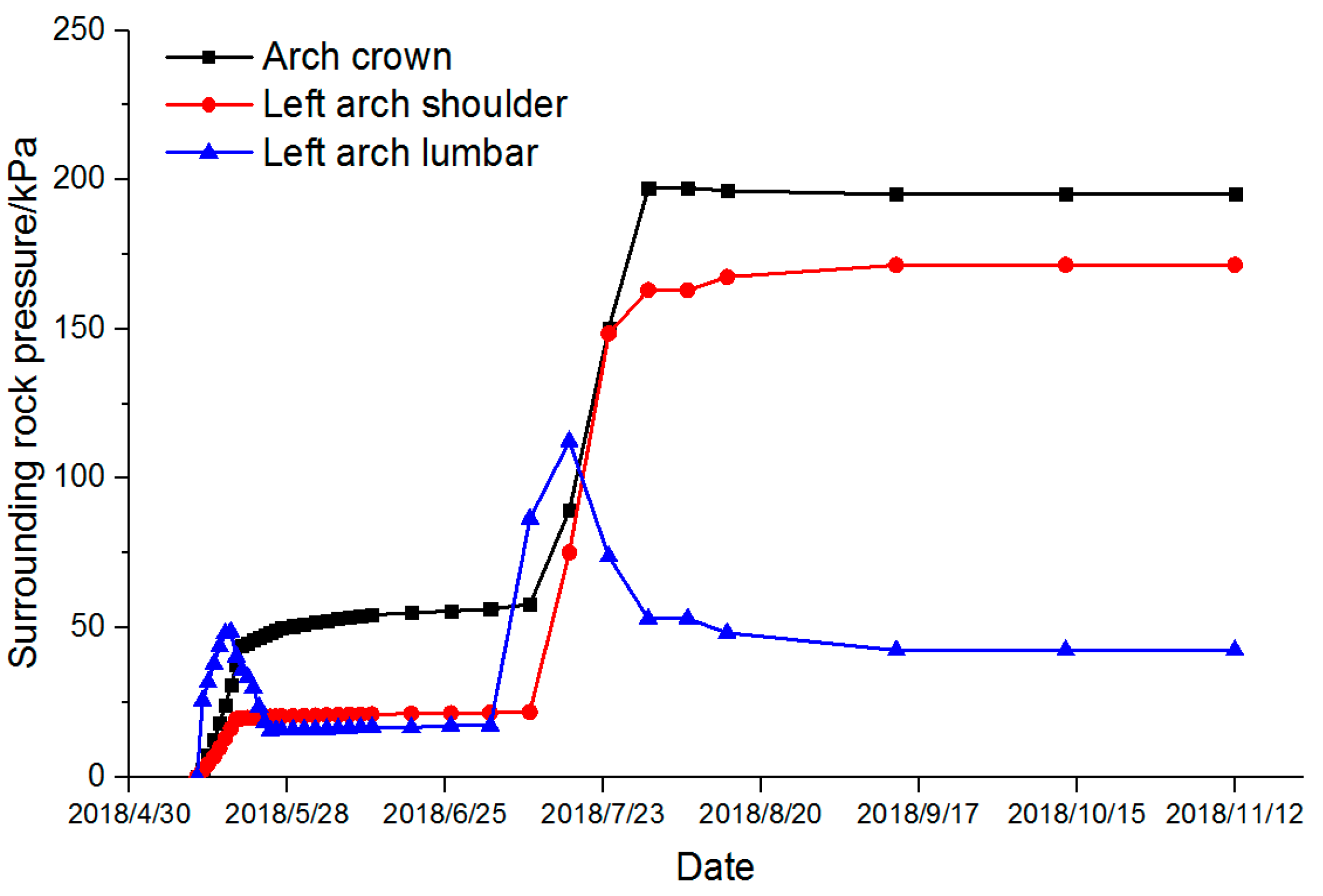
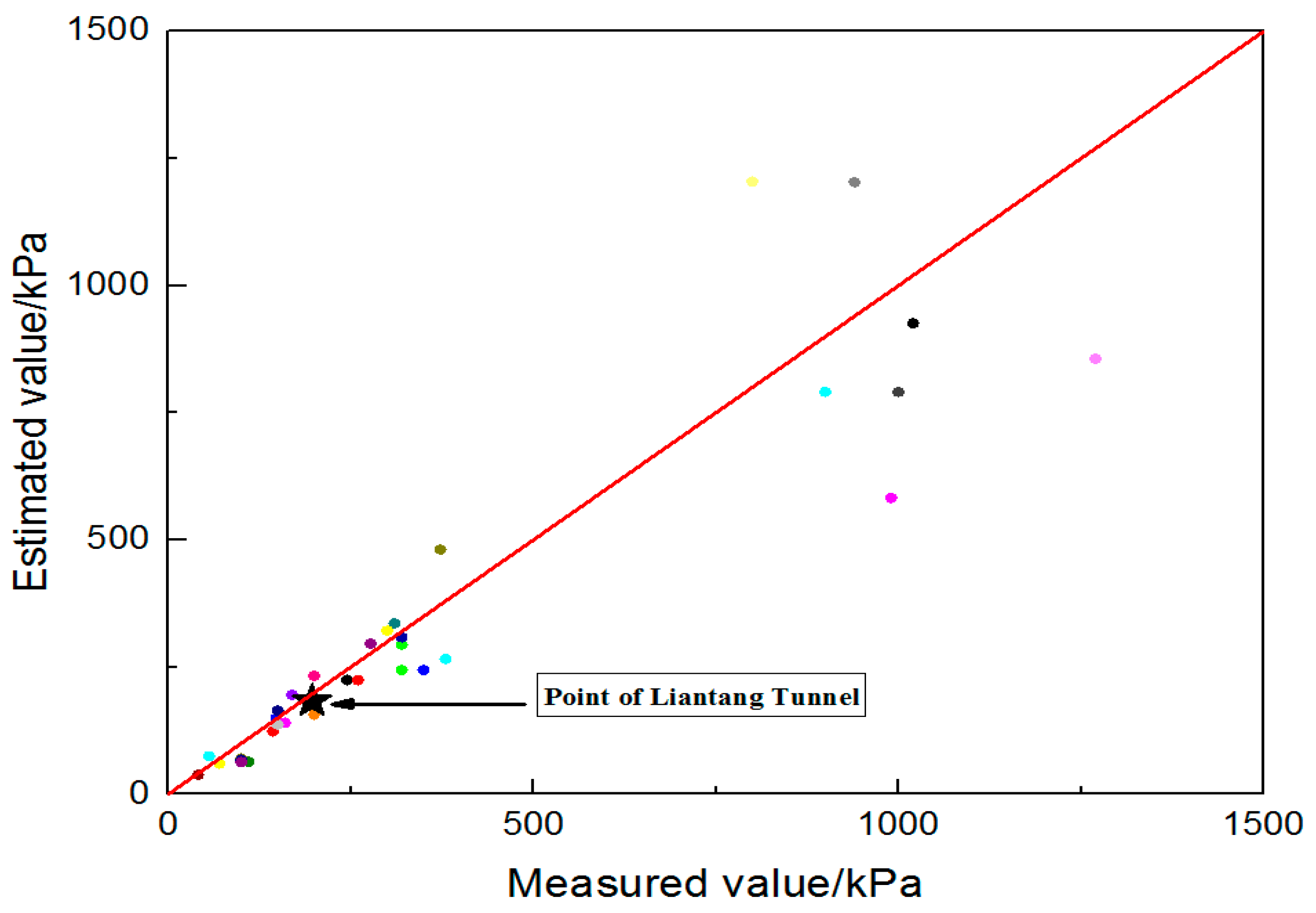
5.2. Comparison between the Results of Correlations and the Measured Values
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guan, B.S. Key Points of Tunnel Engineering Design; China Communication Press: Beijing, China, 2004; Volume 1, pp. 230–303. [Google Scholar]
- Yan, Z.X.; Fang, Y.G.; Liu, T.J. Effect of stress path on surrounding rock pressure of super large-section tunnel. Chin. J. Rock Mech. Eng. 2009, 28, 2228–2234. [Google Scholar]
- Liu, X.Z.; Luo, R.L. Analysis of large-span highway tunnel surrounding rock vertical pressure attributes. J. Tongji Univ. (Nat. Sci.) 2010, 38, 1471–1475. [Google Scholar]
- Li, P.F.; Zhao, Y.; Zhang, D.L. Study of distribution laws of tunnel surrounding rock pressure based on field measured data statistics. Chin. J. Rock Mech. Eng. 2013, 32, 1392–1399. [Google Scholar]
- Zhao, L.J.; He, S.H. Analysis of rock pressure for large span and high side-wall underground cavern. Chin. J. Undergr. Space Eng. 2005, 1, 863–866. [Google Scholar]
- Jiang, D.Y.; Liu, C.; Li, G.Y. Correlation and analysis of calculation valucs of vertical pressure of wall rocks of large-span tunnel. China Min. Mag. 2005, 14, 63–66. [Google Scholar]
- Jiang, Y.Z.; Xu, W.Y.; Wang, R.H. Numerical analysis of the long-term stability of large-scale underground cavern of hydropower station. Rock Soil Mech. 2008, 29 (Suppl. S1), 52–58. [Google Scholar]
- Wang, K.Z.; Li, Z.K.; Bao, Z.J. Study on site monitoring and stability of layered surrounding rocks of underground powerhouses of hydropower station. Chin. J. Rock Mech. Eng. 2007, 26, 2148–2152. [Google Scholar]
- Jiang, Q.; Feng, X.T.; Xiang, T.B. Discussion on method for calculating general safety factor of underground caverns based on strength reduction theory. Rock Soil Mech. 2009, 30, 2483–2488. [Google Scholar]
- Chen, C.N.; Huang, W.Y.; Tseng, C.T. Stress redistribution and ground arch development during tunneling. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2011, 26, 228–235. [Google Scholar] [CrossRef]
- Kong, X.X.; Liu, Q.S.; Zhang, Q.B. A method to estimate the pressure arch formation above underground excavation in rock mass. Tunn. Undergr. Space Technol. 2018, 71, 382–390. [Google Scholar] [CrossRef]
- Prasad, V.V.R.; Dwivedi, R.D.; Swarup, A. Determination of support pressure for tunnels and caverns using block theory. Tunn. Undergr. Space Technol. 2013, 37, 55–61. [Google Scholar] [CrossRef]
- Scussel, D.; Chandra, S. A new approach to obtain tunnel support pressure for polyaxial state of stress. Tunn. Undergr. Space Technol. 2013, 36, 80–88. [Google Scholar] [CrossRef]
- The Professional Standards Compilation Group of People’s Republic of China. TB10003-2016 Code for Design of Railway Tunnel; China Communications Press: Beijing, China, 2016. [Google Scholar]
- Barton, N.R.; Lien, R.; Lunde, J. Engineering Classification of Rock Masses for the Design of Tunnel Support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Zhang, D.L.; Fang, Q.; Hou, Y.J.; Li, P.F.; Wong, L.N.Y. Protection of buildings against damages as a result of adjacent large-span tunneling in shallowly buried soft ground. J. Geotech. Geoenviron. Eng. 2016, 139, 903–913. [Google Scholar] [CrossRef]
- Xu, H.F.; Chen, F.; Wang, B. Relationship between RMR and BQ for rock mass classification and estimation of its mechanical parameters. Chin. J. Geotech. Eng. 2014, 36, 195–198. [Google Scholar]
- Bieniawski, Z.T. Determining rock mass deformability: Experience from case histories. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 237–247. [Google Scholar] [CrossRef]
- Bhasin, R.; Grimstad, E. The Use of Stress-Strengh Relationship in the Assessment of Tunnel Stability. Proc. Recent Adv. Tunn. Technol. 1996, 11, 93–98. [Google Scholar]
- Dwivedi, R.D.; Goel, R.K. Estimation of support pressure during tunnelling through squeezing grounds. Eng. Geol. 2014, 168, 9–22. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. Engineering Rock Mass Classifications; John Wiley & Sons: Hoboken, NJ, USA, 1989; pp. 60–64. [Google Scholar]
- Protodyakonov, M.M. Rock Pressure on Mine Support (Theory of Mine Support); Tipografiya Gubernskogo Zemstva: Yekaterinoslav, Russia, 1907; pp. 23–45. [Google Scholar]
- Terzaghi, K.T. Theoretical Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1965. [Google Scholar]
- Kim, H.J. Estimation for Tunnel Lining Loads; University of Alberta: Edmonton, AB, Canada, 1997; pp. 1–15. [Google Scholar]
- Dong, Y.S. Study of the stability of tunnel early supporting under different lateral pressures ratios. Railw. Stand. Des. 2010, 6, 87–90. [Google Scholar]
- Chen, J.X.; Yang, Z.; Yuan, X.K. Construction monitoring and measuring in segments of large embedded depth in Qinling Zhongnanshan super-long highway tunne. J. Archit. Civ. Eng. 2006, 23, 71–75. [Google Scholar]
- Huang, H.W.; Xu, L. Study on deformation and internal force of surrounding rocks and initial support in Dafengyakou rock road tunnel. Chin. J. Rock Mech. Eng. 2004, 23, 441–452. [Google Scholar]
- Chen, M.C. Force measurement and analysis of tunnel primary support structure. West-China Explor. Eng. 1999, 11, 50–52. [Google Scholar]
- Zhao, W.Z.; Hou, Z.; Wang, B.X. Safety evaluation of lining structure for Huangyanzi tunnel based on on-site pressure monitoring of surrounding rockmass. J. Water Resour. Archit. Eng. 2014, 13, 24–27. [Google Scholar]

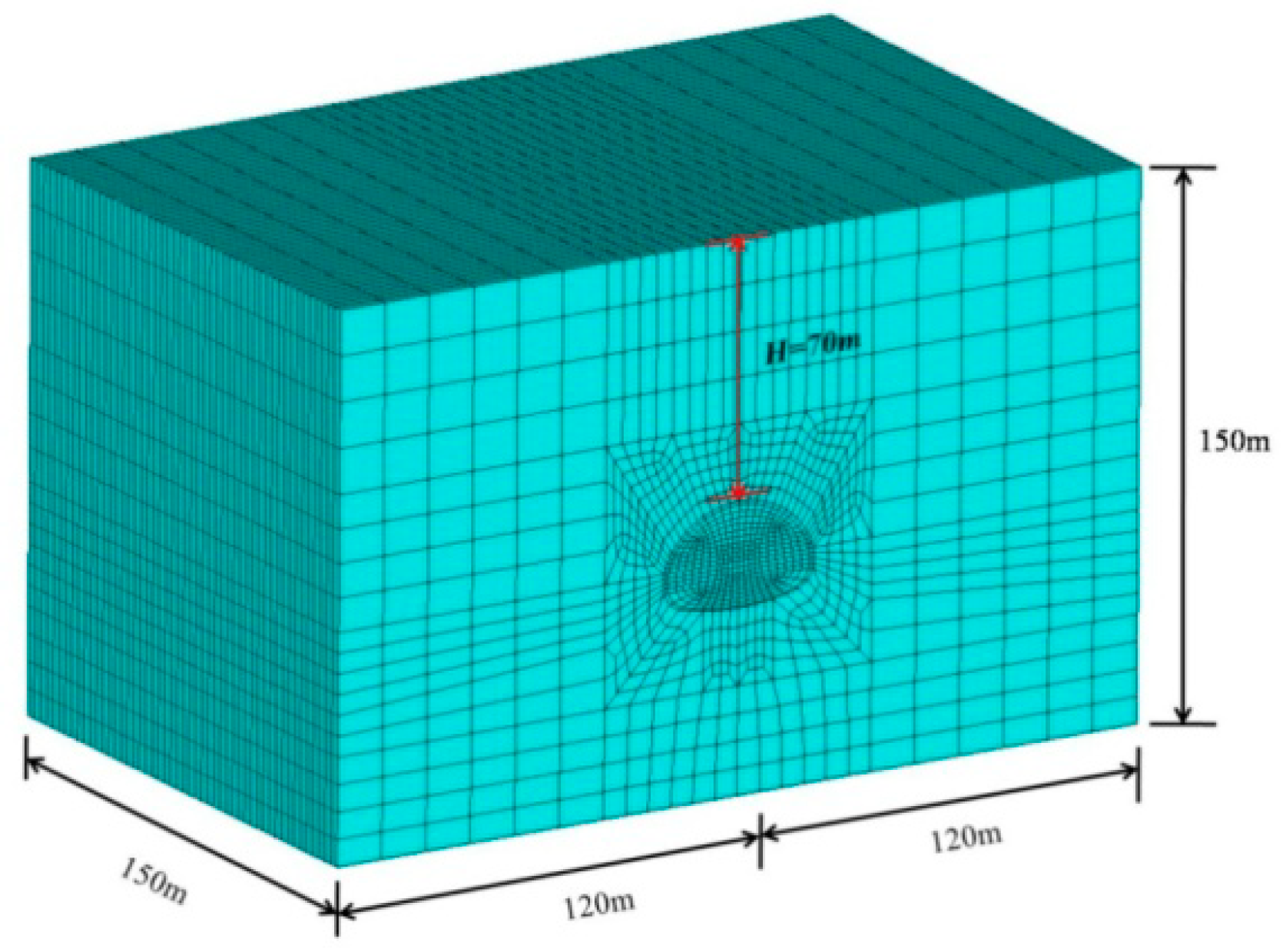



| Section Size | Excavation Area/m2 | Remark |
|---|---|---|
| Standard section | 70~80 | Two-lane highway tunnel |
| Large section | 100~140 | Two-lane highway tunnel with crosswalk |
| Super-large section | > 140 | Highway tunnels with three or more lanes |
| Tunnel | Span/m | Tunnel Height/m | Height-Span Ratio | Excavation Area/m2 | Tunnel Type | Completion Time |
|---|---|---|---|---|---|---|
| Qingdao Jiaozhou Bay | 28.3 | 18.64 | 0.66 | 411.9 | Branch | June 2011 |
| Dalian Hanjialing | 21.2 | 15.52 | 0.731 | 230 | Single Four-lane | April 2003 |
| Guangzhou Longtoushan | 24.5 | 13.56 | 0.63 | 230 | Twin Eight-lane | October 2008 |
| Shenzhen Henglongshan | 29.2 | - | - | 304 | Branch | October 2008 |
| Shenzhen Yabao | 20.9 | 13.48 | 0.645 | 220 | Twin Eight-lane | January 2007 |
| Fuzhou Jinjishan | 41.4 | 13.2 | - | 171 × 2 | Twin-arch | May 2009 |
| Sang-Lim, Korea | 18.77 | 10.48 | 0.56 | 170 | Single Four-lane | 2005 |
| Dongming, Japan | 16.53 | 8.4 | 0.51 | 170~200 | Single Three-lane | 1989 |
| Toshikazu, Japan | 20 | 13.5 | 0.67 | 225 | Water diversion | 1989 |
| The Channel, Europe | 21.2 | 15.4 | 0.73 | 252 | - | - |
| Second, Japan | 24 | - | - | 240 | - | - |
| Kobylish Metro, Czech | 20.35 | 13.75 | 0.68 | 220 | Single | 2006 |
| Value | Class I (Very Good) | Class II (Good) | Class III (Fair) | Class IV (Poor) | Class V (Very Poor) |
|---|---|---|---|---|---|
| [BQ] | >550 | 451~550 | 351~450 | 251~350 | <250 |
| Q | >40 | 10~40 | 4~10 | 1~4 | <1 |
| Number | Section Size | Value of [BQ] | Value of Q | Evaluation of Q | Classification of Surrounding Rock |
|---|---|---|---|---|---|
| 1 | Standard two-lane | 464.98 | 19.97 | Good | II |
| 2 | Maximum section | 395.91 | 5.92 | Fair | III |
| 3 | Gradient section | 395.91 | 5.92 | Fair | III |
| 4 | Gradient section | 346.92 | 2.02 | Poor | IV |
| 5 | Standard four-lane | 346.92 | 2.02 | Poor | IV |
| 6 | Standard four-lane | 243.15 | 0.86 | Very poor | V |
| Number | Correlation | Proposer |
|---|---|---|
| 1 | Protodyakonov [22] | |
| 2 | , | Karl Terzaghi [23] |
| 3 | , | TB10003-2016 of China [14] |
| 4 | Caquot [24] | |
| 5 | , | Barton [15] |
| 6 | Bhasin and Grimstad [19] | |
| 7 | Geol [20] | |
| 8 | Unal [21] |
| Item | Q | ρ (kg/m3) | ϕ | c(kPa) | λ | h(m) | d(m) |
| Value | 5.92 | 2500 | 45° | 700 | 2 | 18.4 | 30 |
| Item | H(m) | Jn | Jr | RMR | k1 | k2 | |
| Value | 0 | 9 | 1 | 60.01 | 0.249 | 0.261 |
| Correlation Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Result/kPa | 503.31 | 194.97 | 157.52 | 52.37 | 155.78 | 50.20 | 756 | 326.10 |
| Number | Value of Q | E(GPa) | ρ(kg/m3) | ν | ϕ | c (kPa) |
|---|---|---|---|---|---|---|
| 1 | 0.86 | 1.3 | 2500 | 0.3 | 22 | 100 |
| 2 | 2.02 | 3 | 2500 | 0.3 | 33 | 500 |
| 3 | 5.92 | 10 | 2500 | 0.3 | 45 | 700 |
| 4 | 19.97 | 27 | 2500 | 0.3 | 50 | 2100 |
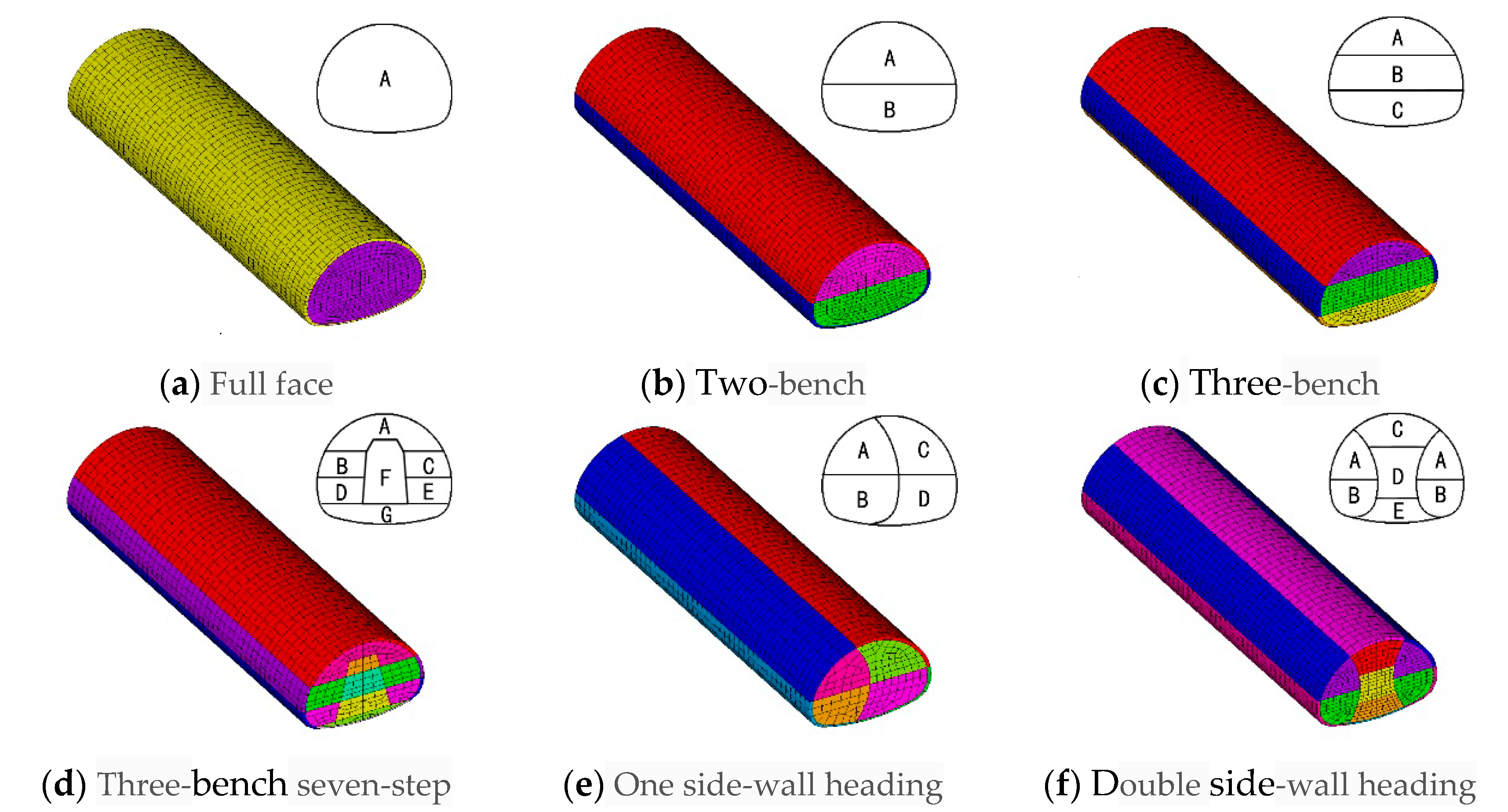
| Span/m | Q = 0.86 | Q = 2.02 | Q = 5.92 | Q = 19.97 |
|---|---|---|---|---|
| 5 | Two-bench excavation | Two-bench excavation | Full face excavation | Full face excavation |
| 10 | Two-bench excavation | Two-bench excavation | Two-bench excavation | Two-bench excavation |
| 15 | Three-bench seven-step excavation | Three-bench excavation | Three-bench excavation | Three-bench excavation |
| 20 | Three-bench seven-step excavation | Three-bench excavation | Three-bench excavation | Three-bench excavation |
| 25 | Three-bench seven-step excavation | Three-bench seven-step excavation | Three-bench seven-step excavation | Three-bench seven-step excavation |
| 30 | Oneside-wallheading excavation | Oneside-wall headingexcavation | One side-wall heading excavation | Three-bench seven-Step excavation |
| 35 | Doubleside-wall headingexcavation | Double side-wall heading excavation | Doubleside-wallheading excavation | One side-wall heading excavation |
| 40 | Doubleside-wallheading excavation | Doubleside-wallheading excavation | Doubleside-wallheading excavation | Double side-wall heading excavation |
| Value of Q | Slope | Fitted Equations | Correlative Coefficients R2 |
|---|---|---|---|
| 0.86 | 3.763 | 0.9477 | |
| 2.02 | 3.223 | 0.9717 | |
| 5.92 | 1.974 | 0.7976 | |
| 19.97 | 1.425 | 0.8394 |
| Number | Engineering Name | Span/m | Measured Value (kPa) | Estimated Value(kPa) | Value of Q | Jn | Jr |
|---|---|---|---|---|---|---|---|
| 1 | Liantang Tunnel | 30 | 197.12 | 183.19 | 5.92 | 1 | 9 |
| 2 | Jiaozhou Bay Tunnel | 28.3 | 245.12 | 224.47 | 0.83 | 1 | 8 |
| 3 | Longtoushan Tunnel | 18 | 143.7 | 123.40 | 0.89 | 1.5 | 9 |
| 4 | Xiangshan Tunne | 9.1 | 320 | 293.95 | 0.19 | 1 | 9 |
| 5 | Zhongnanshan Tunnel | 12.5 | 148 | 149.22 | 2.18 | 1 | 12 |
| 6 | Huangyanzi Tunnel | 15.8 | 56 | 74.54 | 7.39 | 1.2 | 9 |
| 7 | Maozhan Ridge Tunnel | 16.82 | 160 | 140.39 | 0.89 | 1.5 | 12 |
| 8 | Heluoshan Tunnel | 19.65 | 70 | 60.25 | 31.33 | 1 | 9 |
| 9 | Wushaoling tunnel | 7.95 | 373 | 481.19 | 0.11 | 1 | 15 |
| 10 | Bajiaoqing Tunnel | 11 | 150 | 164.18 | 0.51 | 1.2 | 9 |
| 11 | Banzhulin Tunne | 12.5 | 277 | 295.88 | 0.26 | 1.2 | 15 |
| 12 | Zhengyang Tunnel | 12 | 41 | 38.10 | 7.39 | 1.5 | 6 |
| 13 | Alatan Tunnel | 10 | 110 | 63.88 | 2.43 | 1 | 4 |
| 14 | Chhibro-Khodri | 3 | 310 | 335.97 | 0.05 | 1.5 | 12 |
| 15 | Chhibro-Khodri | 3 | 320 | 308.48 | 0.02 | 1.2 | 4 |
| 16 | Giri-Bata | 4.6 | 200 | 156.55 | 0.37 | 1 | 6 |
| 17 | Giri-Bata | 4.6 | 170 | 194.89 | 0.12 | 1 | 4 |
| 18 | Maneri Stage-I | 5.8 | 200 | 232.59 | 0.17 | 1.2 | 9 |
| 19 | Maneri Stage-III | 7 | 290 | 226.96 | 0.19 | 1.2 | 9 |
| 20 | Noonidih Colliery | 7 | 150 | 137.21 | 0.57 | 1 | 6 |
| 21 | Tala Hydro | 6.9 | 940 | 1203.33 | 0.01 | 1 | 15 |
| 22 | Tala HRT | 7.2 | 800 | 1204.65 | 0.01 | 1 | 15 |
| 23 | Kaligandaki | 9.7 | 900 | 791.00 | 0.03 | 1 | 15 |
| 24 | Kaligandaki | 9.7 | 1270 | 855.89 | 0.02 | 1 | 15 |
| 25 | Kaligandaki | 9.7 | 1000 | 791.00 | 0.03 | 1 | 15 |
| 26 | Kaligandaki | 9.7 | 1020 | 925.78 | 0.02 | 1 | 15 |
| 27 | Nathpa Jhakri | 11 | 260 | 224.21 | 0.41 | 1 | 9 |
| 28 | Nathpa Jhakri | 11 | 320 | 244.23 | 0.33 | 1 | 9 |
| 29 | Nathpa Jhakri | 11 | 350 | 244.23 | 0.33 | 1 | 9 |
| 30 | Nathpa Jhakri | 11 | 380 | 265.96 | 0.26 | 1 | 9 |
| 31 | Nathpa Jhakri | 11 | 990 | 582.53 | 0.03 | 1 | 9 |
| 32 | Udhampur rail | 6.5 | 300 | 321.45 | 0.06 | 1.5 | 12 |
| 33 | Chenani-Nashri | 6 | 100 | 70.00 | 2.18 | 1.5 | 12 |
| 34 | Chenani-Nashri | 6 | 100 | 67.47 | 2.43 | 1.5 | 12 |
| 35 | Chenani-Nashri | 6 | 100 | 63.07 | 3.04 | 1.5 | 12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; He, P.; Chen, Z.; Li, X. Study on a Surrounding Rock Pressure Calculation Method for Super-Large Section Highway Tunnels. Symmetry 2019, 11, 1133. https://doi.org/10.3390/sym11091133
Gao H, He P, Chen Z, Li X. Study on a Surrounding Rock Pressure Calculation Method for Super-Large Section Highway Tunnels. Symmetry. 2019; 11(9):1133. https://doi.org/10.3390/sym11091133
Chicago/Turabian StyleGao, Hongjie, Ping He, Zheng Chen, and Xinyu Li. 2019. "Study on a Surrounding Rock Pressure Calculation Method for Super-Large Section Highway Tunnels" Symmetry 11, no. 9: 1133. https://doi.org/10.3390/sym11091133
APA StyleGao, H., He, P., Chen, Z., & Li, X. (2019). Study on a Surrounding Rock Pressure Calculation Method for Super-Large Section Highway Tunnels. Symmetry, 11(9), 1133. https://doi.org/10.3390/sym11091133






