Abstract
Symmetry is a property that has been widely examined clinically as a measurement of health and aesthetic appeal. Many current techniques that assess geometric symmetry rely on interpretation from a trained operator or produce two-dimensional measurements that cannot express the three-dimensional character of an object. In this article, we propose a comprehensive markerless method that describes an object’s symmetry using three types of fundamental symmetry, reflection, rotoinversion—a combination of reflection and rotation—and translation—a process of reflection and rigid movement. This is done by mirroring an object over an arbitrary plane and aligning the mirrored image with the original object in a position that minimizes deviation between both objects. Each object’s symmetry can be displayed in two ways, numerically, with a best plane of symmetry or “Psym”, a fixed point and the mirrored objects rotation and magnitude of translation in relation to the original object, and visually, through a 3D deviation contour map. Three examples were made: Model 1 showed reflection symmetry and resulted in a standard deviation of 0.002 mm, Model 2 expressed rotoinversion symmetry and produced a standard deviation of 0.003 mm and Model 3 expressed translational symmetry which resulted in a translation magnitude difference of 0.015% with respect to model height. This simple procedure accurately recognizes reflection, rotoinversion and translation symmetry, takes minimal time and expertise and has the ability to expand previous case specific methods to a global application of symmetry analysis.
1. Introduction
Symmetry is a property easily recognized by humans [1]. It is customarily associated with visual appeal and can be found in natural objects, manufactured products, and in artwork across the world. Bilateral symmetry especially has been widely examined clinically as an indication of ideal geometry and physiological fitness [2]. The assumption of bilateral symmetry is also frequently made in the assessment of human injury in clinical practice and research studies. In orthopedic applications of the lower extremities, the contralateral unaffected side has been previously applied as a reference for uses such as diagnosing the extent of tibia and femur shaft fractures before corrective osteotomy [3], determining size and position of radial head implants in arthroplasty surgery [4] and as an intra-subject control in assessing the cause and risk factors of osteochondral defects of the ankle joint [5].
In the past, several analysis techniques have been applied to study symmetry of an object. Sun et al. used distance and volume parameters, and the mirroring and overlaying of three-dimensional (3D) models to quantify symmetry in female breasts [6]. 3D torso models were used to derive asymmetry indices to asses scoliosis progression using the outline and area of axial slices [7]. Similarly, dynamic landmarks on surface topography (ST) have been introduced to assess deformities associated with scoliosis [8]. However, many of these methods rely on interpretation from a trained operator and a limited number of markers, thus impedances arise in the consistency and ability to implement these specialized methods to fully describe the symmetry of a 3D object.
Recently, a novel markerless ST asymmetry analysis approach, independent of human interaction was used to assess symmetry to monitor adolescent idiopathic scoliosis (AIS) progression [9] and classify AIS severity. The effectiveness of the approach was initially studied by Ho et al. assessing asymmetry in torsos of healthy adolescents [10] and examined further by Komeili et al. correlating parameters extracted from the markerless ST approach to radiographic data in determining curve severity and location of apical vertebra in scoliosis with promising results [11]. Hill et al. described this procedure in detail, comparing two methods of application to study AIS torso models [12]. These applications of the markerless ST approach have shown the potential to reduce X-ray use [13] and the potential to work as a complementary tool for the diagnosis and monitoring of AIS [14]. The technique relies on creating a mirrored image of the model of an object, and then using a registration algorithm (such as the iterative least-squares method available in the Geomagic software) to register the original model with its reflection. Based on the difference between the two, symmetry, or lack thereof, is assessed. In this article we show that this technique leads to the detection and assessment of three types of symmetry: Reflection, rotoinversion, and translational symmetry. We first introduce the theoretical background to differentiate the three types of symmetry. Then, using three different examples, we discuss how the technique can be used to identify the type of symmetry associated with an object.
2. Theoretical Background
In this work is used to represent the traditional Euclidian linear vector space equipped with the Euclidian norm and the traditional dot product operation.
Given an orthonormal basis set , a vector has components and such that . We also adopt the representation when convenient.
Definition 1.
Let . The tensor product is the linear map: defined such that :
Definition 2.
An orthogonal tensor is a linear map satisfying . Orthogonal tensors have a determinant equal to 1 or −1. Orthogonal tensors form a group, i.e., the composition of two orthogonal tensors is again an orthogonal tensor.
Definition 3.
Orthogonal tensors whose determinant is equal to 1 are called proper orthogonal tensors. Proper orthogonal tensors represent a counterclockwise rotation of an angle around a vector .
The tensor representation of a proper orthogonal tensor has the following form:
where is an orthonormal basis set that follows the right hand rule orientation. A proper orthogonal tensor also has the following traditional matrix form:
Definition 4.
Orthogonal tensors whose determinant is equal to −1 are called improper orthogonal tensors. Improper orthogonal tensors represent a counterclockwise rotation of an angle around a vector in addition to a reflection around the plane perpendicular to .
The tensor representation of an improper orthogonal tensor has the following form:
where is an orthonormal basis set that follows the right hand rule orientation. An improper orthogonal tensor also has the following traditional matrix form:
when , an improper orthogonal tensor becomes symmetric and in that case, it represents a geometric reflection around the plane perpendicular to . The tensor representation of a reflection matrix has the form:
The traditional matrix representation has the following form:
Remark 1.
The following useful relationships are important:
- -
- Given and , an orthogonal tensor . Therefore, every orthogonal tensor can be associated with an angle . Additionally, the transpose of an orthogonal tensor is given by: .
- -
- Given an orthogonal tensor , the cosine of the associated angle can be calculated using the trace of :Assuming the sine of the associated angle can be calculated asThe components of the vector can then be calculated when using the off diagonal components:whereis the Levi–Civita symbol, which is equal to +1 ifare an even permutation of the integers 1, 2, and 3, is equal to −1 ifare an odd permutation of the integers 1, 2, and 3, and is equal to zero otherwise. When, other forms to calculate the componentscan be obtained.
- -
- The composition of two orthogonal tensors is again orthogonal. A reflection followed by a proper orthogonal transformation gives an improper orthogonal tensor.
Remark 2.
Given a proper orthogonal tensor defined by the vector and the angle and given a reflection matrix defined by the vector , their compositions (reflection followed by proper orthogonal transformation) and (proper orthogonal transformation followed by reflection) have the following forms:
where the subscript stands for reflection followed by proper orthogonal transformation, while stands for proper orthogonal transformation followed by reflection, are the vectors associated with the improper orthogonal tensors , respectively, and are the angles associated with respectively. Using Equations (1)–(3):
A natural result is that or is equal to 0 if and/or if and are orthogonal to each other. I.e., pure reflection results in either of these cases. The only difference between and is in the order of the cross product operation. Note that when , i.e., when . This indicates that reflection and proper orthogonal transformations commute when the associated vectors are linearly dependent.
Definition 5.
Let and , then the set defines a hyperplane. A hyperplane in is the analytical representation of a geometric plane. Without loss of generality, . In that case, the vector and can also be represented as
which, given an orthonormal basis set, has the following component form:
It is easy to show that is normal to the plane defined by since .
Definition 6.
Given , a line along the direction of passing through the point is defined in as .
Definition 7.
Given a hyperplane defined by and , the reflection around a hyperplane is the linear operation such that .
Alternatively, using the tensor product defined previously, has the form:
Remark 3.
Clearly, if : .
Definition 8.
Given a line defined by , the geometric rotation around with an angle is given by the linear function defined such that :
Theorem 1.
Given a hyperplane defined by and , and given a line defined by a point and the direction , let the geometric reflection around be defined by . Let the rotation around be defined by . Then, and commute. In addition, is a fixed point for the composition .
Proof of Theorem 1.
Let be the adopted orthonormal basis set. Therefore, and . It is easy to show using Definition 1 that they commute. Setting and since , therefore (Using Remark 3):
Premultiplying by yields:
Since and are linearly dependent, we have .
Therefore,
If the reflection is followed by the rotation, the composition map has the form:
Similarly, if the rotation is followed by the reflection:
Utilizing Equations (8) and (10) renders
Therefore, the composition is commutative. This composition is defined using the general improper orthogonal matrix and an associated translational vector . Under this operation, and using Equations (9) and (11), the point is a fixed point since:
□
Remark 4.
Theorem 1 assers that rotation around a line and reflection around the hyperplane orthogonal to the line commute. In addition, the combined operation is associated with an improper orthogonal tensor, a translational vector, and a fixed point. However, given a general improper orthogonal matrix and a translation vector , it is not always possible to find a fixed point satisfying:
As will be shown in the discussion below, a fixed point can always be found except when the rotation matrix is associated with an angle that is equal to 0 and the translation vector has nonzero components parallel to the hyperplane .
Approximate Symmetry Characterization:
Let be an arbitrary compact set and let be its reflected image using an arbitrary but fixed reflection matrix. Let be a rigid transformation of such that a measure of distance between and is locally minimized with the minimizers being a proper orthogonal tensor and . We seek to distinguish three types of “approximate” symmetry associated with the transformation:
The resulting tensor is an improper orthogonal tensor associated with the vector and an angle which have the analytical forms shown in Equations (5) and (6) above. In the following, an orthonormal basis set is adopted. Let , , and .
Type 1: Reflection symmetry :
In reflection symmetry, the rotoinversion angle is equal to and . In this case, the symmetry is defined by a hyperplane (plane of reflection symmetry) that is defined as
where and . Reflection symmetry is characterized by having a fixed plane since
where , and . Obviously, a set can possess such a reflection symmetry such that as demonstrated in Model 1 in the examples section that follows.
Type 2: Rotoinversion symmetry :
Rotoinversion symmetry is associated with an angle . In this case, rotoinversion symmetry is associated with a fixed point which can be obtained as follows.
since is invertible which guarantees the existence of . Therefore:
In this case, the rotoinversion symmetry is associated with
- -
- a reflection around the hyperplane defined by and , and
- -
- a rotation of angle around the axis defined by the geometric points represented by the two vectors and
A set can possess such a rotoinversion symmetry such that as demonstrated by Model 2 in the examples section that follows.
Type 3: Translational Symmetry (, and/or ):
Translational symmetry is associated with
- -
- a reflection around the hyperplane defined by and .
- -
- A translation parallel to the hyperplane along the vector .
Translational symmetry has the following two properties:
Property 1.
Translational symmetry has no fixed point. Settingand eitherorin Equation (12) shows that no fixed point exists for a translational symmetry.
Theorem 2 and Property 2.
Whenis compact, it is not possible to find a translational symmetry such that.
Proof of Theorem 2.
Without loss of generality, assume and . Let be the vector with the largest value of the component along . This point exists since is compact. Let . . However, since , therefore, . I.e., . □
The examples section below shows a set (Model 3) with an approximate translational symmetry along with a discussion of having translational symmetry when the condition of boundedness is relaxed.
3. Materials and Methods
To represent reflection, rotoinversion and translation symmetry, three models were designed and created using Solidworks 2018. The models were constructed to test the method’s ability to analyze an object and identify the type of symmetry expressed. The method is able, for each object, to identify the plane associated with symmetry (termed: “Psym”), the value of the rotation associated with the rotoinversion symmetry if present, the fixed point if it exists, and finally the magnitude of the associated translation parallel to the plane of symmetry. The reflection and alignment were done using Geomagic Software (3D Systems, North Carolina, USA) while the symmetry parameters were extracted using Mathematica (Wolfram Mathematica, Champaign IL, USA).
3.1. Symmetry Analysis Procedure
The analysis procedure comprises three steps. In the first step, given a cloud of points in 3D (referred to as the original model), a reflection is produced by duplicating the original cloud of points and reflecting the coordinates of the point cloud over an arbitrary plane. The arbitrary plane does not have to intersect any point on the original cloud. In the second step, the reflected point cloud is then aligned with the original point cloud using Geomagic’s Best Fit function where the original model is set as the reference and the reflected model as the test. The evaluation can be made using the predetermined values calculated by the software. To test for translation symmetry, the function must be executed with the selection of automatic deviator elimination found in function options to account for the imperfect alignment of this type of symmetry (see Appendix A). This function initially brings the reference object to a roughly matched position of the original model then uses the iterative least squares method which rigidly transforms the reflected model until the sum of squares of distances between the reflected model and the closest point on the original model is minimized. For each point on the original point cloud the corresponding point is the closest point on the reflected cloud, which is not necessarily the reflected point. In the third step, the resulting transformation matrix describing the reflection and alignment of the reflected cloud is obtained from Geomagic and recorded for analysis.
The transformation matrix is used to determine the normal to the associated plane of symmetry, the angle of rotation, the fixed point, and the magnitude of translation, if any. The values are determined using a subroutine developed in Wolfram Mathematica (see Appendix B). The subroutine compares the resulting transformation matrix with the general form of the matrix given by
where the components of the normal to the plane of reflection are (where ) and is the angle of rotation around the normal to the plane associated with . The components of and the angle are found by minimizing the square of the error between the analytical form of and the numerical values extracted from Geomagic. The subroutine solves , where represents the fixed point. The magnitude of translation parallel to the plane associated with the transformation is calculated as where .
For visual analysis, a colour deviation map illustrating the deviation between the model and the final position of its reflection at each point on the original model can be made using the built-in 3D compare function in Geomagic. It represents both the negative and positive deviations between the original and reflected models. Green represents the smallest distance between the reference cloud and the transformed cloud, shades of blue represent the reference point cloud underneath the original point cloud and shades of red represent the reference point cloud above the original point cloud. Grey indicates an area where the deviation between clouds is very large in comparison to the rest of the model and is omitted in the visual representation. Either object must be wrapped by converting the cloud of points into a triangulated mesh before using the 3D compare function. Due to the comparison of a point cloud to a mesh, areas of slight deviation may occur. In the following section three examples of models with different symmetries are described.
3.2. Symmetry Analysis Example Models
3.2.1. Model 1: Reflection Symmetry
Model 1 represents an object with one plane of reflection symmetry (Figure 1). This was created by mirroring a half object across the XZ plane to represent reflection symmetry. Model 1 has a max height of 135 mm and a max length of 326.653 mm. The model was exported from Solidworks as a STEP file, imported into Geomagic as 400,000 mesh triangles and translated to an arbitrary but known position within the 3D space (Figure 1b). This was achieved by first centering the model to the origin of the world coordinate system (positive X-axis to the front, positive Y-axis to the right and positive Z-axis up). The model was then rotated 330° around the X-axis and 300° around the Z-axis in reference to the objects coordinate system, then rigidly translated {+100, +150, +200} mm. Figure 1b exhibits the final position of the model before performing the analysis procedure in relation to the world coordinate system.

Figure 1.
(a) Model 1 is a purely bilateral symmetric object modelled after an ant and is (b) imported into Geomagic as a mesh, (c) duplicated as a point cloud (grey) and reflected over an arbitrary plane (Step 1), where (d) the reflected model (grey) is aligned to the original model (yellow) using the Best Fit function (Step 2).
A duplicate of 199,613 points was created and used for the mirrored model (Figure 1c). In this position, the plane of symmetry (outlined in red in Figure 1b) has a normal direction of {√3/2, √3/4, 1/4} mm ({0.866, 0.433, 0.25} mm). The model then underwent the three steps in the symmetry analysis procedure described above. For step 1, the arbitrary plane for reflection was chosen as the XZ plane {0, −100, 0} mm from the world coordinate system origin, shown in Figure 1c as the orange plane, with the original model in yellow and the reflected model in grey. For step 2, the reflected model was then aligned to the original model using the Best Fit function (Figure 1d). Finally in step 3, the transformation matrix of the reflected model is extracted from Geomagic.
3.2.2. Model 2: Rotoinversion Symmetry
The second model was created by mirroring a half object across the XZ plane and rotating the mirrored half by 90° to express bilateral and rotational symmetry. The final shape represents a ball held by two opposing set of hands (Figure 2) with a max height of 320 mm and a max length of 425.972 mm. Similar to model 1, model 2 was imported into Geomagic as 400,000 mesh triangles and translated to an arbitrary but known position (Figure 2b). The model is duplicated as a cloud of 199,195 points then experienced the symmetry analysis procedure stated above starting from the position pictured in Figure 2b where the plane of symmetry (outlined in orange) has a normal direction of {√3/2, √3/4, 1/4} mm ({0.866, 0.433, 0.25} mm). For step 1, the arbitrary plane of reflection was chosen as the XZ plane {0, −100, 0} mm from the world coordinate system origin, illustrated in Figure 2c as the orange line between the yellow original model on the right and the grey reflected model on the left. Figure 2d displays the final position of the reflected model projected on the original model after step 2 and the Best Fit function was executed. Once again, the transformation matrix of the reflected model was extracted from Geomagic.
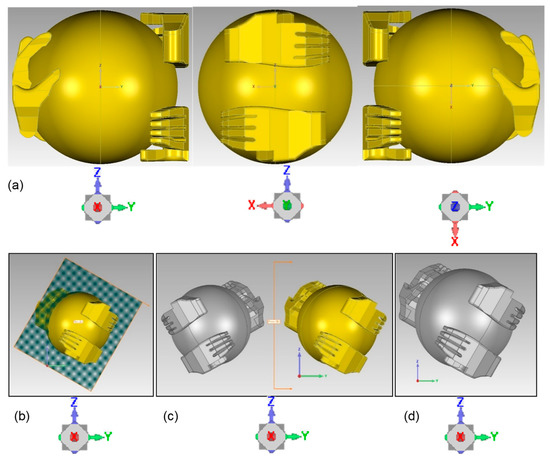
Figure 2.
(a) Model 2 is a bilaterally and rotationally symmetric object reminiscent of two people holding a ball and is (b) imported into Geomagic as a mesh, (c) duplicated as a point cloud and reflected over an arbitrary plane (Step 1), where (d) the reflected model (grey) is aligned to the original model (yellow) using the Best Fit function (Step 2).
3.2.3. Model 3: Translation Symmetry
The third model was created by mirroring protruding features across the XZ plane, and rigidly translating the mirrored half down to show translational symmetry (Figure 3). Model 3 has a max height of 200 mm and a max length of 230 mm. The model imitates an alternating rung ladder where rungs on the same side have a closest distance of 60 mm, thus the mirrored half of the model was rigidly translated {0, 0, −30} mm placing every rung at equal distances between each other. The protruding features resulting in the “rungs” were slanted creating an angle of 43.138° with the XY plane and an angle of 41.668° with the YZ plane (Figure 3) to ensure reflection symmetry is not expressed.
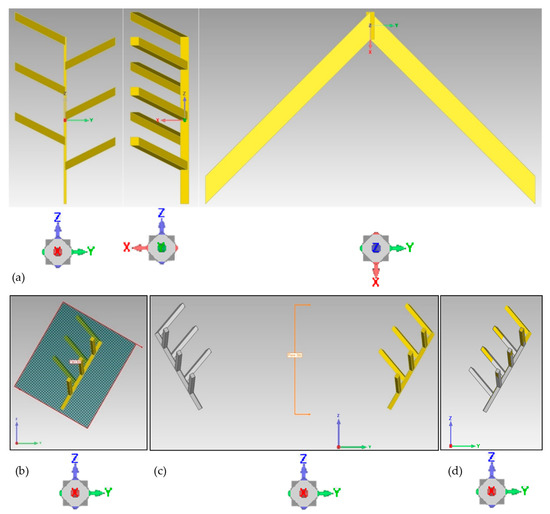
Figure 3.
(a) Model 3 is an object representing an alternating rung ladder and is (b) imported into Geomagic as a mesh, (c) duplicated as a point cloud and reflected over an arbitrary plane (Step 1), where (d) the reflected model (grey) is aligned to the original model (yellow) using the Best Fit function (Step 2).
Similar to the previous models, model 3 was imported into Geomagic as a triangulated mesh of 400,000 mesh triangles. The mesh was then placed in an arbitrary but known position in the world coordinate system and duplicated as a point cloud of 174,114 points. The symmetry analysis procedure was then applied from the position pictured in Figure 3b where the plane of best symmetry (outlined in red) has a normal direction of {√3/2, √3/4, 1/4} mm ({0.866, 0.433, 0.25} mm). For step 1, the arbitrary plane for reflection is chosen as a XZ plane {0, −100, 0} mm from the world coordinate system origin, displayed as the orange plane in Figure 3c. The final projection of the reflected model in grey on the original model in yellow is shown in Figure 3d, where the reflected model is translated down and aligned. For step 3, the transformation matrix of the reflection and alignment of the reflected model is extracted for analysis.
4. Results
The transformation matrices collected from Geomagic following the Best Fit Alignment procedure are shown in Table 1. These matrices represent the combination of reflection and alignment of the duplicated model in the method. The characteristics determined to describe the symmetry of the model, i.e., the normal to the associated plane of symmetry, a fixed point, the rotation angle, and the magnitude of translation within the plane of symmetry after utilizing the Wolfram Mathematica subroutine are shown in Table 2.

Table 1.
Transformation matrices exported from Geomagic after the alignment of the mirrored test models. These matrices are used to extract the characteristics of object’s symmetry in Table 2. Equation (13) is the general form of the matrices which contain components of the Psym normal and rotation.

Table 2.
Characteristics of transformation determined using the Mathematica subroutine.
To visually assess the level of the particular symmetry of the object, Geomagic’s 3D compare function was used to create deviation maps of the distance between the original models and reflected point cloud. Each colour corresponds to the location of the reflected model in relation to the original model with the shade intensity indicative of the magnitude of deviation. Green represents the smallest deviation while grey depicts an area omitted from analysis as the displacement between the models is too substantial in relation to the rest of the model. Since displacement is measured between a triangulated mesh and a cloud of points this can also account for small deviations resulting in small patches of grey found on the maps. Table 3 validates the approach by comparing results of each model with their corresponding theoretical results, explained in depth in the following paragraphs below. It is important to note that in the examples presented here, the examples chosen had perfect symmetry and thus there was minimal deviation between the object and its reflection. However, when assessing the level of symmetry in any object, it is expected that this procedure would identify the “best” symmetry possible. For example, Ghannei et al. assessed the asymmetry associated with a scoliosis spinal deformity based on threshold values of deviation found in a subject torso [8].

Table 3.
Validation of approach. Displaying the measurements outlined above that compare the method’s results to the expected results.
Model 1 created a Psym with the normal {−0.866, 0.433, 0.250} mm which is concurrent to the expected plane normal of {0.866, 0.433, 0.25} mm. The resulting rotation of 0.00° and the translation magnitude of 0.016 mm (difference of 0.012% with respect to model height and 0.005% of the model max length) correspond to the reflection symmetry associated with this object. The values are not exactly zero owing to the fact that the object and its mirrored image are both reduced to distinct point clouds that may not exhibit the same points or exact symmetry sought. The fixed point has no significance as all points lying in the Psym plane are fixed, however, the subroutine finds one possible solution. As shown in Figure 4a, the bilaterally symmetric model is mostly green with an RMS error of 0.007 mm, thus the technique accurately identifies reflection symmetry.
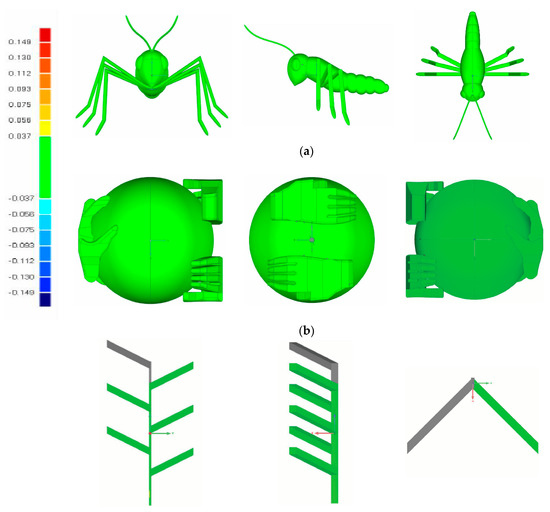
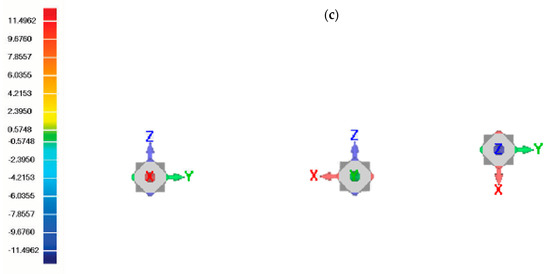
Figure 4.
3D colour contour map of (a) Model 1, (b) Model 2 and (c) Model 3.
The transformation matrix of Model 2 produced a Psym with the normal {0.866, 0.433, −0.250} mm which is once again concurrent with the expected normal of {0.866, 0.433, 0.250} mm. The resulting rotation of 90.026° and fixed point of {99.990, 150.009, 199.836} mm corresponds to the rotation of 90° used to create the model and the object origin coordinates of {100, 150, 200} mm in 3D space. The fixed point difference with respect to model size is 0.038% of max model height and 0.028% of model max length. Figure 4b displays the deviation map of the rotoinverted model as mostly green with an RMS error of 0.026 mm, indicating that the method recognizes rotoinversion symmetry.
Model 3 is described with a Psym normal of {0.866, 0.433, −0.249} mm concurrent to the expected normal of {0.866, 0.433, 0.250} mm. The test model’s movement resulted in a rotation 0.006° and a translation magnitude of 29.899 mm, which corresponds to the rotation of 0.00° and translation of 30.0 mm of the protruding features when creating the model. The difference between the translation and expected translation is 0.050% of the model height and 0.044% of the model max length. The fixed point output by Mathematica is neither found on the model or on the Psym, hence it corresponds to the absence of an expected fixed point and is disregarded as all points are rigidly translated. Figure 4c displays the deviation map of the model with a max/min deviation of 12.1988 mm/−12.1894 mm and an RMS error of 0.00 mm. The model appears nearly green aside from a clear area of imperfect alignment illustrated by the large grey patch found at the top of the model surrounding the topmost middle section and rung. The grey area accounts for the imperfection of translational symmetry and is a result of the reflected model’s translation down to align features detected in both models.
5. Discussions
In this paper, we show a simple technique that can be implemented in any 3D geometric analysis software by which three types of symmetry can be assessed—reflection symmetry, rotoinversion symmetry, and translational symmetry. The theoretical framework portraying the characteristics of each of these is first presented followed by three examples carefully selected to differentiate between the three types of symmetry. The examples showcase the ability of the method to accurately assess and recognize reflection, rotoinversion, and translation symmetry of the 3D models. The method was able to accurately extract the plane of symmetry, the associated normal, the angle of rotation if non-zero, and a fixed point if one exists. The method requires minimal time and expertise or training, only requiring the appropriate software and code.
Author Contributions
Conceptualization, L.W. and S.A.; Data curation, L.W. and S.A.; Formal analysis, L.W. and S.A.; Investigation, M.M.B.; Methodology, M.M.B., L.W. and S.A.; Resources, L.W. and S.A.; Software, L.W. and S.A.; Supervision, L.W. and S.A.; Validation, L.W. and S.A.; Visualization, M.M.B.; Writing—original draft, M.M.B.; Writing—review & editing, L.W. and S.A.
Funding
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Dialog Window for Translation Symmetry
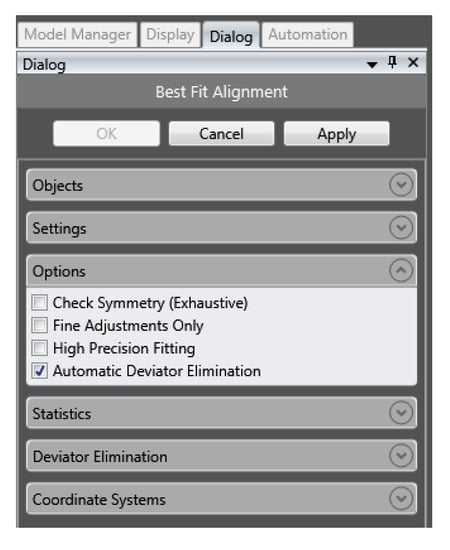
Figure A1.
Dialog Window Before Testing Translational Symmetry.
Appendix B. Subroutine on Wolfram Mathematica to Extract Object Characteristics
#From top left corner 3 × 3 matrix of transformation matrix
Q = {{−0.75, −0.125,0.65}, {−0.625, −0.188, −0.758}, {−0.217, 0.974, −0.063}};
#Translation vector, last column of transformation matrix
c = {63.841,392.18,88.015};
x = {x1, x2, x3};
#Computing fixed point
Solve [x==Q.x+c, {x1, x2, x3}]
p = {p1, p2, p3};
Qq = {{-p1^2(1+Cos[th])+Cos[th], -p1*p2*(1+Cos[th])+p3*Sin[th], -p1*p3*(1+Cos[th])-p2*Sin[th]}, {-p1*p2*(1+Cos[th])-p3*Sin[th], -p2^2(1+Cos[th])+Cos[th], -p2*p3*(1+Cos[th])+p1*Sin[th]}, {-p1*p3*(1+Cos[th])+p2*Sin[th], -p2*p3*(1+Cos[th])-p1*Sin[th], -p3^2 (1+Cos[th])+Cos[th]}};
Qq//MatrixForm
s1 = Table[(Qq[[i,j]]-Q[[i,j]])^2,{i,1,3},{j,1,3}];
s = Sum[(Qq[[i,j]]-Q[[i,j]])^2,{i,1,3},{j,1,3}];
#Computing Psym normal and rotation (in radians)
a = NMinimize[s, {p1,p2,p3,th}]
#Display Psym normal
ptrans = {p1, p2, p3}/.a[[2]]
#Computing translation magnitude
mag = Norm[c-(c.ptrans)*ptrans]
References
- Wagemans, J. Characteristics and models of human symmetry detection. Trends Cogn. Sci. 1997, 1, 346–352. [Google Scholar] [CrossRef]
- Tomkinson, G.R.; Olds, T.S. Physiological correlates of bilateral symmetry in humans. Int. J. Sports Med. 2000, 21, 545–550. [Google Scholar] [CrossRef] [PubMed]
- Santoro, D.; Tantavisut, S.; Aloj, D.; Karam, M.D. Diaphyseal osteotomy after post-traumatic malalignment. Curr. Rev. Musculoskelet Med. 2014, 7, 312–322. [Google Scholar] [CrossRef] [PubMed]
- Ten Berg, P.W.L.; Dobbe, J.G.G.; van Wolfswinkel, G.; Strackee, S.M.; Streekstra, G.J. Validation of the contralateral side as reference for selecting radial head implant sizes. Surg. Radiol. Anat. 2016, 38, 801–807. [Google Scholar] [CrossRef] [PubMed]
- Tümer, N.; Blankevoort, L.; van de Giessen, M.; Terra, M.P.; de Jong, P.A.; Weinans, H.; Tuijthof, G.J.; Zadpoor, A.A. Bone shape difference between control and osteochondral defect groups of the ankle joint. Osteoarthr. Cartil. 2016, 24, 2108–2115. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.-P.; Hsu, K.-W.; Chen, J.-S. The evaluation of female breast symmetry by calculating related physics parameters. J. Med. Biol. Eng. 2007, 27, 87–90. [Google Scholar]
- Jaremko, J.L.; Poncet, P.; Ronsky, J.; Harder, J.; Dansereau, J.; Labelle, H.; Zernicke, R.F. Indices of torso asymmetry related to spinal deformity in scoliosis. Clin. Biomech. 2002, 17, 559–568. [Google Scholar] [CrossRef]
- Oxborrow, N.J. Assessing the child with scoliosis: the role of surface topography. Arch. Dis. Child 2000, 83, 453–455. [Google Scholar] [CrossRef] [PubMed]
- Komeili, A.; Westover, L.; Parent, E.; ElRich, M.; Adeeb, S. Monitoring for Idiopathic Scoliosis Curve Progression Using Surface Topography Asymmetry Analysis of the Torso in Adolescents. Spine J. 2015, 15, 743–751. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.; Parent, E.; Watkins, E.; Moreau, M.J.; Hedden, D.; ElRich, M.; Adeeb, S. Asymmetry Assessment Using Surface Topography in Healthy Adolescents. Symmetry 2015, 7, 1436–1454. [Google Scholar] [CrossRef]
- Komeili, A.; Westover, L.; Parent, E.; El-Rich, M.; Adeeb, S. Correlation between a Novel Surface Topography Asymmetry Analysis and Radiographic Data in Scoliosis. Spine Deform. 2015, 3, 303–311. [Google Scholar] [CrossRef] [PubMed]
- Hill, S.; Franco-Sepulveda, E.; Komeili, A.; Trovato, A.; Parent, E.; Hill, D.; Lou, E.; Adeeb, S. Assessing Asymmetry Using Reflection and Rotoinversion in Biomedical Engineering Applications. J. Eng. Med. 2014, 228, 523–529. [Google Scholar] [CrossRef] [PubMed]
- Hong, A.; Jaswal, N.; Westover, L.; Parent, E.C.; Moreau, M.; Hedden, D.; Adeeb, S. Surface topography classification trees for assessing severity and monitoring progression in adolescent idiopathic scoliosis. Spine 2017, 42, E781–E787. [Google Scholar] [CrossRef] [PubMed]
- Ghaneei, M.; Komeili, A.; Li, Y.; Parent, E.C.; Adeeb, S. 3D Markerless Asymmetry Analysis in the Management of Adolescent Idiopathic Scoliosis. BMC Musculoskelet. Disord. 2018, 19, 385–395. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).