Automatic Retinal Blood Vessel Segmentation Based on Fully Convolutional Neural Networks
Abstract
1. Introduction
- (1)
- We delved into the effects of several data preprocessing methods on network performance. By performing grayscale, normalization, Contrast Limited Adaptive Histogram Equalization (CLAHE), and gamma correction on the retina image, the performance of the model can be improved.
- (2)
- We have devised a new data augmentation method for retinal images to enhance the performance of the model. It can be combined with existing data augmentation methods to achieve better results. We named it Random Crop and Fill (RCF).
- (3)
- We proposed M3FCN, an improved deep fully convolutional neural network structure, for retinal vessel automatic segmentation. Compared with the basic FCN, the M3FCN has the following three improvements: adding a multi-scale input module, expanding to a multi-path FCN, and obtaining the final segmentation result through multi-output fusion. The experimental results show that all three improvements can improve the performance of the model.
- (4)
- We obtain the final segmentation image by overlapping the sampling test patch and the overlapping patch reconstruction algorithm.
- (5)
- We have proved through the ablation analysis experiments that the various improvements proposed in this paper are effective. Experimental results show that the proposed framework is robust and that the improved method has the potential to extend to other methods and medical images.
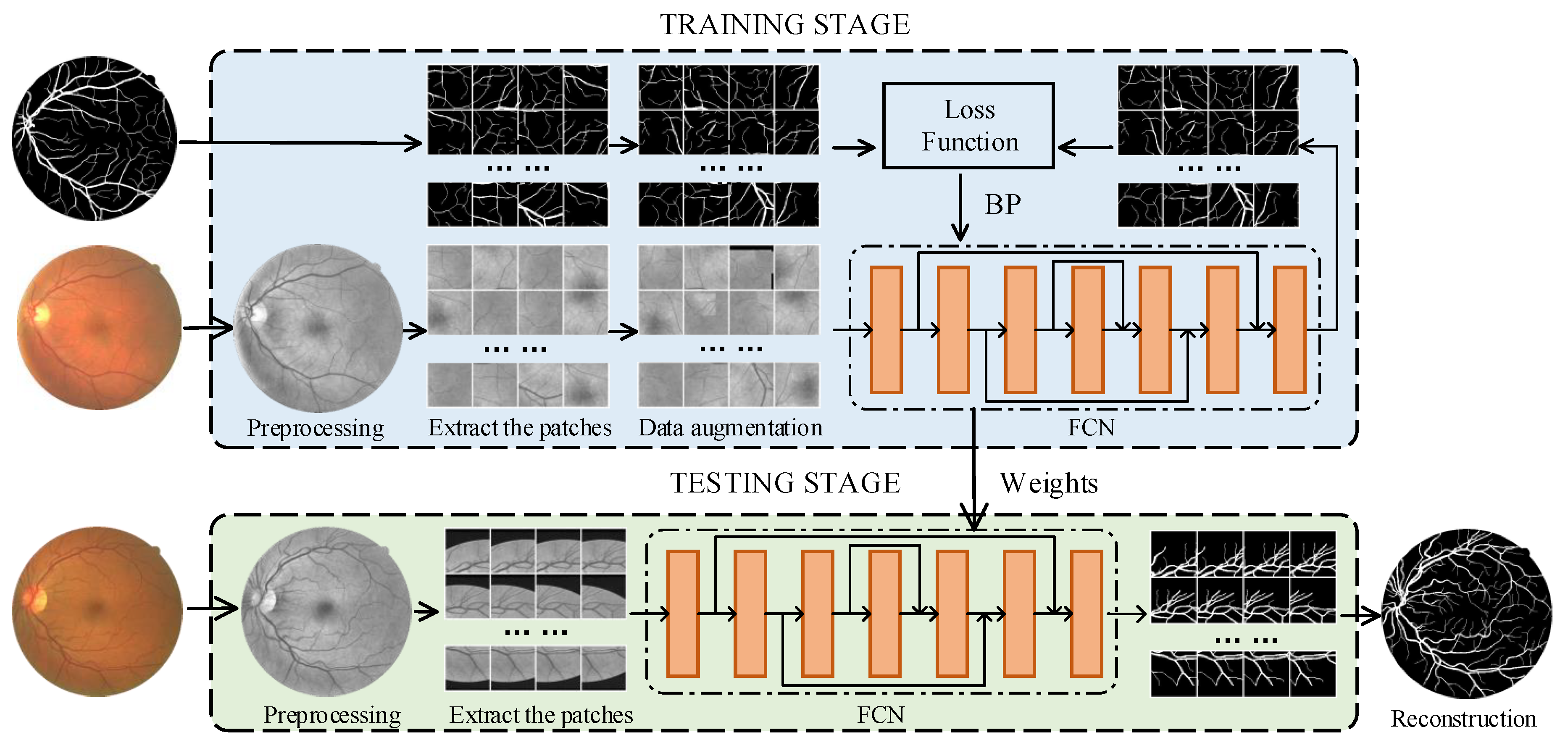
2. Methodology
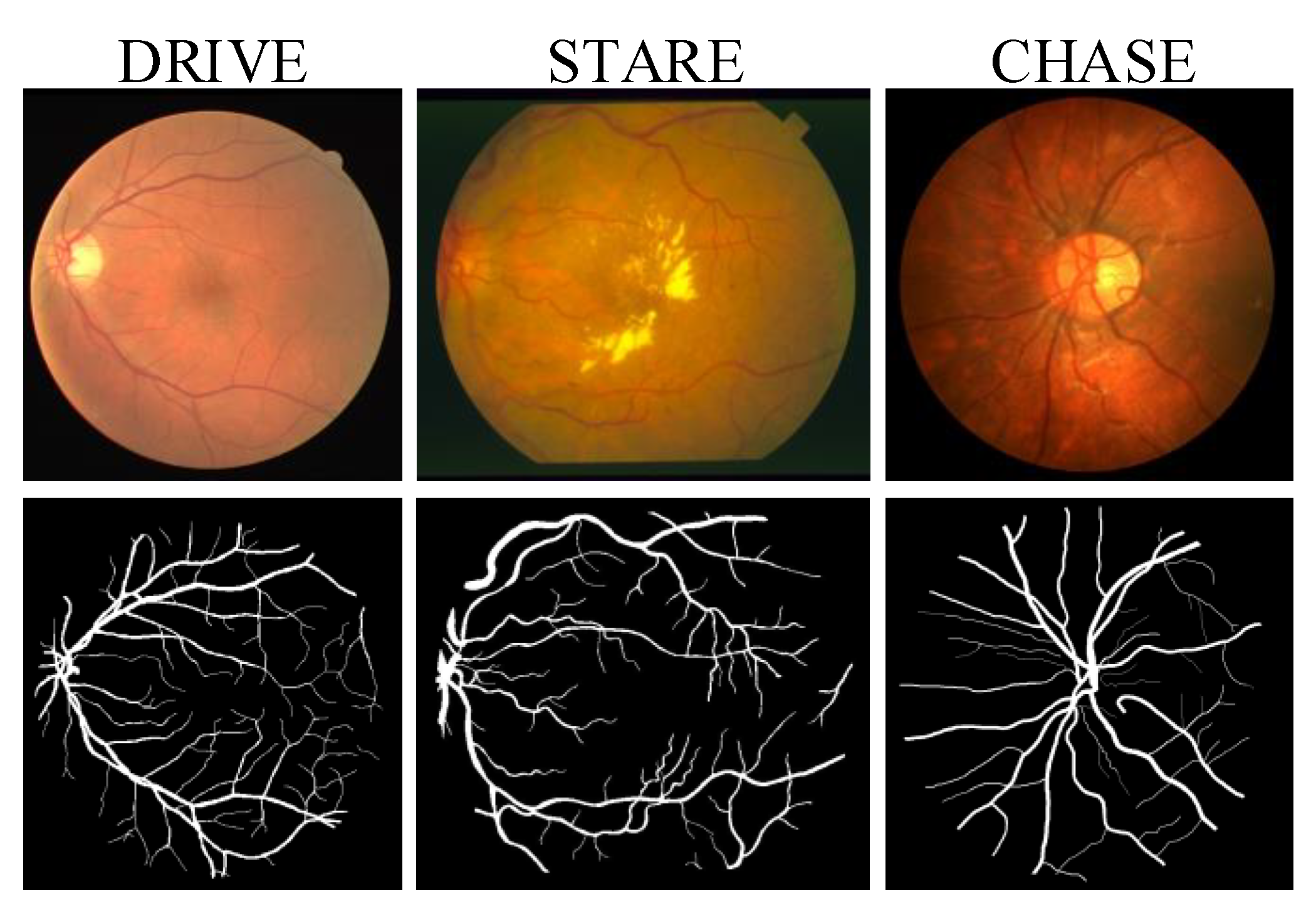
2.1. Materials
2.2. Dataset Preparation and Image Preprocessing
2.2.1. Dataset Preparation
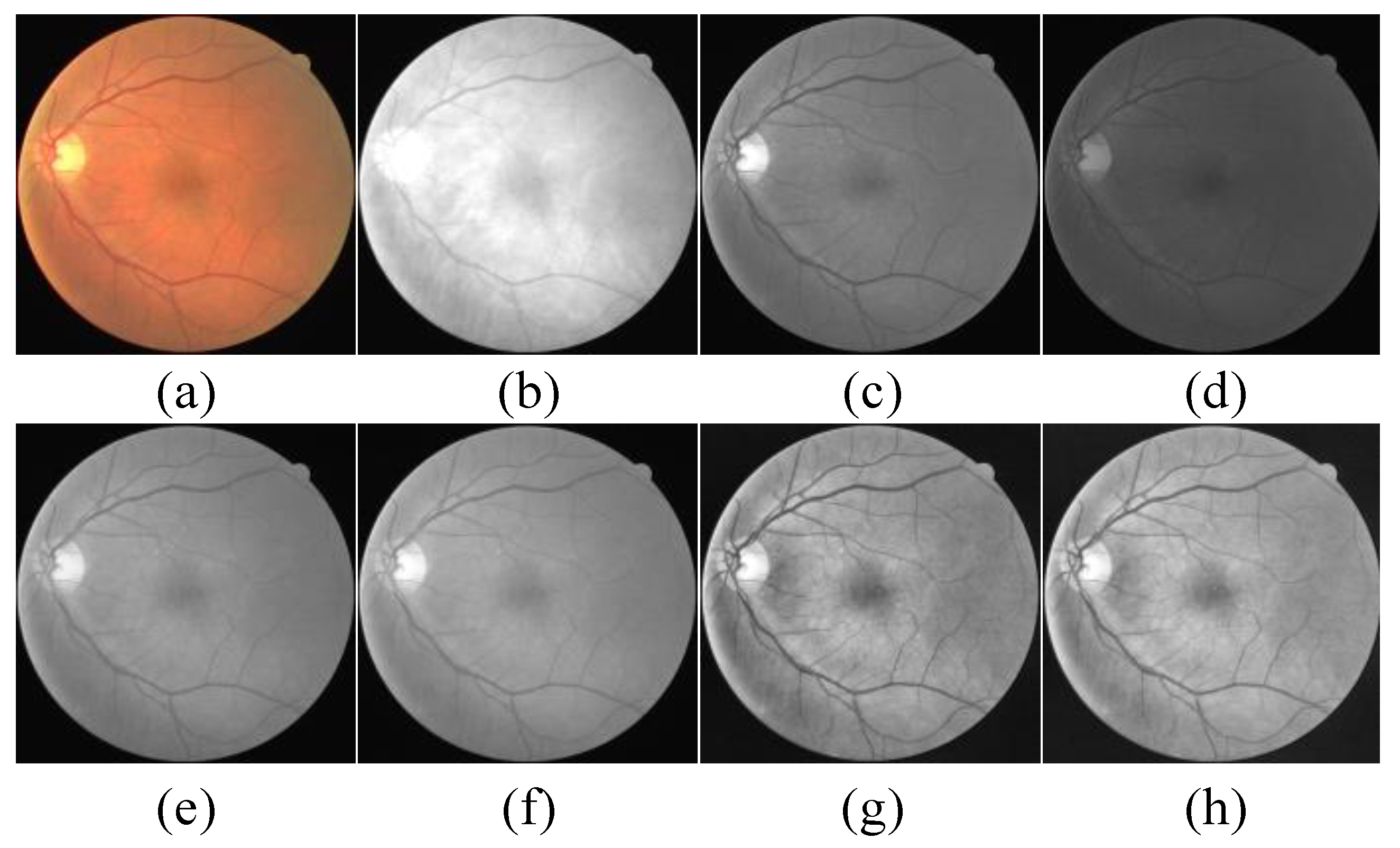
2.2.2. Image Preprocessing
2.3. Dynamic Patch Extraction
| Algorithm 1 Training FCN with dynamic extraction patch strategy |
| Input: Train images , ground truths . Input: Patch size p, dynamic patch number n. Input: Initial FCN parameter , epochs E. Output: FCN parameter . Initialize patch images . Initialize patch labels . for to E do for to N do for to do Randomly generate the center coordinates of the patch. Patches I and labels T are extracted from X and G centered on , respectively. end for end for . Update parameters using the Adam [28] optimizer. end for return . |
| Algorithm 2 Testing FCN with overlapping patches reconstruction algorithm |
| Input: Test images , patch size p, stride size s. Output: Final segmentation result . , . , . Zero padding for X to . Initialize . Initialize . for to N do for to do for to do A patch is extracted with as the upper left coordinate. Input x into the trained FCN to get the output y. Assign y to the corresponding area of . Assign 1 to the corresponding area of . end for end for end for . Crop to get the final segmentation image . return |
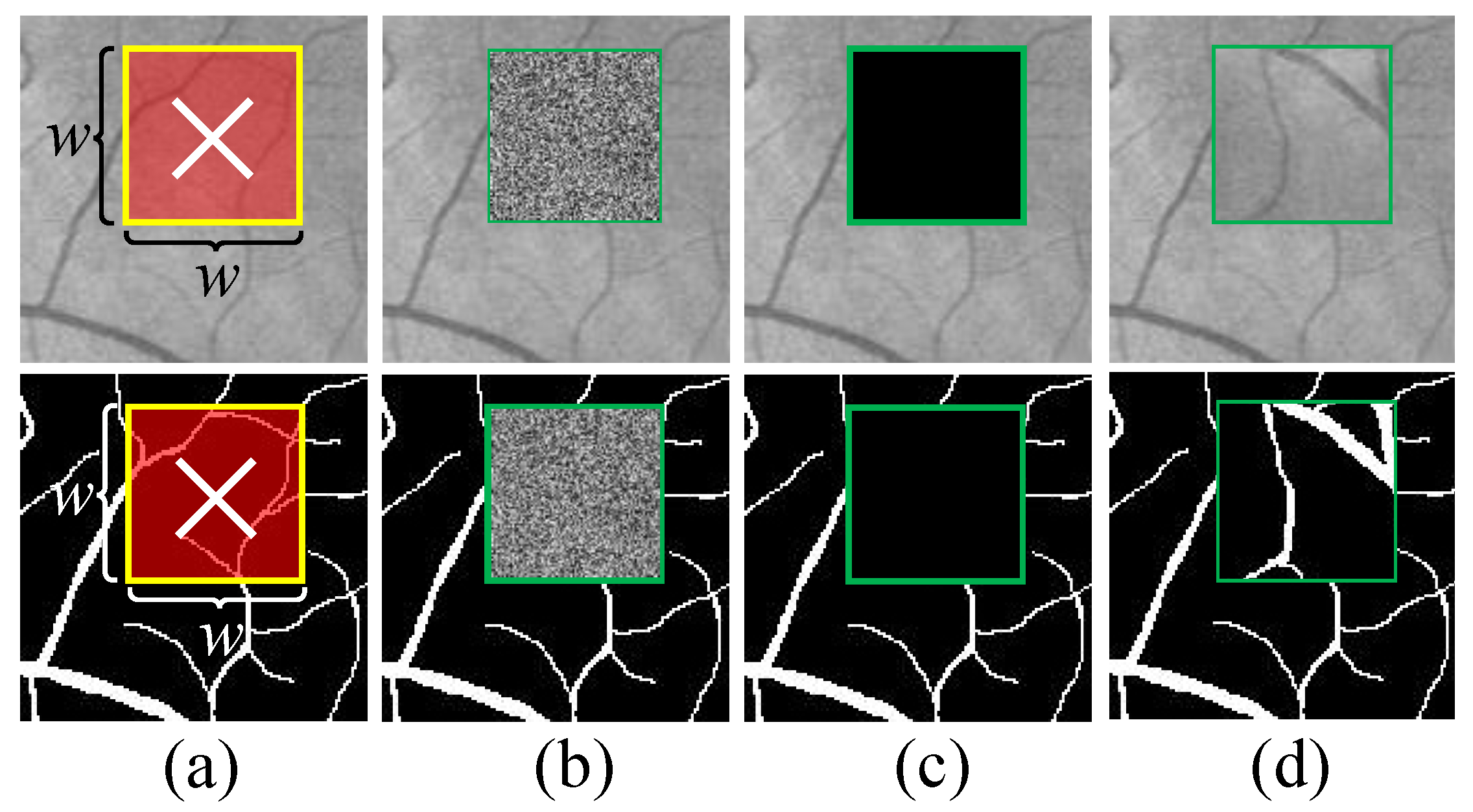
2.4. A Novel Retinal Image Data Augmentation Method
2.5. Fully Convolutional Neural Network (FCN)
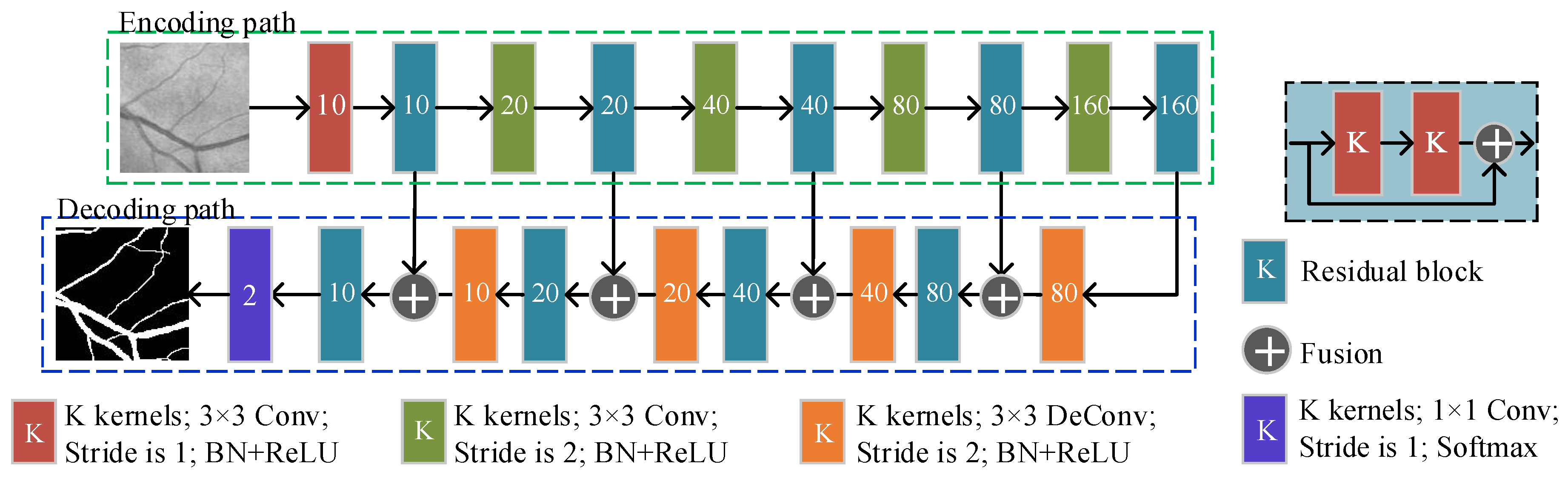
2.5.1. The Basic FCN Architecture
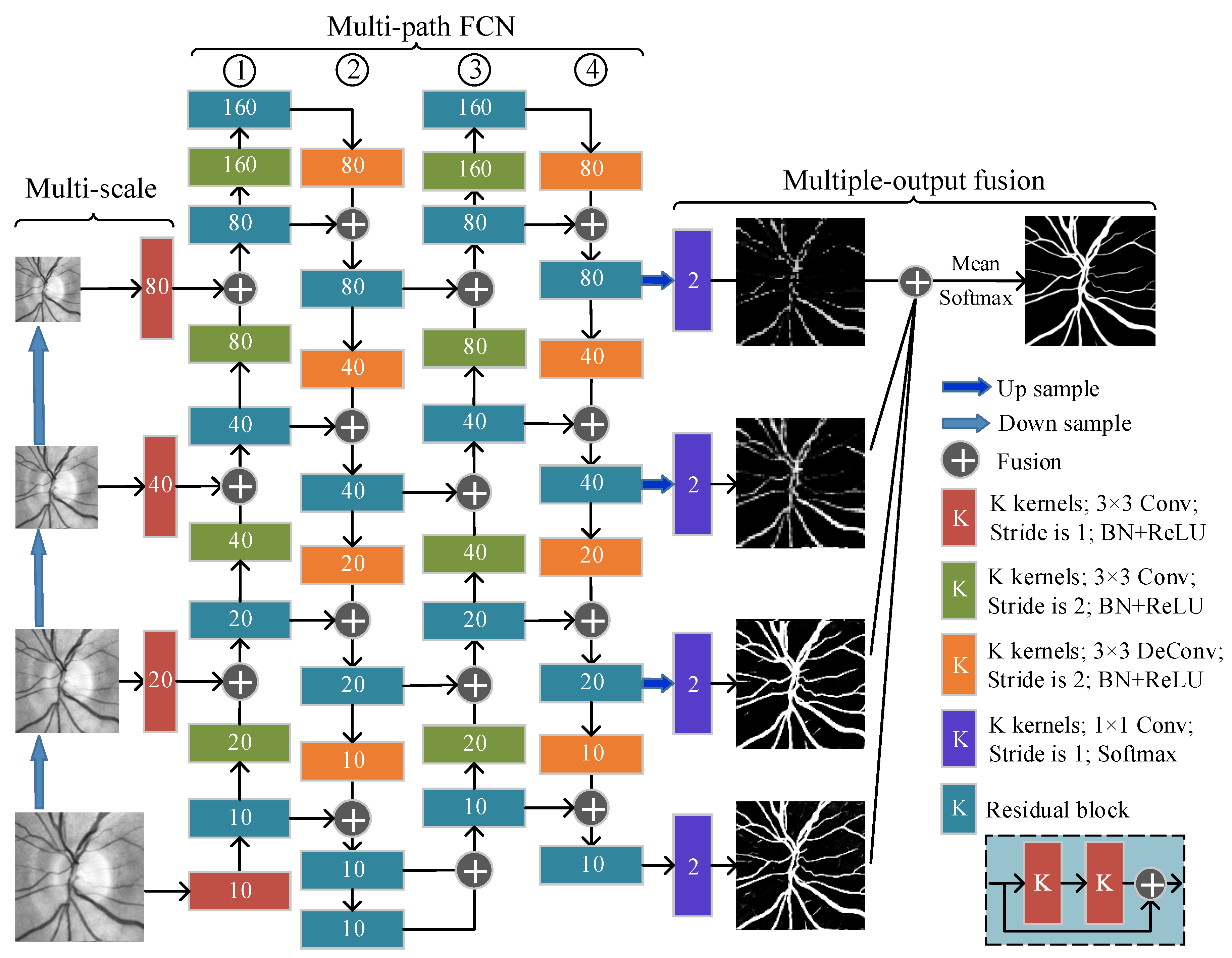
2.5.2. Multi-Scale, Multi-Path, and Multi-Output Fusion FCN (M3FCN)
3. Experimental Setup
3.1. Evaluation Metrics
3.2. Implementation Details
4. Results and Discussion
4.1. Ablation Analysis
4.1.1. Validation of the Image Preprocessing
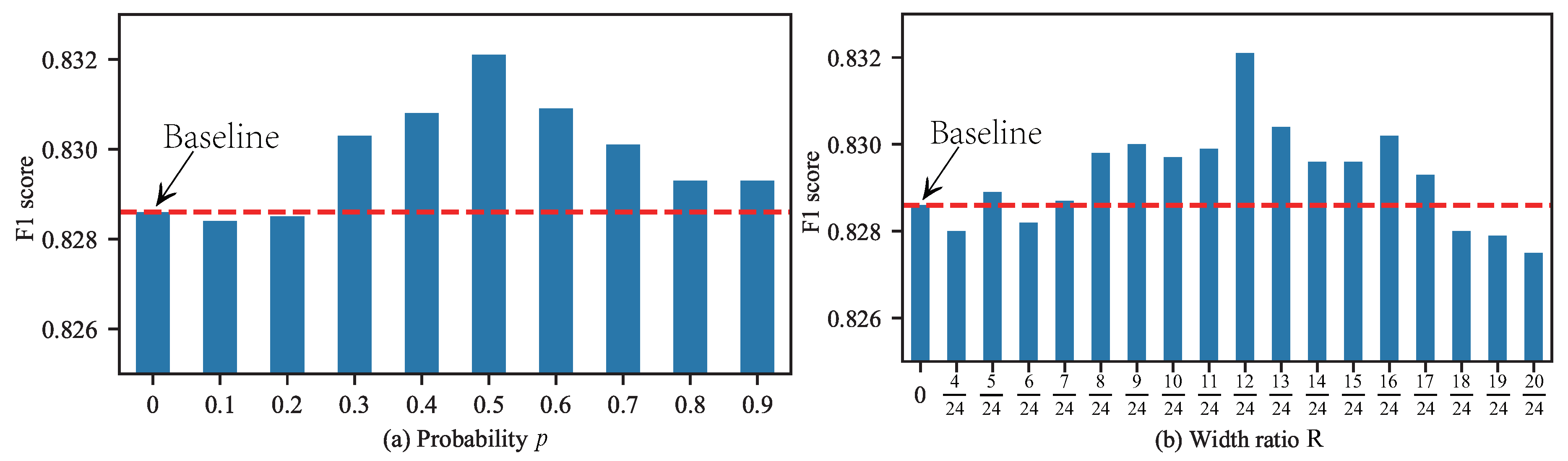
4.1.2. The Impact of RCF’s Hyper-Parameters
4.1.3. Validation of the Data Augmentation and RCF
4.1.4. Comparisons with FCN and M3FCN
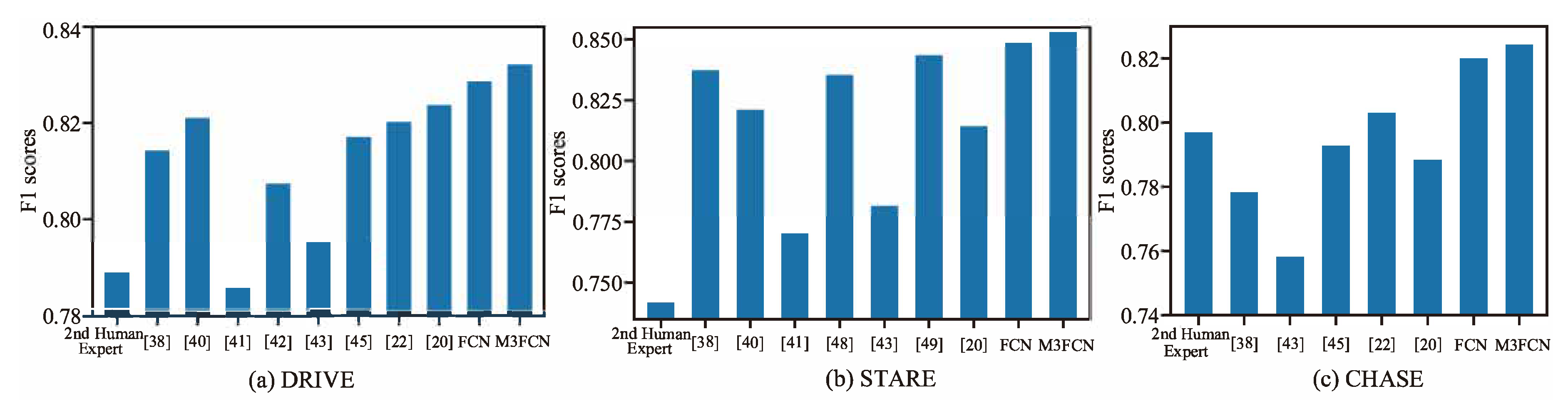
4.2. Comparison with the Existing Methods
4.3. Cross-Testing Evaluation
4.4. Visualize the Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Soomro, T.A.; Khan, T.M.; Khan, M.A.; Gao, J.; Paul, M.; Zheng, L. Impact of ICA-based image enhancement technique on retinal blood vessels segmentation. IEEE Access 2018, 6, 3524–3538. [Google Scholar] [CrossRef]
- Dharmawan, D.A.; Li, D.; Ng, B.P.; Rahardja, S. A New Hybrid Algorithm for Retinal Vessels Segmentation on Fundus Images. IEEE Access 2019, 7, 41885–41896. [Google Scholar] [CrossRef]
- Hoover, A.; Kouznetsova, V.; Goldbaum, M. Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response. IEEE Trans. Med. Imaging 2000, 19, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, W.S.; Teixeira, J.V.; Ren, T.I.; Cavalcanti, G.D.; Sijbers, J. Unsupervised retinal vessel segmentation using combined filters. PLoS ONE 2016, 11, e0149943. [Google Scholar] [CrossRef] [PubMed]
- Zardadi, M.; Mehrshad, N.; Razavi, S.M. Unsupervised Segmentation of Retinal Blood Vessels Using the Human Visual System Line Detection Model. 2016. Available online: https://pdfs.semanticscholar.org/10e1/a203cfdfe9d95e8d5e1b6fb23df03093de40.pdf (accessed on 26 August 2019).
- Fraz, M.M.; Barman, S.A.; Remagnino, P.; Hoppe, A.; Basit, A.; Uyyanonvara, B.; Rudnicka, A.R.; Owen, C.G. An approach to localize the retinal blood vessels using bit planes and centerline detection. Comput. Methods Prog. Biomed. 2012, 108, 600–616. [Google Scholar] [CrossRef] [PubMed]
- Hassan, G.; El-Bendary, N.; Hassanien, A.E.; Fahmy, A.; Snasel, V.; Shoeb, A.M. Retinal blood vessel segmentation approach based on mathematical morphology. Procedia Comput. Sci. 2015, 65, 612–622. [Google Scholar] [CrossRef]
- Liu, I.; Sun, Y. Recursive tracking of vascular networks in angiograms based on the detection-deletion scheme. IEEE Trans. Med. Imaging 1993, 12, 334–341. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Adel, M.; Bourennane, S. Retinal vessel segmentation using a probabilistic tracking method. Pattern Recognit. 2012, 45, 1235–1244. [Google Scholar] [CrossRef]
- Staal, J.; Abràmoff, M.D.; Niemeijer, M.; Viergever, M.A.; Van Ginneken, B. Ridge-based vessel segmentation in color images of the retina. IEEE Transact. Med. Imaging 2004, 23, 501–509. [Google Scholar] [CrossRef]
- You, X.; Peng, Q.; Yuan, Y.; Cheung, Y.M.; Lei, J. Segmentation of retinal blood vessels using the radial projection and semi-supervised approach. Pattern Recognit. 2011, 44, 2314–2324. [Google Scholar] [CrossRef]
- Tan, J.H.; Fujita, H.; Sivaprasad, S.; Bhandary, S.V.; Rao, A.K.; Chua, K.C.; Acharya, U.R. Automated segmentation of exudates, haemorrhages, microaneurysms using single convolutional neural network. Inf. Sci. 2017, 420, 66–76. [Google Scholar] [CrossRef]
- Aslani, S.; Sarnel, H. A new supervised retinal vessel segmentation method based on robust hybrid features. Biomed. Signal Process. Control 2016, 30, 1–12. [Google Scholar] [CrossRef]
- Fraz, M.M.; Remagnino, P.; Hoppe, A.; Uyyanonvara, B.; Rudnicka, A.R.; Owen, C.G.; Barman, S.A. An ensemble classification-based approach applied to retinal blood vessel segmentation. IEEE Trans. Biomed. Eng. 2012, 59, 2538–2548. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Xu, Y.; Wong, D.W.K.; Liu, J. Retinal vessel segmentation via deep learning network and fully-connected conditional random fields. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 13–16 April 2016; pp. 698–701. [Google Scholar]
- Mo, J.; Zhang, L. Multi-level deep supervised networks for retinal vessel segmentation. Int. J. Comput. Assisted Radiol. Surg. 2017, 12, 2181–2193. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Zhang, H.; Hu, G. Automatic Retinal Vessel Segmentation via Deeply Supervised and Smoothly Regularized Network. IEEE Access 2018, 7, 57717–57724. [Google Scholar] [CrossRef]
- Owen, C.G.; Rudnicka, A.R.; Mullen, R.; Barman, S.A.; Monekosso, D.; Whincup, P.H.; Ng, J.; Paterson, C. Measuring retinal vessel tortuosity in 10-year-old children: Validation of the computer-assisted image analysis of the retina (CAIAR) program. Investig. Ophthalmol. Visual Sci. 2009, 50, 2004–2010. [Google Scholar] [CrossRef]
- Jin, Q.; Meng, Z.; Pham, T.D.; Chen, Q.; Wei, L.; Su, R. DUNet: A deformable network for retinal vessel segmentation. Knowl.-Based Syst. 2019, 178, 149–162. [Google Scholar] [CrossRef]
- Soares, J.V.; Leandro, J.J.; Cesar, R.M.; Jelinek, H.F.; Cree, M.J. Retinal vessel segmentation using the 2-D Gabor wavelet and supervised classification. IEEE Trans. Med. Imaging 2006, 25, 1214–1222. [Google Scholar] [CrossRef]
- Zhuang, J. LadderNet: Multi-path networks based on U-Net for medical image segmentation. arXiv 2018, arXiv:1810.07810. [Google Scholar]
- Payette, B. Color Space Converter: R’G’B’to Y’CbCr; Xilinx, XAPP637 (v1. 0); Xilinx: San Jose, CA, USA, 2002. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Jain, A.; Nandakumar, K.; Ross, A. Score normalization in multimodal biometric systems. Pattern Recognit. 2005, 38, 2270–2285. [Google Scholar] [CrossRef]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive histogram equalization and its variations. Comput. Vis. Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library; O’Reilly Media, Inc.: Newton, MA, USA, 2008. [Google Scholar]
- Oliveira, A.; Pereira, S.; Silva, C.A. Retinal vessel segmentation based on fully convolutional neural networks. Expert Syst. Appl. 2018, 112, 229–242. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical evaluation of rectified activations in convolutional network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Washington, DC, USA, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Lam, B.S.; Gao, Y.; Liew, A.W.C. General retinal vessel segmentation using regularization-based multiconcavity modeling. IEEE Trans. Med. Imaging 2010, 29, 1369–1381. [Google Scholar] [CrossRef] [PubMed]
- Fraz, M.M.; Remagnino, P.; Hoppe, A.; Uyyanonvara, B.; Rudnicka, A.R.; Owen, C.G.; Barman, S.A. Blood vessel segmentation methodologies in retinal images—A survey. Comput. Methods Programs Biomed. 2012, 108, 407–433. [Google Scholar] [CrossRef] [PubMed]
- Azzopardi, G.; Strisciuglio, N.; Vento, M.; Petkov, N. Trainable COSFIRE filters for vessel delineation with application to retinal images. Med. Image Anal. 2015, 19, 46–57. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Liskowski, P.; Krawiec, K. Segmenting retinal blood vessels with deep neural networks. IEEE Trans. Med. Imaging 2016, 35, 2369–2380. [Google Scholar] [CrossRef] [PubMed]
- Maninis, K.K.; Pont-Tuset, J.; Arbeláez, P.; Van Gool, L. Deep retinal image understanding. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; pp. 140–148. [Google Scholar]
- Orlando, J.I.; Prokofyeva, E.; Blaschko, M.B. A discriminatively trained fully connected conditional random field model for blood vessel segmentation in fundus images. IEEE Trans. Biomed. Eng. 2016, 64, 16–27. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, A.; Singh, S. A fully convolutional neural network based structured prediction approach towards the retinal vessel segmentation. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 248–251. [Google Scholar]
- Zhang, J.; Chen, Y.; Bekkers, E.; Wang, M.; Dashtbozorg, B.; ter Haar Romeny, B.M. Retinal vessel delineation using a brain-inspired wavelet transform and random forest. Pattern Recognit. 2017, 69, 107–123. [Google Scholar] [CrossRef]
- Xia, H.; Jiang, F.; Deng, S.; Xin, J.; Doss, R. Mapping Functions Driven Robust Retinal Vessel Segmentation via Training Patches. IEEE Access 2018, 6, 61973–61982. [Google Scholar] [CrossRef]
- Alom, M.Z.; Hasan, M.; Yakopcic, C.; Taha, T.M.; Asari, V.K. Recurrent residual convolutional neural network based on u-net (R2U-net) for medical image segmentation. arXiv 2018, arXiv:1802.06955. [Google Scholar]
- Lu, J.; Xu, Y.; Chen, M.; Luo, Y. A Coarse-to-Fine Fully Convolutional Neural Network for Fundus Vessel Segmentation. Symmetry 2018, 10, 607. [Google Scholar] [CrossRef]
- Li, Q.; Feng, B.; Xie, L.; Liang, P.; Zhang, H.; Wang, T. A cross-modality learning approach for vessel segmentation in retinal images. IEEE Trans. Med. Imaging 2015, 35, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Son, J.; Park, S.J.; Jung, K.H. Retinal vessel segmentation in fundoscopic images with generative adversarial networks. arXiv 2017, arXiv:1706.09318. [Google Scholar]
- Li, R.; Li, M.; Li, J. Connection sensitive attention U-NET for accurate retinal vessel segmentation. arXiv 2019, arXiv:1903.05558. [Google Scholar]
- Zhang, B.; Huang, S.; Hu, S. Multi-scale neural networks for retinal blood vessels segmentation. arXiv 2018, arXiv:1804.04206. [Google Scholar]
- Yan, Z.; Yang, X.; Cheng, K.T.T. A three-stage deep learning model for accurate retinal vessel segmentation. IEEE J. Biomed. Health Inform. 2018, 23, 1427–1436. [Google Scholar] [CrossRef]
- Chen, C.; Bai, W.; Davies, R.H.; Bhuva, A.N.; Manisty, C.; Moon, J.C.; Aung, N.; Lee, A.M.; Sanghvi, M.M.; Fung, K.; et al. Improving the generalizability of convolutional neural network-based segmentation on CMR images. arXiv 2019, arXiv:1907.01268. [Google Scholar]
- Dua, S.; Acharya, U.R.; Chowriappa, P.; Sree, S.V. Wavelet-based energy features for glaucomatous image classification. IEEE Trans. Inf. Technol. Biomed. 2011, 16, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
| No. | Grayscale | Data Normalization | CLAHE | Gamma Correction | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.8048 | 0.9546 | 0.7350 | 0.9866 | 0.9771 | ||||
| 1 | ✓ | 0.8199 | 0.9692 | 0.8000 | 0.9855 | 0.9831 | |||
| 2 | ✓ | ✓ | 0.8229 | 0.9697 | 0.8043 | 0.9855 | 0.9852 | ||
| 3 | ✓ | ✓ | 0.8284 | 0.9702 | 0.8215 | 0.9845 | 0.9871 | ||
| 4 | ✓ | ✓ | 0.8168 | 0.9683 | 0.8081 | 0.9836 | 0.9839 | ||
| 5 | ✓ | ✓ | ✓ | 0.8299 | 0.9699 | 0.8376 | 0.9826 | 0.9873 | |
| 6 | ✓ | ✓ | ✓ | 0.8173 | 0.9678 | 0.8234 | 0.9816 | 0.9840 | |
| 7 | ✓ | ✓ | ✓ | 0.8292 | 0.9704 | 0.8206 | 0.9848 | 0.9873 | |
| 8 | ✓ | ✓ | ✓ | ✓ | 0.8321 | 0.9706 | 0.8325 | 0.9838 | 0.9880 |
| Method | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|
| - | 0.8288 | 0.9703 | 0.8198 | 0.9848 | 0.9870 |
| RCF-0 | 0.8299 | 0.9702 | 0.8298 | 0.9837 | 0.9873 |
| RCF-R | 0.8294 | 0.9702 | 0.8269 | 0.9840 | 0.9873 |
| RCF-A | 0.8321 | 0.9706 | 0.8325 | 0.9838 | 0.9880 |
| Method | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|
| 0.8242 | 0.9697 | 0.8111 | 0.9849 | 0.9861 | |
| DA | 0.8288 | 0.9703 | 0.8198 | 0.9848 | 0.9870 |
| RCF-A | 0.8255 | 0.9689 | 0.8392 | 0.9814 | 0.9866 |
| DA + RCF-A | 0.8321 | 0.9706 | 0.8325 | 0.9838 | 0.9880 |
| Model Name | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|
| Basic FCN | 0.8286 | 0.9703 | 0.8196 | 0.9848 | 0.9870 |
| Muiti-scale FCN | 0.8290 | 0.9707 | 0.8115 | 0.9860 | 0.9873 |
| Multi-path FCN | 0.8287 | 0.9706 | 0.8118 | 0.9858 | 0.9871 |
| Multi-output fusion FCN | 0.8293 | 0.9705 | 0.8192 | 0.9850 | 0.9870 |
| Muiti-scale, multi-path FCN | 0.8295 | 0.9703 | 0.8259 | 0.9841 | 0.9870 |
| Muiti-scale, multi-output fusion FCN | 0.8286 | 0.9708 | 0.8063 | 0.9866 | 0.9871 |
| Muiti-path, multi-output fusion FCN | 0.8304 | 0.9701 | 0.8370 | 0.9828 | 0.9873 |
| M3FCN | 0.8321 | 0.9706 | 0.8325 | 0.9838 | 0.9880 |
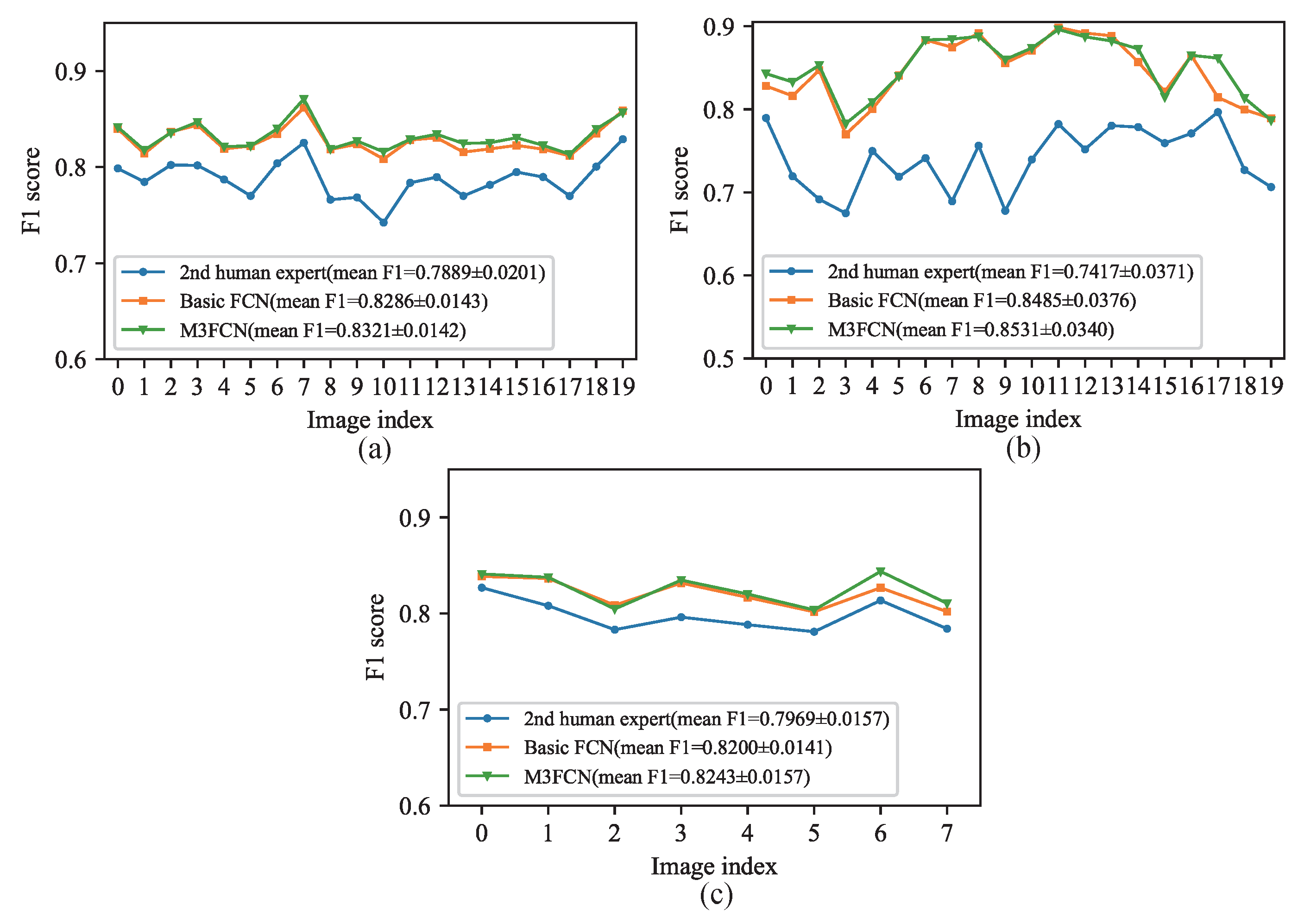
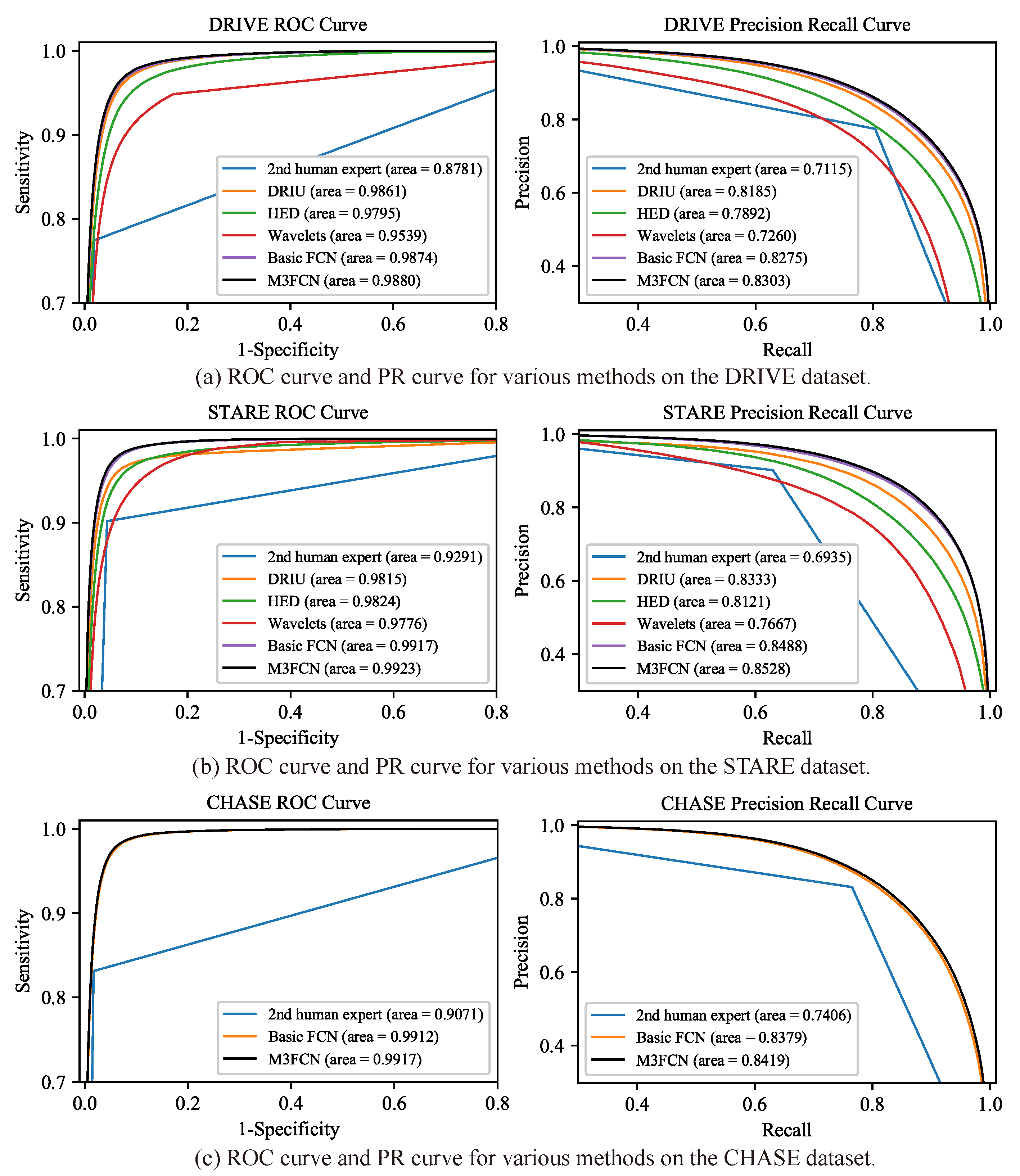
| Methods | Year | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|---|
| 2nd human expert | - | 0.7889 | 0.9637 | 0.7743 | 0.9819 | 0.8781 |
| Lam et al. [35] | 2010 | - | 0.9472 | - | - | 0.9614 |
| You et al. [11] | 2011 | - | 0.9434 | 0.7410 | 0.9751 | - |
| Fraz et al. [36] | 2012 | - | 0.9430 | 0.7152 | 0.9759 | - |
| Azzopardi et al. [37] | 2015 | - | 0.9442 | 0.7655 | 0.9704 | 0.9614 |
| Ronneberger et al. [38] | 2015 | 0.8142 | 0.9531 | 0.7537 | 0.9820 | 0.9755 |
| Liskowsk et al. [39] | 2016 | - | 0.9495 | 0.7763 | 0.9768 | 0.9720 |
| Maninis et al. [40] | 2016 | 0.8210 | 0.9541 | 0.8261 | 0.9115 | 0.9861 |
| Orlando et al. [41] | 2017 | 0.7857 | - | 0.7897 | 0.9684 | - |
| Dasgupta et al. [42] | 2017 | 0.8074 | 0.9533 | 0.7691 | 0.9801 | 0.9744 |
| Zhang et al. [43] | 2017 | 0.7953 | 0.9466 | 0.7861 | 0.9712 | 0.9703 |
| Xia et al. [44] | 2018 | - | 0.9540 | 0.7740 | 0.9800 | - |
| Alom et al. [45] | 2018 | 0.8171 | 0.9556 | 0.7792 | 0.9813 | 0.9784 |
| Zhuang et al. [21] | 2018 | 0.8202 | 0.9561 | 0.7856 | 0.9810 | 0.9793 |
| Lu et al. [46] | 2018 | - | 0.9634 | 0.7941 | 0.9870 | 0.9787 |
| Oliveira et al. [27] | 2018 | - | 0.9576 | 0.8039 | 0.9804 | 0.9821 |
| Jin et al. [19] | 2019 | 0.8237 | 0.9566 | 0.7963 | 0.9800 | 0.9802 |
| Basic FCN (ours) | 2019 | 0.8286 | 0.9703 | 0.8197 | 0.9848 | 0.9874 |
| M3FCN (ours) | 2019 | 0.8321 | 0.9706 | 0.8325 | 0.9838 | 0.9880 |
| Methods | Year | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|---|
| 2nd human expert | - | 0.7417 | 0.9522 | 0.9017 | 0.9564 | 0.9291 |
| Lam et al. [35] | 2010 | - | 0.9567 | - | - | 0.9739 |
| Fraz et al. [36] | 2012 | - | 0.9442 | 0.7311 | 0.9680 | - |
| Azzopardi et al. [37] | 2015 | - | 0.9563 | 0.7716 | 0.9701 | 0.9497 |
| Li et al. [47] | 2015 | - | 0.9628 | 0.7726 | 0.9844 | 0.9879 |
| Ronneberger et al. [38] | 2015 | 0.8373 | 0.9690 | 0.8270 | 0.9842 | 0.9898 |
| Liskowsk et al. [39] | 2016 | - | 0.9566 | 0.7867 | 0.9754 | 0.9785 |
| Maninis et al. [40] | 2016 | 0.8210 | 0.9541 | 0.8261 | 0.9115 | 0.9861 |
| Orlando et al. [41] | 2017 | 0.7701 | - | 0.7680 | 0.9738 | - |
| Son et al. [48] | 2017 | 0.8353 | 0.9657 | 0.8350 | - | 0.9777 |
| Zhang et al. [43] | 2017 | 0.7815 | 0.9547 | 0.7882 | 0.9729 | 0.9740 |
| Oliveira et al. [27] | 2018 | - | 0.9694 | 0.8315 | 0.9858 | 0.9905 |
| Xia et al. [44] | 2018 | - | 0.9530 | 0.7670 | 0.9770 | - |
| Lu et al. [46] | 2018 | - | 0.9628 | 0.8090 | 0.9770 | 0.9801 |
| Li et al. [49] | 2019 | 0.8435 | 0.9673 | 0.8465 | - | 0.9834 |
| Jin et al. [19] | 2019 | 0.8143 | 0.9641 | 0.7595 | 0.9878 | 0.9832 |
| Basic FCN (ours) | 2019 | 0.8485 | 0.9773 | 0.8369 | 0.9888 | 0.9917 |
| M3FCN (ours) | 2019 | 0.8531 | 0.9777 | 0.8522 | 0.9880 | 0.9923 |
| Methods | Year | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|---|
| 2nd human expert | - | 0.7969 | 0.9733 | 0.8313 | 0.9829 | 0.9071 |
| Lam et al. [35] | 2015 | - | 0.9387 | 0.7585 | 0.9587 | 0.9487 |
| Li et al. [47] | 2015 | - | 0.9581 | 0.7507 | 0.9793 | 0.9793 |
| Ronneberger et al. [38] | 2015 | 0.7783 | 0.9578 | 0.8288 | 0.9701 | 0.9772 |
| Liskowsk et al. [39] | 2016 | - | 0.9566 | 0.7867 | 0.9754 | 0.9785 |
| Zhang et al. [43] | 2017 | 0.7581 | 0.9502 | 0.7644 | 0.9716 | 0.9706 |
| Zhang et al. [50] | 2018 | - | 0.9662 | 0.7742 | 0.9876 | 0.9865 |
| Alom et al. [45] | 2018 | 0.7928 | 0.9634 | 0.7756 | 0.9820 | 0.9815 |
| Zhuang et al. [21] | 2018 | 0.8031 | 0.9656 | 0.7978 | 0.9818 | 0.9839 |
| Lu et al. [46] | 2018 | - | 0.9664 | 0.7571 | 0.9823 | 0.9752 |
| Jin et al. [19] | 2019 | 0.7883 | 0.9610 | 0.8155 | 0.9752 | 0.9804 |
| Basic FCN (ours) | 2019 | 0.8200 | 0.9770 | 0.8323 | 0.9867 | 0.9912 |
| M3FCN (ours) | 2019 | 0.8243 | 0.9773 | 0.8453 | 0.9862 | 0.9917 |
| Method | Year | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|---|
| Fraz et al. [14] | 2012 | - | 0.9456 | 0.7242 | 0.9792 | 0.9697 |
| Li et al. [47] | 2015 | - | 0.9486 | 0.7273 | 0.9810 | 0.9677 |
| Yan et al. [51] | 2018 | - | 0.9444 | 0.7014 | 0.9802 | 0.9568 |
| Jin et al. [19] | 2019 | - | 0.9481 | 0.6505 | 0.9914 | 0.9718 |
| Basic FCN(ours) | 2019 | 0.7675 | 0.9646 | 0.6663 | 0.9933 | 0.9780 |
| M3FCN (ours) | 2019 | 0.7845 | 0.9665 | 0.6950 | 0.9926 | 0.9820 |
| Method | Year | F1 | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|---|---|
| Fraz et al. [14] | 2012 | - | 0.9495 | 0.7010 | 0.9770 | 0.9660 |
| Li et al. [47] | 2015 | - | 0.9545 | 0.7027 | 0.9828 | 0.9671 |
| Yan et al. [51] | 2018 | - | 0.9580 | 0.7319 | 0.9840 | 0.9678 |
| Jin et al. [19] | 2019 | - | 0.9445 | 0.8419 | 0.9563 | 0.9690 |
| Basic FCN (ours) | 2019 | 0.7755 | 0.9633 | 0.8332 | 0.9740 | 0.9790 |
| M3FCN (ours) | 2019 | 0.7876 | 0.9647 | 0.8604 | 0.9733 | 0.9826 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Zhang, H.; Tan, N.; Chen, L. Automatic Retinal Blood Vessel Segmentation Based on Fully Convolutional Neural Networks. Symmetry 2019, 11, 1112. https://doi.org/10.3390/sym11091112
Jiang Y, Zhang H, Tan N, Chen L. Automatic Retinal Blood Vessel Segmentation Based on Fully Convolutional Neural Networks. Symmetry. 2019; 11(9):1112. https://doi.org/10.3390/sym11091112
Chicago/Turabian StyleJiang, Yun, Hai Zhang, Ning Tan, and Li Chen. 2019. "Automatic Retinal Blood Vessel Segmentation Based on Fully Convolutional Neural Networks" Symmetry 11, no. 9: 1112. https://doi.org/10.3390/sym11091112
APA StyleJiang, Y., Zhang, H., Tan, N., & Chen, L. (2019). Automatic Retinal Blood Vessel Segmentation Based on Fully Convolutional Neural Networks. Symmetry, 11(9), 1112. https://doi.org/10.3390/sym11091112





