Deep Metric Learning: A Survey
Abstract
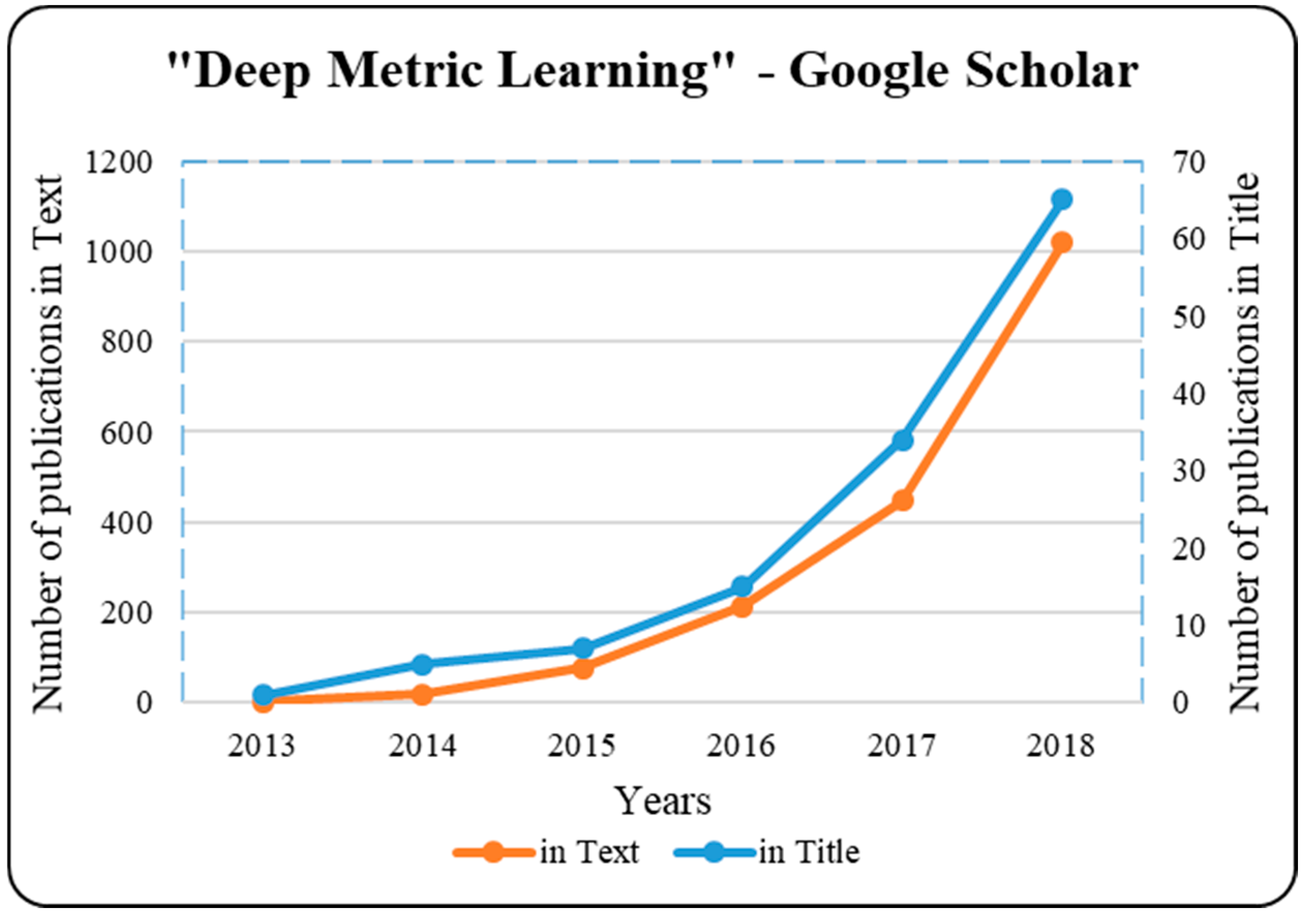
1. Introduction
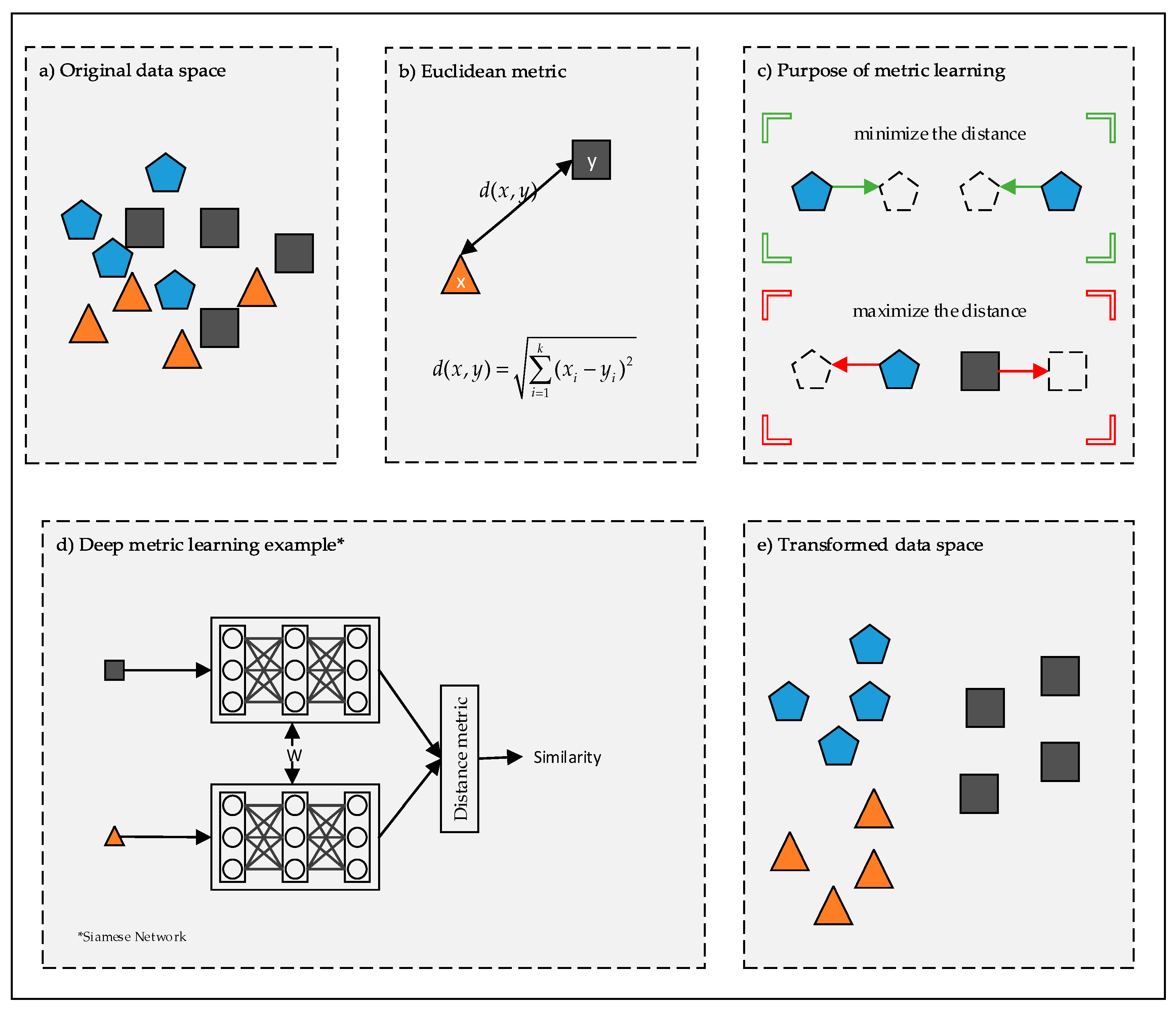
2. Metric Learning
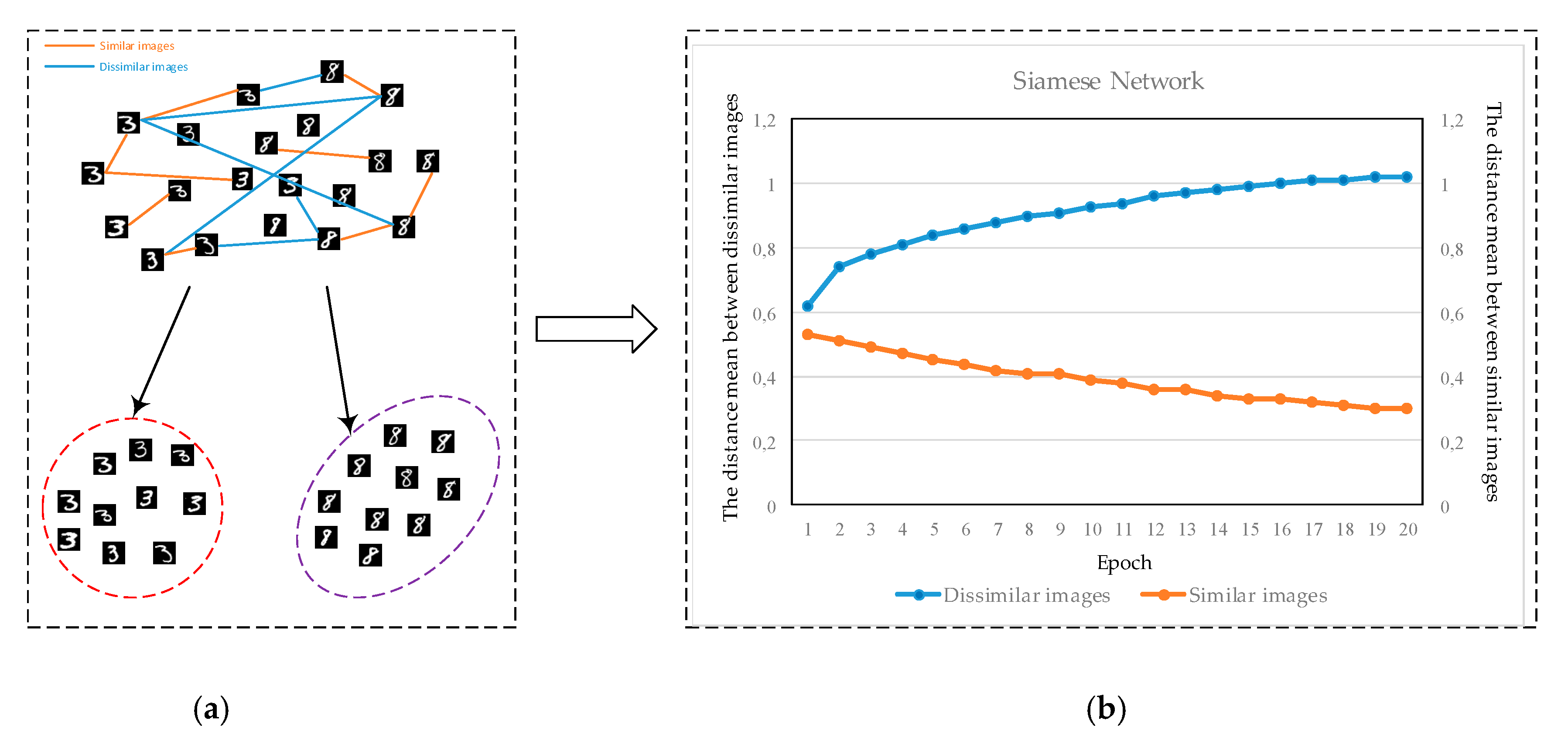
3. Deep Metric Learning
3.1. Deep Metric Learning Problems
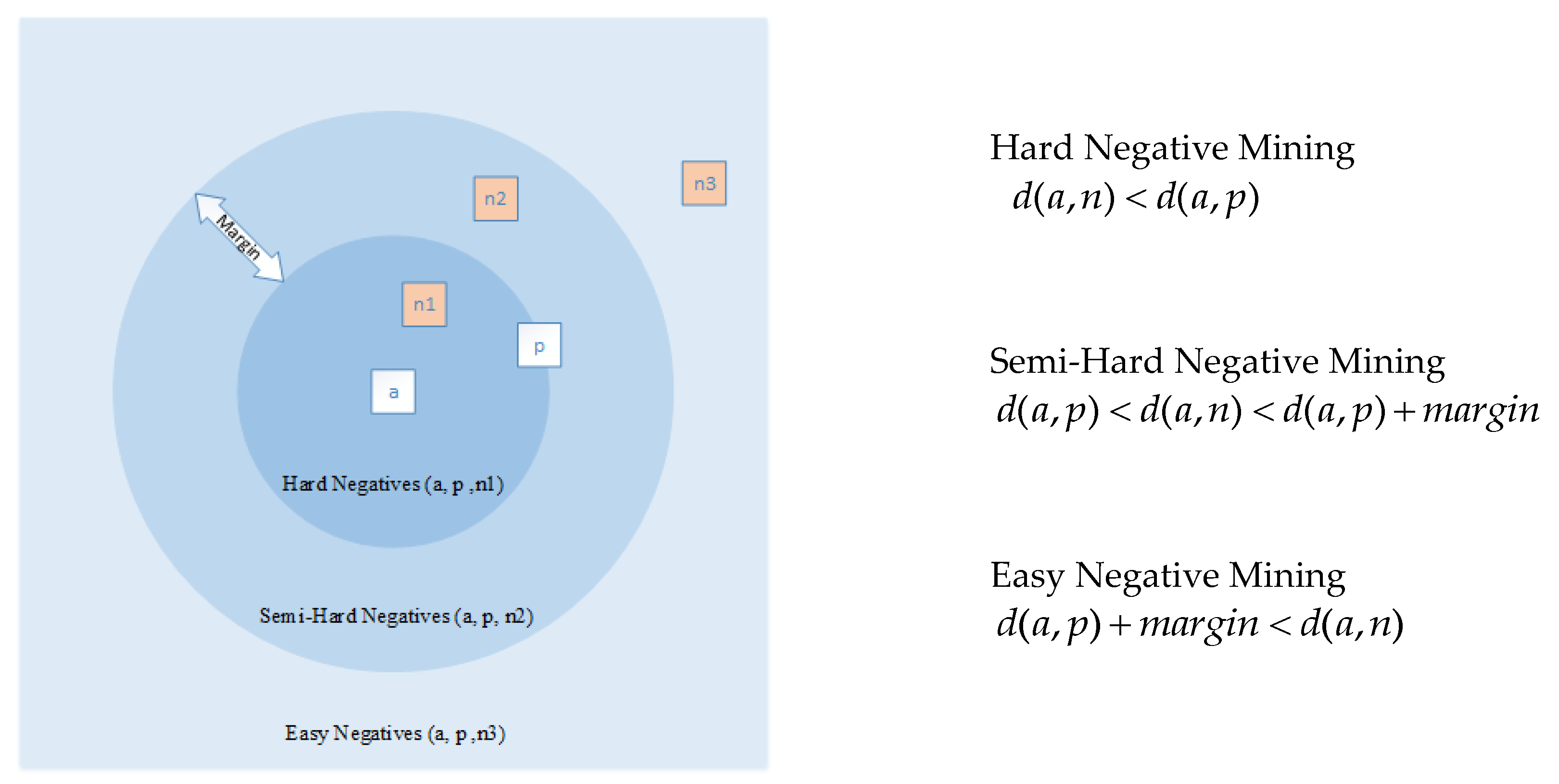
3.2. Sample Selection
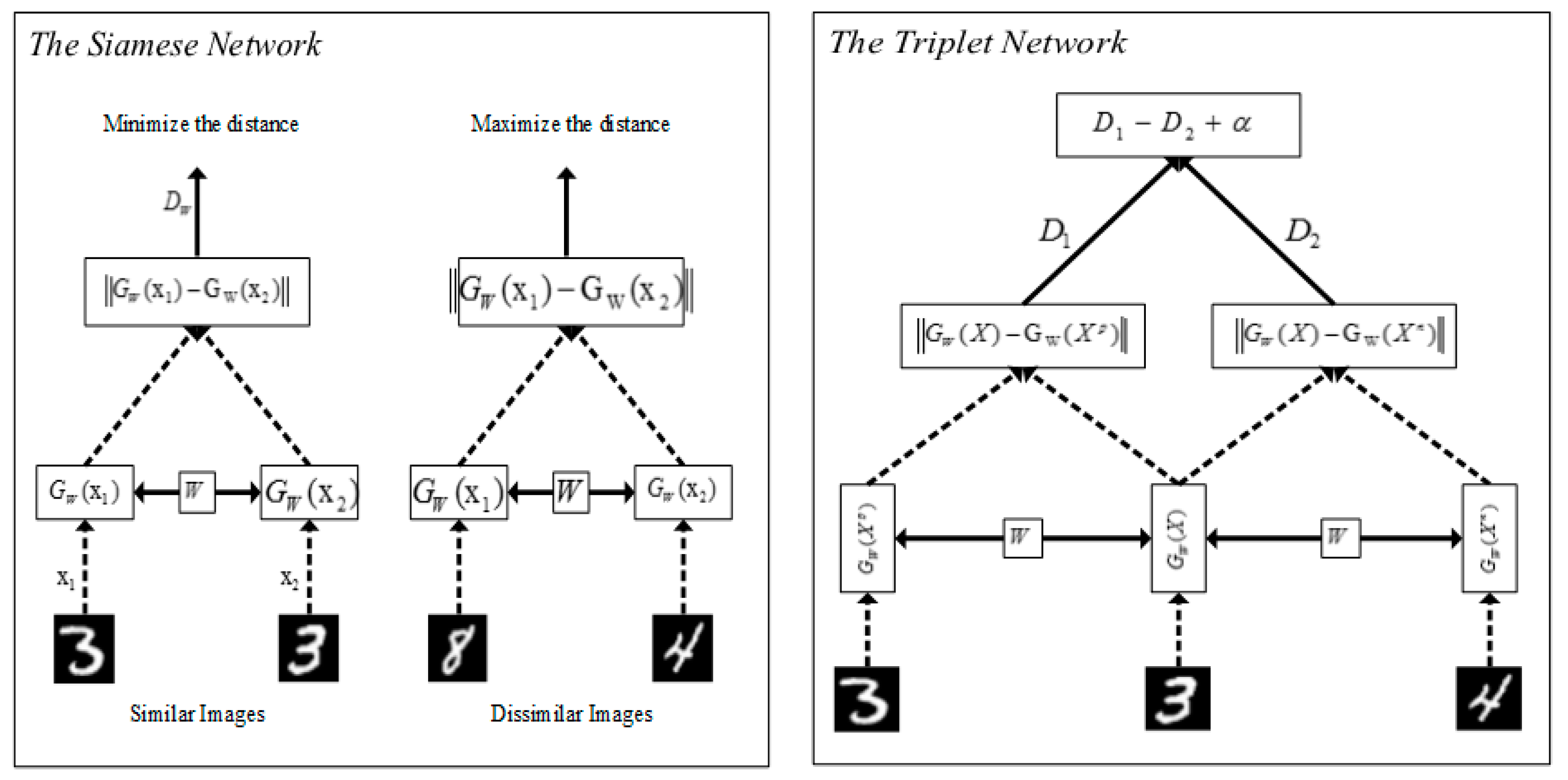
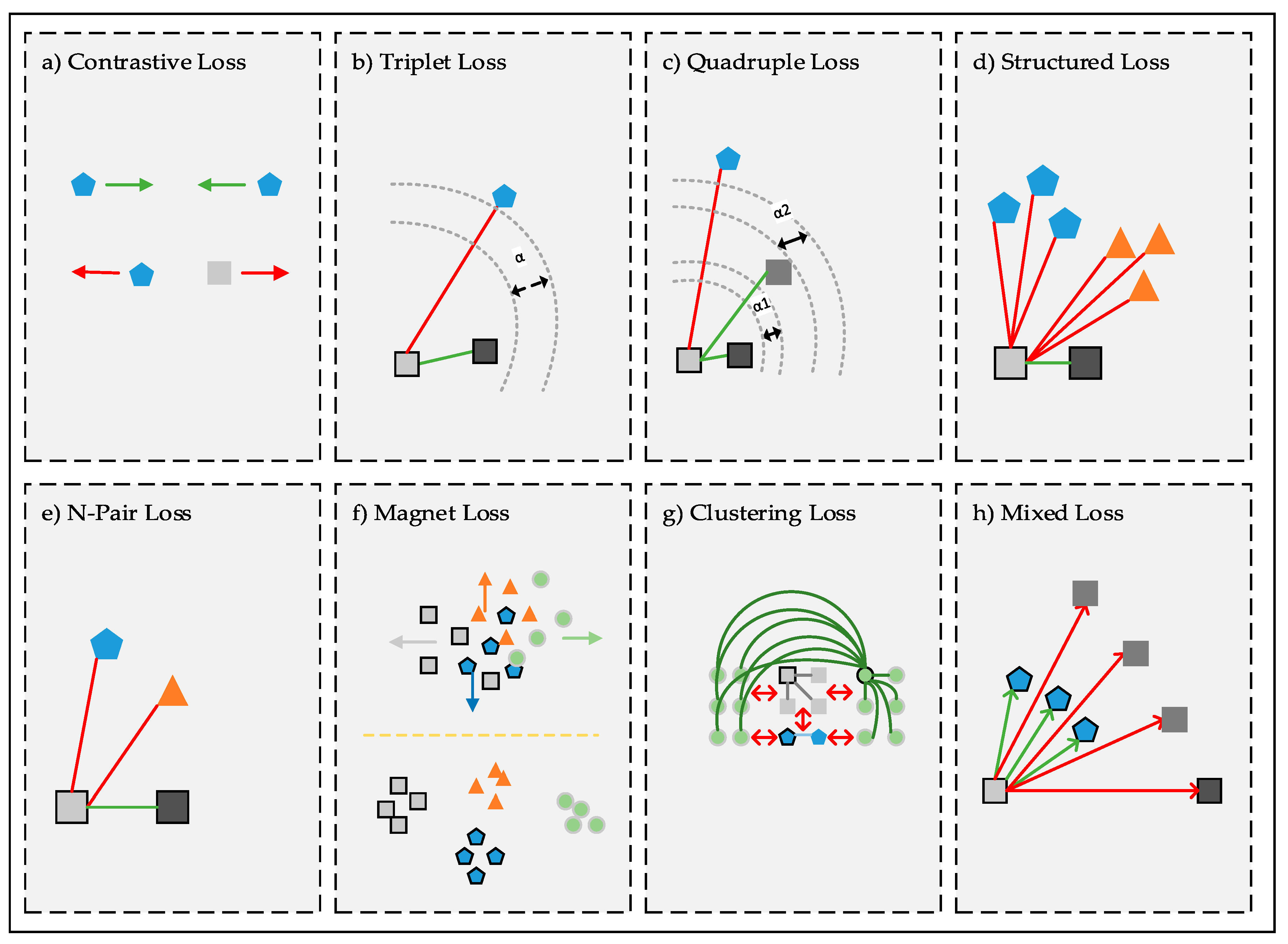
3.3. Loss functions for Deep Metric Learning
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 2000, 44, 206–226. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 1st ed.; O’Reilly Media: Sebastopol, CA, USA, 2017; pp. 1–9. [Google Scholar]
- Malik, S.; Kanwal, N.; Asghar, M.N.; Sadiq, M.A.A.; Karamat, I.; Fleury, M. Data Driven Approach for Eye Disease Classification with Machine Learning. Appl. Sci. 2019, 9, 2789. [Google Scholar] [CrossRef]
- Globerson, A.; Roweis, S. Metric learning by collapsing classes. In Proceedings of the 18th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 451–458. [Google Scholar]
- Wang, F.; Sun, J. Survey on distance metric learning and dimensionality reduction in data mining. Data Min. Knowl. Discov. 2015, 29, 534–564. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Tran, K.; Phan, T.; Tran, T.K.; Phan, T.T. Deep Learning Application to Ensemble Learning—The Simple, but Effective, Approach to Sentiment Classifying. Appl. Sci. 2019, 9, 2760. [Google Scholar] [CrossRef]
- Lu, J.; Hu, J.; Zhou, J. Deep Metric Learning for Visual Understanding: An Overview of Recent Advances. IEEE Signal Process. Mag. 2017, 34, 76–84. [Google Scholar] [CrossRef]
- Xing, E.P.; Jordan, M.I.; Russell, S.J.; Ng, A.Y. Distance metric learning with application to clustering with side-information. In Proceedings of the 15th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 521–528. [Google Scholar]
- Weinberger, K.Q.; Blitzer, J.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 10 December 2005; pp. 1473–1480. [Google Scholar]
- Davis, J.V.; Kulis, B.; Jain, P.; Sra, S.; Dhillon, I.S. Information-theoretic metric learning. In Proceedings of the 24th International Conference on Machine Learning, Corvallis, OR, USA, 20–24 June 2007; pp. 209–216. [Google Scholar]
- Nguyen, H.V.; Bai, L. Cosine similarity metric learning for face verification. In Proceedings of the 10th Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010; pp. 709–720. [Google Scholar]
- Duan, Y.; Lu, J.; Feng, J.; Zhou, J. Deep Localized Metric Learning. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2644–2656. [Google Scholar] [CrossRef]
- Bellet, A.; Habrard, A.; Sebban, M. A Survey on Metric Learning for Feature Vectors and Structured Data. arXiv 2014, arXiv:1306.6709. [Google Scholar]
- Nvidia Developer. Available online: https://developer.nvidia.com/deep-learning-frameworks (accessed on 16 April 2019).
- Matusita, K. Decision Rules, Based on the Distance, for Problems of Fit, Two Samples, and Estimation. Ann. Math. Stat. 1955, 26, 631–640. [Google Scholar] [CrossRef]
- Thacker, N.A.; Aherne, F.J.; Rockett, P.I. The Bhattacharyya metric as an absolute similarity measure for frequency coded data. Kybernetika 1997, 34, 363–368. [Google Scholar]
- Elgammal, A.; Duraiswami, R.; Davis, L.S. Probabilistic tracking in joint feature-spatial spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Madison, WI, USA, 16–22 June 2003; pp. 1–8. [Google Scholar]
- Yu, J.; Yang, X.; Gao, F.; Tao, D. Deep multimodal distance metric learning using click constraints for image ranking. IEEE Trans. Cybern. 2016, 47, 4014–4024. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Wang, C.; Xiao, B.; Chen, X.; Zhou, J. Deep nonlinear metric learning with independent subspace analysis for face verification. In Proceedings of the 20th ACM International Conference on Multimedia, Nara, Japan, 29 October–2 November 2012; pp. 749–752. [Google Scholar]
- Dai, G.; Xie, J.; Zhu, F.; Fang, Y. Deep Correlated Metric Learning for Sketch-based 3D Shape Retrieval. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4002–4008. [Google Scholar]
- Li, Z.; Tang, J. Weakly Supervised Deep Metric Learning for Community-Contributed Image Retrieval. IEEE Trans. Multimedia 2015, 17, 1989–1999. [Google Scholar] [CrossRef]
- Kumar, V.B.; Harwood, B.; Carneiro, G.; Reid, I.; Drummond, T. Smart Mining for Deep Metric Learning. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2821–2829. [Google Scholar]
- Gundogdu, E.; Solmaz, B.; Koç, A.; Yücesoy, V.; Alatan, A.A. Deep distance metric learning for maritime vessel identification. In Proceedings of the 25th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 15–18 May 2017; pp. 1–4. [Google Scholar]
- Liu, J.; Deng, Y.; Huang, C. Targeting Ultimate Accuracy: Face Recognition via Deep Embedding. arXiv 2015, arXiv:1506.07310. [Google Scholar]
- Hoffer, E.; Ailon, N. Semi-supervised deep learning by metric embedding. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 14–26 April 2017. [Google Scholar]
- Hadsell, R.; Chopra, S.; LeCun, Y. Dimensionality Reduction by Learning an Invariant Mapping. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 17–22 June 2006; pp. 1735–1742. [Google Scholar]
- Lim, I.; Gehre, A.; Kobbelt, L. Identifying Style of 3D Shapes using Deep Metric Learning. Comput. Graph. Forum 2016, 35, 207–215. [Google Scholar] [CrossRef]
- Hu, J.; Lu, J.; Tan, Y.-P. Discriminative Deep Metric Learning for Face Verification in the Wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1875–1882. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. FaceNet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 815–823. [Google Scholar]
- Bromley, J.; Bentz, J.W.; Bottou, L.; Guyon, I.; LeCun, Y.; Moore, C.; Sackinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. Int. J. Pattern Recognit. Artif. Intell. 1993, 7, 669–688. [Google Scholar] [CrossRef]
- Lee, J.; Abu-El-Haija, S.; Varadarajan, B.; Natsev, A. Collaborative Deep Metric Learning for Video Understanding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 481–490. [Google Scholar]
- Huang, W.; Ding, H.; Chen, G. A novel deep multi-channel residual networks-based metric learning method for moving human localization in video surveillance. Signal Process. 2018, 142, 104–113. [Google Scholar] [CrossRef]
- Hu, J.; Lu, J.; Tan, Y.-P. Deep Metric Learning for Visual Tracking. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 2056–2068. [Google Scholar] [CrossRef]
- Zheng, L.; Yang, Y.; Hauptmann, A.G. Person Re-identification: Past, Present and Future. arXiv 2016, arXiv:1610.02984. [Google Scholar]
- Chen, M.; Ge, Y.; Feng, X.; Xu, C.; Yang, D. Person Re-Identification by Pose Invariant Deep Metric Learning with Improved Triplet Loss. IEEE Access 2018, 6, 68089–68095. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, P.; Wang, M. Person Reidentification via Structural Deep Metric Learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 1–12. [Google Scholar] [CrossRef]
- Hermans, A.; Beyer, L.; Leibe, B. In Defense of the Triplet Loss for Person Re-Identification. arXiv 2017, arXiv:1703.07737. [Google Scholar]
- Ahmed, E.; Jones, M.; Marks, T.K. An improved deep learning architecture for person re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3908–3916. [Google Scholar]
- Ding, S.; Lin, L.; Wang, G.; Chao, H. Deep feature learning with relative distance comparison for person re-identification. Pattern Recognit. 2015, 48, 2993–3003. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Annarumma, M.; Montana, G. Deep metric learning for multi-labelled radiographs. In Proceedings of the 33rd Annual ACM Symposium on Applied Computing, Pau, France, 9–13 April 2018; pp. 34–37. [Google Scholar]
- Wang, F.; Kang, L.; Li, Y. Sketch-based 3D shape retrieval using Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1875–1883. [Google Scholar]
- Dai, G.; Xie, J.; Fang, Y. Deep Correlated Holistic Metric Learning for Sketch-Based 3D Shape Retrieval. IEEE Trans. Image Process. 2018, 27, 3374–3386. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Dai, G.; Zhu, F.; Shao, L.; Fang, Y. Deep Nonlinear Metric Learning for 3-D Shape Retrieval. IEEE Trans. Cybern. 2018, 48, 412–422. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y.; Zhou, Z.; Bai, S.; Bai, X. Triplet-Center Loss for Multi-view 3D Object Retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 18–22 June 2018; pp. 1945–1954. [Google Scholar]
- Lu, J.; Hu, J.; Tan, Y.-P. Discriminative Deep Metric Learning for Face and Kinship Verification. IEEE Trans. Image Process. 2017, 26, 4269–4282. [Google Scholar] [CrossRef]
- Chen, X.; He, L.; Xu, C.; Liu, J. Distance-Dependent Metric Learning. IEEE Signal Process. Lett. 2019, 26, 357–361. [Google Scholar] [CrossRef]
- Liu, X.; Kumar, B.V.K.V.; You, J.; Jia, P. Adaptive Deep Metric Learning for Identity-Aware Facial Expression Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 522–531. [Google Scholar]
- Liu, H.; Lu, J.; Feng, J.; Zhou, J. Label-Sensitive Deep Metric Learning for Facial Age Estimation. IEEE Trans. Inf. Forensics Secur. 2018, 13, 292–305. [Google Scholar] [CrossRef]
- Mueller, J.; Thyagarajan, A. Siamese recurrent architectures for learning sentence similarity. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 2786–2792. [Google Scholar]
- Benajiba, Y.; Sun, J.; Zhang, Y.; Jiang, L.; Weng, Z.; Biran, O. Siamese Networks for Semantic Pattern Similarity. In Proceedings of the IEEE 13th International Conference on Semantic Computing (ICSC), Newport Beach, CA, USA, 30 January–1 February 2019; pp. 191–194. [Google Scholar]
- Zhu, W.; Yao, T.; Ni, J.; Wei, B.; Lu, Z. Dependency-based Siamese long short-term memory network for learning sentence representations. PLoS ONE 2018, 13, e0193919. [Google Scholar] [CrossRef] [PubMed]
- Ein-Dor, L.; Mass, Y.; Halfon, A.; Venezian, E.; Shnayderman, I.; Aharonov, R.; Slonim, N. Learning Thematic Similarity Metric Using Triplet Networks. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (ACL 2018), Melbourne, Australia, 15–20 July 2018; pp. 49–54. [Google Scholar]
- Narayanaswamy, V.S.; Thiagarajan, J.J.; Song, H.; Spanias, A. Designing an Effective Metric Learning Pipeline for Speaker Diarization. arXiv 2018, arXiv:1811.00183. [Google Scholar]
- Wang, J.; Wang, K.-C.; Law, M.T.; Rudzicz, F.; Brudno, M. Centroid-based Deep Metric Learning for Speaker Recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 12–17 May 2019; pp. 3652–3656. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical Networks for Few-shot Learning. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 4077–4087. [Google Scholar]
- Lu, R.; Wu, K.; Duan, Z.; Zhang, C. Deep ranking: Triplet MatchNet for music metric learning. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 121–125. [Google Scholar]
- Wang, Q.; Wan, J.; Yuan, Y. Deep Metric Learning for Crowdedness Regression. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2633–2643. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, K.; Cong, G. Efficient Similar Region Search with Deep Metric Learning. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 1850–1859. [Google Scholar]
- Wang, X.; Liu, M. Multi-View Deep Metric Learning for Volumetric Image Recognition. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), San Diego, CA, USA, 23–27 July 2018; pp. 1–6. [Google Scholar]
- Fathi, A.; Wojna, Z.; Rathod, V.; Wang, P.; Song, H.O.; Guadarrama, S.; Murphy, K.P. Semantic Instance Segmentation via Deep Metric Learning. arXiv 2017, arXiv:1703.10277. [Google Scholar]
- Cai, S.; Huang, J.; Ding, X.; Zeug, D. Semantic edge detection based on deep metric learning. In Proceedings of the International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Xiamen, China, 6–9 November 2017; pp. 707–712. [Google Scholar]
- Xing, Y.; Wang, M.; Yang, S.; Jiao, L. Pan-sharpening via deep metric learning. ISPRS J. Photogramm. Remote. Sens. 2018, 145, 165–183. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, F.; Wen, S.; Liu, X.; Lin, Y. Deep Metric Learning with Angular Loss. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2593–2601. [Google Scholar]
- Wah, C.; Branson, S.; Welinder, P.; Perona, P.; Belongie, S. The Caltech-UCSD Birds-200-2011 Dataset; Computation & Neural Systems Technical Report, CNS-TR-2011-001; California Institute of Technology: Pasadena, CA, USA, 2011; pp. 1–8. [Google Scholar]
- Song, H.O.; Savarese, S.; Xiang, Y.; Jegelka, S. Deep Metric Learning via Lifted Structured Feature Embedding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4004–4012. [Google Scholar]
- Sohn, K. Improved deep metric learning with multi-class n-pair loss objective. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 1857–1865. [Google Scholar]
- Song, H.O.; Jegelka, S.; Rathod, V.; Murphy, K. Deep Metric Learning via Facility Location. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2206–2214. [Google Scholar]
- Ge, W.; Huang, W.; Dong, D.; Scott, M.R. Deep Metric Learning with Hierarchical Triplet Loss. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 272–288. [Google Scholar]
- Krause, J.; Stark, M.; Deng, J.; Fei-Fei, L. 3D Object Representations for Fine-Grained Categorization. In Proceedings of the IEEE International Conference on Computer Vision Workshops (ICCVW), Sydney, Australia, 1–8 December 2013; pp. 554–561. [Google Scholar]
- Zheng, L.; Shen, L.; Tian, L.; Wang, J.; Tian, Q. Scalable person re-identification: A benchmark. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 1116–1124. [Google Scholar]
- Ustinova, E.; Lempitsky, V. Learning Deep Embeddings with Histogram Loss. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 4170–4178. [Google Scholar]
- Yao, H.; Zhang, S.; Hong, R.; Zhang, Y.; Xu, C.; Tian, Q. Deep Representation Learning with Part Loss for Person Re-Identification. IEEE Trans. Image Process. 2019, 28, 2860–2871. [Google Scholar] [CrossRef]
- Li, W.; Zhao, R.; Xiao, T.; Wang, X. DeepReID: Deep Filter Pairing Neural Network for Person Re-identification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 152–159. [Google Scholar]
- Li, B.; Lu, Y.; Godil, A.; Schreck, T.; Bustos, B.; Ferreira, A.; Furuya, T.; Fonseca, M.J.; Johan, H.; Matsuda, T.; et al. A comparison of methods for sketch-based 3D shape retrieval. Comput. Vis. Image Underst. 2014, 119, 57–80. [Google Scholar] [CrossRef]
- Li, B.; Lu, Y.; Li, C.; Godil, A.; Schreck, T.; Aono, M.; Burtscher, M.; Chen, Q.; Chowdhury, N.K.; Fang, B.; et al. A comparison of 3D shape retrieval methods based on a large-scale benchmark supporting multimodal queries. Comput. Vis. Image Underst. 2015, 131, 1–27. [Google Scholar] [CrossRef]
- Howell, A.J.; Buxton, H. Towards unconstrained face recognition from image sequences. In Proceedings of the Second International Conference on Automatic Face and Gesture Recognition, Killington, VT, USA, 14–16 April 1996; pp. 224–229. [Google Scholar]
- Hu, J.; Lu, J.; Tan, Y.-P. Sharable and Individual Multi-View Metric Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2281–2288. [Google Scholar] [CrossRef]
- Wolf, L.; Hassner, T.; Maoz, I. Face recognition in unconstrained videos with matched background similarity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 21–23 June 2011; pp. 529–534. [Google Scholar]
- Marelli, M.; Bentivogli, L.; Baroni, M.; Bernardi, R.; Menini, S.; Zamparelli, R. SemEval-2014 Task 1: Evaluation of Compositional Distributional Semantic Models on Full Sentences through Semantic Relatedness and Textual Entailment. In Proceedings of the 8th International Workshop on Semantic Evaluation (SemEval 2014), Dublin, Ireland, 23–29 August 2014; pp. 1–8. [Google Scholar]
- Greenberg, C.; Banse, D.; Doddington, G.; GarciaRomero, D.; Godfrey, J.; Kinnunen, T.; Martin, A.; McCree, A.; Przybocki, M.; Reynolds, D. The NIST 2014 Speaker Recognition i-Vector Machine Learning Challenge. In Proceedings of the Odyssey 2014: The Speaker and Language Recognition Workshop, Joensuu, Finland, 16–19 June 2014. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9370, pp. 84–92. [Google Scholar]
- Veaux, C.; Yamagishi, J.; MacDonald, K. Superseded—CSTR VCTK Corpus: English Multi-Speaker Corpus for CSTR Voice Cloning Toolkit; University of Edinburgh, The Centre for Speech Technology Research (CSTR): Edinburgh, UK, 2016. [Google Scholar]
- Chung, J.S.; Nagrani, A.; Zisserman, A. VoxCeleb2: Deep Speaker Recognition. Proc. Interspeech 2018, 1086–1090. [Google Scholar] [CrossRef]
- Bell, S.; Bala, K. Learning visual similarity for product design with convolutional neural networks. ACM Trans. Graph. 2015, 34, 98. [Google Scholar] [CrossRef]
- Simo-Serra, E.; Trulls, E.; Ferraz, L.; Kokkinos, I.; Fua, P.; Moreno-Noguer, F. Discriminative learning of deep convolutional feature point descriptors. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 118–126. [Google Scholar]
- Bucher, M.; Herbin, S.; Jurie, F. Hard Negative Mining for Metric Learning Based Zero-Shot Classification. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 524–531. [Google Scholar]
- Lin, Y.; Cui, Y.; Zhou, F.; Belongie, S. Fine-Grained Categorization and Dataset Bootstrapping Using Deep Metric Learning with Humans in the Loop. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1153–1162. [Google Scholar]
- Movshovitz-Attias, Y.; Toshev, A.; Leung, T.K.; Ioffe, S.; Singh, S. No Fuss Distance Metric Learning Using Proxies. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 360–368. [Google Scholar]
- Manmatha, R.; Wu, C.-Y.; Smola, A.J.; Krähenbühl, P. Sampling matters in deep embedding learning. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2840–2848. [Google Scholar]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005; pp. 539–546. [Google Scholar]
- Filković, I.; Kalafatić, Z.; Hrkać, T. Deep metric learning for person Re-identification and De-identification. In Proceedings of the 2016 39th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 30 May–3 June 2016; pp. 1360–1364. [Google Scholar]
- Jeong, Y.; Lee, S.; Park, D.; Park, K.H. Accurate Age Estimation Using Multi-Task Siamese Network-Based Deep Metric Learning for Frontal Face Images. Symmetry 2018, 10, 385. [Google Scholar] [CrossRef]
- Yi, D.; Lei, Z.; Liao, S.; Li, S.Z. Deep Metric Learning for Person Re-identification. In Proceedings of the 2014 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; pp. 34–39. [Google Scholar]
- Shi, H.; Zhu, X.; Liao, S.; Lei, Z.; Yang, Y.; Li, S.Z. Constrained deep metric learning for person re-identification. arXiv 2015, arXiv:1511.07545. [Google Scholar]
- Wen, Y.; Zhang, K.; Li, Z.; Qiao, Y. A Discriminative Feature Learning Approach for Deep Face Recognition. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Volume 9911, pp. 499–515. [Google Scholar]
- Ni, J.; Liu, J.; Zhang, C.; Ye, D.; Ma, Z. Fine-grained Patient Similarity Measuring using Deep Metric Learning. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 1189–1198. [Google Scholar]
- Gong, Z.; Zhong, P.; Yu, Y.; Hu, W. Diversity-Promoting Deep Structural Metric Learning for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 371–390. [Google Scholar] [CrossRef]
- Wang, X.; Han, X.; Huang, W.; Dong, D.; Scott, M.R. Multi-Similarity Loss with General Pair Weighting for Deep Metric Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5022–5030. [Google Scholar]
- Rippel, O.; Paluri, M.; Dollar, P.; Bourdev, L. Metric learning with adaptive density discrimination. In Proceedings of the International Conference on Learning Representations, San Juan, PR, USA, 2–4 May 2016; pp. 1–15. [Google Scholar]
- Chen, L.; He, Y. Dress Fashionably: Learn Fashion Collocation with Deep Mixed-Category Metric Learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2017; pp. 2103–2110. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- LeCun, Y.; Huang, F.J.; Bottou, L. Learning methods for generic object recognition with invariance to pose and lighting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Washington, DC, USA, 27 June–2 July 2004; pp. 97–104. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. Master’s Thesis, Department of Computer Science, University of Toronto, Toronto, ON, Canada, 2009. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 16 December 2011; pp. 1–9. [Google Scholar]
- Coates, A.; Ng, A.; Lee, H. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 215–223. [Google Scholar]
- Xie, S.; Yang, T.; Wang, X.; Lin, Y. Hyper-class augmented and regularized deep learning for fine-grained image classification. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2645–2654. [Google Scholar]
- Khosla, A.; Jayadevaprakash, N.; Yao, B.; Fei-Fei, L. Novel dataset for fine-grained image categorization: Stanford dogs. In Proceedings of the First Workshop on Fine-Grained Visual Categorization (FGVC) in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 21–23 June 2011; pp. 1–2. [Google Scholar]
- Parkhi, O.M.; Vedaldi, A.; Zisserman, A.; Jawahar, C. Cats, and dogs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 18–20 June 2012; pp. 3498–3505. [Google Scholar]
- Nilsback, M.-E.; Zisserman, A. Automated Flower Classification over a Large Number of Classes. In Proceedings of the 2008 Sixth Indian Conference on Computer Vision, Graphics & Image Processing, Bhubaneswar, India, 16–19 December 2008; pp. 722–729. [Google Scholar]
- Russakovsky, O.; Fei-Fei, L. Attribute learning in large-scale datasets. In Proceedings of the European Conference on Computer Vision (ECCV), Crete, Greece, 5–11 September 2010; pp. 1–14. [Google Scholar]
- Tang, X.; Liu, Z.; Luo, P.; Qiu, S.; Wang, X. DeepFashion: Powering Robust Clothes Recognition and Retrieval with Rich Annotations. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1096–1104. [Google Scholar]
- Gray, D.; Brennan, S.; Tao, H. Evaluating appearance models for recognition, reacquisition, and tracking. In Proceedings of the IEEE International Workshop on Performance Evaluation for Tracking and Surveillance (PETS), Rio de Janeiro, Brazil, 14 October 2007; pp. 1–7. [Google Scholar]
| Dataset | Reference | Task and Comparative Results | Evaluation Protocol | CNN LSTM | Year | |||||||||
| Image Clustering (%) | Image Retrieval Recall@R (%) | |||||||||||||
| NMI | F1 | R=1 | R=2 | R=4 | R=8 | |||||||||
| CUB-200-2011 [68] | Song et al. [69] | 56.2 | 22.7 | 46.5 | 58.1 | 69.8 | 80.2 | 200 classes with 11788 images the first 100 classes for training (5864 images) the rest of the classes for testing (5,924 images) | CNN | 2016 | ||||
| Sohn et al. [70] | 60.3 | 27.2 | 50.9 | 63.3 | 74.2 | 83.2 | CNN | 2016 | ||||||
| Wang et al. [67] | 61.1 | 29.4 | 54.7 | 66.3 | 76.0 | 83.9 | CNN | 2017 | ||||||
| Song et al. [71] | 59.2 | - | 48.1 | 61.4 | 71.8 | 81.9 | CNN | 2017 | ||||||
| Ge et al. [72] | - | - | 57.1 | 68.8 | 78.7 | 86.5 | CNN | 2018 | ||||||
| NMI | F1 | R=1 | R=2 | R=4 | R=8 | |||||||||
| CAR-196 [73] | Song et al. [69] | 55.1 | 21.5 | 48.3 | 61.1 | 71.8 | 81.1 | 198 classes with 16,185 images the first 98 classes for training (8,054 images) the other 98 classes for testing (8,131 images) | CNN | 2016 | ||||
| Sohn et al. [70] | 63.9 | 33.5 | 71.1 | 79.7 | 86.4 | 91.6 | CNN | 2016 | ||||||
| Wang et al. [67] | 63.2 | 32.2 | 71.4 | 81.4 | 87.5 | 92.1 | CNN | 2017 | ||||||
| Song et al. [71] | 59.0 | - | 58.1 | 70.6 | 80.2 | 87.8 | CNN | 2017 | ||||||
| Ge et al. [72] | - | - | 81.4 | 88.0 | 92.7 | 95.7 | CNN | 2018 | ||||||
| NMI | F1 | R=1 | R=10 | R=100 | R=1000 | |||||||||
| Online Products [69] | Song et al. [69] | 87.4 | 24.7 | 63.0 | 80.5 | 91.7 | 97.5 | 22634 products with 120053 images. the first 11318 product categories for training (59,551 images) the other 11316 product categories for testing (60,502 images) | CNN | 2016 | ||||
| Sohn et al. [70] | 88.1 | 28.1 | 67.7 | 83.7 | 92.9 | 97.8 | CNN | 2016 | ||||||
| Wang et al. [67] | 88.6 | 29.9 | 70.9 | 85.0 | 93.5 | 98.0 | CNN | 2017 | ||||||
| Song et al. [71] | 89.4 | - | 67.0 | 83.6 | 93.2 | - | CNN | 2017 | ||||||
| Ge et al. [72] | - | - | 74.8 | 88.3 | 94.8 | 98.4 | CNN | 2018 | ||||||
| Person re-Identification | ||||||||||||||
| R=1 | R=5 | |||||||||||||
| Market-1501 [74] | Ustinova et al. [75] | 59.47 | 80.73 | 1501 identities in total 750 identities for training and 751 identities for test | CNN | 2016 | ||||||||
| Chen et al. [38] | 83.55 | 92.37 | - | CNN | 2018 | |||||||||
| Yang et al. [39] | 84.26 | 93.59 | 1501 identities in total 750 identities for training and 751 identities for test | CNN | 2019 | |||||||||
| Yao et al. [76] | 88.20 | - | 1501 identities in total 750 identities for training and 751 identities for test | CNN | 2019 | |||||||||
| R=1 | R=5 | |||||||||||||
| CUHK03 [77] | Ustinova et al. [75] | 65.77 | 92.85 | 1360 identities in total 1160 identities for training and 100 for test | CNN | 2016 | ||||||||
| Chen et al. [38] | 68.63 | 92.28 | - | CNN | 2018 | |||||||||
| Yang et al. [39] | 39.64 | - | 1367 identities in total 767 identities for training and 700 for test | CNN | 2019 | |||||||||
| Yao et al. [76] | 82.75 | 96.59 | 1360 identities in total 1160 identities for training and 100 for test | CNN | 2019 | |||||||||
| 3D Shape Retrieval | ||||||||||||||
| NN | FT | ST | E | DCG | Map | |||||||||
| SHREC’13 [78] | Dai et al. [23] | 65.0 | 63.4 | 71.9 | 34.8 | 76.6 | 67.4 | 1258 shapes and 7200 sketches, grouped into 90 classes. the number of sketches for each class is equal to 80. 50 sketches for training and 30 for testing for each group. | CNN | 2017 | ||||
| Dai et al. [46] | 73.0 | 71.5 | 77.3 | 36.8 | 81.6 | 74.4 | CNN | 2018 | ||||||
| He et al. [48] | 76.3 | 78.7 | 84.9 | 39.2 | 85.4 | 80.7 | CNN | 2018 | ||||||
| NN | FT | ST | E | DCG | Map | |||||||||
| SHREC’14 [79] | Dai et al. [23] | 27.2 | 27.5 | 34.5 | 17.1 | 49.8 | 28.6 | 13680 sketches and 8987 3D models, grouped into 171 classes. the number of sketches for each class is equal to 80. 50 sketches for training and 30 for testing for each group. | CNN | 2017 | ||||
| Dai et al. [46] | 40.3 | 32.9 | 39.4 | 20.1 | 54.4 | 33.6 | CNN | 2018 | ||||||
| He et al. [48] | 58.5 | 45.5 | 53.9 | 27.5 | 66.6 | 47.7 | CNN | 2018 | ||||||
| Face verification | ||||||||||||||
| Accuracy | ||||||||||||||
| LFW [80] | Hue et al. [31] | 90.68 | 10 folds: each fold has 300 matched pairs and 300 mismatched pairs Image restricted | - | 2014 | |||||||||
| Lu et al. [49] | 94.50 | - | 2017 | |||||||||||
| Hue at al. [81] | 93.27 | - | 2018 | |||||||||||
| Accuracy | ||||||||||||||
| YTF [82] | Hue et al. [31] | 82.34 | 10 folds: each fold has 250 intra-personal pairs and 250 inter-personal pairs Image restricted | - | 2014 | |||||||||
| Lu et al. [49] | 82.50 | - | 2017 | |||||||||||
| Semantic Textual Similarity | ||||||||||||||
| r | MSE | |||||||||||||
| SICK [83] | Mueller et al. [53] | 0.88 | 0.83 | 0.22 | 9927 sentence pairs 5000 for training and 4927 for testing | LSTM | 2016 | |||||||
| Zhu et al. [55] | 0.83 | 0.77 | 0.34 | LSTM | 2018 | |||||||||
| Ein-Dor et al. [56] | 0.81 | 0.72 | 0.33 | LSTM | 2018 | |||||||||
| Speaker Verification | ||||||||||||||
| EER (%) | MDCF | |||||||||||||
| NIST i-vector [84] | Triplet Network [85] | 2.85 | 0.30 | 1306 speakers recorded with 5 i-vectors each. Total 9634 test i-vector and 12582004 trial. randomly divided train subset and test subset. All i-vectors have 600 dimensions | - | 2015 | ||||||||
| Chen et al. [50] | 2.69 | 0.27 | - | 2019 | ||||||||||
| EER (%) | MDCF | |||||||||||||
| VCTK [86] | Triplet Network [85] | 12.26 | - | the first 90 speakers were divided into training, validation and test sets. 18 speakers were used as an “unseen” set | LSTM | 2015 | ||||||||
| Wang et al. [58] | 10.77 | - | LSTM | 2019 | ||||||||||
| EER (%) | MDCF | |||||||||||||
| VoxCeleb2 [87] | Triplet Network [85] | 15.92 | - | selected a subset containing 101 speakers. 71 speakers for training and validation other 30 speakers are used as the “unseen” set | LSTM | 2015 | ||||||||
| Wang et al. [58] | 13.68 | - | LSTM | 2019 | ||||||||||
| Metric | Sample Selection | Topic | Dataset | Purpose | Year |
|---|---|---|---|---|---|
| Contrastive Loss [29] | Hard negative | Image recognition Object recognition | MNIST [105] NORB [106] | calculates a contrastive loss function that aims to obtain a higher value for pairs of dissimilar objects and aims to obtain a lower value for pairs of similar objects | 2006 |
| Triplet Loss [85] | Easy sampling | Image recognition Object recognition | MNIST [105] CIFAR10 [107] SVHN [108] STL10 [109] | calculates the distance difference between anchor-positive samples and anchor-negative samples and aims to bring similar objects closer | 2014 |
| Histogram Loss [75] | Easy sampling | Image recognition Image retrieval Person re-ID | CUB-200-2011 [68] Online Products [69] Market-1501 [74] CUHK03 [77] | aims the distributions of the similarities of less overlapping positive and negative pairs. | 2016 |
| Structured Loss [69] | Hard negative | Image retrieval | CUB-200-2011 [68] Online Products [69] CAR-196 [73] | aims a new metric learning algorithm using the lifted dense pairwise distance matrix within the batch throughout the training. | 2016 |
| N-Pair Loss [70] | Multiple negative “class” | Image retrieval Image clustering Face verification Face identification Object recognition Object verification | CUB-200-2011 [68] Online Products [69] Flower-610 [70] CAR-196 [73] LFW [80] Car-333 [110] | aims to develop triplet loss focusing on pushing a positive sample away from multiple negative samples at each training stage | 2016 |
| Magnet Loss [103] | Hard negative | Image recognition Image annotation | Stanford Dogs [111] Oxford-IIIT Pet [112] Oxford 102 Flowers [113] Object Attributes [114] | aims to retrieve a whole local neighborhood of nearest clusters and punish their overlaps | 2016 |
| Angular Loss [67] | Multiple negative | Image retrieval Image clustering | CUB-200-2011 [68] Online Products [69] CAR-196 [73] | focuses on limiting the angle in the negative sample of triplet triangles. | 2017 |
| Quadruple Loss [100] | Semi-hard negative | Patient similarity | The Ischemic Heart [100] The Cerebrovascular [100] | aims to capture the degree of similarity between patients effectively | 2017 |
| Clustering Loss [71] | Easy sampling | Image retrieval Image clustering | CUB-200-2011 [68] Online Products [69] CAR-196 [73] | aims a new metric learning approach based on the structural prediction that takes the global structure of the embedding space into account by a clustering quality metric. | 2017 |
| Hierarchical Triplet Loss [72] | Anchor-Neighbor sampling | Image retrieval Face recognition | CUB-200-2011 [68] Online Products [69] CAR-196 [73] LFW [80] In-Shop Clothes Retrieval [115] | aims to collect informative samples and capture global data context with an online class-level tree update | 2018 |
| Mixed Loss [104] | Hard-aware online exemplar mining | Image retrieval | Fashion Collocation Dataset [104] | aims to feed multiple positive and negative samples to the neural network per time | 2018 |
| Part Loss [76] | Easy sampling | Person re-ID | Market-1501 [74] CUHK03 [77] VIPeR [116] | aims to reduce empirical classification risks for training and representation learning risks for test by dividing images to K parts | 2019 |
| Multi-Similarity Loss [102] | General pair weighting | Image retrieval | CUB-200-2011 [68] Online Products [69] CAR-196 [73] In-Shop Clothes Retrieval [115] | aims to collect informative paired samples, and weights these pairs both their own and relative similarities | 2019 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
KAYA, M.; BİLGE, H.Ş. Deep Metric Learning: A Survey. Symmetry 2019, 11, 1066. https://doi.org/10.3390/sym11091066
KAYA M, BİLGE HŞ. Deep Metric Learning: A Survey. Symmetry. 2019; 11(9):1066. https://doi.org/10.3390/sym11091066
Chicago/Turabian StyleKAYA, Mahmut, and Hasan Şakir BİLGE. 2019. "Deep Metric Learning: A Survey" Symmetry 11, no. 9: 1066. https://doi.org/10.3390/sym11091066
APA StyleKAYA, M., & BİLGE, H. Ş. (2019). Deep Metric Learning: A Survey. Symmetry, 11(9), 1066. https://doi.org/10.3390/sym11091066





