Abstract
Composite quantile regression (CQR) estimation and inference are studied for varying coefficient models with response data missing at random. Three estimators including the weighted local linear CQR (WLLCQR) estimator, the nonparametric WLLCQR (NWLLCQR) estimator, and the imputed WLLCQR (IWLLCQR) estimator are proposed for unknown coefficient functions. Under some mild conditions, the proposed estimators are asymptotic normal. Simulation studies demonstrate that the unknown coefficient estimators with IWLLCQR are superior to the other two with WLLCQR and NWLLCQR. Moreover, bootstrap test procedures based on the IWLLCQR fittings is developed to test whether the coefficient functions are actually varying. Finally, a type of investigated real-life data is analyzed to illustrated the applications of the proposed method.
1. Introduction
The varying coefficient model, proposed originally by Hastie and Tibshirani [1], is flexible and powerful to examine the dynamic changes of regression coefficients over some factors such as time and age and has gained much popularity during the past few decades (see [2,3,4,5,6]).
A classical varying coefficient model has the following structure:
where is a response variable, is a covariate vector, is an unknown coefficient vector function with a smoothing variable U, and is a random error independent of .
Recently, some estimates of for Model (1) with the least squares regression have attracted many researchers’ attention. Above all, Hastie and Tibshirani [1] considered penalized least squares estimation and attained some good results. Following, Fan et al. [4] and Fan et al. [7] applied the least squares regression to propose a two-step local polynomial estimation procedure and a profile estimator for Model (1), respectively, and designed some suitable statistical inference procedures. However, there arises a dilemma that these estimation procedures of the least squares could be very sensitive to outliers [8]. In order to overcome this problem, quantile regression proposed by Koenker [9] can be thought of as an alternative because as a mean model, traditional least squares regression only gives the effects of the covariates at the center of the distribution, while quantile regression can not only directly estimate the ones at different quantiles, but also characterize the entire conditional distribution of a dependent variable of the regression [8]. Thus, this regression has a much better robust property when processing outlier observations.
Due to its significant theoretical advances, some scholars had integrated the quantile regression into the varying coefficient model. Kim [10] attained the quantile regression model with the varying coefficient. For the processing of time series data, Cai and Xu [11] developed nonparametric quantile estimations with dynamic smooth coefficient models. Later, Cai and Xiao [12] applied dynamic models with partially-varying coefficients to investigate semiparametric quantile regression and obtained some useful results. Tang [13] derived a robust quantile regression estimation using the spatial semiparametric partially-linear regression model with a varying coefficient. Unfortunately, a relative small efficiency may result by a single quantile regression procedure compared with the least squares regression. In order to overcome this drawback, it is very necessary to get a desirable efficient and stable estimator. In recent years, an oracle procedure of composite quantile regression (CQR) was proposed by Zou and Yuan [14] to select the significant variables, and some important theoretical and applied results were derived. So far, the CQR method is widely used in many situations. For example, some efficient estimators based on the CQR method were proposed by Kai et al. [15] and Guo et al. [16] for semi-parametric partially-linear models with a varying coefficient. In addition, a data-driven weighted CQR (WCQR) estimation was studied by Sun et al. [17] and Yang et al. [18] for linear models with a varying coefficient, respectively.
Although the QR has significant theoretical properties such that its literature on the complete data has been rapidly growing, people have paid scant attention to the incomplete data, i.e., the data samples containing missing values since this class of data may lead easily to substantially-distorted results. In fact, as is commonplace, missing data often appear in real life. There are various reasons such as failure on the part of investigators when gathering correct information, the unwillingness of some sampled units when supplying the desired information, loss of information caused by uncontrollable factors, and so forth, resulting in the data missing. In the early 1970s, the advances in computer technology such that many laborious numerical calculations were possible to perform spurred the literature on statistical analysis of real data containing missing values in applied work; see [19,20,21,22,23,24,25]. Despite a long history on missing data analysis, little work on QR has taken missing data into account. Recently, an iterative imputation procedure was developed by Wei et al. [26] in a linear QR model with non-i.i.d. error terms for the covariates with missing values. A smoothed empirical likelihood analysis was discussed by Lv and Li [27] for partially-linear quantile regression with missing response. An inverse probability weighting QR approach was proposed by Sherwood et al. [28] in the last few years for analyzing healthcare cost data with missing covariates at random. The QR for competing risk data was studied by Sun et al. [29] when the failure type was missing. An efficient QR analysis was discussed by Chen [30] with missing observations. Some imputation methods were proposed by Shu [31] for quantile estimation under data missing at random.
In this paper, a coherent inference framework based on CQR estimation and inference is explored for varying coefficient models with response data missing at random. The main contribution of this paper can be summarized as follows:
- A composite quantile regression estimation (CQRE) method is proposed for the analysis of varying coefficient models with response data missing at random. This method has the following two advantages: (1) the CQRE method can effectively overcome not only the drawback of a relative small efficiency that may result from a single quantile regression procedure compared with the least-squares regression, but also the interference of non-normal error; hence, it improves its estimation efficiency significantly; (2) since different quantiles are used in the imputation instead of actually observed responses or means and the robustness of quantile regression is inherited, the CQRE method is less sensitive to outliers; thus, the CQRE method is more effective and robust than the single quantile regression method and the classical least squares method.
- Three estimators including the weighted local linear CQR (WLLCQR) estimator, the nonparametric WLLCQR (NWLLCQR) estimator, and the imputed WLLCQR (IWLLCQR) estimator are proposed for an unknown coefficient function in the varying coefficient model to establish the asymptotic normality of these estimators under some mild conditions.
The rest of this paper is organized as follows. The CQR varying coefficient model will be introduced with missing response data in Section 2 to construct a class of estimators for an unknown coefficient function. Then, some theoretical results on the asymptotic property of the proposed estimators are proposed in Section 3. In Section 4, a bootstrap-based test procedure is developed to perform a simulation study in Section 5 that demonstrates the finite-sample performance of the proposed method. Following, an application to a real dataset illustrates the effectiveness of our approach in Section 6. In addition, some discussions and conclusion remarks are presented in Section 7 and Section 8, respectively. Finally, the proof of the main results is given in Appendix A.
2. Estimation Based on the CQR Varying Coefficient Model With Missing Response
In this section, the CQR varying coefficient model will be introduced with missing response data to construct a class of estimators for an unknown coefficient function. In particular, as the main estimate methods in this paper, three estimators including the weighted local linear CQR (WLLCQR) estimator, the nonparametric WLLCQR (NWLLCQR) estimator, and the imputed WLLCQR (IWLLCQR) estimator are constructed and emphasized.
Let be a random sample coming from Model (1), such that:
where all the and are always observed, and is the coefficient vector function. Further, if is missing and otherwise. We assume that throughout this paper, is missing at random (MAR) for some i. This assumption indicates that and are conditionally independent given and , that is,
where . Moreover, we also assume that across different quantile regression models, there is the same coefficient vector function . Thus, we can express the conditional τ-quantile function of Y as:
where is the -quantile of . If is differentiable, Taylor’s expansion yields that:
for , where u is a fixed value of a random variable and U lies in a neighborhood of u. For the case of no missing response data, minimizing the following criterion:
we can attain the local linear quantile regression (LLQR) estimator of , where is called the quantile loss function of τ-quantile regression, , and is a Gaussian kernel function with bandwidth h. In order to improve the quantile regression estimation efficiently, the local linear composite quantile regression (LLCQR) estimation is adopted from Guo et al. [16] for the varying coefficient models. Let q be the number of quantiles and for The loss function of the LLCQR estimation is defined as:
where is the -quantile of .
In what follows, this technique of LLCQR will be extended to handle the case of response data missing at random.
2.1. WLLCQR Estimation
The inverse probability weighting (IPW) version of local linear CQR estimation will be considered to handle missing responses data at random, that is the CC (complete-case) analysis will be adjusted by using the inverse of the selection probability as the weight. However, the nonparametric smoothing estimation of will encounter the curse of dimensionality when the dimension of Z is high enough. Motivated by Wang [24], we use the inverse marginal probability weighted approach.
Let , i.e., the propensity score just depends on U. When the inverse marginal probability function is known, the WLLCQR estimator of is defined as:
where and . Here, is called the WLLCQR estimator of with .
2.2. Nonparametric WLLCQR Estimation
However, the inverse marginal probability function in practical situations is usually unknown, and thus, it needs to be estimated. We often employ nonparametric smoothing estimation approaches to estimate the unknown selection probability . The Nadaraya–Watson estimation [32] is one of these nonparametric smoothing estimation approaches. We can define the Nadaraya–Watson estimator of as:
where is a density kernel function and is a bandwidth. Therefore, the NWLLCQR estimation procedure with is formally defined as:
where is called the NWLLCQR estimator of with .
2.3. Imputed WLLCQR Estimation
Although both the WLLCQR estimator and NWLLCQR estimator can well estimate the inverse marginal probability function, the information contained in the data is not explored fully. Now, we use quantile regression imputation to resolve the issue by imputing by if is missing, where and is defined in:
Therefore, the imputed WLLCQR estimation procedure can be defined as:
where and is called the IWLLCQR estimator of .
Remark 1.
Since local results in interpolation vary greatly and are unstable, as a smoothing method, the kernel function is used in Equations (4)–(10) such that the interpolation results of these equations are much smoother and stabler.
3. Asymptotic Properties
In this section, the asymptotic distribution will be considered for the estimators proposed in Section 2 to establish some theoretical results of these estimators.
Let and be the density functions of and U, respectively. For simplicity, the following notations: and for for ,⋯, n, and will be used in this section.
Now, the following results are established.
Theorem 1.
Suppose that Conditions–in the Appendix hold. Ifis known, then:
whererepresents the convergence in the distribution,.
Theorem 2.
Supposeis a smoothing function of u, based on Conditions–in the Appendix holding. Then:
where.
Theorem 3.
Assumingis a smoothing function of u, based on the Conditions–in the Appendix hold. Then:
where:
4. A Bootstrap-Based Goodness-of-Fit Test
In investigating the varying coefficient model, how to test whether unknown coefficient functions are actually varying is of importance. In this section, the testing problem is considered for Model (1) under response missing, and then, a goodness-of-fit test is proposed based on the difference between the weighted residual sums of the quantile (WRSQ) and the LLCQR fittings under both the null and alternative hypotheses.
The following testing problem:
for simplicity, is considered, where is a constant vector. The model (1) becomes a classical linear model with missing responses under the null hypothesis. The WRSQ under is defined as:
where , ⋯, and are given by the following IWCQR estimation procedure:
Similarly, the WRSQ under can be defined as:
where and are given in (10). Then, the following test statistic is given as:
For a large value of , the null hypothesis (11) is rejected. In what follows, based on the bootstrap method, we evaluate the p values of the test along the lines of Wong et al. [33] and Guo et al. [16]:
- Step 1.
- Assume the number of complete data is m. We get the IWLLCQR estimator .
- Step 2.
- The bootstrap residuals are generated from series , where:
- Step 3.
- Step 2 is repeated for M times, and then, series sets are obtained for . The bootstrap test statistic is calculated for each bootstrap sample , denoted by .
- Step 4.
- The p value is approximately estimated by , where S is the cardinality of the set .
5. Simulation Study
A simulation study was carried out to investigate the finite-sample properties of our proposed method by a comparison among the WLLCQR estimation method, the NWLLCQR estimation method, the IWLLCQR estimation method, the INWLLCQR (imputed not weighted LLCQR) estimation method, and the WLLCQR estimation method without data missing, defined in (5).
In numerical studies, generally, the kernel function is taken to be . Here, this function is still adopted. It follows that the cross-validation method is used to select the optimal bandwidths . In the subsequent examples, let the composite level
Example 1.
Consider the following model:
where,,are independent,andfollow a uniform distribution on,, and three error distributions ofare considered including, and.
An analysis of the fitting of five different estimators including WLLCQR, NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR is done by using the following three selection probability functions:
The average missing rates of Y corresponding to these three selection probability functions are approximately 0.15, 0.36, and 0.45, respectively. For each of the three cases, we generated 500 Monte Carlo random samples of size 200. The performance of the estimators is illustrated via the MSE. The simulation results are given in Table 1.

Table 1.
The MSE for estimators in Example 1.
From Table 1, we can make the following observations:
Under the same selection probability function and the same sample size n, the MSE of IWLLCQR is only slightly smaller than the ones of WLLCQR and NWLLCQR, respectively; the MSE of INWLLCQR is also slightly smaller than the ones of WLLCQR and NWLLCQR, because much more information on missing data is considered in IWLLCQR and INWLLCQR, while the MSE of INWLLCQR is slightly greater than the one of IWLLCQR. Further the MSE of IWLLCQR is only slightly greater than the one of WLLCQR; this further confirms that the IWLLCQR method is a safe alternative to WLLCQR and NWLLCQR.
Now, the simulated curves are plotted with the case of under different levels of missing rates. Here, the results are presented only when , while the ones for the case of are not given since these results were similar. Figure 1, Figure 2 and Figure 3 summarize the finite sample performance of the NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR methods for under different levels of missing rates. The red dashed curve, the blue dashed curve, the blue dotted curve, and the green dashed-dotted curve represent the results obtained by the NWLLCQR method, the IWLLCQR method, the INWLLCQR method, and the WLLCQR method, respectively. In addition, the red solid curve denotes the real curve of . From Figure 1, Figure 2 and Figure 3, we can see that:
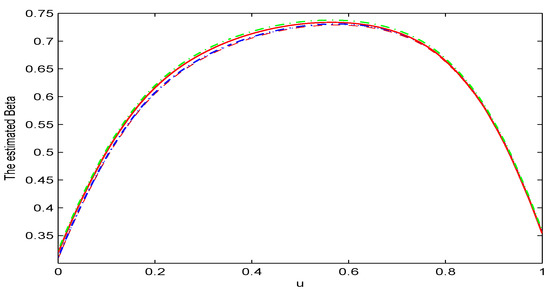
Figure 1.
The comparison between the true curve and the NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR simulation curve when and the selection probability function is .
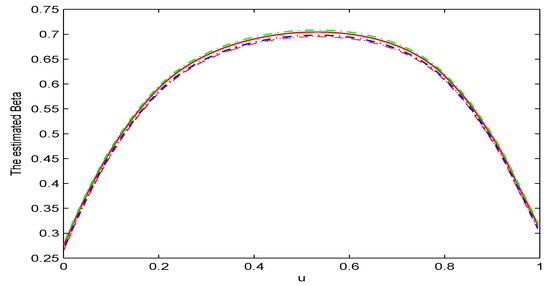
Figure 2.
The comparison between the true curve and the NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR simulation curve when and the selection probability function is .
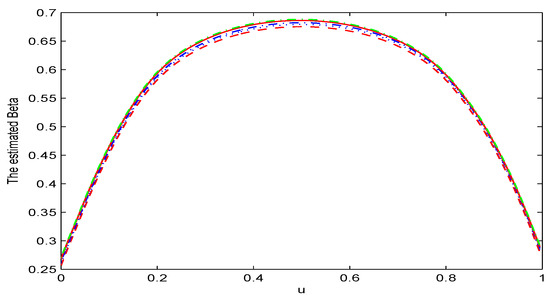
Figure 3.
The comparison between the true curve and the NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR simulation curve when and the selection probability function is .
(1) The simulation results based on the IWLLCQR method were similar to those based on the NWLLCQR method, the INWLLCQR method, and the WLLCQR method under a lower level of missing rate. However, the IWLLCQR method outperformed the INWLLCQR method, and the INWLLCQR method outperformed the NWLLCQR method, under a higher level of missing rate.
(2) It can be easily found that the simulated curve obtained by the IWLLCQR method was very close to the true curve. Thus, the imputed estimation was reasonable. However, the bias of the INWLLCQR method was slightly greater than those for the IWLLCQR and the WLLCQR method.
Example 2.
To examine the performance of the proposed test method, we consider the following model:
where, U follows a uniform distribution on, and, and ε are independent.
In order to illustrate our methods by using the dataset, artificial missing data were created by deleting some of the response values in the dataset at random. Assume that of the response values in this data are missed in this example. Consider the testing problem:
In what follows, the proposed test procedure is applied in a simulation with 500 replications. For each replication, 500 samples were generated, and the bootstrap sampling was repeated 300 times. Suppose the significance level . Figure 4 shows that the simulated powers increased quickly as increased. In particular, the simulated size of the test was 0.043, which is close to the true significant level of , when the null hypothesis holds. This demonstrates that the bootstrap estimate of the null distribution was considerably effective, which shows that our test was very powerful.
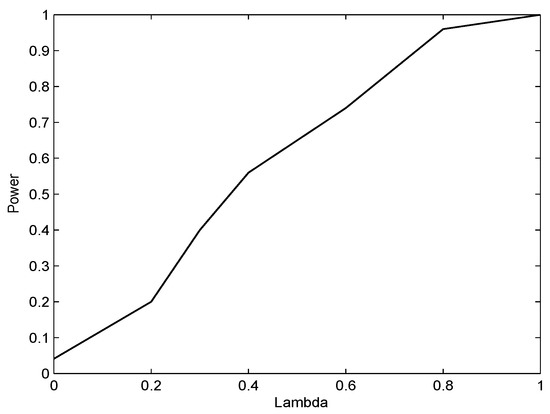
Figure 4.
The comparison between the true curve and the NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR simulation curve when and the selection probability function is .
6. A Real Data Example
In this section, we apply the methods proposed in this paper to the dataset on air pollution that the Norwegian Public Roads Administration collected. The dataset, which can be found in StatLib, consists of 500 observations. The varying coefficient model based on the CQR method was used by Guo and Tian [16] to fit the relation among the hourly values of the logarithm of the number of cars per hour , wind speed , the logarithm of the concentration of NO (Y), and the hour of the day . We deleted about of the completely observed Y randomly to illustrate our proposed methods. Now, we investigate the varying coefficient model with the response data missing:
Since the coefficient functions of the model (15) are really time varying, we need to consider the following testing problem:
where is a constant vector. The model (15) is just a classical linear model if the null hypothesis in (16) is true. For the testing problem (16), we should reject the null hypothesis at a significance level of 0.05 because the p value of test was 0.00 based on 500 resampling bootstraps.
In addition, the estimated functions of and are given, and the computational results came from 500 simulation runs. The estimated coefficients and the standard deviations are summarized in Table 2 for WLLCQR, NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR.

Table 2.
The coefficient estimates and sample standard deviations (in parentheses) for the air pollution data.
From Table 2, we can find that IWLLCQR and WLLCQR had much smaller standard deviations than WLLCQR, WLLCQR, and INWLLCQR, respectively. In what follows, we give estimated functions of and along with the 95% bootstrap confidence bands. The results in Figure 5 and Figure 6 show that and were time varying. Furthermore, we can also see that the IWLLCQR method had almost equal confidence intervals as the WLLCQR method. Hence, the IWLLCQR method was reasonable.
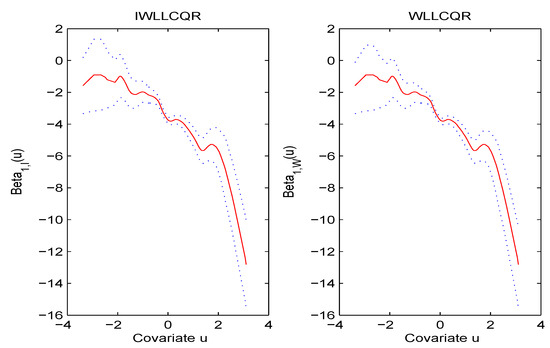
Figure 5.
The comparison between the true curve and the NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR simulation curve when and the selection probability function is .
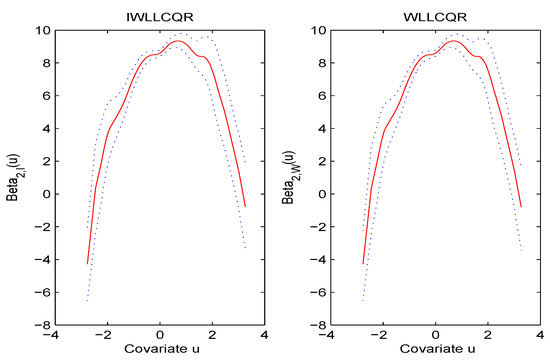
Figure 6.
The comparison between the true curve and the NWLLCQR, IWLLCQR, INWLLCQR, and WLLCQR simulation curve when and the selection probability function is .
7. Discussions
In the simulation study and the practical applications, we mainly found that the CQRE method was much more stable, efficient, and effective for varying coefficient models with response data missing at random than the single QRE method and least squares method when the sample size was large enough and the error faced a different distribution, which means the bias was at a relatively low level and the correct selection rate relatively higher.
In the face of high-dimensional data, these three method were not ideal, but the CQRE method was relatively better. This case arises widely in many research fields such as reliability life testing, genetic data research, medical tracking trials, population census, economics and finance, environment monitoring and biomedical research, etc. How to modify our method to improve the performance of the CQRE method for high-dimensional varying coefficient models with response data missing at random is an important topic that we will study further.
On the other hand, this paper with only response data missing at random studied the CQR estimation and inference for varying coefficient models. However, it did not consider the case of covariant data missing, nor even the more general case of both response and covariant data missing. These problems are more challenging topics that we will explore and study further in the coming year.
8. Concluding Remarks
In this paper, a CQRE method was proposed for varying coefficient models with response data missing at random to develop three estimators including the WLLCQR estimator, the NWLLCQR estimator, and the IWLLCQ estimator for unknown coefficient functions and establish some results on the asymptotic normality of these proposed estimators under some mild conditions. Following, a bootstrap-based test procedure was designed to perform a simulation study, which demonstrated that the unknown coefficient estimators with IWLLCQR were superior to the other two ones with WLLCQR and NWLLCQR. Meanwhile, based on the IWLLCQR fittings, a bootstrap test procedure was also designed to test whether the coefficient functions were actually varying. Finally, a type of investigated real-life dataset was analyzed to illustrate that the CQRE method was much more stable, efficient, and effective for varying coefficient models with response data missing at random than the single QRE method and least squares method.
Author Contributions
All the authors inferred the main conclusions and approved of the current version of this manuscript.
Acknowledgments
The authors would like to thank the anonymous referees for their valuable comments and suggestions, which actually stimulated this work. The work was supported by the National Natural Science Foundations of China (11601409, 71501155 and 11201362), the Natural Science Foundations of Shaanxi Province of China (2016JM1009), and the Natural Science Foundations of the Department of Shaanxi Province of China (2017JK0344).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| QR | quantile regression |
| CQR | composite QR |
| WCQR | weighted CQR |
| CQRE | CQR estimation |
| LLQR | local linear QR |
| LLCQR | local linear CQR |
| WLLCQR | weighted LLCQR |
| NWLLCQR | nonparametric WLLCQR |
| IWLLCQR | imputed WLLCQR |
Appendix A
The following conditions are needed for the results in Section 3.
(C1) are independent and identically distributed random vectors.
(C2) The density function of has a continuous and uniformly-bounded derivative, namely .
(C3) Matrix is a positive definite matrix, and .
(C4) Random variable U has a second-order differentiable density function in some neighborhood of u.
(C5) The coefficient function is second-order differentiable in a neighborhood of a given u, and is continuous.
(C6) The kernel function is a symmetric density function with a compact support, whose bandwidth as .
(C7) The bandwidth , and as .
(C8) The selection probability function has a bounded and continuous second derivative on the support of U.
The following lemma is useful for proving some theorems given in Section 3.
Lemma A1
(See Lemma 2 in [15]). Let be independent and identically distributed (i.i.d) random vectors, where the are scalar random variables. Suppose that and where represents the density of . Let be a bounded positive function with a bounded support, satisfying the Lipschitz condition. Then:
In what follows, the main theorems in Section 3 will be proven.
Proof of Theorem 1.
Let , with , , with a q-dimensional vector with one at the position and zero, elsewhere. Since:
is the minimizer of the criterion:
where . Applying the following identity (see Knight [34]):
we can rewrite as:
where
Then, it follows from Lemma A1 that . Denote:
where:
We observe that by the iterative expectation:
As in Parzen [35], we have:
Based on the above results, we can prove that:
where:
By Corollary 2 of Knight [34], we have . Assume Condition (C3) is satisfied. Then, . Simple calculation of the block matrix yields:
where . Let . It is easy to verify that . As in Parzen [35], we obtain:
By the central limit theorem, we get . Similar to Kai et al. (2011) [15], we can show that:
Proof of Theorem 2.
Let . Similar to the proof of Theorem 1, we have:
where:
Let:
Then, . It is easy to verify that:
Considering the fact that , it follows from (A5) that , and then:
Similar to the proof of Theorem 1, we can prove that:
where . Let . By the proof of Theorem 3 in Wong [33], we can obtain:
where and . Furthermore,
Completing the calculation, we obtain:
Based on the above results, it follows that . Similar to the proof of Theorem 1, we have: . Thus:
By Lemma A1, we get:
Since , then
Thus, we can show that:
Following (A7), (A9), and Theorem 1, we complete the proof of Theorem 2. □
Proof of Theorem 3.
Write . , , then we have:
Similar to the proof of Theorem 2, we have:
where:
We can prove:
Similar to the proof of Theorem 1, we can complete the proof. □
References
- Hastie, T.J.; Tibshirani, R.J. Varying-coefficient models. J. R. Stat. Soc. Ser. 1993, 55, 757–796. [Google Scholar] [CrossRef]
- Chiang, C.T.; Rice, J.A.; Wu, C.O. Smoothing spline estimation for varying coefficient models with repeatedly measured dependent variables. J. Am. Stat. Assoc. 2001, 96, 605–619. [Google Scholar] [CrossRef]
- Eubank, R.L.; Huang, C.; Maldonado, Y.M.; Wang, N.; Wang, S.; Buchanan, R.J. Smoothing spline estimation in varying coefficient models. J. R. Stat. Soc. Ser. 2004, 66, 653–667. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, J.T. Statistical estimation in varying coefficient models. Ann. Stat. 1999, 27, 1491–1518. [Google Scholar]
- Huang, J.; Wu, C.O.; Zhou, L. Varying coefficient models and basis function approximations for the analysis of repeated measurements. Biometrika 2002, 89, 111–128. [Google Scholar] [CrossRef]
- Wu, C.O.; Yu, K.F.; Chiang, C.T. A two-step smoothing method for varying coefficient models with repeated measurements. Ann. Inst. Stat. Math. 2000, 52, 519–543. [Google Scholar] [CrossRef]
- Fan, J.; Huang, T. Profile likelihood inferences on semiparametric varying-cofficient partially linear models. Bernoulli 2005, 11, 1031–1057. [Google Scholar] [CrossRef]
- Whang, Y.J. Smoothed empirical likelihood methods for quantile regression models. Econom. Theory 2006, 22, 173–205. [Google Scholar] [CrossRef]
- Koenker, R. Quantiles Regression; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kim, M.O. Quantile regression with varying coefficients. Ann. Stat. 2007, 35, 92–108. [Google Scholar] [CrossRef]
- Cai, Z.; Xu, X. Nonparametric quantile estimations for dynamic smooth coefficient models. J. Am. Stat. Assoc. 2008, 103, 1595–1608. [Google Scholar] [CrossRef]
- Cai, Z.; Xiao, Z. Semiparametric quantile regression estimation in dynamic models with partially varying coefficients. J. Econom. 2012, 167, 413–425. [Google Scholar] [CrossRef]
- Tang, Q.G. Robust estimation for spatial semiparametric varying coefficient partially linear regression. Stat. Pap. 2015, 56, 1137–1161. [Google Scholar]
- Zou, H.; Yuan, M. Composite quantile regression and the oracle model selection theory. Ann. Stat. 2008, 36, 1108–1126. [Google Scholar] [CrossRef]
- Kai, B.; Li, R.; Zou, H. New efficient estimation and variable selection methods for semiparametric varying coefficient partially linear models. Ann. Stat. 2011, 39, 305–332. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Tian, M.Z. New efficient and robust estimation in varying coefficient models with heteroscedasticity. Stat. Sin. 2012, 22, 1075–1101. [Google Scholar]
- Sun, J.; Gai, Y.; Lin, L. Weighted local linear composite quantile estimation for the case of general error distributions. J. Stat. Plan. Inference 2013, 143, 1049–1063. [Google Scholar] [CrossRef]
- Yang, H.; Lv, J.; Guo, C.H. Weighted composite quantile regression estimation and variable selection for varying coefficient models with heteroscedasticity. J. Korean Stat. Soc. 2015, 44, 77–94. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, C.-Y. Nonparametric M-type regression estimation under missing response data. Stat. Pap. 2016, 57, 641–664. [Google Scholar] [CrossRef]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Sterne, J.; White, I.; Carlin, J.; Spratt, M.; Royston, P.; Kenward, M.; Carpenter, J. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ 2009, 338, b2393. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Linton, O.; HÄrdle, W. Semiparametric regression analysis with missing response at random. J. Am. Stat. Assoc. 2004, 99, 334–345. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, Z. Estimation in partially linear models with missing responses at random. J. Multivar. Anal. 2007, 98, 1470–1493. [Google Scholar] [CrossRef]
- Wang, Q.; Rao, N.K. Empirical Likelihood-based inference under imputation for missing response data. Ann. Stat. 2002, 30, 896–924. [Google Scholar] [CrossRef]
- Xue, L.G. Empirical likelihood confidence intervals for response mean with data missing at random. Scand. J. Stat. 2009, 36, 671–685. [Google Scholar] [CrossRef]
- Wei, Y.; Ma, Y.; Carroll, R. Multiple imputation in quantile regression. Biometrika 2012, 99, 423–438. [Google Scholar] [CrossRef] [PubMed]
- Lv, X.; Li, R. Smoothed empirical likelihood analysis of partially linear quantile regression models with missing response variables. Adv. Stat. Anal. 2013, 97, 317–347. [Google Scholar] [CrossRef]
- Sherwood, B.; Wang, L.; Zhou, X. Weighted quantile regression for analyzing health care cost data with missing covariates. Stat. Med. 2013, 32, 4967–4979. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Q.; Gilbert, P. Quantile regression for competing risks data with missing cause of failure. Ann. Stat. 2012, 22, 703–728. [Google Scholar] [CrossRef]
- Chen, X.; Wan, T.K.; Zhou, Y. Efficient quantile regression analysis with missing observations. J. Am. Stat. Assoc. 2015, 110, 723–741. [Google Scholar] [CrossRef]
- Kim, S.Y. Imputation methods for quantile estimation under missing at random. Stat. Its Interface 2013, 6, 369–377. [Google Scholar]
- Nageswara, S.; Rao, V. Nadaraya-Watson estimator for sensor fusion. Opt. Eng. 1997, 36, 642–647. [Google Scholar]
- Wong, H.; Guo, S.J.; Chen, M.; Wai-Cheung, I.P. On locally weighted estimation and hypothesis testing on varying coefficient models with missing covariates. J. Stat. Plan. Inference 2009, 139, 2933–2951. [Google Scholar] [CrossRef]
- Knight, K. Limiting distributions for L1 regression estimators under general conditions. Ann. Stat. 1998, 26, 755–770. [Google Scholar]
- Parzen, E. On estimation of a probability density function and model. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).