Neutrino Flavor Transitions as Mass State Transitions
Abstract
1. Introduction
2. Four-State Transitions
2.1. Perturbation Induced Transitions between Flavor States
2.2. Flavor State Transitions as Mass State Transitions
3. Transitions between Flavor States: Electron Neutrino Disappearance
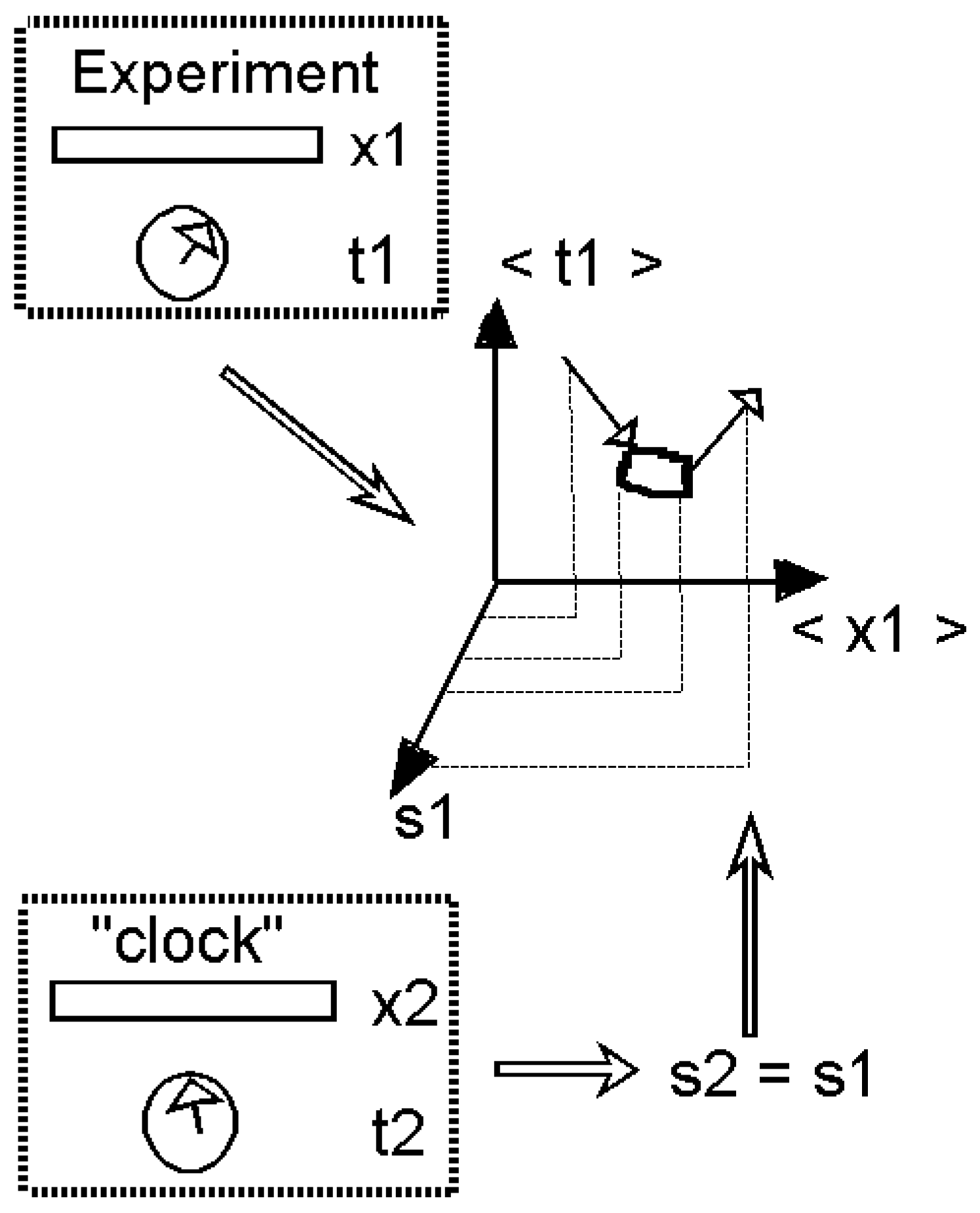
4. Application to Neutrino Oscillation Experiments
5. Conclusions
Funding
Conflicts of Interest
Appendix A. The Physical System
References
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Particle Data Group. Available online: http://pdg.lbl.gov/2019/ (accessed on 15 May 2019).
- Aguilar-Arevalo, A.A.; Brown, B.C.; Bugel, L.; Cheng, G.; Conrad, J.M.; Cooper, R.L.; Dharmapalan, R.; Diaz, A.; Djurcic, Z.; Finley, D.A.; et al. Significant Excess of Electronlike Events in the MiniBooNE Short-Baseline Neutrino Experiment. Phys. Rev. Lett. 2018, 121, 221801. [Google Scholar] [CrossRef] [PubMed]
- Adamson, P.; Anghel, I.; Aurisano, A.; Barr, G.; Bishai, M.; Blake, A.; Bock, G.J.; Bogert, D.; Cao, S.V.; Carroll, T.J.; et al. Search for Sterile Neutrinos in MINOS and MINOS Using a Two-Detector Fit. Phys. Rev. Lett. 2019, 122, 091803. [Google Scholar] [CrossRef] [PubMed]
- Fanchi, J.R. The Mass Operator and Neutrino Oscillations. Found. Phys. 1998, 28, 1521–1528. [Google Scholar] [CrossRef]
- Fanchi, J.R. Parametrized Relativistic Dynamical Framework for Neutrino Oscillations. J. Phys. Conf. Ser. 2017, 845, 1–13. [Google Scholar] [CrossRef]
- Fanchi, J.R. Parametrized Relativistic Quantum Theory; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Fanchi, J.R. Manifestly Covariant Quantum Theory with Invariant Evolution Parameter in Relativistic Dynamics. Found. Phys. 2011, 41, 4–32. [Google Scholar] [CrossRef]
- Pavšič, M. The Landscape of Theoretical Physics: A Global View; Kluwer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Horwitz, L.P. Relativistic Quantum Mechanics; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Fanchi, J.R. The Relativistic Quantum Potential and Non-locality. In Horizons in World Physics 240; Hauppauge: New York, NY, USA, 2003; pp. 117–159. [Google Scholar]
- Fanchi, J.R. Interaction Induced Flavor Oscillations. In Horizons in World Physics 300; Hauppauge: New York, NY, USA, 2019. [Google Scholar]
- Rusov, V.D.; Vlasenko, D.S. Quantization in relativistic classical mechanics: The Stueckelberg equation, neutrino oscillation and large-scale structure of the Universe. J. Phys. Conf. Ser. 2012, 361, 1–15. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fanchi, J.R. Neutrino Flavor Transitions as Mass State Transitions. Symmetry 2019, 11, 948. https://doi.org/10.3390/sym11080948
Fanchi JR. Neutrino Flavor Transitions as Mass State Transitions. Symmetry. 2019; 11(8):948. https://doi.org/10.3390/sym11080948
Chicago/Turabian StyleFanchi, John R. 2019. "Neutrino Flavor Transitions as Mass State Transitions" Symmetry 11, no. 8: 948. https://doi.org/10.3390/sym11080948
APA StyleFanchi, J. R. (2019). Neutrino Flavor Transitions as Mass State Transitions. Symmetry, 11(8), 948. https://doi.org/10.3390/sym11080948



