Retardant Effects of Collapsing Dynamics of a Laser-Induced Cavitation Bubble Near a Solid Wall
Abstract
1. Introduction
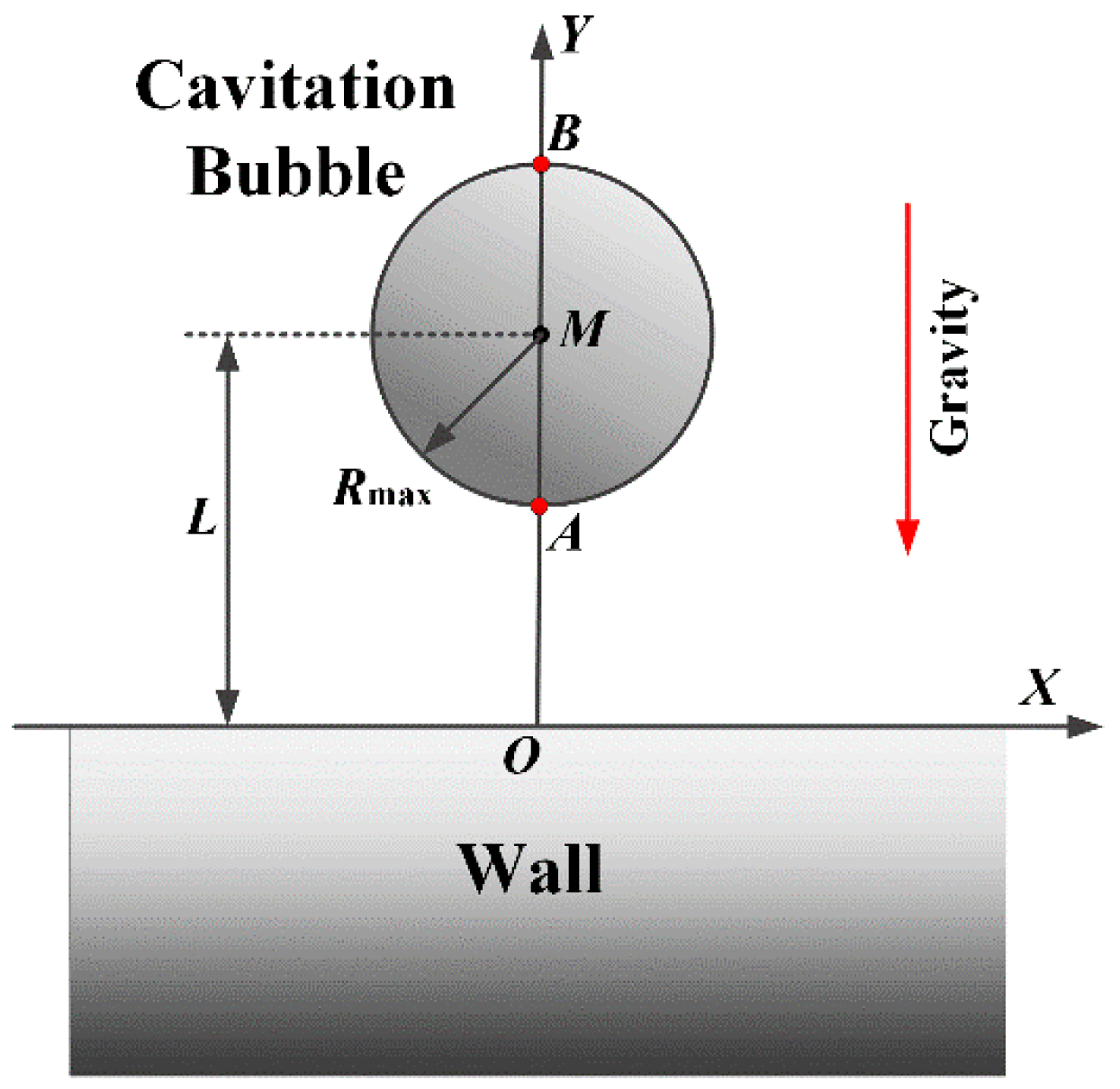
2. Experimental Setup
- Check the connections between different systems, e.g., signal transmission.
- Place the solid wall in a suitable place through the 3D platform.
- Generate bubbles using focused laser. Meanwhile, trigger the camera and the flashing lights. The delays between the three elements could be adjusted for different purposes.
- Save the data and check its quality.
- Repeat the same parameter setup several times for repeatability.
- Try another distance between the bubble and wall or different bubble sizes controlled by the laser energy.
3. Qualitative Descriptions of the Cavitation Bubble Dynamic Behavior Near the Wall
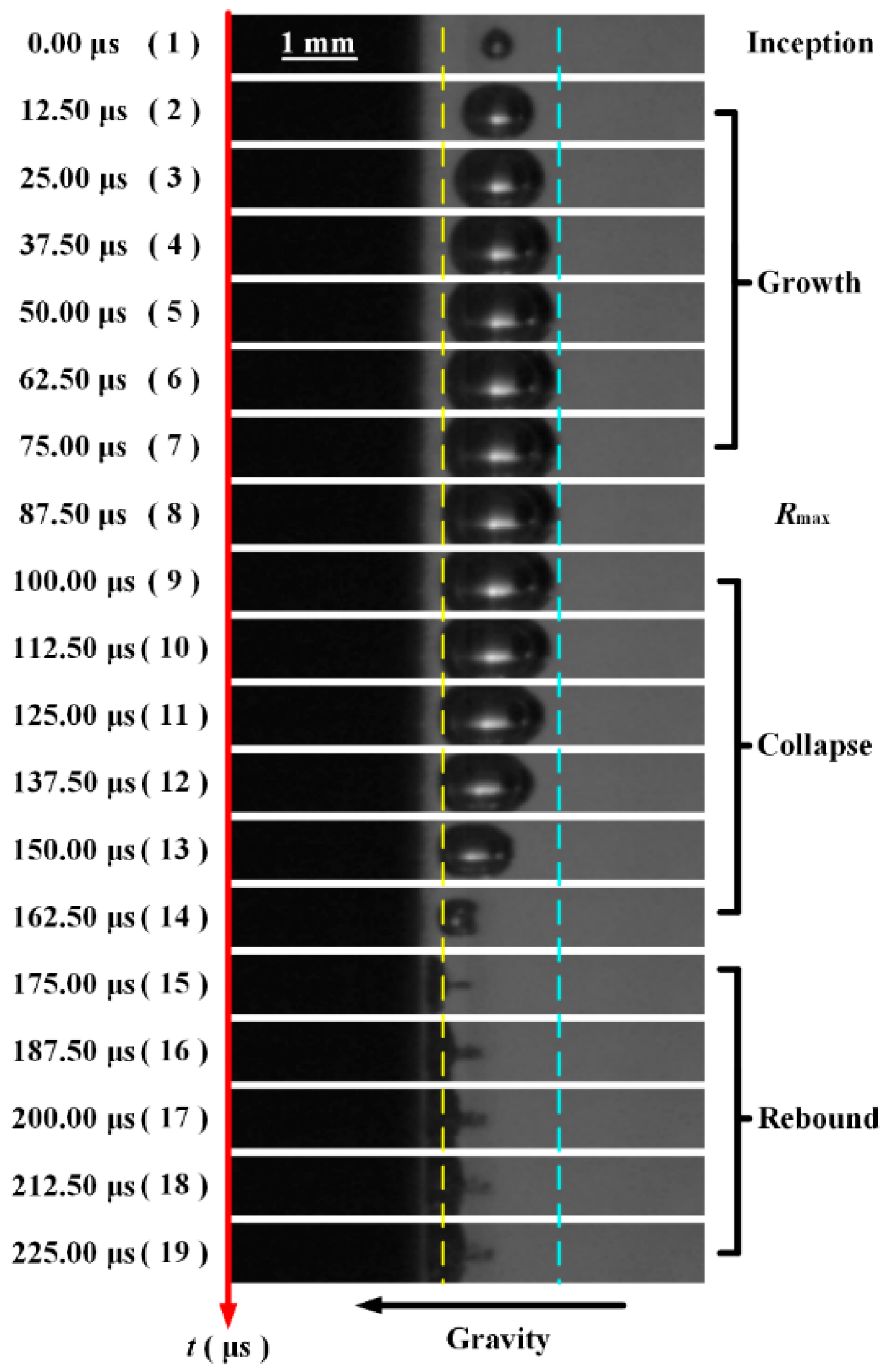
3.1. Typical Examples of the Collapse of a Cavitation Bubble Near a Wall
3.2. Influences of the Bubble–Wall Distance on the Bubble Collapse
- Case 1:
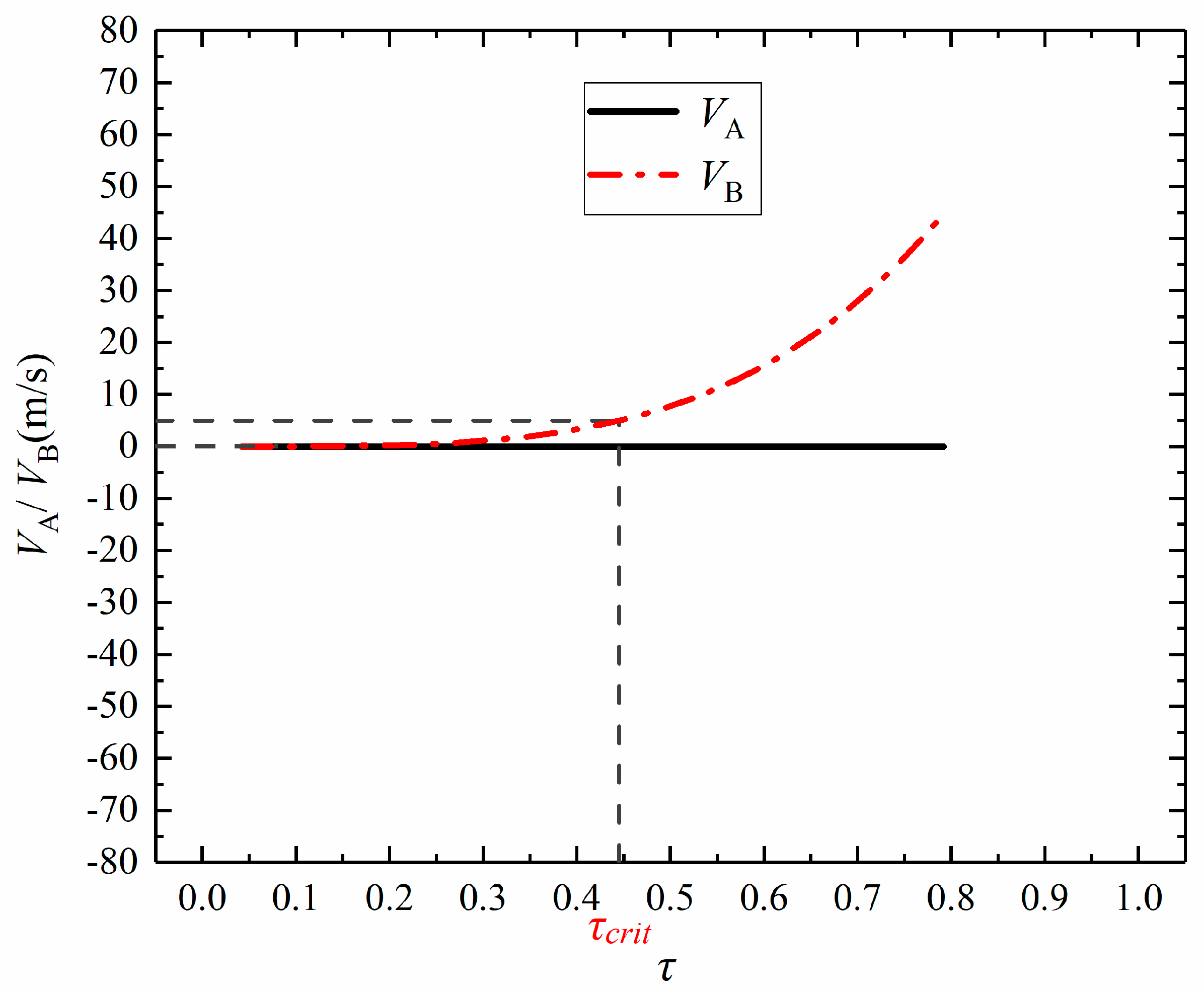
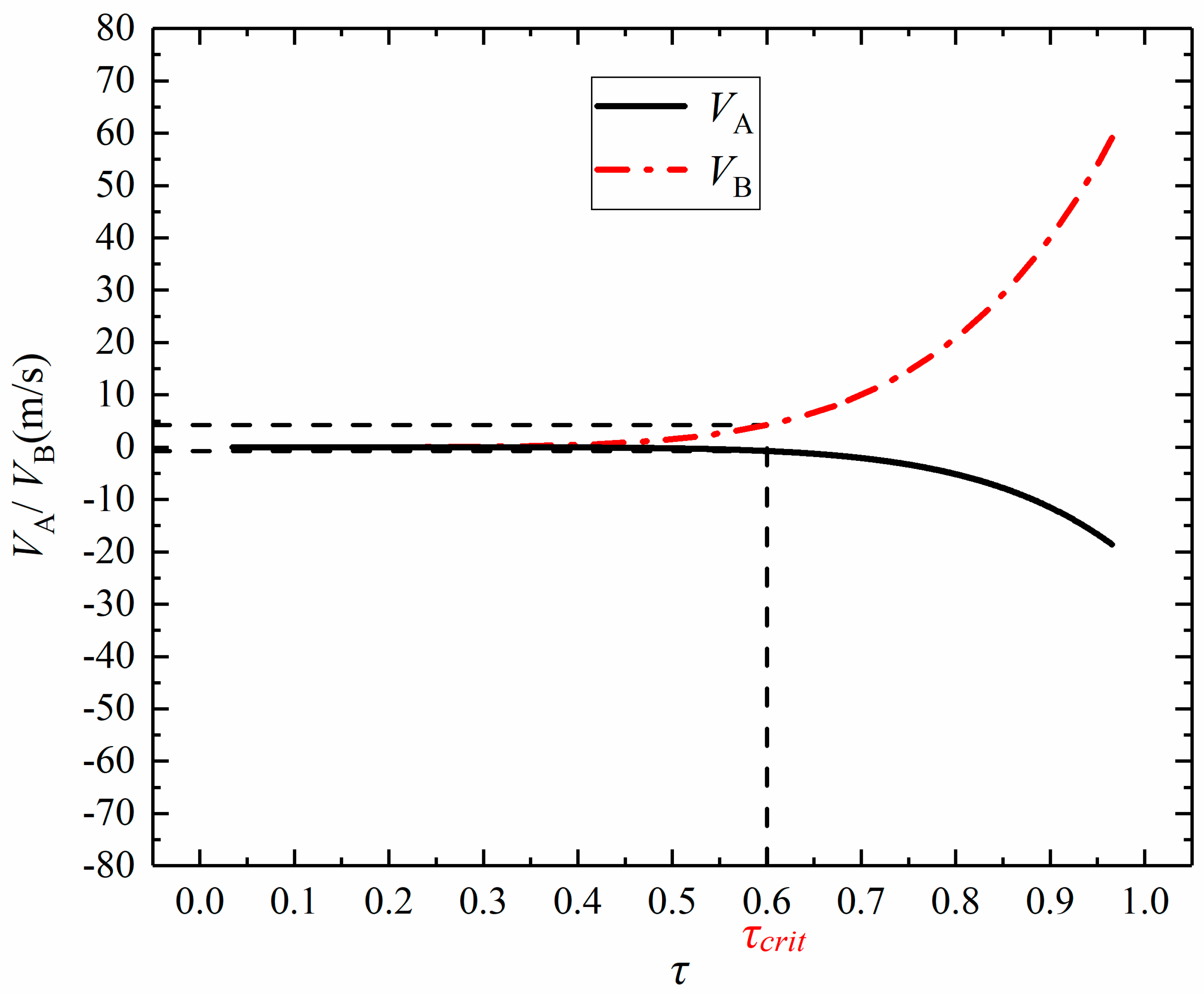
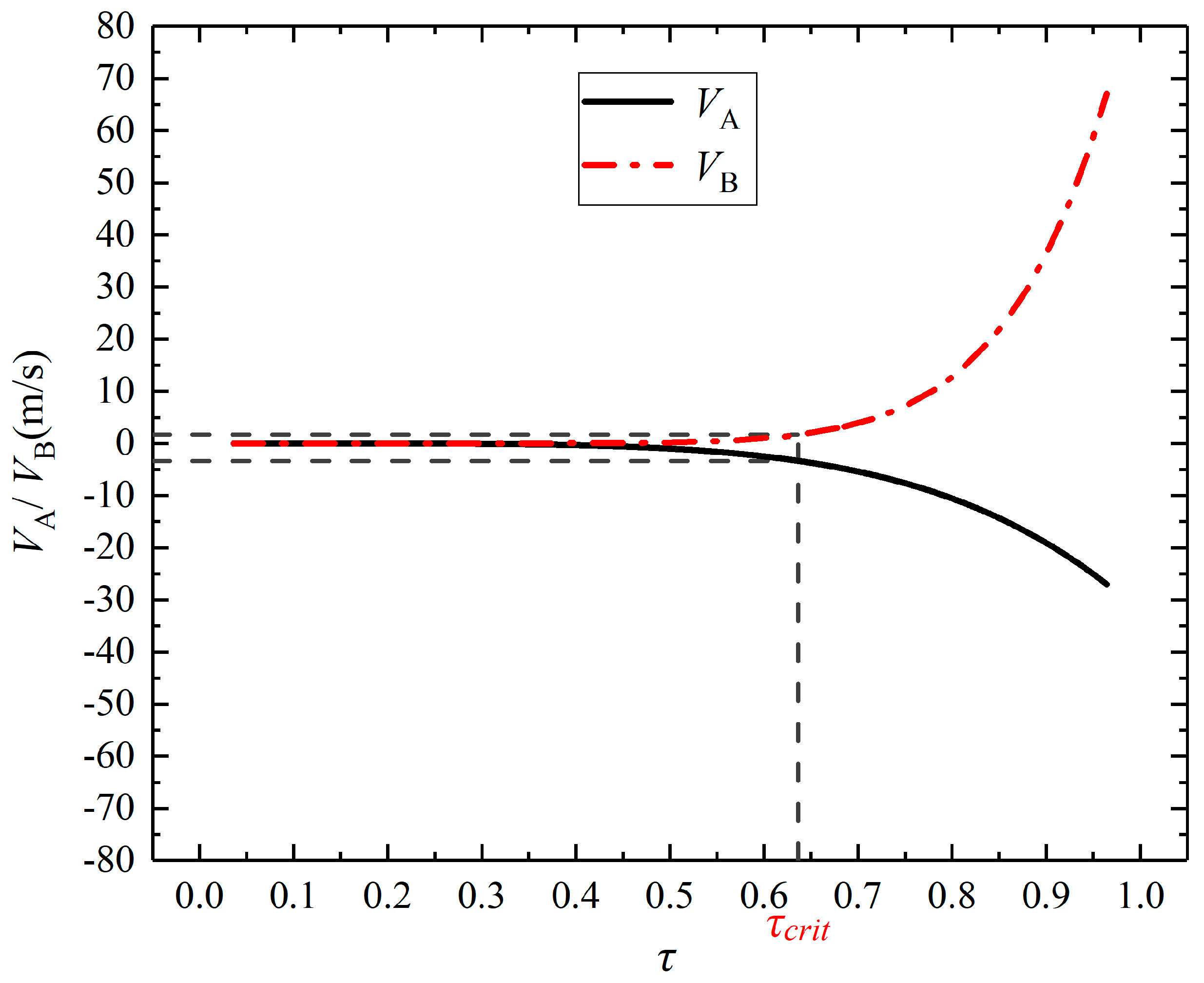
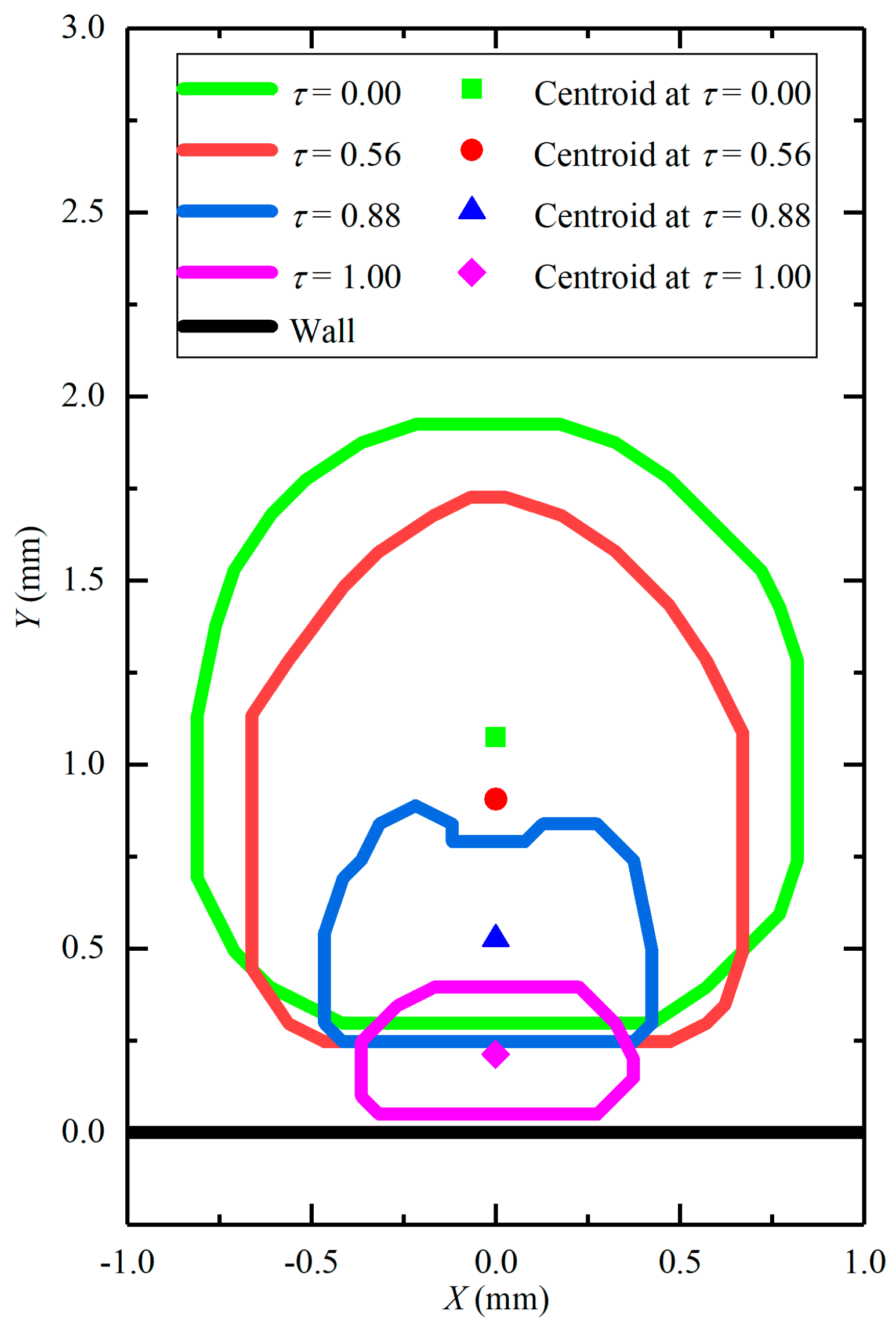
- This case corresponds to the condition with a short distance between the cavitation bubble and the wall (e.g., λ = 1.25). It can be observed from the figure that when the cavitation bubble is very close to the wall, pole A is nearly stationary, while pole B moves to the left significantly. In addition, the overall position of the cavitation bubble also moves toward the wall. If the internal density of the cavitation bubbles is assumed to be uniform, the bubble (mass) centroid continuously moves to the left during the collapsing stage. At the end of the collapsing stage (subplot 18–20 in Figure 3), the left side of the bubble approaches the wall surface while the right side of the bubble shows a toroidal shape in the middle, indicating that the jet may be finally generated.
- Case 2:
- This case corresponds to the condition with a medium distance between the cavitation bubble and the wall (e.g., λ = 2.50). As shown in Figure 4, differently from Figure 3 with a short distance, both poles A and B move towards the inside of the cavitation bubble (Table 1). In addition, the velocity of pole B is much faster than that of pole A, leading to the obvious movement of the bubble towards the wall. Due to the relatively considerable distance, the bubble does not contact the wall during the whole process. At the end of the collapsing stage, similarly to Figure 3, there also exists a toroidal shape on the right side of the cavitation bubble (subplot 20 in Figure 4). However, the display time of the torus is obviously delayed in Figure 4 because of the weak influences of the wall.
- Case 3:
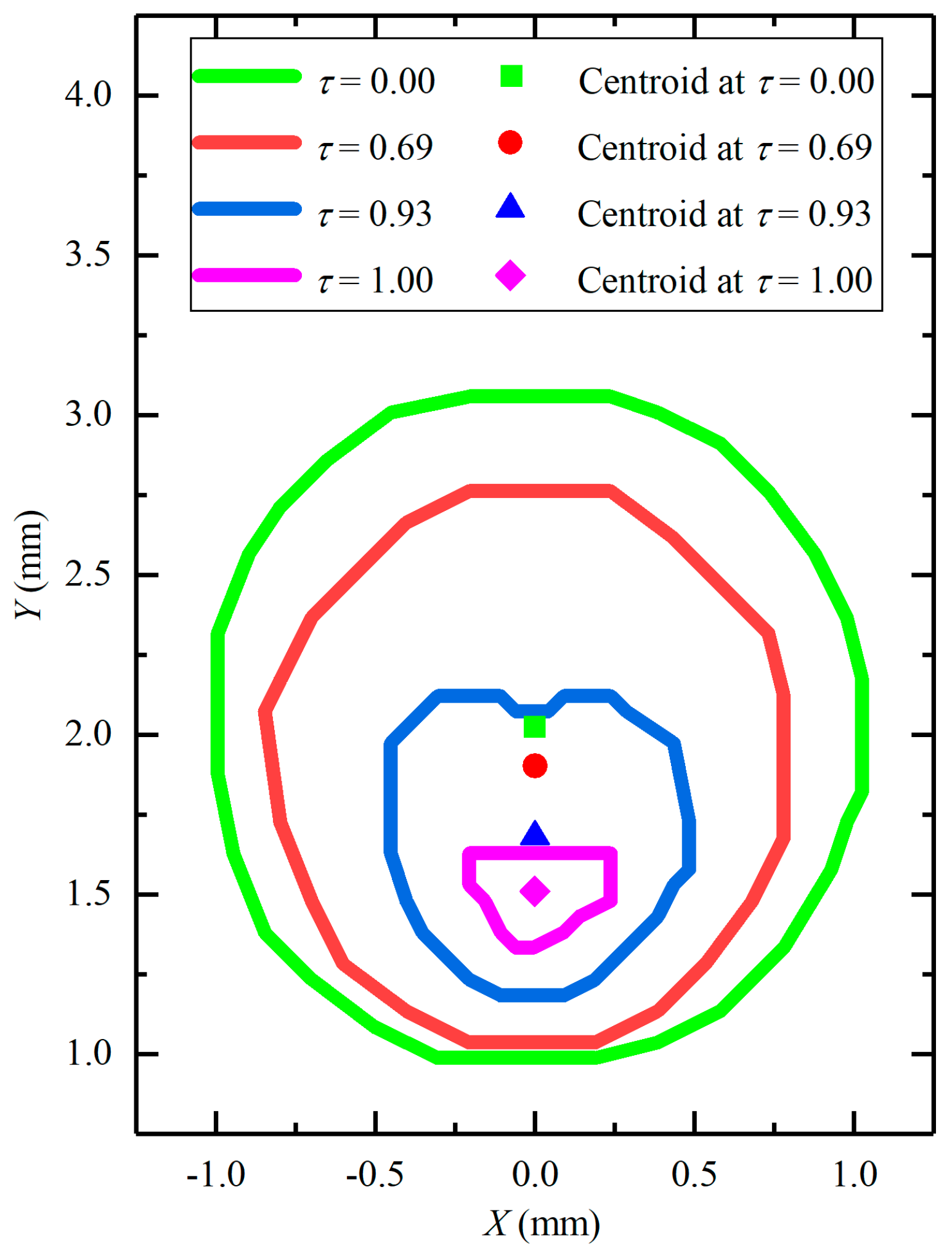
- This case corresponds to the condition with a large distance between the cavitation bubble and the wall (e.g., λ = 3.75). It can be observed from the figure that when the bubble–wall distance is large, the bubble nearly retains a spherical shape during the oscillations. In particular, poles A and B both move toward the inside of the bubble with nearly the same speed. Hence, the movement of the bubble centroid is very marginal during the collapsing stage.
4. The Velocities of Poles A and B of the Cavitation Bubble
5. The Motions of the Bubble Centroid
5.1. The Motions of the Bubble Interface and the Position of the Centroid
5.2. The Relative Movement of the Bubble Centroid
6. Physical Interpretation of the Phenomenon
7. Conclusions
- (1)
- The presence of the wall could significantly alter the collapse contour, leading to a great difference between the movements of poles A and B.
- (2)
- The retardant effect can be observed due to the presence of the wall. With the increase of λ, the retardant effects of the wall will be dismissed and the bubble finally recovers the spherical oscillations.
- (3)
- The cavitation bubble could induce a significant water hammer pressure (up to 87 MPa in our experiment) during the bubble collapse.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Liu, K.; Xian, H.; Du, X. A review of methods for vortex identification in hydroturbines. Renew. Sustain. Energy Rev. 2018, 81, 1269–1285. [Google Scholar] [CrossRef]
- Arndt, R.E.; Voigt, R.L., Jr.; Sinclair, J.P.; Rodrique, P.; Ferreira, A. Cavitation erosion in hydroturbines. J. Hydraul. Eng. 1989, 115, 1297–1315. [Google Scholar] [CrossRef]
- Brennen, C.E. Hydrodynamics of Pumps; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Reuter, F.; Mettin, R. Mechanisms of single bubble cleaning. Ultrason. Sonochem. 2016, 29, 550–562. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Gonzalez-Avila, S.R.; Dijkink, R.; Koukouvinis, P.; Gavaises, M.; Ohl, C.D. Wall shear stress from jetting cavitation bubbles. J. Fluid Mech. 2018, 846, 341–355. [Google Scholar] [CrossRef]
- Philipp, A.; Lauterborn, W. Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 1998, 361, 75–116. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Ellis, A.T. The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Philos. Trans. R. Soc. Lond. Ser. A 1966, 260, 221–240. [Google Scholar] [CrossRef]
- Zhang, S.; Duncan, J.H.; Chahine, G.L. The final stage of the collapse of a cavitation bubble near a rigid wall. J. Fluid Mech. 1993, 257, 147–181. [Google Scholar] [CrossRef]
- Brujan, E.A.; Keen, G.S.; Vogel, A.; Blake, J.R. The final stage of the collapse of a cavitation bubble close to a rigid boundary. Phys. Fluids 2002, 14, 85–92. [Google Scholar] [CrossRef]
- Popinet, S.; Zaleski, S. Bubble collapse near a solid boundary: A numerical study of the influence of viscosity. J. Fluid Mech. 2002, 464, 137–163. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Yeo, K.S.; Khoo, B.C.; Wang, C. 3D jet impact and toroidal bubbles. J. Comput. Chem. Phys. 2001, 166, 336–360. [Google Scholar] [CrossRef]
- Tomita, Y.; Robinson, P.B.; Tong, S.P.; Blake, J.R. Growth and collapse of cavitation bubbles near a curved rigid boundary. J. Fluid Mech. 2002, 466, 259–283. [Google Scholar] [CrossRef]
- Klaseboer, E.; Hung, K.C.; Wang, C.; Wang, C.W.; Khoo, B.C.; Boyce, P.; Debono, S.; Charlier, H. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 2005, 537, 387–413. [Google Scholar] [CrossRef]
- Yusof, N.S.M.; Babgi, B.; Alghamdi, Y.; Aksu, M.; Madhavan, J.; Ashokkumar, M. Physical and chemical effects of acoustic cavitation in selected ultrasonic cleaning applications. Ultrason. Sonochem. 2016, 29, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Prentice, P.; Cuschieri, A.; Dholakia, K.; Prausnitz, M.; Campbell, P. Membrane disruption by optically controlled microbubble cavitation. Nat. Phys. 2005, 1, 107–110. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Zhang, Y.; Du, X. Experimental study of influences of a particle on the collapsing dynamics of a laser-induced cavitation bubble near a solid wall. Exp. Fluid Sci. 2019, 105, 289–306. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, F.; Zhang, Y.; Zhang, Y.; Du, X. Experimental investigations of interactions between a laser-induced cavitation bubble and a spherical particle. Exp. Fluid Sci. 2018, 98, 645–661. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Zhang, Y.; Zhang, Y.X. High-speed experimental photography of collapsing cavitation bubble between a spherical particle and a rigid wall. J. Hydrodyn. 2018, 30, 1012–1021. [Google Scholar] [CrossRef]
- Gonzalez-Avila, S.R.; Klaseboer, E.; Khoo, B.C.; Ohl, C.D. Cavitation bubble dynamics in a liquid gap of variable height. J. Fluid Mech. 2011, 682, 241–260. [Google Scholar] [CrossRef]
- Brujan, E.A.; Takahira, H.; Ogasawara, T. Planar jets in collapsing cavitation bubbles. Exp. Fluid Sci. 2019, 101, 48–61. [Google Scholar] [CrossRef]
- Li, T.; Zhang, A.M.; Wang, S.P.; Li, S.; Liu, W.T. Bubble interactions and bursting behaviors near a free surface. Phys. Fluids 2019, 31, 042104. [Google Scholar] [CrossRef]
- Pearson, A.; Cox, E.; Blake, J.R.; Otto, S.R. Bubble interactions near a free surface. Eng. Anal. Bound. Elem. 2004, 28, 295–313. [Google Scholar] [CrossRef]
- Brujan, E. Cavitation in Non-Newtonian Fluids: With Biomedical and Bioengineering Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Brujan, E.A.; Nahen, K.; Schmidt, P.; Vogel, A. Dynamics of laser-induced cavitation bubbles near an elastic boundary. J. Fluid Mech. 2001, 433, 251–281. [Google Scholar] [CrossRef]
- Hopfes, T.; Wang, Z.; Giglmaier, M.; Adams, N.A. Collapse dynamics of bubble pairs in gelatinous fluids. Exp. Fluid Sci. 2019, 108, 104–114. [Google Scholar] [CrossRef]
- Wu, J.H.; Wang, Y.; Ma, F.; Gou, W.J. Cavitation erosion in bloods. J. Hydrodyn. 2017, 29, 724–727. [Google Scholar] [CrossRef]
- Wan, C.R.; Liu, H. Shedding frequency of sheet cavitation around axisymmetric body at small angles of attack. J. Hydrodyn. 2017, 29, 520–523. [Google Scholar] [CrossRef]
- Blake, J.R.; Gibson, D.C. Cavitation bubbles near boundaries. Annu. Rev. Fluid Mech. 1987, 19, 99–123. [Google Scholar] [CrossRef]
- Lauterborn, W.; Kurz, T. Physics of bubble oscillations. Rep. Prog. Phys. 2010, 73, 106501. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Wang, S.P.; Zhang, A.M.; Liu, Y.L.; Zhang, S.; Cui, P. Bubble dynamics and its applications. J. Hydrodyn. 2018, 30, 975–991. [Google Scholar] [CrossRef]
- Best, J.P. The formation of toroidal bubbles upon the collapse of transient cavities. J. Fluid Mech. 1993, 251, 79–107. [Google Scholar] [CrossRef]
- Lee, M.; Klaseboer, E.; Khoo, B.C. On the boundary integral method for the rebounding bubble. J. Fluid Mech. 2007, 570, 407–429. [Google Scholar] [CrossRef]
- Wang, Q. Multi-oscillations of a bubble in a compressible liquid near a rigid boundary. J. Fluid Mech. 2014, 745, 509–536. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, W.; Zhang, A.M.; Sui, Y. Bubble dynamics in a compressible liquid in contact with a rigid boundary. Interface Focus 2015, 5, 20150048. [Google Scholar] [CrossRef] [PubMed]
- Han, R.; Zhang, A.M.; Li, S.; Zong, Z. Experimental and numerical study of the effects of a wall on the coalescence and collapse of bubble pairs. Phys. Fluids 2018, 30, 042107. [Google Scholar] [CrossRef]
- Koch, M.; Lechner, C.; Reuter, F.; Köhler, K.; Mettin, R.; Lauterborn, W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM. Comput. Fluids 2016, 126, 71–90. [Google Scholar] [CrossRef]
- Lechner, C.; Lauterborn, W.; Koch, M.; Mettin, R. Fast, thin jets from bubbles expanding and collapsing in extreme vicinity to a solid boundary: A numerical study. Phys. Rev. Fluids 2019, 4, 021601. [Google Scholar] [CrossRef]
- Thoroddsen, S.T.; Etoh, T.G.; Takehara, K. High-speed imaging of drops and bubbles. Annu. Rev. Fluid Mech. 2008, 40, 257–285. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, W.; Leppinen, D.M.; Walmsley, A.D. Microbubble dynamics in a viscous compressible liquid near a rigid boundary. IMA J. Appl. Math. 2019, 84, 696–711. [Google Scholar] [CrossRef]
- Klapcsik, K.; Hegedűs, F. Study of non-spherical bubble oscillations under acoustic irradiation in viscous liquid. Ultrason. Sonochem. 2019, 54, 256–273. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Qiu, X.; Chen, F.; Liu, K.; Zhang, Y.; Liu, C. A selected review of vortex identification methods with applications. J. Hydrodyn. 2018, 30, 767–779. [Google Scholar] [CrossRef]
- Dong, X.; Wang, Y.; Chen, X.; Dong, Y.; Zhang, Y.; Liu, C. Determination of epsilon for Omega vortex identification method. J. Hydrodyn. 2018, 30, 541–548. [Google Scholar] [CrossRef]





| λ | |||
|---|---|---|---|
| Small | No Move | ← | Large |
| Medium | → | ← | Medium |
| Large | → | ← | Small |
| Parameters | Case 1 | Case 2 | Case 3 | |||
|---|---|---|---|---|---|---|
| Point A | Point B | Point A | Point B | Point A | Point B | |
| a | 0.00 | 108.98 ± 18.63 | −23.63 ± 3.36 | 71.81 ± 5.14 | −32.40 ± 2.96 | 92.72 ± 7.60 |
| b | 0.00 | 3.81 ± 0.50 | 6.82 ± 1.29 | 5.53 ± 0.54 | 5.03 ± 0.65 | 8.88 ± 0.91 |
| Adjusted | --- | 0.90 | 0.76 | 0.92 | 0.88 | 0.92 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Duan, Y.; Zhang, Y.; Tang, N.; Zhang, Y. Retardant Effects of Collapsing Dynamics of a Laser-Induced Cavitation Bubble Near a Solid Wall. Symmetry 2019, 11, 1051. https://doi.org/10.3390/sym11081051
Li X, Duan Y, Zhang Y, Tang N, Zhang Y. Retardant Effects of Collapsing Dynamics of a Laser-Induced Cavitation Bubble Near a Solid Wall. Symmetry. 2019; 11(8):1051. https://doi.org/10.3390/sym11081051
Chicago/Turabian StyleLi, Xiaofei, Yaxin Duan, Yuning Zhang, Ningning Tang, and Yuning Zhang. 2019. "Retardant Effects of Collapsing Dynamics of a Laser-Induced Cavitation Bubble Near a Solid Wall" Symmetry 11, no. 8: 1051. https://doi.org/10.3390/sym11081051
APA StyleLi, X., Duan, Y., Zhang, Y., Tang, N., & Zhang, Y. (2019). Retardant Effects of Collapsing Dynamics of a Laser-Induced Cavitation Bubble Near a Solid Wall. Symmetry, 11(8), 1051. https://doi.org/10.3390/sym11081051




