Kernel-Based Robust Bias-Correction Fuzzy Weighted C-Ordered-Means Clustering Algorithm
Abstract
1. Introduction
1.1. The Introduction of Fuzzy Clustering
1.2. Introduction to FCM Clustering with Local Spatial Information
1.3. Introduction of Clustering Algorithm Based on Ordered Means
1.4. Introduction of Fuzzy Clustering Based on Kernel Method
- (1)
- The introduction of kernel function avoids the ”dimensional curse” and significantly reduces the computation. It is a perfect trick to shift the ”disaster” effect from the low dimension of the input space to the processing of high-dimensional vector product, thus reducing the computation.
- (2)
- There is no need to know the form and parameters of the non-linear mapping function.
- (3)
- The kernel function method can select different kernel functions and algorithms according to different applications and combine them together to form a variety of different kernel function-based techniques, while the design of kernel functions and algorithms can be performed separately.
- (4)
- The kernel function implicitly turns the originally complicated computation into a mapping computation and changes the initial form and parameters of computation into the mapping from input space to feature space and thus having an effect on the properties of feature space, finally achieving the purpose of computation.
- (1)
- By using robust kernel, a class of robust non-euclidean distance measure is introduced. A new class of robust non-euclidean distance measure is introduced into the input space and then the robust second-order metric (kernel) is used to replace the non-robust Euclidean distance metric. Thus, data clustering or image segmentation can be carried out more effectively.
- (2)
- Maintain the computational simplicity of FCM.
- (3)
- It is more likely to reveal the inherent non-euclidean structure of the data.
- (4)
- The clustering results can be intuitively explained.
- (5)
- Data sets with missing values are easily handled [83].
1.5. Theoretical Classical FCM Algorithm and Its Relationship with KBFWCM Algorithm
1.6. Structure of the Paper
2. Related Work
2.1. Criterion Function for BFWCOM Algorithm
2.2. Clustering Prototype and Bias Field Update
2.3. Calculation of Typicality of Data
3. Kernel-Induced Robust Bias Correction Fuzzy Weighted C-Order Mean Clustering Algorithm
3.1. Definition and Theorem of Kernel Function
3.1.1. Definition of Kernel Function
- 1
- Definiton of feature space: Suppose the pattern maps the input space to a new space by mapping , that is, . Then, F is called the feature space.
- 2
- Definition of kernel function: Let X be a non-empty set, H be a inner product space, be the mapping from X to H, if the function satisfies the condition: for , . Then, K is the kernel function.
- 3
- Definition of positive semi-definite kernel function: if the continuous symmetric function satisfies the following formula:Then, the function is a positive semi-definite kernel function. In the discrete case, for any positive integer n, sample set and constant , if the symmetric function and satisfies the following formula:Then, is a positive semi-definite kernel function.
- 4
- Definition of Mercer conditions: The necessary and sufficient condition for any symmetric function that can be represented as the inner product form is positive semi-definite, that is,For the discrete case, the following matrixis a positive semi-definite matrix for all .The nonnegative condition is as follows:corresponds to the positive semi-definite condition in finite case.
3.1.2. The Fundamentals of Kernel Functions
3.1.3. Gaussian Radial Basis Function Clustering Algorithm
3.2. The Kernel-Induced Distance Based FCM (KFCM)
| Algorithm 1 Kernel-based fuzzy c-means algorithm. |
| Input: Input dataset , the number of clusters , the threshold , the maximum number of iterations t, the fuzziness index m; |
| Output: c clusters of X,U,V. |
| Begin |
| Fix , for some positive constant; |
| Initialize the memberships ; |
| For do: |
| Update all prototypes with Equation (13); |
| Update all memberships with Equation (12); |
| Compute , |
| If , then and goto Step 4 else stop |
| If , then stop |
| end for; |
| return c clusters of X,U,V; |
| end |
3.3. Kernel-Induced Distance Based KBFWCM with Dpatial Constraints
| Algorithm 2 KBFWCM algorithm. | |
| Input: Input Image , the number of clusters , the threshold , the fuzziness index m, the parameter , the parameter , the window size w; | |
| Output: c clusters of X,U,V. | |
| 1: | Begin |
| 2: | Fix ,,,; |
| 3: | Initialize the center ; |
| 4: | Initialize U with random numbers and normalize with constraint (2); |
| 5: | Initialize all with ; |
| 6: | Compute the mean or median filtered image and set the iterative index k = 1; |
| 7: | For t = 1 to N do: |
| 8: | Update the with (23) and constraint (2); |
| 9: | for c = 1 to C do: (for each cluster); |
| 10: | For d = 1 to p do: (for each attribute) |
| 11: | for k = 1 to n do: (for each data item) |
| 12: | (calculate the residual) |
| 13: | end for (for each data item) |
| 14: | sort residual; mark each residual with the number of sequences in the ordered sequence; |
| 15: | for k = 1 to n do: (for each residual); |
| 16: | calculate the characteristics of using formulas (4) and (5) or uniform weighting |
| 17: | end for; (for each residual) |
| 18: | end for; (for each attribute) |
| 19: | Update the prototypes for t-th iteration using (24); |
| 20: | Update the using (25); |
| 21: | end for; (for each cluster) |
| 22: | for k = 1 to n do: (for each data item) |
| 23: | calculate the characteristics of using formula (6) |
| 24: | end for; (for each data item) |
| 25: | if then goto 27 |
| 26: | end for |
| 27: | return c clusters of X,U,V; |
| 28: | end |
4. Algorithm Experiment
4.1. IRIS Data Used for Comparison of Classification Effectiveness
4.1.1. Classification Error Rate (CER)
4.1.2. Deviation Degree (DD) Calculation
4.2. Make Comparisons Between New Algorithm and Other Algorithms in Image Segmentation
4.3. Comparison of Experimental Results Using Brain MR and Lena Images
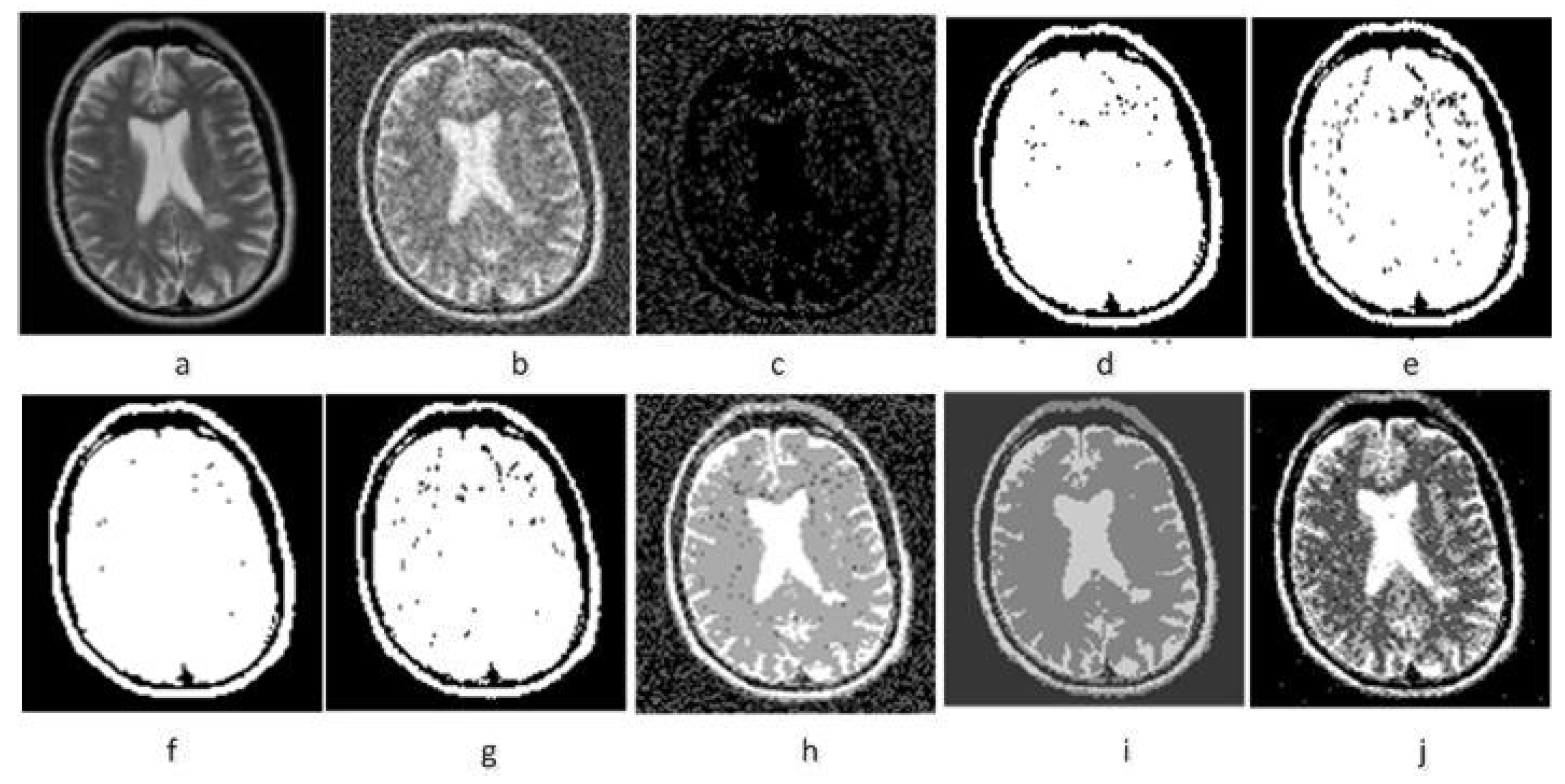
4.3.1. Denoising Experimental Results of MR Image
4.3.2. Denoising Experimental Results of Lena’s Head Images
5. Conclusions
- (1)
- The local spatial information of the image and the typicality of the data item are used to improve the segmentation results and the kernel method is used to reduce the computation.
- (2)
- KBFWCM uses the membership filtering algorithm to exploit the local spatial constraint. Since noise points will have low compatibility in all clusters, the membership functions obtained by this algorithm more approach to the concept of typicality, making their impact on clustering negligible. Therefore, this algorithm is naturally more immune to noise.
- (3)
- This algorithm has additional advantages in calculation. It is a natural mechanism, assigning ’fuzzy labels’ to data in each iteration. Therefore, it can be used for more complex pattern recognition.
- (4)
- Experimental results show that the proposed KBFWCM can provide better segmentation results without adjusting parameters for different grayscale.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sghaier, G. A K-Means Clustering-Based Security Framework for Mobile Data Mining. Wirel. Commun. Mob. Comput. 2016, 16, 3449–3454. [Google Scholar]
- Subbalakshmi, C.; Ramakrishna, G.; Rao, S.K.M. Evaluation of Data Mining Strategies Using Fuzzy Clustering in Dynamic Environment. In Proceedings of the 3rd International Conference on Advanced Computing, Networking and Informatics, Orissa, India, 23–25 June 2016; pp. 529–536. [Google Scholar]
- Wan, L.; Zhang, T.; Xiang, Y.M. A Robust Fuzzy C-means Algorithm Based on Bayesian Nonlocal Spatial information for SAR Image Segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 896–906. [Google Scholar] [CrossRef]
- Gharieb, R.; Gendy, G.; Selim, H. A Hard CMeans Clustering Algorithm Incorporating Membership KL Divergence And Local Data Information for Noisy Image Segmentation. Int. J. Pattern Recognit. Artif. Intell. 2018, 32, 758–769. [Google Scholar] [CrossRef]
- Naz, S.; Majeed, H.; Irshad, H. Image segmentation using fuzzy clustering: A survey. In Proceedings of the IEEE International Conference on Emerging Technologies, Cagliari, Italy, 10–13 September 2013; Volume 2, pp. 2927–2929. [Google Scholar]
- Ouma, Y.O.; Hahn, M. Pothole Detection on Asphalt Pavements from 2D-Colour Pothole Images Using Fuzzy C-means Clustering and Morphological Reconstruction. Autom. Constr. 2017, 83, 196–211. [Google Scholar] [CrossRef]
- Baraldi, A.; Blonda, P. A survey of fuzzy clustering algorithms for pattern recognition I. IEEE Syst. Man Cybern. Soc. 1999, 29, 778–785. [Google Scholar] [CrossRef] [PubMed]
- Shabia, S.K.; Quadri, S.M.K. Structure Identification and IO Space Partitioning In a Nonlinear Fuzzy System for Prediction of Patient Survival after Surgery. Int. J. Intell. Comput. Cybern. 2017, 10, 166–182. [Google Scholar]
- Huang, H.C.; Chuang, Y.Y.; Chen, C.S. Multiple Kernel Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2012, 20, 120–134. [Google Scholar] [CrossRef]
- Masulli, F.; Rovetta, S. Soft Transition from Probabilistic to Possibilistic Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2006, 14, 516–527. [Google Scholar] [CrossRef]
- Cao, H.; Deng, H.W.; Wang, Y.P. Segmentation of M-FISH Images for Improved Classification of Chromosomes with an Adaptive Fuzzy C-means Clustering Algorithm. IEEE Trans. Fuzzy Syst. 2012, 20, 1–8. [Google Scholar] [CrossRef]
- Javed, A.; Kim, Y.C.; Khoo, M.C.K.; Ward, S.L.D.; Nayak, K.S. Dynamic 3D MR Visualization and Detection of upper Airway Obstruction during Sleep Using Region Growing Segmentation. IEEE Trans. Biomed. Eng. 2016, 63, 431–437. [Google Scholar] [CrossRef]
- Grau, V.; Mewes, A.U.J.; Alcaniz, M.; Kikinis, R.; Warfield, S.K. Improved Watershed Transform for Medical Image Segmentation Using Prior Information. IEEE Trans. Med. Imaging 2004, 23, 447–458. [Google Scholar] [CrossRef] [PubMed]
- Gong, M.; Li, H.; Zhang, X.; Zhao, Q.; Wang, B. Nonparametric Statistical Active Contour Based on Inclusion Degree of Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2016, 24, 1176–1192. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean Shift: A Robust Approach toward Feature Space Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Mahapatra, D. Semi-Supervised Learning and Graph Cuts for Consensus Based Medical Image Segmentation. Pattern Recognit. 2017, 5, 700–709. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J. Super pixel Segmentation Using Linear Spectral Clustering. In Proceedings of the IEEE Conference Computer Vision Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; Volume 10, pp. 1356–1363. [Google Scholar]
- Chatzis, S.P.; Varvarigou, T.A. A Fuzzy Clustering Approach Toward Hidden Markov Random Field Models for Enhanced Spatially Constrained Image Segmentation. IEEE Trans. Fuzzy Syst. 2008, 16, 1351–1361. [Google Scholar] [CrossRef]
- Pathak, D.; Krahenbuhl, P.; Darrell, T. Constrained Convolutional Neural Networks for Weakly Supervised Segmentation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, USA, 7–13 December 2015; pp. 2380–7504. [Google Scholar]
- Wang, B.; Tu, Z. Affinity Learning via Self-Diffusion for Image Segmentation and Clustering. In Proceedings of the IEEE Conference Computer Vision Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2312–2319. [Google Scholar]
- Kim, S.; Yoo, C.D.; Nowozin, S.; Kohli, P. Image Segmentation Using Higher-Order Correlation Clustering. IEEE Trans. Pattern Anal. Mach. Intel. 2014, 36, 1761–1774. [Google Scholar] [CrossRef] [PubMed]
- Pont-Tuset, J.; Arbelaez, P.; Barron, J.; Marques, F.; Malik, J. Multiscale Combinatorial Grouping for Image Segmentation and Object Proposal Generation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 128–140. [Google Scholar] [CrossRef] [PubMed]
- Hasnat, M.A.; Alata, O. Joint Color- Spatial-Directional Clustering and Region Merging (JCSDRM) for Unsupervised RGB-D Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2255–2268. [Google Scholar] [CrossRef]
- Bampis, C.G.; Maragos, P.; Bovik, A.C. Graph-Driven Diffusion and Random Walk Schemes for Image Segmentation. IEEE Trans. Image Process. 2017, 26, 35–50. [Google Scholar] [CrossRef]
- Saha, P.K.; Basu, S.; Hoffman, E.A. Multiscale Opening of Conjoined Fuzzy Objects: Theory and Applications. IEEE Trans. Fuzzy Syst. 2016, 24, 1121–1133. [Google Scholar] [CrossRef]
- Dunnt, J.C. Well-Separated Clusters and Optimal Fuzzy Partitions. J. Cybern. 2008, 4, 95–104. [Google Scholar]
- Dunn, J.C. A fuzzy relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Dunnt, J.C. Some Recent Investigations of a New Fuzzy Partitioning Algorithm and Its Application to Pattern Classification Problems. J. Cybern. 1974, 4, 1–15. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Gitman, I.; Levine, M.D. An Algorithm for Detecting Unimodal Fuzzy Sets and Its Application as a Clustering Technique. IEEE Comput. Soc. 1970, 100, 583–593. [Google Scholar] [CrossRef]
- Bezdek, J.C. Cluster Validity with Fuzzy Sets. J. Cybern. 1974, 3, 58–73. [Google Scholar] [CrossRef]
- Bezdek, J.C. Numerical Taxonomy with Fuzzy Sets. J. Math. Biol. 1974, 10, 57–71. [Google Scholar] [CrossRef]
- Bezdek, J.C. Convex Decompositions of Fuzzy Partitions. J. Math. Anal. Appl. 1979, 10, 490–512. [Google Scholar] [CrossRef]
- Bezdek, J.C. A Convergence Theorem for the Fuzzy C-means Clustering Algorithms. IEEE Trans. PAMI 1980, 2, 1–8. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms. Adv. Appl. Pattern Recognit. 1981, 22, 203–239. [Google Scholar]
- Bezdek, J.C.; Trivedi, M.; Ehrlich, R.; Full, W. Fuzzy Clustering: A New Approach for Geostatistical Analysis. Syst. Meas. Decis. 1982, 10, 142–149. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The Fuzzy C-means Clustering Algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Pal, N.; Bezdek, J. On cluster validity for the fuzzy c-means model. IEEE Trans. Fuzzy Syst. 1995, 3, 370–379. [Google Scholar] [CrossRef]
- Gong, M.; Su, L.; Jia, M.; Chen, W. Fuzzy Clustering With a Modified MRF Energy Function for Change Detection in Synthetic Aperture Radar Images. IEEE Trans. Fuzzy Syst. 2014, 22, 98–109. [Google Scholar] [CrossRef]
- Chiang, I.J.; Liu, C.H.; Tsai, Y.H.; Kumar, A. Discovering Latent Semantics in Web Documents using Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2015, 23, 2122–2134. [Google Scholar] [CrossRef]
- Nguyen, T.; Wu, J. Online feature selection based on fuzzy clustering and its applications. IEEE Trans. Fuzzy Syst. 2016, 24, 1294–1306. [Google Scholar] [CrossRef]
- Hu, L.; Chan, K.C. Fuzzy clustering in a complex network based on content relevance and link structures. IEEE Trans. Fuzzy Syst. 2016, 24, 456–470. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J.M. A possibilistic approach to clustering. IEEE Trans. Fuzzy Syst. 1993, 1, 98–110. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J.M. The possibilistic C-means algorithm: Insights and recommendations. IEEE Trans. Fuzzy Syst. 1996, 4, 385–393. [Google Scholar] [CrossRef]
- Pal, N.R.; Pal, K.; Bezdek, J.C. A mixed C-means clustering model. In Proceedings of the IEEE International Conference on Fuzzy Systems, Barcelona, Spain, 5– July 1997; Volume 1, pp. 11–21. [Google Scholar]
- Pal, N.R.; Pal, K.; Keller, J.M.; Bezdek, J.C. A Possibilistic Fuzzy C-means Clustering Algorithm. IEEE Trans. Fuzzy Syst. 2005, 13, 517–530. [Google Scholar] [CrossRef]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters Department of Theoretical and Applied Mechanics. J. Cybern. 1974, 3, 32–57. [Google Scholar] [CrossRef]
- Tolias, Y.A.; Panas, S.M. Image Segmentation by a Fuzzy Clustering Algorithm Using Adaptive Spatially Constrained Membership Functions. IEEE Trans. SMC-PART A 1998, 28, 359–369. [Google Scholar] [CrossRef]
- Ahmed, M.N.; Yamany, S.M.; Mohamed, N.; Farag, A.A.; Moriarty, T. A Modified Fuzzy C-means Algorithm for Bias Field Estimation and Segmentation of MRI Data. IEEE Trans. Med. Imaging 2002, 21, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Pham, D.L. Spatial Models for Fuzzy Clustering. Comput. Vis. Image Underst. 2001, 84, 295–297. [Google Scholar] [CrossRef]
- Liew, A.W.C.; Leung, S.H.; Lau, W.H. Fuzzy Image Clustering Incorporating Spatial Continuity. IEEE Proc. Vis. Image Signal Process. 2000, 147, 185–192. [Google Scholar] [CrossRef]
- Chuang, K.; Tzeng, H.; Chen, S.; Wu, J.; Chen, T.J. Fuzzy c-means clustering with spatial information for image segmentation. Comput. Med. Imaging Graph. 2006, 30, 9–15. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, D. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 1907–1916. [Google Scholar] [CrossRef]
- Szilagyi, L.; Benyo, Z.; Szilagyi, S.M.; Adam, H.S. MR Brain Image Segmentation Using an Enhanced Fuzzy CMeans Algorithm. In Proceedings of the International Conference of the IEEE Engineering in Medicine & Biology Society, Milano, Italy, 25–29 August 2003; Volume 10, pp. 724–726. [Google Scholar]
- Cai, W.L.; Chen, S.C.; Zhang, D.Q. Fast And Robust Fuzzy C-means Clustering Algorithms Incorporating Local Information For Image Segmentation. Pattern Recognit. 2007, 40, 825–838. [Google Scholar] [CrossRef]
- Hathaway, R.J.; Bezdek, J.C.; Hu, Y.H.Y. Generalized fuzzy c-means clustering strategies using Lp norm distances. IEEE Trans. Fuzzy Syst. 2000, 8, 576–582. [Google Scholar] [CrossRef]
- Zhu, L.; Chung, F.L.; Wang, S. Generalized Fuzzy C-Means Clustering Algorithm With Improved Fuzzy Partitions. J. Comput. Res. Dev. 2009, 39, 578–591. [Google Scholar]
- Crammer, K.; Singer, Y. On the Algorithmic Implementation of Multiclass Kernel-based Vector Machines. J. Mach. Learn. Res. 2002, 2, 265–292. [Google Scholar]
- Yang, X.; Zhang, G.; Lu, J.; Ma, J. A Kernel Fuzzy c-Means Clustering-Based Fuzzy Support Vector Machine Algorithm for Classification Problems With Outliers or Noises. IEEE Trans. Fuzzy Syst. 2014, 10, 105–115. [Google Scholar] [CrossRef]
- Zhao, F.; Jiao, L.; Liu, H. Kernel generalized fuzzy C-means clustering with spatial information for image segmentation. Digit. Signal Process 2013, 23, 184–199. [Google Scholar] [CrossRef]
- Yang, M.S.; Tsai, H.S. A Gaussian Kernel-Based Fuzzy C-means Algorithm with a Spatial Bias Correction. Pattern Recognit. Lett. 2008, 29, 1713–1725. [Google Scholar] [CrossRef]
- Wang, J.Z.; Kong, J.; Lu, Y.H.; Qi, M.; Zhang, B.A. Modified FCM Algorithm for MRI Brain Image Segmentation Using Both Local and Non-Local Spatial Constraints. Comput. Med. Imaging Graph. 2008, 32, 685–698. [Google Scholar] [CrossRef] [PubMed]
- Krinidis, S.; Chatzis, V. A Robust Fuzzy Local Information C-means Clustering Algorithm. IEEE Trans. Image Process. 2010, 19, 1328–1337. [Google Scholar] [CrossRef]
- Gong, M.; Zhou, Z.; Ma, J. Change Detection in Synthetic Aperture Radar Images Based on Image Fusion and Fuzzy Clustering. IEEE Trans. Image Process. 2012, 21, 2141–2151. [Google Scholar] [CrossRef]
- Elazab, A.; Wang, C.; Jia, F.; Wu, J.; Li, G.; Hu, Q. Segmentation of Brain Tissues from Magnetic Resonance Images Using Adaptively Regularized Kernel-Based Fuzzy C-Means Clustering. Comput. Math. Methods Med. 2015, 5, 1–12. [Google Scholar] [CrossRef]
- Lei, T.; Jia, X.; Zhang, Y.; He, L.; Meng, H.; Nandi, A.K. Significantly Fast and Robust Fuzzy C-means Clustering Algorithm Based on Morphological Reconstruction and Membership Filtering. IEEE Trans. Fuzzy Syst. 2018, 26, 3027–3041. [Google Scholar] [CrossRef]
- Saranathan, A.M.; Parente, M. Uniformity-Based Superpixel Segmentation of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1419–1430. [Google Scholar] [CrossRef]
- Zhao, Z.; Lizhi, C.; Guangquan, C. Neighbourhood Weighted Fuzzy C-means Clustering Algorithm for Image Segmentation. IET Image Process. 2014, 8, 150–161. [Google Scholar]
- Guo, F.; Wang, X.; Shen, J. Adaptive Fuzzy C-means Algorithm Based on Local Noise Detecting for Image Segmentation. IET Image Process. 2016, 10, 272–279. [Google Scholar] [CrossRef]
- Jacek, M.L. Fuzzy C-Ordered Means Clustering. Fuzzy Sets Syst. 2016, 10, 114–133. [Google Scholar]
- Huber, P.J. Robust Covariance and Correlation Matrices. In Robust Statistics; Wiley: New York, NY, USA, 1981; pp. 199–204. [Google Scholar]
- Yager, R.R. On Ordered Weighted Averaging Aggregation Operators in Multicriteria Decision Making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Krzysztof, S. Fuzzy Weighted C-Ordered Means Clustering Algorithm. Fuzzy Sets Syst. 2017, 318, 1–33. [Google Scholar]
- Muller, K.R.; Mika, S. An introduction to kernel-based learning algorithms. IEEE Trans. Neural Netw. 2001, 12, 181–202. [Google Scholar] [CrossRef] [PubMed]
- Cristianini, N.L. 3-Kernel-Induced Feature Spaces. In Support Vector Machines; Taylor, J.S., Ed.; Cambridge University: London, UK, 2013; pp. 26–51. [Google Scholar]
- Vapnik, V.N. Support Vector Learning Machines. In Statistical Learning Theory; Simon, H., Ed.; Wiley: New York, NY, USA, 1998; pp. 375–380. [Google Scholar]
- Scholkopf, B.L. Incorporating invariances in support vector learning machines. In Artificial Neural Networks-ICANN 96; Scholkopf, B., Burges, C., Vapnik, V., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 47–52. [Google Scholar]
- Volker, R.; Volker, S.L. Nonlinear Discriminant Analysis Using Kernel Functions. In Advances Neural Information Processing Systems 12; Solla, S.A.F., Leen, T.K., Muller, K.R., Eds.; MIT Press: Cambridge, MA, USA, 2000; pp. 568–574. [Google Scholar]
- Scholkopf, B.; Smola, A.; Muller, K.-R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Chen, J.H.; Chen, C.S. Fuzzy kernel perceptron. EEE Trans. Neural Netw. 2002, 13, 1364–1373. [Google Scholar] [CrossRef] [PubMed]
- Girolami, M. Mercer kernel-based clustering in feature space. IEEE Trans. Neural Netw. 2002, 10, 780–784. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Chen, S.C. Fuzzy clustering using kernel methods. In Proceedings of the International Conference Control Automation, Xiamen, China, 19 June 2002; Volume 10, pp. 123–127. [Google Scholar]
- Zhang, D.Q.; Chen, S.C. Clustering Incomplete Data Using Kernel-Based Fuzzy C-means Algorithm. Neural Process. Lett. 2003, 18, 155–162. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawetaylor, J. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods. Kybernetes 2001, 32, 1–28. [Google Scholar]
- Bernhard, S. Kernel Principal Component Analysis. In Advances in Kernel Methods-Support Vector Learning; Christopher, J.C., Alexauder, J.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 327–373. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 10, pp. 67–75. [Google Scholar]
- Wu, Z.D.; Xie, W.X.; Yu, J.P. Fuzzy C-means Clustering Algorithm based on Kernel Method. In Proceedings of the 15th International Conference on Computational Intelligence and Multimedia Applications, Las Vegas, NV, USA, 16–18 August 2003; Volume 10, pp. 49–54. [Google Scholar]
- Wu, K.L.; Yang, M.S. Alternative C-means clustering algorithms. Pattern Recognit. 2002, 35, 2267–2278. [Google Scholar] [CrossRef]
- Mathworks, N.M. Image Processing Toolbox. Available online: http://www.mathworks.Com (accessed on 4 June 2017).
- Sanjith, S. Fusion of DWT-DCT algorithm for satellite image compression. Int. J. Appl. Eng. Res. 2015, 10, 130–137. [Google Scholar]
- Sanjith, S.; Ganesan, R.; Rimal, I.R.S. Experimental Analysis of Compacted Satellite Image Quality Using Different Compression Methods. Adv. Sci. Eng. Med. 2015, 7, 227–233. [Google Scholar] [CrossRef]
- Cavouras, D.; Kandarakis, I.; Kanellopoulos, M.; Nomicos, C.D.; Panayiotakis, G.S. Signal-to-noise-ratio (SNR) of X-ray imaging scintillators determined by luminescence measurements. Appl. Radiat. Isot. 1999, 51, 59–68. [Google Scholar] [CrossRef]
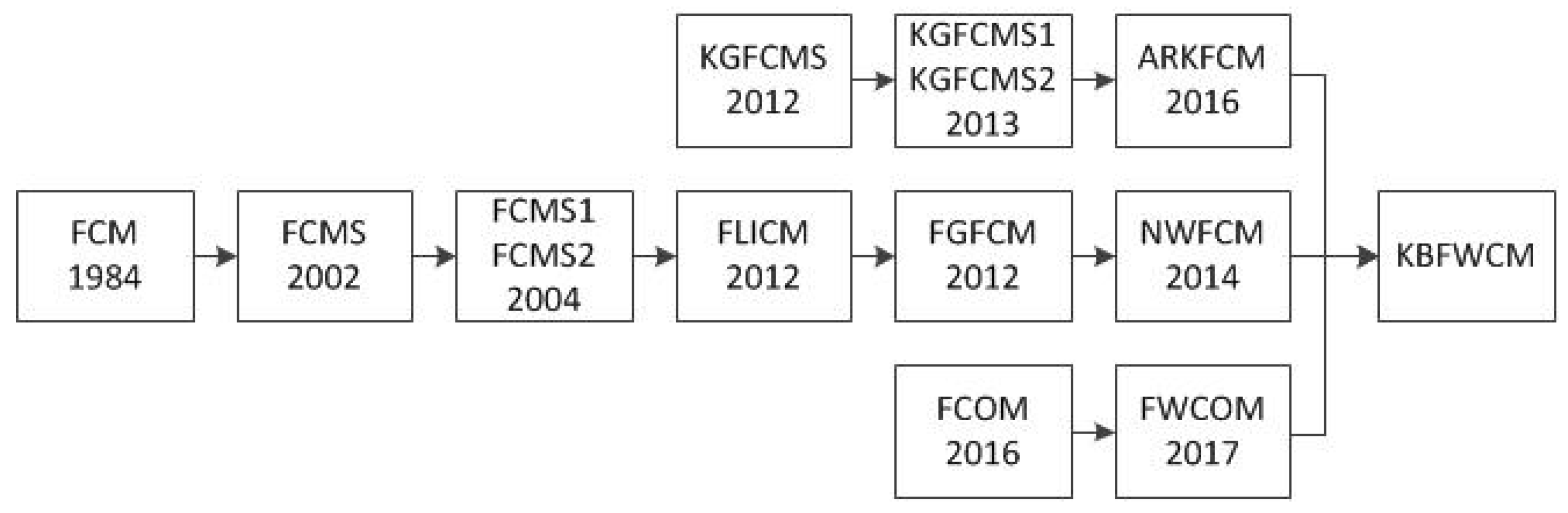
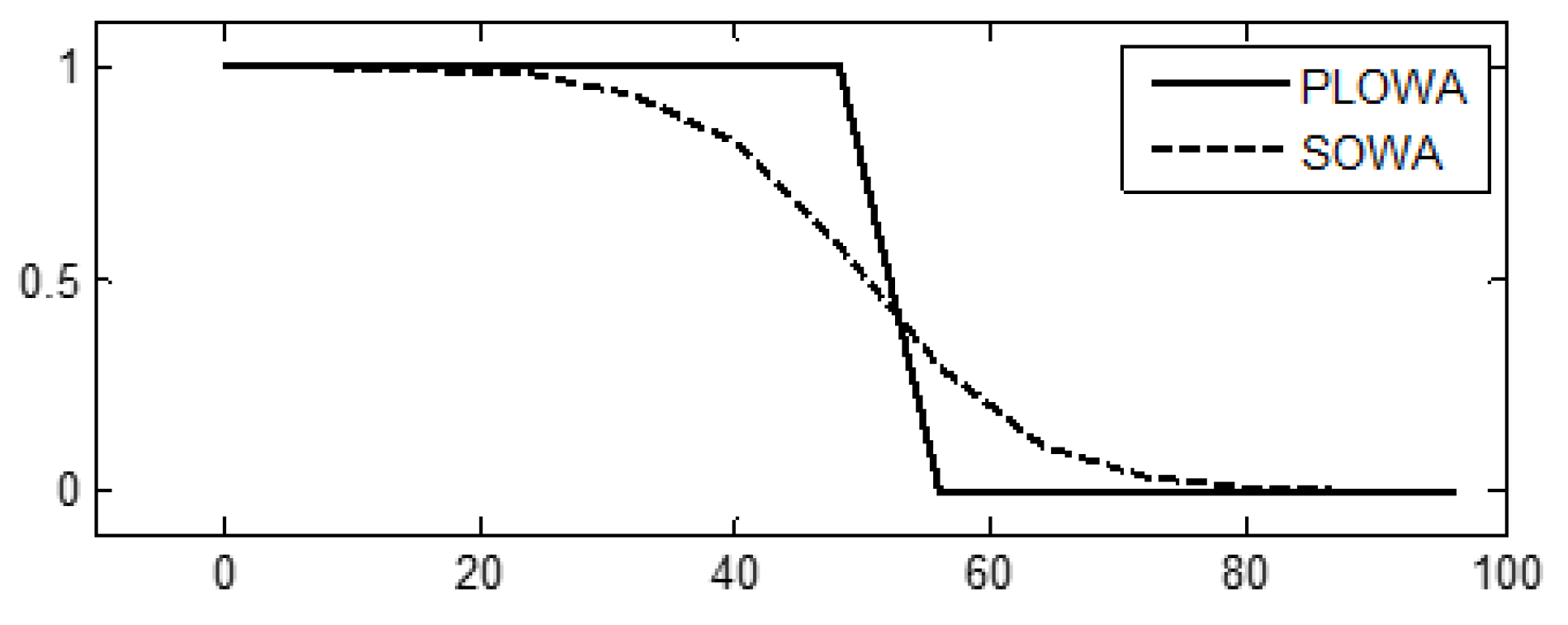
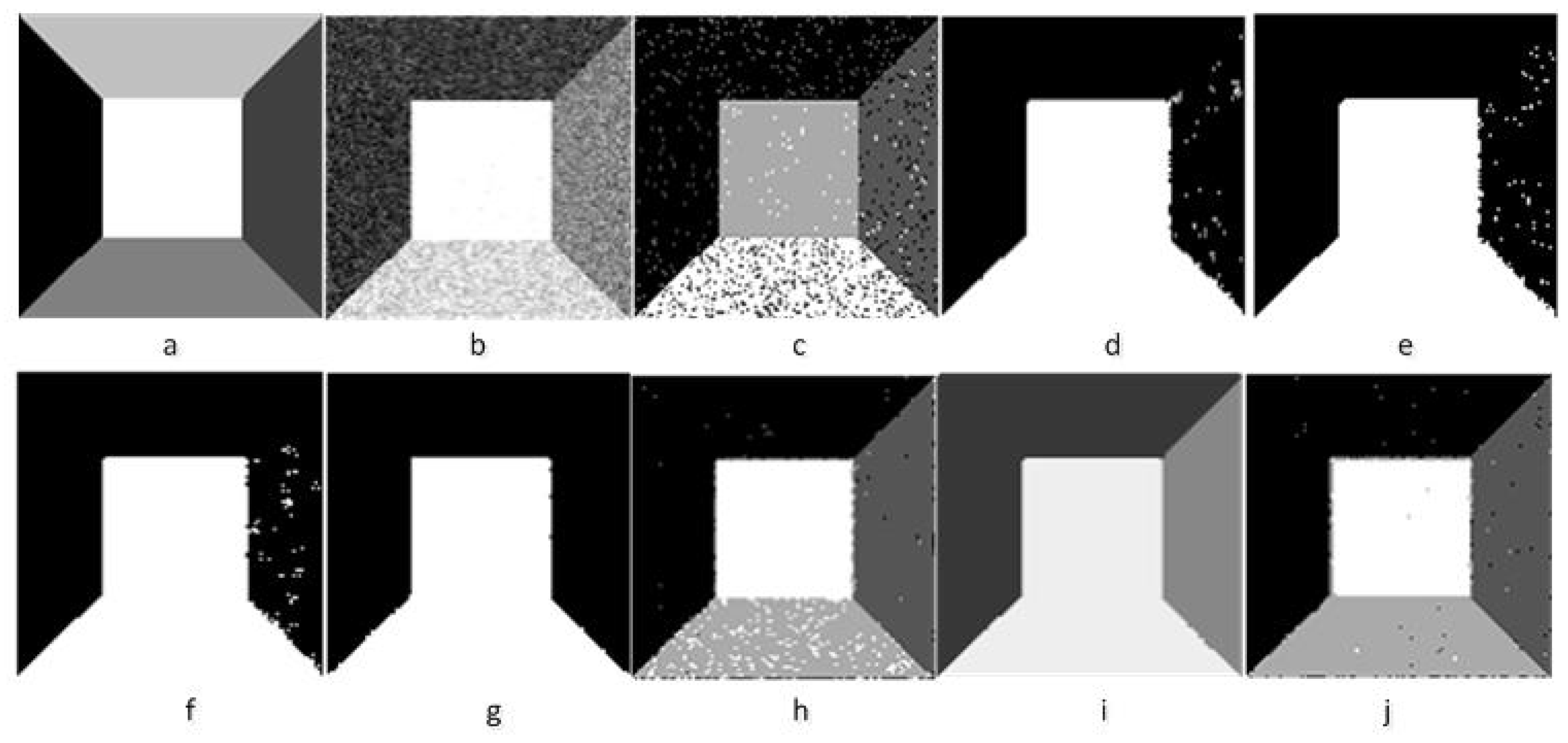

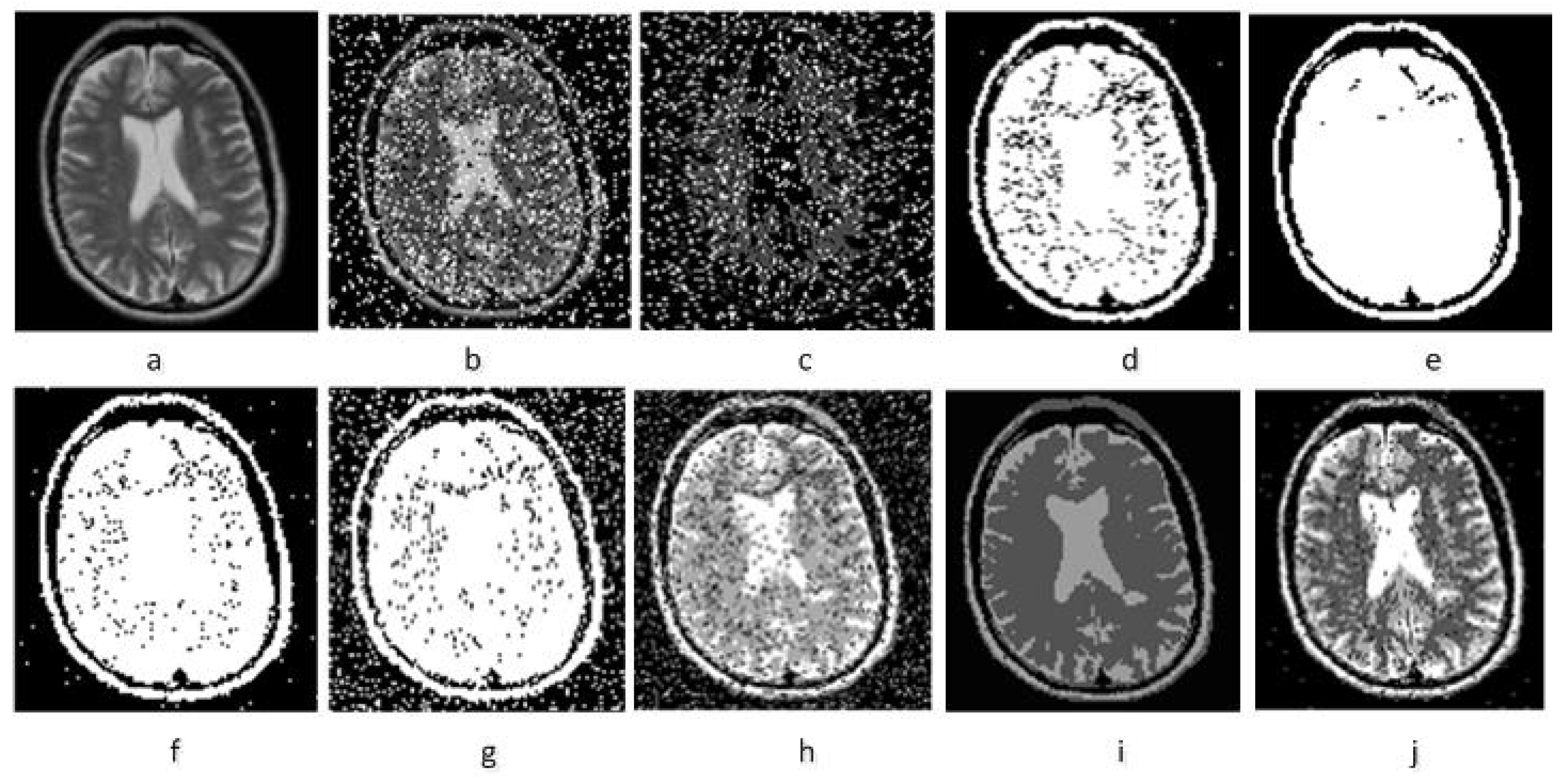

| Algorithm Name | Abbreviation | Objective Function | Time |
|---|---|---|---|
| Fuzzy C-Means [37] | FCM | 1984 | |
| FCM with spatial constraints [49] | FCMS | 2002 | |
| Enhanced FCM [54] | EnFCM | 2003 | |
| Two variants of FCMS [53] | FCMS1 FCMS2 | 2004 | |
| Spatial FCM [52] | SFCM | 2006 | |
| Fuzzy Local Information C-Means [64] | FLICM | 2012 | |
| Two Kernel variants of GIFPFCM [60] | KGFCMS1 KGFCMS2 | 2013 | |
| New Weighted Fuzzy C-Means [68] | NWFCM | 2014 | |
| Adaptively Regularized Kernel-based FCM [69] | ARKFCM | 2016 | |
| Fuzzy C-Ordered-Means [70] | FCOM | 2016 | |
| Fuzzy weighted C-ordered-means [73] | FWCOM | 2017 | |
| Reconstruction and membership Filtering FCM [66] | FRFCM | 2018 |
| Algorithm | Misclassification Numbers | CER | Clustering Center | DD |
|---|---|---|---|---|
| FCM | 16 | 10.7% | 0.081 | |
| FCMS | 10 | 6.7% | 0.063 | |
| KFCMS | 9 | 6% | 0.057 | |
| FWCOM | 8 | 5.3% | 0.049 | |
| ARKFCM | 7 | 4.7% | 0.046 | |
| FRFCM | 5 | 3.3% | 0.037 | |
| KBFWCM | 5 | 3.3% | 0.035 |
| Algorithm | = 10 | = 20 | = 25 | Salt & Pepper (5%) | Salt & Pepper (10%) | Salt & Pepper (20%) |
|---|---|---|---|---|---|---|
| KFCM | 85.94 | 86.16 | 85.34 | 92.71 | 93.41 | 95.35 |
| KFCMS1 | 86.07 | 86.17 | 87.05 | 93.68 | 94.56 | 95.78 |
| KFCMS2 | 89.15 | 87.40 | 86.44 | 94.68 | 95.85 | 94.89 |
| KGFCMS | 71.50 | 94.74 | 94.90 | 98.84 | 96.97 | 99.32 |
| FLICM | 96.64 | 96.64 | 96.64 | 97.34 | 96.44 | 97.28 |
| ARKFCM | 93.17 | 93.17 | 93.17 | 94.23 | 95.84 | 97.84 |
| FRFCM | 97.84 | 98.78 | 96.97 | 95.96 | 96.94 | 97.92 |
| KBFWCM | 98.91 | 98.93 | 97.86 | 98.35 | 97.77 | 97.98 |
| Denosing Method | MSE | MSE | PSNR/db | SNR/db |
|---|---|---|---|---|
| Image with noise | 640.5461 | 100 | 20.0653 | 13.4480 |
| KFCM | 138.6119 | 21.64 | 26.7128 | 21.0557 |
| KFCMS1 | 179.6752 | 28.05 | 26.1314 | 20.0553 |
| KFCMS2 | 182.4737 | 28.49 | 25.5188 | 19.8616 |
| KGFCMS | 105.4836 | 16.47 | 26.0125 | 20.6052 |
| FLICM | 107.1739 | 16.73 | 26.1670 | 20.5099 |
| ARKFCM | 91.4922 | 14.28 | 28.8986 | 22.2414 |
| FRRCM | 67.5066 | 10.54 | 29.5425 | 23.8853 |
| KBFWCM | 54.9023 | 8.53 | 31.5349 | 24.6808 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Guo, X.; Huang, T.; Liu, J.; Chen, J. Kernel-Based Robust Bias-Correction Fuzzy Weighted C-Ordered-Means Clustering Algorithm. Symmetry 2019, 11, 753. https://doi.org/10.3390/sym11060753
Zhang W, Guo X, Huang T, Liu J, Chen J. Kernel-Based Robust Bias-Correction Fuzzy Weighted C-Ordered-Means Clustering Algorithm. Symmetry. 2019; 11(6):753. https://doi.org/10.3390/sym11060753
Chicago/Turabian StyleZhang, Wenyuan, Xijuan Guo, Tianyu Huang, Jiale Liu, and Jun Chen. 2019. "Kernel-Based Robust Bias-Correction Fuzzy Weighted C-Ordered-Means Clustering Algorithm" Symmetry 11, no. 6: 753. https://doi.org/10.3390/sym11060753
APA StyleZhang, W., Guo, X., Huang, T., Liu, J., & Chen, J. (2019). Kernel-Based Robust Bias-Correction Fuzzy Weighted C-Ordered-Means Clustering Algorithm. Symmetry, 11(6), 753. https://doi.org/10.3390/sym11060753





