Abstract
By using sample units (SUs), the generalized data envelopment analysis (DEA) method can evaluate the efficiency of decision making unit (DMU) through different reference sets, but the existing models are radial models, and the DMU is treated as a black box, rarely taking the operations of the internal divisions into account. This paper proposes a generalized network slacks-based measure (SBM) approach based on the SUs. First, the generalized network SBM approach for a basic two-stage structure is proposed. This paper considers the intermediate products in calculating the divisional efficiency for each DMU. Overall efficiency of DMU is a weighted average of the divisional efficiency. The weight of each division does not need to be given in advance. Since the DMUs set and SUs set are not necessarily the same, this paper proposes an improved generalized network SBM approach for a basic two-stage structure to solve the problem that the original model may be infeasible. Then, the approach for basic two-stage structure is extended to general multi-stage structure. Finally, an example is given to show the practicability of the generalized network SBM approach.
1. Introduction
Data envelopment analysis (DEA) as proposed by Charnes, Cooper, and Rhodes [1], is an approach for measuring the relative efficiency of a set of homogenous decision making units (DMUs) with multiple inputs and multiple outputs [2]. There are many theoretical developments and practical applications being reported (see, for example, the review of Zhou et al. [3]; Liu et al. [4]; Kao [5]; Sueyoshi et al. [6]; Emrouznejad et al. [7]).
In traditional DEA approaches, DMUs are treated as a whole unit, or a black box, and only the inputs supplied from the outside and the outputs sent to the outside are considered in measuring efficiency, ignoring the intermediate products produced and consumed within the system, without taking the operations of the internal divisions into account [8]. There are two major drawback of this; one is that inefficiencies arising from the organization of activities within this internal structure cannot be addressed, which limits the amount information that can be gained to improve the system efficiency [9], and the other is that this may produce misleading results, for example, the system is efficient, while the component divisions are not.
The early papers that discussed the component stages of DMU are Färe and Grosskopf [10] and Wang et al. [11]. Färe and Grosskopf [12] firstly proposed network DEA which considers multi-stage processes with inputs, outputs, and intermediate measures that connect the internal components of DMUs [13]. To measure the efficiency of the DMU more appropriately, several models for measuring the overall efficiency and divisional efficiency of a network have been proposed. Every study on network DEA is associated with a structure, based on which a model for measuring efficiency is developed, and an application to real world problems is carried out [5]. The existing network structures include basic two-stage structure, general two-stage structure, series structure, parallel structure, mixed structure, and dynamic structure.
Most of the studies concentrate on the basic two-stage structure which is a closed system, where the outputs from the first stage become the inputs to the second stage, and where no other inputs enter the process at the second stage. Based on the basic two-stage structure, several studies measured the overall and divisional efficiency, and also derived mathematical relationships between overall efficiency and divisional efficiency. In modeling two-stage network DEA from the efficiency decomposition perspective, both multiplicative efficiency decomposition and additive efficiency decomposition are proposed depending on the variations of two-stage structures and assumptions of constant returns to scale and variable returns to scale [14]. Kao and Hwang [15] developed a relational model which is able to decompose the overall efficiency into the product of the two divisional efficiencies under the assumption of constant returns to scale. Based on this work, Liang et al. [16] developed multiplicative efficiency decomposition using the game theory concept. Based on multiplicative efficiency decomposition, studies have been carried out. For example, Chen et al. [17], Zha and Liang [18], and Du et al. [19] defined the overall efficiency as the product of divisional efficiency. Different from the multiplicative efficiency decomposition, Chen et al. [20] decomposed the overall efficiency into a weighted average of the two divisional efficiencies, where the constant returns to scale was not required. This is additive efficiency decomposition. However, additive efficiency decomposition has its own computational issues as demonstrated by Guo et al. [13]. Chen et al [14] showed that additive efficiency decomposition can be solved using second order cone programming. Hundreds of papers that apply basic two-stage network DEA models to solve real world problems have been published. For example, Luo [21] examined the performance of the 245 banks in the US with assets greater than one billion US dollars, where the operations of a bank are divided into two stage to measure profitability and marketability. Based on the above network DEA approach, Lo et al. [22] studied US S&P 500 firms; Tsolas [23] discussed 19 construction firms in Greece; Yang et al. [24] integrated a two-stage series performance model and fuzzy multi-objective model to measure managerial efficiency in Taiwan bank branches. Based on the relational model proposed by Kao and Hwang [15], Cao and Yang [25] measured the marketability and profitability of 40 internet companies; Chen et al. [26] evaluated the design performance of 534 carlines from more than 20 manufacturers that aim to have lower environmental impacts.
While the basic two-stage structure does exist, the more prevalent case is that where both stages are allowed to consume exogenous inputs and to produce exogenous outputs. This structure is general network structure which is open system. Li et al. [27] extended Liang et al. [16] by assuming that the inputs to the second stage include both the outputs from the first stage and additional inputs to the second stage. Cook et al. [28] extended the methodology of Chen et al. [20] to general multi-stage network structures, which is applicable under the assumption of constant returns to scale and variable returns to scale, but it is biased towards the second division when setting the weight. Despotis et al. [29] proposed a new method to calculate the overall efficiency of the system, ensuring the uniqueness of the efficiency value and the unbiasedness of weight setting. Ang et al. [30] extended this method to the general two-stage network structure and multi-stage structure. Kao [31] proposed two approaches for discussing the relationship between overall efficiency and divisional efficiency, and developed a relational model from the perspective of efficiency decomposition. For a parallel system of several processes, Kao [32] developed a relational model to decompose the system efficiency into a weighted average of the process efficiencies under the assumption of constant returns to scale. The general two-stage network DEA is also widely used. For example, Yang [33] studied a problem of farrow-to-finish swine production; Simon et al. [34] analyzed the productivity growth of 34 Spanish university libraries using Malmquist productivity index.
All of these studies are based on radial efficiency measures, which assume that all inputs or outputs change proportionally. To solve this problem, Tone [35] proposed a slacks-based measure (SBM) approach to measure the efficiency. Tone and Tsutsui [36,37] then extended this to general network structure and dynamic structure. Compared with the traditional SBM model, the network SBM is better in identifying the effectiveness of DMUs. However, the slack variables of intermediate products are not taken into account when calculating the overall and divisional efficiency of DMU. Fukuyama et al. [38] proposed an improved two-stage network SBM, which includes the slack variables of intermediate products in the formula for calculating the overall efficiency of DMU, but the weight of each division in the formula needs to be given in advance according to its importance to DMU. Kao [39] proposed a general SBM model for network systems, and decomposed the overall efficiency into a weighted average of the divisional efficiencies. The weight of each division in the formula does not need specified beforehand. This relationship holds for all types of network structure. Kao [8] proposed different ways to study the intermediate products that link the component divisions based on the production possibility set. Chen et al. [9] developed both envelopment-based and multiplier-based models to obtain simultaneously both the frontier projection and the efficiency decomposition based on SBM. Kao [40] proposed an SBM model to decompose the system efficiency of a closed series system into the product of the division efficiencies divided by the linkage efficiencies, which are expressed as the product of the efficiencies of the intermediate product. Network SBM has been widely used in environmental efficiency, airline efficiency, and efficiency of the waste sector, etc. since it was proposed. For example, Lozano [41], Bian et al. [42], Simoes and Marques [43], Zhou et al. [44], Li et al. [45], Zhu et al. [46], and Wang et al. [47].
The above studies are evaluation methods based on a self-assessment system, in which the evaluated DMU can only be compared with efficient DMUs among its peers, and the decision maker cannot choose the reference set freely. However, in reality, there are many evaluation problems, and the objects that the DMU need to compare are not efficient DMUs among its peers; for instance, they might use specified special units or standard units as comparison objects. In light of these issues, Ma [48] proposed a generalized DEA approach based on sample units (SUs). The generalized DEA not only has all the properties of traditional DEA, but also can evaluate DMUs according to any reference set. The reference set can be composed by the DMUs themselves or the SUs. The SUs can be specific DMUs, such as standards or objects that the decision maker is interested in. Muren [49] proposed a generalized fuzzy DEA method along this idea.
The generalized DEA method can provide multiple perspectives for decision makers to measure the efficiency of DMUs. However, the existing generalized DEA models are basically radial models, and the DMUs are regarded as a black box, and the internal structure of system and relevance of divisions are rarely studied. In this paper, we develop a generalized network SBM approach based on SUs. This approach can measure the overall efficiency and divisional efficiency through different reference sets under assumptions of constant returns to scale and variable returns to scale. We consider the intermediate products in calculating the divisional efficiency for each DMU. Moreover, the overall efficiency is a weighted average of the divisional efficiency.
This paper is organized as follows. In Section 2, the basic SBM model is briefly reviewed. In Section 3, the generalized network SBM approach for basic two-stage structure is proposed. This paper considers the intermediate products in calculating the divisional efficiency for each DMU. Overall efficiency of DMU is a weighted average of the divisional efficiency. Since the DMUs set and SUs set are not necessarily the same, an improved generalized network SBM model for basic two-stage structure is proposed, then the relationship between overall and divisional efficiency is derived. In Section 4, a generalized network SBM approach for general multi-stage structure is proposed. Numerical examples are demonstrated in Section 5. Finally, some concluding remarks are made in Section 6.
2. The Slacks-Based Measure Model
Suppose there are n DMUs. Each DMU has m inputs and s outputs. Let , where denotes the ith input of DMU j, , where denotes the rth output of DMU j. Assume that all data are positive, i.e., for all possible , , and .
The production possibility set P is defined as
Tone [35] proposed the SBM model to evaluate the efficiency of DMU ,
The left-hand sides of the constraints in the SBM model form the efficient frontier of the model. The objective function in SBM is a function of input and output slacks that would otherwise be neglected in the classical DEA model. The SBM efficiency score is bounded between zero and one, and the lower the score, the lower the relative efficiency [35]. This paper will use a superscript “*” to denote the optimal solution value of a variable in the SBM model.
The SBM model is a fractional programming problem which can be transformed into a linear problem by using the Charnes–Cooper transformation (see Charnes et al. [1]). Refer to Tone [35] for details. Let the optimal solution of SBM be . Tone [35] defines that a DMU is SBM-efficient if . Equivalently, a DMU is SBM-efficient if for all i and r.
Tone and Tsutsui [36] proposed a network DEA with slacks-based measure to evaluate both divisional and overall efficiencies of DMUs.
3. The Generalized Network Slacks-Based Measure Approach for Basic Two-Stage Structure
The reference set in a traditional network SBM approach is the efficient DMUs. However, in reality, there are many evaluation problems, and the objects that the DMUs need to compare are not efficient ones, they might use specified special units or standard ones; for instance, in the transition from the planned economy of China to a market-oriented economy of China, the decision maker does not compare with efficient enterprise, but compare with the model of reform according to the market economy allocation. Based on the study in Ma [48], we propose the generalized network SBM approach. In the generalized network SBM approach, the reference set can be the efficient DMUs, normal DMUs, inefficient DMUs, special DMUs, or non-DMUs [49]. These five categories are called the sample units (SUs) (see Figure 1 [49]).
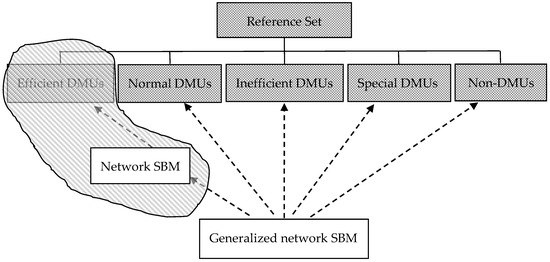
Figure 1.
The reference set of traditional network slacks-based measure (SBM) and generalized network SBM.
From the reference set of evaluation, Figure 1 illustrates that the perspective of generalized network SBM is different from that of a traditional network SBM when dealing with problems. In the traditional network SBM approach, the reference set is made of all the efficient DMUs. The decision maker can only get information which is compared with efficient DMUs. In the generalized network SBM approach, the decision maker can get more information by choosing the reference set freely. The objects to be compared are not only efficient DMUs, but also normal DMUs (such as the criterion for judging a university’s level of scientific research), inefficient DMUs, or special DMUs (such as the selected sample, standards or some specific objects).
Let A be DMUs set, B be the reference set (or SUs set). The relationship between DMUs set and SUs set in the generalized network SBM approach is shown in Figure 2.
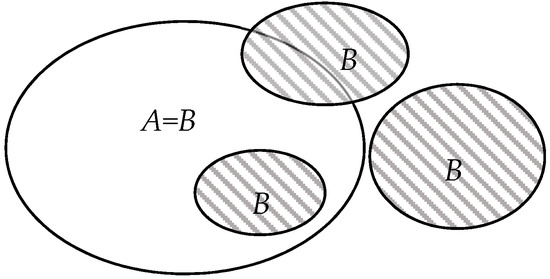
Figure 2.
The relationship between the decision making units (DMUs) set and sample units (SUs) set in generalized network SBM.
Consider the basic two-stage structure in Figure 3. We assume that there are n DMUs are observed, and there are SUs in the reference set. The DMUs and SUs have m inputs and s outputs, and contain two divisions. There are h intermediate products between two divisions.

Figure 3.
The basic two-stage structure.
DMU , . SU , . The Division 1 uses m exogenous inputs to produce h endogenous outputs (intermediate products) . The Division 2 treats as endogenous inputs to produce s exogenous outputs .
is the SUs set.
is the DMUs set. If , it was the self-evaluation system.
Kao [15] believes that there may be potential conflicts between the intermediate products of the two divisions. As shown in Figure 3, the Division 1 may need to increase intermediate outputs to improve its efficiency, but such an approach will increase the inputs of the Division 2, thus reducing the efficiency of the Division 2 [15]. For intermediate products, Tone and Tsutsui [36] proposed two cases. One is the free-link value case, and the other is the fixed link value case. To resolve this potential conflict between the two divisions, and to discuss the projection properties of the DMU, Chen et al. [9] proposed the variable intermediate measures SBM (VSBM) model. Intermediate measures is a variable, and can increase or decrease freely in the VSBM model.
According to the study of Chen et al. [9], and structural nature of the production possibility set in Tone and Tsutsui [36], the production possibility set of SUs is defined as
The parameter is a binary parameter which equals only 0 or 1. Here indicates constant returns to scale, while indicates variable returns to scale. is called the sample production possibility set.
Based on model in Chen et al. [9], and the sample production possibility set , we propose the generalized network SBM model for basic two-stage structure (hereinafter referred to as the G-BNSBM2 model), see model (4). Intermediate measures are variables.
The model (4) is fractional programming, which can be transformed into a linear programming problem by the Charnes–Cooper transformation [1]. Since the DMUs set and SUs set are not necessarily the same, the model (4) may not have a feasible solution.
When the model (4) has a feasible solution, this paper will use a superscript “*” to denote the optimal solution value of a variable in model (4). The optimal solution of model (4) is , .
Chen et al. [9] proposed the definition of VSBM efficient, and derived efficient frontier projection for each DMU based on the VSBM model. According to Kao’s study [8], this definition of VSBM efficient is the external evaluation. The intermediate products are not considered in calculating the VSBM efficiency for each DMU. Based on studies in Kao [8,39], this paper considers the intermediate products in calculating the overall efficiency for each DMU. This paper firstly calculates the divisional efficiency.
is the target intermediate product value of the DMU . can be regarded as the target point of the endogenous output of the Division 1 and the endogenous input of the Division 2. is the actual intermediate product value of the DMU . If are regarded as the endogenous outputs of the Division 1, let . Denote as the insufficient amount of the intermediate product as endogenous output of the Division 1. The slack variable can be positive, negative or zero. If is negative, the actual endogenous output of the Division 1 is higher than the expected endogenous output . This indicates that the endogenous output of the Division 1 is efficient. If are regarded as the endogenous inputs of the Division 2, let . Denote as the excessive amount of the intermediate product as endogenous input of the Division 2. The slack variable can be positive, negative or zero. If is negative, the actual endogenous input of the Division 2 is lower than the expected endogenous input . This indicates that the endogenous input of the Division 2 is efficient. Due to is the opposite of , with . The efficiencies of the two divisions are calculated as Definition 1.
Definition 1.
If the model (4) has a feasible solution, the divisional efficiencies of the DMUrelative to the SUs are
Kao [39] proposed the internal evaluation efficiency which is a weighted average of the divisional efficiency. Based on the study of Kao [39], we let the weights of the two divisions be
Considering the intermediate products, this paper calculates the overall efficiency as Definition 2.
Definition 2.
If the model (4) has a feasible solution, the overall efficiency of the DMUrelative to the SUs is
If the model (4) is infeasible, the overall efficiency and divisional efficiency of the DMU cannot be calculated concretely. The model (4) is infeasible, because there is exogenous input of Division 1 which is smaller relative to SUs, or there is exogenous output of Division 2 which is bigger relative to SUs. Let be the expected increased amount of exogenous input of Division 1 relative to SUs. Let be the expected reduction amount of the exogenous outputs of Division 2 relative to SUs. Based on the above consideration, we propose the improved generalized network SBM model for basic two-stage structure (hereinafter referred to as the model), see model (8). Intermediate measures are variables.
The model (8) is fractional programming, which can be transformed into a linear programming problem by the Charnes–Cooper transformation [1]. This paper will use a superscript “*” to denote the optimal solution value of a variable in model (8). The optimal solution of model (8) is , .
is the target intermediate product value of the DMU . can be regarded as the target point of the endogenous output of the Division 1 and the endogenous input of the Division 2. is the actual intermediate product value of the DMU . If are regarded as the endogenous outputs of the Division 1, let . Denote as the expected reduction amount of the intermediate product as endogenous output of the Division 1. The variable can be positive, negative or zero. If , are regarded as the endogenous inputs of the Division 2, let . Denote as the expected increased amount of the intermediate product as endogenous input of the Division 2. The variable can be positive, negative or zero. Due to is the opposite of , with . The efficiencies of the two divisions are calculated as Definition 3.
Definition 3.
If the model (4) is infeasible, model (8) is calculated. The divisional efficiencies of the DMUrelative to the SUs are
We let the weights of the two divisions be
Definition 4.
If the model (4) is infeasible, model (8) is calculated. The overall efficiency of the DMUrelative to the SUs is
4. The Generalized Network Slacks-Based Measure Approach for General Multi-Stage Structure
In this paper, we have proposed a generalized network SBM approach for basic two-stage structure which is a closed system, where the outputs from Division 1 become the inputs to the Division 2, and where no other inputs enter the process in Division 2 as shown in Figure 3. While the basic two-stage structure does exist in production processes, there are processes whose structure do not fulfill the condition in Figure 3. The more prevalent production processes are those where both stages are allowed to consume exogenous inputs and to produce exogenous outputs. This structure is a general network structure which is open system. This section extends our proposed approach to general network structure.
We assume that there are n DMUs are observed, and there are SUs in the reference set. The DMUs and SUs have m inputs and s outputs, and contain K divisions. There are h intermediate products between divisions. The network structure of DMUs and SUs is the general multi-stage structure as shown in Figure 4.
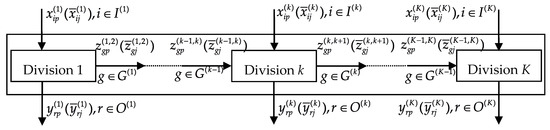
Figure 4.
The general multi-stage structure.
The Division k of DMU and SU consumes exogenous inputs and the endogenous inputs produced by Division k-1 to produce the exogenous outputs and the endogenous outputs for Division k + 1 to use. Let denote the set of the indices of the exogenous inputs of the Division k. are disjoint for all divisions, and . Let denote the set of the indices of the exogenous outputs of the Division k. are disjoint for all divisions, and [8]. are the intermediate products connecting the Division k-1 and the Division k. Let denote the set of the indices of the endogenous inputs of the Division k. are the intermediate products connecting the Division k and the Division k+1. Let denote the set of the indices of the endogenous outputs of Division k. are disjoint for all divisions, and . The Division k of DMU and SU has endogenous inputs, exogenous inputs, exogenous outputs and endogenous outputs. It should be noted that the Division 1 does not have an endogenous input and the Division K does not have an endogenous output.
is the SUs set.
is the DMUs set. If , it was the self-evaluation system.
Similar to the basic two-stage structure, the production possibility set determined by SUs is defined as follows,
The parameter is a binary parameter which equals only 0 or 1. Here indicates constant returns to scale, while indicates variable returns to scale. is called sample production possibility set.
According to the construction idea of the G-BNSBM2 model, we propose the generalized network SBM model for general multi-stage structure (hereinafter referred to as the G-GNSBMK model), see model (13). Intermediate measures are variables.
The model (13) is fractional programming, which can be transformed into linear programming by Charnes–Cooper transformation [1]. Since the DMUs set and the SUs set are not necessarily the same, the model (13) may not have a feasible solution.
When the model (13) has a feasible solution, this paper will use a superscript “*” to denote the optimal solution value of a variable in model (13). The optimal solution of model (13) is , .
is the target intermediate product value of the DMU . is the actual intermediate product value of the DMU . If are regarded as the endogenous outputs of the Division k, let . Denote as the insufficient amount of the intermediate product as endogenous output of the Division k. The slack variable can be positive, negative or zero. If is negative, the actual endogenous output of the Division k is higher than the expected endogenous output . This indicates that the endogenous output of the Division k is efficient. If are regarded as the endogenous inputs of the Division k+1, let . Denote as the excessive amount of the intermediate product as endogenous input of the Division k+1. The slack variable can be positive, negative or zero. If is negative, the actual endogenous input of the Division k+1 is lower than the expected endogenous input . This indicates that the endogenous input of the Division k+1 is efficient. Obviously, . The efficiencies of the two divisions are calculated as Definition 5.
Definition 5.
If the model (13) has a feasible solution, the divisional efficiencies of the DMUrelative to the SUs are
Similar to the basic two-stage structure, the overall efficiency is defined as a weighted average of the divisional efficiencies. Let the weight associated with Division k be
Definition 6.
If the model (13) has a feasible solution, the overall efficiency of the DMUrelative to the SUs is
If the model (13) is infeasible, the overall efficiency and divisional efficiency of the DMU cannot be calculated concretely. The model (13) is infeasible, there is exogenous input of Division k which is smaller relative to SUs, or there is exogenous output of Division k which is bigger relative to SUs. Let be the expected increased amount of exogenous inputs of Division k relative to SUs. Let be the expected reduction amount of the exogenous outputs of Division k relative to SUs. Based on the above consideration, we propose an improved generalized network SBM model for general multi-stage structure (hereinafter referred to as the model), see model (19). Intermediate measures are variables.
The model (19) is fractional programming, which can be transformed into a linear programming problem by the Charnes–Cooper transformation [1]. This paper will use a superscript “*” to denote the optimal solution value of a variable in model (19). The optimal solution of model (19) is .
is the target intermediate product value of the DMU . is the actual intermediate product value of the DMU . If are regarded as the endogenous outputs of the Division k, let . Denote as the expected reduction amount of the intermediate product as endogenous output of the Division k. The variable can be positive, negative or zero. If are regarded as the endogenous inputs of the Division k+1, let Denote as the expected increased amount of the intermediate product as endogenous input of the Division k+1. The variable can be positive, negative or zero. Obviously, . The efficiencies of the two divisions are calculated as Definition 7.
Definition 7.
If the model (13) is infeasible, model (19) is calculated. The divisional efficiencies of the DMUrelative to the SUs are
Similar to the basic two-stage structure, the overall efficiency is defined as a weighted average of the divisional efficiencies. Let the weight associated with division k be
Definition 8.
If the model (13) is infeasible, model (19) is calculated. The overall efficiency of the DMUrelative to the SUs is
5. Numerical Examples
Suppose there are 10 power companies of the same type. The operation of the power company is divided into three stages, as shown in Figure 5.
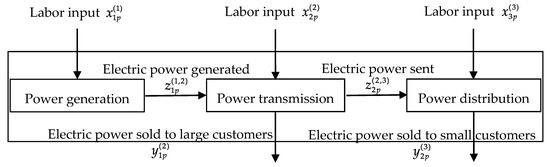
Figure 5.
Three-stage network structure of power company operation.
In order to further improve productivity, the 10 power companies have introduced advanced technology and equipment, thus effectively improving production. This paper uses the generalized network SBM model to analyze the efficiency changes before and after technological innovation. The inputs, outputs, and intermediate product indicators for the DMUs and SUs are listed as below:
- Power generation (Division 1):
- Input 1: : Labor input (numbers of employees)
- Power transmission (Division 2):
- Input 2: : Labor input (numbers of employees)
- Output 1: : Electric power sold to larger customers
- Power distribution (Division 3):
- Input 3: : Labor input (numbers of employees)
- Output 2: : Electric power sold to small customers
- Intermediate products:
- : Electric power generated (output from Division 1 and input to Division 2)
- : Electric power sent (output from Division 2 and input to Division 3)
Table 1 and Table 2 are the relevant data of power companies before and after technological innovation (some of the data are from Tone and Tsutsui [36]). A simple descriptive statistical analysis of data is given in Table 3.

Table 1.
Index data of power company before technological innovation [36].

Table 2.
Index data of power company after technological innovation.

Table 3.
Descriptive statistical analysis of data.
In the following, the generalized network SBM model is applied to calculate the efficiency of 10 power companies before and after technological innovation under the condition of variable returns to scale, taking the index data of 10 power companies before technological innovation as reference SUs. In the model (13) and (19), let , . The model based on (13) is:
In the model (25), are the data of SUs. SUs are 10 power companies before technological innovation.
The model (25) is fractional programming, let . . Model (25) can be transformed into linear programming as follows:
This paper will use a superscript “*” to denote the optimal solution value of a variable in model (25). The calculation result of model (25) is shown in Table 4 and Table 5.

Table 4.
Overall efficiencies and divisional efficiencies of 10 companies before technological innovation under the condition of variable returns to scale.

Table 5.
Overall efficiencies and divisional efficiencies of 10 power companies after technological innovation under the condition of variable returns to scale.
When the index data of 10 power companies before technological innovation are taken as reference SUs for evaluation, the overall efficiency and divisional efficiency of each power company before technological innovation are calculated (Table 4). The DMUs set and the SUs set are the same. That is the self-evaluation system. At this time, the model (25) degenerates into the traditional network SBM model, which can measure the overall efficiencies and divisional efficiencies of all power companies, and the calculation results are consistent with Kao [8].
Table 4 shows the overall efficiencies and three divisional efficiencies of the 10 companies. The efficiencies of the three divisions are shown in columns 4, 8, and 11 of Table 4. The numbers in parentheses are the weights of the corresponding divisions for calculating the overall efficiency. The calculation of divisional efficiency is shown in Definition 5. is the insufficient amount of endogenous output of the Division 1, and . is the excessive amount of the endogenous input of the Division 2, and . . is the insufficient amount of endogenous output of the Division 2, and . is the excessive amount of the endogenous input of the Division 3, and . . Division 3 does not have endogenous output. . Denote the weights associated with the three divisions as where and
Divisions with smaller efficiencies are those that cause unsatisfactory system performance. For most DMUs, the efficiency of Division 1 is lower compared to that of the other two divisions. The Division 1 is the power generation division. The last column in Table 4 shows the overall efficiencies of 10 power companies. The calculation of overall efficiency is shown in Definition 6. The overall efficiency is a weighted average of the divisional efficiencies. For example, the overall efficiency of company 2 is 0.5170, which is equal to 0.3314 × 0.2111 + 0.3756 × 0.5633 + 0.2930 × 0.8038.
When the index data of 10 power companies before technological innovation are taken as the reference SUs for evaluation, the overall efficiency and divisional efficiency of each power company after technological innovation are calculated (Table 5). The DMUs set and the SUs set are different. Based on model (25), Table 5 shows the overall efficiencies and three divisional efficiencies of the 10 companies after technological innovation.
The variables in Table 5 are consistent with Table 4. The efficiencies of the three divisions are shown in columns 4, 8, and 11 of Table 5. The numbers in parentheses are the weights of the corresponding divisions for calculating the overall efficiency. The last column in Table 5 shows the overall efficiency of DMU. As can be seen from Table 5, when the model (25) is used to calculate the efficiencies of 10 power companies, it is infeasible for companies 3, 5, 8, and 9. At this time, the efficiencies of these four companies cannot be obtained by the application of model (25). The efficiency score can be further calculated by the improved model (19). The model based on (19) is:
In model (27), are the data of SUs. SUs are 10 power companies before technological innovation.
The model (27) is fractional programming, let , . Model (27) can be transformed into linear programming as follows:
This paper will use a superscript “*” to denote the optimal solution value of a variable in model (27). The calculation result of model (27) is shown in Table 6.

Table 6.
Overall efficiencies and divisional efficiencies of companies 3, 5, 8, and 9 after technological innovation under the condition of variable returns to scale with the model (27).
Table 6 shows the overall efficiencies and three divisional efficiencies of companies 3, 5, 8, and 9. The efficiencies of the three divisions are shown in columns 4, 8, and 11 of Table 6. The numbers in parentheses are the weights of the corresponding divisions for calculating the overall efficiency. The calculation of divisional efficiency is shown in Definition 7. is the expected reduction amount of endogenous output of the Division 1, and . is the expected increased amount of the endogenous input of the Division 2, and . Denote the efficiency of Division 1 as . is the expected reduction amount of endogenous output of the Division 2, and . is the expected increased amount of the endogenous input of the Division 3, and . Denote the efficiency of Division 2 as . Division 3 does not have endogenous output. Denote the efficiency of Division 3 as . Denote the weights associated with the three divisions as where and The last column in Table 6 shows the overall efficiencies of 10 power companies. The calculation of overall efficiency is shown in Definition 8. The overall efficiency is a weighted average of the divisional efficiencies. The overall efficiencies of 10 power companies after technological innovation is obviously higher than that before technological innovation.
6. Conclusions
In this paper, we have proposed generalized network SBM approach based on SUs to extend the study of Ma [48]. Unlike the generalized DEA approach, our generalized network SBM model allows inputs or outputs to change non-proportionally, and take the operations of the internal divisions into account in measuring efficiency of DMU. Unlike Tone and Tsutsui’s approach [36], the proposed model does not require the weight of each division to be given in advance according to its importance to DMUs. Unlike Kao’s approach [8], the generalized network SBM approach can evaluate the DMU based on any reference set.
This paper firstly proposed a generalized network SBM model for basic two-stage structure, and then proposed a generalized network SBM model for general multi-stage structure. This generalized network SBM model can be employed to measure the overall efficiency and divisional efficiency, which consider the intermediate products in the calculating formula. The overall efficiency is a weighted average of the divisional efficiency, and is divisional efficiency aggregation.
In the generalized network SBM approach, the DMUs set and SUs set are not necessarily the same. When the DMUs set and the SUs set are the same, the generalized network SBM model degenerates into the traditional network SBM model. When the DMUs set and the SUs set are different, the generalized network SBM model may be infeasible. This paper proposed an improved generalized network SBM model, which can further solve the problem of no feasible solution.
The generalized network SBM approach can measure efficiency of DMU from the viewpoint of inside managers. The inside managers evaluate the overall efficiency of DMU taking all the exogenous (endogenous) inputs and outputs that are observable into consideration. The overall efficiency shows the aggregate performance of the divisions. The decision maker can use the overall efficiency to identify inefficient divisions to make improvements. Moreover, the generalized network SBM approach can evaluate the DMU based on any reference set. This provides a method for decision makers to evaluate the efficiency of DMU from multi-dimensions, not only by self-evaluation. The decision maker can get more information than from self-evaluation.
There is a related topic about the generalized network SBM approach for future research. We can study the decomposition of overall efficiency and discuss the relationship between overall efficiency and divisional efficiency in future research.
Author Contributions
Methodology, and writing—original draft, N.S.; conceptualization, and resources, N.Z.; writing—review and editing, Z.-X.M.
Funding
This research was funded by the General Program of Natural Science Foundation of China, grant number 61471083, National Natural Science Foundation of China, grant number 71661025 and 71261017, Inner Mongolia higher school scientific research project, grant number NJZY16320 and NJZY17373.
Acknowledgments
The authors would like to thank the editor and referees for their very constructive comments in revising this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Khoveyni, M.; Fukuyama, H.; Eslami, R.; Yang, G.L. Variations effect of intermediate products on the second stage in two-stage processes. Omega-Int. J. Manag. Sci. 2019, 85, 35–48. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Poh, K.L. A survey of data envelopment analysis in energy and environmental studies. Eur. J. Oper. Res. 2008, 189, 1–18. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, L.Y.Y.; Lu, W.M.; Lin, B.J.Y. A survey of DEA applications. Omega-Int. J. Manag. Sci. 2013, 41, 893–902. [Google Scholar] [CrossRef]
- Kao, C. Network data envelopment analysis: A review. Eur. J. Oper. Res. 2014, 239, 1–16. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G.L. A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Kao, C. A classification of slacks-based efficiency measures in network data envelopment analysis with an analysis of the properties possessed. Eur. J. Oper. Res. 2018, 270, 1109–1121. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.J.; Liang, L.; Salo, A.; Wu, H.Q. Frontier projection and efficiency decomposition in two-stage processes with slacks-based measures. Eur. J. Oper. Res. 2016, 250, 543–554. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Productivity and intermediate products: A frontier approach. Econ. Lett. 1996, 50, 65–70. [Google Scholar] [CrossRef]
- Wang, C.H.; Gopal, R.D.; Zionts, S. Use of data envelopment analysis in assessing information technology impact on firm performance. Ann. Oper. Res. 1997, 73, 191–213. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Network DEA. Socio-Econ. Plan. Sci. 2000, 34, 35–49. [Google Scholar] [CrossRef]
- Guo, C.; Shureshjani, R.A.; Foroughi, A.A.; Zhu, J. Decomposition weights and overall efficiency in two-stage additive network DEA. Eur. J. Oper. Res. 2017, 257, 896–906. [Google Scholar] [CrossRef]
- Chen, K.; Zhu, J. Second order cone programming approach to two-stage network data envelopment analysis. Eur. J. Oper. Res. 2017, 262, 231–238. [Google Scholar] [CrossRef]
- Kao, C.; Hwang, S.N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan. Eur. J. Oper. Res. 2008, 185, 418–429. [Google Scholar] [CrossRef]
- Liang, L.; Cook, W.D.; Zhu, J. DEA models for two-stage processes: Game approach and efficiency decomposition. Nav. Res. Logist. 2008, 55, 643–653. [Google Scholar] [CrossRef]
- Chen, Y.; Du, J.; Sherman, H.D.; Zhu, J. DEA model with shared resources and efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 339–349. [Google Scholar] [CrossRef]
- Zha, Y.; Liang, L. Two-stage cooperation model with input freely distributed among the stages. Eur. J. Oper. Res. 2010, 205, 332–338. [Google Scholar] [CrossRef]
- Du, J.; Liang, L.; Chen, Y.; Cook, W.D.; Zhu, J. A bargaining game model for measuring performance of two-stage network structures. Eur. J. Oper. Res. 2011, 210, 390–397. [Google Scholar] [CrossRef]
- Chen, Y.; Cook, W.D.; Li, N.; Zhu, J. Additive efficiency decomposition in two-stage DEA. Eur. J. Oper. Res. 2009, 196, 1170–1176. [Google Scholar] [CrossRef]
- Luo, X.M. Evaluating the profitability and marketability efficiency of large banks-An application of data envelopment analysis. J. Bus. Res. 2003, 56, 627–635. [Google Scholar] [CrossRef]
- Lo, S.F.; Lu, W.M. An integrated performance evaluation of financial holding companies in Taiwan. Eur. J. Oper. Res. 2009, 198, 341–350. [Google Scholar] [CrossRef]
- Tsolas, I.E. Modeling Profitability and Stock Market Performance of Listed Construction Firms on the Athens Exchange: Two-Stage DEA Approach. J. Constr. Eng. Manage. 2013, 139, 111–119. [Google Scholar] [CrossRef]
- Yang, C.Y.; Liu, H.M. Managerial efficiency in Taiwan bank branches: A network DEA. Econ. Model. 2012, 29, 450–461. [Google Scholar] [CrossRef]
- Cao, X.F.; Yang, F. Measuring the performance of Internet companies using a two-stage data envelopment analysis model. Enterp. Inf. Syst. 2011, 5, 207–217. [Google Scholar] [CrossRef]
- Chen, C.L.; Zhu, J.; Yu, J.Y.; Noori, H. A new methodology for evaluating sustainable product design performance with two-stage network data envelopment analysis. Eur. J. Oper. Res. 2012, 221, 348–359. [Google Scholar] [CrossRef]
- Li, Y.J.; Chen, Y.; Liang, L.; Xie, J.H. DEA models for extended two-stage network structures. Omega-Int. J. Manag. Sci. 2012, 40, 611–618. [Google Scholar] [CrossRef]
- Cook, W.D.; Zhu, J.; Bi, G.B.; Yang, F. Network DEA: Additive efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 1122–1129. [Google Scholar] [CrossRef]
- Despotis, D.K.; Koronakos, G.; Sotiros, D. Composition versus decomposition in two-stage network DEA: A reverse approach. J. Prod. Anal. 2016, 45, 71–87. [Google Scholar] [CrossRef]
- Ang, S.; Chen, C.M. Pitfalls of decomposition weights in the additive multi-stage DEA model. Omega-Int. J. Manag. Sci. 2016, 58, 139–153. [Google Scholar] [CrossRef]
- Kao, C. Efficiency decomposition and aggregation in network data envelopment analysis. Eur. J. Oper. Res. 2016, 255, 778–786. [Google Scholar] [CrossRef]
- Kao, C. Efficiency measurement for parallel production systems. Eur. J. Oper. Res. 2009, 196, 1107–1112. [Google Scholar] [CrossRef]
- Yang, C.C.; Hsiao, C.K.; Yu, M.M. Technical efficiency and impact of environmental regulations in farrow-to-finish swine production in Taiwan. Agric. Econ. 2008, 39, 51–61. [Google Scholar] [CrossRef]
- Simon, J.; Simon, C.; Arias, A. Changes in productivity of Spanish university libraries. Omega-Int. J. Manag. Sci. 2011, 39, 578–588. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. Network DEA: A slacks-based measure approach. Eur. J. Oper. Res. 2009, 197, 243–252. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. Dynamic DEA with network structure: A slacks-based measure approach. Omega-Int. J. Manag. Sci. 2014, 42, 124–131. [Google Scholar] [CrossRef]
- Fukuyama, H.; Mirdehghan, S.M. Identifying the efficiency status in network DEA. Eur. J. Oper. Res. 2012, 220, 85–92. [Google Scholar] [CrossRef]
- Kao, C. Efficiency decomposition in network data envelopment analysis with slacks-based measures. Omega-Int. J. Manag. Sci. 2014, 45, 1–6. [Google Scholar] [CrossRef]
- Kao, C. Inefficiency identification for closed series production systems. Eur. J. Oper. Res. 2019, 275, 599–607. [Google Scholar] [CrossRef]
- Lozano, S. Technical and environmental efficiency of a two-stage production and abatement system. Ann. Oper. Res. 2017, 255, 199–219. [Google Scholar] [CrossRef]
- Bian, Y.W.; Liang, N.N.; Xu, H. Efficiency evaluation of Chinese regional industrial systems with undesirable factors using a two-stage slacks-based measure approach. J. Clean Prod. 2015, 87, 348–356. [Google Scholar] [CrossRef]
- Simoes, P.; Marques, R.C. On the economic performance of the waste sector. A literature review. J. Environ. Manage. 2012, 106, 40–47. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.Y.; Luo, R.; Yao, L.M.; Cao, S.; Wang, S.Y.; Lev, B. Assessing integrated water use and wastewater treatment systems in China: A mixed network structure two-stage SBM DEA model. J. Clean Prod. 2018, 185, 533–546. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.Z.; Cui, Q. Evaluating airline efficiency: An application of Virtual Frontier Network SBM. Transp. Res. Pt. e-Logist. Transp. Rev. 2015, 81, 1–17. [Google Scholar] [CrossRef]
- Zhu, Y.C.; Li, Y.J.; Liang, L. A variation of two-stage SBM with leader-follower structure: An application to Chinese commercial banks. J. Oper. Res. Soc. 2018, 69, 840–848. [Google Scholar] [CrossRef]
- Wang, C.N.; Hsu, H.P.; Wang, Y.H.; Pham, T.T.H. Performance assessment for electronic manufacturing service providers using two-stage super-efficiency SBM model. Appl. Econ. 2017, 49, 1963–1980. [Google Scholar] [CrossRef]
- Ma, Z.X. DEA model with generalized reference set and its properties. J. Syst. Eng. Electron. 2012, 34, 709–714. (In Chinese) [Google Scholar]
- Muren; Ma, Z.X.; Wei, C. Generalized fuzzy data envelopment analysis methods. Appl. Soft. Comput. 2014, 19, 215–225. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).