Abstract
Studying the interaction between demand forecasting and train stop planning is important, as it ensures the sustainable development of high-speed rail (HSR). Forecasting the demand for high-speed rail (HSR), which refers to modal choice or modal split in this paper, is the first step in high-speed rail (HSR) planning. Given the travel demand and the number of train trips on each route, the train stop planning problem (TSPP) of line planning involves determining the stations at which each train trip stops, i.e., the stop-schedule of each train trip, so that the demand can be satisfied. To integrate and formulate the two problems, i.e., the modal choice problem (MCP) and train stop planning problem (TSPP), a nonlinear model is presented with the objective of maximizing the total demand captured by a high-speed rail system. To solve the model, a heuristic iterative algorithm is developed. To study the relationship between the demand and the service, the Beijing–Shanghai high-speed rail (HSR) corridor in China is selected. The empirical analysis indicates that combining modal choice and train stop planning should be considered for the sustainable design of high-speed rail (HSR) train services. Furthermore, the model simulates the impact of the number of stops on its mode share by reflecting changes in travelers’ behaviors according to HSR train stop planning, and it also provides a theoretical basis for the evaluation of the adaptability of the service network to travel demand.
1. Introduction
As an emerging transportation mode, high-speed rail (HSR) has attracted attention from passengers and operators due to its rapidity, safety, and comfort when compared to other modes. High-speed rail, together with other transportation modes, such as bus, traditional rail, and air transport, constitute a transportation system. The introduction of high-speed rail services has significantly changed the transportation market. However, some competition occurs between HSR and other transport modes for travel demand. As shown in Figure 1, for short-distance travel demand, bus and traditional rail are the main competitors of high-speed rail (HSR), whereas air transport has become the major competitor of high-speed rail (HSR) for medium- and long-distance travel demand. Empirical studies (Caseetta and Coppola [1], and Borjesson [2]) have shown that transportation mode choice is determined by many factors, especially by travel time and ticket price. Thus, the more stops a HSR train trip makes, the more time is required for the passenger to travel, which reduces the market share of HSR. A stop-schedule, sometimes called a stop pattern or a halt pattern in the literature, identifies the stations at which a train trip stops. According to Cordone and Redaelli [3], travel demand and train services interact. HSR train services are determined by the travel demand for HSR trains, and the travel demand for HSR trains depends on the HSR train services provided. Thus, for the sustainable development of both high-speed rail and travel demand, demand forecasting, including travel behavior or modal choice, should be integrated into the train stop planning of line planning. In this paper, an integrated model for the modal choice and train stop planning problem (MC-TSPP) is proposed. The modal choice problem (MCP), involves estimating the travel demand for HSR, which is an important component in developing a sustainable HSR system. The train stop planning problem (TSPP) of line planning involves determining the stop-schedule plan for HSR train trips. For a clear description, all abbreviations used in this paper are summarized in Table 1.
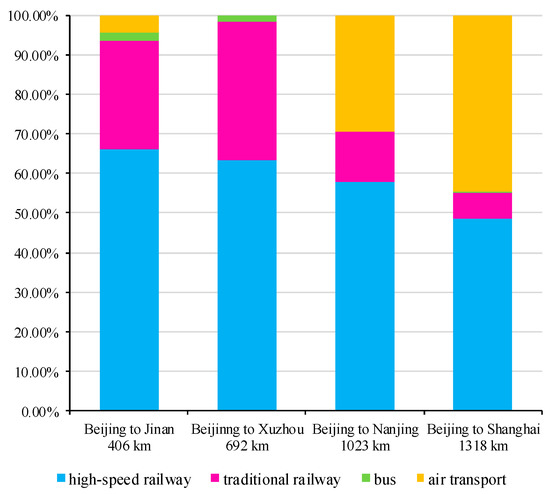
Figure 1.
Travel mode choices among city pairs for the respondents.

Table 1.
Abbreviations.
The contributions of this paper are as follows: (1) an integrated model simultaneously considering mode choice and train stop planning is presented, (2) a decomposition-based heuristic iterative algorithm is proposed, and (3) a detailed analysis of travel behavior and train services is provided.
The remainder of the paper is structured as follows. Section 2 reviews the literature related to our study. In Section 3, we outline an integrated model for modal choice and train stop planning. A heuristic iterative algorithm is developed in Section 4. A case study is detailed in Section 5. Section 6 concludes this paper and suggests directions for future work.
2. Related Literature
2.1. Train Stop Planning Under Given Demand
Given the travel demand, which is constant and independent of the service supplied, the TSPP of line planning determines the stop-schedule plan for train trips or lines (Table 2). To optimize a stop-schedule plan, a multiobjective programming model was presented by Chang et al. [4]. Goossens et al. [5] tackled the problem of altering the stops along the lines by both upgrading and downgrading stations. They assumed that the types of lines were given and focused on finding a line type for each station. To model this problem, a line-event graph was presented. A multicommodity flow model was formulated, which was also a mixed integer programming formulation. Several models were used to handle the line planning problem (LPP) with different stop patterns by Goossens et al. [6]. Based on a heuristic algorithm, a stop-schedule plan was constructed by Shi et al. [7]. Deng et al. [8] presented a bilevel programming model for the optimization of stop-schedules. To optimize all-stop, short-turn, and express transit services, a mixed integer nonlinear model was adopted by Ulusoy et al. [9]. In their approach, the stop-schedules of the express transit services were determined. They also considered the passenger assignment and transfer stations. By applying a two-layer nonlinear optimization model, Wang et al. [10] determined the stop-schedule of each individual train trip. Passenger assignment was also considered in their model. To tackle the TSPP, a two-stage approach was proposed by Fu et al. [11] under the assumption that the number of train stop patterns was given. For the passengers whose travel distance was beyond the train-set maintenance kilometers, they split them into several separate origin-destinations (ODs) at major transfer hubs. Huang and Peng [12] concentrated on designing a stop-schedule plan for HSR and a two-stage heuristic algorithm was presented to handle this problem. A nonlinear programming model was presented to optimize HSR stopping patterns by Jong et al. [13], which became infeasible when dealing with large-scale problems. The authors assumed that each passenger OD only chose the pattern with the shortest travel time. To solve the model, a genetic algorithm was presented that could solve small-scale problems, such as the Taiwan HSR system, to the optimal or a near-optimal solution. A new model with a restricted passenger flow assignment procedure was presented for the TSPP by Fu et al. [14]. Li et al. [15] focused on the TSPP and a nonlinear planning model was presented based on the concept of node service. Park et al. [16] handled the line planning problem (LPP) where the stop patterns were determined based on a multicommodity flow model. To solve the model, they applied the Dantzig–Wolfe decomposition and column generation. An integrated optimization method for the TSPP was proposed by Zhang et al. [17] based on classified stations and categorized passenger flows. For each type of train stop pattern of categorized passenger flows, an integer programming model was used.

Table 2.
Train stop planning problem (TSPP) studies.
Wang and Luo [18] presented a nonlinear programming model to optimize the TSPP. Lai et al. [19] focused on the TSPP for a HSR system based on a novel network structure. Yang et al. [20] integrated the TSPP and train scheduling problem. Yue et al. [21] also incorporated train stopping patterns into train scheduling optimization. Qi et al. [22] extended the research of Yang et al. [20] by considering the number of passengers boarding or alighting at each station for each train trip.
2.2. Modal Choice
To estimate travel demand, we needed to model the travel behavior in the form of decisions. Most research on travel behavior has emphasized the use of discrete choice theory, and many variants of logit models have been developed. With regard to the travel behavior, Ben-Akiva and Lerman [23] applied the theory of discrete choice to study the travel behavior within public transport. Cascetta et al. [24] proposed the C-Logit model to tackle path overlapping problems. To consider the cross similarities between different pure and combined modes, the cross-nested logit model was developed by Vovsha [25]. To handle the route overlapping problem, a new logit model, the link-nested logit model, was presented by Vovsha and Bekhor [26]. Ben-Akiva and Bierlaire [27] reviewed the discrete choice models and applied these models to short-term travel decisions. Ramming [28] considered network knowledge in both route generation and route choice. Almost all route choice models were compared based on the Boston case study data. Prashker and Bekhor [29] reviewed the route choice models and applied these models to the traffic assignment problem.
A large and growing body of studies has investigated the impact of service on travel behavior (Table 3). To estimate travelers’ preferences in multimodal networks, Arentze and Molin [30] designed a series of stated preference (SP) experiments to estimate a multimodal travel choice model. Caseetta and Coppola [1] proposed a trip-frequency model to forecast the short-term demand induced by HSR that depends directly on the generalized travel cost (i.e., travel time, travel cost, and service frequency). In order to forecast the diverted demand for considerably reduced travel times, when new HSR lines were introduced, Borjesson [2] validated the Swedish long-distance model, Sampers, and proposed a new model. To study the impact of the stations’ architectural quality on the users’ choices, a quantitative analysis based on a binomial logit model was conducted by Cascetta and Carteni [31], which showed a significant impact of the stations’ quality on the travelers’ preference. Based on a multinomial logit model, Baek and Sohn [32] conducted an investigation of passenger behavior for express trains during peak hours for the metro line nine in Seoul, South Korea. To investigate the mode choice behavior for passengers among air transport, HSR, and integrated air and high-speed rail (AH) services, Li and Sheng [33] proposed a modal split model. Some important results were produced. The mode choice behavior of commuters with the introduction of a new rail transit mode was studied by Sohoni et al. [34]. Carteni et al. [35] quantitatively analyzed the impacts of hedonic quality, including faster transit services and a number of hedonic characteristics of the services, on the students’ domestic tourist travel behavior. Mattson et al. [36] presented a mixed logit model to estimate demand for rural intercity bus services. It can be clearly seen that modelling long-distance travel is a different kind of modelling than modelling of daily commuter traffic because of different kind of trips.

Table 3.
Studies on the impact of services on travel behavior.
2.3. Integrated Model of Modal Choice and Transportation Services
Relatively few studies have been published concerning the interaction between travel behavior and service network design (Table 4). To consider the relationship between the travel demand and the service network design, Cordone and Redaelli [3] integrated timetable design into demand estimation. A solution procedure was proposed based on branch-and-bound and a heuristic algorithm. Borndorfer [37] presented an optimization approach for fare planning based on a discrete choice model in public transport where the line operation frequency were also considered in their models. Different fare structures, optimization objectives, and scenarios were analyzed in detail. An optimization model for railway timetabling was proposed by Espinosa-Aranda [38] that considered the mode choice and the travel behavior among different services based on a constrained nested logit model.

Table 4.
Studies on the interaction between travel behavior and service network design.
Cantarella et al. [39] and Li and Yang [40] conducted some relevant analyses of day-to-day dynamic modal choice with responsive transit service frequency for only one OD pair, which was not based on the logit-based model. Canca et al. [41] defined a mathematical programming model that integrated network design and line planning. The elasticity of demand was considered by the model and was used to determine the proportion of demand that each mode captured for each OD pair, assuming that the market share between modes was given and not determined. Li et al. [42] focused on the interaction between fare, frequency, and transit demand in a bimodal transportation network where transit frequency and fare were handled in an aggregate way, and a more detailed transit service design was not considered. Robenek et al. [43] combined timetable design with a multinomial logit-based passenger assignment to present the demand elasticity under the assumption that the mode choice model was solved in advance. Wen et al. [44] studied the autonomous vehicle operation problem considering the interaction between demand and supply, which provided new ideas for our research.
According to the literature review, it can be seen that recent research has begun to pay attention to the interaction between travel behavior and service network design. However, the literature on the interaction between travel behavior and line planning is fairly limited. In addition, most studies are restricted to frequency setting and modal choice and do not consider the interaction between stop-schedules and transit demand due to the difficulty of investigation. Differently, we explore how the travel demand interacts with the stop-schedule plan, and thus we adjust the stop-schedule plan. Compared to other studies, this method can be used to analyze passenger travel choice behavior caused by the number of stops in more detail. In addition, this integration can help make HSR more competitive than other modes of transport.
3. An Integrated Model for Modal Choice and Train Stop Planning
This section presents our integrated model for the modal choice and train stop planning problem (MC-TSPP). For convenience, the list of sets, parameters, and variables used are given in Table 5, Table 6 and Table 7, respectively.

Table 5.
Sets.

Table 6.
Parameters.

Table 7.
Decision variables.
3.1. Train Stop Planning Model
To formulate the TSPP, some assumptions are required, as stated below.
Assumption 1.
The set of potential operated routes is known and given. If there is no train trip that runs on a route, the route will not operate. Additionally, the running time between any two stations is given, which is obtained from the official timetable. The stop time at an intermediate station, which contains the acceleration and deceleration time, is assumed to be given and constant and independent of passenger flow (alighting and boarding) at the station.
Assumption 2.
Travel demand depends on the quality of the train service, which will be illustrated in the next subsection.
The TSPP considered in this paper can be stated as follows. Given a set of feasible routes and the possible number of train trips for each route, the TSSP involves determining (1) the optimal stop-schedule for each train trip, (2) the passenger volume served by the corresponding train trip, and (3) the number of passengers on board when the train trip stops at an intermediate station.
To formulate the TSPP, the following constraints need to be satisfied:
Equation (1) states that the travel demand between any two stations must be conveyed by the train trips whose routes pass these two stations simultaneously. The capacity constraints for tracks and stations are specified by Equations (2) and (3), respectively.
To construct a stop-schedule for a train trip, the constraints in Equations (4) and (5) must be imposed. That is, a train trip on route is required to start from one terminal station of route and end at the other terminal station of route . Otherwise the train trip on route will not be operated. Constraint (6) specifies that no passenger can get on or get off a train trip at station if a train trip does not halt at station .
The seating capacity constraint of a train trip is imposed by Equation (7). That is, the number of passengers served by a train trip on route cannot exceed the seating capacity of the corresponding train trip. Equation (8) defines the number of passengers on board when a train trip on route stops at an intermediate station . The number of passengers on board is determined by the passengers that alight at a station before station and disembark at a station after station . Constraints in Equations (9)–(11) provide the restrictions on the decision variables.
3.2. Modal Choice Model
Modal choice, which involves estimating the amount of demand captured by a transport mode, is a common problem in transportation research. Modal choice or modal split is the third step of the four-step model, which consists of four steps, i.e., trip generation, trip distribution, modal split, and traffic assignment. Discrete choice methods, especially logit-based models, have been widely used to model the problem. Logit-based models assume that decision-makers, i.e., travelers, are rational and choose a transport mode that maximizes their own utility, which is not completely known. The utility is usually related to the quality of the transportation service, such as travel time and ticket price. Empirical studies have shown that transportation mode choice is determined by many factors, particularly travel time and ticket price. In our paper, we assumed that the ticket price is given and constant. Thus, we mainly focused on the travel time. For simplicity, we used the average travel time of one transport mode to represent the travel time as follows:
For HSR, the average travel time can be calculated below, which is related to the stop time:
Then, the utility function of one transport mode can be defined as follows:
where represents the utility of mode between city and city . , the deterministic utility, accounts for all of the attributes that are known and influence the mode choice of the travelers. As stated above, for simplicity, we only selected the travel time and ticket price. is usually a linear combination of the attributes with suitable coefficients. denotes the ignored attributes and individual differences between the travelers, which are assumed to be independent and an identically distributed Gumbel variable with zero mean. In our model, the deterministic utility is defined as follows:
where represents the ticket price of alternative from to , and and are unknown coefficients that need to be estimated. We assumed that the ticket price for all transport modes between any two stations or cities are known and constant. The travel time for all modes, except for HSR, between any two stations or cities are known. The travel time for HSR depends on the average stop time. Therefore, the deterministic utilities for all transport modes apart from HSR are constant, whereas the deterministic utility of HSR is a function of the stop-schedules. Then, the estimated demand of HSR can be defined as
3.3. An Integrated Model
The logit formulation and TSPP formulation can be integrated to study the interaction between travel demand and HSR train services. From the demand perspective, we maximized the total demand of HSR mode. Then, the integrated model, i.e., MC-TSPP model, is
Constraints (1)–(11)
The objective function in Equation (17) maximizes the total demand that uses the HSR mode. The constraint in Equation (18) relates the HSR demand of each origin and the destination pair to the associated travel time. Constraint (19) relates the travel time to the HSR train running time and average stop time. The other constraints are directly obtained from the TSPP formulation.
4. Solution Procedure
The MC-TSPP formulation is a mixed integer nonlinear programming (MINLP) problem. Therefore, we cannot directly solve it with a commercial solver. By analyzing the structure of the MC-TSPP formulation, we see that the formulation can be decomposed back into the modal choice problem (MCP) and the train stop planning problem (TSPP) with fixed demand. Then, the TSPP, which is a mixed integer linear programming (MILP) problem, can be solved by a commercial solver, such as ILOG Cplex. The solution procedure was based on the idea of Cordone and Redaelli [3]: we started from the demand estimating based on the current attributes of the modes; then, with the demand, we solved the TSPP and used the results to estimate another demand, and iterate. To illustrate the solution procedure, we outline the process below.
Step 1. Calculate the initial average travel time for the HSR based on the current HSR timetable.
To start, we calculated the average travel time of the HSR between any two stations based on the current HSR timetable, which is used to obtain the initial demand.
Step 2. Estimate the initial demand of the HSR.
Based on the obtained initial average travel time for the HSR, we calculated the logit model to estimate the initial demand of the HSR.
Step 3. Solve the TSPP and estimate the demand of the HSR.
Since the objective is to maximize the total demand captured by the HSR, which mostly depends on the number of times it stops, we solved the TSPP by minimizing the total time loss for all demand:
Based on Objective (21) and Constraints (1)–(11) the TSPP can be solved with ILOG Cplex, from which we obtained the optimal solution . Then, based on the optimal solution, we estimated the demand with Constraints (18) and (19), which can be applied to the next iteration.
Step 4. If , , and the number of iterations is no more than a limited number, go to Step 3; otherwise, terminate the algorithm and return the train service plan that generates the maximum demand. denotes the maximum demand that the HSR can transport. can be obtained with and Constraints (2)–(11), i.e., . and represent the demand of the current iteration and previous iteration, respectively; and is a threshold.
5. Case Study
This section presents the results obtained based on the integrated model and solution procedure. We selected the Beijing–Shanghai corridor to conduct the case study.
5.1. Data Collection
For the case study, the Beijing–Shanghai corridor was selected for the following reasons. First, the Beijing–Shanghai HSR operates along a corridor, which has attracted a large amount of passenger traffic. Second, several transportation modes operate in the corridor, including HSR, traditional rail, bus, and air transport. We considered the 23 cities along the Beijing–Shanghai HSR. Thus, there were 253 OD pairs in one direction. We were given the HSR demand for a normal operating day; then, the total demand for all modes and all OD pairs were derived from calculations using the HSR demand and the estimated share rate of the HSR.
To estimate the modal split models, we conducted stated preference (SP) surveys to determine the travel mode choice of the individuals. SP attempts to directly measure preferences or utility by survey. In terms of attribute selection, all attributes affecting mode choice should be considered. However, for practicality and simplicity, only the travel time and ticket prices were considered. The travel time for each transportation mode was derived from the official timetable. HSR fares were derived from the second class fare. Seat fares were selected as the traditional rail (TR) fares and bus fares. Economy class ticket prices were selected as the air transport fares. The SP survey questionnaires were distributed at stations or airports between September and December 2018. The coefficients were estimated using TransCAD Transportation Planning software.
5.2. Beijing–Shanghai HSR
The Beijing–Shanghai HSR, a double track rail line, consists of 23 stations and 22 tracks in one direction. There are five terminal stations: Beijing South, Jinan West, Xuzhou East, Nanjing South, and Shanghai Hongqiao, which can be used as start or end stations. The running time of a HSR train between any two stations was derived from the official timetable. For simplicity, let numbers 1 to 23 represent the stations from Beijing South to Shanghai Hongqiao, respectively. Other parameters related to the proposed model are given in Table 8.

Table 8.
Input parameters for our model.
As mentioned by Jeong et al. [45], ILOG Cplex sometimes does not work for all instances with all the Cplex parameters at their default values. To get a feasible solution, we need to revise the Cplex parameters to ensure that both the quality of the solution and the solution time are acceptable. Thus, before applying the proposed heuristic algorithm, we record the mixed integer programming (MIP) relative error of ILOG Cplex with different time limits under the condition of maximum demand (see Table 9). This is because and for the same MIP relative error, each TSPP needs less solution time. The results show that the more computational time is allowed, the higher the quality of the solution is. However, it is noteworthy that the improvement of solution quality becomes less significant with the increase of time when computation time is more than 2 h. Besides, the quality of solution is acceptable when the time limit is 7200 s, i.e., 2 h. Thus, the time limit was set to 7200 s for each TSPP with fixed demand. In this paper, the proposed heuriustic solution procedure is implemented by using ILOG Cplex and Visual C# on a laptop with a CPU based on a 2.53 GHz Intel Core i3 processor and 8 GB RAM.

Table 9.
Mixed integer programming (MIP) relative error with different time limit under the maximum demand.
Using the proposed solution procedure and the time limit for ILOG Cplex, the iterative process terminated after about eight iterations when the total demand of all OD pairs converged. The total travel demand of the HSR increases by around 7.45% to 1,059,136 in one direction, mainly due to the fact that the travel time for some OD pairs is shorter, caused by fewer stops. In addition, the extent to which the solution reaches maximum demand is also indicated as Table A1 in Appendix A. It is shown that for most OD pairs, the demand does not reach the maximum demand that HSR can serve.
To explore how the service level impacts the demand at the stations, the statistics for demand at stations in one direction are given in Figure 2. The results show that increases in demand at stations 1, 6, 11, 16, and 23 are significant, and corresponded with Beijing South, Jinan West, Xuzhou East, Nanjing South, and Shanghai Hongqiao, respectively. Increases in passenger flow at terminal stations are usually higher than that at intermediate stations. For example, the increase in passenger flow for these five terminal stations is 73,462, which accounted for 56.18% of the total increase for all stations. This reflects the fact that terminal stations have more potential to attract more passenger trips. Thus, the operators should pay more attention to the train services at terminal stations.
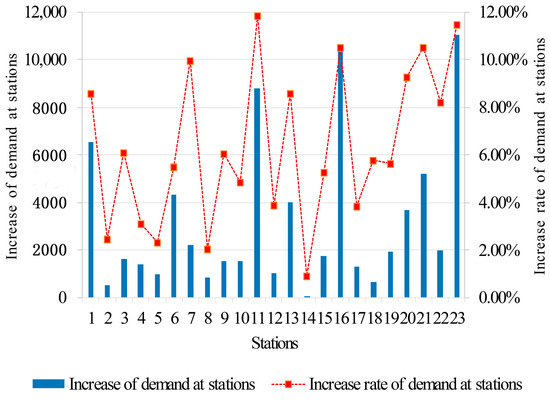
Figure 2.
Demand changes at the stations in one direction.
Table A2 in Appendix A shows the growth rate of the maximum passenger flow compared with the current passenger flow in one direction. As a result, only 12 OD pairs have reduced passenger flow and 241 OD pairs have increased demand. This reflects the fact that the travel time of most OD pairs decreases because the stop times for most OD pairs are reduced. In addition, this seems to indicate that the ridership growth rates of the OD pairs with long distances and more intermediate stations are usually greater than that of OD pairs with shorter distances and fewer intermediate stations. This indicates that the more stations an OD pair passes, the higher the possibility of an increase in passenger flow. This also shows that the number of stops can be further improved. Then, a new HSR train service plan in one direction, i.e., a new line plan, is generated (see Figure A1 in Appendix B), which is more competitive than the existing one. This indicates that operators can improve the current Beijing–Shanghai HSR train service based on our method.
To analyze the competition relationship and the diverted demand, the modal share of each transportation mode for four OD pairs is illustrated in Figure 3. The data on the left represents the current modal share, while the data on the right denotes the optimized results. The increase rate in the HSR market share increases with the increase in distance. For short-distance transportation, such as Beijing–Jinan and Beijing–Xuzhou, the diverted demand of HSR is, to a large extent, from traditional rail, whereas for medium- and long-distance transportation, the diverted demand of HSR is mainly from air transport. This shows that HSR and TR compete in the short-distance transport market, and air transport and HSR compete in the medium- and long-distance transport market.
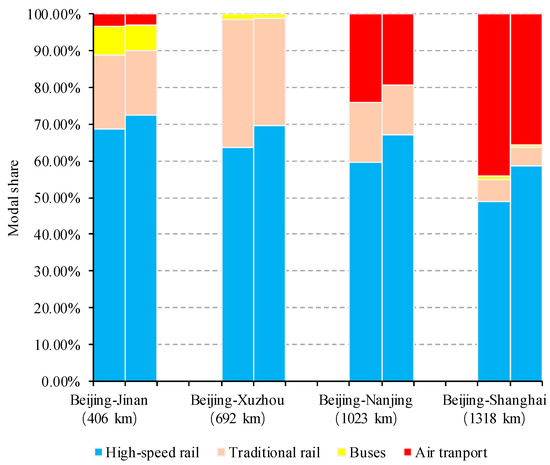
Figure 3.
Modal share of each transportation mode for four OD pairs.
6. Conclusions
In this paper, we proposed an integrated model that combines modal choice and train stop planning. To solve the problem, we presented a decomposition-based heuristic algorithm. Based on a case study, some further conclusions can be drawn:
(1) It would be better to integrate modal choice and train stop planning for designing a sustainable and competitive HSR train service plan.
(2) Terminal stations usually have more potential to attract more ridership. In addition, based on our method, the HSR train service can be improved further.
(3) HSR and TR compete for the short-distance transport market, and air transport and HSR compete for the medium- and long-distance transport market.
(4) The results seem to indicate that the more stations an OD pair passes, the higher the possibility of an increase in passenger flow.
(5) Long-distance passengers are more sensitive to travel time than short-distance passengers. For short-distance passengers, other factors, such as price, may be more important, which needs further analysis.
Although we concentrated on HSR, as a planning decision aid, the model can also be applied to other modes. In addition, our model can easily take other considerations into account.
Although important discoveries have been revealed by this paper, some interesting topics remain to be explored:
(1) Fare planning was not considered in our model, which is an important aspect. In our next study, we will incorporate fare planning into our model.
(2) Travel behavior between HSR trains was not considered, which could be incorporated in future studies.
(3) Train timetable design considering travel behavior is also an interesting topic.
(4) A more effective algorithm is needed to reduce computation time.
(5) In order to be more realistic, different mode choice models for different ODs or distances should be explored based on investigation data.
(6) In addition, to make the results more realistic, the specific characteristics of individual and latent factors should be taken into account.
Author Contributions
Conceptualization, G.J.; Methodology, G.J.; Software, G.J. and H.X.; Formal analysis, G.J.; Supervision, S.H.; Writing—original draft preparation, G.J.; Writing—review and editing, G.J., J.L., Y.L., X.G. and H.X.
Funding
This paper is supported by National Key R&D Program of China (2018YFB1201402, 2016YFE0201700), National Natural Science Foundation of China (U1734204) and Key projects of CRRC Corporation Limited (CIJS18-KJ004).
Acknowledgments
We appreciate editors and reviewers very much for their positive and constructive comments and suggestions for our paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The extent to which the solution reaches maximum demand.
Table A1.
The extent to which the solution reaches maximum demand.
| Station | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.05 | 0.22 | 0.18 | 0.26 | 0.97 | 0.97 | 0.97 | 0.95 | 0.94 | 0.97 | 0.99 | 0.98 | 0.96 | 0.94 | 0.97 | 0.96 | 0.98 | 0.97 | 0.94 | 0.96 | 0.94 | 0.99 |
| 2 | 0.03 | 0.07 | 0.16 | 0.14 | 0.50 | 0.97 | 0.95 | 0.98 | 0.95 | 0.96 | 0.99 | 0.95 | 1.00 | 0.99 | 0.97 | 0.99 | 1.00 | 0.98 | 0.99 | 0.98 | 0.98 | |
| 3 | 0.09 | 0.16 | 0.14 | 0.94 | 0.99 | 0.96 | 0.99 | 0.99 | 0.66 | 0.94 | 0.97 | 0.96 | 0.99 | 0.95 | 0.98 | 0.97 | 0.96 | 0.97 | 1.00 | 0.94 | ||
| 4 | 0.16 | 0.44 | 0.32 | 1.00 | 0.95 | 0.94 | 0.98 | 0.57 | 0.98 | 0.79 | 0.97 | 0.96 | 0.96 | 0.95 | 0.95 | 0.99 | 0.95 | 0.95 | 0.95 | |||
| 5 | 0.13 | 0.96 | 0.90 | 0.97 | 0.74 | 0.95 | 0.99 | 0.94 | 0.98 | 0.99 | 0.96 | 0.98 | 0.94 | 0.99 | 0.97 | 0.95 | 0.97 | 1.00 | ||||
| 6 | 0.04 | 0.29 | 0.25 | 0.46 | 1.00 | 0.57 | 0.95 | 0.98 | 0.94 | 0.99 | 0.98 | 0.94 | 0.99 | 0.96 | 0.95 | 0.96 | 0.99 | |||||
| 7 | 0.08 | 0.16 | 0.16 | 0.94 | 0.33 | 0.96 | 0.33 | 0.31 | 1.00 | 0.96 | 1.00 | 0.96 | 0.97 | 0.99 | 1.00 | 0.97 | ||||||
| 8 | 0.16 | 0.19 | 0.21 | 0.48 | 0.97 | 0.96 | 0.99 | 0.95 | 0.98 | 0.94 | 1.00 | 0.97 | 0.97 | 0.94 | 0.94 | |||||||
| 9 | 0.10 | 0.25 | 0.86 | 0.49 | 0.98 | 0.33 | 0.99 | 0.96 | 0.96 | 0.50 | 0.98 | 1.00 | 0.98 | 0.95 | ||||||||
| 10 | 0.27 | 0.20 | 0.33 | 0.20 | 0.35 | 0.99 | 0.95 | 0.99 | 0.94 | 0.96 | 0.96 | 0.98 | 0.97 | |||||||||
| 11 | 0.36 | 0.89 | 0.24 | 0.48 | 0.50 | 0.99 | 0.95 | 0.97 | 0.98 | 0.96 | 1.00 | 0.95 | ||||||||||
| 12 | 0.19 | 0.09 | 0.33 | 1.00 | 0.31 | 0.49 | 0.27 | 0.47 | 1.00 | 0.96 | 0.97 | |||||||||||
| 13 | 0.17 | 0.24 | 0.73 | 0.96 | 0.50 | 0.42 | 0.26 | 0.99 | 0.97 | 0.94 | ||||||||||||
| 14 | 0.10 | 0.57 | 0.80 | 0.91 | 0.53 | 0.95 | 0.94 | 0.53 | 0.98 | |||||||||||||
| 15 | 0.35 | 0.32 | 0.59 | 0.96 | 0.98 | 0.98 | 0.37 | 0.99 | ||||||||||||||
| 16 | 0.18 | 0.32 | 0.99 | 0.98 | 0.98 | 0.94 | 0.95 | |||||||||||||||
| 17 | 0.10 | 0.09 | 0.34 | 0.49 | 0.96 | 1.00 | ||||||||||||||||
| 18 | 0.07 | 0.14 | 0.52 | 0.24 | 0.98 | |||||||||||||||||
| 19 | 0.09 | 0.15 | 0.18 | 0.94 | ||||||||||||||||||
| 20 | 0.18 | 0.11 | 0.97 | |||||||||||||||||||
| 21 | 0.03 | 0.09 | ||||||||||||||||||||
| 22 | 0.03 |

Table A2.
Growth rate of the maximum passenger flow compared with the current passenger flow in one direction (%).
Table A2.
Growth rate of the maximum passenger flow compared with the current passenger flow in one direction (%).
| Station | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.02 | −0.27 | −1.73 | 2.51 | 5.18 | 7.99 | 16.80 | 10.99 | 13.03 | 9.60 | 21.99 | 23.21 | 0.00 | 24.98 | 12.62 | 0.00 | 0.00 | 15.17 | 15.11 | 19.74 | 9.60 | 20.20 |
| 2 | 0.15 | 0.00 | −2.11 | 1.68 | 1.08 | 0.00 | 12.64 | 4.78 | 5.60 | 1.65 | 3.28 | 0.00 | 0.60 | 20.08 | 0.00 | 0.00 | 13.64 | 0.70 | 1.71 | 11.76 | 11.75 | |
| 3 | 0.20 | 0.00 | 11.20 | 5.86 | 3.00 | 3.47 | 22.62 | 16.18 | 3.52 | 1.30 | 0.00 | 0.61 | 16.11 | 0.85 | 83.33 | 1.18 | 1.61 | 1.44 | 2.51 | 15.21 | ||
| 4 | 6.19 | 0.05 | 8.16 | 8.43 | 1.84 | 2.82 | 16.63 | 9.22 | 16.83 | 0.00 | 3.68 | 2.85 | 0.37 | 63.07 | 3.28 | 0.73 | 1.78 | 0.57 | 2.80 | |||
| 5 | 0.02 | 1.43 | 0.00 | 2.47 | 1.86 | 2.93 | 0.07 | 4.89 | 0.00 | 3.19 | 5.34 | 2.05 | 0.99 | 26.32 | 4.03 | 2.24 | 0.68 | 1.04 | ||||
| 6 | 0.07 | −0.27 | 9.35 | 2.90 | 13.59 | 6.04 | 7.61 | 0.26 | 22.52 | 15.28 | 6.74 | 17.60 | 1.04 | 61.65 | 3.82 | 4.74 | 11.44 | |||||
| 7 | 0.15 | −0.22 | 4.39 | 17.14 | 10.29 | 4.39 | 0.00 | 14.46 | 14.76 | 2.33 | 3.48 | 0.29 | 1.93 | 51.53 | 2.47 | 2.30 | ||||||
| 8 | 0.05 | 0.07 | 0.93 | 0.07 | 1.63 | 0.00 | 1.90 | 3.83 | 0.00 | 1.89 | 0.00 | 0.00 | 0.11 | 6.25 | 1.20 | |||||||
| 9 | 0.16 | −1.48 | 5.36 | 1.59 | 0.00 | 7.04 | 6.04 | 11.00 | 1.91 | 1.06 | 76.42 | 2.53 | 53.30 | 7.49 | ||||||||
| 10 | 0.01 | 8.84 | 1.73 | 0.00 | 22.13 | 3.51 | 18.08 | 1.60 | 8.12 | 17.05 | 4.81 | 51.43 | 5.37 | |||||||||
| 11 | 0.01 | 6.47 | 0.00 | 5.87 | 13.29 | 2.94 | 9.65 | 8.01 | 26.57 | 12.16 | 42.89 | 24.80 | ||||||||||
| 12 | 0.03 | 0.00 | 3.48 | 5.66 | 2.95 | 0.00 | 15.96 | 3.30 | 7.19 | 2.22 | 6.79 | |||||||||||
| 13 | 0.87 | −0.62 | 5.11 | 3.34 | 2.21 | 12.42 | 1.22 | 48.11 | 12.50 | 11.31 | ||||||||||||
| 14 | 0.67 | 0.56 | 0.00 | 2.65 | 1.00 | 2.05 | 3.53 | 3.43 | 3.88 | |||||||||||||
| 15 | 0.98 | 7.28 | 2.76 | 2.57 | 4.02 | 6.17 | 4.18 | 11.25 | ||||||||||||||
| 16 | 1.07 | 0.10 | 3.94 | 5.46 | 18.84 | 10.87 | 18.16 | |||||||||||||||
| 17 | 0.49 | −0.19 | −0.67 | 0.53 | −0.51 | 11.26 | ||||||||||||||||
| 18 | 0.36 | −1.11 | 1.60 | 4.55 | 1.93 | |||||||||||||||||
| 19 | 0.21 | 11.40 | 5.70 | 6.41 | ||||||||||||||||||
| 20 | 0.85 | 6.31 | 7.89 | |||||||||||||||||||
| 21 | 0.50 | −0.26 | ||||||||||||||||||||
| 22 | 0.97 |
Appendix B

Figure A1.
A new HSR train service plan in one direction designed with our method and given data.
References
- Caseetta, E.; Coppola, P. High Speed Rail (HSR) Induced Demand Models. Available online: https://www.sciencedirect.com/science/article/pii/S1877042814000482 (accessed on 3 March 2019).
- Borjesson, M. Forecasting demand for high speed rail. Transp. Res. Pt. A-Policy Pract. 2014, 70, 81–92. [Google Scholar] [CrossRef]
- Cordone, R.; Redaelli, F. Optimizing the demand captured by a railway system with a regular timetable. Transp. Res. Pt. B-Methodol. 2011, 45, 430–446. [Google Scholar] [CrossRef]
- Chang, Y.H.; Yeh, C.H.; Shen, C.C. A multiobjective model for passenger train services planning: application to Taiwan’s high-speed rail line. Transp. Res. Pt. B-Methodol. 2000, 34, 91–106. [Google Scholar] [CrossRef]
- van Hoesel, C.; Goossens, J.; Kroon, L. Optimising Halting Station of Passenger Railway Lines. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.528.4097&rep=rep1&type=pdf (accessed on 3 March 2019).
- Goossens, J.W.; van Hoesel, S.; Kroon, L. On solving multi-type railway line planning problems. Eur. J. Oper. Res. 2006, 168, 403–424. [Google Scholar] [CrossRef]
- Shi, F.; Deng, L.; Huo, L. Bi-level programming model and algorithm of passenger train operation plan. China Railw. Sci. 2007, 28, 110–116. [Google Scholar]
- Deng, L.; Shi, F.; Zhou, W. Stop schedule plan optimization for passenger train. China Railw. Sci. 2009, 30, 102–107. [Google Scholar]
- Ulusoy, Y.Y.; Chien, S.I.J.; Wei, C.H. Optimal All-Stop, Short-turn, and express transit services under heterogeneous demand. Transp. Res. Rec. 2010, 8–18. [Google Scholar] [CrossRef]
- Wang, L.; Jia, L.M.; Qin, Y.; Xu, J.; Mo, W.T. A two-layer optimization model for high-speed railway line planning. J. Zhejiang Univ.-Sci. A 2011, 12, 902–912. [Google Scholar] [CrossRef]
- Fu, H.L.; Nie, L.; Sperry, B.R.; He, Z.H. Train stop scheduling in a high-speed rail network by utilizing a two-stage approach. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Huang, J.; Peng, Q. Two-stage optimization algorithm for stop schedule plan of high-speed train. J. Southwest Jiaotong Univ. 2012, 47, 484–489. [Google Scholar]
- Jong, J.C.; Suen, C.S.; Chang, S.K. Decision support system to optimize railway stopping patterns application to taiwan high-speed rail. Transp. Res. Rec. 2012, 2289, 24–33. [Google Scholar] [CrossRef]
- Fu, H.L.; Sperry, B.R.; Nie, L. Operational impacts of using restricted passenger flow assignment in high-speed train stop scheduling problem. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Li, D.-W.; Han, B.-M.; Li, X.-J.; Zhang, H.-J. High-speed railway stopping schedule optimization model based on node service. J. China Railw. Soc. 2013, 35, 1–5. [Google Scholar] [PubMed]
- Park, B.H.; Seo, Y.I.; Hong, S.P.; Rho, H.L. Column generation approach to line planning with various halting patterns—application to the Korean high-speed railway. Asia Pac. J. Oper. Res. 2013, 30. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, H.; Tong, L. Optimizing the high speed train stop schedule using flexible stopping patterns combination. In Proceedings of the 2014 17th IEEE International Conference on Intelligent Transportation Systems (ITSC 2014), Qingdao, China, 8–11 October 2014; pp. 2398–2403. [Google Scholar]
- Wang, Z.-P.; Luo, X. Stopping schedule optimization of express/local trains in urban rail transit. J. South China Univ. Technol. 2015, 43, 91–98. [Google Scholar]
- Lai, Y.C.; Shih, M.C.; Chen, G.H. Development of efficient stop planning optimization process for high-speed rail systems. J. Adv. Transp. 2016, 50, 1802–1819. [Google Scholar] [CrossRef]
- Yang, L.X.; Qi, J.G.; Li, S.K.; Gao, Y. Collaborative optimization for train scheduling and train stop planning on high-speed railways. Omega-Int. J. Manage. Sci. 2016, 64, 57–76. [Google Scholar] [CrossRef]
- Yue, Y.X.; Wang, S.F.; Zhou, L.S.; Tong, L.; Saat, M.R. Optimizing train stopping patterns and schedules for high-speed passenger rail corridors. Transp. Res. Pt. C-Emerg. Technol. 2016, 63, 126–146. [Google Scholar] [CrossRef]
- Qi, J.G.; Li, S.K.; Gao, Y.; Yang, K.; Liu, P. Joint optimization model for train scheduling and train stop planning with passengers distribution on railway corridors. J. Oper. Res. Soc. 2018, 69, 556–570. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Lerman, S.R. Discrete Choice Analysis: Theory And Application To Travel Demand; MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Cascetta, E.; Nuzzolo, A.; Russo, F.; Vitetta, A. A modified logit route choice model overcoming path overlapping problems. Specification and some calibration results for interurban networks. In Proceedings of the 13th International Symposium on Transportation and Traffic Theory, Lyon, France, 24–26 July 1996. [Google Scholar]
- Vovsha, P. Application of cross-nested logit model to mode choice in Tel Aviv, Israel, metropolitan area. Trans. Res. Rec. 1997, 1607, 6–15. [Google Scholar] [CrossRef]
- Vovsha, P.; Bekhor, S. Link-nested logit model of route choice—Overcoming route overlapping problem. In Forecasting, Travel Behavior, And Network Modeling; National Academy of Sciences: Washington, DC USA, 1998; pp. 133–142. [Google Scholar]
- Ben-Akiva, M.; Bierlaire, M. Discrete choice methods and their applications to short term travel decisions. In Handbook of Transportation Science; Springer: Boston, MA, USA, 1999; pp. 5–33. [Google Scholar]
- Ramming, M.S. Network knowledge and route choice. Unpublished. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Prashker, J.N.; Bekhor, S. Route choice models used in the stochastic user equilibrium problem: A review. Transp. Rev. 2004, 24, 437–463. [Google Scholar] [CrossRef]
- Arentze, T.A.; Molin, E.J.E. Travelers’ preferences in multimodal networks: Design and results of a comprehensive series of choice experiments. Transp. Res. Pt. A-Policy Pract. 2013, 58, 15–28. [Google Scholar] [CrossRef]
- Cascetta, E.; Carteni, A. The hedonic value of railways terminals. A quantitative analysis of the impact of stations quality on travellers behaviour. Transp. Res. Pt. A-Policy Pract. 2014, 61, 41–52. [Google Scholar] [CrossRef]
- Baek, J.; Sohn, K. An investigation into passenger preference for express trains during peak hours. Transportation 2016, 43, 623–641. [Google Scholar] [CrossRef]
- Li, Z.C.; Sheng, D. Forecasting passenger travel demand for air and high-speed rail integration service: A case study of Beijing-Guangzhou corridor, China. Transp. Res. Pt. A-Policy Pract. 2016, 94, 397–410. [Google Scholar] [CrossRef]
- Sohoni, A.V.; Thomas, M.; Rao, K.V.K. Mode shift behavior of commuters due to the introduction of new rail transit mode. In Transportation Research Procedia; Elsevier: Amsterdam, The Netherlands, 2017; pp. 2607–2622. [Google Scholar]
- Carteni, A.; Pariota, L.; Henke, I. Hedonic value of high-speed rail services: Quantitative analysis of the students’ domestic tourist attractiveness of the main Italian cities. Transp. Res. Pt. A-Policy Pract. 2017, 100, 348–365. [Google Scholar] [CrossRef]
- Mattson, J.; Hough, J.; Varma, A. Estimating demand for rural intercity bus services. Res. Transp. Econ. 2018, 71, 68–75. [Google Scholar] [CrossRef]
- Borndorfer, R.; Karbstein, M.; Pfetsch, M.E. Models for fare planning in public transport. Discret Appl. Math. 2012, 160, 2591–2605. [Google Scholar] [CrossRef]
- Espinosa-Aranda, J.L.; Garcia-Rodenas, R.; Ramirez-Flores, M.D.; Lopez-Garcia, M.L.; Angulo, E. High-speed railway scheduling based on user preferences. Eur. J. Oper. Res. 2015, 246, 772–786. [Google Scholar] [CrossRef]
- Cantarella, G.E.; Velona, P.; Watling, D.P. Day-to-day Dynamics & Equilibrium Stability in A Two-Mode Transport System with Responsive bus Operator Strategies. Netw. Spat. Econ. 2015, 15, 485–506. [Google Scholar]
- Li, X.W.; Yang, H. Dynamics of modal choice of heterogeneous travelers with responsive transit services. Transp. Res. Pt. C-Emerg. Technol. 2016, 68, 333–349. [Google Scholar] [CrossRef]
- Canca, D.; De-Los-Santos, A.; Laporte, G.; Mesa, J.A. A general rapid network design, line planning and fleet investment integrated model. Ann. Oper. Res. 2016, 246, 127–144. [Google Scholar] [CrossRef]
- Li, X.W.; Liu, W.; Yang, H. Traffic dynamics in a bi-modal transportation network with information provision and adaptive transit services. Transp. Res. Pt. C-Emerg. Technol. 2018, 91, 77–98. [Google Scholar] [CrossRef]
- Robenek, T.; Azadeh, S.S.; Maknoon, Y.; de Lapparent, M.; Bierlaire, M. Train timetable design under elastic passenger demand. Transp. Res. Pt. B-Methodol. 2018, 111, 19–38. [Google Scholar] [CrossRef]
- Wen, J.; Chen, Y.X.; Nassir, N.; Zhao, J.H. Transit-oriented autonomous vehicle operation with integrated demand-supply interaction. Transp. Res. Pt. C-Emerg. Technol. 2018, 97, 216–234. [Google Scholar] [CrossRef]
- Jeong, Y.; Saha, S.; Chatterjee, D.; Moon, I. Direct shipping service routes with an empty container management strategy. Transp. Res. Pt. e-Logist. Transp. Rev. 2018, 118, 123–142. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).