Abstract
A novel adaptive filtering (AF) algorithm is proposed for group-sparse system identifications. In the devised algorithm, a novel mixed error criterion (MEC) with two-order logarithm error, p-order errors and group sparse constraint method is devised to give a resistant to the impulsive noise. The proposed group-sparse MEC can fully use the known group-sparse characteristics in the cluster sparse systems, and it is derived and analyzed in detail. Various simulations are presented and analyzed to give a verification on the effectiveness of the developed group-sparse MEC algorithms, and the simulated results shown that the developed algorithm outperforms the previously developed sparse AF algorithms for identifying the systems.
1. Introduction
Adaptive filters (AF) is an important field of signal processing, which has been utilized for system identification (SI) [1,2]. For the AF applications, the least mean square (LMS) and its variants based on the two-order error cost function have been used widely since they are low in complexity and simple in practical implementations [1,2,3,4,5]. However, these algorithms might diverge, especially in the presence of outliers. The least mean fourth (LMF) has been reported by using the four-order error, resulting in improved performance at low signal-to-noise ratio (SNR) [6,7]. The LMF algorithm becomes unstable unless a small step size is used, resulting in that it is less accurate and has higher misalignment than the LMS algorithm. Then, mixed AF algorithms have been proposed by introducing a weighted factor to combine the two-order and higher-order errors to construct new cost function for improving the performance without sacrificing the simplicity and stability of the LMS [8,9,10,11,12]. Specifically, the least mean square/fourth (LMS/F) and the least mean mixed norm (LMMN) algorithms have been presented [8,11,12]. However, the early reported algorithms mentioned above cannot use the prior sparse-structure information in practical systems, and their performance might be reduced in the presence of the impulsive noise because of the use of the squared error criterion.
In practical engineering applications, many systems have inherent sparse features, such as the channel impulse response (CIR) of the digital television transmissions, acoustic echo paths and satellite linked echo paths which are typical sparse systems [13,14,15]. In these CIRs, most of the channel coefficients, which are inactive, are equal to zero, while a few active coefficients have larger amplitudes [13,14,15]. In these sparse systems, the convergence speed rate can be accelerated by taking advantage of the prior sparse information structures. Then, proportional update scheme has been proposed to implement the sparse SI, such as proportionate normalized LMS (PNLMS) which yields better convergence at the initial stage by assigning larger gain to the larger taps in comparison to the inactive taps, and the convergence rate for the gain allocated PNLMS algorithm can even be slower than that of the classical normalized LMS (NLMS) algorithm at the later adaptation stage [15]. To further enhance the behavior of the gain assigned PNLMS, several enhanced proportionate-type (Pt) algorithms have been reported, including the improved PNLMS (IPNLMS) algorithm [16]. Additionally, in recent years, zero-attraction (ZA) techniques have been carried out to use the sparse system characteristics to optimize the behavior of the classical LMS algorithm by considering both the convergence and steady-state mean-square-error (MSE). Then, the zero-attraction LMS (ZA-LMS) and its reweighted form (RZA-LMS) were presented by exerting the -norm on the estimated filter coefficient vector to form a penalty to modify the basic LMS’s cost function [17]. However, the ZA-based AF algorithms are not good enough to deal with the group sparse systems.
According to the active coefficient distribution in these sparse systems, the sparse systems are divided into three types [18,19,20,21,22,23]: (1) General sparse systems; (2) one-group sparse systems, and (3) multi-group sparse systems. It is known to us that the network echo paths are modeled as a typical one-group system while the satellite link echo paths have been modeled as multi-group systems, owing to the bulk delays which are always extant in network encoding and jitter buffer delays [19,21]. Then, a block sparse LMS (BS-LMS) was developed by introducing the hybrid -norm into the basic LMS’s cost function to identify group-sparse systems [18] and a block sparse PNLMS (BS-PNLMS) is also realized by integrating mixed -norm of coefficient vector into the basic PNLMS algorithm to provide enhanced performance for dealing with group bulked system identification [19].
In this article, we put our effort to propose a mixed error criterion (MEC) algorithm based on squared error and p-order sign errors for identifying sparse systems in impulsive noise, and a family of generalized group-sparse mixture adaptive filtering (GGS-MAF) algorithms are realized by integrating proportionate group-update approach into the MEC algorithm to utilize the prior group-sparse information. Simulation results reveal that the devised GGS-MAF algorithms converge faster and has lower normalized misalignment (NM) for identifying group-sparse systems in impulsive noises (IN).
2. Traditional Adaptive Algorithms
NLMS Algorithm
Considering the application in the SI, we give the assumptions that an input signal vector is , and a CIR unknown system denotes , where n represents the time index and L denotes the total elements in the discrete CIR system. Thus, the expected signal is [1]
where is an additive noise that is an IN. is considered as the estimation of the CIR, and then, the estimated error is described as [1]
Within the AF framework of SI, our purpose is to minimize the statistical measure of error signal. Two statistical measures, namely, squared error and fourth error, are employed to construct the cost function of the classical LMS and LMF [1,6], which are
Based on the two measurements, many AF algorithms have been derived to implement the SI. For example, the well-known LMS algorithm aims to minimize the squared error to form the cost function (CF) . Considering the commonly used stochastic gradient method (SGM), the LMS’s updating equation is
where denotes the overall step-size. Considering the normalized AF theory, the NLMS’s updating equation is given by
where is to prevent dividing from zero, is a step-size, and means the Euclidean norm. Then, the LMF is reported by using instead of , and its updating equation is
3. The Proposed GGS-MAF Algorithms
The devised algorithms, which are named as generalized group-sparse mixture adaptive filtering (GGS-MAF) algorithms, propose a novel gain allocation scheme for the MEC algorithm, which will be derived in detail. We first proposed a mixed error criterion (MEC) algorithm to give a resistant to the impulsive noise in the context of the SI. Then, a family of constructed GGS-MAF algorithms is presented in detail.
3.1. Mixed Error Criterion Algorithm
As we know, the disturbance in the error signal with a shape of an outlier probably affects the performance of the LMSs such as the impulsive noise. To improve the LMS’s performance, two estimation errors called two-order logarithm error and p-order sign errors are constructed and used to realize the MEC algorithm. Within the AF theory, we can write the modified CF for the MEC algorithm as
where the parameter controls the mixed freedom between the two different errors. Taking the gradient on by , we have
Then, the MEC’s update equation obtained from the SGM is
with a step-size of . is used for preventing the denominator from zero. It is worth noting that the MEC algorithm behaves like the squared error algorithms for , while it works toward p-order sign error algorithm when is close to 0.
3.2. The GGS-MAF Algorithms
In the well-known SGM, we attempt to seek out the minimum of the cost functions regardless of the unknown parameter space. Herein, we use a Riemannian metric structure (RMS) presented in [24] instead of the Euclidean space for providing a rapid convergence within the Pt updating method. In the RMS, the cost functions are given by [24], where the distance between and becomes
with Riemannian metric tensor [24]. According to the proportionate-type AF updating scheme, we can write the reported proportionate-type algorithms via finding out the solution of the following generic updating [25,26]
where represents the step-size. To make the MEC suitable for exploiting the group-sparse characteristics in the blocked echo systems, we introduce proportionate group-update approach to the MEC algorithm for further utilizing the prior group-sparse information. In this case, the GGS-MAF algorithms aim to seek a solution by solving the giving equation
where and . Then, the mixed-norm constraint coefficient vectors are developed to obtain the and which are obtained from . Then, we have
and
Herein, the approximation -norm scheme in [27] is considered to implement , and N denotes the number of groups defined as , and B denotes the length of the group, and is a regularization parameter. Considering the combination of the and , we can have four different GGS-MAF algorithms, named GGS-MAF-1, GGS-MAF-2, GGS-MAF-3 and GGS-MAF-4 algorithms, which are
Then, we can achieve GGS-MAF-1 when is implemented by using (13). The GGS-MAF-2 algorithm is obtained when is achieved from (13) and is from (14). The GGS-MAF-3 algorithm is achieved when is achieved from (14) and is from (13). If and they are both implemented by using (14), we can obtain the GGS-MAF-4. We can see that the proposed GGS-MAF algorithms are realized by the combination of and that control the gain assignment matrix. Herein, the and are given by
where in (16) denotes B-length row-vector, and are calculated by
in which
for utilizing and . Similarly,
for using , where time index n is ignored.
From the derivation of the GGS-MAF algorithms, we can see that the proposed GGS-MAF algorithms are realized by using mixture errors and the mixed - norm to give a resistant to the impulsive noise and to use the prior sparse-structure-information. In the GGS-MAF algorithms, the -norm penalty aims to divide the groups, while the -norm exploits the sparseness of the systems.
4. Results Analysis
Various simulation experiments are setup in order to discuss the estimated performance of the developed GGS-MAF algorithms by considering different inputs. In all the simulations, the additive noise , where denotes a white Gaussian noise (WGN) with SNR of 30 dB, and represents the impulsive interference which is modeled by the Bernoulli-Gaussian (BG) distribution, and . Herein, is another WGN and denotes a Bernoulli process which has a probability of , and the signal-interference ratio (SIR) is 15 dB, and . In these simulations, the regularization parameters are set to be , [26], the step sizes are set to be , , , , and . The performance of GGS-MAF algorithms, defined by using NM which has a definition of , is discussed over two group sparse systems. The first group sparse system has one group active channel coefficients distributed in [267,282], and the second one possesses two group active coefficients appeared in [267,282] and [778,793], which are given in Figure 1.
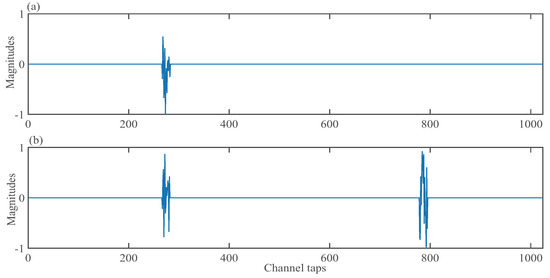
Figure 1.
Performance comparisons of the four generalized group-sparse mixture adaptive filtering (GGS-MAF) algorithms.
4.1. Performance Comparisons of Four GGS-MAF Algorithms
From the Equation (15), it is clear to see that there are four forms of GGS-MAF algorithms. An experiment is created to discuss the performance of these GGS-MAF algorithms with colored noise (CN) input. One group system is used for the first 7000 iterations, and we use the two group system for the next 7000 iterations. The experiment is similar to those in [9,14,19]. The CN is realized by the WGN filtering via a first-order autoregressive process at a pole of 0.8. Herein, and are selected for all the GGS-MAF algorithms, and the simulation results are demonstrated in Figure 2. We can see from the results that the GGS-MAF-1 algorithm behaves the best since it only uses the -norm constraints where the -norm can well exploit the sparsity properties in the systems. Thus, we only choose GGS-MAF-1 to give a comparison with previous AF algorithms with different group sizes.
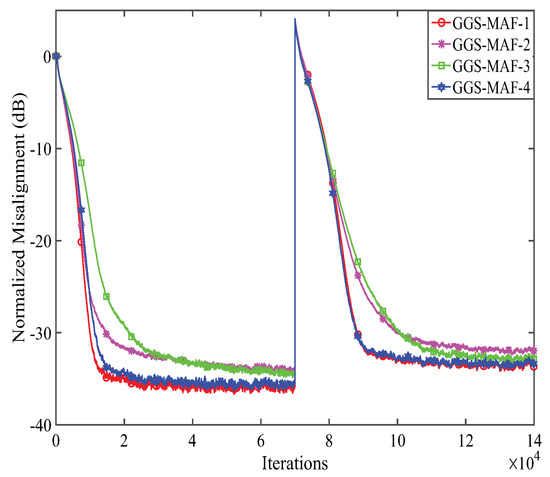
Figure 2.
Performance comparisons of the four GGS-MAF algorithms.
4.2. Performance of the Proposed GGS-MAF-1 Algorithm with Different B
The effects of parameter B on the estimated system performance for the GGS-MAF-1 are discussed with different inputs (WGN, CN and speech signal (SS)). Herein, four different B of 4, 8, 16 and 64 are selected for evaluating the GGS-MAF-1 algorithm. The ZA factors are set to be , , for WGN input, , for CN input, and , for SS input, where , and corresponds to the ZA-LMS, RZA-LMS and ZA-PNLMS algorithms. Parameter is set to be 20 under the condition that the input signal is WGN or CN, and , , are selected for SS input. Simulation results with different inputs are presented in Figure 3. From the results in Figure 3a, it is obvious to see that the GGS-MAF-1 algorithm converges quickly and arrives at the lower steady state error for the sake of comparison with the other algorithms when the input is WGN signal. Figure 3b,c show that the convergence speed of the GGS-MAF-1 algorithm degrades for CN and SS inputs, but the performance of the GGS-MAF-1 algorithm is still better than the other algorithms. Note that the GGS-MAF-1 algorithm with exhibits the best performance while GGS-MAF-1 algorithm with behaves the worst. This is because that the size for each group is 16 in the two different systems. If the group size B is greater than 16, each group will cover much more inactive taps, and hence, the performance will be degraded. In addition, we can see that there is a sudden jump in Figure 2 and Figure 3 because the system is changed from one group system to two group system. This is to say that the proposed algorithm can track the time-varying systems, which is similar to [9,14,19]. Since the active system coefficients in the two group system are doubled in comparison with the one group system, the two group system is less sparse, and hence, the original normalized misalignment is higher.
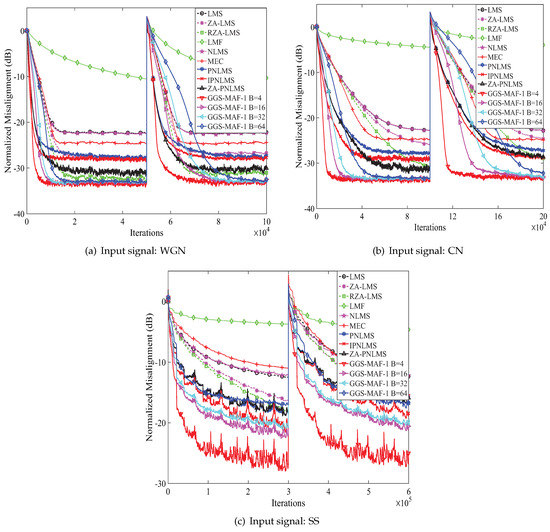
Figure 3.
Performance of the proposed GGS-MAF-1 algorithm with different B. White Gaussian noise (WGN), colored noise (CN), speech signal (SS), least mean square (LMS), zero-attraction LMS (ZA-LMS), reweighted ZA-LMS (RZA-LMS), least mean fourth (LMF), normalized LMS (NLMS), mixed error criterion (MEC), proportionate normalized LMS (PNLMS), improved PNLMS (IPNLMS).
4.3. SNR Effects on the Proposed GGS-MAF-1 Algorithm
In this experiment, different (from 0 dB to 40 dB) are used to analyze the NM of the proposed GGS-MAF-1 algorithm for CN input. is chosen for GGS-MAF-1 algorithm, and other parameters are same as previous experiments. Simulation performance of the GGS-MAF-1 algorithm with different SNRs is shown in Figure 4. Figure 4 demonstrates that the NM decreases when SNR increases from 0 to 40 dB. We can see that the NM of the proposed GGS-MAF-1 algorithm is lower than other algorithms.
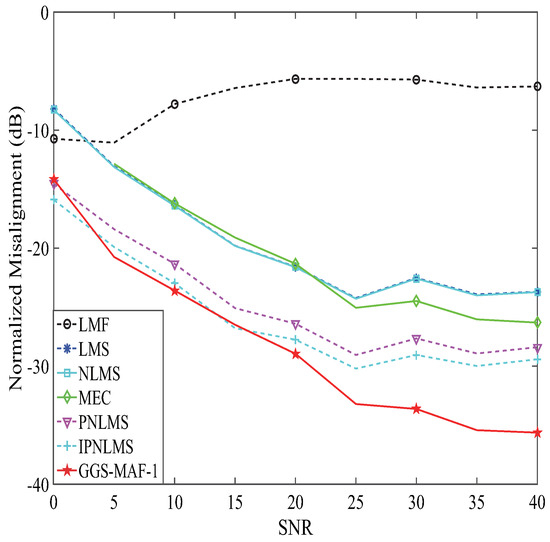
Figure 4.
Signal-to-noise ratio (SNR) effects on the proposed GGS-MAF-1 algorithm.
5. Conclusions
A group of GGS-MAF algorithms obtained from the mixed error criterion have been proposed, investigated and discussed for identifying group-sparse systems. The constructed GGS-MAF algorithm has been achieved by incorporating mixed norm constraints into the MEC’s cost function to exploit the prior group-sparse information. The proposed GGS-MAF is derived in detail. Different parameters are considered to discuss the performance of GGS-MAF algorithms under three different inputs. The results shown that the devised GGS-MAF algorithms converges faster and gives lower NM compared with the traditional AF algorithms for both one-group and two-group systems. In the future, the proposed algorithm can be investigated for multi-channel network applications.
Author Contributions
Conceptualization, Y.L. and A.C.; methodology, Y.L.; software, Y.L.; validation, Y.L., A.C. and Z.J.; formal analysis, Y.L.; investigation, Z.J.; resources, W.S.; data curation, W.S.; writing origional draft preparation, Y.L. and Z.J.; writing—review and editing, J.W.; visualization, J.W.; supervision, Y.L.; project administration, Y.L.; funding acquisition, Y.L.
Funding
This research is partly supported by the National Key Research and Development Program of China (2016YFE0111100), the National Science Foundation of China (61571149), the Science and Technology Innovative Talents Foundation of Harbin (2016RAXXJ044), the Opening Fund of Acoustics Science and Technology Laboratory (SSKF2016001), the Key Research and Development Program of Heilongjiang Province (GX17A016), the China Postdoctoral Science Foundation (2017M620918), the Natural Science Foundation of Beijing (4182077).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Diniz, P.S.R. Adaptive Filtering: Algorithms and Practical Implementation, 4th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU-Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Cheng, H.; Xia, Y.; Huang, Y.; Yang, L.; Mandic, D.P. A normalized complex LMS based blind I/Q imbalance compensator for GFDM receivers and its full second-order performance analysis. IEEE Trans. Signal Process. 2018, 66, 4701–4712. [Google Scholar] [CrossRef]
- Li, Z.; Xia, Y.; Pei, W.; Wang, K.; Mandic, D.P. An augmented nonlinear LMS for digital self-interference cancellation in full-duplex direct-conversion transceivers. IEEE Trans. Signal Process. 2018, 66, 4065–4078. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Wang, Y. Noise-free maximum correntropy criterion algorithm in non-gaussian environment. IEEE Trans. Circuits and Syst. II 2019. [Google Scholar] [CrossRef]
- Walach, E.; Widrow, B. The least mean fourth (LMF) adaptive algorithm and its family. IEEE Trans. Inf. Theory 1984, 30, 275–283. [Google Scholar] [CrossRef]
- Eweda, E.; Zerguine, A. A normalized least mean fourth algorithm with improved stability. In Proceedings of the 2010 Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2010; pp. 1002–1005. [Google Scholar]
- Lim, S.J.; Harris, J.G. Combined LMS/F algorithm. Electron. Lett. 1997, 33, 467–468. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Ma, M.; Qin, X.; Duan, J.; Li, Y.; Chen, B. Kernel recursive generalized mixed norm algorithm. J. Frankl. Inst. 2018, 355, 1596–1613. [Google Scholar] [CrossRef]
- Chambers, J.A.; Tanrikulu, O.; Constantinides, A.G. Least mean mixed-norm adaptive fltering. Electron. Lett. 1994, 30, 1574–1575. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Sparse least mean mixed-norm adaptive filtering algorithms for sparse channel estimation applications. Int. J. Commun. Syst. 2016, 30, 1–14. [Google Scholar] [CrossRef]
- Cotter, S.F.; Rao, B.D. Sparse channel estimation via matching pursuit with application to equalization. IEEE Trans. Commun. 2002, 50, 374–377. [Google Scholar] [CrossRef]
- Gui, G.; Mehbodniya, A.; Adachi, F. Least mean square/fourth algorithm for adaptive sparse channel estimation. In Proceedings of the IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 296–300. [Google Scholar]
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptation in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Benesty, J.; Gay, S.L. An improved PNLMS algorithm. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; pp. 1881–1884. [Google Scholar]
- Chen, Y.; Gu, Y.; Hero, A.O. Sparse LMS for system identification. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 3125–3128. [Google Scholar]
- Jiang, S.; Gu, Y. Block-sparsity-induced adaptive filter for multi-clustering system identification. IEEE Trans. Signal Process. 2015, 63, 5318–5330. [Google Scholar] [CrossRef]
- Liu, J.; Grant, S.L. Proportionate affine projection algorithms for block-sparse system identification. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 529–533. [Google Scholar]
- Li, Y.; Jiang, Z.; Jin, Z.; Han, X.; Yin, J. Cluster-sparse proportionate NLMS algorithm with the hybrid norm constraint. IEEE Access 2018, 6, 47794–47803. [Google Scholar] [CrossRef]
- Jin, Z.; Li, Y.; Liu, J. An improved set-membership proportionate adaptive algorithm for a block-sparse system. Symmetry 2018, 10, 75. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Shi, W.; Han, X.; Chen, B.D. Blocked maximum correntropy criterion algorithm for cluster-sparse system identification. IEEE Trans. Circuits Syst. II 2019. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Omer-Osman, O.M.; Han, X.; Yin, J. Mixed norm constrained sparse APA algorithm for satellite and network channel estimation. IEEE Access 2018, 6, 65901–65908. [Google Scholar] [CrossRef]
- Sayin, M.O.; Yilmaz, Y.; Demir, A.; Kozat, S.S. The Krylov-proportionate normalized least mean fourth approach: Formulation and performance analysis. Signal Process. 2015, 109, 1–13. [Google Scholar] [CrossRef]
- Wagner, K.; Doroslovački, M. Proportionate-Type Normalized Least Mean Square Algorithms; John Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Benesty, J.; Paleologu, C.; Ciochina, S. On regularization in adaptive filtering. IEEE Trans. Audio Speech Languag. Process. 2011, 19, 1734–1742. [Google Scholar] [CrossRef]
- Gu, Y.; Jin, J.; Mei, S. l0 Norm Constraint LMS Algorithm for Sparse System Identification. IEEE Signal Process. Lett. 2009, 16, 774–777. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).