1. Introduction
There are graph invariants that describe certain properties of a graph, which we call topological indices. Various topological indices are proposed and researched by both theoretical chemists and mathematicians. Topological index is mainly used to study the quantitative relationship between structure and performance and between structure and activity. It would be helpful for describing partially biological and chemical properties. Some of them have been proved to be successful [
1]. Recently, finding the extreme value for the topological indices, as well as the related problem of characterizing the extremal graphs, attracted the attention of many researchers, and many results were obtained.
Among these topological indices, one of most widely known topological description is the Wiener index, which was proposed in 1947 and represents the sum of the distances of all pairs of vertices in the graph, i.e.,
Another graph invariant based on distance is called the Harary index, has been introduced independently by Placšić et al. [
2] and by Ivanciuc et al. [
3] in 1993, which is the sum of the reciprocal distances of any vertex pair in graph
G, i.e.,
More results on the Harary index can be found in the literature [
4,
5,
6,
7].
Recently, graph invariants based on resistance distance have attracted the attention of theorists, such as the Kirchhoff index. The resistance distance is what Klein and Randić [
8] came up with as a function of the distance of the graph. The resistance distance between two vertices
u and
v of
G, denoted by
, represents the effective resistance of two elements
u and
v in a circuit, and each edge in
G means the cell resistance.
Similar to the distance in the path graph, the resistance distance is also closely related to the structure of the graph, and not only has good mathematics and physics characteristics [
9,
10], but also has widespread chemistry applications.
The Kirchhoff index is one of the most studied topological indices, which is defined as
With the continuous development and improvement of electrical network theory, D.J. Klein and O. Ivanciue [
11] investigated the global cyclictiy index
, defined as
Y. Yang [
12] obtained some results on global cyclicity index.
Inspired by the Harary index, S. Chen et al. [
13] modify the global cyclicity index and put forward the Resistance–Harary index, described as
In [
14], the structure of the graph with maximum
value is described among the connected graph with given order and cut edges.
All graphs considered here are connected and simple. Let G be a graph with vertex set and edge set , and the degree of each vertex v is expressed as , which means the number of neighbors of v in G. is the distance between u and v in G, the longest distance between any two vertices in the graph is called the diameter.
As usual, let , and be a cycle, a star, and a path with n vertices, respectively. represents the subgraph obtained by deleting an edge from graph G. Similarly, represents the graph obtained by adding an edge to graph G. Let U and W be all the vertex sets of G. Where , then represents the complement of W in U. The pendant vertex of G refers to the vertex of graph G with degree 1. The pendant edge is the edge adjacent to the pendant vertex.
A bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets X and Y, such that every edge connects a vertex in X to one in Y. Vertex sets X and Y are usually called the parts of the graph. If a graph G is a bipartite graph, and all vertices in X are connected to all vertices in Y, then G is a completed bipartite graph.
If the number of vertices in each part of the completed bipartite is
m and
n, respectively, denoted it by
. The
cut vertex (edge) will increase the number of branches of the graph if it is removed. Other terms not defined here are referred to [
15].
A matching M in graph G is a set of non-adjacent edges, that is, no two edges share a common vertex. A maximum matching (also known as maximum-cardinality matching) is a matching that contains the largest possible number of edges. There may be many maximum matchings. The matching number of a graph G is the size of a maximum matching.
Inspired by the above results, it is natural to consider these extremal problems from the class of general connected graphs to the bipartite graphs. Our aim in this article is to study the extremal bipartite graphs with given parameters on Resistance–Harary index. First, we give the upper bound and lower bound of index, and describe the corresponding extremal graphs in the bipartite graph of a given order. We also describe the graphs with maximum index in terms of graph parameters such as vertex bipartiteness , (where ), cut edges, and matching numbers.
2. General Connected Bipartite Graphs
In this section, we give the upper bound and lower bound of
index, and describe the corresponding extremal graphs in the bipartite graph of a given order. In the simple connected acyclic graph, the Resistance distance and distance from the two points in the graph are equal, that is, the Resistance–Harary index and the Harary index are the same in the acyclic graph. There is a formula for this scenario:
However, when the connected graph contains cycles, the resistance distance is different from the general distance. Our calculation is based on electrical network theory, given a fixed resistor on each edge, the shortest distance between two vertices represents the effective resistance of the corresponding two components in the circuit. Let
be the cycle on
k vertices, where
. By Ohm’s law, any two components in a circuit
with
, we have
then, we have
We start with some useful lemmas.
Lemma 1 ([
8]).
w is the cut vertex of graph G, and let u and v be two vertices of different components of . There must be . Lemma 2 ([
14]).
Let G be a graph that is not complete. Add an edge from G and we get the graph . So there is . That is to say, increases with addition of edges. Corollary 1. G is a connected graph with n vertices, and H is a connected spanning subgraph of G. Then , the equal sign is true when .
Lemma 3 ([
13]).
Let T be a tree on n vertices different from and . Then Theorem 1. is the graph with maximum index among all connected bipartite graphs of order n.
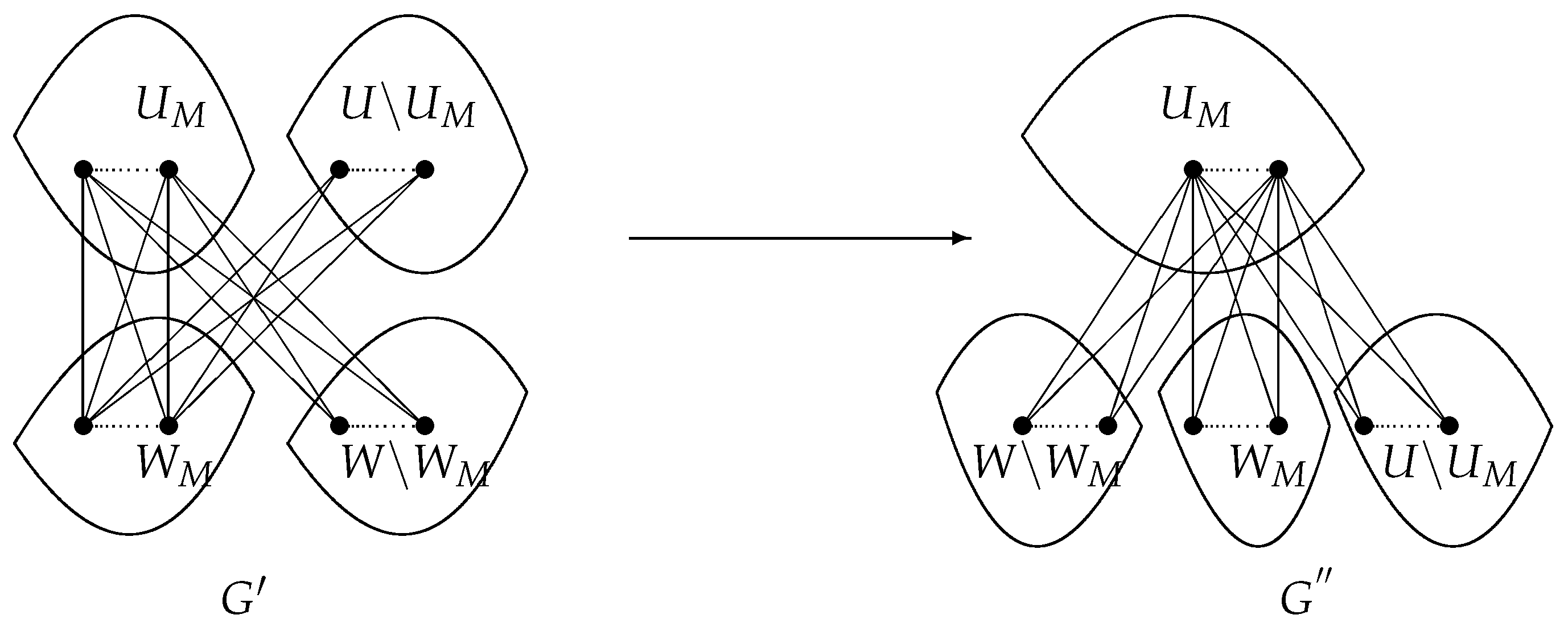
Proof. Choose as the graph such that its Resistance–Harary index is as large as possible, let be its two divisions, where . We first prove the following two claims.
Claim 1. is a complete bipartite graph.
Suppose to the contrary that is a graph that is not complete. Thus we can add one edge from to to form a new graph . It is obvious that is still a bipartite graph. By Lemma 2, we know that , which contradicts the maximality of .
Claim 2..
From Claim 1, we denote
as
. In a complete connected bipartite graph
, Klein [
16] obtain that the resistance distance between vertices from
X and
Y, respectively, is
. The resistance distance between any two vertices in
X and in
Y is
and
, respectively, hence, by Lemma 1 and the definition of
index, we can get that
Let
, if
, then, we have
So obtain the extremal value if and only if . This completes the proof. ◻
Theorem 2. For any bipartite graph G of order n, we have Proof. By Lemma 3 and Corollary 1, we can deduce that
has minimal
index in the bipartite graphs of order
n. By Theorem 1, one can see that
has the maximum Resistance–Harary index. By direct calculation, we have
and
This completes the proof. ◻
4. Graphs with Given Vertex Bipartiteness
In this section, we described the extremal graph with a given vertex bipartiteness for Resistance–Harary index. Let
and
be the graphs where any two vertices do not intersect. We obtain the joint graph of
and
through the correlation of every vertex of graph
with every vertex of graph
, denoted it by
. The vertex bipartiteness of a graph
G is the minimum number of vertices removed makes the graph
G a bipartite graph, which is denoted by
, see [
17]. Let
be the set of the graphs with
n vertices and
, where
is the positive integer that does not exceed
.
Lemma 5. Let G be the graph in . There is a pair of positive integers s and t that satisfies , we have for all graphs , and the equality holds if and only if .
Proof. By Lemma 2, we know that is a topological index whose value increases with the number of edges. Let be the graph with the largest index value, that is to say, for all graphs . Since , there are () such that is a bipartite graph, let be its vertex sets, and and . Thus, . If , then there exists two vertices u, v that are not adjacent and , . We get another graph by getting a new edge , then , and we get the contradiction, so . In addition, if there are two vertices that are not adjacent to each other and , then we get a new graph , by adding a new edge into , then , again, a contradiction. This suggests that the subgraph induced by is , so . At last, we prove that . To the contrary, assume that or . Naturally, we set . Pick a vertex v from Y, and add the edges to , where , the resulting graph is , and it has edges more than graph , implying that , which is a contradiction. Therefore, and . Complete the proof of the theorem. ◻
Lemma 6. Let and . If , then .
Proof. By the definition of the
index and by Lemma 1, we have
where
. We have
where
. So
where
. Then
This completes the proof. ◻
Next, we describe the graphs with extremal Resistance–Harary index values in the graph with given vertex bipartiteness. The following conclusion is easy to deduce by applying Lemmas 2, 5, and 6.
Theorem 4. Let G be the graph of . Where , then
(a) If is even, then holds, where .
(b) If is odd, then holds, where .
5. Bipartite Graph with a Given Cut Edges
In this section, we determine bipartite graph given cut edges with maximum Resistance–Harary index.
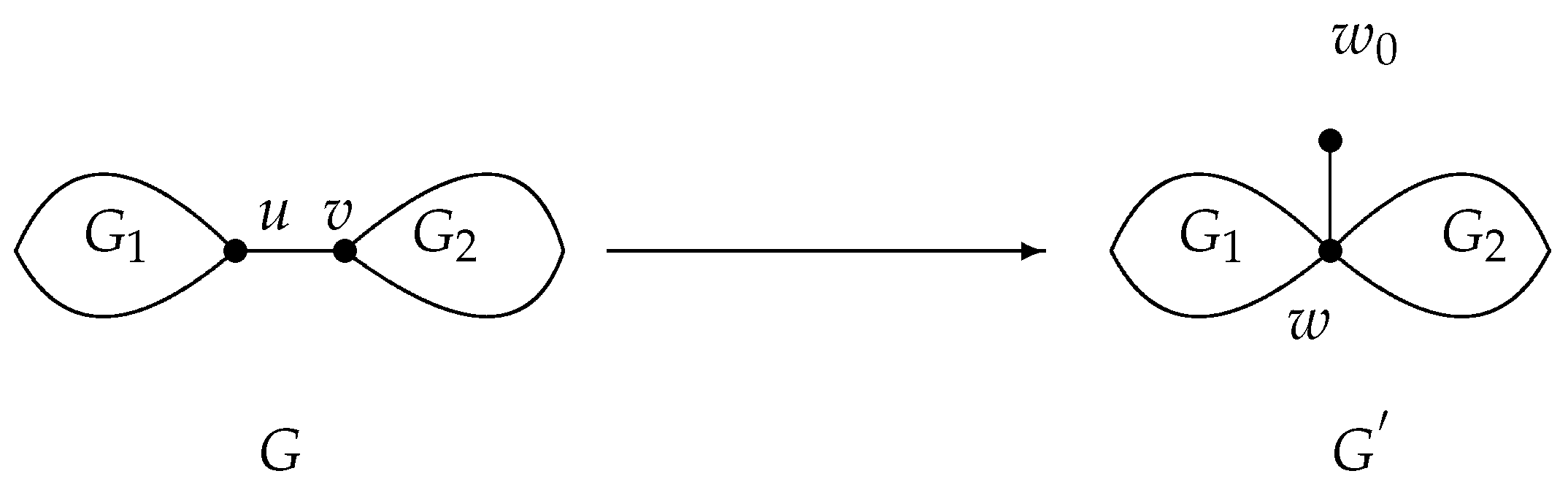
Lemma 7. and are connected graphs whose vertices do not intersect, assume that and . We connect u and v to get G, and if we identified two vertices u with v in G, we get graph . Let the new vertex be w, which is adjacent to a pendant vertex (see Figure 2). Then . Proof. By Lemma 1 and the definition of
index, we have
Then
This completes the proof. ◻
Lemma 8 ([
13]).
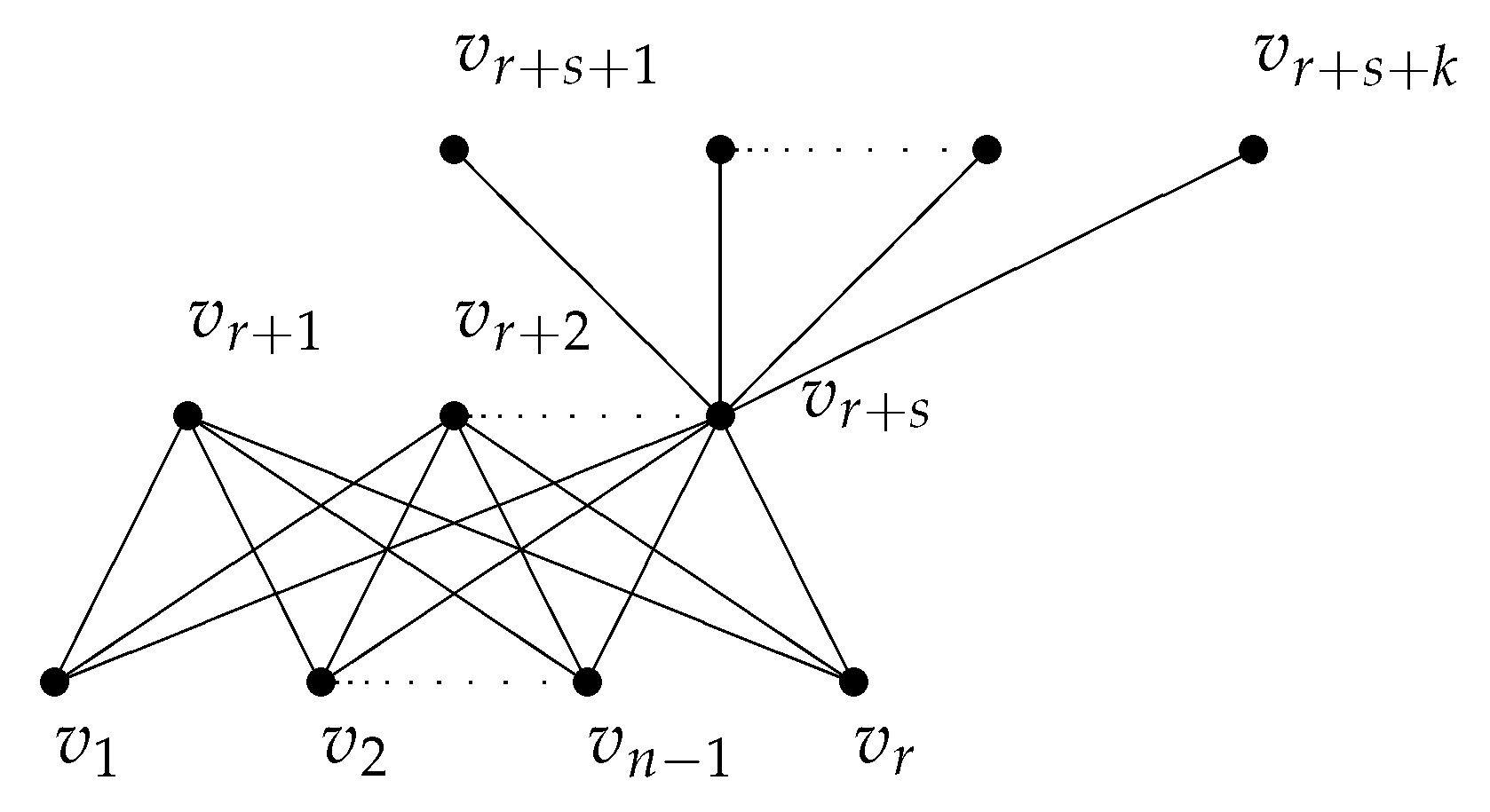
Let G be a graph from a connect graph by attaching some pendant vertices. If u and v are two vertices in graph , pendant vertices are attached to the vertex u and b pendant vertices are attached to the vertex v. Let and . Then or . Lemma 9. For bipartite graph with and (see Figure 3). One has . Proof. By Lemmas 1 and direct calculations, we can get the value of
of
.
Let
. Then we know from the proof of Theorem 1,
. Similarly, let
, by comparison, we have
. Thus, we have
This completes the proof. ◻
By Lemma 9, it is straightforward to see that
Corollary 2. Let be the bipartite graphs of order n with k cut edges obtained by identifying the center of order star graph and one vertex of a complete graph with vertices. For , we have , and equality is attained if and only if .
Let be the set of connected bipartite graphs with n order and k cut edges. For , from Theorem 1, then the graph with maximum index is isomorphic to graph . For , the bipartite graph is a tree, so the Resistance distance and distance between the vertices in the tree are equal, that is, the Resistance–Harary index in the tree was the same as the index. So the maximum Resistance–Harary index is obtained uniquely at .
Next, we focus on the case .
Theorem 5. In all connected bipartite graphs with n order and k cut edges, where , the maximum Resistance–Harary index is founded at .
Proof. Let be the graph having the maximum index value in and be the set of cut edges of . Where and are bipartite graphs, then by Lemma 2, we can know that each component of is a complete bipartite graph. In addition, by Lemma 7, every edge of must be pendant edges. Hence, must be the graph constructed from by hanging k pendant edges. Finally, by Lemma 8, all these pendant edges in must be attached to one common vertex. That is to say, must be one of the graph , furthermore, by Corollary 2, we get that . This completes the proof. ◻