Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion
Abstract
1. Introduction
2. Modeling the Equations of Motion
3. RANS Solver (ANSYS-CFX)
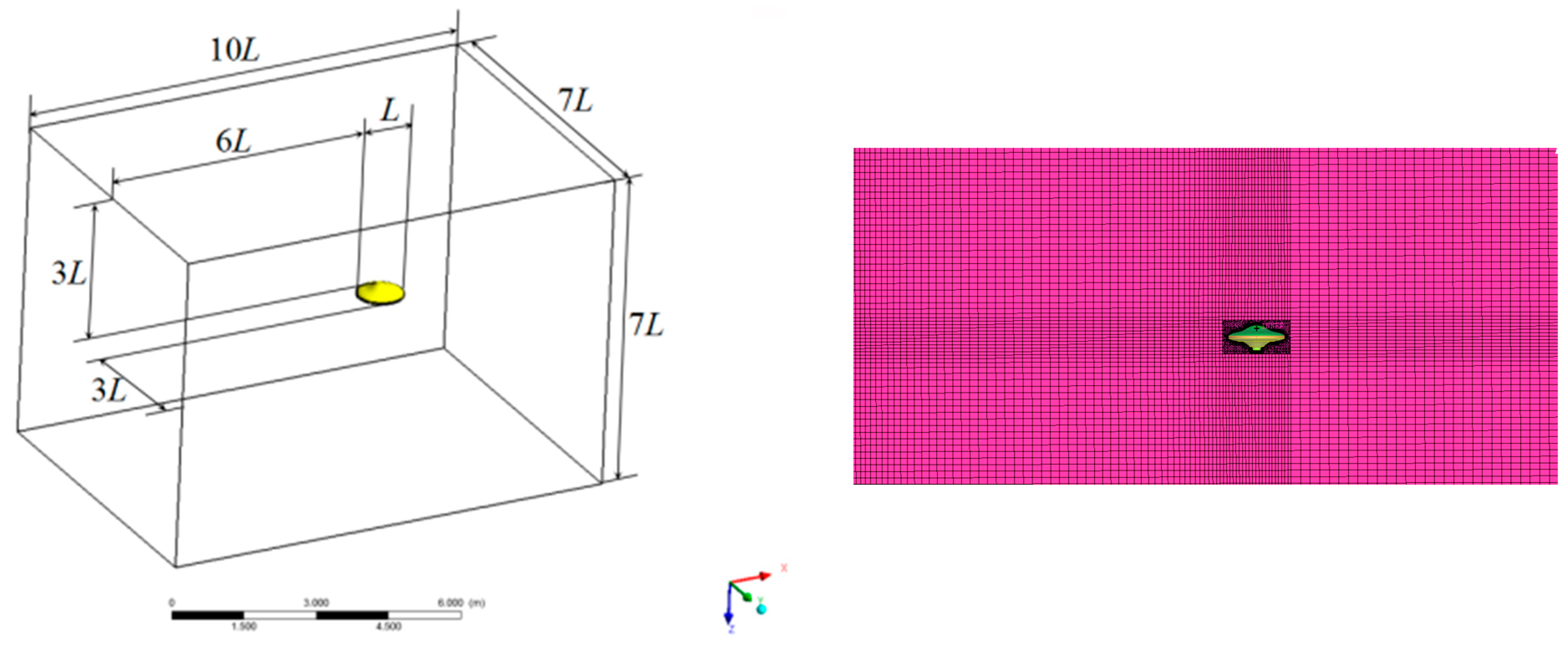
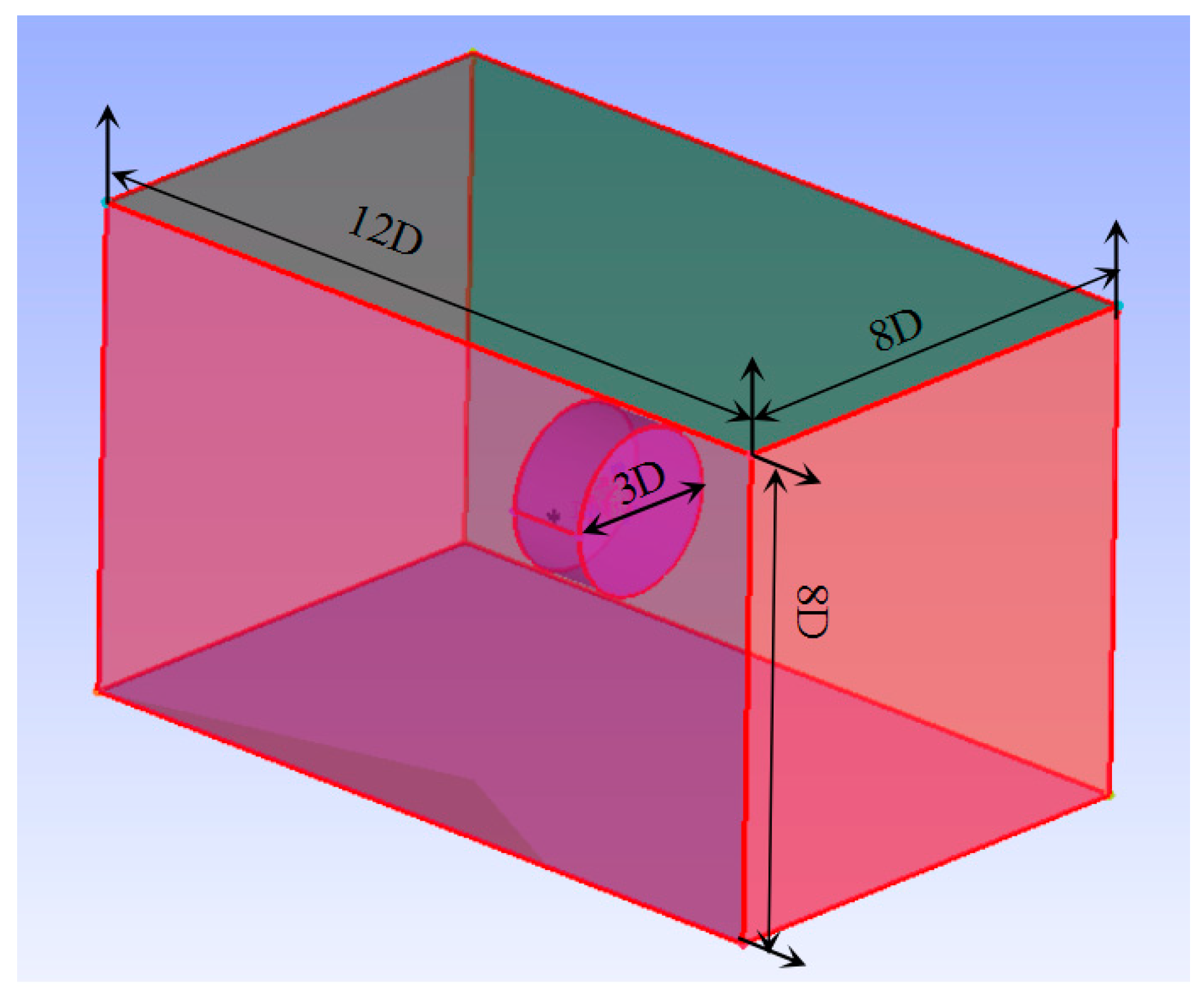
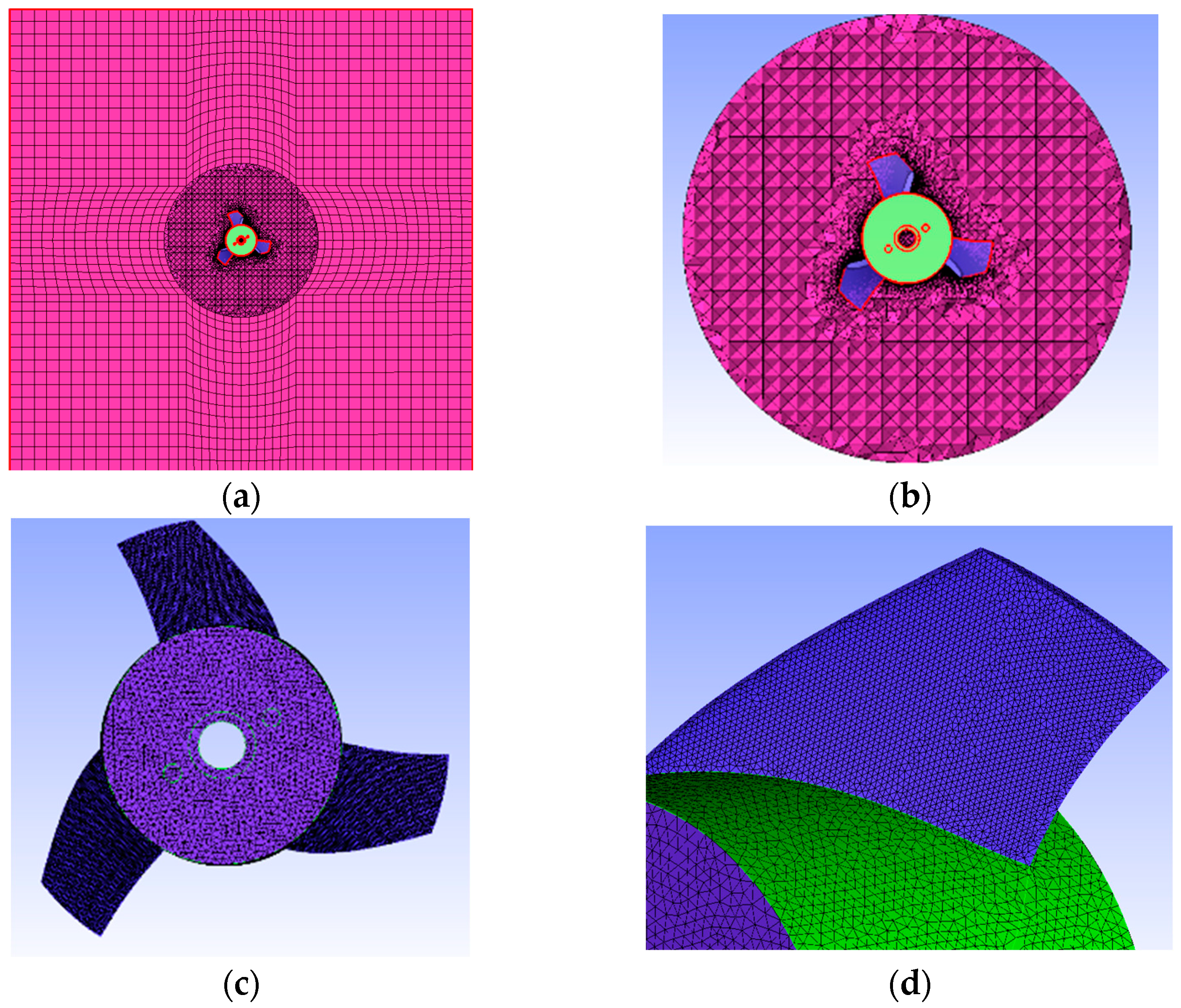
3.1. Mesh Generation
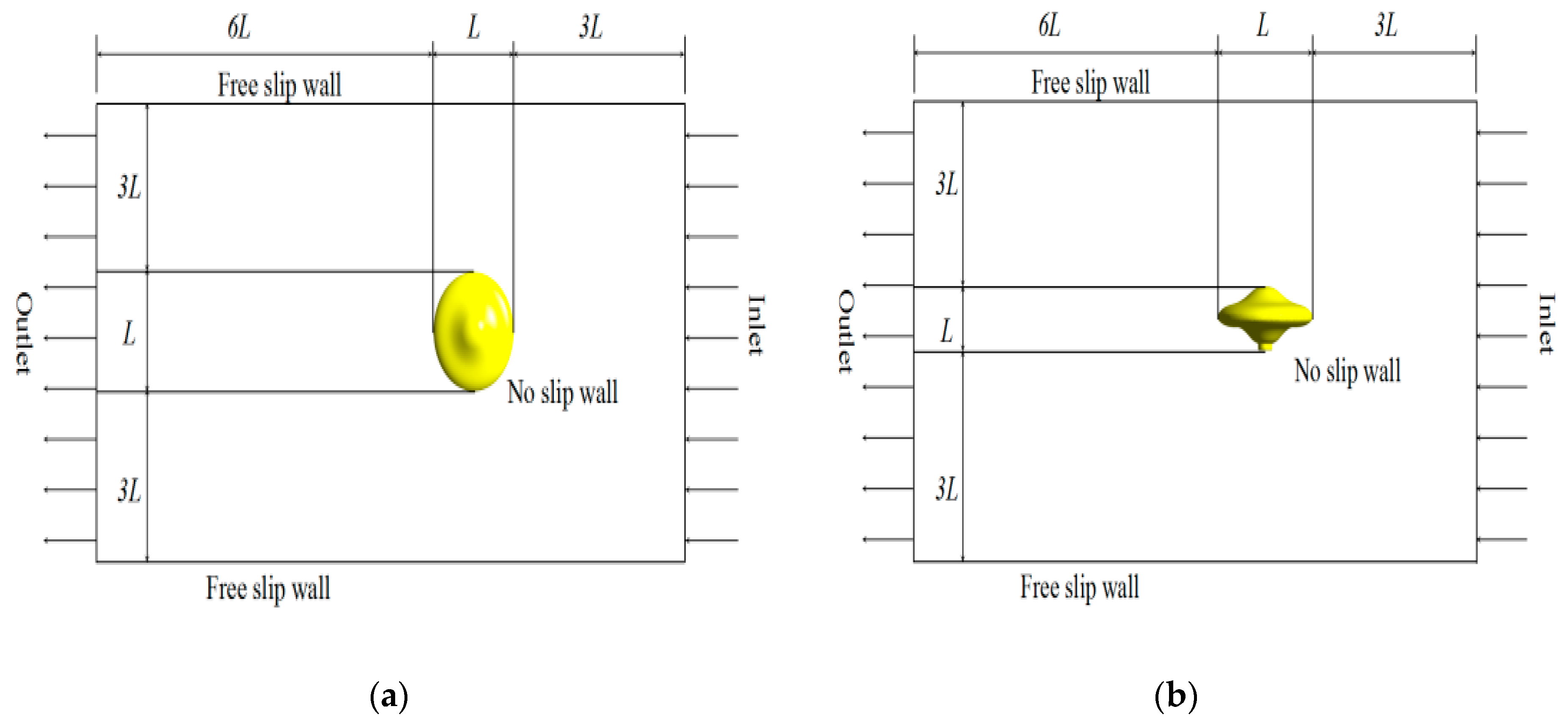
3.2. Boundary Conditions
3.3. Computer Simulation
4. Simulation Results of Magnus Force
4.1. Formulation of Hydrodynamic Performance
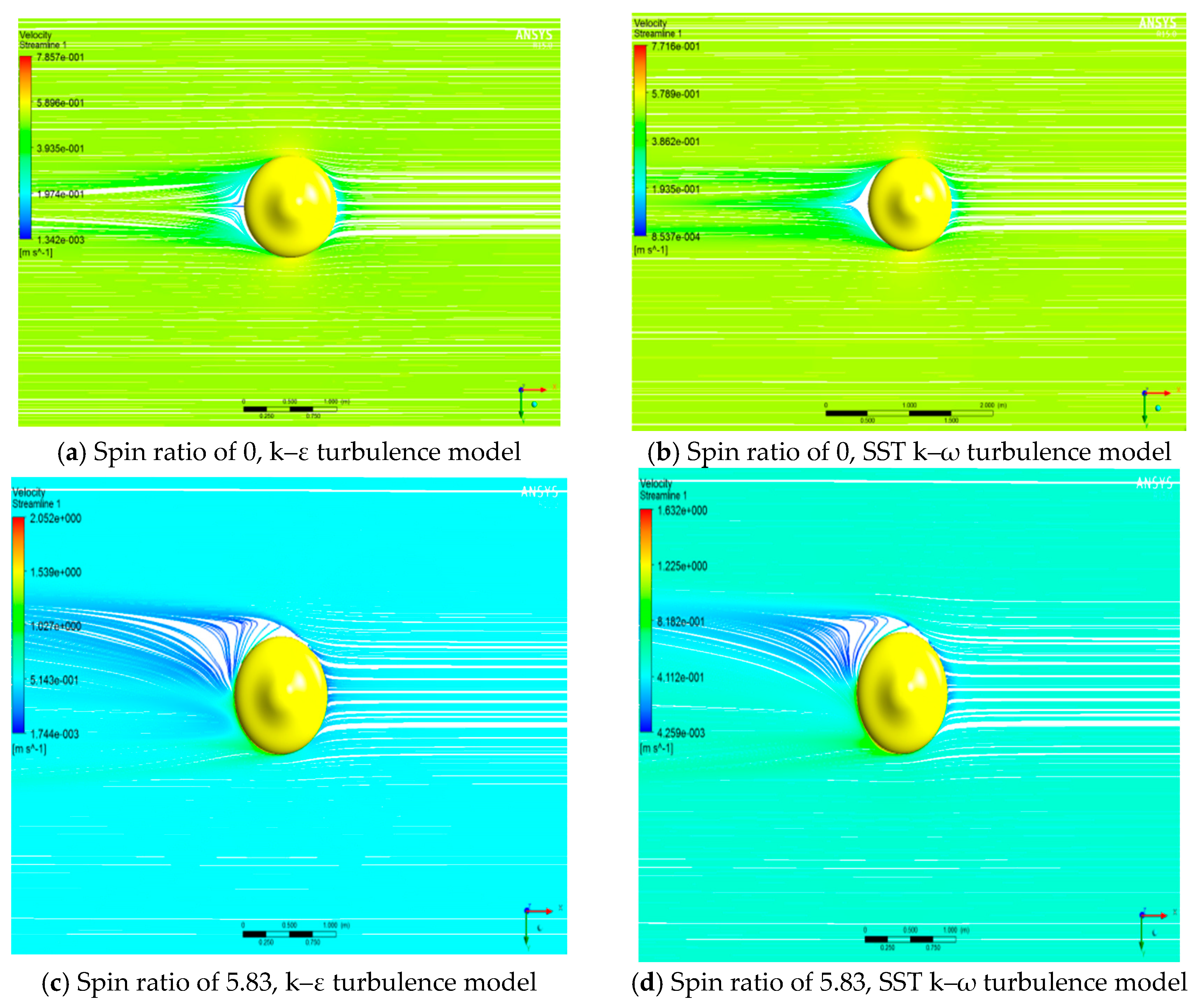
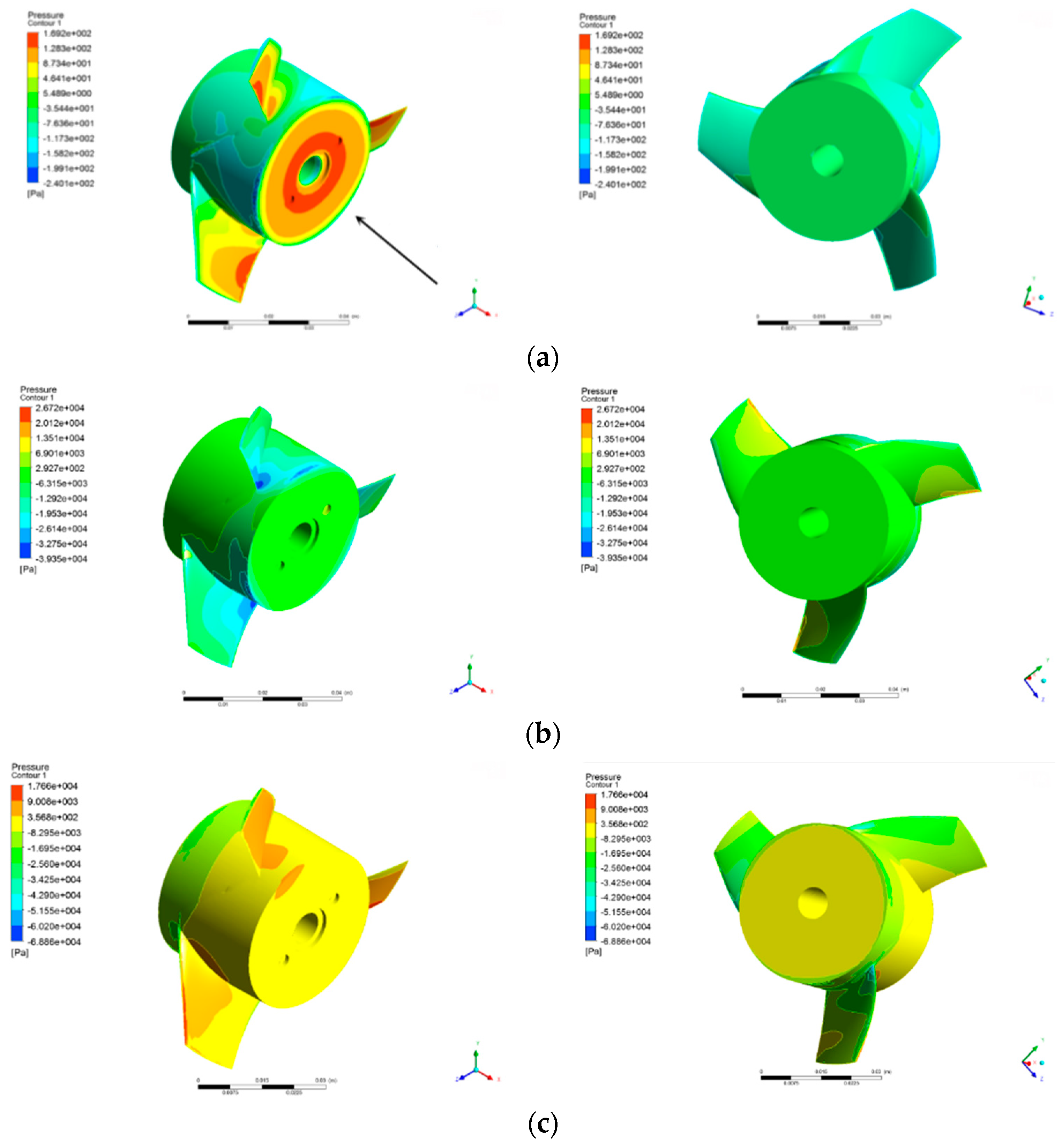
4.2. Distribution of Pressure and Streamlines
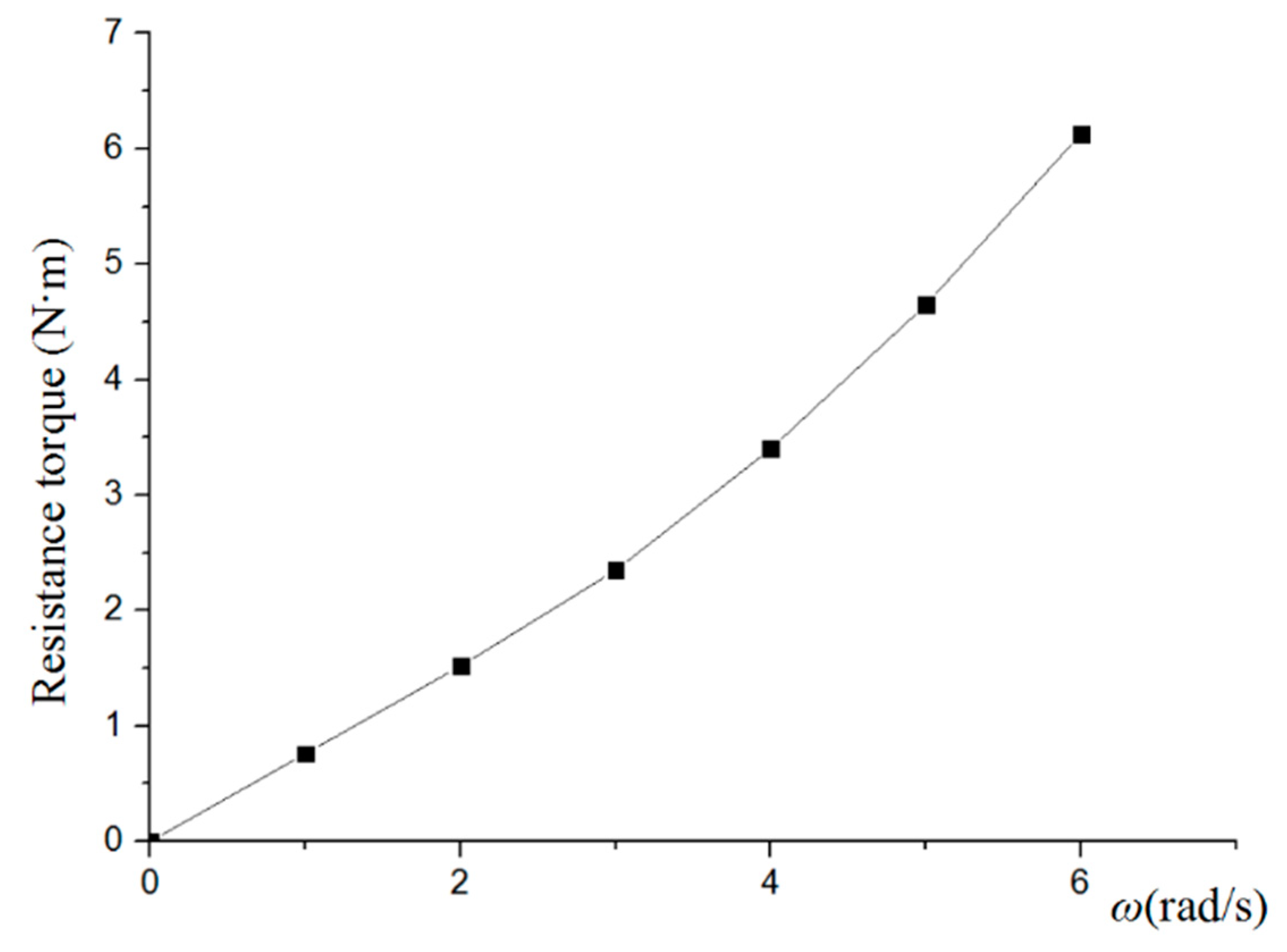
4.3. CFD Prediction of Hydrodynamic Coefficients
5. Hydrodynamic Performance of the High-Speed Propeller
5.1. Mesh Generation
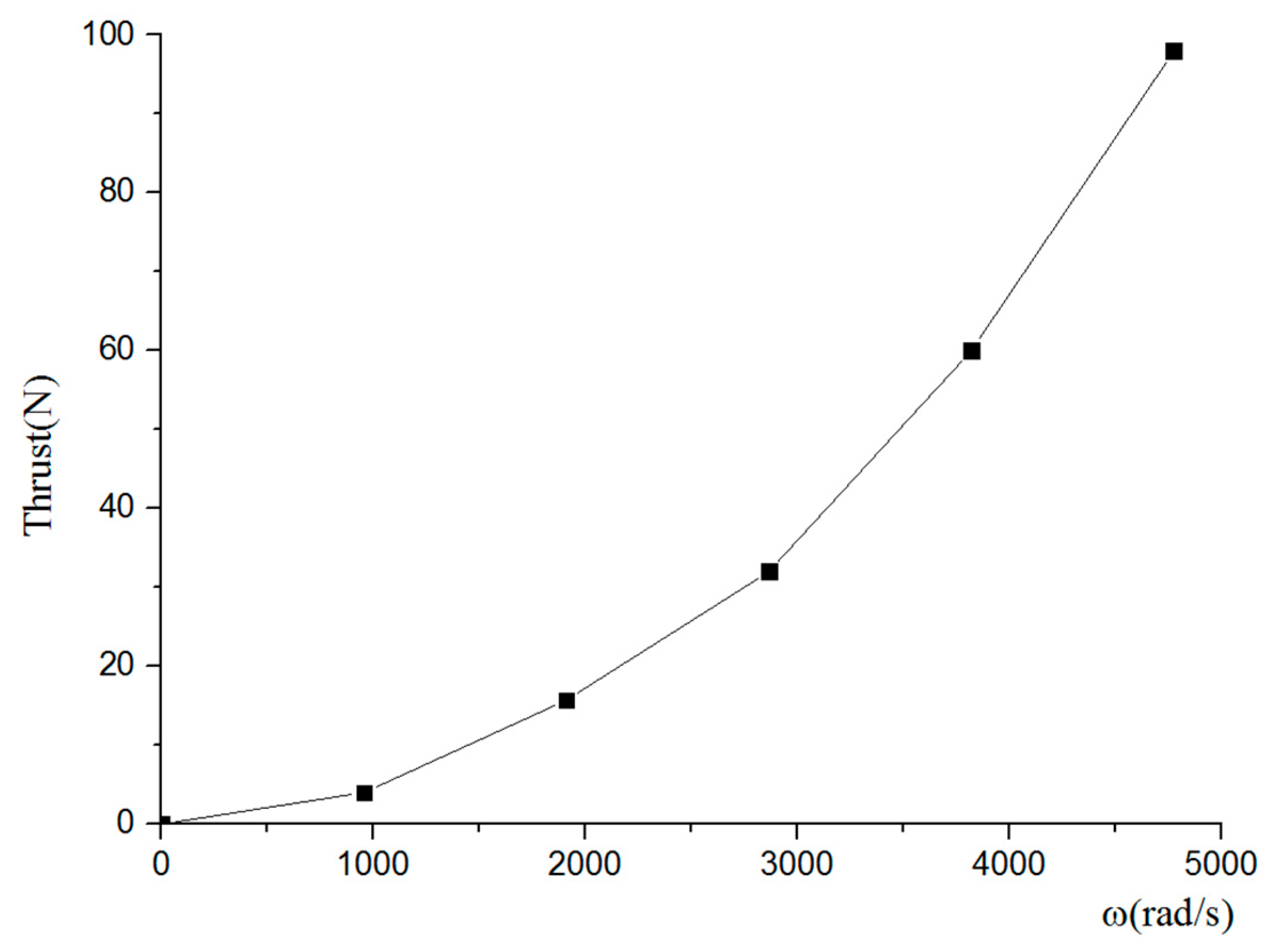
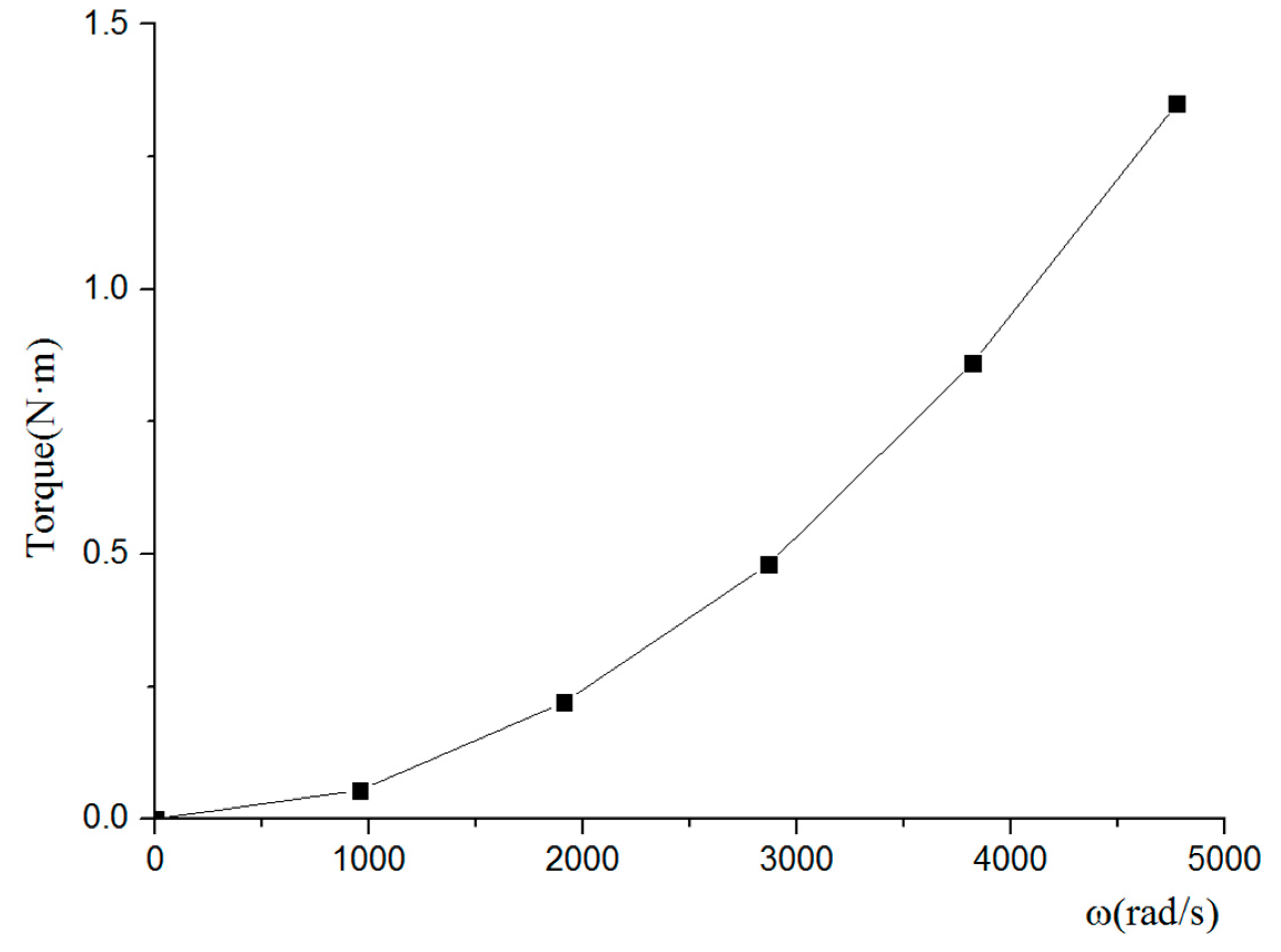
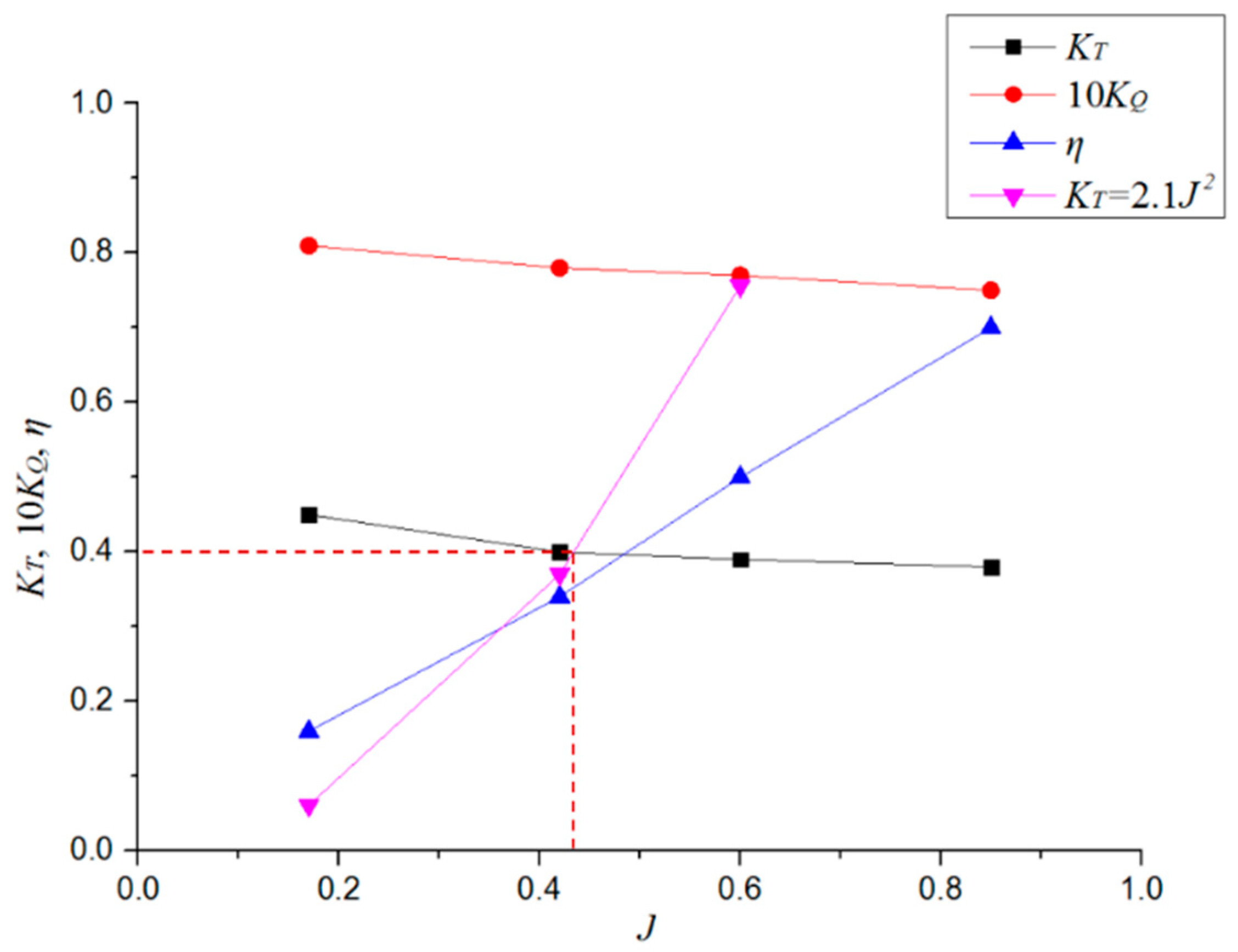
5.2. Hydrodynamic Performance of the Propeller
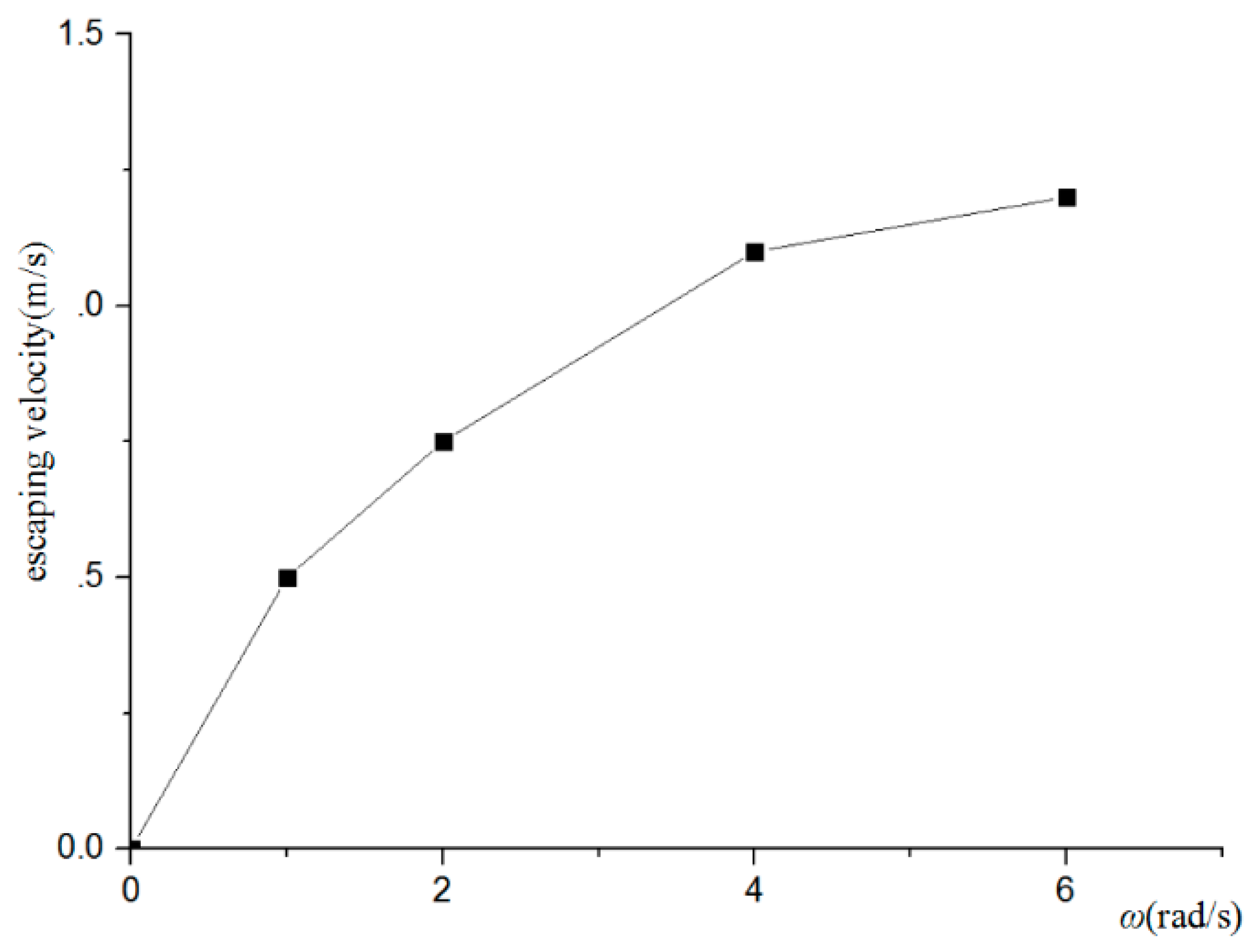
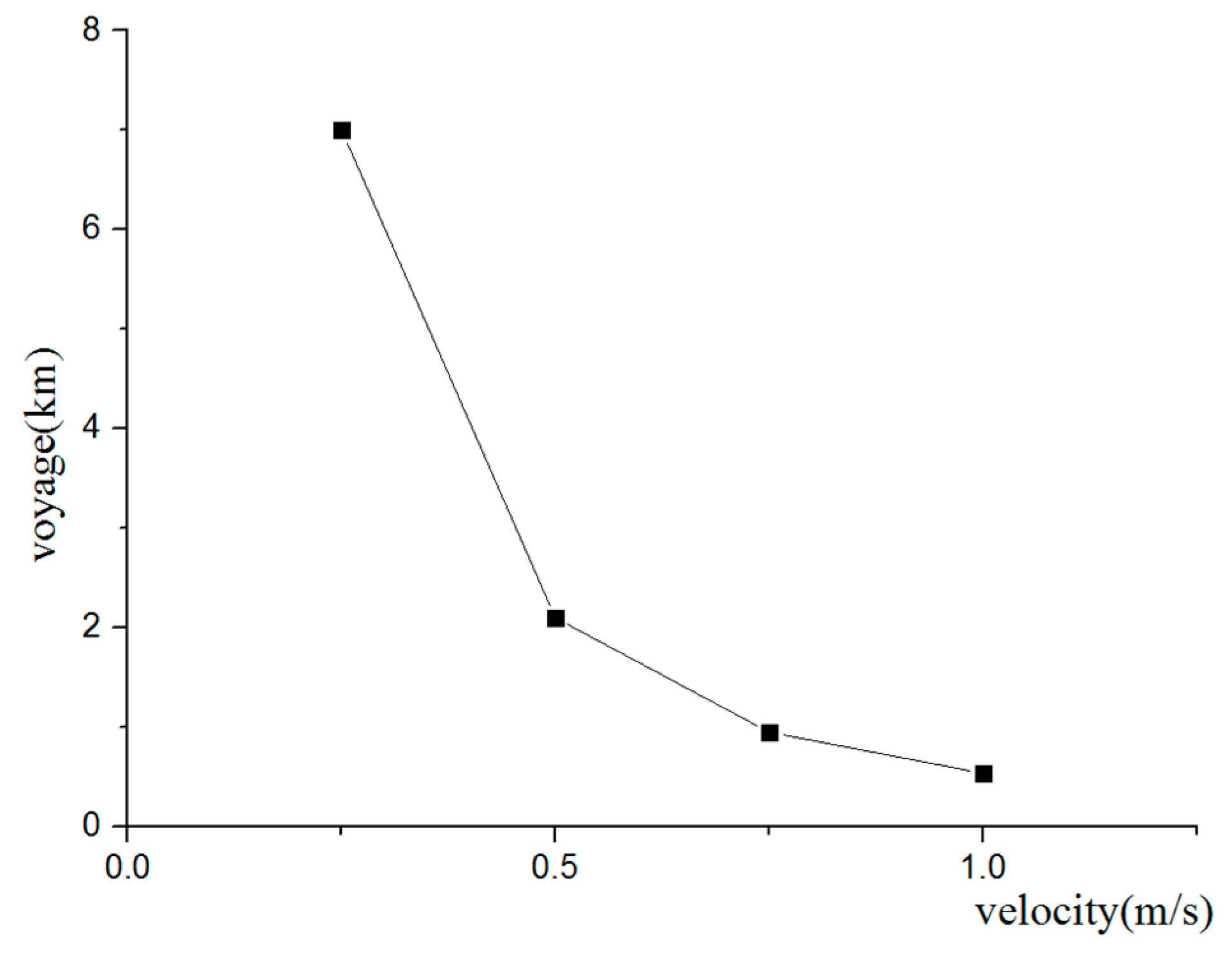
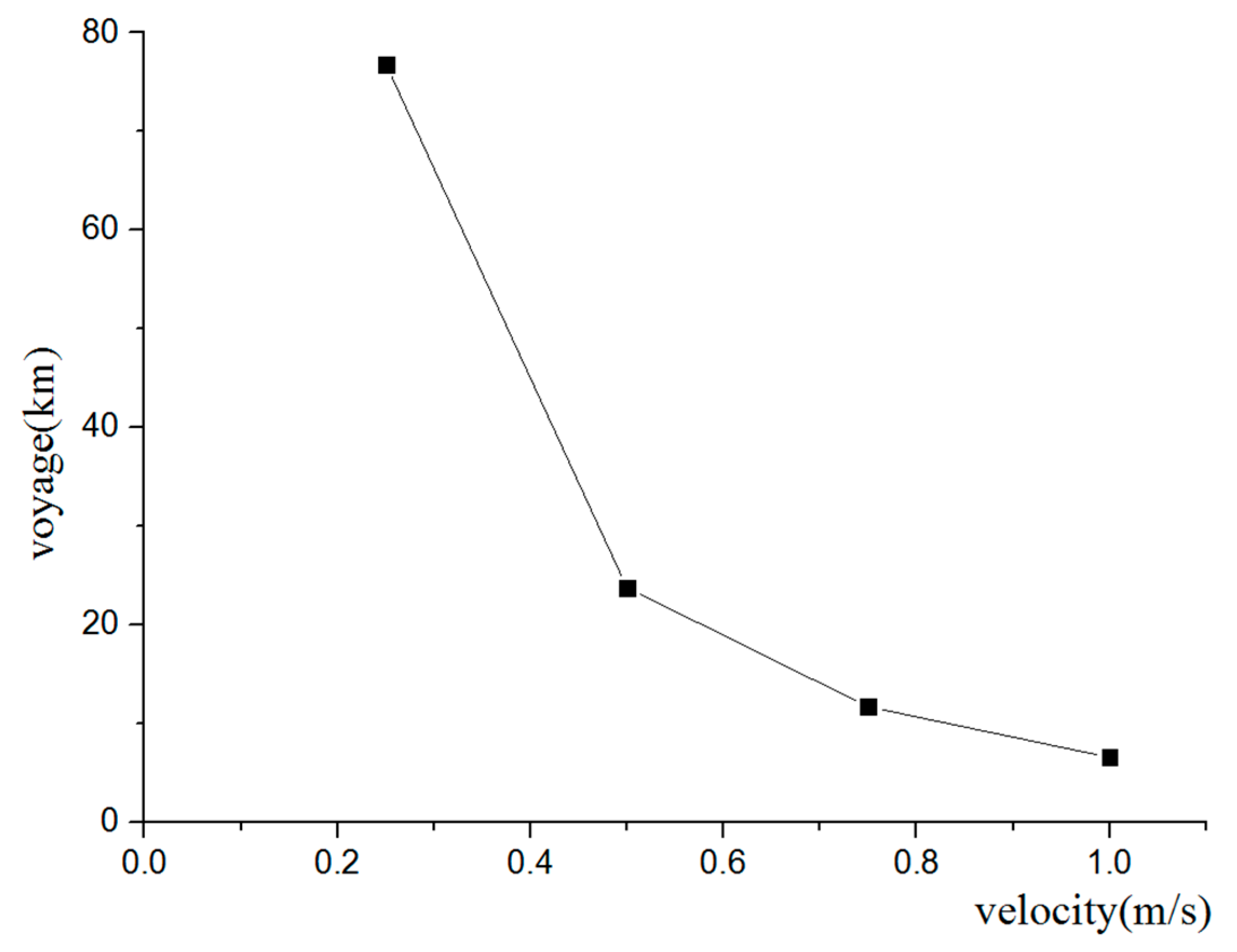
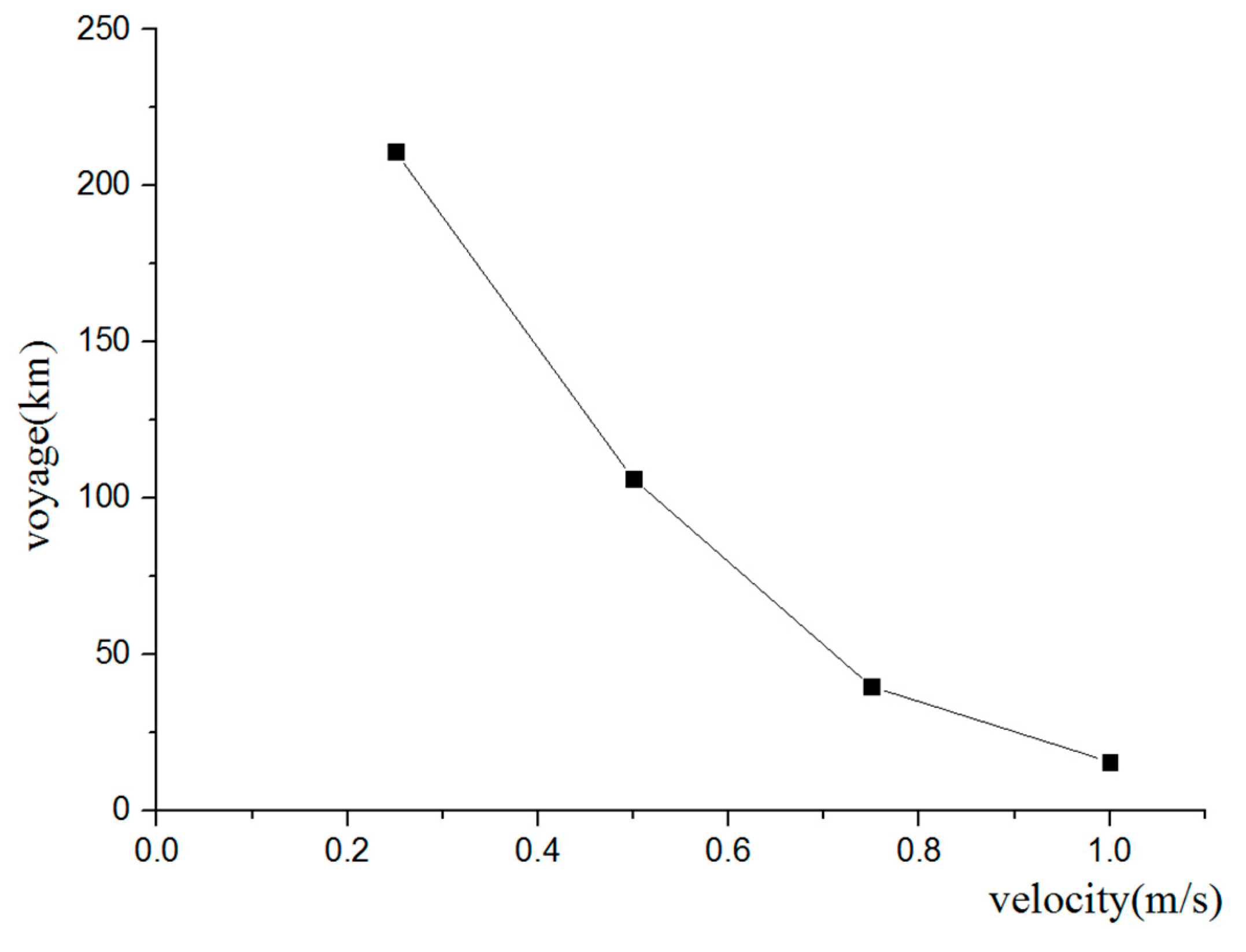
6. A Comparison Using Three Different Methods to Escape Currents
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Evans, J.; Nahon, M. Dynamics modeling and performance evaluation of an autonomous underwater vehicle. Ocean Eng. 2004, 31, 1835–1858. [Google Scholar] [CrossRef]
- Pyo, J.; Cho, H.; Joe, H.; Ura, T.; Yu, S.C. Development of hovering type AUV “Cyclops” and its performance evaluation using image mosaicing. Ocean Eng. 2015, 109, 517–530. [Google Scholar] [CrossRef]
- Phillips, A.; Furlong, M.; Turnock, S.R. The Use of Computational Fluid Dynamics to Determine the Dynamic Stability of an Autonomous Underwater Vehicle. 2007. Available online: https://core.ac.uk/download/pdf/28341.pdf?repositoryId=34 (accessed on 18 March 2018).
- Lapierre, L.; Soetanto, D. Nonlinear path-following control of an AUV. Ocean Eng. 2008, 33, 89–102. [Google Scholar] [CrossRef]
- Phillips, A.B.; Turnock, S.R.; Furlong, M. The use of computational fluid dynamics to aid cost-effective hydrodynamic design of autonomous underwater vehicles. Proc. Inst. Mech. Eng. Part M J. Eng. Mar. Environ. 2010, 224, 239–254. [Google Scholar] [CrossRef]
- Chen, C.W.; Jiang, Y.; Huang, H.C.; Ji, D.X.; Sun, G.Q.; Yu, Z.; Chen, Y. Computational fluid dynamics study of the motion stability of an autonomous underwater helicopter. Ocean Eng. 2017, 143, 227–239. [Google Scholar] [CrossRef]
- Minnick, L.M. A Parametric Model for Predicting Submarine Dynamic Stability in Early Stage Design; Virginia Tech: Blacksburg, VA, USA, 2006. [Google Scholar]
- Tanakitkorn, K.; Wilson, P.A.; Turnock, S.R.; Phillips, A.B. Depth control for an over-actuated, hover-capable autonomous underwater vehicle with experimental verification. Mechatronics 2017, 41, 67–81. [Google Scholar] [CrossRef]
- Lin, X.; Guo, S. Development of a Spherical Underwater Robot Equipped with Multiple Vectored Water-Jet-Based Thrusters. J. Intell. Robot. Syst. 2012, 67, 307–321. [Google Scholar] [CrossRef]
- Ba, X.; Luo, X.; Shi, Z.; Zhu, Y. A vectored water jet propulsion method for autonomous underwater vehicles. Ocean Eng. 2013, 74, 133–140. [Google Scholar]
- Chen, C.W.; Jiang, Y.; Huang, C.H.; Leng, J.X.; Yu, Z.; Su, H.; Chen, Y. Computational Fluid Dynamics Study on Magnus Force of an Autonomous Underwater Helicopter. In Proceedings of the OCEANS 2017, Anchorage, AK, USA, 18–21 September 2017; pp. 1–6. [Google Scholar]
- Kray, T.; Franke, J.; Frank, W. Magnus effect on a rotating sphere at high Reynolds numbers. J. Wind Eng. Ind. Aerodyn. 2012, 110, 1–9. [Google Scholar] [CrossRef]
- Yang, C.; Peng, S.; Fan, S.; Zhang, S.; Wang, P.; Chen, Y. Study on docking guidance algorithm for hybrid underwater glider in currents. Ocean Eng. 2016, 125, 170–181. [Google Scholar] [CrossRef]
- Chen, C.W.; Kouh, J.S.; Tsai, J.F. Maneuvering Modeling and Simulation of AUV Dynamic Systems with Euler-Rodriguez Quaternion Method. China Ocean Eng. Int. J. 2013, 27, 403–416. [Google Scholar] [CrossRef]
- Chen, C.W.; Kouh, J.S.; Tsai, J.F. Modeling and Simulation of an AUV Simulator with Guidance System. IEEE J. Ocean. Eng. 2013, 38, 211–225. [Google Scholar] [CrossRef]
- Bettle, M.C.; Gerber, A.G.; Watt, G.D. Using reduced hydrodynamic models to accelerate the predictor–corrector convergence of implicit 6-DOF URANS submarine maneuvering simulations. Comput. Fluids 2014, 102, 215–236. [Google Scholar] [CrossRef]
- Bettle, M.C.; Gerber, A.G.; Watt, G.D. Unsteady analysis of the six DOF motion of a buoyantly rising submarine. Comput. Fluids 2009, 38, 1833–1849. [Google Scholar] [CrossRef]
- CFX. Innovative Turbulence Modeling: SST Model in ANSYS CFX. 2006. Available online: https://support.ansys.com/staticassets/ANSYS/staticassets/resourcelibrary/techbrief/cfx-sst.pdf (accessed on 18 March 2018).










| Design Parameters | Symbol | Physical Unit | Value |
|---|---|---|---|
| Diameter | L | m | 1.0 |
| Design depth | h | m | 0–1000 |
| Height | H | m | 0.43–0.48 |
| Mass | m | kg | 50–150 |
| Design velocity | V | kn | 1 |
| Center of gravity | G(xG, yG, zG) | mm | (0, 0, 0) |
| Center of buoyancy | B(xB, yB, zB) | mm | (0, 0, −39.5) |
| Parameters | Setting |
|---|---|
| Computing performance | 4 Intel Xeon CPUs, 72 cores, 36 threads, 2.1 GHz, 256 GB of RAM |
| No. of meshing elements | 2.05 million |
| Mesh type | Structured, sliding meshes |
| Turbulence models | k–ε, k–ω (SST) |
| Advection scheme | ANSYS-CFX high resolution |
| Residual convergence | RMS residual < 10–5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-W.; Jiang, Y. Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion. Symmetry 2019, 11, 397. https://doi.org/10.3390/sym11030397
Chen C-W, Jiang Y. Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion. Symmetry. 2019; 11(3):397. https://doi.org/10.3390/sym11030397
Chicago/Turabian StyleChen, Chen-Wei, and Yong Jiang. 2019. "Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion" Symmetry 11, no. 3: 397. https://doi.org/10.3390/sym11030397
APA StyleChen, C.-W., & Jiang, Y. (2019). Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion. Symmetry, 11(3), 397. https://doi.org/10.3390/sym11030397





