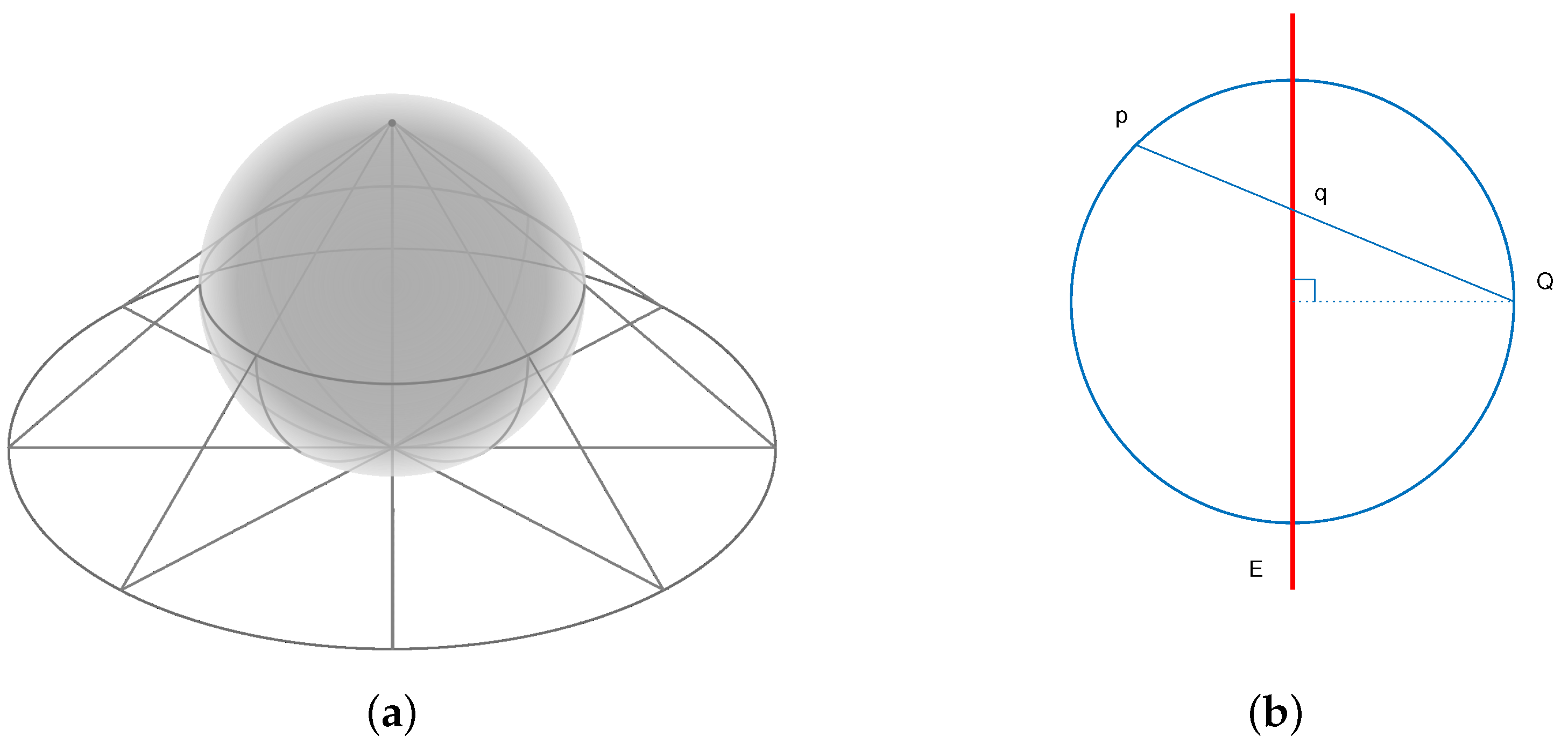1. Introduction
Regular polytopes (RPs) are an extension of 2D regular polygons and 3D regular polyhedra in
n-dimensional Euclidean space
(
), which have high abstraction and perfect symmetry [
1,
2,
3]. For instance, the 5D hypercube
has 32 vertices, 80 edges, 80 squares, 40 3D cubes, and 10 4D regular polytopes
. Those vertices, edges, squares, cubes, and 4D cells combine together to form a very coordinated and symmetrical structure, which in total consists of 1920 symmetries. The strong symmetrical structure of RPs thus gives them an aesthetic quality that has had a continuous and deep influence in the fields of math, computer graphics, art, and commercial design [
4,
5,
6,
7,
8].
The history of scientific and technological progress shows that the study of symmetry is of great significance [
9,
10]. It has greatly promoted the integration and development of natural sciences and has a far-reaching impact in practical fields. For example, the research of 2D symmetries produces the profound result of planar symmetry groups, which is widely used in the fields of architecture and decoration [
4,
11,
12]. The study of 3D symmetrical structures has laid the foundation of modern crystallography [
13]. The exploration of RPs in higher dimensional space impels a profound intersection between geometry and algebra and further makes many branches of mathematics flourish [
14]. The resulting technology has brought rapid innovation in the fields of physics, chemistry, materials, etc.
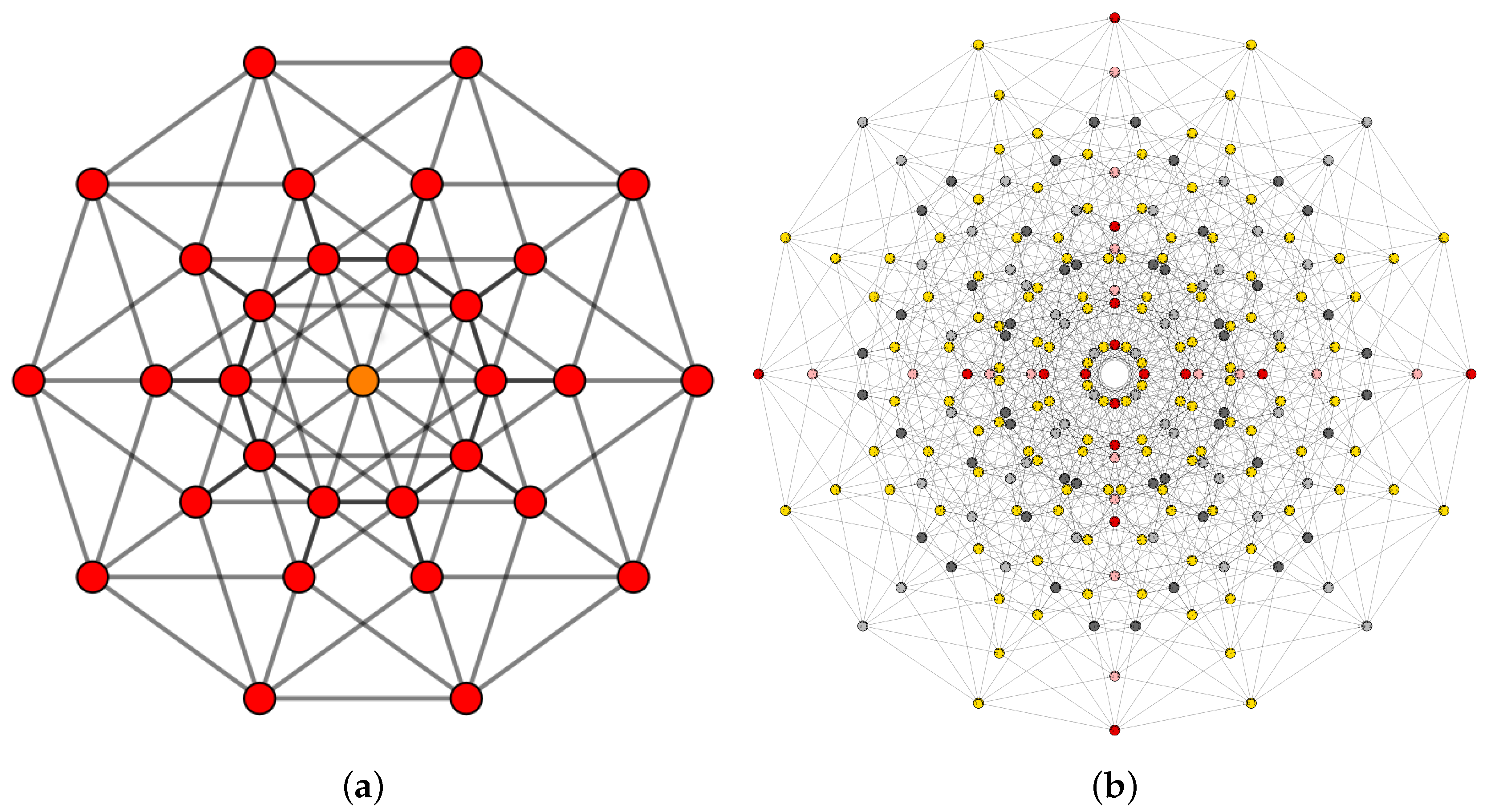
In 2D or 3D space, people can construct and observe real models of regular polygons or polyhedra so that they can understand their structures well. However, we cannot do that for RPs in more than three dimensions. As a subject closely related to geometry, it is very important to establish the 2D or 3D visualization methods for RPs. Based on the idea of reducing dimensions, many projection methods have been developed to visualize RPs, such as perspective [
15], orthogonal [
16], and canonical [
17] projections. However, these methods mainly aim to maintain symmetries of an RP to the highest degree; the resulting images thus only transmit vertex and edge information. Therefore, a major defect of existing projections is that they lack crucial metric or topological data; see the examples illustrated in
Figure 1. In fact, using traditional projections, it is difficult to establish their detailed geometric structure. To this end, in [
7], we studied the generalized stereographic projection to observe 4D RPs. This method preserves both the metric and topological data of 4D RPs, from which one can identify their general symmetrical structure better.
Compared to 4D RPs [
18,
19], 5D RPs are more complex and have richer symmetries. In this paper, by generalizing the idea of [
7], we study in detail the 2D and 3D stereographic projections of 5D RPs. It is a simple and universal strategy that can be extended to RPs in higher dimensional space. The remainder of this paper is outlined as follows. In
Section 2, we briefly introduce the structure of 5D RPs, including the symmetry group, fundamental root system, and an important algorithm that transforms an arbitrary point of
into the fundamental region. Then, in
Section 3, we describe the 3D and 2D visualization implementations of 5D RPs. Finally,
Section 4 concludes the paper and shows future directions on this subject.
2. Geometrical Features of 5D RPs
In this section, we briefly describe the geometrical features of 5D RPs, including their geometrical structures, group representations, fundamental region systems, and common notations. Moreover, we will present an important algorithm that transforms an arbitrary point of into a fundamental region symmetrically.
5D RPs are the analogs of regular polytopes in . Their geometrical structure is precisely specified by the concise Schläfli symbols , where p is the number of sides of each regular polygon, q the number of regular polygons meeting at each vertex in a cell, r the number of regular polyhedra meeting along each edge, and s the number of 4D RP meeting around each 4D face. It is well known that there are only three regular polytopes in : 5-simplex , 5-cube , and 5-orthoplex .
To understand the Schläfli symbol better, let us take the five-simplex
as an example. The first three tells us that face
is an equilateral triangle. The second three shows that there are three
s meeting at each vertex. Thus we see that
is the familiar regular tetrahedron, which is called a cell. The third three means that there are three
s meeting along each edge, which forms a 4D RP
, called a facet. Finally, the last three means that 5D
has three 4D RPs
around each 4D face. In short, the five-simplex
has in total 6 vertices, 15 edges, 20 equilateral triangles, 15 tetrahedrons, and 6 4D-RPs. The main geometrical features of 5D RPs are summarized in
Table 1.
Each 5D RP has a dual RP . They share the same reflection symmetry group, which is usually denoted by . The five-simplex is self-dual and corresponds to the reflection symmetry group , which is usually denoted as . The other two 5D RPs, five-cube and five-orthoplex , are dual and share the same reflection symmetry group , called . and have 3840 and 1920 symmetries, respectively.
Group
is generated by five proper reflections
. The abstract representation of group
is:
where the last one represents the unit element. The abstract representation of group
is:
Assume
is a nonzero normal vector with respect to hyperplane
P, then the reflection
associated with
P is:
where
denotes the inner product of vectors. Obviously,
if
and
if
(the orthogonal space of
P). The fundamental root system with respect to
is a vector set formed by certain vectors so that the associated reflections are precisely generators of
. In this paper, the fundamental root system associated with
is denoted by
. The fundamental root systems of
and
are listed in
Table 2 [
20].
The fundamental region under group
is a connected set, whose transformed copies under the action of
cover the entire space without overlapping except at boundaries [
1]. The fundamental region of 5D RP can be elegantly described by the fundamental root system [
20]: it is a closed set of points in
satisfying:
Assume
is the hyperplane passing through the origin with normal vector
(
). Then, geometrically, the fundamental region
is a 5D cone surrounded by hyperplanes
whose vertex is the origin. Though it is a little bit difficult to imagine the appearance of
, the 3D cone is familiar; see a 3D example illustrated in
Figure 2.
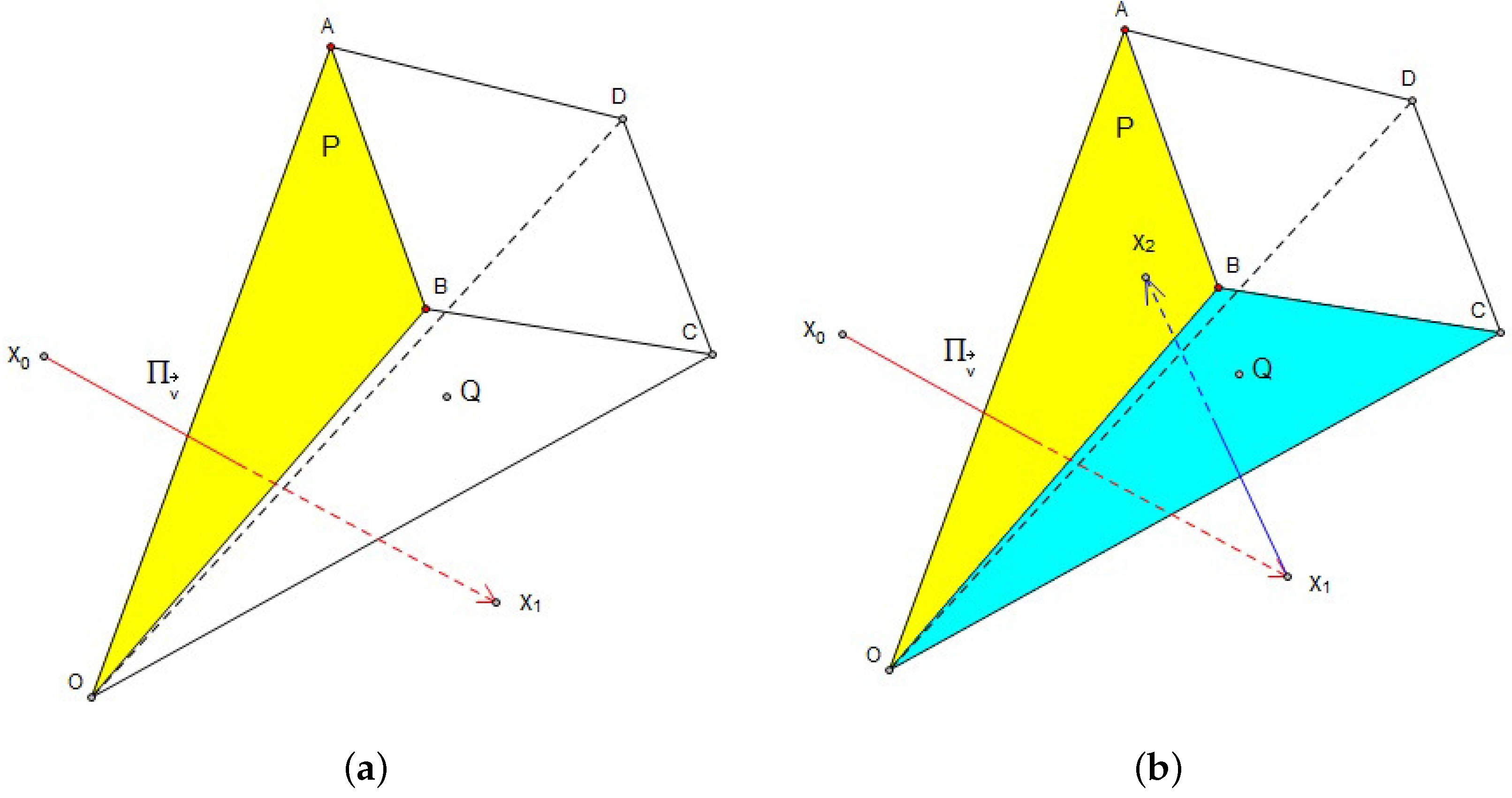
For outside , there is a fast algorithm to transform symmetrically into the fundamental region . To show how this algorithm works, we first introduce a lemma.
Lemma 1. Assume is a nonzero normal vector with respect to the hyperplane P. Points and are points on different sides of P, i.e.,wheredenotes the inner product of vectors. Then:whereis the reflection associated with P andis the Euclidean norm. Proof. By (
1), we see
Thus, we have (
2). □
We use a diagram to explain the geometric meaning of Lemma 1. In
Figure 2a, assume
and
are points on different sides of a plane
P. Then,
and
Q lie on the same side of
P. Lemma 1 says that the distance between
and
Q is smaller than
and
Q. In other words, for two points on the different sides of a plane, the reflection transformation associated with
P can shorten their distance.
Theorem 1. Letbe the fundamental region with respect to group. For a pointoutside, there exists a transformationand a symmetrically-placed pointsuch that.
Proof. Assume
Q is an interior point of the fundamental region
. For
, recalling the definition of
, there must exist a
so that
. In other words,
and
Q lie on different sides of the hyperplane
(
is the hyperplane passing through the origin with normal vector
); denoted by
. By Lemma 1, we have:
If , there exists a so that , where .
Thus, each time a chosen reflection is employed, the transformed will get nearer to Q and eventually fall into . Let n be the reflection times and be the product of the employed , then . □
Theorem 1 describes an algorithm that transforms points into
symmetrically.
Figure 2b illustrates an example of how Theorem 1 works. For convenience, we call it the fundamental region algorithm (FRA) and summarize the corresponding pseudocode in Algorithm 1 so that the interested readers can create their own projection patterns. Essentially, it is the kaleidoscope principle in higher dimension Euclidean space [
1,
2,
3].
| Algorithm 1 Fundamental region algorithm (FRA). |
Input: Point and fundamental root system
Output: Point and reflection number n- 1:
Let - 2:
Compute sign: - 3:
for–5 do - 4:
if then - 5:
- 6:
end if - 7:
end for - 8:
whiledo - 9:
- 10:
for to 5 do - 11:
if then - 12:
- 13:
- 14:
Compute sign: - 15:
for to 5 do - 16:
if then - 17:
- 18:
end if - 19:
end for - 20:
break - 21:
end if - 22:
end for - 23:
end while - 24:
n is the repeated Steps 8–23, then point
|
3. Visualizations of 5D RPs from Generalized Stereographic Projection
In this section, we first introduce the generalized stereographic projection. Then, we describe 2D or 3D visualization methods for 5D RPs.
Denote by
the unit sphere and
. Suppose
is a hyperplane. Then, the stereographic projection of a point
is the intersection point
q between line
and
E.
Figure 3 demonstrates the situation of 2D and 3D stereographic projections. Assume
. According to the stereographic projection, the relation between
q and
p is:
Then, the inverse of the stereographic projection is:
It is easy to check that , which means that the pre-image of under projection always lies on .
For a point
, we can compute the corresponding point
by using stereographic projection twice, that is:
where:
and
is the parameters specifying the radii of
-dimensional sphere
.
Assume
N is the number of steps employed in FRA. On average, each point of
will be transformed into the fundamental region
of 5D RPs within 10–13 times, a little larger than 4D RPs (8–10 times [
8]) and regular polyhedra (4–7 [
7]). According to
N odd or even, one can use two colors to color a 3D point
and obtain a two-color interlaced image of 5D RPs. We next use this scheme to create some projection patterns in
and
.
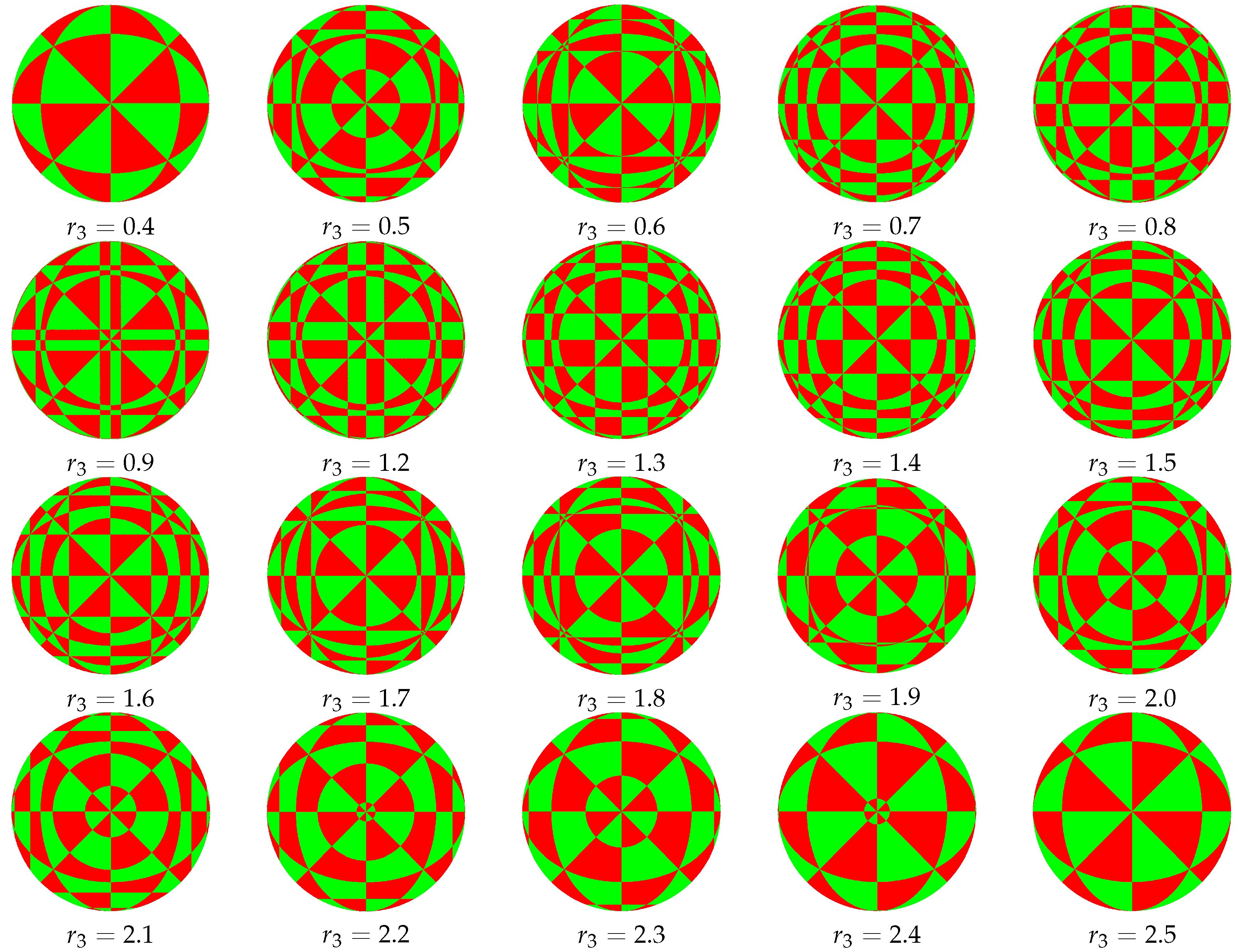
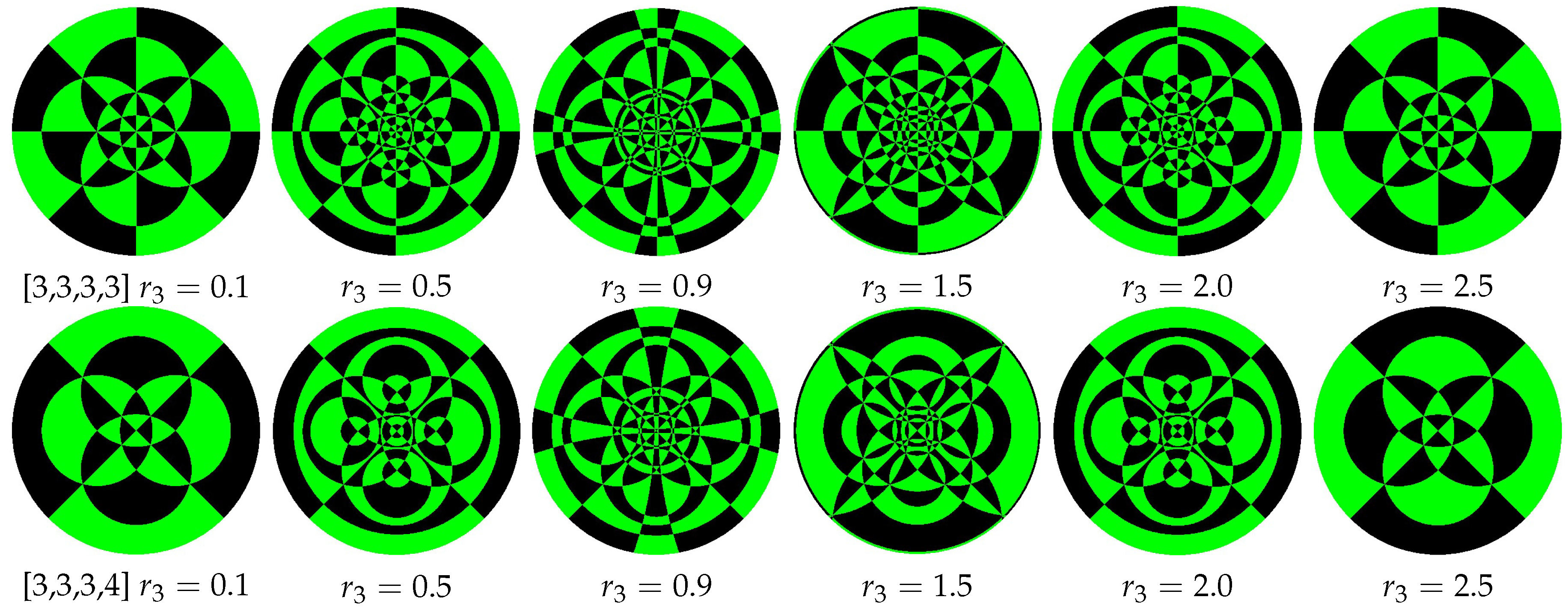
In the first situation, by fixing
= 2 and varying
,
Figure 4 shows the sphere projections of 5D RPs. In the second situation, by fixing
= 0.5 and varying
,
Figure 5 and
Figure 6, respectively, illustrate the sphere projections of
and
. As the order of
is twice that of
, it is easy to see that the projection of
is more complex than
. The value of
can be sensitive to small changes, so in these two images, we have chosen certain values so that the change of projections is relatively obvious. We observe an interesting phenomenon: at first, projections tend to be complex as
increases; however, projections become simpler once
exceeds a certain threshold.
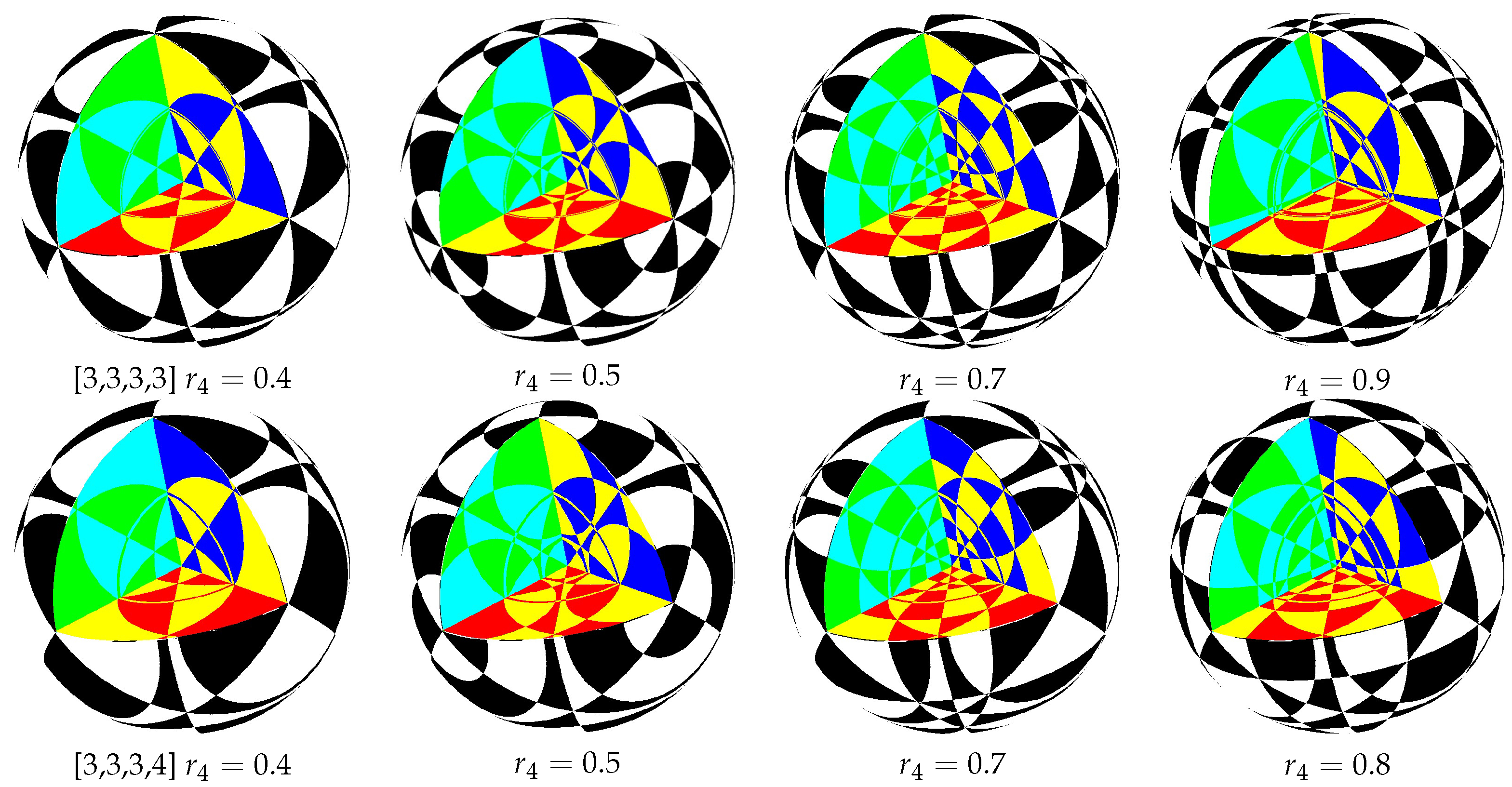
Figure 7 and
Figure 8, respectively, display the effect of unit solid sphere projections of 5D RPs, where
and
of the spherical solids are cut off so that they exhibit some inner details. For clarity, several colors are used in the sections.
We next consider 2D projections of 5D RPs. For a point
, we can similarly compute its corresponding point
by using stereographic projection three times. More precisely,
where:
and
are parameters specifying the radii of the
-dimensional sphere. By fixing
and varying
and
separately,
Figure 9 and
Figure 10 demonstrate the 2D projections of 5D RPs. Again, we see, as
or
is increasing, those projections will first change from simple to complex and then back to simple.
4. Conclusions
Based on the geometrical meaning of RPs, this paper presents a convenient strategy to visualize 5D RPs, which could be extended to treat n-dimensional RPs (). We first introduced their structure, Schläfli symbol, group representation, and fundamental root system. Then, we proved the generalized kaleidoscope principle that transforms an arbitrary point of into a fundamental region symmetrically. For convenience, the kaleidoscope principle was summarized in Algorithm 1. Using the algorithm, we finally presented the visualization implementations of 5D RPs.
The foundations of RPs were laid by the Greeks over two thousand years ago. Over the past two hundred years, many excellent mathematicians around the world have made a systematic, extensive, and in-depth study of RPs. In the bibliography of the classic Regular Polytopes, H.S.M.Coxeter listed the name of 110 mathematicians: 30 German, 27 British, 12 American, 11 French, 7 Dutch, 8 Swiss, 4 Italian, 2 Austrian, 2 Hungarian, 2 Polish, 2 Russian, 1 Norwegian, 1 Danish, and 1 Belgian. He commented that “the chief reason for studying regular polyhedra is still the same as in the time of the Pythagoreans, namely, that their symmetrical shapes appeal to one’s artistic sense”. The first edition of the Regular Polytopes was published in 1948, but there has been no major change in the following. Due to the early completion of the book—the computer had just been born–much of the visualization study of RPs is not discussed in depth.
The fundamental root system and fundamental region, which in practice helped H.S.M. Coxeter to complete the classification of irreducible reflective groups [
20], constituted the core theoretical tool of this study. In this paper, we saw that those tools can be used easily to create infinite exotic spherical tilings. Generally speaking, the construction of spherical tilings is not easy. For the past decade, many very complex methods have been reported to construct spherical tilings; see [
21,
22] and the references therein. In the future, we plan to investigate the relation between Algorithm 1 and the associated spherical tilings, which aims to present a simple and efficient approach to construct rich spherical tilings.