Nonlinear Management of Topological Solitons in a Spin-Orbit-Coupled System
Abstract
1. Introduction
2. The Model and Analytical Results
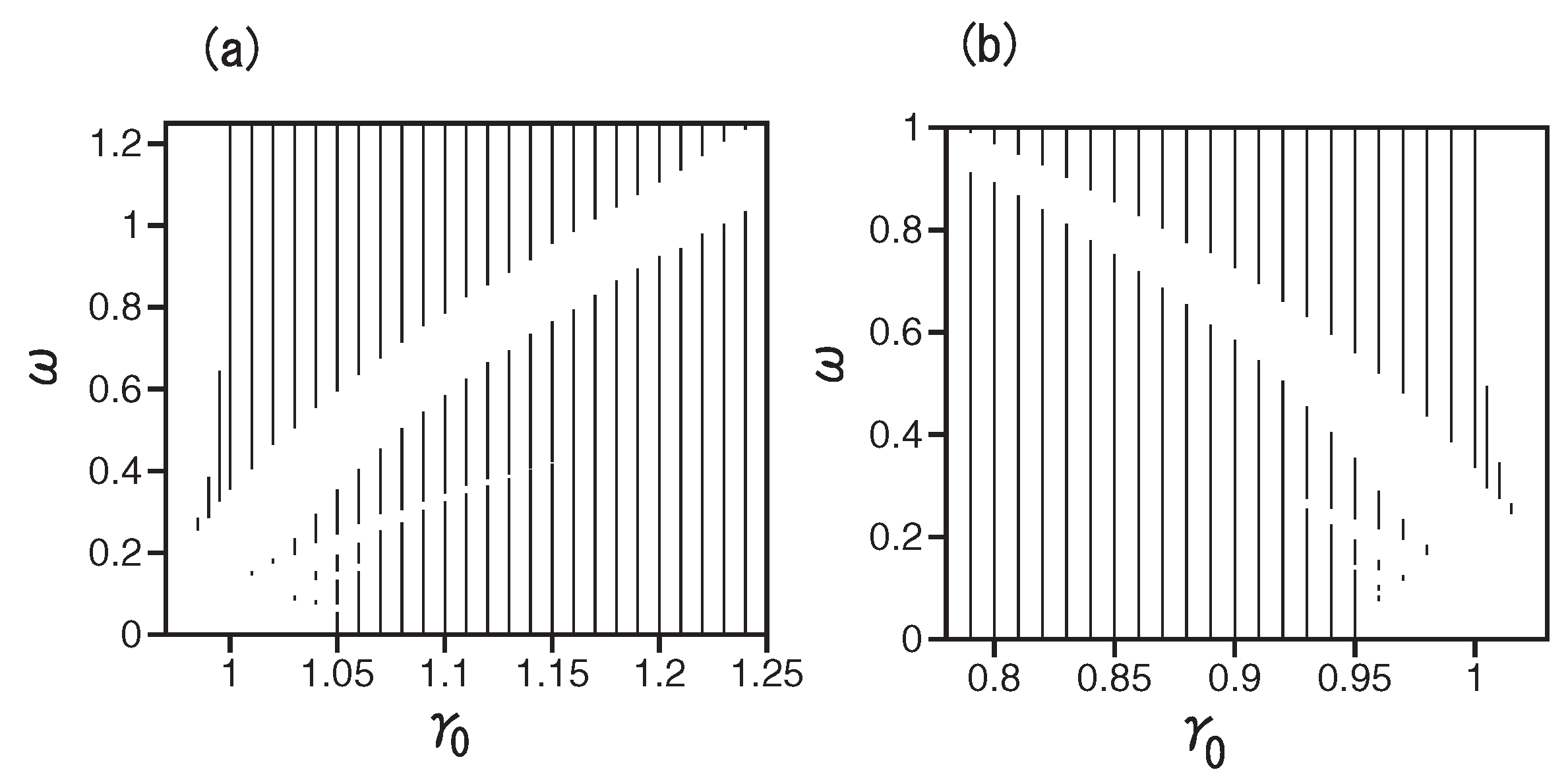
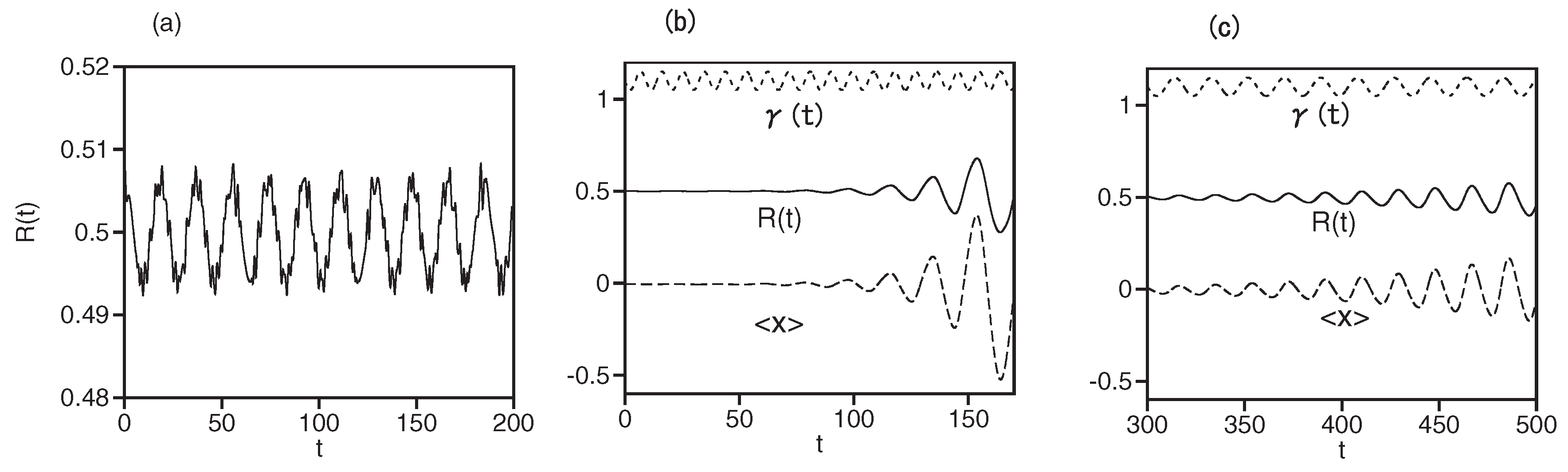
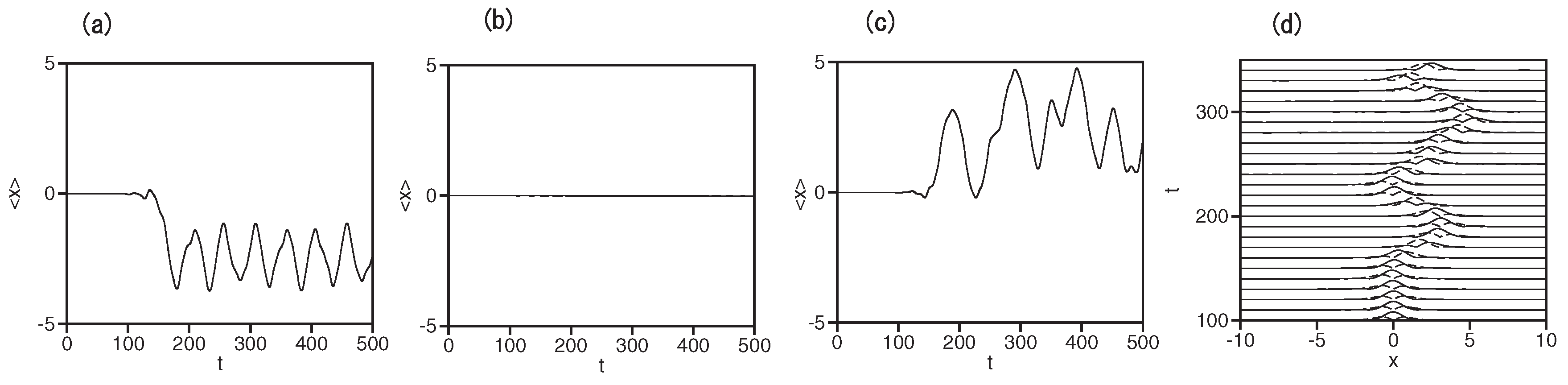
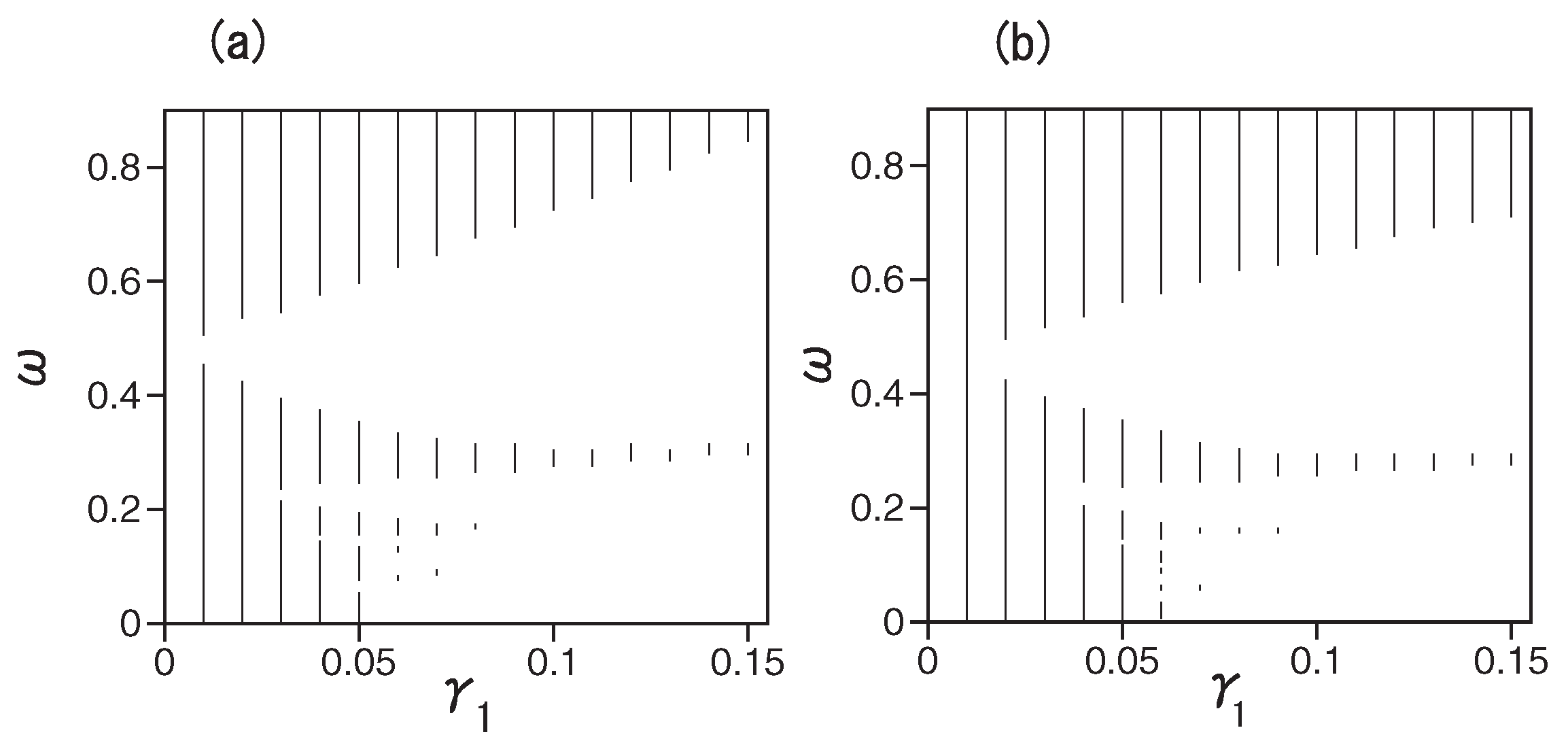
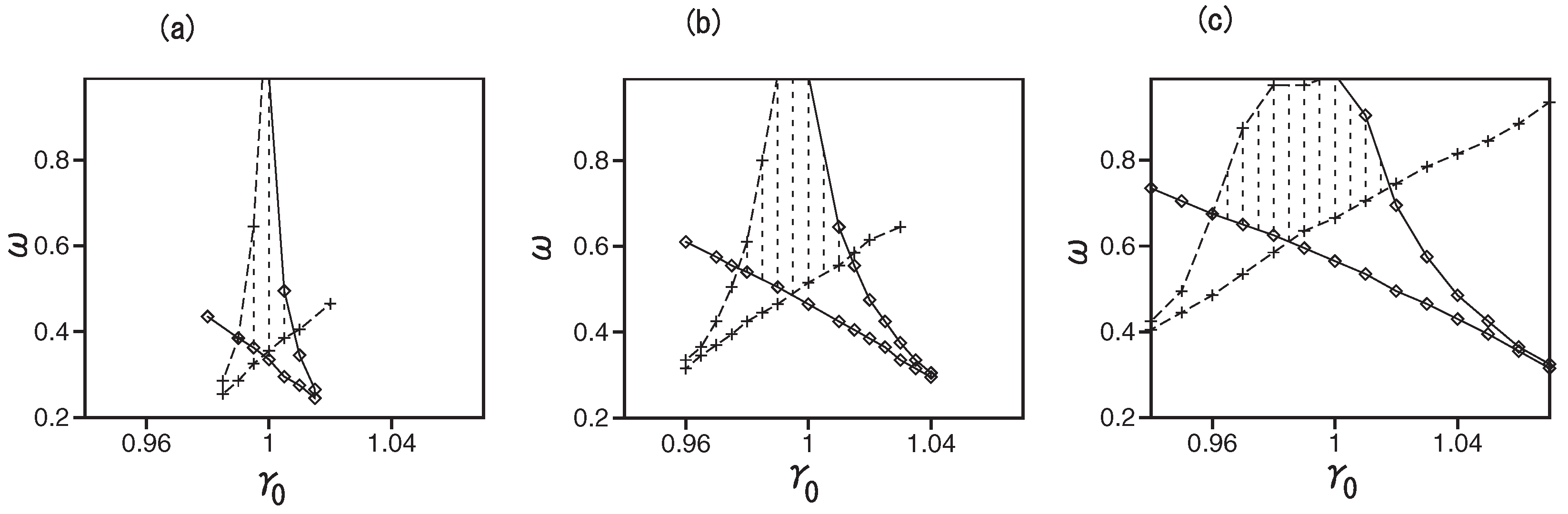
3. Results: Stability Regions for Solitons under the Action of the Management
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hauke, P.; Cucchietti, F.M.; Tagliacozzo, L.; Deutsch, I.; Lewenstein, M. Can one trust quantum simulators? Rep. Prog. Phys. 2012, 75, 082401. [Google Scholar] [CrossRef]
- Johnson, T.H.; Clark, S.R.; Jaksch, D. What is a quantum simulator? EPJ Quantum Technol. 2014, 1, 10. [Google Scholar] [CrossRef]
- Zohar, E.; Cirac, J.I.; Reznik, B. Quantum simulations of lattice gauge theories using ultracold atoms in optical lattices. Rep. Prog. Phys. 2016, 79, 014401. [Google Scholar] [CrossRef] [PubMed]
- Dresselhaus, G. Spin-orbit coupling effects in zinc blende structures. Phys. Rev. 1955, 100, 580–586. [Google Scholar] [CrossRef]
- Bychkov, Y.A.; Rashba, E.I. Oscillatory effects and the magnetic-susceptibility of carriers in inverse-layers. J. Phys. C 1984, 17, 6039–6045. [Google Scholar] [CrossRef]
- Lin, Y.J.; Jimenez-Garcia, K.; Spielman, I.B. Spin-orbit-coupled Bose-Einstein condensates. Nature 2011, 471, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Dalibard, J.; Gerbier, F.; Juzeliūnas, G.; Öhberg, P. Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523–1543. [Google Scholar] [CrossRef]
- Galitski, V.; Spielman, I.B. Spin-orbit coupling in quantum gases. Nature 2013, 494, 49–54. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Cai, Z.; Wu, C. Unconventional states of bosons with the synthetic spin-orbit coupling. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 134001. [Google Scholar] [CrossRef]
- Goldman, N.; Juzeliūnas, G.; Öhberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Progr. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef] [PubMed]
- Zhai, H. Degenerate quantum gases with spin–orbit coupling: A review. Rep. Prog. Phys. 2015, 78, 026001. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, L.; Sun, W.; Xu, X.-T.; Wang, B.-Z.; Ji, S.-C.; Deng, Y.; Chen, S.; Liu, X.-J.; Pan, J.-W. Realization of two-dimensional spin-orbit coupling for Bose-Einstein condensates. Science 2016, 354, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Pitaevskii, L.P.; Stringari, S. Bose-Einstein Condensation; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Lahaye, T.; Menotti, C.; Santos, L.; Lewenstein, M.; Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 2009, 72, 26401. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Konotop, V.V. Solitons in Bose-Einstein condensates with helicoidal spin-orbit coupling. Phys. Rev. Lett. 2017, 118, 190401. [Google Scholar] [CrossRef] [PubMed]
- Lobanov, V.E.; Kartashov, Y.V.; Konotop, V.V. Fundamental, multipole, and half-vortex gap solitons in spin-orbit coupled Bose-Einstein condensates. Phys. Rev. Lett. 2014, 112, 180403. [Google Scholar] [CrossRef] [PubMed]
- Chiquillo, E. Harmonically trapped attractive and repulsive spin-orbit and Rabi coupled Bose-Einstein condensates. J. Phys. A Math. Theor. 2017, 50, 105001. [Google Scholar] [CrossRef]
- Malomed, B.A. Creating solitons by means of spin-orbit coupling. Europhys. Lett. 2018, 122, 36001. [Google Scholar] [CrossRef]
- Sinha, S.; Nath, R.; Santos, L. Trapped two-dimensional condensates with synthetic spin-orbit coupling. Phys. Rev. Lett. 2011, 107, 270401. [Google Scholar] [CrossRef]
- Wu, C.J.; Mondragon-Shem, I.; Zhou, X.-F. Unconventional Bose-Einstein Condensations from Spin-Orbit Coupling. Chin. Phys. Lett. 2011, 28, 097102. [Google Scholar] [CrossRef]
- Deng, Y.; Cheng, J.; Jing, H.; Sun, C.P.; Yi, S. Spin-orbit-coupled dipolar Bose-Einstein condensates. Phys. Rev. Lett. 2012, 108, 125301. [Google Scholar] [CrossRef]
- Kawakami, T.; Mizushima, T.; Machida, K. Textures of F = 2 spinor Bose-Einstein condensates with spin-orbit coupling. Phys. Rev. A 2011, 84, 011607. [Google Scholar] [CrossRef]
- Ramachandhran, B.; Opanchuk, B.; Liu, X.-J.; Pu, H.; Drummond, P.D.; Hu, H. Half-quantum vortex state in a spin-orbit-coupled Bose-Einstein condensate. Phys. Rev. A 2012, 85, 023606. [Google Scholar] [CrossRef]
- Conduit, G.J. Line of Dirac monopoles embedded in a Bose-Einstein condensate. Phys. Rev. A 2012, 86, 021605(R). [Google Scholar] [CrossRef]
- Ruokokoski, E.; Huhtamäki, J.A.M.; Möttönen, M. Stationary states of trapped spin-orbit-coupled Bose-Einstein condensates. Phys. Rev. A 2012, 86, 051607. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Li, B. Vortex lattice solutions to the Gross-Pitaevskii equation with spin-orbit coupling in optical lattices. Phys. Rev. A 2013, 87, 015602. [Google Scholar] [CrossRef]
- Fetter, A. Vortex dynamics in spin-orbit-coupled Bose-Einstein condensates. Phys. Rev. A 2014, 89, 023629. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Umeda, K. Solitons and vortex lattices in the Gross-Pitaevskii equation with spin-orbit coupling under rotation. J. Phys. Soc. Jpn. 2016, 85, 064402. [Google Scholar] [CrossRef]
- Kawakami, T.; Mizushima, T.; Nitta, M.; Machida, K. Stable skyrmions in gauged Bose-Einstein condensates. Phys. Rev. Lett. 2012, 109, 015301. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Garmire, E.; Townes, C.H. Self-trapping of optical beams. Phys. Rev. Lett. 1964, 13, 479–482. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Vlasov, R.A. Spiral self-trapping propagation of optical beams. Phys. Lett. A 1985, 111, 401–404. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Logvin, Y.A.; Volkov, V.M. The theory of spiral laser beams in nonlinear media. J. Mod. Opt. 1992, 39, 2277–2291. [Google Scholar] [CrossRef]
- Malomed, B.A.; Mihalache, D.; Wise, F.; Torner, L. Spatiotemporal optical solitons. J. Optics B Quant. Semicl. Opt. 2005, 7, R53–R72; Viewpoint: On multidimensional solitons and their legacy in contemporary Atomic, Molecular and Optical physics. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 170502. [Google Scholar] [CrossRef]
- Kartashov, Y.; Astrakharchik, G.; Malomed, B.; Torner, L. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys. 2019, 1, 185–197. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Li, B.; Malomed, B.A. Creation of two-dimensional composite solitons in spin-orbit-coupled self attractive Bose-Einstein condensates in free space. Phys. Rev. E 2014, 89, 0329020. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, H.; Sherman, E.Y.; Malomed, B.A. Vortex solitons in two-dimensional spin-orbit coupled Bose-Einstein condensates: Effects of the Rashba-Dresselhaus coupling and the Zeeman splitting. Phys. Rev. E 2016, 94, 032202. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, H.; Li, B.; Sherman, E.Y.; Malomed, B.A. Composite solitons in two-dimensional spin-orbit coupled self-attractive Bose-Einstein condensates in free space. Rom. Rep. Phys. 2018, 70, 502. [Google Scholar] [CrossRef]
- Maimistov, A.I. Solitons in nonlinear optics. Quantum Electron. 2010, 40, 756. [Google Scholar] [CrossRef]
- Zhong, R.; Chen, Z.; Huang, C.; Luo, Z.; Tan, H.; Malomed, B.A.; Li, Y. Self-trapping under the two-dimensional spin-orbit-coupling and spatially growing repulsive nonlinearity. Front. Phys. 2018, 13, 130311. [Google Scholar] [CrossRef]
- Sakaguchi, H. New models for multi-dimensional stable vortex solitons. Front. Phys. 2019, 14, 1230. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Konotop, V.V.; Lobanov, V.E.; Torner, L. Stabilization of solitons in bulk Kerr media by dispersive coupling. Opt. Lett. 2015, 40, 1045–1048. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, H.; Malomed, B.A. One- and two-dimensional solitons in -symmetric systems emulating spin–orbit coupling. New J. Phys. 2016, 18, 105005. [Google Scholar] [CrossRef]
- Chiang, K.S. Intermodal dispersion in 2-core optical fibers. Opt. Lett. 1995, 20, 997–999. [Google Scholar] [CrossRef]
- Abdullaev, F.K.; Caputo, J.G.; Kraenkel, R.A.; Malomed, B.A. Controlling collapse in Bose-Einstein condensation by temporal modulation of the scattering length. Phys. Rev. A 2003, 67, 013605. [Google Scholar] [CrossRef]
- Saito, H.; Ueda, M. Dynamically stabilized bright solitons in a two-dimensional Bose-Einstein condensate. Phys. Rev. Lett. 2003, 90, 040403. [Google Scholar] [CrossRef] [PubMed]
- Kevrekidis, P.G.; Theocharis, G.; Frantzeskakis, D.J.; Malomed, B.A. Feshbach resonance management for Bose-Einstein condensates. Phys. Rev. Lett. 2003, 90, 230401. [Google Scholar] [CrossRef] [PubMed]
- Montesinos, G.D.; Perez-Garcia, V.M.; Michinel, H. Stabilized two-dimensional vector solitons. Phys. Rev. Lett. 2004, 92, 133901. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, H.; Malomed, B.A. Resonant nonlinearity management for nonlinear Schrödinger solitons. Phys. Rev. E 2004, 70, 066613. [Google Scholar] [CrossRef]
- Itin, A.; Morishita, T.; Watanabe, S. Reexamination of dynamical stabilization of matter-wave solitons. Phys. Rev. A 2006, 74, 033613. [Google Scholar] [CrossRef]
- Towers, I.; Malomed, B.A. Stable (2+1)-dimensional solitons in a layered medium with sign-alternating Kerr nonlinearity. J. Opt. Soc. Am. B 2002, 19, 537–543. [Google Scholar] [CrossRef]
- Malomed, B.A. Soliton Management in Periodic Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Papp, S.B.; Pino, J.M.; Wieman, C.E. Tunable miscibility in a dual-species Bose-Einstein condensate. Phys. Rev. Lett. 2008, 101, 040402. [Google Scholar] [CrossRef]
- Gubeskys, A.; Malomed, B.A.; Merhasin, I.M. Alternate solitons: Nonlinearly-managed one- and two-dimensional solitons in optical lattices. Stud. Appl. Math. 2005, 115, 255–277. [Google Scholar] [CrossRef]
- Achilleos, V.; Frantzeskakis, D.J.; Kevrekidis, P.G.; Pelinovsky, D.E. Matter-wave bright solitons in spin-orbit coupled Bose-Einstein condensates. Phys. Rev. Lett. 2013, 110, 264101. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics; Nauka Publishers: Moscow, Russia, 1988. [Google Scholar]
- Jiang, X.; Fan, Z.; Chen, Z.; Pang, W.; Li, Y.; Malomed, B.A. Two-dimensional solitons in dipolar Bose-Einstein condensates with spin-orbit coupling. Phys. Rev. A 2016, 93, 023633. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakaguchi, H.; Malomed, B. Nonlinear Management of Topological Solitons in a Spin-Orbit-Coupled System. Symmetry 2019, 11, 388. https://doi.org/10.3390/sym11030388
Sakaguchi H, Malomed B. Nonlinear Management of Topological Solitons in a Spin-Orbit-Coupled System. Symmetry. 2019; 11(3):388. https://doi.org/10.3390/sym11030388
Chicago/Turabian StyleSakaguchi, Hidetsugu, and Boris Malomed. 2019. "Nonlinear Management of Topological Solitons in a Spin-Orbit-Coupled System" Symmetry 11, no. 3: 388. https://doi.org/10.3390/sym11030388
APA StyleSakaguchi, H., & Malomed, B. (2019). Nonlinear Management of Topological Solitons in a Spin-Orbit-Coupled System. Symmetry, 11(3), 388. https://doi.org/10.3390/sym11030388





