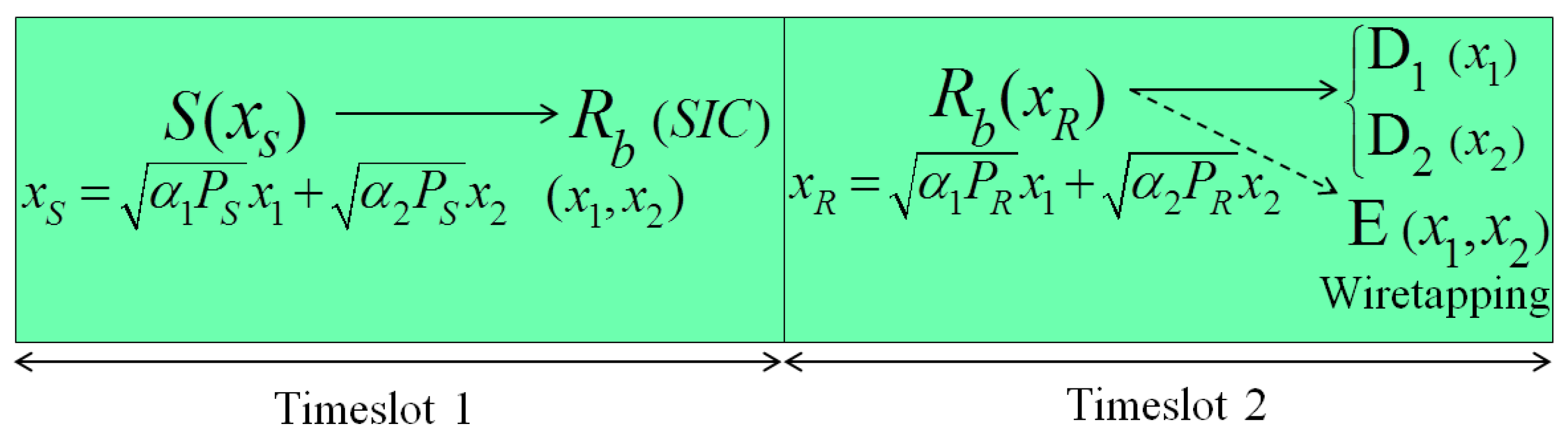1. Introduction
Today, the development of smart devices has led to the increase in the number of wireless connections, the mobile data rate, and the consumed energy in the next generation of wireless communication systems [
1,
2]. The users always wants to connect and get the data quickly and safely. Therefore, in order to deploy and improve the range of the wireless communication system and the connection speed, non-orthogonal multiple access (NOMA) has recently received great attention from researchers in the field of wireless systems as a promising technique to achieve enhanced spectrum efficiency of the 5G mobile network [
3,
4]. In the NOMA technique, the users can share both time and frequency resources and only adjust their power allocation ratios. In particular, the user with better channel conditions can be allocated to a channel that is occupied by a user with poor channel conditions. The users with strong channel conditions can serve as relays to enhance the system performance by using successive interference cancellation (SIC) [
5].
In recent times, there has been many research investigations into NOMA in wireless communication systems [
6,
7,
8]. Cooperative NOMA can achieve the maximum diversity gain for wireless networks. The researchers in [
6] studied the cooperative relaying system using the NOMA technique to improve the spectral efficiency. In [
7], the authors considered the performance of the NOMA system in amplify-and-forward (AF) relaying systems to increase the data transmission rate for 5G communications. Approaches based on the role of chaos in game theory have been investigated in [
9,
10] and can be applied in multiple access schemes. The combination of cooperative communication and PLS is an effective approach to overcome the disadvantages of the fading environment, as well as to increase the security capacity of the wireless network.
PLS has been presented by published researches in [
8,
11]. In [
8], the authors evaluated the secrecy performance of cooperative protocols with relay selection methods under the impact of co-channel interference. The authors in [
11] studied the impact of correlated fading on the secrecy performance of multiple DFrelaying with the optimal relay selection method. Besides, the authors researched the NOMA technique combined with PLS in [
12,
13]. In [
12], the authors solved the problem of maximizing the minimum confidential information rate among users subject to the secrecy outage constraint and instantaneous transmit power constraint. Cooperative NOMA systems with PLS were investigated in [
13] in cases of both AF and DF operations.
In addition, the underlay cognitive radio networks applying the NOMA technique were also proposed by some authors in [
14,
15,
16,
17]. In [
14], a cooperative transmission scheme has been proposed for a downlink NOMA in CR systems, and this research exploited the maximal spatial diversity. Considering the security principle [
18,
19,
20], the authors in [
19] studied secure communication in cognitive DF relay networks in which a pair of cognitive relays is opportunistically selected for security protection against eavesdroppers. In [
20], the authors investigated tradeoffs between security and reliability in cooperative cognitive radio networks with the NOMA solution.
In most of the above research, the authors have not considered the combination of NOMA with PLS in UCCN. Excited by the above ideas, in this article, we propose a UCCN using the NOMA scheme in which the intermediate relays help to decode and forward two signals and from a source node to two destination nodes D1 and D2, respectively, under wiretapping of an eavesdropper. The best relay selection strategy is investigated in three types of relay selection criteria: the first and second best relay selection is based on maximizing the value of the channel gains from the links R-D1, R-D2, respectively; the third one is to ensure the minimum value of the channel gains from the R-E link. Then, we analyze and evaluate the secrecy performances of the transmissions and in the proposed UCCN-NOMA scheme in terms of the SOPs over Rayleigh fading channels to advance the spectral efficiency and secure communication in which the best intermediate relay supports power to the destination nodes and perform digital network coding (DNC) to compress the received data and then to forward the signals to the destination nodes.
The article is summarized with the main contributions as follows. Firstly, we propose a DF-formed cooperation UCCN scheme in which the best relay uses the NOMA and considers PLS to enhance the system performance in 5G wireless networks. Secondly, the SOPs over Rayleigh fading channels are derived and are confirmed by Monte Carlo simulations. Thirdly, the secrecy performances of the transmissions
and
in the three best relay selection strategies are compared with each other in the proposed UCCN-NOMA system. The organization of paper is as follows:
Section 2 describes a UCCN system model with the best relay using NOMA combined with PLS and the operation methods of the proposed system;
Section 3 analyses the results of the SOPs for the eavesdropping of the signals
and
in the proposed UCCN-NOMA system; the simulation results are presented in
Section 4; and
Section 5 summarizes our conclusions.
2. System Model
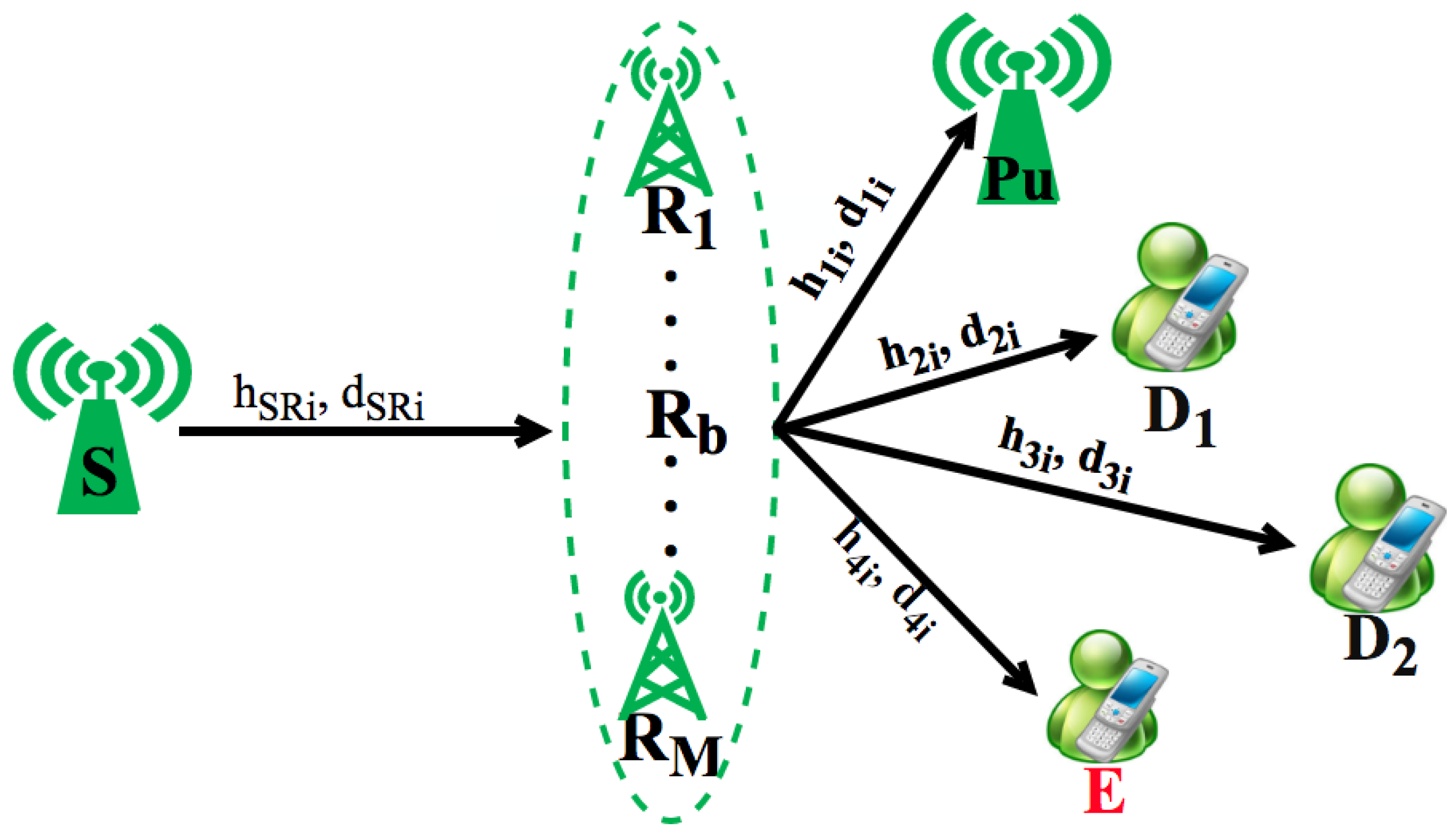
In this paper, as shown in
Figure 1, we consider a wireless communication system of a UCCN, which contains one source node S, two destination nodes D
and D
, multi-wireless relay nodes using the NOMA principle, and one eavesdropper node E to wiretap the signals of the links S-D
and S-D
. In this figure, we assume that the communication between the source S and the destinations D
and D
is not transmitted directly, and they are linked through the intermediate relays with the presence of the eavesdropper E. Hence, the source node transmits its packets to the destination nodes (
is sent to D
, and
is sent to D
). The R
-D
link distance is farther than the R
-D
link distance. In order to transmit data optimally, the best relay node using the NOMA method was selected to help the source node exchange data with destination nodes D
and D
. The best relay selection strategy is presented by three types of relay selection criteria: the first and second best relay selection is based on the maximum channel gain of the links R
-D
and R
-D
, respectively; the third one is to ensure the minimum channel gain of the link R
-E.
There are some assumptions as follows. Firstly, each node has a private antenna. Secondly, the variances of zero-mean white Gaussian noises (AWGNs) are equal, denoted similarly as N
. Thirdly, all channels are designated for flat and block Rayleigh fading. Finally, the channel state information (CSI) regarding the sources-to-eavesdropper, sources-to-relays, and relays-to eavesdropper channels is known at the source node S and the destination nodes D
and D
[
5].
In
Figure 1,
,
are Rayleigh fading channel coefficients and the link distances of S-R
, R
-D
, R
-E, and R
-Pu, respectively, where
,
, and
. Hence, the random variables
have an exponential distribution with the parameter
, where
is a path-loss exponent. The respectively distances of R
-D
, R
-E, and R
-Pu are illustrated in
Figure 1. The cumulative distribution function (cdf) and probability density function (pdf) of random variables
are expressed as
and
, respectively. With the assumptions in this paper, the fading channels
are fixed during a block time
T, and the variables
are independent and identically distributed between two continuous block times.
Based on a time division channel model, the operation method of the proposed UCCN-NOMA system is divided into two timeslots as presented in
Figure 2. In the first timeslot, the source node S broadcasts its signal
, which contains signals
and
, to the best relay
. The signal
is created by the superposition coding method [
21]. The selection criteria of the best relay
will be discussed in the next section. The best relay
uses the SIC technique to decode the signals
and
sequentially based on the allocated powers to the signals
and
at the source node S. In the second timeslot, the best relay
combines the signals
and
to the coded signal
by the superposition coding and then sends the signal
to the destinations D
and D
. The transmitted
can be wiretapped by the eavesdropper E in the wireless environment.
3. Secrecy Outage Probability Analysis
In this section, we analyze the sum SOP for the eavesdropping of the signals and in the proposed UCCN-NOMA system. We assume that a node successfully and safely decodes the received packet if its achievable secrecy capacity is larger than a target secrecy capacity SCth.
At the first timeslot, the source node S creates the signal
by the superposition coding [
21] and then broadcasts the
to all of the relays R
. The signal
is given by:
where
is the power at source node S,
and
are the power allocation coefficients, and
and
are the messages sent to D
and D
. Following the principle of the NOMA, we assume that
with
.
The received signal at the relay R
from the source node S for the decoding of
and
is given by:
where
denote the AWGNs at the relay R
with the same variance N
,
,
(
denotes the expectation process of
x).
Based on the NOMA scheme, firstly, the relay R
decodes
from (
1) and removes it using SIC, then
will be decoded and forward to D
without the component
in (
2). Therefore, the signal received at R
after decoding
is expressed as follows:
In the second timeslot, the signals received at the destinations D
and D
related to links R
-D
and R
-D
, respectively, can be written as:
where
denote the AWGNs at the destination D
with the same variance N
and P
is the transmit power of the relay R
.
Similarly, the node E also wiretaps the packets
and
from R
, respectively, and the received signals at node E are obtained as follows:
where
denote the AWGNs at E with the same variance N
.
In the system model, under the interference constraint at the Pu node, the relays R
have to adjust their transmitting powers so that the interference power at the Pu must be less than a threshold value,
. The maximum powers of nodes S and R
are given, respectively, as:
With Formulas (
4) and (
5), the received signal-to-interference and noise ratios (SINRs) at the destination D
for decoding the information signals
and
are obtained, respectively, as follows:
Applying Formulas (
6) and (
7), the received SINRs at the node E for eavesdropping the information signal
of D
and the signal
of D
from the relay R
are obtained, respectively, as follows:
Applying the Shannon capacity formula, the achievable rates of the links R
-Y are formulated as:
where the ratio 1/2 represents the fact that data transmission is split into two time slots, and
.
The secrecy capacity of the UCCN system with DF-based NOMA for the R
-D
communication can be expressed as:
where
;
;
are the secrecy capacities from the relay R
to the destination D
, given, respectively, as:
3.1. The Sum SOP of the Secrecy Transmission in the Proposed UCCN-NOMA System with the Best Relay Selection: Case ST1
In this section, firstly, we find the best relay
based on the maximum channel gain of the R
-D
link. Then, we calculate the SOPs of the ST1case in which the destination nodes D
and D
do not get the signal safely from the source node S through
under the malicious attempt of the eavesdropper E. Finally, we calculate their sum SOPs to compare fairly with the sum SOPs of the ST2 and ST3 cases in
Section 3.2 and
Section 3.3.
First, the best relay is selected based on a criterion as follows:
From the definition of
in (
16), the CDF of
is obtained as:
The pdf of
is inferred as:
The next, we calculate the SOP of the ST1 case in which the destination node D
does not receive the signal safely from the best relay under the malicious attempt of the eavesdropper E, presented by a math expression as follows:
Substituting Formula (
15) into (
19),
is obtained as:
Replacing Formula (
13) in (
20),
is expressed as:
where
.
In this paper, we consider the worst case in which the node E can take the data of D
with the best conditions. From (
21), we have an upper constraint of
as follows:
where
,
,
,
To solve
in (
22), we use two lemmas as follows:
Lemma 1. A is obtained by a closed-form expression as follows:where . Lemma 2. The following expression is valid for A: Proof. The proof of Lemma 2 is presented clearly in
Appendix B.
The exact upper expression of the SOP is provided in the following theorem. ☐
Theorem 1. The upper expression is obtained by the expression as:where and .
Proof. Substituting Lemma 1 and Lemma 2 into (
22),
is shown in two cases as:
-When
:
where
A
in (
26b) is calculated as
where
The A
in (
26b) is presented as:
By setting
, A
in (
28) is given as:
where
Substituting A
in (
27) and A
in (
29) into (
26b),
is obtained as:
With the results of (
29) and (
26b), Theorem 1 in (
25) is proven successfully.
Finally, we calculate the SOP of the ST1 case in which the destination node D
does not receive the signal safely from the source node S through the best relay R
under the malicious attempt of the eavesdropper E as follows:
Substituting Formula (
15) into (
31),
is obtained as:
Replacing Formula (
13),
,
into (
32),
is expressed as:
By performing the pdf of the random variables
,
and the cdf of the random variable
, (
33) is achieved by the closed-form expression as:
Finally, from (
25) and (
34), the sum SOP of ST1 is constrained by the upper expression as:
☐
3.2. The SOP of the Secrecy Transmission in the Proposed UCCN-NOMA System with the Best Relay Selection: Case ST2
Similar to
Section 3.1, first, we find the best relay
based on the maximum channel gain of the R
-D
link. Next, we calculate the SOPs of the ST2 case in which the destination nodes D
, D
do not receive the signal safely from the source node S through
under the malicious attempt of the eavesdropper E. Finally, we calculate their sum SOPs.
Firstly, we calculate the best relay similarly as the expression of the best relay
in
Section 3.1, and the best relay
is selected based on a criterion as follows:
The cdf and pdf of the random variable
is expressed similarly as (
17) and (
18) and is shown as
,
The SOP of the ST2 case occurs when the destination D
does not receive signals
safely from the source node S. The SOP of the ST2 is obtained by a math expression as follows:
Substituting Formula (
15) into (
37),
is calculated as:
Replacing Formula (
13),
,
into (
37),
is expressed as:
Similar to (
33), the probability
in (
39) is shown by the closed-form expression as follows:
Second, we calculate the SOP of the ST2 case in which the destination node D
does not receive the signal safely from the source node S through the best relay R
under the malicious attempt of the eavesdropper E as follows:
By substituting (
9) and (
13) into (
40), we have an expression of
as follows:
Similar to solving
, we consider the worst case in which the node E can take data
with the best condition. We rewrite (
41), an upper constraint of
, as follows:
We calculate
similar to
, and after some algebra, the probability of
can be expressed as:
where
.
From Formulas (
40) and (
43), we have the sum SOPs of ST2 constrained by the upper expression as:
3.3. The SOP of the Secrecy Transmission in the Proposed UCCN-NOMA System with the Best Relay Selection: Case ST3
In this case, we find the best relay
based on the minimum channel gain of the R
-E link. The SOPs of the ST3 case in which the destination nodes D
and D
do not receive the signal safely from the source node S under the malicious attempt of the eavesdropper E are expressed next. Finally, we calculate their sum SOPs. The best relay selection is given as:
The cdf and pdfof the random variable
are calculated as:
The SOP of the ST3 case is similar to those in
Section 3.1 and
Section 3.2 and is shown by two math expressions, respectively, as follows:
By replacing Formula (
13),
,
into (
48) and (
49), finally, we can easily calculate the probability
,
, respectively, as:
-When
:
where
From Formulas (
51), (
52a), and (
52b),
is obtained as:
I
in (
35), I
in (
45), and I
in (
53) contain the complex integrals, and solving of these integrals is not practical. However, we can use numerical methods to find the value of I
, I
, and I
.
4. Simulation Results
In this section, the SOPs of ST1, ST2 and ST3 are analyzed and evaluated using the theoretical analyses and the Monte Carlo simulations. In the two-dimensional plane, the coordinates of S, R
, D
, D
, Pu, and E were set as S(0, 0), R
, D
(1, 0), D
, Pu
, E
, respectively, satisfying
. Therefore,
,
,
,
, and
. We assumed that the target secrecy capacity and the path-loss exponent were set to constants,
(bits/s/Hz) and
. The value range of
can be from 2–7, which depends on the transmission environments. To simplify the presentation, the parameters used to simulate and analyze are summarized in
Table 1 as follows.
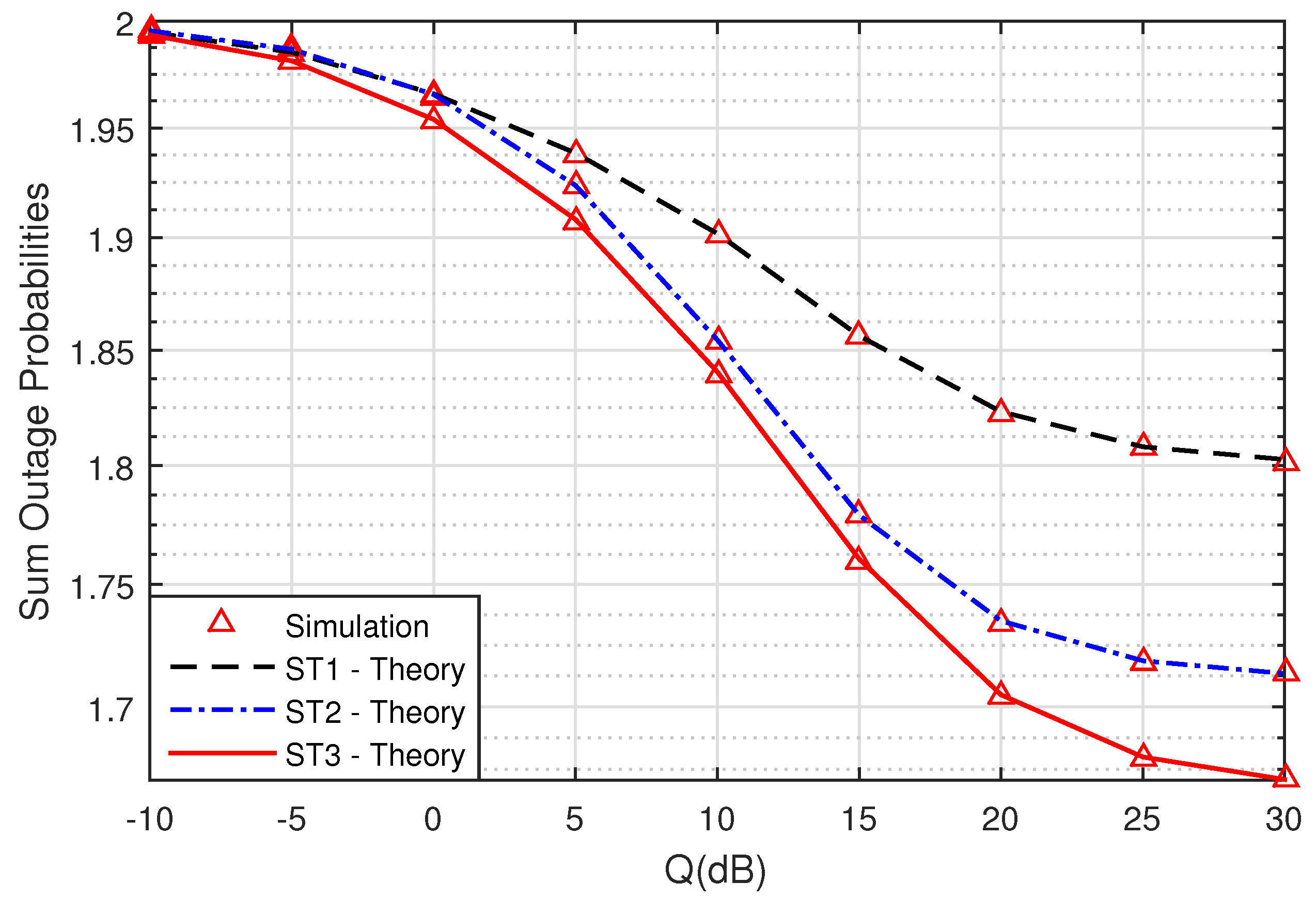
Figure 3 presents the sum SOPs of ST1, ST2 and ST3 versus Q(dB) when the symmetric network model is considered with M = 3,
,
,
, SC
= 1 (bit/s/Hz),
,
,
,
. As shown in
Figure 3, we can see that the secrecy performance of ST3 outperformed ST1 and ST2. The sum SOPs of ST1, ST2 and ST3 decreased when Q(dB) increased due to the increment of transmit powers. This can be explained by applying the NOMA technique and the selected relay method as in
Section 3.1,
Section 3.2 and
Section 3.3.
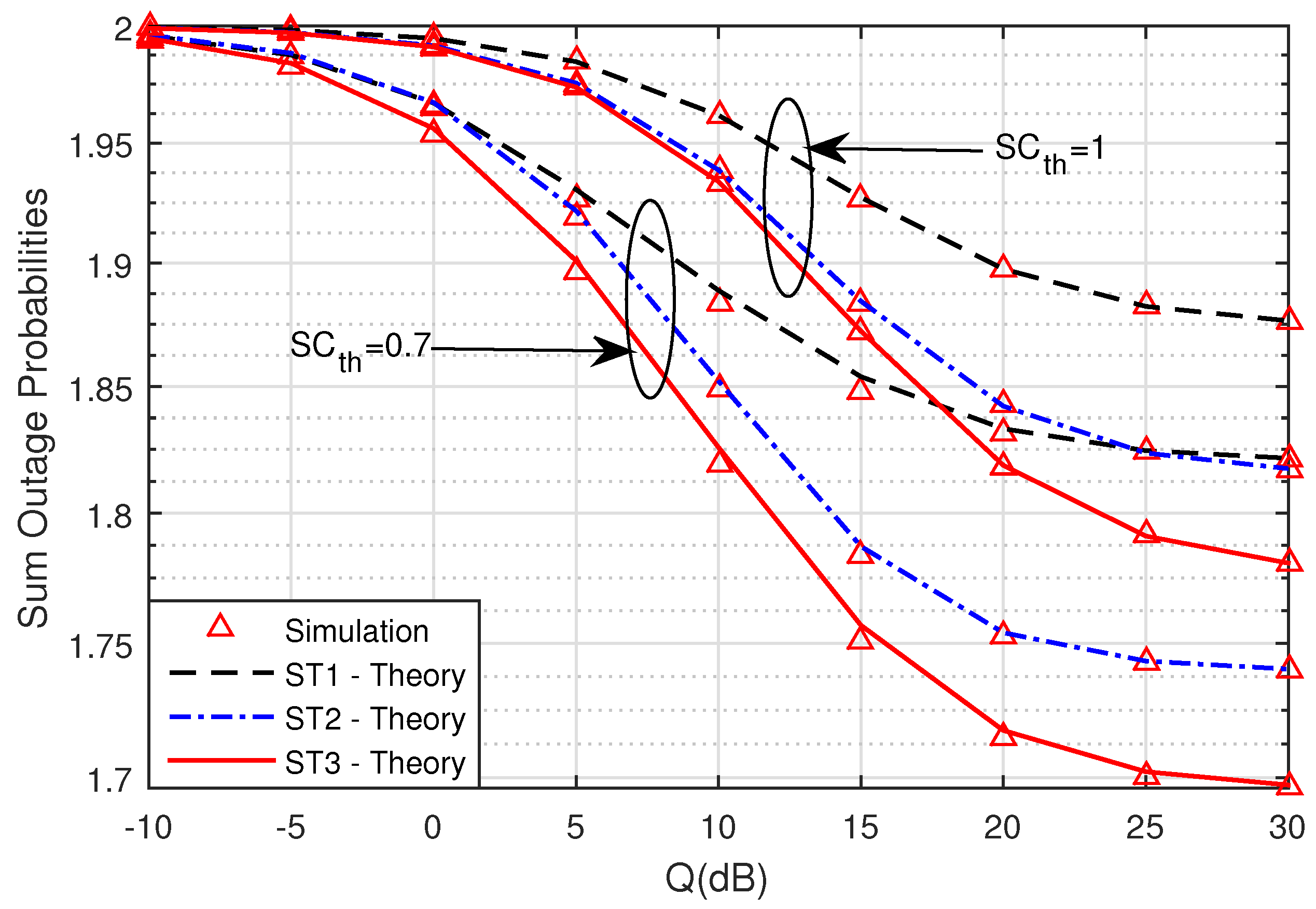
In
Figure 4, we compare the sum SOPs with two defined thresholds in two values: Case 1, SC
= 0.7 (bit/s/Hz), and Case 2, SC
= 1 (bit/s/Hz). It is clear that the lower the threshold is, the better the sum SOPs becomes. Lastly, the simulation results in
Figure 3 and
Figure 4 were suitable for the theoretical results of ST1, ST2, and ST3. Hence, we can conclude that the derived formulas during the analysis were accurate.
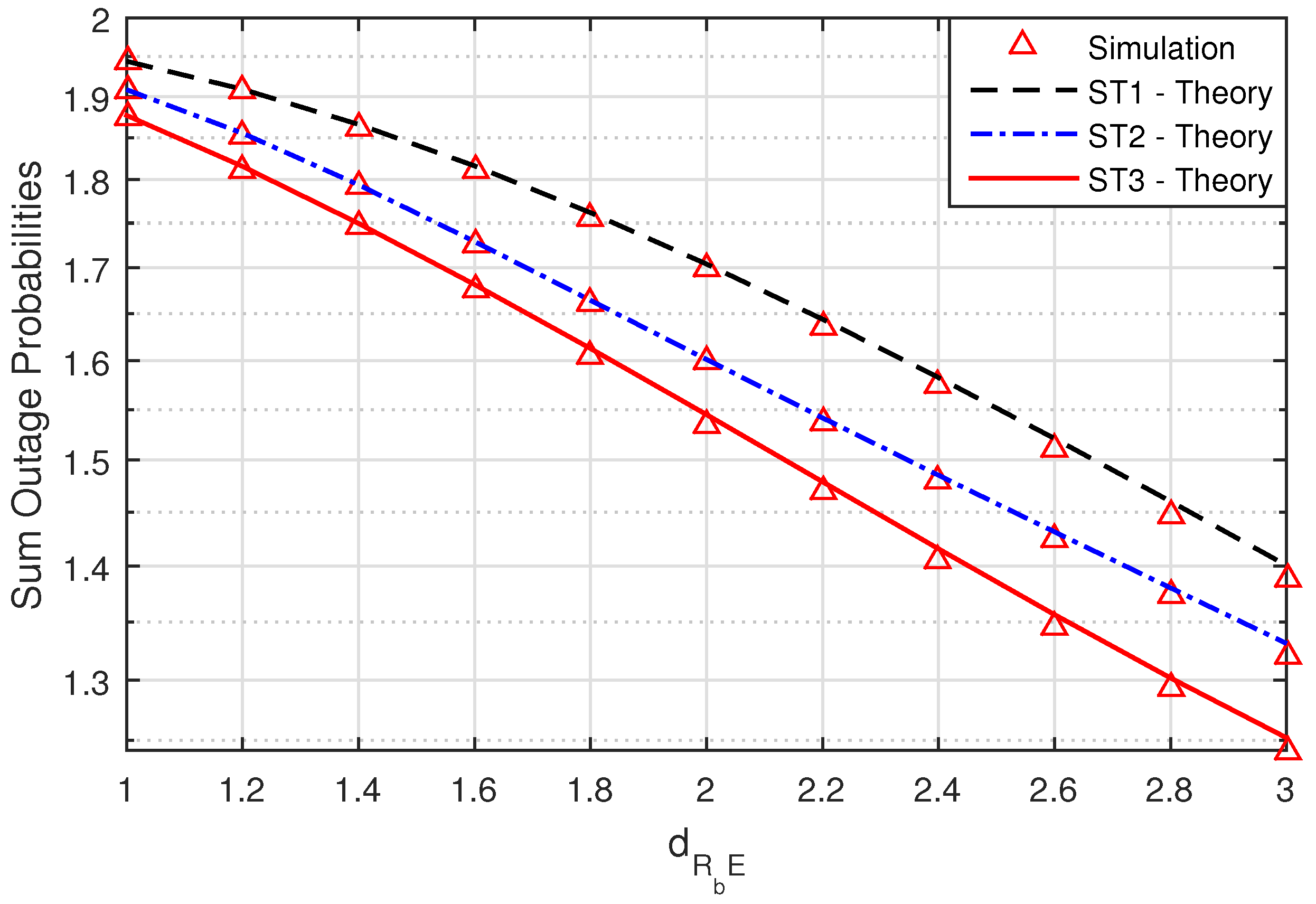
Figure 5 presents the sum SOPs versus the location of the eavesdropper node E when the symmetric network model is considered with M = 3,
,
,
, Q (dB) = 10 dB, SC
= 1 (bit/s/Hz), and
moves from one to three. In
Figure 5, the sum SOPs of ST3 are also smaller than the sum SOPs of ST1 and ST2. The simulation results and the theoretical results are logical. In addition, we can see that if the
value increased, the sum SOPs decreased. This result means that the security of the system is very good when eavesdropper node E is far from the source and cooperative relay.
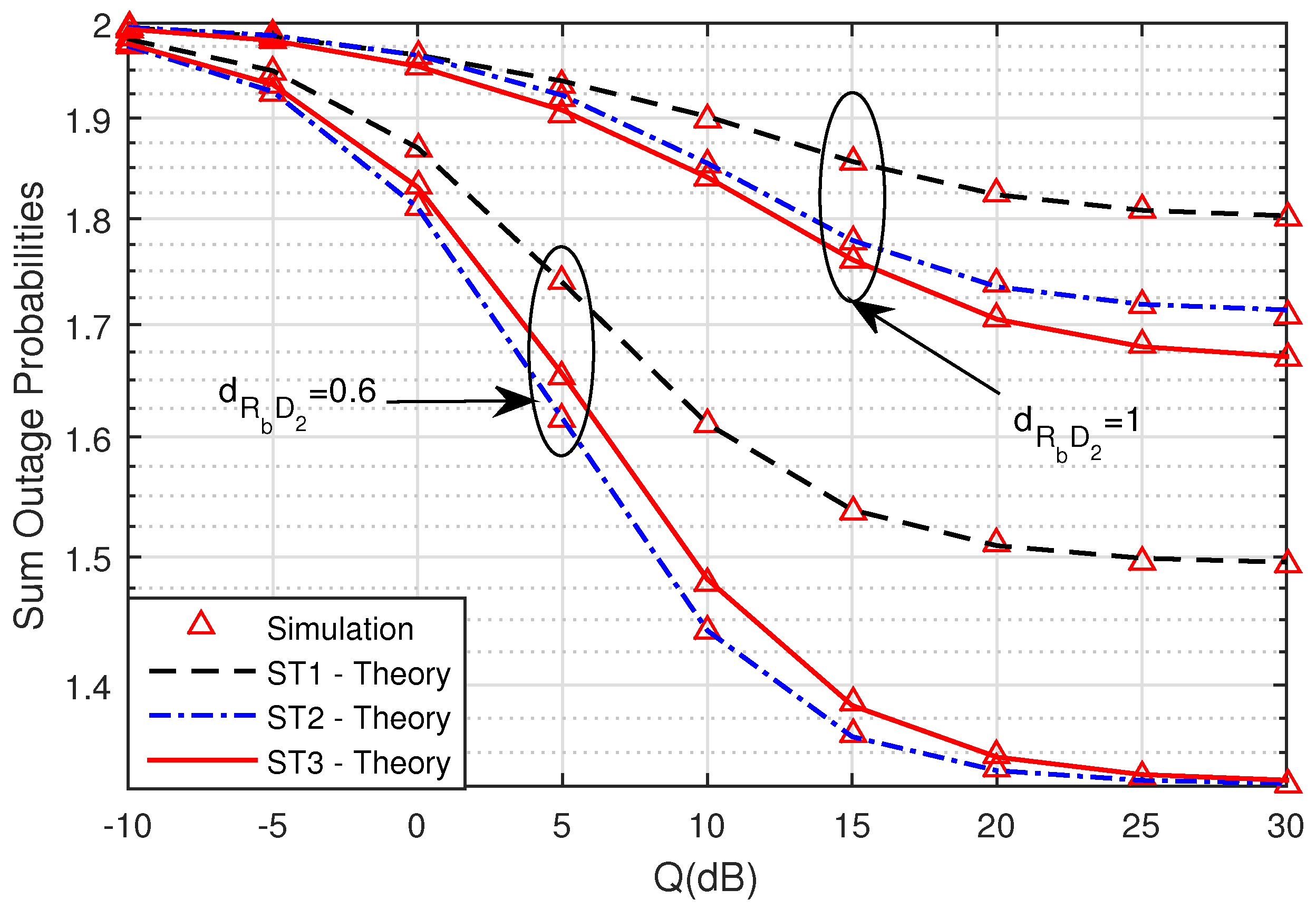
Figure 6 presents the sum SOPs versus Q(dB) when M = 3,
,
,
, SC
= 1 (bit/s/Hz),
, and
. As can be observed from
Figure 6, the sum SOPs of ST1, ST2, and ST3 decreased at the higher Q(dB) regions. This clear because the proposed UCCN-NOMA system used NOMA, and the considered PLS with the best relay selection achieved higher secrecy efficiency. When link distance
, the security of the system is better than when
. However, the security of system in ST2 is smaller than two for the remaining cases due to D
being near the relay.
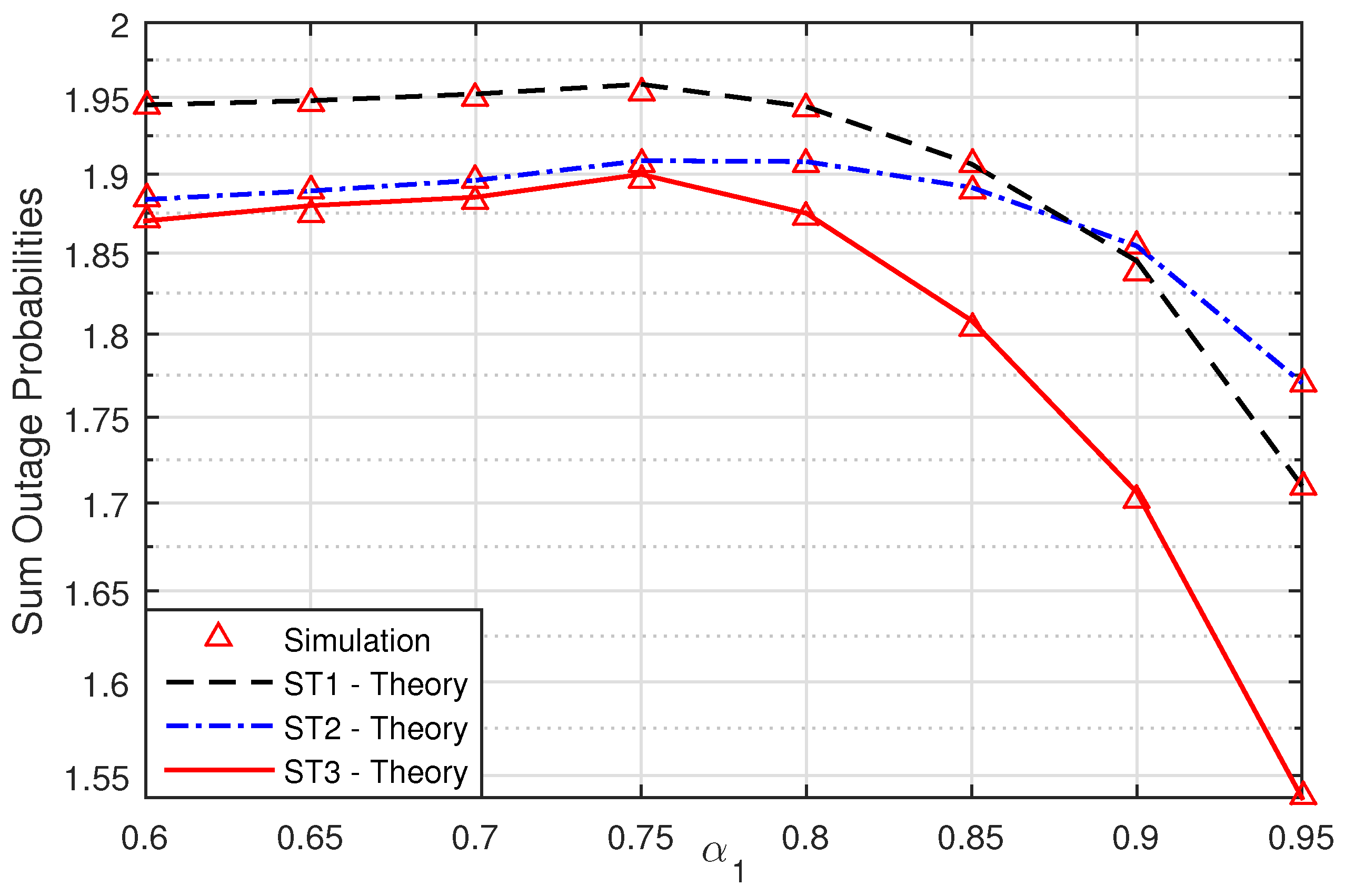
In
Figure 7, we investigate the impact of power allocation coefficients on the security performance of the UCCN system with the NOMA solution. In this figure, we show the impacts of varying
and
on the system. When
increased, the SOPs of the secrecy transmission of the signals
and
decreased and moved to small values. It is noticed that the power allocation coefficients in
Figure 7 can result in significant capacity gains in the UCCN system with NOMA and the best relay selection solution.