Tactical and Operational Cooperative Empty Container Repositioning Optimization Model Based on Business Flow and Initial Solutions Generation Rules

Abstract

Due to the special role of empty containers in the container transportation process, empty container repositioning is a focal point in the shipping industry. For this problem, highly efficient and feasible optimization models are critical in improving the benefit for shipping companies and increasing their market competitiveness. Operational decisions are affected by tactical ones. Aimed at this point, we propose a tactical and operational cooperative empty container repositioning optimization model. To cut the search space and obtain the optimal solution quickly, several initial solutions generation rules are extracted, based on business flow. Furthermore, the reachable shipping distance may change when the calling sequence is different. An algorithm which calculates the reachable shipping distance matrix between ports is presented to solve this problem. Simulated cases are used to test the proposed model and algorithm. The results show that the cases can cope with the tactical and operational cooperative empty container repositioning optimization model. Moreover, some interesting conclusions also are deduced about the relationships among number of calling ports, total profits, leasing cost, calling port fee, number of Empty Containers Repositioned (ECR), and laden containers. All these can guide and assist the various decisions to be made. According to the homepage of Symmetry, its subject areas include Mathematics, Computer Science, Theory, and Methods. Their branches include information theory, computer-aided design, and so on. The topic of our paper is to solve this engineering application problem by using a mathematical optimization model and computer methods. That is, applying mathematical theory and computer methods to make decision results for the empty container repositioning problem in the shipping industry. It has certain economic value and practical significance. Obviously, it is consistent with the theme of Symmetry.

1. Introduction

Container transportation has become a widely-used mode of transportation, due to its advantages of efficient and reliable operation, comprehensive service, low cost, and easy intermodal transport. However, due to the imbalance of national trade and other complex factors, such as the location of container maintenance ports, different ports of production and use, and so on, the distribution of empty containers in ports is almost unbalanced. How to reposition them is a difficult problem, which all shipping companies have to face, not only in meeting customer demand for empty containers in time, but also in making the overall cost as low as possible.

Generally speaking, the costs relating to containers include transportation costs, stock costs, repairing costs, leasing costs, unload costs, load costs, and other operation costs. For shipping companies, there are also huge differences in the various costs consisting of laden container transportation, empty container repositioning (ECR), calling ports, and calling sequence of vessels, as well as the operating costs of liners. Moveover, since these above problems may by interrelated, it is necessary to consider them simultaneously. Therefore, this problem has become one of the key problems to be dealt with urgently for shipping companies to consider the calling port set, calling sequence, and the transportation of two typical containers together, so as to make the overall cost as low as possible. Basically, the above problem is a typical NP problem in optimization field. At present, one of the research streams about this kind of optimization solution is heuristic algorithms, which mainly imitate natural body algorithms, such as genetic algorithms (GA), ant colony algorithms (ACA), simulated annealing (SA), artificial neural networks (ANN), list search algorithms (ST), and so on.

For a heuristic algorithm solving laden container transportation, ECR, and related optimization problems, many research works and corresponding solutions have been presented. Shintani et al. [1] relaxed the constraints of calling sequence and calling port set, and designed the corresponding shipping lines for ECR problem. This problem is formalized into a two-tier model. The upper level is the knapsack problem, in order to select the best calling port set. The lower level is to determine the calling sequence under the decision of the upper level. GA is used to solve them. Supposing that the demand number of container transportation is a fuzzy one, Chuang et al. [2] solved the shipping lines planning through fuzzy GA. Lam et al. [3] proposed an approximate dynamic programming method to cope with the ECR of two ports and two routes. The feasibility of the method was verified by simulated data. For the empty container coding problem, Hottung and Tierney [4] gave a novel biased-random key genetic algorithm encoder, which can study how to move a single container or container group to the yard quickly. Iris et al. [5] also presented a metaheuristic algorithm for the efficient handling of containers in the yard.

Yoonjea et al. [6] proposed a two-way, four-echelon container supply chain management mechanism to solve bilateral trade between two countries. This mechanism can reduce high shipping costs and shorten the transportation time prolonged by transit. The paper discussed, in depth, how the choice of ports, leasing empty containers, and shipping routes affected the number of ECR. Dang et al. [7] assumed that customer demand and returned containers per unit time were sequence-dependent and dependent on random variables. They considered the ECR between one port and four yards. Under this situation, it included three cases: Repositioning empty containers from other ports, repositioning between yards, and empty container leasing mechanisms. Rahime and Shahin [8] proposed a modelling framework, which made joint problems of network design, fleet deployment, and ECR. Zheng et al. [9] focused on the coordination of empty container allocations among liner carriers. To solve the problem, they proposed a two-stage optimization method. In stage I, liner carriers pursued a centralized optimization solution of ECR. In stage II, inverse optimization techniques are used to define the exchange costs. Under the situation of the Chinese One Belt One Road, Katarzyna and Erwin [10] analyzed the models and a variety of solutions to ECR problems through the prism of Eurasian intermodal transportation. From the view of container transport chains, Lee and Song [11] gave the extant study in ocean container transport, in which many wide issues were discussed. Notteboom et al. [12] studied how the alliance mode and vertical integration in container operations have influenced the selection of calling ports. Furthermore, this article also described the interplay between changes in the organizational routines of shipping lines as part of alliances, changes at the level of terminal operations, and changes in the port calling pattern.

Bandeira et al. [13] proposed a heuristic method for integrated distribution of empty and laden containers in an intermodal network. Zhang et al. [14] analyzed multi-period and multi-port ECR with stochastic demand and lost sales. Song and Dong [15] considered the laden container routing and ECR at the operational level. To solve this problem, a shortest-path based integer programming method and a heuristic-rules based integer programming method were given. They presented a heuristic algorithm to implement the static assignment plan in dynamic, multiple-period situations. It is reasonable to assume that laden containers have priority over empty containers. Chang et al. [16] adopted container substitution between different types, in order to reduce the cost of empty container interchange. The proposed heuristic approach for the multi-commodity substitution problem used a branch and bound (B&B) procedure, to find an integer solution to the reduced problem. Lai et al. [17] adopted a simulation model to optimize the ECR from the Middle East to ports in the Far East. In order to search for cost-effective ways, some heuristic search methods were used. Bell et al. [18] presented a frequency-based assignment model to allocate laden and empty containers over shipping services. Its objective was to minimize the sailing time plus container dwell time, at the original port and any intermediate trans-shipment ports.

Braekers et al. [19] proposed a decision support model for service network design in intermodal barge transportation. This model determined optimal shipping routes for roundtrip services between a major seaport and several hinterland ports, where the vessel capacity and service frequency decisions also were analyzed. Chou et al. [20] built a two-stage model. In stage one, a fuzzy backorder quantity inventory mechanism was proposed, to determine the optimal quantity of empty container at a port. In stage two, an optimization mathematical programming network model was used, to determine ECR between ports. Di Francesco et al. [21] adopted the concept of flexible destination port repositioning and used multi-scenario mixed-integer programming to address the ECR problem in maritime networks under possible port disruptions. Epstein et al. [22] developed an empty container logistics optimization system (ECO) to support the repositioning and stocking of empty containers in a large shipping company. However, the movements and routing of laden containers were not involved. Long et al. [23] formulated a two-stage stochastic programming model for the ECR problem in a maritime shipping network with uncertainties. The sample average approximation method and the progressive hedging strategy were applied to solve the optimization problem. Zheng et al. [24] also measured container leasing prices with ECR. There are also other collaborative studies between liner shipping companies and ports. Venturini et al. [25] addressed the integrated problem of call port sequencing and berth allocation.

At present, existing methods have studied the problem of ECR from many views, and have given corresponding solutions. However, from the literature, it can be observed that the existing methods only pay attention to laden container transportation and ECR on the operation layer to a certain extent, and ignore the direct influence of relevant decisions on the tactical layer. As we know, within industry fields, decision-making in the shipping industry is usually divided into three levels: The strategic layer, the tactical layer, and the operational layer. They depend on each other, complement each other, and cannot be separated. Therefore, only considering the two types of container transportation planning on the operation layer may be contrary to the actual business. For example, if the decision maker ignores the stocks of port, which typically belongs to the decision problem on the strategy level, they only focus on the container transportation. It may cause unnecessary repositioning cost, as stocking empty containers can meet the demand. In addition, most of the existing methods for solving models use classical optimization methods, such as mathematical programming methods and combinational optimization methods, which cannot cope with shipping-related models on a large scale, having many parameters and variables, and involving big datasets.

To solve the above problems, we propose a two-layer collaborative optimization model based on business flow, which contains the main decision-making problem of the tactical and operation layers. This model can optimize not only the calling port set and calling sequence on the tactical layer, but also the ECR and laden container transportation on the operation layer. For the former, we have proposed a initial solution generation coding method, based on business flow, which can reduce the search space and improve the performance. These extracted business rules are constructed through intuition or experience, which can obtain the best solution, given accepted costs (e.g., time and space). In addition, differences in calling port set and calling sequence may change sailing distances for shipping lines between ports. How to calculate the reachable shipping distance matrix, some rules, and the corresponding algorithm has been given. The latter can further be optimized with the decision problem of two types of containers on the operation layer, by using a mathematical programming method. Case-simulated experiments show that the proposed method can better solve the two-layer cooperative decision problem, simultaneously. The contributions of this paper mainly include the following three aspects.

(1) A coding method and several solution generation rules for the initial solution space are designed for the shipping business flow, which can greatly reduce the search space, decrease the computational complexity, and improve the search efficiency for the best solution.

(2) Two algorithms, which can generate the initial feasible solutions and calculate the reachable shipping line distance matrix between ports, are proposed.

(3) We present and construct a two-layer collaborative optimization model, and solve the main decision problems on the tactical layer and operational layers, consisting of calling port set, calling sequence, ECR, and laden container transportation, and so on.

The rest of this paper is given as follows. The problem description is given in Section 2. The detailed design of the proposed model is discussed in Section 3. Experimental results and analysis are demonstrated in Section 4. Conclusions and future work are presented in Section 5.

2. Problem Description

As was mentioned above, the decision-making problem in the shipping field can be divided into three levels. For the strategic level, because the scope of its involvement is usually the overall business policy of long-term development of a company, its cycle is longer, some for as long as 30 years. It is difficult to control and quantify the processing. However, relevant decisions made on the strategic level have important and direct impacts on the lower layers, including tactical and operational layers. For example, the typical issue, on the strategic level, is strategic alliances. Forming an alliance, or breaking one, will immediately determine the relevant issues on the two lower levels. Basically, the tactical level decisions consist of route planning, liner deployment, and port inventories. This layer and the operational layer are jointly considered, and interact with each other. Meanwhile, they are consistent with the actual business, and the decision results are more reasonable and feasible. Due to the numerous decision-making problems on the tactical layer and the operation layer, the factors involved are very complicated. Here, only the calling port set and calling sequence on the tactical layer, and the two types of container transportation problems on the operation layer are involved in the models. The details of the problem are as follows.

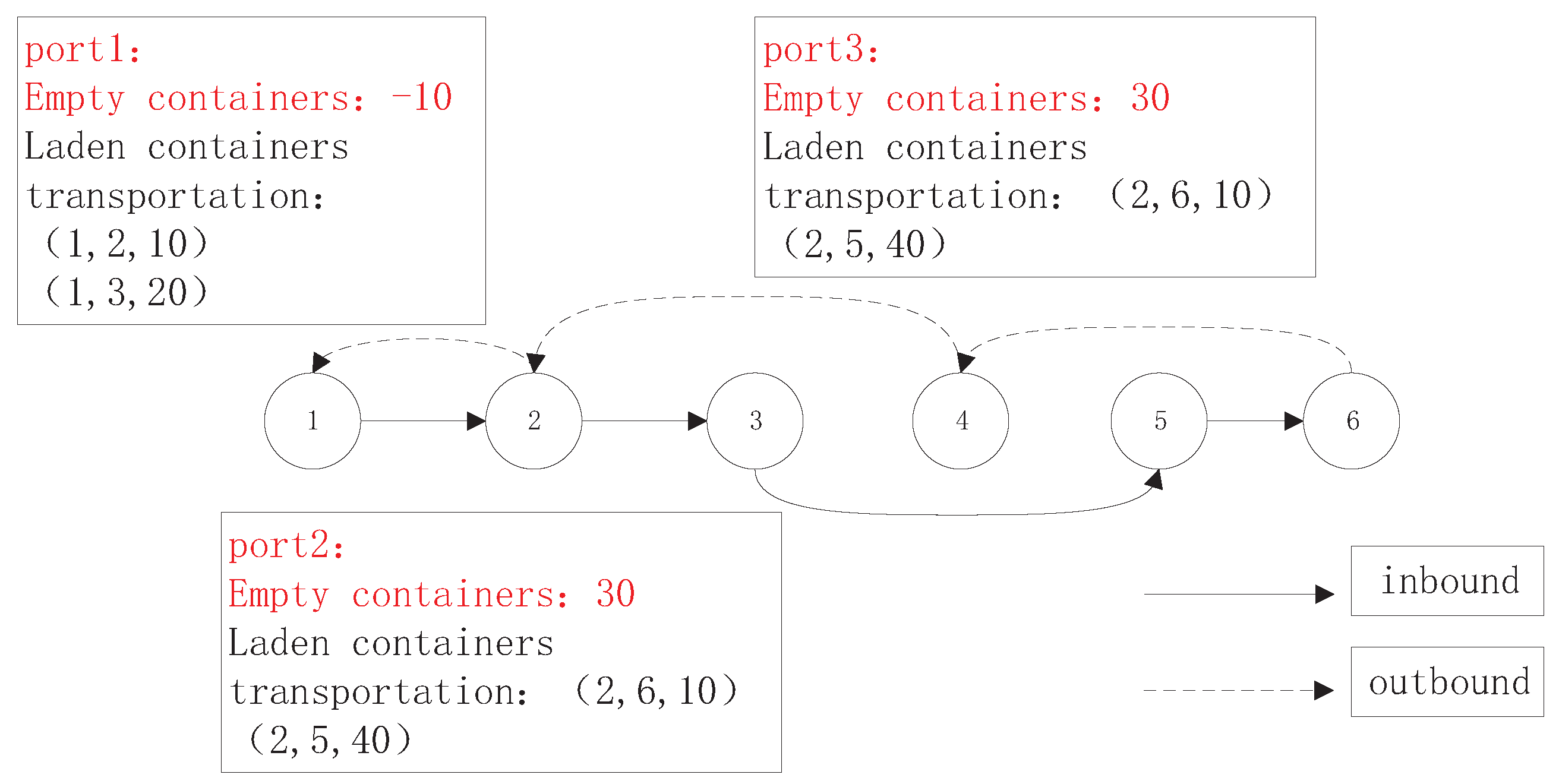
Suppose that one shipping route, $lin{e}_1$, is provided (shown as Figure 1). There are six candidate calling ports. In order to describe the problem succinctly, the port numbers are named ①, ②, ③, ④, ⑤, and ⑥, respectively. The beginning port and end port of this shipping route are both ①. The process, travelling through several ports from port ① and back to port ①, is called a voyage, where the solid line is the inbound journey, including the calling port set and the corresponding sequence. It is: ①-②-③-⑤-⑥. The dotted line is the return trip or outbound one. Its calling port set and sequence is: ⑥-④-②-①. For example, based on the given supply and demand of empty containers in the port, and transportation tasks of the laden containers, for port ①, the number of empty containers is $-10$. The negative value indicates that this port is deficit. Namely, empty containers need to be unloaded at or leased to port ①. A positive value indicates that surplus empty containers exist in the corresponding port. The workloads of the laden container transport between ports are formalized as triples (1):

$$(originatingport,destinationport,transportationvolume).$$

(1)

Taking port ① as an example, the transportation numbers of laden containers are $L_1(1,2,10)$ and $L_2(1,3,20)$, which describes that port ① needs to transport 10 laden containers to port ②, and 20 laden containers to port ③. Based on the situation where laden container transportation and empty container demand must be satisfied, how to choose the calling port set and plan the calling sequence will be solved here. The objective function is to maximize the total profit or minimize the total cost of a voyage.

As the factors involved in the above problems are various and complex, the following assumptions are given for building and solving the problem: For liner shipping, schedules and services are given and fixed in advance. Ignore the repair and scrapping of the containers, and all containers within the study scope are available. All required and supplied containers are measured in 20-foot equivalent unit (TEU) containers. There is no limit to the amount of empty containers at each port at anytime. The tasks of laden container transportation among ports are always satisfied, and the amount of empty containers required for each port must be met. The transportation cost between ports is proportional to the distance between them.

3. Optimization Models

The above problem is a typical combinatorial optimization problem. Since this problem has decisions at two levels, consisting of tactical level and operational level decisions, involved, we divide it into two stages and solve them separately. In first stage, the visiting sequence is determined and, in the second stage, the optimization model for ECR is solved.

3.1. Initial Solutions Generation Mechanism of Calling Port Set and Calling Sequence on the Tactical Level

When the problem scale increases exponentially, the existing classical combinatorial optimization methods will be usually fruitless and frustrating. Therefore, inspired by the coding method of classical GA, a coding method based on business flow is proposed to adapt this problem. After studying the related business flows on the tactical layer, Rule 1 and Rule 2 are extracted as the basis for the initial solution sequence generation mechanism, as shown below.

Rule 1: Considering that the beginning port and ending port of one voyage in the shipping business are both port ①, the corresponding values of start and end positions of all the solution sequences are both ‘1’. The ‘1’ indicates that the corresponding port is called, and ‘0’ for the opposite side. Generally, because port ⑥ is the farthest port, it must be called; otherwise, it may be isolated. So, its value is also ‘1’.

Some of the initial solutions (calling sequences) are presented in

Table 1. Initial feasible solution generation sequences.

s	Feasible Solution
$s_1$	1	2	3	0	5	6	0	4	0	2	1
$s_2$	1	2	3	4	5	6	0	0	0	0	1
$s_3$	1	0	0	0	0	6	5	4	3	2	1
$s_4$	1	2	3	0	0	6	0	4	3	2	1
⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯

. For example, the solution $s_1$ describes the calling port sequence ①-②-③-⑤-⑥-④-②-①. Basically, $s_1$ shows the case in Figure 1. For solution $s_2$, the inbound trip calls each port, but the outbound trip only visits ports ⑥ and ①. The corresponding port calling sequence is ①-②-③-④-⑤-⑥-①. According to Rule 1, both of them are feasible solutions.

The feasible solution sequence generation algorithm is given (from line 4 to 21) in Algorithm 1.

Rule 2: For one voyage, including the outbound and inbound trips, the same port should be called at least once and up to 2 times. The former can ensure the connectivity between this port with any other ports, and the latter can avoid the route forming a self-loop.

It is easy to find that, after applying these two rules, the initial solution space size can be reduced from $2^{11}$ to $3^4$ and greatly cut the search space. For example, as shown in

Table 2. Infeasible solution sequences.

$\mathit{n}\mathit{s}$	Infeasible Solution
$n{s}_1$	1	2	0	0	5	6	0	4	0	2	1
$n{s}_2$	1	0	0	0	0	6	0	0	0	0	1
$n{s}_3$	1	2	0	0	0	6	0	0	0	0	1
$n{s}_4$	1	2	0	4	0	6	5	0	0	0	1
⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯

, for sequence $n{s}_1$, the corresponding positions of outbound and inbound are both 0 for port ③, representing that there is no calling at port ③ at all in both directions. This completely deviates from the actual business flow. Another example is $n{s}_2$: Except for ports ① and ⑥, the other ports are not linked, which is also out of the actual business flow. Similarly, the sequences $s{n}_3$ and $s{n}_4$ are both infeasible solutions, shown in Table 2.

3.2. Generation Mechanism of Reachable Shipping Lines Matrix Between Ports

Due to the difference between calling port set and calling sequences among ports, the transportation distances of containers that can be reached among the various ports will be quite different. The distances between ports are formalized as (2), which indicates that the distance between $port1$ and $port2$ is d standard units.

$$(port1-port2:d).$$

(2)

Without loss the generality, assume that the distances between ports are (①-②: 50), (②-③: 40), (③-④: 80), (④-⑤: 50), and (⑤-⑥: 70). In Figure 1, since the outbound trip does not call at port ④, the shipping route distance between port ③ and ④ can be calculated as below: ③-④-⑤-⑥-⑤-④. The shipping route distance is 80 + 50 + 70 + 70 + 50 = 320.

Based on the above analysis, the following five rules were extracted as the relevant basis for generating the shipping distance matrix between ports, according to the actual service flow.

Rule 3: If one port is called on both inbound and outbound journeys, the distance between the other ports to this port has 2 values, and the corresponding shipping distance value in the matrix is taken to be the smaller one.

By way of illustration, for the feasible solution $sn\left(111111111111\right)$, this port sequence indicates that all ports are visited in both directions. Our method will calculate two values when deciding the shipping route distance from port ② to ④. One is docked at port ② and ④ for inbound journey. The calling ports sequence is ②-③-④, and its shipping line distance is 120. Another is calling at port ④ when returning. The calling port sequence is ②-③-④-⑤-⑥-⑤-④. Its shipping route distance is 460. So, the corresponding value in the route distance matrix between port ② and ④, according to rules 3, is 120.

Algorithm 1 Pseudo-code for calling port set generation mechanism and reachable shipping distance matrix.

Require: 1: number of candidate ports: n. $dis[2n-2]$;// distances of neighbour ports. Ensure: 2: $path[2n-1]$;//calling ports set and calling sequence. $dis\_mat\left[n\right]\left[n\right]$; //shipping distance matrix: SDS. 3: procedure 4:  $pos\_bef\left[n\right]$;//represents the calling ports set of inbound trip. 5:  $pos\_aft\left[n\right]$;//represents the calling ports set of outbound trip. 6:  //calling sequences generation. 7:  $pos\_bef\left[\right]=path[0:n]$; $pos\_aft\left[\right]=path[n:2n-1]$; 8:  for each i in $2n-1$ do 9:   //Initialize path, where the corresponding positions are 0 and length of each calling sequence is $2n-1$. 10:   //position 1, n and $2n-1$ must be called, and its position value equals to 1. 11:   $path\left[1\right]=path\left[n\right]=path[2n-1]=1$; 12:   for (int $i=2;i<n-1;i++$) do 13:    $path\left[i\right]=$ random(0,1);//random value generation: 1 or 0. 14:    if ($path\left[i\right]==0$) then 15:     $path[2n-i]=1$;//port must be called once. 16:    end if 17:    if ($path\left[i\right]==1$) then 18:     $path[2n-i]=1$ or $path[2n-i]=0$; 19:    end if 20:   end for 21:  end for 22:  //calculate the distance matrix. 23:  for each i in range(n) do 24:   for each j in range(n) do 25:    if ($i==j$) then 26:     $dis\_mat\left[i\right]\left[j\right]=0;$ //set the distance from port A to A is 0. 27:    else 28:     //if both two ports are in $pos\_bef$ and not 0. 29:     //both two port are located in “pos_bef” respectively. Both their values are not ‘0’. 30:     //judge the positions of two ports, get port “$t1$” from A to B. 31:     if ($pos\_bef\left[i\right]!=0\&\&pos\_bef\left[j\right]!=0$) then 32:      $t1=Fun(pos\_bef[i],pos\_bef[j\left]\right)$ 33:      // Fun is to obtain the passing port set from i to j. 34:      for (t in range($t1$)) do 35:       $temp1+=dis\left[t\right]$; 36:      end for 37:     end if 38:     //both two port are located in “pos_aft” respectively. Both their values are not ‘0’. 39:     //judge the positions of two ports, get port “$t2$” from A to B. 40:     if ($pos\_aft\left[i\right]!=0\&\&pos\_aft\left[j\right]!=0$) then 41:      $t2=Fun(pos\_aft[i],pos\_aft[j\left]\right)$ 42:      for (t in range($t2$)) do 43:       $temp2+=dis\left[t\right]$; 44:      end for 45:     end if 46:     // two ports are located in “pos_bef” and “pos_aft” respectively. 47:     // Both their values are not ‘0’. 48:     //judge the positions of two ports, get port “$t3$” from A to B. 49:     if ($pos\_bef\left[i\right]!=0\&\&pos\_aft\left[j\right]!=0$) then 50:      $t3=Fun(pos\_bef[i],pos\_aft[j\left]\right)$ 51:      for (t in range($t3$)) do 52:       $temp3+=dis\left[t\right]$; 53:      end for 54:     end if 55:     $dis\_mat\left[i\right]\left[j\right]=min(temp1,temp2,temp3)$; // get the minimum value of three values. 56:    end if 57:   end for 58:  end for 59: end procedure

Rule 4: Within one voyage, if one port only has an inbound calling, the other ports to this port cannot reachable in the outbound journey. That is, non-connected for outbound. For this situation, the shipping route distance has only one value and reaches its maximum.

Take the calling sequence $s{n}_m\left(11011111101\right)$, as example. For the inbound journey, it calls in at port ②; but in the outbound, it does not call in at port ②. So, the shipping line from port ③ to ② is ③-②-①-②. Their value in the distance matrix is $40+50+50=140$.

Rule 5: When calculating the shipping route distance matrix, the maximum distance of any two ports cannot exceed the values of one voyage.

Since each port calls one time at least, the maximum distance between this port to other ports is across both inbound and outbound journeys. Its values are less than the distance of one voyage.

Rule 6: For a feasible solution, every two ports are connected.

If one solution can not guarantee that any two ports can reach one another, it may appear to have an isolated port. Furthermore, if two ports are not connected, the possible transportation task cannot be executed. This port also loses the existing necessity.

Rule 7: For each port, the distance from the port to itself equals to 0.

For example, for feasible solution sequence $s{n}_p\left(11111111111\right)$, its distance matrix is as in Formula (3). The Pseudo-code is described (from line 23 to 58) in Algorithm 1.

$$\left[\begin{array}{cccccc}0& 50& 90& 170& 270& 340\\ 50& 0& 40& 120& 220& 290\\ 90& 40& 0& 80& 180& 250\\ 170& 120& 80& 0& 100& 170\\ 270& 220& 180& 100& 0& 70\\ 340& 290& 250& 170& 70& 0\end{array}\right]$$

(3)

3.3. Relevant Parameters of Two Types of Containers on the Operational Level

To describe the model of ECR and laden container transportation conveniently, some notation is given:

$i,j$: port;

$defP:deficitportset$, the port set to which the empty containers need to be imported;

$surP:surplusportset$, the port set from which the empty containers need to be exported;

$balP:balanceportset$, the ports set which needs neither importing nor exporting;

P: port set—$P=\{defP,surP,balP\}$;

M: profit coefficient of laden containers;

Q: transportation cost coefficient of laden containers;

N: transportation cost coefficient of empty containers;

$empt{y}_i$: the number of empty containers in port i;

$lease{C}_i$: the leasing cost of unit containers in port i;

$load{C}_i$: the loading cost of unit containers in port i;

$unload{C}_i$: the unloading cost of unit containers in port i;

$stock{C}_i$: the inventory cost of unit containers in port i;

$portCall{C}_i$: the calling cost of vessel in port i;

$lade{n}_{ij}$: number of laden containers from port i to j;

$di{s}_{ij}$: the distance between port i to j.

3.4. Optimization Model of ECR and Laden Container Transportation on the Operational Level

According to the business process of ECR and laden container transportation on the operation layer, the corresponding objective function, decision variables, and constraints are given as follows.

3.4.1. Decision Variables

The decision variables are as follow:

• $transNu{m}_{ij}$: number of empty containers from i to j;
• $s_i$: inventory number of empty containers in i;
• $l_i$: leasing number of empty containers in i.

3.4.2. Objective Function

According to the objective function, which maximized the revenue, we give the details of model as formula 4 and corresponding constraints as formulas (5)–(9), where, the objective function (4) describes that the goal of the model is to maximize revenue, which is the total income minus the total cost.

$$\begin{array}{cc}\hfill maximize& \sum _i\sum _{j}lade{n}_{ij}\times di{s}_{ij}\times M-\sum _i\sum _{j}transNu{m}_{ij}\times (di{s}_{ij}\times N+load{C}_i+unload{C}_j)\hfill \\ & -\sum _i\sum _{j}lade{n}_{ij}\times (di{s}_{ij}\times Q+load{C}_i+unload{C}_j)\hfill \\ & -\sum _i{l}_i\times lease{C}_i-\sum _i{s}_i\times stock{C}_i-\sum _{i}portCall{C}_i.\hfill \end{array}$$

(4)

3.4.3. Constraints

According to the above hypothesis and problem description, the corresponding constraints are given:

$$\sum _{j}transNu{m}_{ij}\le empt{y}_i,\mathrm{for}i\in surP;$$

(5)

$$\sum _{i}transNu{m}_{ij}\le \left|empt{y}_j\right|,\mathrm{for}j\in defP;$$

(6)

$$\sum _{j}transNu{m}_{ji}\le 0,\mathrm{for}i\in surP;$$

(7)

$$\sum _{j}transNu{m}_{ij}+s_i=empt{y}_i,\mathrm{for}i\in surP;$$

(8)

$$\sum _{i}transNu{m}_{ij}+l_j=\left|empt{y}_j\right|,\mathrm{for}j\in defP.$$

(9)

The first item of the objective function is the freight income of laden containers. The second items are the transportation cost and (un)loading cost of the empty containers, respectively. The third item is the leasing cost of the deficit ports. The fourth item is stock cost of empty containers in surplus ports. The last one is the cost of the vessel calling ports, which is usually a constant. The constraint (5) indicates that the number of empty containers exported from the surplus ports cannot exceed the ones available at the same port. The constraint (6) describes that the number of empty containers imported into the deficit ports should be less than or equal to the absolute value of required ones. The constraint (7) ensures that the deficit ports do not export empty containers; otherwise, it will be contrary to the actual business. The constraint (8) declares that, for the surplus ports, the exporting amount of empty containers plus the inventory ones are equal to the excess. The last constraint (9) limits the leasing mechanism, and is employed if the imported empty containers do not meet the demand ones in deficit ports. The number of leased empty containers is the demand ones minus the importing ones. This is due to the fact that the empty container demand must be met, which was mentioned in the above hypothesis.

4. Experimental Results and Analysis

Aimed at the calling port set and a calling sequence of 6 ports, we have constructed and discussed the optimization model, based on the tactical and operational cooperative decision problem. The Algorithm 1 was written in Java and the model from Section 3.4 was solved by means of CPLEX 12.5.

4.1. Case Data

Based on an actual business, simulated data were generated and used to evaluate the proposed model. The details of the various costs are shown in

Table 3. Best solution under different calling sequences.

Calling Cost		${\mathit{callC}}_1=\mathrm{20,000}$	${\mathit{callC}}_2=\mathrm{10,000}$	${\mathit{callC}}_3=5000$
Calling Sequence		1 2 3 0 0 6 5 4 0 0 1	1 2 3 0 0 6 5 4 0 0 1	1 2 3 0 0 6 5 4 0 0 1
Matrix of ECR		$\left[\begin{array}{cccccc}0& 80& 0& 10& 0& 10\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 50\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 70& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 80& 0& 10& 0& 10\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 50\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 70& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 80& 0& 10& 0& 10\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 50\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 70& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$
Number of leased empty containers		$\left[\begin{array}{cccccc}0& 0& 0& 20& 0& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 0& 0& 20& 0& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 0& 0& 20& 0& 0\end{array}\right]$
Number of calling ports		6	6	6
Transportation matrix of laden containers		$\left[\begin{array}{cccccc}0& 30& 0& 50& 10& 30\\ 20& 0& 0& 50& 0& 10\\ 0& 0& 0& 0& 10& 20\\ 20& 30& 0& 0& 30& 10\\ 0& 0& 0& 10& 0& 20\\ 70& 0& 60& 20& 30& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 30& 0& 50& 10& 30\\ 20& 0& 0& 50& 0& 10\\ 0& 0& 0& 0& 10& 20\\ 20& 30& 0& 0& 30& 10\\ 0& 0& 0& 10& 0& 20\\ 70& 0& 60& 20& 30& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 30& 0& 50& 10& 30\\ 20& 0& 0& 50& 0& 10\\ 0& 0& 0& 0& 10& 20\\ 20& 30& 0& 0& 30& 10\\ 0& 0& 0& 10& 0& 20\\ 70& 0& 60& 20& 30& 0\end{array}\right]$
Cost	Inventory cost	0	0	0
	Empty container cost	114,600	114,600	114,600
	Cost of calling ports	120,000	60,000	30,000
	Cost of leasing	40,000	40,000	40,000
Revenue	Freight charge of laden containers	464,800	464,800	464,800
Net profit	Best solution	1,119,400	1,179,400	1,209,400

. In the case of Table 3, the leasing cost of each port was $leaseCos{t}_1=\left[200030004000200030002000\right]$. They were keep constant throughout the experimental sections (Section 4.2.1 and Section 4.2.2). In order to test the influence of leasing cost, we supposed that it will be changed from $leaseCos{t}_1$ to $leaseCos{t}_2=\left[200030004000400030004000\right]$. Namely, the corresponding leasing costs of port 4 and 6 are increased, due to higher demand. For the calling port set and a calling sequence of 6 ports, there were 81 cases. Limited by space,

Table 4. Vessel calling sequences of ports.

s	Calling Sequences	s	Calling Sequences
$s_1$	1 0 0 0 0 6 5 4 3 2 1	$s_6$	1 0 0 4 5 6 0 0 3 2 1
$s_2$	1 0 0 0 5 6 0 4 3 2 1	$s_7$	1 0 0 4 5 6 0 4 3 2 1
$s_3$	1 0 0 0 5 6 5 4 3 2 1	$s_8$	1 0 0 4 5 6 5 0 3 2 1
$s_4$	1 0 0 4 0 6 5 0 3 2 1	$s_9$	1 0 0 4 5 6 5 4 3 2 1
$s_5$	1 0 0 4 0 6 5 4 3 2 1	$s_{10}$	1 0 3 0 0 6 5 4 0 2 1

only shows ten of them, where part of the reachable shipping distance matrix among ports is given in

Table 5. Part of the reachable shipping route matrix for different calling sequences.

Calling Sequence	Reachable Shipping Distance Matrix Among Ports
$s_1$	$\left[\begin{array}{cccccc}0& 630& 590& 510& 410& 340\\ 50& 0& 640& 560& 460& 390\\ 90& 40& 0& 600& 500& 430\\ 170& 120& 80& 0& 580& 510\\ 270& 220& 180& 100& 0& 610\\ 340& 290& 250& 170& 70& 0\end{array}\right]$
$s_2$	$\left[\begin{array}{cccccc}0& 630& 590& 510& 270& 340\\ 50& 0& 640& 560& 320& 390\\ 90& 40& 0& 600& 360& 430\\ 170& 120& 80& 0& 440& 510\\ 410& 360& 320& 240& 0& 70\\ 340& 290& 250& 170& 610& 0\end{array}\right]$
$s_3$	$\left[\begin{array}{cccccc}0& 630& 590& 510& 270& 340\\ 50& 0& 640& 560& 320& 390\\ 90& 40& 0& 600& 360& 430\\ 170& 120& 80& 0& 440& 510\\ 270& 220& 180& 100& 0& 70\\ 340& 290& 250& 170& 70& 0\end{array}\right]$
$s_4$	$\left[\begin{array}{cccccc}0& 630& 590& 170& 410& 340\\ 50& 0& 640& 220& 460& 390\\ 90& 40& 0& 260& 500& 430\\ 510& 460& 420& 0& 240& 170\\ 270& 220& 180& 440& 0& 610\\ 340& 290& 250& 510& 70& 0\end{array}\right]$
$s_5$	$\left[\begin{array}{cccccc}0& 630& 590& 170& 410& 340\\ 50& 0& 640& 220& 460& 390\\ 90& 40& 0& 260& 500& 430\\ 170& 120& 80& 0& 240& 170\\ 270& 220& 180& 100& 0& 610\\ 340& 290& 250& 170& 70& 0\end{array}\right]$

.

4.2. Results and Analysis

4.2.1. Relationship among Cost of Calling Port, Number of ECR, Number of Leasing Empty Containers, and Net Profit

For different costs of calling port: $call{C}_1=\mathrm{20,000}$, $call{C}_2=\mathrm{10,000}$, and $call{C}_3=5000$, we give their corresponding net profits, shown in

Table 6. Net profit of different costs of calling ports.

s	${\mathit{callC}}_1=\mathrm{20,000}$	${\mathit{callC}}_2=\mathrm{10,000}$	${\mathit{callC}}_3=5000$
$s_1$	1,103,800	1,163,800	1,193,800
$s_2$	1,082,600	1,142,600	1,172,600
$s_3$	941,400	1,011,400	1,046,400
$s_4$	926,400	996,400	1,031,400
$s_5$	736,000	806,000	841,000
$s_6$	979,600	1,039,600	1,069,600
$s_7$	742,000	812,000	847,000
$s_8$	827,200	897,200	932,200
$s_9$	589,600	669,600	709,600
$s_{10}$	1,097,000	1,157,000	1,187,000
⋯	⋯	⋯	⋯
Best solution: $s_{56}$	1,119,400	1,179,400	1,209,400

and Figure 2 ($load{C}_i$ and $unload{C}_i$ can be obtained from Iris et al. [5]). The explicit optimal solutions are given in Table 3. It can be observed that, for the above three cases, the optimal solution appears when the calling sequence is $s_{56}$: ①-②-③-⑥-⑤-④-①. The essential cause is that, in the current situation, all ports on the shipping lines are in deficit states; namely, all ports require more containers than supply ones and, so, the inventory cost of empty containers is 0. However, the number and cost of ECR are much larger than the corresponding ones for the leasing mechanism. Compared with other factors, the cost of ECR directly determines the overall profit. Under the current supply and demand of empty container, the numbers of ECR in the three cases are exactly the same, which is: $80+10+10+50+70=220$. According to distance matrix of shipping lines in Table 3, the originating port, destination port, and transportation numbers are, respectively: (1, 2, 80), (1, 4, 10), (1, 6, 10), (2, 6, 50), and (5, 4, 70). Therefore, the costs of ECR corresponding to these three cases are also the same (i.e., 114,600). Furthermore, because both the freight charge of laden container income and various costs are the same, the net profit is determined by the calling port fee. The higher the cost, the lower the net profit. On the contrary, the lower the calling cost, the higher the net profit.

4.2.2. Relationship among Number of Calling Ports, Whole (Total) Profits, and Total Costs

For $call{C}_1$, the relationship among total profit, total cost, and calling port number was studied. The corresponding two-dimensional graph was constructed with 81 sets of data, as shown in Figure 3 and Figure 4. It can be observed that the fewer the number of calling ports, the higher the total profit was, and vice versa. The optimal solution appeared in such calling sequences, whose number of calling ports equalled six. The worst solution occured when each port in the shipping line was called. The main reason was that the cost of calling ports was far greater than other expenses, such as cost of ECR, leasing cost, and so on. It made the number of calling ports (that is, the total cost of calling the ports) have a direct impact on the total profits. Obviously, because the calling port cost of one vessel at a certain port is fixed, its influence was weakened as other costs gradually increased. Moreover, when other costs are gradually reduced, the impact of the cost of calling ports on the total profit became crucial.

In addition, Figure 4 shows the relationship between whole cost and the number of calling ports. The more calling ports, the lesser the cost, and vice versa. For Figure 2, its maximal value occurs when the number of calling ports is six. Differing from Figure 2, here the peak max appeared when the corresponding value was seven. This was caused by the increase in freight charge for laden container transportation.

Furthermore, the headway is not involved here. Once the speed is reduced by 20% from the planning speed in advance, the daily fuel consumption can be reduced by almost 50%. If, within a given voyage (for example, a voyage taking one week), the higher the number of calling ports, the larger the shipping speed. At the same time, the corresponding fuel costs will rise. Basically, if the customer’s satisfaction is to be taken into consideration, more ports are docked, and the more the customer’s transportation needs can be met. To some extent, making these decisions can improve the customer stickiness.

4.2.3. Relationship between Total Profit and Leasing Cost

Consider that the leasing costs may fluctuate with the supply and demand of different ports. Without loss of generality, suppose that, for ports 4 and 6, the leasing costs increased due to higher demand. Their rental costs are changed from $leaseCos{t}_1$ to $leaseCos{t}_2$. Observe the impact on the total profit by changing the cost of leasing containers; the details are shown in

Table 7. Best solution under different leasing costs.

Leasing Cost		${\mathit{leaseCost}}_1$	${\mathit{leaseCost}}_2$
Sequence		1 2 3 0 0 6 5 4 0 0 1	1 0 3 0 0 6 5 4 0 2 1
Cost	Empty container cost	114,600	202,200
	Matrix ECR	$\left[\begin{array}{cccccc}0& 80& 0& 10& 0& 10\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 50\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 70& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 0& 0& 90& 0& 10\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 50\\ 0& 0& 0& 0& 0& 0\\ 0& 60& 0& 10& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$
	Matrix of leasing empty containers	$\left[\begin{array}{cccccc}0& 0& 0& 20& 0& 0\end{array}\right]$	$\left[\begin{array}{cccccc}0& 20& 0& 0& 0& 0\end{array}\right]$
	Cost of leasing empty containers	40,000	60,000
Revenue	Freight charge of laden containers	464,800	511,600
Net profit	Best solution	1,119,400	1,082,200

.

It is easy to find that, at this time, unlike the case where the optimal solution sequence and the ECR matrix were exactly the same, as in Table 3, the corresponding calling port sequence of the best solution has changed. The cost of ECR increased by 87,600, which rised by about 76.44%. The port location of empty container leasing were moved from port 4 to port 2. The root cause is due to the increase in the cost of empty container leasing in port 4, which is consistent with the actual situation. That is, the cost of empty container leasing in the port is positively correlated with the supply and demand of empty containers in the port. Both the seasonal changes and port demand degree will cause the supply and demand of empty containers to fluctuate, which will directly affect the company’s net profit.

Figure 5 shows the profit fluctuations if the rental cost is changed. It can be observed that, for the whole dataset, when the renting cost was changed from $leaseCos{t}_1$ to $leaseCos{t}_2$, the profit of each feasible solution increased, to some different extent. However, nearly 92% (where the demand for empty containers was 240, and number of ECR was 220), was met by ECR, and not by the leasing mechanism. Therefore, although the rental costs of port 2 and port 4 increased significantly, it had little impact on the overall cost. So, it can be seen, from Figure 5, that there was little relationship with the leasing cost. As above, the fewer the number of calling ports, the greater the profit.

5. Conclusions

This paper proposes a cooperative optimization model at the tactical and operational levels, in which many factors, consisting of calling port set, calling sequence, and two types of container transportation, are involved. As this problem is complex, we study the business flow and extract some initial solutions generation rules, in order to reduce the search space and improve performance. Additionally, because different calling sequences may change the reachable shipping line distance between ports, an algorithm is proposed to generate the corresponding matrix. To evaluate the presented model, we analyze various relationships among indicators and obtain some interesting conclusions. Results show that our constructed model can effectively solve the main optimization problems on the tactical and operational levels, simultaneously.

In this paper, the proposed model considers the calling port set and calling sequence, according to the number of supplied and demanded empty containers, given in advance. In reality, it can not exactly match the practice, since many uncertain factors may exist in the actual transportation process. So, one of the extensions of this paper is to develop uncertainty factors in the proposed model. Another possible future work is to add alliance modes among different shipping companies; once the alliance mechanism has been adopted, all of the above planning must be dispatched. For example, under an alliance, the ECR and laden container transportation may be adjusted among all alliance members. The vessels will have their necessary tasks of calling ports and have calling sequences constrained within the treaty of alliance. In essence, because the alliance mode belongs to the high level decision making, a slight change may affect all aspects on the tactical and operational levels.