Time Series ARIMA Model for Prediction of Daily and Monthly Average Global Solar Radiation: The Case Study of Seoul, South Korea
Abstract
1. Introduction
1.1. Motivations of the Study
1.2. Problem Statement
1.3. Literature Review
1.4. Contributions of the Study
- A time series ARIMA model is built to forecast the daily and monthly solar radiation of Seoul, South Korea, considering the accuracy, suitability, adequacy, and timeliness of the collected data.
- The reliability, accuracy, suitability, and performance of the model are investigated in comparison with those of established tests, such as standardized residual, ACF, and PACF, and the results are compared with the results forecasted by the Monte Carlo method.
- The trend of monthly solar radiation in Seoul for the coming years is analyzed and compared based on solar radiation data obtained from the KMS over 37 years.
1.5. Paper Organization
2. Case Study: Seoul, South Korea
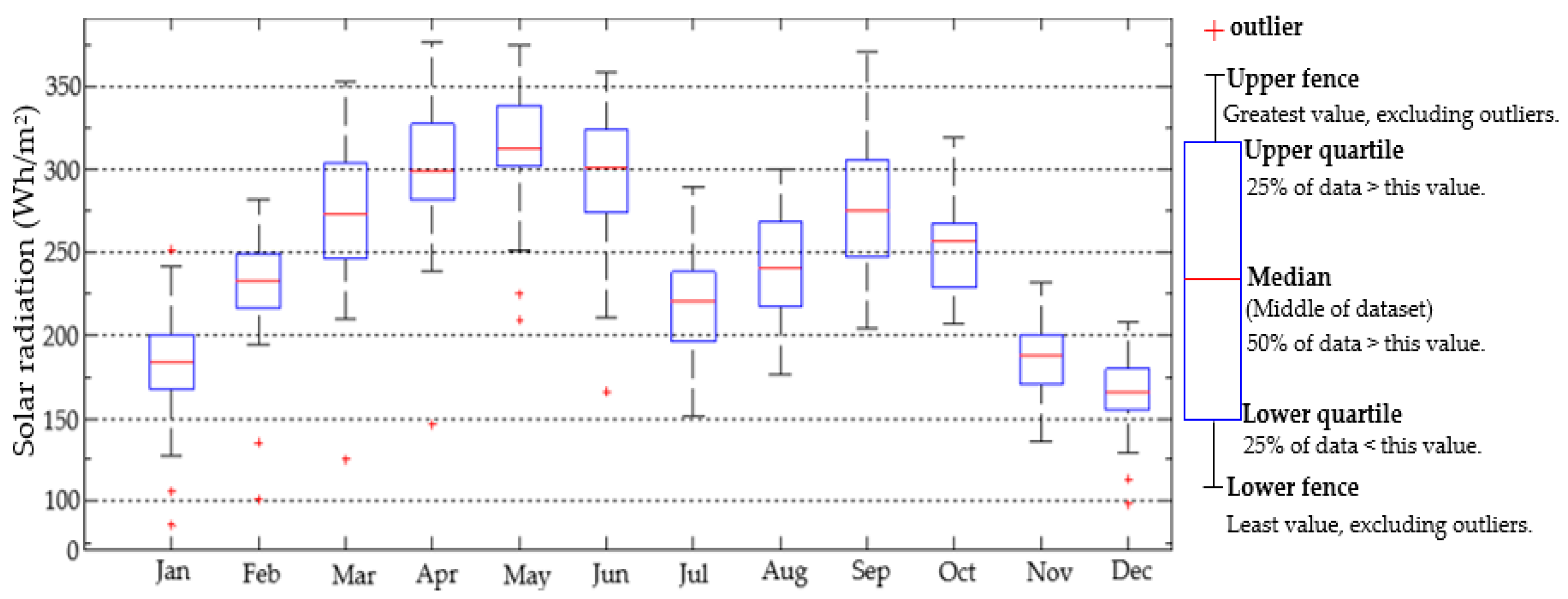
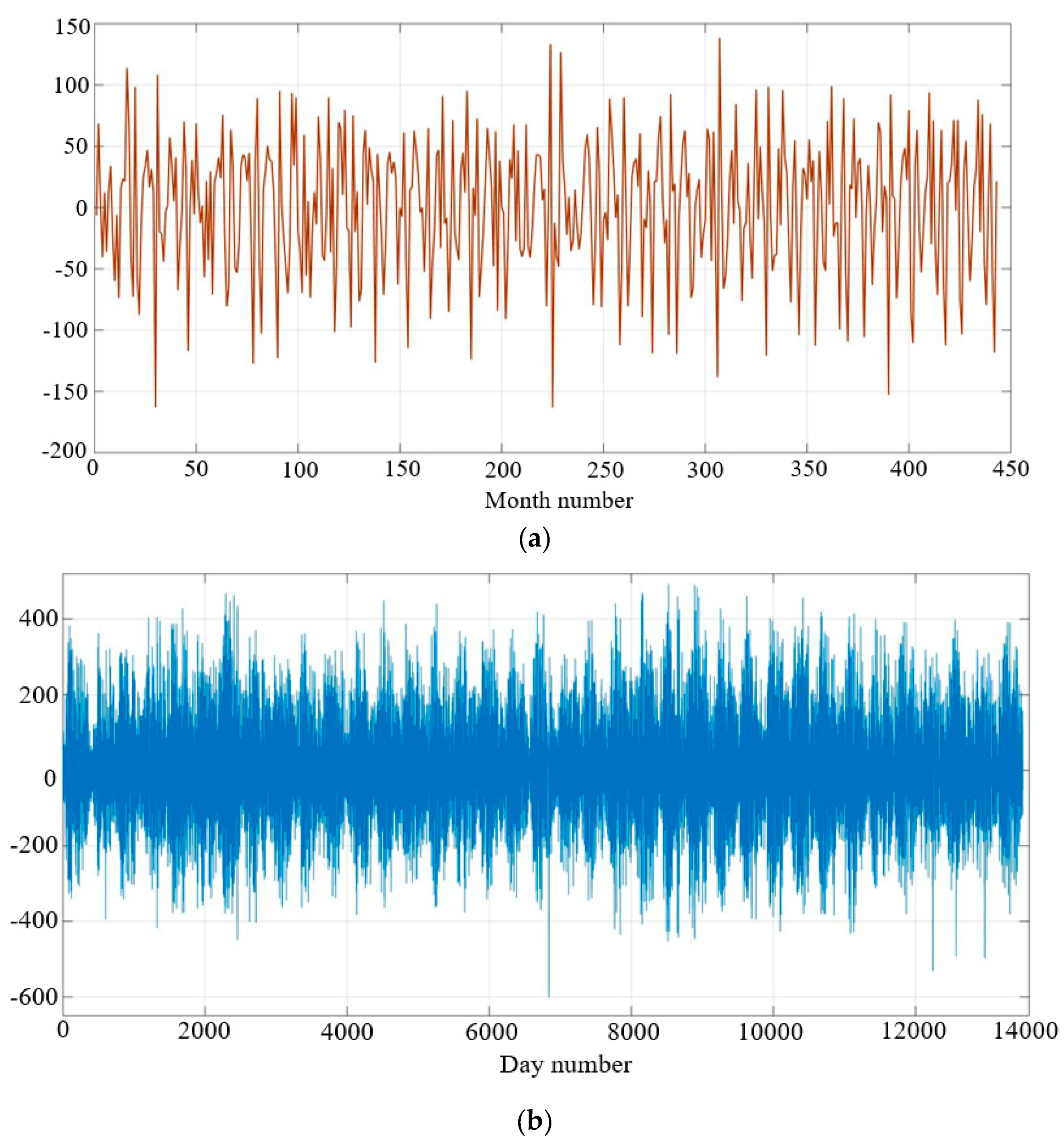
3. Data Collection
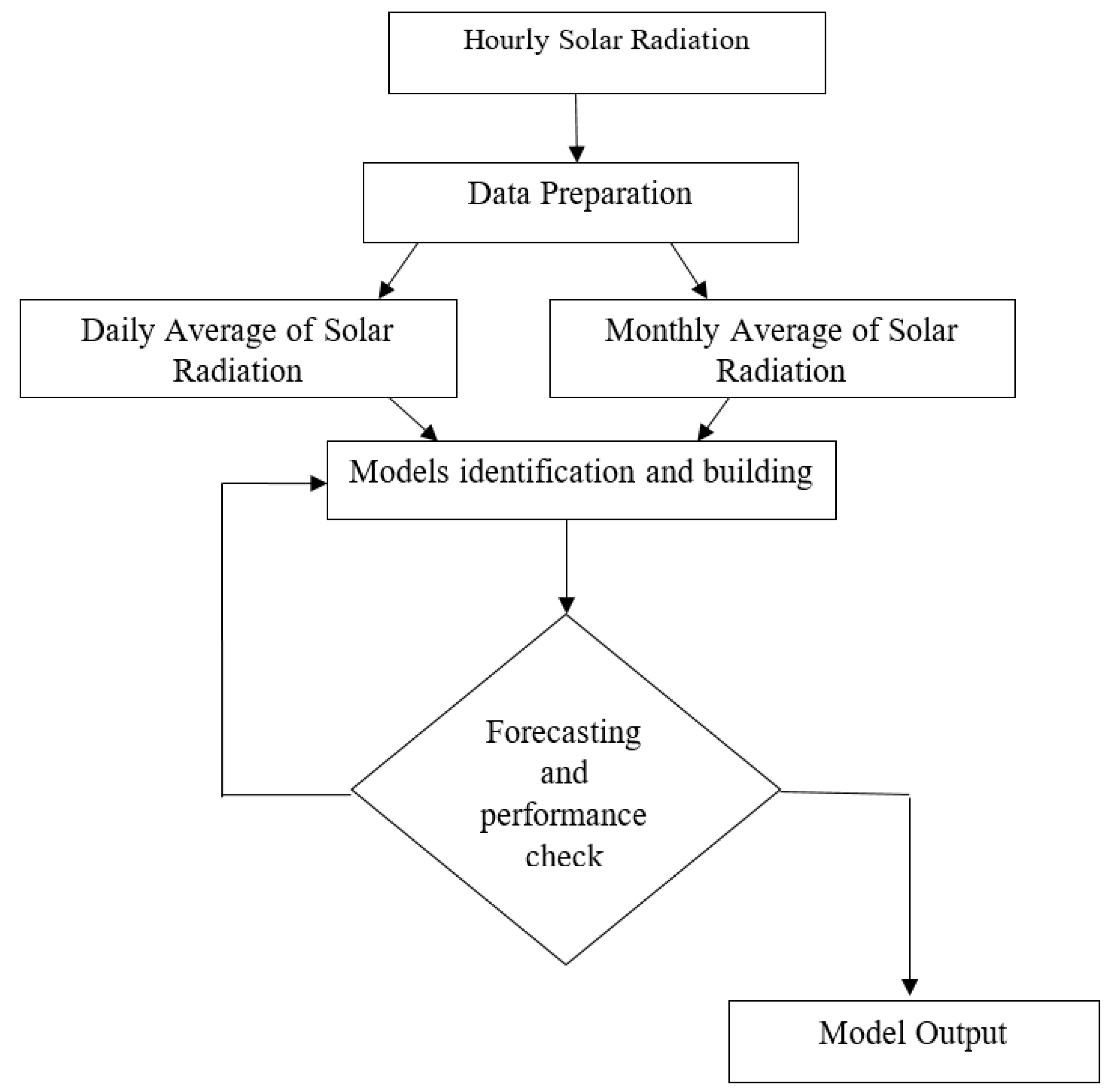
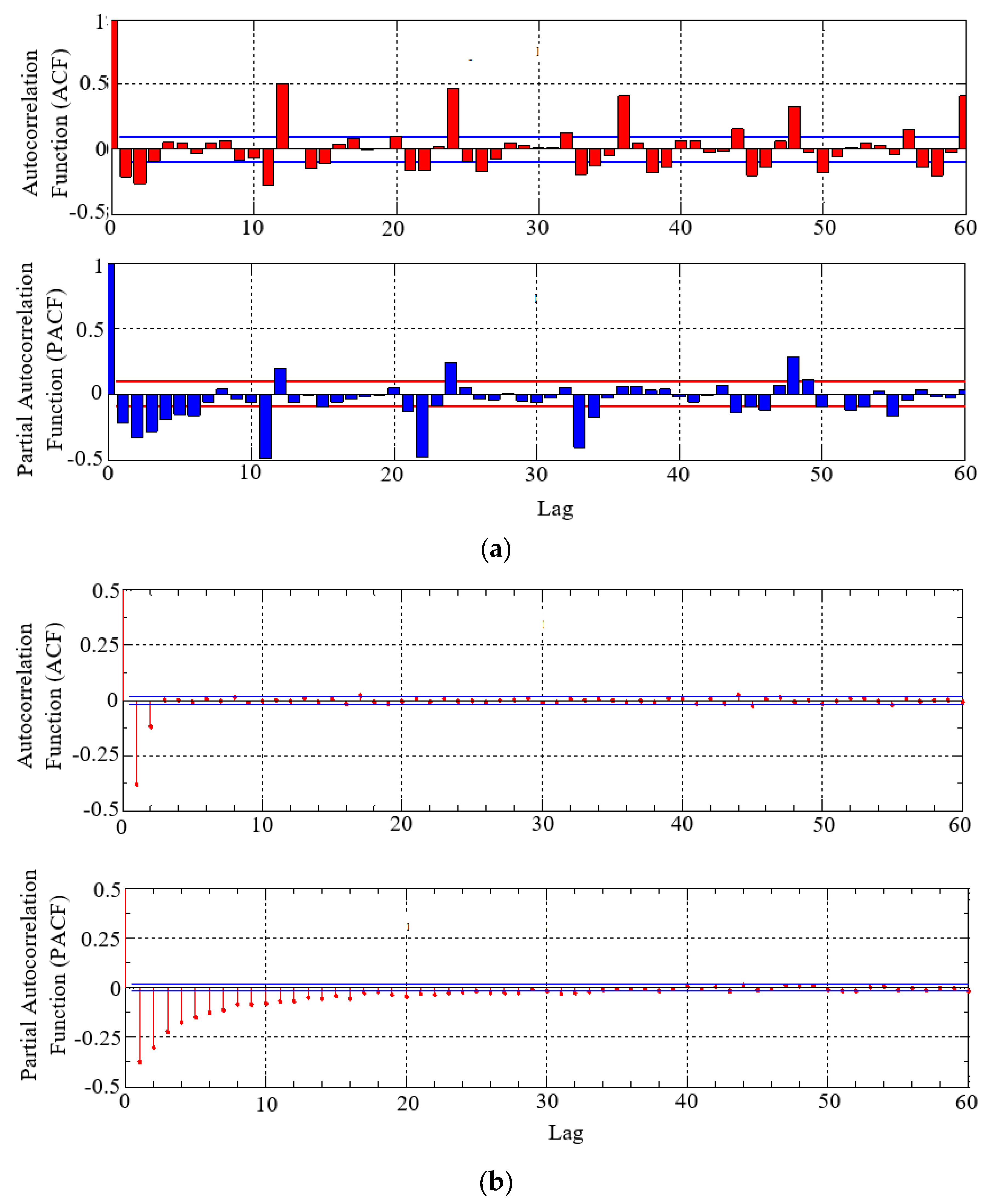
4. ARIMA Forecasting Model
5. Result and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. List of Abbreviations
| Abbreviation | Meaning |
|---|---|
| ACF | Autocorrelation Function |
| ANNs | Artificial Neural Networks |
| AR | Auto-regression |
| ARIMA | auto-regressive Integrated Moving Average |
| KMA | Korean Meteorological Administration |
| MA | Moving Average |
| NWP | Numerical Weather Prediction |
| PACF | Partial Autocorrelation Function |
| PV | Photovoltaic |
| RMSE | Root Mean Square Error |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| UV | Ultraviolet |
Appendix B. List of Symbols
| Symbols | Meaning |
|---|---|
| d | Number of non-seasonal differences needed for stationarity |
| p | Number of autoregressive terms |
| q | Number of lagged forecast errors in the prediction equation |
| B | Backshift operator. |
| Φp(B) | An autoregressive operator of order p |
| θq(B) | A moving average operator of order q |
| Xt | Forecasted observation |
| Xo | Actual observation |
| yt | Daily average of solar radiation |
References
- Alsharif, M.H.; Kim, J.; Kim, J.H. Green and sustainable cellular base stations: An overview and future research directions. Energies 2017, 10, 587. [Google Scholar] [CrossRef]
- Kim, K.-G. Evolution of Climate Resilience and Low-Carbon Smart City Planning: A Process. In Urban Governance and Informal Settlements; Springer Nature: Berlin, Germany, 2017; pp. 1–76. [Google Scholar]
- Lee, J.-S.; Kim, J.-W. South Korea’s urban green energy strategies: Policy framework and local responses under the green growth. Cities 2016, 54, 20–27. [Google Scholar] [CrossRef]
- Alsharif, M.H. A solar energy solution for sustainable third generation mobile networks. Energies 2017, 10, 429. [Google Scholar] [CrossRef]
- Kwon, T.-H. Is the renewable portfolio standard an effective energy policy?: Early evidence from South Korea. Util. Policy 2015, 36, 46–51. [Google Scholar] [CrossRef]
- Korean Energy Agency (KEA). Annual Report 2015. Available online: http://www.energy.or.kr/renew_eng/resources/resources_view.aspx?no=12&page=1 (accessed on 22 January 2019).
- Sindhu, S.; Nehra, V.; Luthra, S. Solar energy deployment for sustainable future of India: Hybrid SWOC-AHP analysis. Renew. Sustain. Energy Rev. 2017, 72, 1138–1151. [Google Scholar] [CrossRef]
- Park, E.; Yoo, K.; Ohm, J.Y.; Kwon, S.J. Case study: Renewable electricity generation systems on Geoje Island in South Korea. J. Renew. Sustain. Energy 2016, 8, 015904. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Benmouiza, K.; Cheknane, A. Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models. Energy Convers. Manag. 2013, 75, 561–569. [Google Scholar] [CrossRef]
- Beaumont, C.; Makridakis, S.; Wheelwright, S.C.; McGee, V.E. Forecasting: Methods and Applications. J. Oper. Res. Soc. 1984, 35, 79. [Google Scholar] [CrossRef]
- Koca, A.; Öztop, H.F.; Varol, Y.; Koca, G.O. Estimation of solar radiation using artificial neural networks with different input parameters for Mediterranean region of Anatolia in Turkey. Expert Syst. Appl. 2011, 38, 8756–8762. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.-L. Optimization of an artificial neural network dedicated to the multivariate forecasting of daily global radiation. Energy 2011, 36, 348–359. [Google Scholar] [CrossRef]
- Ramedani, Z.; Omid, M.; Keyhani, A.; Shamshirband, S.; Khoshnevisan, B. Potential of radial basis function based support vector regression for global solar radiation prediction. Renew. Sustain. Energy Rev. 2014, 39, 1005–1011. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Generalized three phase robust load-flow for radial and meshed power systems with and without uncertainty in energy resources using dynamic radial basis functions neural networks. J. Clean. Prod. 2018, 174, 96–113. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Three-phase AC/DC power-flow for balanced/unbalanced microgrids including wind/solar, droop-controlled and electronically-coupled distributed energy resources using radial basis function neural networks. IET Power Electron. 2017, 10, 313–328. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Bagahee, H.R.; Gharehpetian, G.B.B. Power Calculation using RBF Neural Networks to Improve Power Sharing of Hierarchical Control Scheme in Multi-DER Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetan, G.B.; Talebi, H.A. Nonlinear Load Sharing and Voltage Compensation of Microgrids Based on Harmonic Power-Flow Calculations Using Radial Basis Function Neural Networks. IEEE Syst. J. 2018, 12, 1–11. [Google Scholar] [CrossRef]
- Reikard, G. Predicting solar radiation at high resolutions: A comparison of time series forecasts. Sol. Energy 2009, 83, 342–349. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef]
- Shamim, M.A.; Remesan, R.; Bray, M.; Han, D. An improved technique for global solar radiation estimation using numerical weather prediction. J. Atmos. Sol. -Terr. Phys. 2015, 129, 13–22. [Google Scholar] [CrossRef]
- Farhath, Z.A.; Arputhamary, B.; Arockiam, D.L. A Survey on ARIMA Forecasting Using Time Series Model. Int. J. Comput. Sci. Mobile Comput. 2016, 5, 104–109. [Google Scholar]
- Colak, I.; Yesilbudak, M.; Genc, N.; Bayindir, R. Multi-period Prediction of Solar Radiation Using ARMA and ARIMA Models. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Institute of Electrical and Electronics Engineers (IEEE), Miami, FL, USA, 9–11 December 2015; pp. 1045–1049. [Google Scholar]
- Ferrari, S.; Lazzaroni, M.; Piuri, V.; Cristaldi, L.; Faifer, M. Statistical models approach for solar radiation prediction. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Institute of Electrical and Electronics Engineers (IEEE), Minneapolis, MN, USA, 6–9 May 2013; pp. 1734–1739. [Google Scholar]
- Boualit, S.B.; Mellit, A. SARIMA-SVM hybrid model for the prediction of daily global solar radiation time series. In Proceedings of the 2016 International Renewable and Sustainable Energy Conference (IRSEC), Institute of Electrical and Electronics Engineers (IEEE), Marrakesh, Morocco, 14–17 November 2016; pp. 712–717. [Google Scholar]
- David, M.; Ramahatana, F.; Trombe, P.; Lauret, P. Probabilistic forecasting of the solar irradiance with recursive ARMA and GARCH models. Sol. Energy 2016, 133, 55–72. [Google Scholar] [CrossRef]
- Korean Statistical Information Service (KOSIS). Available online: http://kosis.kr/statHtml/statHtml.do?orgId=111&tblId=DT_1B040A4&vw_cd=&list_id=&scrId=&seqNo=&lang_mode=ko&obj_var_id=&itm_id=&conn_path=E1 (accessed on 22 January 2019).
- Byrne, J.; Taminiau, J.; Kurdgelashvili, L.; Kim, K.N. A review of the solar city concept and methods to assess rooftop solar electric potential, with an illustrative application to the city of Seoul. Renew. Sustain. Energy Rev. 2015, 41, 830–844. [Google Scholar] [CrossRef]
- Nematollahi, O.; Kim, K.C. A feasibility study of solar energy in South Korea. Renew. Sustain. Energy Rev. 2017, 77, 566–579. [Google Scholar] [CrossRef]
- Korean Ministry of Trade, Industry and Energy (MOTIE) & Korea Energy Economics Institute (KEEI). Available online: https://www.keei.re.kr/main.nsf/index_en.html (accessed on 22 January 2019).
- Alsharif, M.H.; Kim, J.; Kim, J.H. Opportunities and Challenges of Solar and Wind Energy in South Korea: A Review. Sustainability 2018, 10, 1822. [Google Scholar] [CrossRef]
- Korea Meteorological Administration (KMA), Synoptic weather observation. Available online: https://data.kma.go.kr/data/grnd/selectAsosList.do?pgmNo=34 (accessed on 22 January 2019).
- Khashei, M.; Bijari, M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl. Soft Comput. 2011, 11, 2664–2675. [Google Scholar] [CrossRef]
- Chung, S.S. Projecting municipal solid waste: The case of Hong Kong SAR. Resour. Conserv. Recycl. 2010, 54, 759–768. [Google Scholar] [CrossRef]
- Xu, L.; Gao, P.; Cui, S.; Liu, C. A hybrid procedure for MSW generation forecasting at multiple time scales in Xiamen City, China. Waste Manag. 2013, 33, 1324–1331. [Google Scholar] [CrossRef]
- Younes, M.K.; Nopiah, Z.M.; Basri, N.E.A.; Basri, H. Medium term municipal solid waste generation prediction by autoregressive integrated moving average. Stat. Oper. Res. Int. Conf. (SORIC 2013) 2014, 427–435. [Google Scholar] [CrossRef]
- Antanasijević, D.Z.; Pocajt, V.V.; Povrenović, D.S.; Ristić, M.Đ.; Perić-Grujić, A.A. PM10 emission forecasting using artificial neural networks and genetic algorithm input variable optimization. Sci. Total Environ. 2013, 443, 511–519. [Google Scholar] [CrossRef]
- Miswan, N.H.; Said, R.M.; Anuar, S.H.H. ARIMA with regression model in modelling electricity load demand. J. Telecommun. Electr. Comput. Eng. 2016, 8, 113–116. [Google Scholar]
- MathWorks, Phillips-Perron Test. Available online: https://www.mathworks.com/help/econ/pptest.html (accessed on 31 January 2019).
- Kleiner, B. Time Series Analysis: Forecasting and Control. Technometrics 1977, 19, 343–344. [Google Scholar] [CrossRef]
- Chatfield, C.; Weigend, A.S. Time series prediction: Forecasting the future and understanding the past. Int. J. Forecast. 1994, 10, 161–163. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Badran, A.; Dwaykat, B. Prediction of Solar Radiation for the Major Climates of Jordan: A Regression Model. J. Ecol. Eng. 2018, 19, 24–38. [Google Scholar] [CrossRef]
- MathWorks, Jarque-Bera Test. Available online: https://www.mathworks.com/help/econ/pptest.html (accessed on 31 January 2019).
- Häder, D.-P.; Wängbergke, S.Å.; Rose, K.C.; Helbling, E.W.; Sinha, R.P.; Worrest, R.; Williamson, C.E.; Rautio, M.; Gao, K. Effects of UV radiation on aquatic ecosystems and interactions with other environmental factors. Photochem. Photobiol. Sci. 2015, 14, 108–126. [Google Scholar]
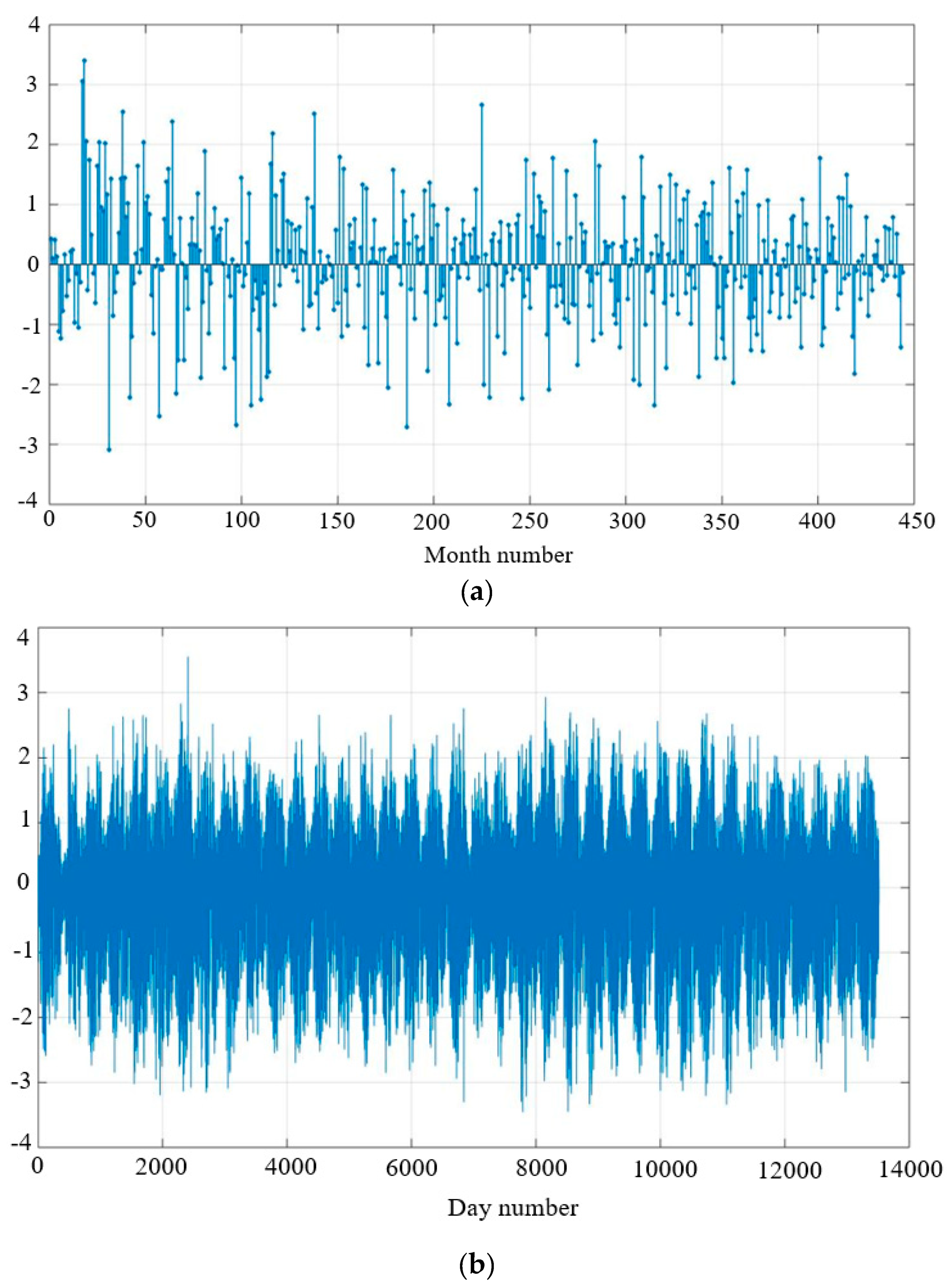
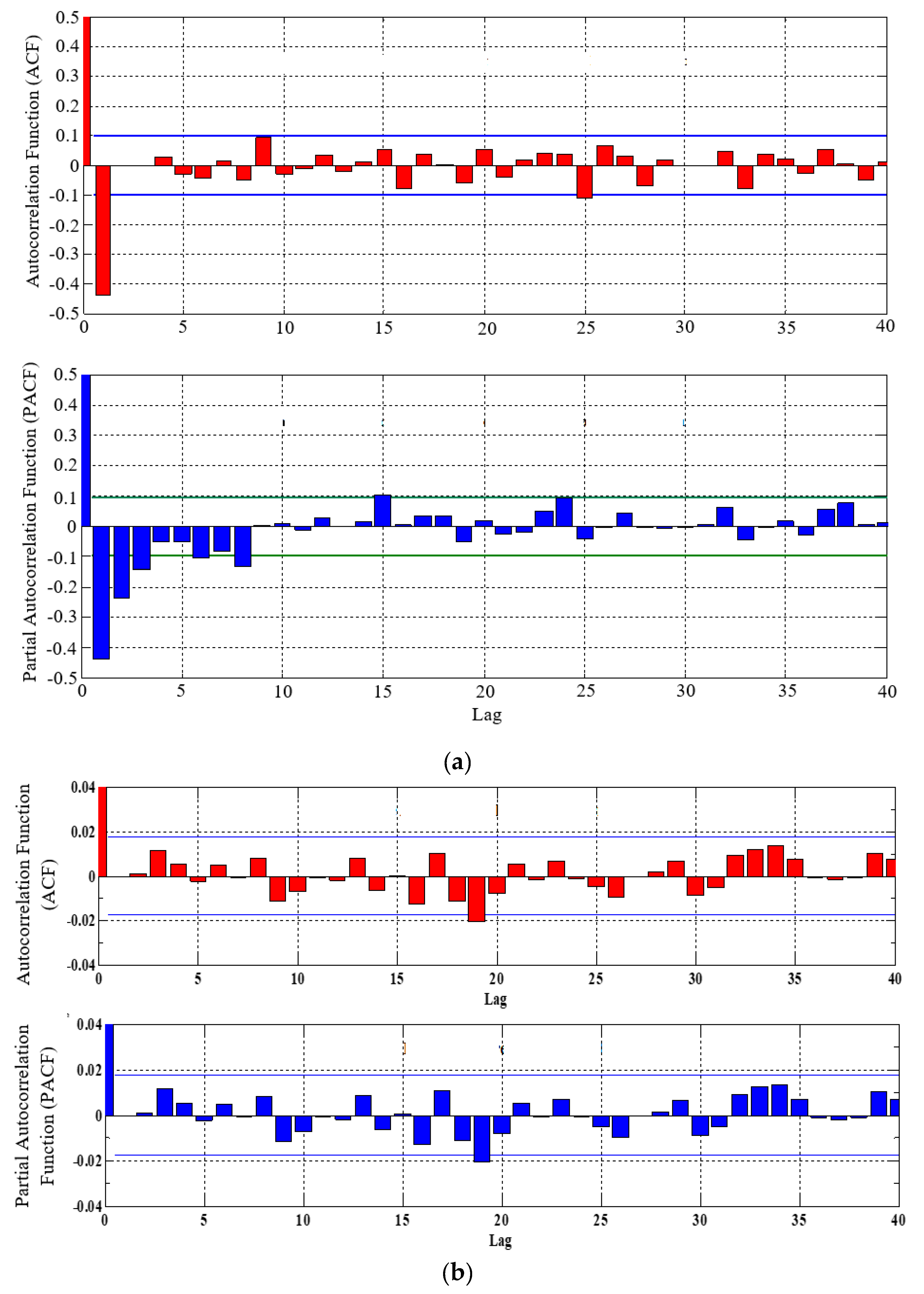
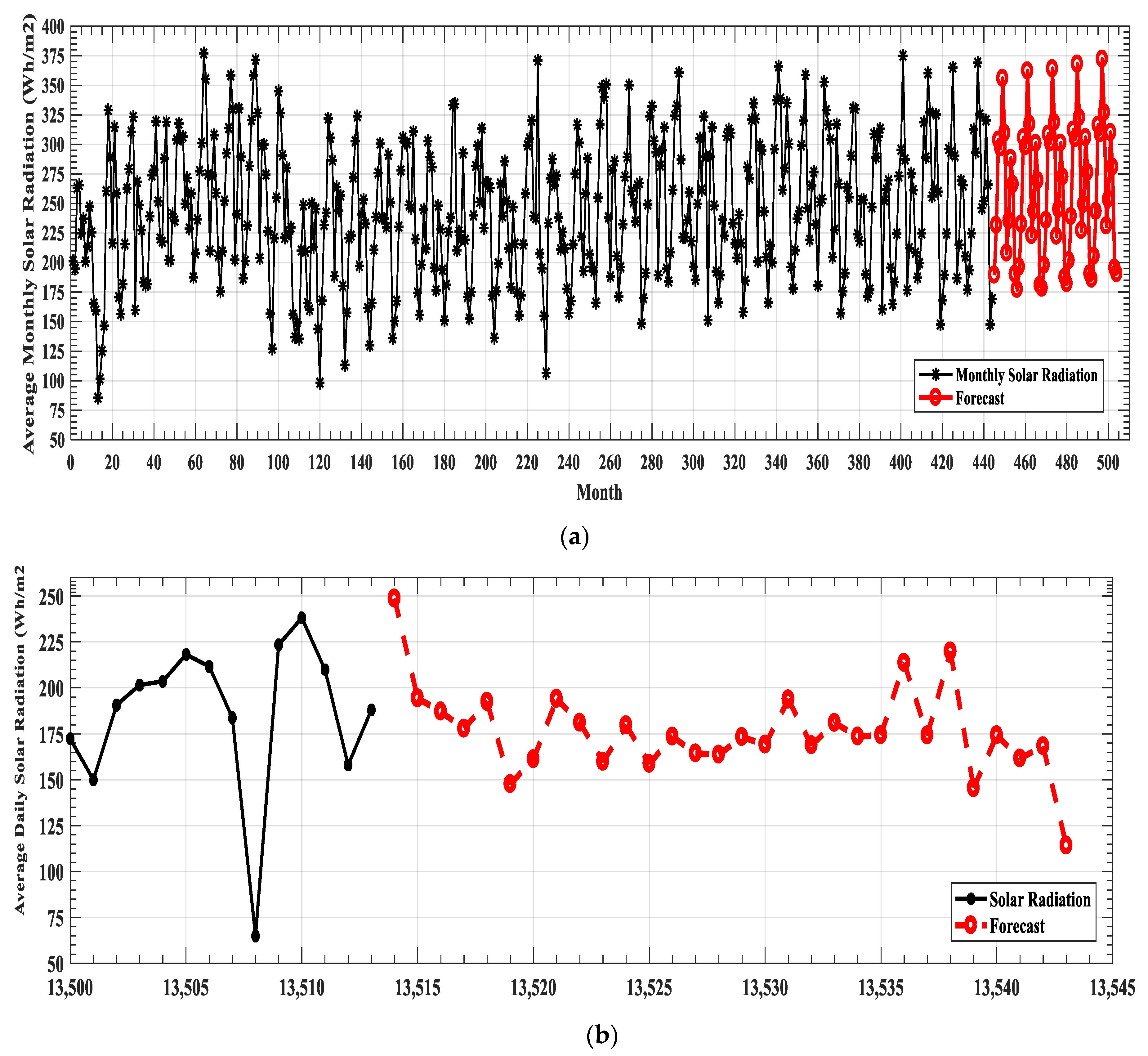
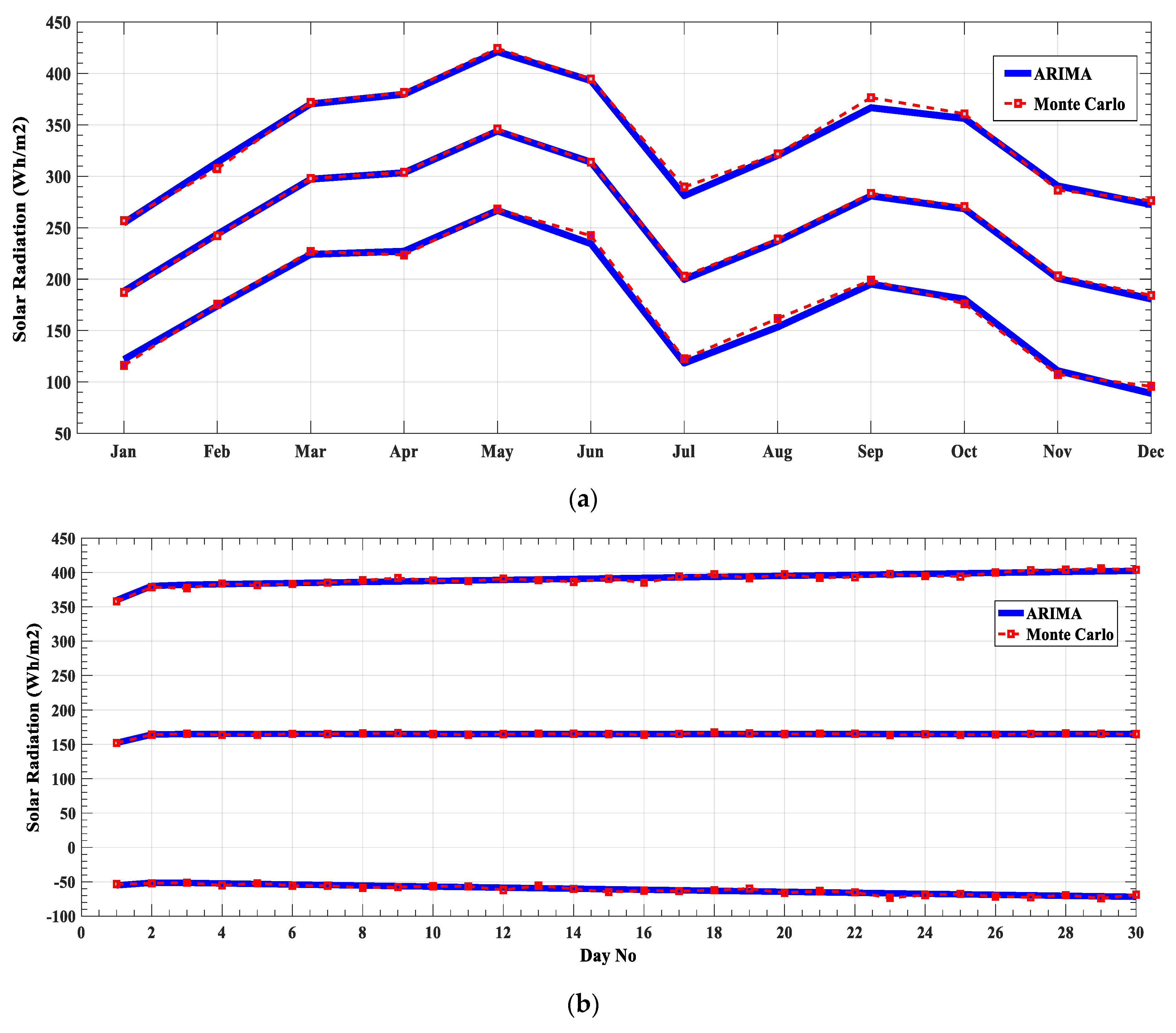
| Variables | Daily Average Value | Monthly Average Value |
| Number of readings | 13,513 | 444 |
| Minimum (Wh/m2) | 9.4 | 85.6 |
| Maximum (Wh/m2) | 676.2 | 377 |
| Mean (Wh/m2) | 244.6 | 244 |
| Median (Wh/m2) | 244.8 | 244.5 |
| Standard Deviation | 117.25 | 58.6 |
| Range | 666.8 | 291.4 |
| Parameter | Value | Standard Error | T Statistic |
|---|---|---|---|
| Constant | 0.08 | 0.201 | 0.395 |
| AR(4) | −0.152 | 0.044 | −3.441 |
| SAR(12) | −0.296 | 0.037 | −8.073 |
| MA(1) | −0.676 | 0.032 | −21.018 |
| SMA (12) | −0.656 | 0.041 | −16.128 |
| Variance | 1101.03 | 71.413 | 15.417 |
| Parameter | Value | Standard Error | T Statistic |
|---|---|---|---|
| Constant | −0.002 | 0.081 | −0.027 |
| AR(1) | 0.0565 | 0.039 | 1.446 |
| MA (1) | −0.767 | 0.040 | −19.662 |
| MA (2) | −0.148 | 0.034 | −4.247 |
| Variance | 10,870.5 | 146.211 | 74.347 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsharif, M.H.; Younes, M.K.; Kim, J. Time Series ARIMA Model for Prediction of Daily and Monthly Average Global Solar Radiation: The Case Study of Seoul, South Korea. Symmetry 2019, 11, 240. https://doi.org/10.3390/sym11020240
Alsharif MH, Younes MK, Kim J. Time Series ARIMA Model for Prediction of Daily and Monthly Average Global Solar Radiation: The Case Study of Seoul, South Korea. Symmetry. 2019; 11(2):240. https://doi.org/10.3390/sym11020240
Chicago/Turabian StyleAlsharif, Mohammed H., Mohammad K. Younes, and Jeong Kim. 2019. "Time Series ARIMA Model for Prediction of Daily and Monthly Average Global Solar Radiation: The Case Study of Seoul, South Korea" Symmetry 11, no. 2: 240. https://doi.org/10.3390/sym11020240
APA StyleAlsharif, M. H., Younes, M. K., & Kim, J. (2019). Time Series ARIMA Model for Prediction of Daily and Monthly Average Global Solar Radiation: The Case Study of Seoul, South Korea. Symmetry, 11(2), 240. https://doi.org/10.3390/sym11020240






